机械原理典型例题第七章轮系1124
机械原理第七版西北工业大学课后习题答案(7-11章)
第7章课后习题参考答案7—1等效转动惯量和等效力矩各自的等效条件是什么?7—2在什么情况下机械才会作周期性速度波动?速度波动有何危害?如何调节?答:当作用在机械上的驱动力（力矩)周期性变化时，机械的速度会周期性波动。
机械的速度波动不仅影响机械的工作质量，而且会影响机械的效率和寿命。
调节周期性速度波动的方法是在机械中安装一个具有很大转动惯量的飞轮。
7—3飞轮为什么可以调速?能否利用飞轮来调节非周期性速度波动，为什么?答：飞轮可以凋速的原因是飞轮具有很大的转动惯量，因而要使其转速发生变化．就需要较大的能量，当机械出现盈功时，飞轮轴的角速度只作微小上升，即可将多余的能量吸收储存起来；而当机械出现亏功时，机械运转速度减慢．飞轮又可将其储存的能量释放，以弥补能最的不足，而其角速度只作小幅度的下降。
非周期性速度波动的原因是作用在机械上的驱动力(力矩)和阻力(力矩)的变化是非周期性的。
当长时问内驱动力(力矩)和阻力(力矩)做功不相等，机械就会越转越快或越转越慢．而安装飞轮并不能改变驱动力(力矩)或阻力(力矩)的大小也就不能改变驱动功与阻力功不相等的状况，起不到调速的作用，所以不能利用飞轮来调节非周期陛速度波动。
7—4为什么说在锻压设备等中安装飞轮可以起到节能的作用?解：因为安装飞轮后，飞轮起到一个能量储存器的作用，它可以用动能的形式把能量储存或释放出来。
对于锻压机械来说，在一个工作周期中，工作时间很短．而峰值载荷很大。
安装飞轮后．可以利用飞轮在机械非工作时间所储存能量来帮助克服其尖峰载荷，从而可以选用较小功率的原动机来拖动，达到节能的目的，因此可以说安装飞轮能起到节能的作用。
7—5由式J F=△W max／(ωm2[δ])，你能总结出哪些重要结论(希望能作较全面的分析)?答：①当△Wmax与ωm一定时，若[δ]下降，则J F增加。
所以，过分追求机械运转速度的均匀性，将会使飞轮过于笨重。
②由于J F不可能为无穷大，若△W max≠0，则[δ]不可能为零，即安装飞轮后机械的速度仍有波动，只是幅度有所减小而已。
南京理工大学机械原理题库 轮系及其设计
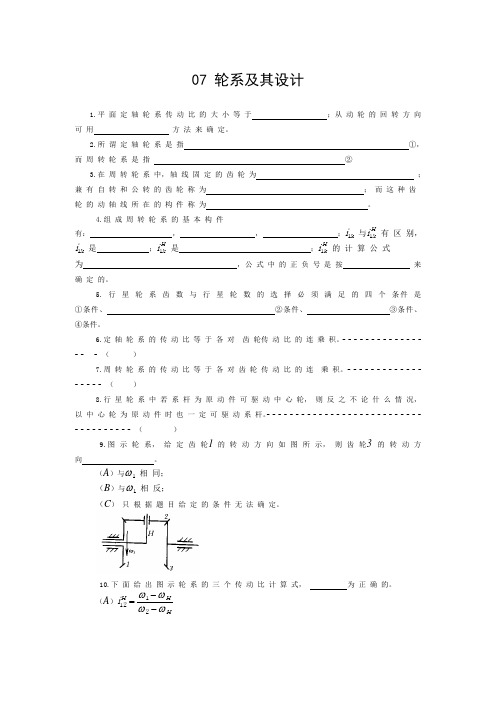
07 轮系及其设计1.平 面 定 轴 轮 系 传 动 比 的 大 小 等 于 ；从 动 轮 的 回 转 方 向 可 用 方 法 来 确 定。
2.所 谓 定 轴 轮 系 是 指 ①， 而 周 转 轮 系 是 指 ②3.在 周 转 轮 系 中， 轴 线 固 定 的 齿 轮 为 ；兼 有 自 转 和 公 转 的 齿 轮 称 为 ； 而 这 种 齿 轮 的 动 轴 线 所 在 的 构 件 称 为 。
4.组 成 周 转 轮 系 的 基 本 构 件有： ， ， ；i k 1 与i k H1 有 区 别，i k 1 是 ；i k H1 是 ；i k H1 的 计 算 公 式为 ， 公 式 中 的 正 负 号 是 按 来确 定 的。
5. 行 星 轮 系 齿 数 与 行 星 轮 数 的 选 择 必 须 满 足 的 四 个 条件 是①条件、 ②条件、 ③条件、 ④条件。
6.定 轴 轮 系 的 传 动 比 等 于 各 对 齿 轮传 动 比 的 连 乘 积。
- - - - - - - - - - - - - -- - - （ ）7.周 转 轮 系 的 传 动 比 等 于 各 对 齿 轮 传 动 比 的 连 乘 积。
- - - - - - - - - - - - -- - - - - （ ）8.行 星 轮 系 中 若 系 杆 为 原 动 件 可 驱 动 中 心 轮， 则 反 之 不 论 什 么 情 况， 以 中 心 轮 为 原 动 件 时 也 一 定 可 驱 动 系 杆。
- - - - - - - - - - - - - - - - - - - - - - - - - - -- - - - - - - - - - （ ）9.图 示 轮 系， 给 定 齿 轮1 的 转 动 方 向 如 图 所 示， 则 齿 轮3 的 转 动 方 向 。
（A ）与ω1 相 同；（B ）与ω1 相 反；（C ） 只 根 据 题 目 给 定 的 条 件 无 法 确 定。
机械原理课后答案——第七章--齿轮系及其设计PPT课件
-
6
11-17 解：此轮系为一个3K型周转轮 系，即有三个中心轮（1、3和4）。
i1H1i1 H 3 1(z z1 2 z z2 3 ')15 6 71.5 0 i4 H 1 i4 H 3 1 (z z2 4 'z z2 3) 1 5 2 6 5 5 2 7 5 5 16 i14 ii1 4H H1.5 0(5)6 58(n1 8 与 n4转向 ) 相反
齿轮系及其设计
习题11-11 习题11-16 习题11-17 习题11-18- Nhomakorabea1
11-11 解：
i1 5zz 1 2 zz 2 '3 z z3 4 'z z5 4 ' 5 2 0 3 0 1 0 4 5 1 1 0 58 25.7 77 8
-
2
-
3
11-16 解：此轮系为一复合轮系。
在1-2(3)-4定轴轮系中
画箭头表示的是构件在转化轮系中的转向关系，而不 是在周转轮系中的转向关系。 n1Hn1nH18.461r5/min n1=200r/min
n3Hn3nH11.538r5/min n3= -100r/min
n1H与n3H反向，与图中箭 方头 向所 相示 同。
若转化轮系传动比的“”判断错误，不仅会影响到 周转轮系传动比的大小，还会影响到周转轮系中构件的转
i 1 H i 1 i 4 ' 7 i 7 H 3 . 5 2 5 . 8 1 2 9 . 7 9 2 7 . 5 8 7 87
故 n H n 1 /i 1 H 3/ 5 2 .5 4 8 8 1 9 .1 7 2 (5 r 4转 /m 4 转 向 in) ) 向 与
-
4
11-16 解：1) 图a： i1 H3 n n 1 3 n n H Hz z1 2zz2 3 ' 2 2 0 4 4 3 0 01.6
《机械原理》 轮系的传动比
原周转轮系角速度
1 2
3
H
转化轮系中的角速度
1H 1 H 2H 2 H
3H 3 H
HH H H 0
2.传动比计算的基本思路与方法
根据定轴轮系传动比的公式，可写出转化轮系传动比
iH
13
i1H3
1H 3H
1 H 3 H
z2z3 z1 z 2
z3 z1
“－”号表示在转化机构中1H
z3 z1
2.2 周转轮系传动比的计算
1.周转轮系的组成与类型 2.传动比计算的基本思路与方法 3.注意事项 4.计算实例
例1 已知：双排外啮合行星轮系
z1 100, z2 101, z2 100, z3 99
求：传动比 iH1
解：
i1H3
1H
H 3
1 3
H H
z2 z3 z1 z2
第7章 轮系
1 轮系的类型 2 轮系的传动比 3 轮系的功能 4 轮系的设计 5 其他类型的行星传动简介
第7章 轮系
2 轮系的传动比
2.1 定轴轮系传动比的计算 2.2 周转轮系传动比的计算 2.3 混合轮系传动比的计算
2.1 定轴轮系传动比的计算
1.传动比大小的计算 2.主、从动轮转向关系的确定
只起改变方向作用
称为惰轮
定 轴 轮 系 的 传 动 比
所 有 从 动 轮 齿 数 的 连 乘积 所 有 主 动 轮 齿 数 的 连 乘积
2.1 定轴轮系传动比的计算
2 .传动比方向的确定
平面定轴轮系 所有齿轮均为直齿或斜齿圆柱齿轮，
可用(-1)m 来确定从动轮的转动方向。
m —— 外啮合的对数。
传动比为正,说明主、从动轮转向
机械原理轮系
蜗杆右旋，右手法则
右旋
右旋
蜗杆左旋，左手法则
左旋
左旋
定轴轮系转动方向判断举例：
1
3
3'
2
'
6'
7
4
2
5
6
5'
7-3 周转轮系传动比的计算
行星轮有自转和公转，所以不能直接 应用定轴轮系传动比的计算方法。
3
2
H
O1
3
O2
2
O2
2
O1
H
OH
H
O3
1
OH
O3
1
3
1
3
2
H
O1
3
O2
2
2
轮系运动分析的主要内容是确定传动比
反之，设计轮系时
？
设计轮系的一般步骤：
使用要求
确定要实现的传动比
确定输入输出轴的位置关系、转向关系 选定轮系类型 确定各轮齿数、布置方案……
7-2 定轴轮系传动比的计算
一、主、从动轮传动比大小的计算 二、主、从动轮转向关系的确定
7-2 定轴轮系传动比的计算
一、主、从动轮传动比大小的计算
轮系的应用很广泛。
小到精密仪器，大到航天航空工程。
一对圆柱齿轮，传动比一般不大于5～7
12小时：
时针：1圈
i = 12
分针：12圈 秒针：720圈
i = 60
i = 720
问题1：多个执行构件、大传动比传动
精密仪器中的轮系
问题2：变速、换向
问题2：变速、换向
大型机械中的轮系
为什么轮系的应用很广泛？
1
1
2
2
机械原理第7章
∵3=0，代入上式得
9999 3 H 100 100 iH 1 i1 H 1 10000 ∴iH1=-100
i13
， 1
H H 10000 10000
1
例2:如图所示轮系中,已知z1=z2=30， z3=90，轮1与系杆转速n1=nH=1r/min，转 向相反，求n3。 z3 n1 nH H 解: i13
1
z1
2
z2 z2
2
i12
1 z2 2 z1
i12
1 z2 2 z1
3.一对蜗轮蜗杆传动
4.一对锥齿轮传动
n2 n1 n1 1 z2 2 z1 n2
i12
i12
1 z 2 2 z1
方向如图所示。
方向如图所示。
7.2.2 定轴轮系传动比的计算 1.平面定轴轮系传动比的计算 已知图示轮系中各 1 轮齿数，求i15。 3
1 2 3 4 i12 i23 i34 i45 2 3 4 5
z 2 z 3 z4 z5 z z z z 1 2 3 4
z z 3 z4 z5 z 2 z 3 z5 1 、z 、z 2是从1至5每对齿轮中从动 3 即从式中可见：z2 5 i15 z4大小并不影响传动比的数值，只改 5 z1 z2 z3 z4 z1 z2 z3 轮的齿数； z1、z2′、z3′是主动轮的齿数，传动比数 变传动方向，这种齿轮称为惰轮或过轮。 值为从动轮齿数积与主动轮齿数积之比。
3. 1
2
定轴轮系：
(1)1-2
6
4 H 5
(2)6-7 周转轮系：
3
7机械原理第七章课后习题解答
机械原理课后习题解答
第7章 机械的运转及其速度波动的调节
7－7图示为一机床工作台的传动系统。
设已知各齿轮的齿
数，齿轮3的分度圆半径r 3，各齿轮的转动惯量J 1、J 2、J 2'、J 3，
齿轮1直接装在电动机轴上，故J 1中包含了电动机转子的转动
惯量；工作台和被加工零件的重量之和为G 。
当取齿轮1为等
效构件时，试求该机械系统的等效转动惯量J e 。
7 -12某内燃机的曲柄输出力矩M d
随曲柄转角φ的变化曲线如图所示，其运动周期φT=π，曲柄的平均转速n m=620 r/min。
当用该内燃机驱动一阻抗力为常数的机械时，如果要求其运转不均匀系数δ= 0. 01。
试求：
(1)曲轴最大转速n max和相应的曲柄转角位置φmax；
(2)装在曲轴上的飞轮转动惯量J F（不计其余构件的转动惯量）。
机械原理典型例题(第七章轮系)
3
自行车变速器
自行车的变速器是基于齿轮传动原理设计的。
数据分析及计算
通过数据分析和计算，可以更好地了解和优化齿轮传动系统的性能。
胶带传动原理
胶带传动是一种基于摩擦的传动方式，适用于轻载、低转速的传动。
胶带传动设计
胶带传动的设计要考虑传递力、张紧装置和传动比力的计算，可以确定轮胎传递给地面的力。
传动比计算
1 计算方法
传动比等于从动齿轮的齿数除以主动齿轮的齿数。
2 影响因素
齿轮传动的传动比受到齿数、齿轮模数等因素的影响。
3 传动比的重要性
传动比决定了齿轮传动系统的输出速度和扭矩。
齿轮传动的应用
1
机床
齿轮传动广泛应用于机床上，如铣床、车床、刨床等。
2
工程机械
挖掘机、推土机等工程机械中常使用齿轮传动。
机械原理典型例题(第七 章轮系)
本节将讨论机械原理中的轮系。我们将探索它的定义、分类以及在机械传动 和制造中的应用。
齿轮传动
一种效率高的传动方式
齿轮传动以齿轮的啮合为基础，具有高效率和较大的传递力。
常见的齿轮类型
齿轮传动包括直齿轮、斜齿轮、蜗轮蜗杆等不同类型，适用于不同的工程需求。
应用广泛
齿轮传动广泛应用于机械设备、汽车、船舶等领域。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2019.11
例1. 在图示轮系中，已知：蜗杆为单头且右旋，转速 n1=1440r/min, 转动方向如图示，其余各轮齿数为： Z2 = 40 ，Z2‘ = 20，Z3 = 30 ，Z3 ' = 18 ，Z4 = 54 ， 试： （1） 说明轮系属于何种类型； (2 ） 计算齿轮4 的转速n4;（3） 在图中标出齿轮4的转动方向。
解：
（1）1-2-3-4- H(5) 行 星 轮 系
i514 =(n1-n5)/(n4-n5)=1-i 15 =(-1) 2(Z2· Z4)/(Z1· Z3) =+ 16/25
故 i15 =1- i 514 = + 9/25 (2)5 、6 定 轴 轮 系
i56 =n5/n6= - Z6/Z5= - 1/5 (3) 混合轮系
=1-
i
B 2'4
=1+(Z3·Z4)/(Z2' ·Z3')=
+ 20
(3) 混 合 轮 系 i1B =i 12 ·i2'B =40 ×20=800
例3 图示轮系中，Z1 = Z3=25, Z5 = 100 ，Z2 = Z4 = Z6 = 20, 试区分哪些构件组成定轴轮系？哪些构件组成 周转轮系？哪个构件是转臂H？传动比i16 =?
3
2 2' 4
H 1
行星轮 — Z2，Z2' 联动关系 — n2=n 2' 系杆 — H 中心轮 — 1，3，4 3K-H 型周转轮系
解法一：
差动轮系1-2- 2‘-4-H
行星轮系1-2-3-H
i1H4
?
n1 ? nH n4 ? nH
? ? z2z3 = ? 174 z1z2 ' 33
i1H3
?
n1 ? nH n3 ? nH
? 200 ? nH ?? 8 ? 100 ? nH 5
nH
?
? 1800 3
?
? 600/r
min
1
i1H3
?
n1 ? nH n3 ? nH
??
b
z2 z3 z1z 2 '
? 200 ? nH ?? 8 ? 100 ? nH 5
200 nH ? 13 ? 15.38r /m in
注意：
? 转化轮系传动比的“±”号的确定错误， 将导致整个计算结果的错误。
i16 =i 15 ·i56 =(9/25) ×(- 1/5) =- 9/125 轮1和6的方向相反
例4 图示为里程表中的齿轮传动，已知各轮的齿数为Z１ = 17 ，Z2 = 68 ，Z3 = 23 ，Z4 = 20 ，Z4' =19 ，Z5 = 24 。试求传动比i15 。
解：（1） Z１、Z2 为 定 轴 轮 系。
如图示。
解：
(1) 定 轴 轮 系1-2
i12 =n1/n2= Z2/Z1=40( 向下) (2) 周 转 轮 系 :2' -(3- 3') -4-H(B)
iB 2'4 =(n2' -nH)/(n4-nH) =1-n2'/nH=1 - i 2'H =- (Z3· Z4 )/(Z2' ·Z3')
故
i2'H
1
5
i12
?
n1 n2
?
Z2 Z1
i1' 4'
?
n1' n4 '
= Z5'Z4' Z1'Z5
H
?
n2 ?
n1Z1 Z2
?
n4' ?
n1' Z1' Z5 Z5' Z 4 '
2' 2
4
3 4'
差动：
i2H'4?n2' ? nH n4 ? nH
?
?
z4 = ? 1 z2'
2' -3-4-H 差动轮系 1-2 空间定轴轮系 1' -5' -5- 4' 空间定轴轮系
i12 = - Z2/Z1=-68/17= - 4
（2）Z3 –(Z4' -Z4)- Z5- H(2) 为 行 星
轮 系， n3=0 。 i53 H=(n5-nH)/(n3-nH)
=1-n5/nH= + (Z4·Z3)/(Z5· Z4') i5H =1-i 53 H=1-(20 ×23)/(24 ×19) iH5 =1/i 5H =-114 (3) 混合轮系，n2=nH i15 =i 12 ·i25 =i 12 ·iH5 =(-4) ×(-114)
? 它不仅表明在转化机构中中心轮之间的 转向之间的关系，而且将直接影响到周 转轮系传动比的大小和正负号。
? 用箭头确定的构件的转向关系，是指转 化机构中各构件的转向关系，而非该周 转轮系中各构件绝对运动的转向关系。
例6 ：已知 Z1=18 ，Z2=36 ，Z2' =33 ，Z3=90 ， Z4=87 ，求i14
? 1 ? n1 nH
? ? z3 = ? 5
z1
?
i14 ?
n1 n4
?
n1 n4
? 116
解二：
行星轮系3-2- 2‘-4-H
行星轮系3-2-1-H
i3H4
?
n3 ? nH n4 ? nH
? ? z2z4 = ? 174 z3z2 ' 165
i3H1
?
n3 ? nH n1 ? nH
?
?
z1 = ? 1 z3 5
+
Z1 Z2
n1
?
n1
? ?1
?
Z1Z5 Z5'Z4'
n1
?
nH
?
i1H
?
n1 nH
? 1980000
联动n1=n1' ， n2=n2' ， n4=n4' ，n5=n5'
? t ? i1H / n1 ? 1440 min ? 24h
解：
（1） 空间定轴轮系
（2 ）i14 =n 1/n 4 = (Z2·Z3 ·Z4)/(Z1·Z2' ·Z3')
故n4 ＝ 8 r/min （ 3）n4 方 向 ←。
例2. 计算图示轮系的传动比i1H ，并确定输出杆H 的转 向。已知各轮齿数Z1 = 1 ，Z2 = 40 ，Z2' = 24 ， Z3 = 72 ，Z3' = 18 ，Z4 = 114 ，蜗杆左旋，转向
?
i14
?
n1 n4
? 116
例7 ：已知Z1 =1( 右)，Z1'=101 ，Z2=99 ，Z 2'=Z4 ，Z4'=100 ，
Z5'=100 ，Z5=1( 右)，求i1；求当n 1=1375r/min ，输出轴 H 转一
周的时间 t 。
1' n1
5'
定轴： n2 和n4' 转向相反，n2' 和n4 转向相反
=456
例5: 图a 、b 为两个不同结构的锥齿轮周转轮系，已知 Z1=20 ，Z2=24 ，Z2 '=30，Z3 =40 ，n1 =200r/min ， n3=-100r/min 。求两轮系的nH=?
2' 3 H1
2'
3 2
H
2
i1H3
?
n1 ? nH n3 ? nH
??
a
z2 z3 z1z 2 '