结构稳定理论-第二章
第二章 有机化合物的结构理论
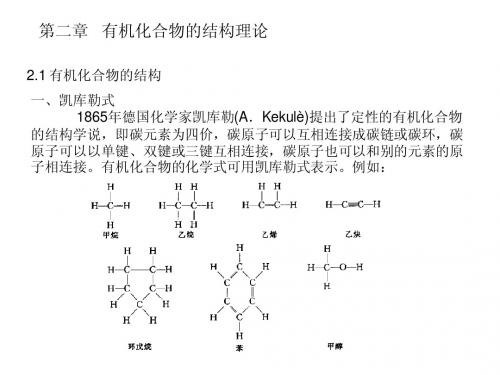
H—H键的电子云是围绕键轴对称分布的，这种类型的键叫做σ键。
2．共价键的饱和性。 如果一个未成对电子已经配对，就不能再与别的原子的未成对电 子配对。例如氯化氢分子中的氢原子和氯原子的未成对电子已互相配 对，就不能再与其它的原子形成共价键。
3．共价键的方向性。 原子轨道互相重叠程度越大，体系能量就越低，形成的共价键也 就越牢固，因而应使原子轨道最大限度地互相重叠。例如两个2px轨道 只有在x轴方向上才能最大限度地互相重叠形成σ键。两个原子的p轨 道若互相平行，则在侧面能有最大的重叠，这种类型的共价键叫做π 键，π电子云分布在两个原子键轴的平面的上方和下方。
2．异裂(heterolytic) 共价键异裂时，成键的一对电子为某一个原子或基团占有，生 成正离子和负离子。通过共价键的异裂的反应叫做离子型反应。 大多数有机反应都是离子型反应或自由基反应。此外还有协同 反应，在协同反应中，既无自由基也无离子生成，共价键的断裂 和形成是同时进行的。
2.3. 分子间的弱相互作用力 一. 分子间的弱相互作用力类型 分子中相连原子之间存在强烈的吸引力，这种吸引力叫做化学键， 它是决定分子化学性质的重要因素。在物质的聚集态中，分子之间还存在 着一种弱的吸引力，把它统称为范德华（van der Waals)引力，它是决定 物质的沸点、熔点、气化热、熔化热、溶解度、粘度、表面张力等物理化 学性质的重要因素。从本质上讲，这种吸引力是由于分子中电荷分布不均 匀[或瞬间分布不均)而出现的静电作用力。常见的有如下3种。 (1). 偶极-偶极作用力(静电力)：这种作用力产生于极性分子的静电相互作 用。如氯甲烷分子中，氯原子电负性较大，氯原子一端带有部分负电荷， 而碳原子上带有部分正电荷。一个分子带负电荷的一端吸引另一个分子带 正电荷的一端，于是分子间出现正负极相吸的排列，即
结构稳定理论(第2版)
2022年3月7日，《结构稳定理论（第2版）》由高等教育出版社出版发行。
内容简介
《结构稳定理论（第2版）》共计9章，第1章介绍结构稳定问题概述，第2章介绍结构稳定计算的能量法，第 3章介绍轴心受压杆件的整体稳定，第4章和第5章介绍杆件的扭转与梁的弯扭屈曲、受压杆件的扭转屈曲与弯扭 屈曲，第6章和第7章介绍压弯杆件在弯矩作用平面内的稳定、刚架的稳定，第8章和第9章介绍拱的平面内屈曲以 及薄板的屈曲等内容。
郑宏，男，哈尔滨人，工学博士，长安大学建筑工程学院教授，研究生导师。研究领域：钢结构基本理论及 其应用、结构稳定理论、结构抗震及减震。
石宇，工学博士，重庆大学土木工程学院教授，硕士生、博士生导师。研究方向：钢结构基本原理及其应用、 钢—混凝土组合结构。
感谢观看
教材目录
（注：目录排版顺序为从左列至右列）
教学资源
《结构稳定理论（第2版）》的数字课程与纸质教材一体化设计，内容涵盖教学课件、动画、失稳案例分析、 练习题及答案等。
《结构稳定理论（第2版）》配有数字化资源。
作者简介
周绪红，男，1956年9月出生，汉族，湖南南县人，工学博士，中国工程院院士，日本工程院外籍院士，重 庆大学钢结构工程研究中心主任，重庆大学土木工程学院教授。研究方向：钢结构、钢-混凝土混合结构、高层结 构、大跨结构、桥梁结构、风电结构。
结构稳定理论（第2版）
3月高等教育出版社出版的图书
01 成书过程
03 教材目录 05 作者简介
目录
02 内容简介 04 教学资源
《结构稳定理论（第2版）》是由周绪红主编，高等教育出版社于2022年3月7日出版的“十二五”普通高等 教育本科国家级规划教材，新世纪土木工程系列教材。该教材可作为高等学校土木工程专业高年级本科生及相关 专业研究生教材，也可供相关专业教师和工程技术人员参考。
结构第二章第四章综合
1、单选1 用紫外光照射某双原子分子，使该分子电离出一个电子。
如果电子电离后该分子的核间距变短了，则表明该电子 ( ) CA 从成键MO 上电离出去的B 从非键MO 上电离出去的C 从反键MO 上电离出去的D 不能断定是从哪个轨道上电离出去的2 组成有效分子轨道需要满足下列哪三条原则？( ) DA 对称性匹配，能级相近，电子配对。
B 能级相近，电子配对，最大重叠C 对称性匹配，电子配对，最大重叠D 对称性匹配，能级相近，最大重叠3 对于极性双原子分子AB，如果分子轨道中的一个电子有90％的时间在A原子轨道φa上，有10％的时间在B的原子轨道φb上，描述该分子轨道归一化的形式为：( ) CA ψ =0.9φa + 0.1 φbB ψ =0.1φa + 0.9 φbC ψ =0.949φa + 0.316φb Dψ =0.994φa + 0.110 φb4 下列四种分子或离子中为顺磁性的是( ) BA N2B NOC CN ‒D O 2‒5 下列分子或离子中磁矩最大的是( ) DA N2B C2C C2 +D B26 按分子轨道理论, 下列分子(离子)中键级最大的是( ) BA F2BC D7 OF，OF+，OF– 三者间，键长顺序正确的是 ( ) BA OF > OF + > OF –B OF – > OF > OF +C OF + > OF > OF –D OF + > OF – > OF8 对于"分子轨道"的定义，下列叙述中正确的是： ( ) BA 分子中电子在空间运动的波函数。
B 分子中单个电子空间运动的波函数。
C 分子中单电子完全波函数(包括空间运动和自旋运动) 。
D 原子轨道线性组合成的新轨道。
9 下面对于分子中电子排布说法正确的是( ) BA 电子不能排入反键轨道，因为反键轨道能量较高。
B 电子可以排入反键轨道，但排入后轨道能量升高。
钢结构稳定理论-2
有：A 0 B 1 C 0 D 0
Ak 1 Bk 0 C 0 0
A
sin
kl
B
cos
k
l
Cl
D
0
Ak cos kl Bk sin kl C 0 0
为使关于A、B、C、 D的齐次方程组有非 0解，则其系数行列 式应为0。
0
1 01
k sin kl
0 10 0
cos kl l 1
挠度关系； ❖ 大挠度理论使用了弹性假设，因此屈曲后荷载有所提
高，但当挠度达到构件长度3％以上时，跨中弯曲应 力将使截面进入弹塑性状态，出现下降段，如上图所
示。因此轴心压杆的屈曲后强度提高时没有意义的。
§2-4 理想轴心压杆的弹塑性屈曲
(inelastic buckling)
1）理想弹性轴压杆屈曲的适用范围
§2-2 理想轴压杆的弹性屈曲(perfect columns)
1）理想轴压杆的欧拉临界力Euler critical load
基本假设： ❖ 同一材料制成的等截面直杆，两端铰接； ❖ 荷载作用在截面形心上； ❖ 平截面假定，仅考虑弯曲变形（忽略剪切变形）； ❖ 材料为弹性；
❖ 构件变形非常微小（小挠度理论 y 1 ）。
采用图形曲线法得： kl 1.43 k 1.43
l
Pcr
1.43
l
2
EI
2EI
(l /1.43)2
2EI
(0.7l)2
❖ 工况三：一端嵌固、一端自由的轴心压杆
y x0 0, y' x0 0
y'' xl 0, y''' xl k 2 y' xl 0
有： B D 0 Ak C 0 Ak 2 sin kl Bk 2 cos kl 0 Ak3 cos kl Bk 3 sin kl k 2 ( Ak cos kl Bk sin kl C) 0
受压构件的稳定(结构稳定原理)
127第2章 受压构件的稳定2.1 轴心受压构件的稳定轴心压杆就其自身的截面形状和尺寸而言，有较长细的杆，也有较中短的杆，这可用长细比i l /0=λ来表达。
对于长细比大的长细压杆，可以认为是在弹性范围内失稳；对于长细比小的中短杆件，则可能是在弹塑性范围内失稳。
因此，应该分别按弹性范围和弹塑性范围来分析理想轴心压杆的临界荷载。
2.1.1 理想轴心压杆的弹性稳定用理想轴心压杆的欧拉荷载E P 除以杆件的截面积A ，可得轴心压杆欧拉临界应力22202)/(λππσE i l E A P E cr===，式中i 为回转半径，AIi =。
由此可计算出应力值为材料比例极限p σ时的长细比p λ，并以此作为长细杆和中短杆的分界；压杆的长细比大于p λ时称为长细杆或大柔度杆，长细比小于p λ时称为中短杆或小柔度杆。
对于理想轴心压杆来说，长细杆是在弹性范围内工作的，所以压杆的稳定分析为弹性稳定问题。
通过弹性压杆的静力平衡条件,可以建立理想轴心压杆的平衡微分方程式，解平衡微分方程则可求得轴心压杆的临界荷载。
下面来看几个边界条件不同的理想轴心压杆的弹性稳定分析。
1）一端固定一端铰接的压杆 （1）用静力法求解如图2－1所示一端固定一端铰接的等截面轴心受压弹性直杆，设其已处于新的曲线平衡形式，则取任意截面的弯矩为)(x l Q Py M -+-=式中Q 为上端支座反力。
由y EI M ''-=，压杆挠曲线的平衡微分方程为:)(x l Q Py y EI -+-='' 图2－1一端固定一端铰接压杆128即 )(x l EIQ y EI P y -=+'' （2.1） 令EIPk =2，则有 )(22x l PQk y k y -=+'' （2.2） 此微分方程的通解为)(sin cos x l PQkx B kx A y -++= （2.3） 式中A 、B 为积分常数，Q ／P 也是未知的。
钢结构稳定原理ppt课件
2016《钢结构稳定原理》
02.1 典型算例1
【典型算例1】 能量法
UVUW
r2 /2Nl1cos
r N ls in 0
小变形状态下
sin
N cr
r l
【思考02.1】请根据最小势能原理判别 变形后的平衡状态是否稳定？
同济大学建筑工程系
2016《钢结构稳定原理》
04.2 平衡方程
A. 两端铰接理想压杆的平衡方程
基本假定：
z
z
等直杆；弹性；小变形；
平截面；荷载作用在形心；
N
由内外弯矩的平衡可得：
N
Mx内EIxv M x外 Nv
EIxvNv0
【思考04.1】右图压杆失稳后，支座处有没有 水平反力？画出右图压杆变形后的弯矩图和剪 力图；压杆中的剪力是如何产生的？
典型焊接残余应力分布
平板
工字形截面
纵向残余应力； 焊缝处后冷却，为残余拉应力； 残余应力在截面上自平衡；
同济大学建筑工程系
2016《钢结构稳定原理》
04 轴压构件的弯曲失稳
可编辑课件PPT
42
04.1 失稳形式
轴压构件整体失稳形式
➢弯曲失稳： H型截面柱
➢扭转失稳 十字截面柱
➢弯扭失稳 T型截面柱
大应力，原因：
fy fe
fp
（1）fe、fp、fy非常接近，三者合一，可认
为弹性与塑性的分界点；
（2）fy以后，塑性变形很大，一旦超载，易 o 被发现加固补救；
（3）fy 发展到fu，有很大一段区域，可作为 fy 强度储备，称fu/fy为强屈比，要求大于1.2
结构稳定概述(结构稳定原理)
第1章结构稳定概述工程结构或其构件除了应该具有足够的强度和刚度外，还应有足够的稳定性，以确保结构的安全。
结构的强度是指结构在荷载作用下抵抗破坏的能力；结构的刚度是指结构在荷载作用下抵抗变形的能力；而结构的稳定性则是指结构在荷载作用下，保持原有平衡状态的能力。
在工程实际中曾发生过一些由于结构失去稳定性而造成破坏的工程事故，所以研究结构及其构件的稳定性问题，与研究其强度和刚度具有同样的重要性。
1.1 稳定问题的一般概念结构物及其构件在荷载作用下，外力和内力必须保持平衡，稳定分析就是研究结构或构件的平衡状态是否稳定的问题。
处于平衡位置的结构或构件在外界干扰下，将偏离其平衡位置，当外界干扰除去后，仍能自动回到其初始平衡位置时，则其平衡状态是稳定的；而当外界干扰除去后，不能自动回到其初始平衡位置时，则其平衡状态是不稳定的。
当结构或构件处在不稳定平衡状态时，任何小的干扰都会使结构或构件发生很大的变形，从而丧失承载能力，这种情况称为失稳，或者称为屈曲。
结构的稳定问题不同于强度问题，结构或构件有时会在远低于材料强度极限的外力作用下发生失稳。
因此，结构的失稳与结构材料的强度没有密切的关系。
结构稳定问题可分为两类：第一类稳定问题（质变失稳）—结构失稳前的平衡形式成为不稳定，出现了新的与失稳前平衡形式有本质区别的平衡形式，结构的内力和变形都产生了突然性变化。
结构丧失第一类稳定性又称为分支点失稳。
第二类稳定问题（量变失稳）—结构失稳时，其变形将大大发展（数量上的变化），而不会出现新的变形形式，即结构的平衡形式不发生质的变化。
结构丧失第二类稳定性又称为极值点失稳。
无论是结构丧失第一类稳定性还是第二类稳定性，对于工程结构来说都是不能容许的。
结构失稳以后将不能维持原有的工作状态，甚至丧失承载能力，而且其变形通常急剧增加导致结构破坏。
因此，在工程结构设计中除了要考虑结构的116强度外，还应进行其稳定性校核。
1.1.1 第一类稳定问题首先以轴心受压杆来说明第一类稳定问题。
第二章-结构可靠性的基本概念和原理
若结构或结构构件达到正常使用或耐久性能的某项规
定限值，则认为其达到正常使用极限状态。如：影响正常
使用或外观的变形；影响正常使用或耐久性能的局部损坏。
(3)整体性极限状态(抗连续破坏极限状态)
结构由于局部损坏而达到其余部分将发生连续破坏(或
连续20倒21/塌4/)9状态限值。
5
2.2 可靠度基本概念
第二章：结构可靠性的基本概念和原理
2.2 可靠度基本概念
2.2.1 极限状态
1、工程结构的功能函数
无论是房屋、桥梁、隧道等工程结构设计时，应使其在
使用期内，力求在经济合理前提下满足下列各项要求：
(1)能承受正常施工和正常使用期间可能出现的各种作用
(包括荷载及外加变形或约束变形)—结构的安全性；
(2)在正常使用时具有良好的性能—结构的适用性；
N(S,S )
对R，S作标准化变
换
Sˆ
Rˆ
S S S
R R
R
显然, Sˆ , Rˆ 均服从 N (0 ,1分) 布.
Z R ˆR R (S ˆSS ) 0
c
o
s
S
用
2 R
2除上式得
S
S ˆcosSR ˆcosˆR0
c
o
s
R
S
2 R
2 S
R
2 R
2 S
2021/4/9
14
由解析几何知，在标准正态化坐标系SˆOˆ Rˆ 中，上式为极 限状态直线的标准法线式方程。 为原点 O ˆ 到极限状态 直线的法线距离 Oˆ p (见图2-4)。cosS,cosR为法线对各 坐标向量的方向余弦。 的几何意义为标准正态坐标 系中原点 O ˆ 到极限状态直线的最短距离。对结构极限 状态方程为若干相互独立、正态变量构成非线性方程 情况，同样可证明 的合理近似取值为标准正态坐标 系中原点 O ˆ 到极限状态曲面的最短距离。
结构稳定理论与设计-2(110303)
7 23 U V 4EIa l Pa1 l 3
2 1
2.1 轴心受压构件的弯曲失稳
2.1.1 理想轴心受压构件的弹性弯曲失稳 能量法： 用里兹法求解图示轴心受压构件 的临界荷载Pcr。 d 0 由势能驻值原理 da1
4EIl 1.714EI P 3 cr 3 7l l 2 级数、 三角函数！ 1.358EI Pcr 精确解 2 l 例题图 无限自由度轴心压杆
切线模量理论采用如下假定： ①杆件是挺直的； ②杆件两端铰接，荷载沿杆轴 线作用； ③杆件产生微小的弯曲变形 （小变形假定）； ④弯曲前的平截面弯曲变形后 仍为平面； ⑤弯曲变形时全截面没有出现 反号应变?
Pt
2 Et I
l0
2
2 Et t 2
2.1 轴心受压构件的弯曲失稳
2.1.2 理想轴心受压构件的非弹性弯曲失稳 2.双模量理论
挠曲线方程成为：
y A sin kz Cz
z l 由 ； y 0
z l 得 y 0
A sin kl Cl 0 Ak cos kl C 0
为一关于A、C 的线形齐次方程组，为使其有非零解
（否则 y 0），则必有其系数行列式等于零，即：
2.1.1 理想轴心受压构件的弹性弯曲失稳
静力法：
2） 柱的高阶微分方程（对其他支承及荷载情况）
考虑图示杆件承受一组竖向力系， 由脱离体的平衡可得：
EIy Fy M A Vz
对上式求导两次可消去 等式右端的杆端约束力：
EIy Fy 0
2.1 轴心受压构件的弯曲失稳
sin kl
l
k cos kl 1
结构稳定理论计算和原理
静力法
静力法即静力平衡法，也称中性平衡法，此法是 求解临界荷载的最基本方法。
对第一类弹性稳定问题，在分支点存在两个临近 的平衡状态：
初始直线平衡状态和产生了微小弯曲变形的平衡 状态。
静力法就是根据已发生了微小弯曲变形后结构的 受力条件建立平衡微分方程，而后解出临界荷载。
静力法举例
两端铰接轴心受压构件
挠曲线的平衡微分方程
由内力矩-EIy〞=M与外力矩 P y
相平衡
或 EIy〞+Py=0
当两端铰接时，边界条件为 x=0, y=0； x=l, y=0
解平衡微分方程，得到P的最小值:
Pcr =π2EI / l2 即 临界荷载或“ 欧拉荷载”
能量法
静力法是通过建立轴心受压构件微弯状态时的平 衡方程，求出临界荷载的精确解。
影响结构稳定性能的各种主要因素；
为增强结构稳定可能采取的各种措施等。
本课程为考试课。
第一章 概 述
工程结构或其构件除了应该具有足够的强度和刚度外， 还应有足够的稳定性，以确保结构的安全。
强度 结构的强度是指结构在荷载作用下抵抗 破坏的能力；
刚度 结构的刚度是指结构在荷载作用下抵抗 变形的能力；
当作用着外力的弹性结构偏离原始平衡位置而产生 新的微小位移时，如果应变能的增量ΔU大于外力功的增 量ΔW，即此结构具有恢复到原始平衡位置的能力，则结 构处于稳定平衡状态；如果ΔU <ΔW，则结构处于不稳 定平衡状态而导致失稳；临界状态的能量关系为
ΔU =ΔW
势能驻值原理
势能驻值原理指：受外力作用的结构，当位移有 微小变化而总势能不变，即总势能Π 有驻值时，结构处 于平衡状态。或者说
荷载—位移曲线
结构稳定理论
1.理想压杆：受压杆件两端铰支荷载作用于形心轴，杆轴线沿杆长完全平直，横截面双轴对称且沿杆长均匀不变，杆件无初应力，材料符合胡=胡克定律2.极限状态：承载能力极限状态和正常使用极限状态。
3.保守力：如果力在它作用的任意可能位移上所做的功与力作用点移动路径无关，只依赖与移动的起点和终点。
4.势能驻值原理与最小势能的区别：势能驻值原理方法比较简单，但从教学角度δp=0只是平衡条件，它不表示从稳定平衡过度到不稳定平衡的临界条件，而最小势能原理方法更加严密。
（势能驻值原理：虚位移，基本条件δp=0）5.伽辽金法瑞利-里兹法的区别：①瑞利里兹法只需要满足几何边界条件即可，而伽辽金法需要满足几何边界条件，力学边界条件；②伽辽金法直接与微分方程相联系，而瑞利里兹法需要写出体系的总势能。
6.计算长度系数μ，将非两端铰支的理想轴心压杆构件，临界荷载公式换算成相当于两端铰支理想轴心压杆构件，求解临界荷载的形式的所利用的计算长度，几何意义：杆件绕由曲线上两反弯点的间距7.自由度：用来表示约束条件允许的体系，可能变形时所必须的独立几何参数的数目。
8.柱子曲线：临界应力δcr与长细比的关系曲线，可作为轴心受压构件设计的依据。
9.残余应力：降低比例极限，使柱子提前出现弹塑性屈曲，当超过比例极限后，残余应力使杆件应力应变曲线，同时减小了截面的有效面积和有效惯性矩，从而降低了刚度和稳定性。
10.翘曲：非圆形截面的杆件扭转时，截面处绕杆件轴线转动外，截面上个点还会发生不同的轴向位移而使截面出现凹凸，不像圆截面杆件那样扭转后不保持平面。
11.影响弯曲荷载Mor的因素：①截面的形状，尺寸。
②截面的残余应力。
③初始几何缺陷。
④荷载类型及其作用特点。
⑤构件端部和侧向支撑条件。
12．梁的弯曲屈曲5个假设：①构件为各向同性完全弹性体，②弯曲和扭转时，构件截面形状不变，③小变形（侧面）。
④构件为等截面无截面。
⑤主弯矩作用平面内刚度很大，屈曲前变形对弯扭屈曲的影响的忽略。
结构力学稳定理论
解。即在荷载达到临界值前后，总势能由正定过渡到非正定θ。 3）如以原始平衡位置作为参考状态，当体θ系处于中性平衡P=Pcr
时，必有总势能θ=0。对于多自由度体系，结论仍然成立。
2）能量法
•在新的平衡位 置各杆端的相 对水平位移
A
YA=Py1/l
y1
Bk
R1=ky1
y2
kC
R2=ky2
Dλ P YD=Py2/l
l
l
l cos
2l sin 2
2
1 2
l能①2量给法出12步新l(骤的ly )平:2 衡 形12 式yl 2 ;②写出
体系具有足够的应变能克服荷载势能，使压杆恢复到原有平
衡位置)当θ=0，Π为极小值0。
对于稳定平衡状态，真实的位移使Π为极小值
2）P>k/l ，当θ≠0，Π恒小于零（Π为负定） (即U<UP表示体系缺 少足够的应变能克服荷载势能，压杆不能恢复到原有位置) 。当 θ=0，Π为极大值0。原始的平衡状态是不稳定的。
对于具有n找个新自的由平度衡的位结置构，，列新平的衡平方衡程形，式需E要I=∞n个独立的位
l
移参数确定，由在此新求的临平界衡荷形载式。下也可列出n个独立的平衡方程，
它们是以n个独立的位移参数为未知量的齐次代数方θ程组。根据
临P(l界Pl状Mkk态)A的静00 力θ特=0征，，原该始齐平次衡方程组除零解转外动（刚对应于原有平
二类稳定分析
桥墩二类稳定分析报告2009.12.11.结构稳定分析理论按照结构在逐渐加载过程中平衡形式是否发生质变的观点，将结构的失稳区分为第一类稳定问题和第二类稳定问题，如图l －图2所示。
前者表示在加载过程中，构件的平衡状态将出现分枝现象，使原有的平衡状态失去稳定性而转向新的平衡状态；而后者在加载过程中平衡形式并不发生质变。
在第一类稳定同题中，当加载至P cr 时，表示平衡的分枝即将出现，称P cr 为压屈荷载。
在第二类稳定问题中，当加载到P cr 时，表示构件的承载能力即将降低，称为压溃荷载。
工程上通常把两者统称为失稳的临界荷载。
工程问题中研究结构稳定问题的目的，在于寻求相应的临界荷载及其临界状态，防止不稳定平衡状态的发生，从而确保结构安全。
结构的第一类稳定问题，在数学上归结为广义特征值问题，()0d g K K λδ+= (1)式中，d K 为弹性刚度矩阵，g K 为几何刚度矩阵，它只与结构的轴力有关；δ为结构的位移增量；λ为载荷稳定系数。
式(1)数学上表现为广义特征问题，应用各种迭代方法，如逆矢量迭代法、子空间迭代法等都可以很方便地求解。
结构的几何非线性是指大位移问题。
在载荷作用下，当位移大到足以使得结构的几何形状发生显著的改变时，必须按已变形的位置建立平衡方程。
弹性大变形问题与变形的历史不相关，可以采用全量方法研究，也就是直接求在已知载荷的约束下的总变形和应力，结构全量形式的非线性平衡方程可表示为：{}()0K F δδ−= (2)式中：()K δ为非线性刚度矩阵，δ为节点位移，F 为等效节点载荷。
非线性稳定分析的基本方法是逐步地施加一个恒定的载荷增量直到解变得开始发散为止。
由于特征值屈曲载荷是预期的线性屈曲载荷的上限，故可以作为非线性屈曲的给定载荷，在渐进加载达到此载荷前，非线性求解应该发散。
设λ为特征值屈曲分析时的稳定系数，在这里取非线性屈曲分析的给定载荷系数。
将给定载荷分为n 个载荷增量，010t n λλλλλ=<⋅⋅⋅⋅<⋅⋅⋅⋅<= (3)在每一个载荷步内对非线性方程(2)进行线性化，可得增量形式的平衡方程：0t K F δΔ−Δ= (4) 0t l K K K K σ=++ (5) 1()t t F F λλ−Δ=− (6)式中：t K 为切线刚度矩阵，F Δ为等效节点载荷增量矩阵，δΔ为节点位移增量，0K 为小位移线性刚度矩阵，l K 为大位移矩阵，K σ为初应力矩阵，F 为等效节点载荷矩阵。
结构稳定理论2
We Wi
We 为外力在虚位移上作的功，即外力虚功； Wi 为内力在虚位移上作的功，即内力虚功。
用应变能和外力势能来表示：
Ep (E W ) 0
E p —— 为总势能； E —— 为应变能；
W —— 为外力势能；
0
E
EI 2
l
0
2a1(l 3x) 6a2 (l
2x)x
2 dx
EI 2
(4l 3a12
8l 4a1a2
4.8l5a22 )
外力势能
W F l y/ 2 dx 20
W F 2
l 0
a1(2l
3x)x a2 (3l
4x)x2
2.4 瑞利—里兹法
瑞利—里兹法：建立在势能驻值原理基础上的近似方法， 用求解代数方程式代替求解微分方程。
假设体系在中性平衡时，沿坐标轴x,y,z方向的位移分量分 别为：
n
其中，ai ,bi , ci 是3n个独立
u aii (x, y, z)
参数，成为广义坐标；
i 1
2 dx
F 2
(0.1333l 5a12
0.2l 6a1a2
0.0857l7a22 )
压杆的总势能： EP E W
令：
EP a1
(4EI 0.1333Fl2 )l3a1 (4EI 0.1Fl2 )l 4a2
0
EP a2
(4EI 0.1Fl2 )l 4a1 (4.8EI 0.085Fl2 )l5a2
2 dx
由临界荷载的基本方程： W Es
结构稳定理论绪论.ppt
结构稳定理论 福州大学土木工程学院 林翔
绪论
一。稳定与失去稳定的概念
狭义的概念： 稳定（Stability）： 体系保持某种情形或状态 失稳（Instability）:体系丧失某种情形或状态，通常是突然
sin
e
cos
l
(0 11)
线性化（0－11）得：
p
PL 2K
e
l
或
(0 12) 图0－15 荷载缺陷的影响
1 e e
1 p L L
(2 13)
结构稳定理论 福州大学土木工程学院 林翔
3。2 能量方法
U 1 K (2 )2
2
1 2L(1 cos )
图1－11 小球平衡位置附近稳 定性
结构稳定理论 福州大学土木工程学院 林翔
2。判别平衡稳定性的三个准则
2。1 静力准则
平衡稳定的静力准则可表达为：若结构系统处于某一平衡 状态，且与其无限接近的相邻位置也是平衡的，则这一平衡状 态是随遇的。用静力准则确定平衡分支荷载，首先要对新的平 衡状态建立静力平衡方程。这种在外荷载不变的情况下，考虑 干扰变形影响的静力平衡方程显然是对干扰状态的一组齐次方 程。这组方程如果存在非零解，就表示非零的干扰状态是另一 平衡位置，则原来的平衡状态处于随遇平衡状态，因而平衡稳 定问题便转化为在齐次边界条件下求解齐次方程组的特征值问 题。这样求得的状态对应于分支点A，最小特征值即为稳定性 问题的临界荷载。对应于每个特征值都可得到特征函数，即失 稳波形。用静力准则确定临界荷载的方法称为静力平衡法。静 力准则广泛应用于连续弹性体系稳定性问题的求解。
桥梁结构稳定理论演示文稿
第21页，共59页。
日期 6月
6月 8月6日 8月23日 8月27日
施工过程中杆件变形
构件 A3R、A4R、A7R、
A8R、A9R A8R、A9R
7L、8L 5R、6R
A9L
变形量/mm 1.5~6.5
19 19 13 57
第22页，共59页。
1907年 Quebec桥 第一次事故
根据能量准则，令 程：
，又 0 是任意的，则可得体系的平衡方
故有： P k 或 l sin
其中：
Pkp k l
稳定平衡判别：
sin 0
sin
Pkp P
1 cos
第52页，共59页。
2.0
1.8
1.6
1.4
平衡状态方程：
λ<1时，θ=0
λ=1时，θ=0
λ>1时，两个解
1.2
1.0
sin
线性屈曲分析
非线性屈曲分析
第5页，共59页。
参考教材
李国豪. 桥梁结构稳定与振动. 中国铁道出版社,1992
Timoshenko. S.P, Gere. J. Theory of Elastic Stability, 2nd. Ed. McGraw Hill Inc. 1961
刘光栋，罗汉泉. 杆系结构稳定. 人民交通出版设, 1988
论和折算模量理论；
➢ 1910年，Timoshenko导出了均匀受压两端铰支圆弧拱的屈曲临界 荷载公式；
➢ 1940年，符拉索夫(Vlasov)引入极值点失稳的观点以及跳跃现象
的稳定理论。
➢ 1947年，Shanley提出简化的弹塑性压杆模型。
➢ ………
钢结构稳定原理
N′Ex=π2EA/(1.1λx2 )，大体相当于欧拉力除以分项系数。
受弯构件的腹板稳定性 受弯构件的腹板稳定性
• 不同受力状态下的临界应力 •相关方程 •考虑腹板屈曲后强度q
挠度
跃越屈曲
• 4.1.2一阶和二阶分析 一阶和二阶分析
1
x
δ
P
αP
ρ
=
y ′′ 1 + ( y ′)
3 2
=−
M EI
1
ρ
= y′′ = −
M EI
h
是否考虑变形对平衡方程的影响而分别写出一阶和二阶弯矩：
M1 = αP(h − x) ,
M 2 = αP(h − x) + P(δ − y)
EI y ′′ = α P (h − x ) ,
(1) (2) (3)
λb
0.6 0.85 1.25
h t 0 w λb = 177 h0 t w 153
(受压翼缘扭转受到约束时) (受压翼缘扭转未受约束时)
(λ s ≤ 0.8) (0.8 < λs ≤ 1.2) (λs > 1.2)
fy 235 fy 235 (a h0 ≤ 1.0) (a h0 > 1.0)
(λb ≤ 0.85) (0.85 < λb ≤ 1.25) (λb > 1.25)
♦研究表明，当边缘正应力达到屈服点时，工字形截面焊接梁的腹板还可承受 剪力0.6Vu。在弯剪联合作用下，剪力不超过0.5Vu时，腹板抗弯屈曲后强度不 下降。有鉴于此，国家规范将工字形截面焊接梁屈曲后承载力表达为如下相关 方程： 2 M −Mf V 0 . 5V − 1 + M − M ≤ 1 u eu f 式中 M，V 同一梁截面的弯矩和剪力设计值； 但是，当V<0.5Vu，取V=0.5Vu；当M<Mf，取M = Mf ； Mf 梁两翼缘所承担的弯矩设计值，Mf=(Af1h12/h22+Af2h2)f； Af1，h1 较大翼缘的截面积及其形心至中和轴的矩离； Af2，h2 较小翼缘的截面积及其形心至中和轴的矩离； Meu，Vu 梁抗弯和抗剪设计值。 如果仅设置支承加劲肋不能满足时，应在腹板两侧成对设置横向加劲肋以 减小区格的长度。横向加劲肋的间距通常取(1～2)h0 。
结构稳定理论伽辽金法
y( 0 ) y l ( ) ，即 0 i (0) i (l ) 0
则
L( y )
( 4 ) 2 y y
= a1[24 2 2 (6x2 6xl l 2 )] a 2[120(2x l ) 2 2 (20x 30lx2 12lx l 3 )] 伽辽金方程组为
DK,1,ALL DK,2,UX DK,2,UY DK,2,ROTX DK,2,ROTY DK,2,ROTZ F,2,FZ,-1 /SOL !静力计算 ANTYPE,STATIC PSTRES,ON SOLVE FINISH /SOL !线性屈曲分析 ANTYPE,BUCKLE BUCOPT,LANB,3,0,0 MXPAND,3,0,0,1,0.001, SOLVE FINISH
模态图
一阶模态图
临界荷载为 49809.7N 与精确解 49937.56N 相比，01584N
三阶模态图
临界荷载为 197505N
体会与总结
（1） 当杆件的长度取的太短时，ANSYS 中模态变化有问题 （2） 对于两端固接，并在一端加力的模型，ANSYS 中是将一端约束全位移，另一端是留 一个与力方向相同的轴向位移，其他都约束。
0.8 0.0191 2l 2
0
6 2l 2
展开后，解得
(0.5714 0.006349 2l 2 )l
=0
2l 2 41.99
2 由 F / EI 得最小根为 Fcr 41.99
EI EI ，与精确解 Fcr 39.48 2 相比，偏大约 6.3%。 2 l l
L( y)
0 l 0
l
1
dx
1
a ( 0 .8
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
由此可得临界力公式为： P
2 EIn 2
西北农林科技大学
参数 k
或 Pcrn在数学上称为固有值、本征值或特征值 (eigenvalue)。
n
在参数取特征值时，方程有非0解，所以数学上也叫求解
特征值问题。
轴向压力 9 2 EI P3 l2
4 2 EI P2 l2 l
nx y A sin l
其中A、B、C、D为四个由边界条件确定的待定系数。
其中k
对通解求导，可得其各阶导数： y ' Ak cos kx Bk sin kx C
y ' ' Ak 2 sin kx Bk 2 cos kx y ' ' ' Ak 3 cos kx Bk 3 sin kx
P EI
结构稳定理论
西北农林科技大学
§2-1
轴心受压构件的失稳类型
φ φ
（a）弯曲屈曲（绕z轴） （b）扭转屈曲（绕x轴） （c）弯扭屈曲
图2.1 轴心受压构件的失稳类型
轴心受压构件的失稳形式主要取决于：截面的形状和几何尺寸，杆件长度和杆端的连接条件 。
结构稳定理论
西北农林科技大学
§2-2
轴心受压构件的弯曲失稳
任意一截面弯矩(对A点取矩)：
x y P M Q x
M P y Qx M A
弯矩与曲率的关系 M EIy ' ' 则有二阶常系数微分方程：
y
Q MA P
Q P MA
其中：
EIy' ' Py Qx M A
MA MB Q l
结构稳定理论
西北农林科技大学
则方程的通解为： y A sin kx B cos kx Cx D
西北农林科技大学
第二章 轴心受压构件的失稳
(flexural buckling of axial compressed members) 轴心受压构件在工程结构中应用广泛， 如钢结构中桁架、网架中的杆件，工业厂房 及高层钢结构的支撑，操作平台和其他结构 的支柱等。
本章着重讨论：
轴心受压构件的整体稳定问题
结构稳定理论
西北农林科技大学
则力矩平衡方程为：
M P y EI EI y' ' EI y' ' Py 0
为二阶齐次常微分方程
y ' ' k y 0
2
P k EI
2
该微分方程的通解为：
y A sin kx B cos kx
A,B为待定系数，由边界条件确定
为使关于A、B、C、 D的齐次方程组有非 0解，则其系数行列 式应为0。
结构稳定理论
西北农林科技大学
则： 2 sin kl (2 sin kl kl cos kl ) 0 2 2 2 因此有：sin kl 0 或 tg kl kl 2 2 2 由第一式得：
kl 2n P 4n 2 2 EI min 4 2 EI n k Pcrn Pcr 2 2 l EI l l2
结构稳定理论
EIy' ' Py 0 2 3/ 2 [1 ( y ' ) ]
西北农林科技大学
2）大挠度理论的解
应采用特殊的变换和数值解法才能求解。 （大多数非齐次微分方程都没有解析解） 可以得到大挠度理论轴心受压构件的荷载挠度曲线。
结构稳定理论
西北农林科技大学
结构稳定理论
西北农林科技大学
结构稳定理论
西北农林科技大学
轴心受压构件的大挠度理论 1）大挠度方程
基本假设： 同一材料制成的等截面直杆； 荷载作用在截面形心上； 平截面假定，仅考虑弯曲变形； 材料为弹性； y' ' 构件曲率与变形的关系： Φ
与小挠度 理论相同
[1 ( y ' ) ]
2 3/ 2
因此大挠度方程为：
结构稳定理论
西北农林科技大学
一、理想轴心受压构件的弹性弯曲失稳
基本假设： 同一材料制成的等截面直杆； 荷载作用在截面形心上； 平截面假定，仅考虑弯曲变形（忽略剪切变形）； 材料为弹性； 构件变形非常微小（小挠度理论 y ' 1 ）。
y' ' Φ y' ' 2 3/ 2 [1 ( y ' ) ]
结构稳定理论
西北农林科技大学
工况四：一端嵌固、另一端侧向可动但不转动的轴心
压杆
有：
y y'
x 0 x l
0, 0,
y'
x 0 x l
0 k y'
2 x l
y' ' '
0
B D 0 Ak C 0 Ak cos kl Bk sin kl C 0 Ak 3 cos kl Bk 3 sin kl 2 k ( Ak cos kl Bk sin kl C ) 0 B D 0 Bk sin kl 0
B 0, D 0, C 0
EI
2
(2l ) 2
结构稳定理论
西北农林科技大学
注：从上述五种工况的结果可以看出，临界力Pcr可表达 为： 2 EI Pcr 2 l0
l0 l
2 EI Pcr ( l ) 2
l0－有效长度、或计算长度；
l－实际杆长；
μ－杆件计算长度系数。
PE P 1
2 EI
l2
2 EI 最低的临界力即为欧拉临界力 P 1 2
横向挠度
结构稳定理论
西北农林科技大学
边界效应与计算长度的概念
(boundary conditions and effective length concept) （求解两端为任意支承情况时的临界力）
MB P Q
结构稳定理论
西北农林科技大学
结构稳定理论
西北农林科技大学
Pcr 2 EI 2E 临界应力： cr 2 A l0 A l0 I A
2
l0 i
2E
2
2E 2
其中：
l0 l i i
屈曲临界应力与 长细比的关系：
超过屈服点fy时 以虚线表示
工况一：两端嵌固轴心压杆
西北农林科技大学
y x0 0,
y'
x 0
0,
y xl 0,
y'
x l
0
有： A 0 B 1 C 0 D 0
Ak 1 Bk 0 C 0 0 A sin kl B cos kl Cl D 0 Ak cos kl Bk sin kl C 0 0 0 1 k 0 sin kl cos kl k cos kl k sin kl 0 1 l 1 1 0 0 1 0
结构稳定理论
西北农林科技大学
y x 0 0 y x l 0
B 0,
y A sin kx
A sin kl 0
A 0 否则方程的解为0，没有意义。 sin kl 0
n kn l
P n 即 EI l
crn
2
l2 nx 与之对应的挠曲线为： y A sin l 结构稳定理论
A 0 , C 0
结构稳定理论
西北农林科技大学
1 1 0 k sin kl 0 k sin kl 0 sin kl 0
kl n
(n 1, 2, 3)
2
nπ P EI l 2 EI Pcr 2 l
结构稳定理论
西北农林科技大学
3）几点结论
当P<PE时，小、大挠度理论都表明构件处于直线稳
定平衡状态； 当P≥PE时，小挠度理论只能指出构件处于随遇平衡 状态，只能给出分岔点和屈曲变形形状，不能给出确 定的挠度值；而大挠度理论不仅能说明构件屈曲后仍 处于稳定平衡状态，而且可以得到不同时刻的荷载与 挠度关系； 大挠度理论使用了弹性假设，因此屈曲后荷载有所提 高，但当挠度达到构件长度3％以上时，跨中弯曲应 力将使截面进入弹塑性状态，出现下降段，如上图所 示。因此轴心压杆的屈曲后强度提高时没有意义的。
确定轴心受压构件临界荷载值不简单的原因： (1)理想轴心受压构件在实际结构中并不存在，因此在 理想条件下求出的临界荷载值并不能直接应用于轴 心受压构件的稳定设计。
• （2）轴心受压构件的弹性分析与弹塑性分析差别 • （3）将理论分析结果用于结构轴心受压构件的设
很大。对于某一构件，用弹性方法还是用弹塑性方 法确定其临界荷载取决于构件的具体情况。 计是稳定分析的目的，由于影响因素众多，研究工 作仍不完善，需要做大量的工作。
结构稳定理论
西北农林科技大学
二、 理想轴心受压构件的非弹性弯曲失稳
(inelastic buckling)
理想弹性轴压杆屈曲的适用范围
当σcr>比例极限σp时，欧拉公式
不
再适用。
因为前面推导时用到 M EIy '， ' E为弹性模量，应该是不变的；而 弹塑性阶段时模量将发生变化。
各种支承情况的边界条件为： 铰支： y 0,
y' ' 0 y' 0 y ' ' ' k y ' 0
2
剪力Q＝0， 由前面的微分方程得：
固支： y 0,
自由端： y ' ' 0,
EIy' ' Py M A