横截面上的最大正应力共67页文档
合集下载
第三章 杆件横截面上的应力
z
计算任一点的正应力时，可不考虑M、y的正负，一律以绝
y 对值代入。M为正，梁中性轴下边纤维受拉，中性轴以下部分
均为正的正应力，而中性轴以上部分纤维受压，均为负的正应 力；M为负时，应力正负号则相反。
M
max
M z y max Mz Iz Wz
Wz I z / ymax 抗弯截面模量。
目录
例题3-4 已知E轴所传递的功率P1＝14kW, H轴、 C轴所传递的功率 P2= P3=P1/2。n1=n2=120r/min，z1=36，z3=12；d1=70mm， d 2=50mm, d3=35mm。求:各轴横截面上的最大切应力。 解：1、计算各轴的功率与转速
3
P1=14kW, P2= P3= P1/2=7 kW z1 n3＝n1 ＝360r/min z3
本章重点
杆件基本变形时横截面上应力的计算
第一节 应力、应变极其相互关系
问题的提出
一、正应力、切应力
1. 应力 内力的集度（单位面积上的内力）
F
C
2.一点处的应力 平均应力 令
F4
A
F3
一点处应力
F pm A
F dF p lim A 0 A dA
p
τ
σ
p 垂直于截面的分量σ －－正应力
16 716.2 D2 3 0.046m=46mm 4 6 π 1- 40 10
实心轴
d2＝0.5D2=23 mm M x 16M x max1 40MPa 3 WP1 πd1
2
d1=45 mm
长度相同的情形下，二轴的重量之比即为横截面面积之比：
A1 d12 1 45 10 3 2 ＝ .28 1 2 3 2 A2 D2 1 46 10 1 0.5
横截面上的最大正应力
B max
4 88 Iz
46.1MPa
例8：简支梁AΒιβλιοθήκη ，在Ｃ截面下边缘贴一应变片，测得其应变ε= 6×10-4，材料的弹性 模量 E=200GPa，求载荷P的大小。
P
A
CD
B
40
0.5 m
0.4 m
20
1m
解：C点的应力 C E 200 103 6 104
120MPa
C截面的弯矩 MC C Wz 640 N m
第六章
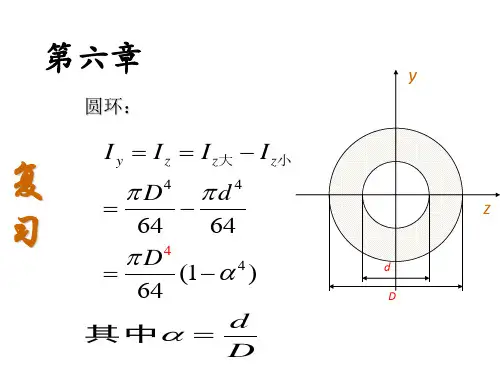
圆环：
复 习
I y I z I z大 I z小
D4 d 4
64 64
D4 (1 4 )
64
其中 d
D
y
z
d D
bh3 I Z 12
d4
I Z 64
WZ
bh2 6
WZ
d 3
32
h
Z
b
d
Z
IZ
(D4
64
d4)
D4
64
(1 4 )
WZ
D3
32
(1 4 )
Z
d D
横截面上的最大正应力：
15 11.25
max
M max Wz
20 103 0.1 0.22
6
30MPa < [ ]
该梁满足强度条件，安全 20
例7：图示铸铁梁，许用拉应力[σ+ ]=30MPa，
许用压应力[σ- ]=60MPa,Ｉz=7.63×10-6m4，
试校核此梁的强度。
9 kN
4 kN
A
C
B
52
D
Cz
1m 1m 1m
例2：两矩形截面梁，尺寸和材料的许用应力
轴向拉伸与压缩时横截面上的应力
解1计算轴力由截面法可求得杆中各横截面上的轴力均为ffnf20knf20kn1212ffafnff图47nb2计算最大正应力图47bba1hha2h0cahh0b251020mm2300mm2则杆件内的最大正应力则杆件内的最大正应力为为maxmax由于整个杆件轴力相同故最大正应力发生在面积较小的横截面上即开槽部分的横截面上如图47c其面积为maxmpa667mpaa300fn10203?负号表示最大正应力为压应力
例 一正中开槽的直杆，承受轴向载荷F =20kN的作用， 如图4-7a所示。已知h = 25mm，h0 = 10mm，b = 20mm。试求 杆内的最大正应力。
1 2
F
1 2
F
解 (1) 计算轴力 由截面法可求得杆中 各横截面上的轴力均为
a)
FN F
b)
图4-7
FN = -F = -20kN
A1
图4-6
由材料的均匀性、连续性假设可以推断出轴力在横截面 上的分布是均匀的，而且都垂直于横截面，故横截面上的正 应力也是均匀分布的，如图4-6c所示。因此，轴向拉伸与压 缩时的横截面上的正应力计算公式为
FN σ= A
σ 式中， 为横截面上的正应力；FN 为横截面上的内力（轴
力）；A 为横截面面积。 正应力的正负号与轴力的正负号一致。即拉应力正， 压应力为负。
h0 h
A2
h
b b
c)
(2)计算最大正应力 图4-7 由于整个杆件轴力相同，故最大正应力发生在面积较小 的横截面上，即开槽部分的横截面上如图4-7c,其面积为
A = (h-h0 )b = (25-10)
则杆件内的最大正应力 σ max 为
×20mm2 =
300mm2
σ max
例 一正中开槽的直杆，承受轴向载荷F =20kN的作用， 如图4-7a所示。已知h = 25mm，h0 = 10mm，b = 20mm。试求 杆内的最大正应力。
1 2
F
1 2
F
解 (1) 计算轴力 由截面法可求得杆中 各横截面上的轴力均为
a)
FN F
b)
图4-7
FN = -F = -20kN
A1
图4-6
由材料的均匀性、连续性假设可以推断出轴力在横截面 上的分布是均匀的，而且都垂直于横截面，故横截面上的正 应力也是均匀分布的，如图4-6c所示。因此，轴向拉伸与压 缩时的横截面上的正应力计算公式为
FN σ= A
σ 式中， 为横截面上的正应力；FN 为横截面上的内力（轴
力）；A 为横截面面积。 正应力的正负号与轴力的正负号一致。即拉应力正， 压应力为负。
h0 h
A2
h
b b
c)
(2)计算最大正应力 图4-7 由于整个杆件轴力相同，故最大正应力发生在面积较小 的横截面上，即开槽部分的横截面上如图4-7c,其面积为
A = (h-h0 )b = (25-10)
则杆件内的最大正应力 σ max 为
×20mm2 =
300mm2
σ max
第八章 弹性杆件横截面上的正应力分析-2
Iz
I z y 2 dA
A
惯性矩
EIz 梁的抗弯刚度
My Iz
将上式代入 E y
工 程 力 学
第 八 章 弹 性 杆 件 横 截 面 上 的 应 力
在横截面上离中性轴最远的各点处，正应力最大。
max
Mymax Iz
令:
Iz Wz ymax
max
F
C
Fa
B D
x
Fs
在CD段内，梁的横截面上 剪力为零，而弯矩为常量，这 种情况称为纯弯曲。 梁在纯弯曲变形时，横截面 上只有与弯矩有关的正应力。
F A C
D
B F
x
M A C
Fa D B
x
工 程 力 学
第 八 章 弹 性 杆 件 横 截 面 上 的 应 力
二、梁在纯弯曲时的正应力
1、变形几何关系
工 程 力 学 aa 变形前的长度等于中性层的长度
第 八 aa O1O2 O1 O2 d 章 弹 纵向线aa变形后的长度为: 性 ' ' a a ( y) d 杆 件 纵向线aa的应变为 横 截 y ( y) d d 面 d 上 即：纯弯曲时横截面上各点的纵向线应变沿截面 的 应 高度呈线性分布。 力
作如下假设： (1) 梁的横截面变形后仍保持为平面，且垂直于变形后 的轴线，即弯曲变形的平面假设。 (2) 纵向纤维间无挤压作用，各纵向纤维均处于单向受拉 或受压状态。
工 程 力 学
第 八 章 弹 性 杆 件 横 截 面 上 的 应 力
☆ 中性层
对称轴
中性层
中性轴
中性层：构件内部既不伸长也不收缩的纤维层。 中性轴：横截面与中性层的交线。
第4章杆件横截面上的正应力分析
3 N BC 4 10 6 N 12.7 10 2 m ABC π 202 106 4
=12.7MPa(拉)
σ AB N AB 3.46 10 6 N 6.4 10 2 6 m AAB 540 10
3
= 6.4MPa(压)
第4章
杆件横截面上的正应力分析
30
y1
Ay A
i
i
200
z y1
30 170 170 2 30 170 (139 ) 12 2
3
85 30 85 y
40.3106 (mm)4 40.3106 m4
第4章
杆件横截面上的正应力分析
(2) 画弯矩图
q =10kN/m
A 2m P=20kN C 3m 20kNm 1m D
§4-2 梁的弯曲正应力
一、概述
第4章
杆件横截面上的正应力分析
一般平面弯曲时，梁的横截面上将有剪力和弯矩两个 内力分量。如果梁的横截面上只有弯矩一个内力分量， 这种平面弯曲称为纯弯曲。此时由于梁的横截面上只 有弯矩，因而便只有垂直于横截面的正应力。
c
c
c
c
第4章
杆件横截面上的正应力分析
在垂直梁轴线的横力作用下，梁横截面 上将同时产生剪力和弯矩。这时，梁的横截面 上不仅有正应力，还有剪应力。这种弯曲称为 横向弯曲。
第4章
杆件横截面上的正应力分析
第4章
杆件横截面上的正应力分析
第4章
杆件横截面上的正应力分析
第4章
杆件横截面上的正应力分析
解：先确定危险截面
故取b=43mm
第4章
杆件横截面上的正应力分析
例 求图示梁的最大拉应力和最大压应力。 q =10kN/m A B P=20kN C 1m D
=12.7MPa(拉)
σ AB N AB 3.46 10 6 N 6.4 10 2 6 m AAB 540 10
3
= 6.4MPa(压)
第4章
杆件横截面上的正应力分析
30
y1
Ay A
i
i
200
z y1
30 170 170 2 30 170 (139 ) 12 2
3
85 30 85 y
40.3106 (mm)4 40.3106 m4
第4章
杆件横截面上的正应力分析
(2) 画弯矩图
q =10kN/m
A 2m P=20kN C 3m 20kNm 1m D
§4-2 梁的弯曲正应力
一、概述
第4章
杆件横截面上的正应力分析
一般平面弯曲时，梁的横截面上将有剪力和弯矩两个 内力分量。如果梁的横截面上只有弯矩一个内力分量， 这种平面弯曲称为纯弯曲。此时由于梁的横截面上只 有弯矩，因而便只有垂直于横截面的正应力。
c
c
c
c
第4章
杆件横截面上的正应力分析
在垂直梁轴线的横力作用下，梁横截面 上将同时产生剪力和弯矩。这时，梁的横截面 上不仅有正应力，还有剪应力。这种弯曲称为 横向弯曲。
第4章
杆件横截面上的正应力分析
第4章
杆件横截面上的正应力分析
第4章
杆件横截面上的正应力分析
第4章
杆件横截面上的正应力分析
解：先确定危险截面
故取b=43mm
第4章
杆件横截面上的正应力分析
例 求图示梁的最大拉应力和最大压应力。 q =10kN/m A B P=20kN C 1m D
p51-梁弯曲时横截面上的正应力(精)
My max M max Iz Wz 式中，Wz=Iz /ymax ——横截面对中性轴 z 的弯曲截面系数。它只与截面的形 状及尺寸有关，是衡量截面抗弯能力的一个几何量，单位为mm3或m3。
第6章 杆件的应力与强度\梁弯曲时的应力与强度\梁弯曲时横截面上的正应力
对于矩形、圆形及圆环形等常见简单截面的惯性矩和弯曲截面系数
第6章 杆件的应力与强度\梁弯曲时的应力与强度\梁弯曲时横截面上的正应力
如图 a 所示，取一具有纵向对称面的梁，例如矩形截面梁，在其侧面 画两条代表两个横截面的横向线 m m 和 nn，再在两横向线间靠近梁顶面和 底面处画两条代表纵向纤维的纵向线 a a 和 b b ，在梁的两端施加外力偶 Me ， 使梁发生纯弯曲。此时可观察到下列现象：
MC
(b) 横截面
Fl 40 2 20 kN m 4 4
2) 截面对中性轴的惯性矩为
(c) M图
bh3 0.15m 0.33 m3 Iz 3.375 104 m4 12 12
第6章 杆件的应力与强度\梁弯曲时的应力与强度\梁弯曲时横截面上的正应力
3) 计算横截面C上a、b、c、d 四点处的正应力
MC ya 20 103 N m 0.15m 6 a 8 . 89 10 Pa 8.89MPa（拉应力） -4 4 IZ 3.375 10 m
b 0
c
MC yC Iz 20 103 N m 0.075m 6 （压应力） 4 . 44 10 Pa 4.44MPa -4 4 3.375 10 m
d a 8.89MPa（压应力）
▲ a、d 两点处的正应力也可以用
力也比较大，这样的点称为危险点。
拉压杆横截面上的正应力
∑ X = 0 , N 2 − N 1 cos 45
N1 = 2[P]
o
σ
2
=
N2 [P] = A A
=0
N1 45o C [P]
N2 = [ P ]
σ
1
[P]=Min{15,14.14} =14.14kN x
=
N1 = A
2[ P ] A
N2
A
α B
α C
σ max ≤ [ σ ]
N 4N = σ max = A πd 2 4N 4 × 266 × 10 3 d≥ = 6 = 53 .2 mm π[σ ] 3.14 × 120 × 10
P
支架 1、2杆的横截面积均为100mm2,许用拉应力[σ+]=200MPa, 许用压应力[σ-]=150MPa。计算许可荷载[P]。 A
max
为构件设计截面。
A
≤ [σ ] N max σ max = A N max ∴ A ≥ [σ ]
max
σ
∴ N
≤ [σ ] A
作动筒 校核活塞杆的 强度。 p Pmax=300kN, [σ]=300MPa, 退刀槽处的直径 d=44mm.
P
退刀槽
P
P
300 × 103 N max Pmax 解∶ = 197 MPa = 2 = σ max = 2 −6 π × 44 × 10 πd A 4 4 [ σ ] = 300MPa
∴ σ max ≤ [ σ ]
活塞杆符合拉伸的强度要求。
吊环 α=20o,P=500kN,[σ]=120MPa,求杆AB和AC的直径d. y 解∶ P ∑ Y = 0 P − 2 N cosα = 0
P
P N = 2 cos α 500 = = 266kN N 2 cos 20o
N1 = 2[P]
o
σ
2
=
N2 [P] = A A
=0
N1 45o C [P]
N2 = [ P ]
σ
1
[P]=Min{15,14.14} =14.14kN x
=
N1 = A
2[ P ] A
N2
A
α B
α C
σ max ≤ [ σ ]
N 4N = σ max = A πd 2 4N 4 × 266 × 10 3 d≥ = 6 = 53 .2 mm π[σ ] 3.14 × 120 × 10
P
支架 1、2杆的横截面积均为100mm2,许用拉应力[σ+]=200MPa, 许用压应力[σ-]=150MPa。计算许可荷载[P]。 A
max
为构件设计截面。
A
≤ [σ ] N max σ max = A N max ∴ A ≥ [σ ]
max
σ
∴ N
≤ [σ ] A
作动筒 校核活塞杆的 强度。 p Pmax=300kN, [σ]=300MPa, 退刀槽处的直径 d=44mm.
P
退刀槽
P
P
300 × 103 N max Pmax 解∶ = 197 MPa = 2 = σ max = 2 −6 π × 44 × 10 πd A 4 4 [ σ ] = 300MPa
∴ σ max ≤ [ σ ]
活塞杆符合拉伸的强度要求。
吊环 α=20o,P=500kN,[σ]=120MPa,求杆AB和AC的直径d. y 解∶ P ∑ Y = 0 P − 2 N cosα = 0
P
P N = 2 cos α 500 = = 266kN N 2 cos 20o
工程力学 第8章 杆件横截面上的正应力分析
2 A 2 A A
展开后，并利用静矩、惯性矩和惯性积的定义，得
I z1 = I z + 2aS z + a 2 A I y1 z1 = I y z + aS y + bSz + abA I y1 = I y + 2bS y + b 2 A
(8－17)
如果 y、z 轴通过图形形心，则上述各式中的 Sy＝Sz ＝0，于是，由上式得到
S z = AyC S y = Az C
(8－2)
或
ydA A S y ∫AzdA zC = = A A yC = Sz = A
∫
A
(8－3)
这就是图形形心坐标与静矩之间的关系。 根据上述关于静矩的定义以及静矩与形心之间的关系可以看出：
n 静矩与坐标轴有关，同一平面图形对于不同的坐标轴有不同的静矩。对 某些坐标轴静矩为正；对另外一些坐标轴静矩则可能为负；对于通过形心的坐标 轴，图形对其静矩等于零。 n 如果已经计算出静矩，就可以确定形心的位置；反之，如果已知形心在 某一坐标系中的位置，则可计算图形对于这一坐标系中坐标轴的静矩。
I P = ∫ r 2 dA,
A
(8－7)
为图形对于点 O 的截面二次极矩 或极惯性矩 （second polar moment of an area） 。 定义积分
I yz = ∫A yzd A,
பைடு நூலகம்
(8－8)
为图形对于通过点 O 的一对坐标轴 y、z 的惯性积 (product of inertia) 。 定义
(8－4)
再利用式（8－3） ，即可得组合图形的形心坐标：
S yC = z = A
∑Ay
展开后，并利用静矩、惯性矩和惯性积的定义，得
I z1 = I z + 2aS z + a 2 A I y1 z1 = I y z + aS y + bSz + abA I y1 = I y + 2bS y + b 2 A
(8－17)
如果 y、z 轴通过图形形心，则上述各式中的 Sy＝Sz ＝0，于是，由上式得到
S z = AyC S y = Az C
(8－2)
或
ydA A S y ∫AzdA zC = = A A yC = Sz = A
∫
A
(8－3)
这就是图形形心坐标与静矩之间的关系。 根据上述关于静矩的定义以及静矩与形心之间的关系可以看出：
n 静矩与坐标轴有关，同一平面图形对于不同的坐标轴有不同的静矩。对 某些坐标轴静矩为正；对另外一些坐标轴静矩则可能为负；对于通过形心的坐标 轴，图形对其静矩等于零。 n 如果已经计算出静矩，就可以确定形心的位置；反之，如果已知形心在 某一坐标系中的位置，则可计算图形对于这一坐标系中坐标轴的静矩。
I P = ∫ r 2 dA,
A
(8－7)
为图形对于点 O 的截面二次极矩 或极惯性矩 （second polar moment of an area） 。 定义积分
I yz = ∫A yzd A,
பைடு நூலகம்
(8－8)
为图形对于通过点 O 的一对坐标轴 y、z 的惯性积 (product of inertia) 。 定义
(8－4)
再利用式（8－3） ，即可得组合图形的形心坐标：
S yC = z = A
∑Ay
弹性杆件横截面上的正应力分析 PPT
32
;
e、圆环截面的极惯性矩
IP
d 4
32
(1 4 );
d; D
4、形心主惯性矩 图形对形心主轴的惯性矩称形心主惯性矩,
与应力分析相关的截面图形几何性质
例4-1、求图中剖面线部分的惯性矩惯性矩 Iy ;Iz ;
解:由负面积法, Iz=H b³/ 12 – h b³/ 12 = b³( H - h) / 12; Iy = b H³/ 12 – b h³/ 12 = b( H³- h³) /12;
4、常见形体的惯性矩、极惯性矩 a、矩形截面的惯性矩
IY
hb3 ; 12
IZ
bh3 ; 12
b、圆形截面的惯性矩
d 4
I Y I Z 64 ;
y
z
h
b
y
z
d
C、圆环截面的惯性矩
Iy
Iz
D 4
64
(1 4 );
d; D
y
zபைடு நூலகம்
dD
与应力分析相关的截面图形几何性质
d、圆形截面的极惯性矩
IP
d 4
192103 m3;
FN 4.8 103 N ; M z 4.8 103 0.04 192(Nm); M y 4.8 103 0.025 120(Nm);
弯矩和轴力同时作用时杆件横截面上的正应力
2、判断最大应力作用位置:
在内力作用下A、E 分别是最大压应
力和拉应力作用点 3、计算ABDE各点的应力,作图:
x
M z y1 10103 0.452 0.03 0.02 0.033 42.2106 Pa
Iz
8
4
12
M
-
为拉伸应力
;
e、圆环截面的极惯性矩
IP
d 4
32
(1 4 );
d; D
4、形心主惯性矩 图形对形心主轴的惯性矩称形心主惯性矩,
与应力分析相关的截面图形几何性质
例4-1、求图中剖面线部分的惯性矩惯性矩 Iy ;Iz ;
解:由负面积法, Iz=H b³/ 12 – h b³/ 12 = b³( H - h) / 12; Iy = b H³/ 12 – b h³/ 12 = b( H³- h³) /12;
4、常见形体的惯性矩、极惯性矩 a、矩形截面的惯性矩
IY
hb3 ; 12
IZ
bh3 ; 12
b、圆形截面的惯性矩
d 4
I Y I Z 64 ;
y
z
h
b
y
z
d
C、圆环截面的惯性矩
Iy
Iz
D 4
64
(1 4 );
d; D
y
zபைடு நூலகம்
dD
与应力分析相关的截面图形几何性质
d、圆形截面的极惯性矩
IP
d 4
192103 m3;
FN 4.8 103 N ; M z 4.8 103 0.04 192(Nm); M y 4.8 103 0.025 120(Nm);
弯矩和轴力同时作用时杆件横截面上的正应力
2、判断最大应力作用位置:
在内力作用下A、E 分别是最大压应
力和拉应力作用点 3、计算ABDE各点的应力,作图:
x
M z y1 10103 0.452 0.03 0.02 0.033 42.2106 Pa
Iz
8
4
12
M
-
为拉伸应力
轴向拉伸与压缩—轴向拉(压)杆横截面上的正应力(工程力学课件)
• 与截面垂直的应力称为正应力，用σ表示。 • 与截面相切的应力称为剪应力，用τ表示。
应力单位：帕（Pa）、千帕（kPa）、兆帕 （MPa）、吉帕（GPa）。
➢ 2.轴向拉（压）杆横截面上的正应力 平面假设：变形前原为平面的横截面，变形后仍保持为平面，
且垂直于杆轴线。
结论：轴向拉（压）杆横截面上只有正应力，且均匀分布。
第一节 轴向拉（压）杆的内力与轴力图 第二节 轴向拉（压）杆横截面上的正应力 第三节 轴向拉（压）杆的强度计算 第四节 轴向拉（压）杆的变形计算 第五节 材料在拉伸和压缩时的力学性能
➢ 1.应力的概念
应力——内力在单位面积上的分布集度。反映了内力在横截面上分布 的密集程度。
1Pa 1N / m2 1kPa 103 Pa 1Mpa 1N / mm2 106 Mpa 1Gpa 109 Pa
X 0 N BA sin 30 P 0
Y 0 N BA cos 30 N BC 0
P 15 NBA sin 30 0.5 30kN
N BC N BA cos 30 30 0.866 26kN
（2）计算各杆的应力
AB
N BA ABA
4 N BA
d 2
4 30 103 3.14 162
149.3MPa
BC
N BC ABC
26 10 2
103 10 2
2.6MPa
结论：拉杆横截面上产生的应力为均匀分布的正应力。 轴向拉（压）杆横截面上的正应力计算公式为：
N
A
N——横截面上的轴力； A——横截面面积。
σ 的符号：正号表示拉应力；Байду номын сангаас号表示压应力。
例题3 有一根钢丝绳，其截面积为0.725 cm2，受到3000N 的拉力，试求这根钢丝绳的应力是多少？
第八章 弹性杆件横截面上的正应力分析-2
64
C截面：
Iz
64
D 4 636 10-9 m4
3、计算最大应力
B截面： ( ) M z ymax 82.5MPa max B
Iz
C截面： ( max )c
M z ymax Iz
55.2MPa
轴中的最大正应力发生在Ｃ截面处（即实心部分）。
工 程 力 学
第 八 章 弹 性 杆 件 横 截 面 上 的 应 力
P1
c z x
P1 P2
c y
z
x
c y
z
P2
y
工 程 力 学
第 八 章 弹 性 杆 件 横 截 面 上 的 应 力
P1
c x z
P1 P2
c
y z x c y
z
P2
y
x
这样，可以分别计算每一种基本变形各自引起 的内力、应力、应变和位移，然后把所得的结果进 行叠加，便是构件在组合变形下的内力、应力、应 变和位移。这就是叠加原理。 条件： 要求内力、应力、应变和位移等与外力呈线性关系
F
C
Fa
B D
x
Fs
在CD段内，梁的横截面上 剪力为零，而弯矩为常量，这 种情况称为纯弯曲。 梁在纯弯曲变形时，横截面 上只有与弯矩有关的正应力。
F A C
D
B F
x
M A C
Fa D B
x
工 程 力 学
第 八 章 弹 性 杆 件 横 截 面 上 的 应 力
二、梁在纯弯曲时的正应力
1、变形几何关系
工 程 力 学
(3)求最大正应力 截面B：上边缘有最大拉应力， 第 下边缘有最大压应力
八 章 弹 性 杆 件 横 截 面 上 的 应 力
C截面：
Iz
64
D 4 636 10-9 m4
3、计算最大应力
B截面： ( ) M z ymax 82.5MPa max B
Iz
C截面： ( max )c
M z ymax Iz
55.2MPa
轴中的最大正应力发生在Ｃ截面处（即实心部分）。
工 程 力 学
第 八 章 弹 性 杆 件 横 截 面 上 的 应 力
P1
c z x
P1 P2
c y
z
x
c y
z
P2
y
工 程 力 学
第 八 章 弹 性 杆 件 横 截 面 上 的 应 力
P1
c x z
P1 P2
c
y z x c y
z
P2
y
x
这样，可以分别计算每一种基本变形各自引起 的内力、应力、应变和位移，然后把所得的结果进 行叠加，便是构件在组合变形下的内力、应力、应 变和位移。这就是叠加原理。 条件： 要求内力、应力、应变和位移等与外力呈线性关系
F
C
Fa
B D
x
Fs
在CD段内，梁的横截面上 剪力为零，而弯矩为常量，这 种情况称为纯弯曲。 梁在纯弯曲变形时，横截面 上只有与弯矩有关的正应力。
F A C
D
B F
x
M A C
Fa D B
x
工 程 力 学
第 八 章 弹 性 杆 件 横 截 面 上 的 应 力
二、梁在纯弯曲时的正应力
1、变形几何关系
工 程 力 学
(3)求最大正应力 截面B：上边缘有最大拉应力， 第 下边缘有最大压应力
八 章 弹 性 杆 件 横 截 面 上 的 应 力
梁横截面上的应力共73页文档
D4 14
W z
64 D
2
D3 14
32
•
轧制型钢（工字钢、槽钢等）的Iz 、
W值可从型钢表中查得。
横力弯曲作用为：
一 般 截 面 上 下 不 对 称 m a x M m a Ix z ym a x
z o y
一 般 截 面 上 下 对 称 m a xM W m z a x
z
y
例1：两矩形截面梁，尺寸和材料的许用应力 均相等，但放置如图(a)、(b)。按弯曲正应力强 度条件确定两者许可载荷之比 P1／P2＝？
此外还假设：梁的各纵向纤维 （上层的）互不挤压，（下层的）互 不牵拉，即梁的纵截面上无正应力作 用。
根据上述假设，梁弯曲后，其纵
向层一部分产生伸长变形，另一部分 则产生缩短变形，二者交界处存在既 不伸长也不缩短的一层，这一层称为 中性层。如图所示，中性层与横截面 的交线为截面的中性轴。因此横截面 绕着中性轴转过一个角度。
1）梁的校核强度
max
Mmaxymax Iz
[]
max
Mmax Wz
[]
2）设计梁的（最小）截面尺寸 3）确定梁的（最大）许用外载荷 [ F ] （难点）。
解题的基本过程： 1，分析题意是等直梁，还是变截面梁，是塑
性材料, 还是脆性材料。 2，是三类问题中的那一类问题。 3，先求梁或结构的反力 4，求作每一梁的内力图（这里是弯矩图）
45、法律的制定是为了保证每一个人 自由发 挥自己 的才能 ，而不 是为了 束缚他 的才能 。—— 罗伯斯 庇尔
§7-2 梁横截面上的应力
7.2.1 纯弯曲梁横截 面上的正应力
观察梁受力时的表面变形特点
提出合理假设(平面假设) 几何关系(变形协调关系) ：推断梁内部变形
纯弯曲时梁横截面上的正应力
截面几何参数的定义，可得
E E Sz N Aσ dA A ydA o ρ ρ
(g)
Байду номын сангаас
E I yz E o M y A zσ dA A zydA ρ ρ E E Iz 2 M M z A yσ dA A y dA ρ ρ
(h)
(I)
E E Sz N Aσ dA A ydA o ρ ρ
o2
（ f）
(c)
将梁的轴线取为 x 轴，横截
面的对称轴取为 y 轴，中性 轴取为 z 轴。
C
d
o1
Z O x
dx
o2
(d)
y
(c)
在横截面上取距中性轴为 y 处
的纵向线 AB。
C
d
作 o2B1 与 o1 A 平行（图5-1 c）
为中性层上的纵向线段o1o2
变弯后的曲率半径
A
A B1 为变形前 AB 的长度
o1
y
dx
o2
B1
B
B1B为 A B1 的伸长量
AB1
(c)
y (d θ ) AB1 B1 B ε dx O1 O2 AB1
为 A 点的纵向线应变。
C
d
O1 O2 dx 为中性层上纵向线段的
长度 A
o1
y
dx
o2
B1
B
中性层的曲率为
1 dθ ρ dx
(c)
y (d θ ) AB1 B1 B ε dx O1 O2 AB1
O
m Z
dA y
因此，只可能组成三个内力分量
N Aσ dA
0
(d) (e) (f)
E E Sz N Aσ dA A ydA o ρ ρ
(g)
Байду номын сангаас
E I yz E o M y A zσ dA A zydA ρ ρ E E Iz 2 M M z A yσ dA A y dA ρ ρ
(h)
(I)
E E Sz N Aσ dA A ydA o ρ ρ
o2
（ f）
(c)
将梁的轴线取为 x 轴，横截
面的对称轴取为 y 轴，中性 轴取为 z 轴。
C
d
o1
Z O x
dx
o2
(d)
y
(c)
在横截面上取距中性轴为 y 处
的纵向线 AB。
C
d
作 o2B1 与 o1 A 平行（图5-1 c）
为中性层上的纵向线段o1o2
变弯后的曲率半径
A
A B1 为变形前 AB 的长度
o1
y
dx
o2
B1
B
B1B为 A B1 的伸长量
AB1
(c)
y (d θ ) AB1 B1 B ε dx O1 O2 AB1
为 A 点的纵向线应变。
C
d
O1 O2 dx 为中性层上纵向线段的
长度 A
o1
y
dx
o2
B1
B
中性层的曲率为
1 dθ ρ dx
(c)
y (d θ ) AB1 B1 B ε dx O1 O2 AB1
O
m Z
dA y
因此，只可能组成三个内力分量
N Aσ dA
0
(d) (e) (f)
《材料力学》课件4-4梁横截面上的正应力.梁的正应力条件
kN m
如果T截面倒置会如何???
例题 4.25
铸铁制作的悬臂梁，尺寸及受力如图示，图中F＝20kN。梁 的截面为T字形，形心坐标yc=96.4mm。已知材料的拉伸许用应 力和压缩许用应力分别为[σ]+＝40MPa， [σ]－＝100MPa。试 校核梁的强度是否安全。 y
F
B
A
C
B
A
50
150 96.4
150kN吊车
B
200kN吊车
1.确定F加在辅助梁的位置
A
C
辅助梁
M M
A
0 0
FA
F
l
x
FB
B
FP l x F F B B l F l x 0 l F Fx FAl 0 FAx l
令: FA Fx 200kN l
FB
F l x l
( A) max (a ) max (b) max (c)； ( B ) max (a ) max (b) max (c)； (C ) max (a ) max (b) max (c)； ( D) max (a ) max (b) max (c)。
m
n o
dA
z
y
y:到中性轴的距离
o
m
dx
n
z
IZ:截面对中性轴的惯性矩
M M
y
Mz Mzy max Wz Iz
max
M x Wz
中性轴
例题 4.20
A
l 2
FL
长为l的矩形截面悬臂梁，在自由端作用一集中力F， 已知b＝120mm，h＝180mm、l＝2m，F＝1.6kN， 试求B截面上a、b、c各点的正应力。 h 6 a F B h b C l 2 h2
第四章 杆件横截面上的应力
0
b bh y (h y ) dy h 6
例7：求半径为r的半圆对底边z轴的
静矩，并确定其形心坐标。 y
2 r y
2 2
解：取平行于z轴的狭长条作为面积元素
dy y
C
dA 2 r 2 y 2 dy
z
2
o
S z y dA y 2 r y dy
p d t
p
200 5
解：
m FN m
y
d
R
n
n FN
圆环在内压力作用下要均匀 涨大，故在包括圆环轴线的 任何径向截面上，作用有相 同的法向拉力FN
此半环上的内压力沿y方向的合力R为： b· R= л (p· d· sin = p· d 壁厚远小于内径，可 ∫ 0 b· d/2)· 近似认为m-m、n-n FN =R/2= p· d/2 b· 上各点处正应力相等。 当t d/20时，这种近 = FN /A= p· d/(2· t)= p· t) 似足够精确。 b· b· d/(2· =2 · 6 · /(2 · 10 0.2 0.005 )Pa=40MPa
起吊重物Q=15kN，求AB的最大工作应力。
B
0.8m
C
1.9m
A
Q
解：1）分析AB受力、并求其内力:
当Q移到A点时AB杆受力最大，取结点A研究 FN 0: F y
AB
N FNAB sinα Q 0 Q N FNAB sin 0.8 sin
2
B
FN
AC
A
Q
FN AB
0.8 1.9 15 103 38.7 103 ( N ) 0.388
请思考:
纯弯曲梁横截面上的正应力课件
正应力的定义
正应力指的是在受力物体的单位面积 上所承受的垂直作用力，也称为法向 应力。
正应力的计算
正应力的大小可以通过公式σ=F/A来 计算，其中σ为正应力，F为作用力， A为受力物体的横截面积。
横截面上的正应力分布
均匀分布
在纯弯曲梁的横截面上，正应力呈现出均匀分布的特点。即在整个析法
通过数学公式推导，求解梁横截面上的应力分布和最大应力 值。
有限元法
利用有限元分析软件，建立梁的有限元模型，通过计算求解 梁横截面上的应力分布和最大应力值。
05
纯弯曲梁的实例分析
实例一：简单梁的弯曲分析
简单梁是指长度远大于高度和宽 度的梁，其弯曲变形可以简化为
纯弯曲变形。
纯弯曲梁的受力分析
01
02
03
受力特点
纯弯曲梁在弯曲过程中， 只受到弯矩的作用，没有 剪力和扭矩。
弯矩分析
弯矩是使梁产生弯曲变形 的力矩，其大小取决于外 力的大小和作用点位置。
应力分布
由于弯矩的作用，梁的横 截面上会产生正应力和剪 应力，其中正应力是本节 重点讨论的内容。
纯弯曲梁的位移分析
位移特点
横截面上的正应力分布不再呈现对称性，需要采用更精确的分析方法进行计算。
实例三：实际工程中的纯弯曲梁分析
在实际工程中，纯弯曲梁的应 用非常广泛，如桥梁、建筑结 构等。
对于实际工程中的纯弯曲梁， 需要考虑材料特性、载荷大小 和分布、支撑条件等因素对正 应力的影响。
实际工程中的纯弯曲梁分析需 要采用有限元分析、实验测试 等方法进行验证和优化。
脆性断裂失效
当梁受到的应力超过材料的强度极限 时，会发生脆性断裂失效，导致梁断 裂。
强度条件的建立
正应力指的是在受力物体的单位面积 上所承受的垂直作用力，也称为法向 应力。
正应力的计算
正应力的大小可以通过公式σ=F/A来 计算，其中σ为正应力，F为作用力， A为受力物体的横截面积。
横截面上的正应力分布
均匀分布
在纯弯曲梁的横截面上，正应力呈现出均匀分布的特点。即在整个析法
通过数学公式推导，求解梁横截面上的应力分布和最大应力 值。
有限元法
利用有限元分析软件，建立梁的有限元模型，通过计算求解 梁横截面上的应力分布和最大应力值。
05
纯弯曲梁的实例分析
实例一：简单梁的弯曲分析
简单梁是指长度远大于高度和宽 度的梁，其弯曲变形可以简化为
纯弯曲变形。
纯弯曲梁的受力分析
01
02
03
受力特点
纯弯曲梁在弯曲过程中， 只受到弯矩的作用，没有 剪力和扭矩。
弯矩分析
弯矩是使梁产生弯曲变形 的力矩，其大小取决于外 力的大小和作用点位置。
应力分布
由于弯矩的作用，梁的横 截面上会产生正应力和剪 应力，其中正应力是本节 重点讨论的内容。
纯弯曲梁的位移分析
位移特点
横截面上的正应力分布不再呈现对称性，需要采用更精确的分析方法进行计算。
实例三：实际工程中的纯弯曲梁分析
在实际工程中，纯弯曲梁的应 用非常广泛，如桥梁、建筑结 构等。
对于实际工程中的纯弯曲梁， 需要考虑材料特性、载荷大小 和分布、支撑条件等因素对正 应力的影响。
实际工程中的纯弯曲梁分析需 要采用有限元分析、实验测试 等方法进行验证和优化。
脆性断裂失效
当梁受到的应力超过材料的强度极限 时，会发生脆性断裂失效，导致梁断 裂。
强度条件的建立