自动控制原理实验一控制系统的阶跃响应.
自动控制原理实验一

KTδ(t)+K
实测:μo(t)=
+
e-t/R3C
Ro=
100K R2=
100K
C=1uF
R3=
10K
R1=
100K
R1=
200K
典型
环节
传递函数参数与模拟电路参数
关 系
单位阶跃响应
理想阶跃响应曲线
实测阶跃响应曲线
PID
KP=
TI=Ro C1
TD=
理想:μo(t)= TDδ(t)+Kp+
答:传递函数的相角始终大于零,a>1。
3.你能解释校正后系统的瞬态响应变快的原因吗?
答:由于实际控制系统具有惯性、摩擦、阻尼等原因。
表3-1
参数
项目
Mp(%)
Ts(s)
阶 跃 响 应 曲 线
未校正
0.6
4
校正后
0.125
0.42
实验四 控制系统的频率特性
一、被测系统的方块图及原理:
图4—1 被测系统方块图
关 系
单位阶跃响应
理想阶跃响应曲线
实测阶跃响应曲线
惯性
K=
T=R1C
μo(t)=
K(1-e-t/T)
R1=
250K
Ro=
250K
C=
1μF
C=
2μF
I
T=RoC
μo(t)=
Ro=
200K
C=
1μF
C=
2μF
PI
K=
T=RoC
μo(t)=K+
R1=
100K
Ro=
200K
C=
自动控制原理实验实验指导书

自动控制原理实验目录实验一二阶系统阶跃响应(验证性实验) (1)实验三控制系统的稳定性分析(验证性实验) (9)实验三系统稳态误差分析(综合性实验) (15)预备实验典型环节及其阶跃响应一、实验目的1.学习构成典型环节的模拟电路,了解电路参数对环节特性的影响。
2.学习典型环节阶跃响应测量方法,并学会由阶跃响应曲线计算典型环节传递函数。
二、实验内容搭建下述典型环节的模拟电路,并测量其阶跃响应。
1.比例(P)环节的模拟电路及其传递函数示于图1-1。
2.惯性(T)环节的模拟电路及其传递函数示于图1-2。
3.积分(I)环节的模拟电路及其传递函数示于图1-3。
4. 比例积分(PI)环节的模拟电路及其传递函数示于图1-4。
5.比例微分(PD)环节的模拟电路及其传递函数示于图1-5。
6.比例积分微分(PID)环节的模拟电路及其传递函数示于图1-6。
三、实验报告1.画出惯性环节、积分环节、比例积分环节、比例微分环节、比例积分微分环节的模拟电路图,用坐标纸画出所记录的各环节的阶跃响应曲线。
2.由阶跃响应曲线计算出惯性环节、积分环节的传递函数,并与由模拟电路计算的结果相比较。
附1:预备实验典型环节及其阶跃响应效果参考图比例环节阶跃响应惯性环节阶跃响应积分环节阶跃响应比例积分环节阶跃响应比例微分环节阶跃响应比例积分微分环节阶跃响应附2:由模拟电路推导传递函数的参考方法1. 惯性环节令输入信号为U 1(s) 输出信号为U 2(s) 根据模电中虚短和虚断的概念列出公式:整理得进一步简化可以得到如果令R 2/R 1=K ,R 2C=T ,则系统的传递函数可写成下面的形式:()1KG s TS =-+当输入r(t)为单位脉冲函数时 则有输入U 1(s)=1输出U 2(s)=G(s)U 1(s)= 1KTS-+由拉氏反变换可得到单位脉冲响应如下:/(),0t TK k t e t T-=-≥ 当输入r(t)为单位阶跃函数时 则有输入U 1(s)=1/s输出U 2(s)=G(s)U 1(s)= 11K TS s-+由拉氏反变换可得到单位阶跃响应如下:/()(1),0t T h t K e t -=--≥当输入r(t)为单位斜坡函数时 则有输入U 1(s)=21s输出U 2(s)=G(s)U 1(s)=2323R R C T R R =+2Cs12Cs-(s)U R10-(s)U 21R R +-=12212)Cs (Cs 1(s)U (s)U )(G R R R s +-==12212)Cs 1((s)U (s)U )(G R R R s +-==由拉氏反变换可得到单位斜坡响应如下:/()(1),0t T c t Kt KT e t -=--≥2. 比例微分环节令输入信号为U 1(s) 输出信号为U 2(s) 根据模电中虚短和虚断的概念列出公式:(s)(s)(s)(s)(s)U100-U U 0U 2=1R1R23(4)CSU R R '''---=++由前一个等式得到 ()1()2/1U s U s R R '=- 带入方程组中消去()U s '可得1()1()2/11()2/12()1134U s U s R R U s R R U s R R R CS+=--+由于14R C〈〈,则可将R4忽略,则可将两边化简得到传递函数如下: 2()23232323()(1)1()11123U s R R R R R R R R G s CS CS U s R R R R R ++==--=-++如果令K=231R R R +, T=2323R R C R R +,则系统的传递函数可写成下面的形式:()(1)G s K TS =-+当输入r(t)为单位脉冲函数时,单位脉冲响应不稳定,讨论起来无意义 当输入r(t)为单位阶跃函数时 则有输入U 1(s)=1/s输出U 2(s)=G(s)U 1(s)=(1)K TS S-+由拉氏反变换可得到单位阶跃响应如下:()(),0h t KT t K t δ=+≥当输入r(t)为单位斜坡函数时 则有输入U 1(s)=21s输出U 2(s)=G(s)U 1(s)=2(1)K TS S -+由拉氏反变换可得到单位斜坡响应如下:(),0c t Kt KT t =+≥实验一 二阶系统阶跃响应(验证性实验)一、实验目的研究二阶系统的两个重要参数阻尼比ξ和无阻尼自然频率n ω对系统动态性能的影响。
自动控制原理实验报告 (1)

实验1 控制系统典型环节的模拟实验(一)实验目的:1.掌握控制系统中各典型环节的电路模拟及其参数的测定方法。
2.测量典型环节的阶跃响应曲线,了解参数变化对环节输出性能的影响。
实验原理:控制系统模拟实验采用复合网络法来模拟各种典型环节,即利用运算放大器不同的输入网络和反馈网络模拟各种典型环节,然后按照给定系统的结构图将这些模拟环节连接起来,便得到了相应的模拟系统。
再将输入信号加到模拟系统的输入端,并利用计算机等测量仪器,测量系统的输出,便可得到系统的动态响应曲线及性能指标。
实验内容及步骤实验内容:观测比例、惯性和积分环节的阶跃响应曲线。
实验步骤:分别按比例,惯性和积分实验电路原理图连线,完成相关参数设置,运行。
①按各典型环节的模拟电路图将线接好(先接比例)。
(PID先不接)②将模拟电路输入端(U i)与阶跃信号的输出端Y相连接;模拟电路的输出端(Uo)接至示波器。
③按下按钮(或松开按钮)SP时,用示波器观测输出端的实际响应曲线Uo(t),且将结果记下。
改变比例参数,重新观测结果。
④同理得积分和惯性环节的实际响应曲线,它们的理想曲线和实际响应曲线。
实验数据实验二控制系统典型环节的模拟实验(二)实验目的1.掌握控制系统中各典型环节的电路模拟及其参数的测定方法。
2.测量典型环节的阶跃响应曲线,了解参数变化对环节输出性能的影响。
实验仪器1.自动控制系统实验箱一台2.计算机一台实验原理控制系统模拟实验采用复合网络法来模拟各种典型环节,即利用运算放大器不同的输入网络和反馈网络模拟各种典型环节,然后按照给定系统的结构图将这些模拟环节连接起来,便得到了相应的模拟系统。
再将输入信号加到模拟系统的输入端,并利用计算机等测量仪器,测量系统的输出,便可得到系统的动态响应曲线及性能指标。
实验内容及步骤内容:观测PI,PD和PID环节的阶跃响应曲线。
步骤:分别按PI,PD和PID实验电路原理图连线,完成相关参数设置,运行①按各典型环节的模拟电路图将线接好。
自动控制原理1实验指导书

《自动控制原理Ⅰ》实验指导书2013年9月修订实验一 典型环节及其阶跃响应一. 实验目的1.学习构成典型环节的模拟电路。
2.熟悉各种典型环节的阶跃响应曲线,了解参数变化对典型环节动态特性的影响。
3.学会由阶跃响应曲线计算典型环节的传递函数。
4.掌握仿真分析软件multisim的使用。
二. 物理模拟说明用电子线性运算放大器和各种反馈电路能够模拟线性系统典型环节。
同时,模拟典型环节是有条件的,即是将运算放大器视为满足以下条件的理想放大器:(1)输入阻抗为∞,进入运算放大器的电流为零,同时输出阻抗为零;(2)电压增益为∞;(3)通频带为∞;(4)输入与输出间呈线性特性.可是,实际运算放大器毕竟不是理想的;电子元件和电路仍然有惯性(尽管非常小)其通频带有限,并非达到∞,输入输出功率也是有限的;一般的运算放大器,在开环使用时,其通频带仅为10-100Hz,当将其接成K=1的比例器,其通频带也不过MHz左右。
所以,以线性运算放大器和各种反馈电路去模拟系统的各种线性和非线环节也不是无条件的,它仍然是在一定条件下,在一定程度上模拟出线性典型环节的特性,超出条件的范围和要求过份精确都是办不到的。
因此,需要说明以下几点事项:(1)用实际的运算放大器模拟线性系统各种典型环节都是有条件的近似关系,不可能得到理想化典型环节的特性。
其主要原因是:1实际运算放大器输出幅值受其电源所限,根本不可能达到∞,此即非线性影响;2实际运算放大器不是无惯性的。
尽管惯性很小,但通频带不会达到∞。
(2)实际运算放大器输出幅值受限的非线性因素对所有各种模拟环节都有影响,但情况迥异。
对比例环节、惯性环节、积分环节、比例积分环节和振荡环节,只要控制了输入量的大小或是输入量施加的时间长短(对于积分或比例积分环节),不使其输出在工作期间内达到最高饱和度,则非线性因素对上述环节特性的影响可以避免;但是非线性因素对模拟比例微分环节和微分环节的影响却无法避免。
《自动控制》一二阶典型环节阶跃响应实验分析报告
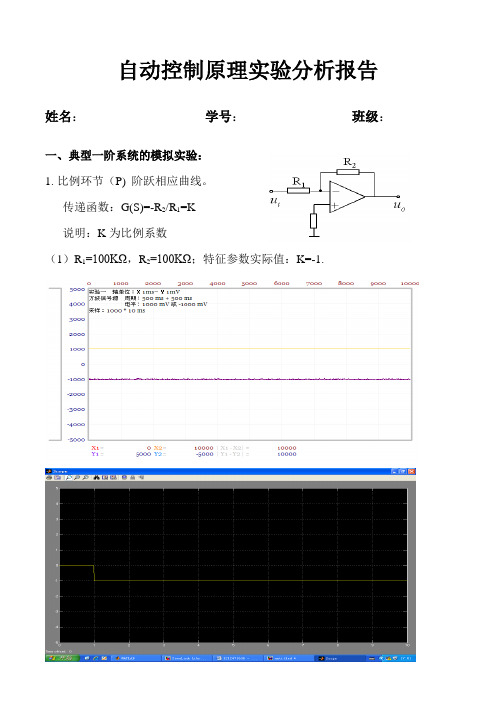
自动控制原理实验分析报告姓名:学号:班级:一、典型一阶系统的模拟实验:1.比例环节(P) 阶跃相应曲线。
传递函数:G(S)=-R2/R1=K说明:K为比例系数(1)R1=100KΩ,R2=100KΩ;特征参数实际值:K=-1.(2)(2)R1=100KΩ,R2=200KΩ;即K=-2.〖分析〗:经软件仿真,比例环节中的输出为常数比例增益K;比例环节的特性参数也为K,表征比例环节的输出量能够无失真、无滞后地按比例复现输入量。
2、惯性环节(T) 阶跃相应曲线及其分析。
传递函数:G(S)=-K/(TS+l) K=R2/R1 , T=R2C说明:特征参数为比例增益K和惯性时间常数T。
(1)、R2=R1=100KΩ , C=1µF;特征参数实际值:K=-1,T=0.1。
(2)、R2=R1=100KΩ , C=0.1µF;特征参数实际值:K=-1,T=0.01。
〖分析〗:惯性环节的阶跃相应是非周期的指数函数,当t=T时,输出量为0.632K,当t=3~4T时,输出量才接近稳态值。
比例增益K表征环节输出的放大能力,惯性时间常数T表征环节惯性的大小,T越大表示惯性越大,延迟的时间越长,反之亦然。
传递函数:G(S)= -l/TS ,T=RC说明:特征参数为积分时间常数T。
(1)、R=100KΩ , C=1µF;特征参数实际值:T=0.1。
(2)R=100KΩ , C=0.1µF;特征参数实际值:T=0.01。
〖分析〗:只要有一个恒定输入量作用于积分环节,其输出量就与时间成正比地无限增加,当t=T时,输出量等于输入信号的幅值大小。
积分时间常数T表征环节积累速率的快慢,T越大表示积分能力越强,反之亦然。
4、比例积分环节(PI) 阶跃相应曲线及其分析。
传递函数:G(S)=K( l+l/TS) K=-R2/R1, T=R2C说明:特征参数为比例增益K和积分时间常数T。
(1)、R2=R1=100KΩ , C=1µF;特征参数实际值:K=-1,T=0.1。
自动控制原理实验报告 (2)

实验一 典型环节的模拟研究及阶跃响应分析1、比例环节可知比例环节的传递函数为一个常数:当Kp 分别为0.5,1,2时,输入幅值为1.84的正向阶跃信号,理论上依次输出幅值为0.92,1.84,3.68的反向阶跃信号。
实验中,输出信号依次为幅值为0.94,1.88,3.70的反向阶跃信号, 相对误差分别为1.8%,2.2%,0.2%. 在误差允许范围内可认为实际输出满足理论值。
2、 积分环节积分环节传递函数为:(1)T=0.1(0.033)时,C=1μf (0.33μf ),利用MATLAB ,模拟阶跃信号输入下的输出信号如图: T=0.1 T=0.033与实验测得波形比较可知,实际与理论值较为吻合,理论上T=0.033时的波形斜率近似为T=0.1时的三倍,实际上为8/2.6=3.08,在误差允许范围内可认为满足理论条件。
3、 惯性环节惯性环节传递函数为:if i o R RU U -=TS1CS R 1Z Z U U i i f i 0-=-=-=1TS K)s (R )s (C +-=K = R f /R 1,T = R f C,(1) 保持K = R f /R 1 = 1不变,观测T = 0.1秒,0.01秒(既R 1 = 100K,C = 1μf ,0.1μf )时的输出波形。
利用matlab 仿真得到理论波形如下: T=0.1时 t s (5%)理论值为300ms,实际测得t s =400ms 相对误差为:(400-300)/300=33.3%,读数误差较大。
K 理论值为1,实验值2.12/2.28,相对误差为(2.28-2.12)/2.28=7%与理论值较为接近。
T=0.01时t s (5%)理论值为30ms,实际测得t s =40ms 相对误差为:(40-30)/30=33.3%由于ts 较小,所以读数时误差较大。
K 理论值为1,实验值2.12/2.28,相对误差为(2.28-2.12)/2.28=7%与理论值较为接近(2) 保持T = R f C = 0.1s 不变,分别观测K = 1,2时的输出波形。
自动控制原理实验(1)

实验一 典型环节的电路模拟一、实验目的1.熟悉THKKL-5型 控制理论·计算机控制技术实验箱及“THKKL-5”软件的使用; 2.熟悉各典型环节的阶跃响应特性及其电路模拟;3.测量各典型环节的阶跃响应曲线,并了解参数变化对其动态特性的影响。
二、实验设备1.THKKL-5型 控制理论·计算机控制技术实验箱;2.PC 机一台(含“THKKL-5”软件)、USB 数据采集卡、37针通信线1根、16芯数据排线、USB 接口线。
三、实验内容1.设计并组建各典型环节的模拟电路;2.测量各典型环节的阶跃响应,并研究参数变化对其输出响应的影响。
四、实验原理自控系统是由比例、积分、微分、惯性等环节按一定的关系组建而成。
熟悉这些典型环节的结构及其对阶跃输入的响应,将对系统的设计和分析十分有益。
本实验中的典型环节都是以运放为核心元件构成,其原理框图 如图1-1所示。
图中Z 1和Z 2表示由R 、C 构成的复数阻抗。
1.比例(P )环节比例环节的特点是输出不失真、不延迟、成比例地复现输出信号的变化。
图1-1 它的传递函数与方框图分别为:KS U S U S G i O ==)()()(当U i (S)输入端输入一个单位阶跃信号,且比例系数为K 时的响应曲线如图1-2所示。
2.积分(I )环节 图1-2积分环节的输出量与其输入量对时间的积分成正比。
它的传递函数与方框图分别为:设U i (S)为一单位阶跃信号,当积分系数为T 时的响应曲线如图1-3所示。
TsS U S Us G i O1)()()(==图1-33.比例积分(PI)环节比例积分环节的传递函数与方框图分别为:)11(11)()()(21211212CSR R R CSR R R CSR CS R S U S U s G i O +=+=+==其中T=R 2C ,K=R 2/R 1设U i (S)为一单位阶跃信号,图1-4示出了比例系数(K)为1、积分系数为T 时的PI 输出响应曲线。
自动控制原理实验报告

自动控制原理实验报告班级自动化1204姓名焦雍堡学号12212153组员黄寅峰学号:12212124任课老师苗宇实验一经典环节及其阶跃响应1.各个环节的模拟电路图及其阶跃响应曲线(1)比例环节(2)惯性环节(3)积分环节(4)微分环节(5)比例微分环节2.由阶跃响应曲线计算出传递函数(1)惯性环节K=R2/R1=200K/100K=2 T=R2C=0.2G(S)=-2/(0.2S+1)由图可得,输入1000mv的阶跃信号,输出信号稳定在-2000mv 与理论值相符。
(2)积分环节T=RC=0.1G(S)=1/TS=10/s由图可得,R(S)=100/S,C(S)=1000/2S,与理论值相符。
实验二二阶系统阶跃响应1.画出二阶系统的模拟电路图,讨论经典二阶系统性能指标与ξ,nω的关系。
(1)R2=0,ξ=0,nω=10 rad/s(2)R2=50K,ξ=0.25,nω=10 rad/s(3)R2=100K,ξ=0.5,nω=10 rad/s(4)R2=150K,ξ=0.75,nω=10 rad/s(5)R2=200K,ξ=1,nω=10 rad/s(6)R2=400K,ξ=2,nω=10 rad/s(7)ξ=0.5,nω=100 rad/s2.不同ξ,n ω条件下的Mp 和ts 值。
实际测量值: n ωξMpTs (ms )10 rad/s 0 无 无穷 10 rad/s 0.25 41.1% 1098 10 rad/s 0.5 15.9% 665 10 rad/s 0.75 17.3% 333 10 rad/s 1 0 - 10 rad/s 2 0 - 100 rad/s0.515.3%73当ξ=0时,系统处于零阻尼状态,等幅振荡;当0<ξ<1时,系统处于欠阻尼状态,在相同自然角频率的情况下,通过改变ξ可以减小系统的响应时间并减少超调量,且在0.5<ξ<0.75存在最佳阻尼比。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验一 控制系统的阶跃响应一、实验目的1. 掌握控制系统多项式模型和零极点模型的建立方法及它们之间的相互转换。
2.观察学习控制系统的单位阶跃响应。
3.记录单位阶跃响应曲线。
4.掌握时间响应分析的一般方法。
5.分析系统阶跃响应曲线与传递函数参数的对应关系。
二、实验设备PC 机,MATLAB 仿真软件。
三、实验内容1.作以下二阶系统的单位阶跃响应曲线10210)(2++=s s s G 2.分别改变该系统的ζ和n ω,观察阶跃响应曲线的变化。
3.作该系统的脉冲响应曲线。
四、实验原理1. 建立系统模型在MATLAB 下,系统数学模型有三种描述方式,在本实验中只用到多项式模型和零极点模型。
(1)多项式模型num 表示分子多项式的系数,den 表示分母多项式的系数,以行向量的方式输入。
例如,程序为num=[0 1 3]; %分子多项式系数den=[1 2 2 1]; %分母多项式系数printsys (num, den) %构造传递函数并显示(2)零极点模型z 表示零点,p 表示极点,以行向量的方式输入,k 表示增益。
例如,程序为k=2; %赋增益值,标量z=[1]; %赋零点值,向量p=[-1 2 -3]; %赋极点值,向量[num, den]=zp2tf(z, p, k); %零极点模型转换成多项式模型printsys(num, den) %构造传递函数并显示(3)相关MATLAB 函数函数tf(num, den) 用来建立控制系统的多项式模型;函数zpk(z, p, k)用来建立控制系统的零极点模型;[num, den]=zp2tf (z, p, k) %零极点模型转换成多项式模型[z, p, k]=tf2zp (num, den) %多项式模型转换成零极点模型[num, den]=ord2(ωn , ξ) %用来建立二阶系统标准模型2. 控制系统的单位阶跃响应(1)给定系统传递函数的多项式模型,求系统的单位阶跃响应。
函数格式1:step(num, den) %给定num ,den ,求系统阶跃响应,时间向量t 的范围自动设定。
函数格式2:step(num, den, t) %时间向量t 的范围可以由人工给定(如t=0:0.1:10).函数格式3:[y, x]=step(num, den) %返回变量格式。
计算所得的输出y 、状态x 及时间向量t 返回至MATLAB 命令窗口,不做图。
(2)给定特征多项式系数向量,计算系统的闭环根、阻尼比、无阻尼振荡频率。
函数格式:damp(den)五、实验步骤1.二阶系统为 10210)(2++=s s s G (1)键人程序 观察并纪录阶跃响应曲线程序:clear;closenum=[10]; %多项式分子系数den=[1,2,10]; %多项式分母系数step(num,den); %系统阶跃响应figure(1) %绘图title('G(s)的阶跃响应')(2)键入 damp (den ),计算系统的闭环根、阻尼比、无阻尼振荡频率,并作记录。
程序:clear;closenum=[10]; %多项式分子系数den=[1,2,10]; %多项式分母系数damp(den) %计算系统的闭环根,阻尼比,无阻尼振荡频率计算结果如下:Eigenvalue Damping Freq. (rad/s)-1.00e+000 + 3.00e+000i 3.16e-001 3.16e+000-1.00e+000 - 3.00e+000i 3.16e-001 3.16e+000 闭环根为:s1=-1+3j,s2=-1-3j阻尼比:ζ=0.316无阻尼振荡频率:ωn=3.16(3)键入[y,x,t]=step(num,den) %返回变量输出y与时间t(变量x为状态变量矩阵)[y,t'] %显示输出向量y与时间向量t(t为自动向量)记录实际测取的峰值大小Cmax (tp)、峰值时间tp、调节时间ts,并与理论值相比较。
ans =0 00.0133 0.05250.0509 0.10490.1096 0.15740.1856 0.20980.2752 0.26230.3749 0.31480.4809 0.36720.5899 0.41970.6987 0.47210.8045 0.52460.9049 0.57700.9977 0.62951.0814 0.68201.1546 0.73441.2165 0.78691.2666 0.83931.3048 0.89181.3312 0.94431.3463 0.99671.3509 1.04921.3459 1.10161.3324 1.15411.2847 1.2590 1.2531 1.3115 1.2180 1.3639 1.1807 1.4164 1.1425 1.4688 1.1043 1.5213 1.0672 1.5738 1.0321 1.6262 0.9996 1.6787 0.9704 1.7311 0.9448 1.7836 0.9233 1.8361 0.9059 1.8885 0.8926 1.9410 0.8835 1.9934 0.87832.0459 0.8769 2.0983 0.8787 2.1508 0.8836 2.2033 0.8910 2.2557 0.9005 2.3082 0.9116 2.3606 0.9240 2.4131 0.9371 2.4656 0.9505 2.5180 0.9639 2.5705 0.9769 2.62290.9892 2.67541.00052.7278 1.0107 2.7803 1.0197 2.8328 1.0272 2.8852 1.0332 2.9377 1.0378 2.9901 1.04103.0426 1.0427 3.0951 1.0432 3.1475 1.0425 3.2000 1.0408 3.2524 1.0381 3.3049 1.0348 3.3573 1.0309 3.4098 1.0265 3.46231.0172 3.5672 1.0125 3.6196 1.0079 3.6721 1.0036 3.7246 0.9997 3.7770 0.9961 3.8295 0.9930 3.8819 0.9904 3.9344 0.9883 3.9869 0.9867 4.0393 0.9856 4.0918 0.9850 4.1442 0.9848 4.1967 0.9851 4.2491 0.9857 4.3016 0.9867 4.3541 0.9878 4.4065 0.9892 4.4590 0.9908 4.5114 0.9924 4.5639 0.9940 4.6164 0.9957 4.6688 0.9973 4.72130.9988 4.77371.0002 4.8262 1.0014 4.8786 1.0025 4.9311 1.0034 4.9836 1.0041 5.0360 1.0047 5.0885 1.0051 5.1409 1.0053 5.1934 1.0053 5.2459 1.0052 5.2983 1.0050 5.3508 1.0047 5.4032 1.0042 5.4557 1.0038 5.5082 1.0032 5.5606 1.0027 5.6131 1.0021 5.6655 1.0015 5.7180 1.0009 5.77040.9999 5.87540.9995 5.92780.9991 5.9803理论值计算:xcm= 1+e-ζπ/√1-ζ*ζ=1.3535峰值时间t p=π/√1-ζ2 *ωn=1.0472过渡时间:ts=(±5%)=3/ζωn=3.0022过渡时间:ts=(±2%)=4/ζωn=4.0029实际值理论值峰值 Cmax (tp) 1.3509 1.3535峰值时间tp1.0491 1.0472过渡时间ts%5± 2.5399 3.0022 %2± 3.5889 4.0029理论值与实际值比较,峰值和过渡时间,理论值比实际值大,但在峰值时间上比实际值短2.修改参数,分别实现ζ=1, ζ=2的响应曲线,并作记录。
程序为:n0=10;d0=[1 2 10];step(n0,d0 ) %原系统ζ=0.316hold on %保持原曲线n1=n0,d1=[1 6.32 10];step(n1,d1) %ζ=1n2=n0;d2=[1 12.64 10];step(n2,d2) %ζ=2修改参数,写出程序分别实现1n ω=021n ω和2n ω=20n ω的响应曲线,并作记录。
(100=n ω)。
程序: clear;closen0=10;d0=[1 2 10];step(n0,d0) %原系统振荡角频率=3.16hold on %保持原曲线 n1=2.5;d1=[1 1 2.5];step(n1,d1) %振荡角频率=1.58n2=40;d2=[1 4 40];step(n2,d2) %振荡角频率=6.323.试作以下系统的阶跃响应,并比较与原系统响应曲线的差别与特点,作出相应的实验分析结果。
(a)102102)(21+++=s s s s G ,有系统零点情况,即s=-5。
(b) 102105.0)(222++++=s s s s s G ,分子分母多项式阶数相等,即n=m=2。
(c)1025.0)(223+++=s s s s s G ,分子多项式零次项系数为零。
(d)102)(24++=s s s s G ,原响应的微分,微分系数为1/10。
程序:clear;close n0=10;d0=[1 2 10];step(n0,d0) %原系统hold on %保持原曲线 n1=[2,10];d1=[1 2 10];step(n1,d1) %G1(s)n2=[1,0.5,10];d2=[1 2 10];step(n2,d2) %G2(s)n3=[1,0.5,0];d3=[1 2 10];step(n3,d3)%G3(s)n4=[1,0];d4=[1 2 10];step(n4,d4)%G4(s)六、预习要求1.仔细阅读实验指导书。
2.预习相关控制理论知识。
3.完成相关仿真程序的书面设计。
4.有条件的可提前上机练习。
七、实验报告要求1. 分析系统的阻尼比和无阻尼振荡频率对系统阶跃响应的影响。
答:系统的阻尼比ζω决定了其振荡特性,阻尼比(0<ζ<1)越大,其阶跃响应超调量越小,上升时间越长。
