正方形的性质及判定复习课程
3.正方形的性质与判定第1课时正方形的性质PPT课件(北师大版)

第一章
特殊平行四边形 3.正方形的性质与判定
第1课时 正方形的性质
第1课时 正方形的性质
1 …知…识…回…顾…. 2 …新…知…导…航…. 3 …轻…松…过…招….
第1课时 正方形的性质
知识回顾
正方是轴对称图形,它有 4 条对称轴,即经 过对边中点的直线或两对角线所在直线:正方形又 是中心对称图形,两对角线交点是它的对称中心 (也是对边中点的直线的交点)。 .
第1课时 正方形的性质
新知导航
变式训练
1.已知正方形ABCD的对角线相交于点O. (1)若周长为8,则对角线长为 2 2 , 面积为 4 ; (2)图中共有 8 个等腰直角三角形.
第1课时 正方形的性质
新知导航
2.如图,过正方形ABCD的顶点B作直线l,过点A,C 作l的垂线,垂足分别为E,F,若 AE=1,CF=3.求AB的长.
第1课时 正方形的性质
轻松过招
3.如图,正方形ABCD中,E为CD边上一点,F为 BC延长线上一点,且CE=CF. (1)求证:△BCE≌△DCF;
(1)证明:∵四边形ABCD是正方形,
∴BC=DC,∠BCE=∠DCF=90°
CE=CF
在△BCE和△DCF中, ∠BCE=∠DCF ,
∴△BCE≌△DCF.
解:∵四边形ABCD是正方形, ∴∠CBF+∠FBA=90°,AB=BC, ∵CF⊥BE,∴∠CBF+∠BCF=90°, ∴∠BCF=∠ABE, ∵∠AEB=∠BFC=90°,AB=BC, ∴△ABE≌△BCF(AAS),∴AE=BF=1,BE=CF=3, ∴AB= AE2+BE2 = 1+9 = 10 .
第1课ห้องสมุดไป่ตู้ 正方形的性质
轻松过招
第05讲 正方形的性质与判定(原卷版)-初中数学暑假自学课讲义(9年级北师大版)
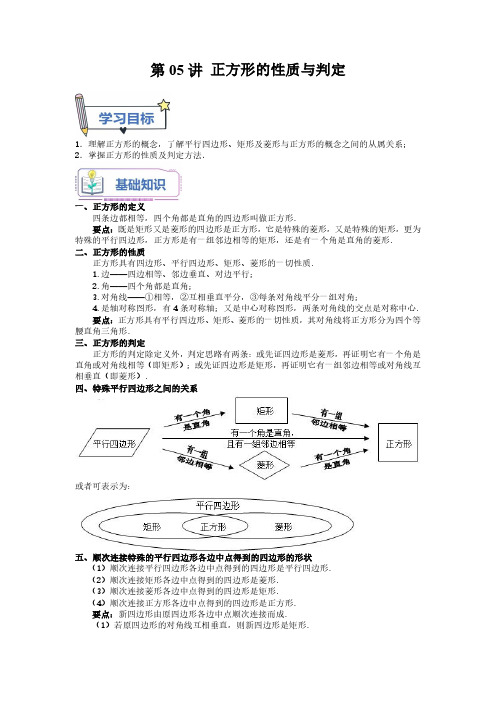
第05讲正方形的性质与判定1.理解正方形的概念,了解平行四边形、矩形及菱形与正方形的概念之间的从属关系;2.掌握正方形的性质及判定方法.一、正方形的定义四条边都相等,四个角都是直角的四边形叫做正方形.要点:既是矩形又是菱形的四边形是正方形,它是特殊的菱形,又是特殊的矩形,更为特殊的平行四边形,正方形是有一组邻边相等的矩形,还是有一个角是直角的菱形.二、正方形的性质正方形具有四边形、平行四边形、矩形、菱形的一切性质.1.边——四边相等、邻边垂直、对边平行;2.角——四个角都是直角;3.对角线——①相等,②互相垂直平分,③每条对角线平分一组对角;4.是轴对称图形,有4条对称轴;又是中心对称图形,两条对角线的交点是对称中心.要点:正方形具有平行四边形、矩形、菱形的一切性质,其对角线将正方形分为四个等腰直角三角形.三、正方形的判定正方形的判定除定义外,判定思路有两条:或先证四边形是菱形,再证明它有一个角是直角或对角线相等(即矩形);或先证四边形是矩形,再证明它有一组邻边相等或对角线互相垂直(即菱形).四、特殊平行四边形之间的关系或者可表示为:五、顺次连接特殊的平行四边形各边中点得到的四边形的形状(1)顺次连接平行四边形各边中点得到的四边形是平行四边形.(2)顺次连接矩形各边中点得到的四边形是菱形.(3)顺次连接菱形各边中点得到的四边形是矩形.(4)顺次连接正方形各边中点得到的四边形是正方形.要点:新四边形由原四边形各边中点顺次连接而成.(1)若原四边形的对角线互相垂直,则新四边形是矩形.(2)若原四边形的对角线相等,则新四边形是菱形.(3)若原四边形的对角线垂直且相等,则新四边形是正方形.考点1:正方形的性质例1.正方形、矩形、菱形都具有的特征是()A .对角线互相平分B .对角线相等C .对角线互相垂直D .对角线平分一组对角例2.正方形具有而菱形不一定有的性质是()A .对角线相等B .对角线互相垂直C .对角相等D .四条边相等考点2:利用正方形的性质求长度例3.正方形一条对角线长为22,则周长为()A .4B .42C .8D .82例4.如图,菱形ABCD 的面积为2120cm ,正方形AECF 的面积为250cm ,则菱形的边长是()A .13cm B .15cm C .17cm D .20cm例5.如图,在正方形ABCD 中,点E 是对角线AC 上一点,作EF AB ⊥于点F ,连接DE ,若114BC BF ==,,则DE 的长为()A .36B .62C .213D 65考点3:利用正方形的性质求角度例6.一个正方形和一个直角三角形的位置如图所示,若1∠=α,则2∠=()A .45α-︒B .90α-︒C .270α︒-D .180α︒-例7.如图,以正方形ABCD 的一边BC 向正方形外作等边EBC ,则AED ∠的度数是()A .30︒B .20︒C .15︒D .10︒例8.如图,已知正方形ABCD 中,DA DE =,CF AE ∥,则ECF ∠的度数是()A .30︒B .35︒C .40︒D .45︒考点4:利用正方形的性质求面积例9.如图,正方形ABCD 的边长为8,在各边上顺次截取6AE BF CG DH ====,则四边形EFGH 的面积是()A .34B .36C .40D .100例10.如图,在菱形ABCD 中,=60B ∠︒,4AB =,则正方形ACEF 的面积为()A .8B .12C .16D .20例11.如图,在ABC 中,90B Ð=°,2AB =,4BC =.四边形ADEC 是正方形,则正方形ADEC 的面积是()A .8B .12C .18D .20例12.如图将边长为a 的大正方形与边长为b 的小正方形放在一起(0,0)a b >>,则三角形AEG 的面积()A .与a 、b 大小都有关B .与a 、b 的大小都无关C .只与a 的大小有关D .只与b 的大小有关考点5:正方形的判定例13.如图,在矩形ABCD 中,对角线AC BD 、交于点O ,下列条件中,能使矩形ABCD 成为正方形的是()A .AC BC =B .60AOB ∠=︒C .OA AD =D .BC CD =例14.有下列四个条件:①90ABC ∠=︒;②AC BD ⊥;③AB BC =;④AC BD =;从中选两个作为补充条件,使平行四边形ABCD 为正方形,现有下列四种选法,你认为错误的是()A .①②B .①③C .②③D .②④考点6:中点四边形例15.连接菱形各边中点,可得到的“中点四边形”是矩形,主要是因为()A .菱形的四条边都相等B .菱形的对角线互相垂直C .菱形的对角线互相平分D .以上答案都不对例16.如图,AC 、BD 是四边形ABCD 的两条对角线,顺次连接四边形ABCD 各边中点得到四边形EFGH ,要使四边形EFGH 为矩形,应添加的条件是()A .AC ⊥BDB .AB =CDC .AB ∥CD D .AC =BD例17.若顺次联结一个四边形各边的中点得到的图形是矩形,则这个四边形的对角线()A .互相平分B .相等C .互相垂直D .互相垂直且平分考点7:正方形的判定与性质综合例18.如图,点E 是正方形对角线AC 上一点,过E 作EF AD ∥交CD 于F ,连接BE ,若5BE =,4DF =,则AC 的长为()A .42B .52C .62D .72例19.如图,正方形ABCD 的边长为1,E 为AD 边上一点(与点A 、D 不重合),连接CE ,交BD 于点F .当DEF 是等腰三角形时,则AE 的长为()A .12B .23C .21-D .22-例20.如图,正方形ABCD 边长为10,点M 在对角线AC 上运动,N 为DC 上一点,DN =2,则DM +MN 长的最小值为()A .8B .10C .241D .102例21.如图,ABCD 为正方形,O 为AC 、BD 的交点,△DCE 为Rt △,∠CED=90°,∠DCE=30°,若OE=,则正方形的面积为()A .5B .4C .3D .2例22.ABCD 是边长为1的正方形,BPC 是等边三角形,则BPD 的面积为()A .14B 314-C .18D .318考点8:正方形的判定与性质解答题例23.如图,若四边形ABCD 的对角线AC 与BD 相交于点O ,且2OA OB OC OD AB ===,则四边形ABCD 是正方形吗?例24.如图,M 、N 分别是正方形ABCD 的边AD CD 、的中点,CM 与BN 交于点P ,连结AP ,求证:AP AB =.例25.如图,在正方形ABCD 中,E 是AB 上一点,F 是AD 延长线上一点,且DF =BE .(1)求证:CE =CF ;(2)若点G 在AD 上,且∠GCE =45°,则GE =BE +GD 成立吗?为什么?例26.如图,E ,F 是正方形ABCD 的对角线BD 上的两点,且BE =DF .(1)≌△CDF ;(2)若AB =2,BE =2,求四边形AECF 的面积.例27.如图,正方形ABCD 中,AE BF =.(1)求证:BCE CDF ≌;(2)求证:CE DF ⊥;(3)若6CD =,且2241DG GE +=,则BE =_______.一、单选题1.(2022·湖南衡阳·统考中考真题)下列命题为假命题的是()A .对角线相等的平行四边形是矩形B .对角线互相垂直的平行四边形是菱形C .有一个内角是直角的平行四边形是正方形D .有一组邻边相等的矩形是正方形2.(2021·广西玉林·统考中考真题)一个四边形顺次添加下列中的三个条件便得到正方形:a .两组对边分别相等b .一组对边平行且相等c .一组邻边相等d .一个角是直角顺次添加的条件:①a→c→d ②b→d→c ③a→b→c则正确的是:()点F是边AB上一点,连接A.45︒B.侧作正方形APCD、正方形PBEF,A.2αB.90°﹣度数为()A.50°B.55°二、填空题、相交于点O,6.(2021·黑龙江·统考中考真题)如图,在矩形ABCD中,对角线AC BD在不添加任何辅助线的情况下,请你添加一个条件______,使矩形ABCD是正方形.7.(2015·广西南宁·中考真题)如图,在正方形ABCD外作等边ADE,则∠=___________︒.BED8.(2020·江苏镇江·统考中考真题)如图,点P 是正方形ABCD 内位于对角线AC 下方的一点,∠1=∠2,则∠BPC 的度数为_____°.三、解答题9.(2022·湖北恩施·统考中考真题)如图,已知四边形ABCD 是正方形,G 为线段AD 上任意一点,CE BG ⊥于点E ,DF CE ⊥于点F .求证:DF BE EF =+.10.(2019·四川内江·统考中考真题)如图,在正方形ABCD 中,点E 是BC 上的一点,点F 是CD 延长线上的一点,且BE DF =,连结,,AE AF EF .(1)求证:ABE ∆≌ADF ∆;(2)若5AE =,请求出EF 的长.11.(2021·山东泰安·统考中考真题)四边形ABCD 为矩形,E 是AB 延长线上的一点.(1)若AC EC =,如图1,求证:四边形BECD 为平行四边形;(2)若AB AD =,点F 是AB 上的点,AF BE =,EG AC ⊥于点G ,如图2,求证:DGF △是等腰直角三角形.12.(2020·黑龙江鹤岗·统考中考真题)以Rt ABC ∆的两边AB 、AC 为边,向外作正方形ABDE 和正方形ACFG ,连接EG ,过点A 作AM BC ⊥于M ,延长MA 交EG 于点N .(1)如图1,若90BAC ∠=︒,AB AC =,易证:EN GN =;(2)如图2,90BAC ∠=︒;如图3,90BAC ∠≠︒,(1)中结论,是否成立,若成立,选择一个图形进行证明;若不成立,写出你的结论,并说明理由.13.(2023·陕西·模拟预测)已知,四边形ABCD 是正方形,DEF 绕点D 旋转(DE AB <),90EDF ∠=︒,DE DF =,连接AE ,CF .(1)如图1,求证:ADE V ≌CDF ;(2)直线AE 与CF 相交于点G .①如图2,BM AG ⊥于点M ,⊥BN CF 于点N ,求证:四边形BMGN 是正方形;②如图3,连接BG ,若4AB =,2DE =,直接写出在DEF 旋转的过程中,线段BG 长度的最小值.一、单选题长为()A .5cm4.如图,四边形ABCDA.22.5°B 5.如图,正方形A.406.如图,在正方形若AB=4,则线段AE的长为(A.22B交CD于点G.若1AE=,A.2B.1 AF相交于点G,点A.3439.如图,在正方形接DE,F是DE的中点,连接CF的距离为()A .235B .435()A .①③二、填空题11.正方形是有一组邻边_______,并且有一个角是_______的平行四边形,因此它既是______又是________.12.若正方形的边长为a ,则它的对角线长为__________.13.已知矩形ABCD ,给出三个关系式:①;AB BC =②;AC BD =③,AC BD ⊥如果选择关系式__________作为条件(写出一个即可),那么可以判定矩形为正方形,理由是_______________________________.14.在正方形ABCD 中,E 是对角线AC 上一点,且AE =AB ,则∠EBC 的度数是___________.15.作正方形ABCD 中对角线AC 的平行线BF ,点E 在直线BF 上,且四边形AEFC 是菱形,贴EAB ∠=_______.16.如图,E 是正方形ABCD 的对角线BD 上一点,连接CE ,过点E 作EF AD ⊥,垂足为点F .若6AF =,10EC =,则正方形ABCD 的面积为___.17.如图,在正方形ABCD交AD于F.当∠18.如图,点P是正方形⑤PD=2EC,其中正确结论的序号是=+.求证:AF DF BE20.如图,若四边形ABCD则四边形21.如图,求证:22.如图,交AG23.如图,E ,F 是正方形(1)求证:△ABE ≌△CDF ;(2)若AB =32,BE =2,求四边形24.如图,正方形ABCD 中,EF ED ⊥,交AB 于点F ,以(1)求证:①EFB EBF ∠=∠②矩形DEFG 是正方形;(2)求AG AE +的值.25.已知,四边形ABCD 是正方形,连接AE ,CF(1)如图1,求证:ADE CDF V V ≌;(2)直线AE 与CF 相交于点G .①如图2,BM AG ⊥于点M ,⊥BN CF 点N ,证明矩形BMGN 是正方形②如图3,连接BG ,若4AB =,2DE =直接写出在DEF 旋转的过程中,线段最小值.。
正方形的性质与判定(优秀教案)

正方形的性质与判定(1)主讲:叶良国课题:正方形的性质与判定(1)课型:新授课教学目标:1.了解正方形概念,理解并掌握正方形的性质和判定方法,通过由一般到特殊的研究方法,分析平行四边形、矩形、菱形、正方形的概念及性质之间的区别与联系.并形成文本信息与图形信息相互转化的能力.2.在观察、操作、推理、归纳等探索明正方形的性质和判定定理过程中,发展合情推理能力,进一步培养自己的说理习惯与能力3.培养学生勇于探索、团结协作交流的精神.激发学生学习的积极性与主动性.教学重难点:重点:探索正方形的性质与判定。
难点:掌握正方形的性质和判定的应用方法。
关键:把握正方形既是矩形又是菱形这一特性来学习本节内容教学过程教学过程:一、回忆童年,情境引入想一想:什么是矩形?是菱形?做一做:大家小时候都做过风车吗?在准备材料的时候我们往往会先折一张正方形的纸片,大家来做一做用一张长方形的纸片折出一个正方形.设计意图:学生在动手中对正方形产生感性认识,并感知正方形与矩形的关系.猜一猜:什么样的平行四边形是正方形?正方形定义:有一组邻边相等.....叫做正方形.......并且有一个角是直角.......的平行四边形看一看:几何画板演示动画设计意图:从学生的生活实际出发,从制作、动画中,提出问题,创设情境,激发学生强烈的好奇心和求知欲。
我们这节课就来研究正方形.板书课题【正方形的性质与判定】二、实践探究,交流新知师:其定义包括了两层意:⑴有一组邻边相等的平行四边形(菱形)⑵有一个角是直角的平行四边形(矩形),所以说正方形既是菱形又是矩形.平行四边形、菱形、矩形、正方形之间有什么关系?你能用一个图直观地表示它们之间的关系吗?与同伴交流.生:画图展示设计意图:锻炼学生文本信息图形化的能力.构建他们之间的逻辑关系;重建学生的认知结构.师:正方形都具有什么性质呢?生:由正方形的定义可以得知,正方形既是有一组邻边相等的矩形,又是有一个角是直角的菱形.所以它应该具备菱形和矩形的所有性质.(多媒体补充显示性质)正方形性质①正方形的四个角都是直角,四条边都相等.②正方形的两条对角线相等并且互相垂直平分.师:同学们从正方形定义中能尝试口述这两个命题的证明过程吗?生:学生独立完成,并相互交流师:正方形有几条对称轴?生:思考或者画图验证师:什么样的矩形是正方形?什么样的菱形是正方形?(多媒体演示)设计意图:通过分析让学生感受到正方形与矩形和菱形、平行四边形的紧密联系,明确正方形的判定。
1.3正方形的性质与判定(教案)2018-2019学年九年级上学期数学教材(北师大版)

此外,我也注意到,在小组讨论环节,学生们表现得积极主动,能够提出自己的观点和想法。但在分享成果时,部分学生表达不够清晰,逻辑性不强。因此,我打算在接下来的课程中,加强学生的表达和逻辑思维能力训练,让他们在分享成果时能够更加自信和清晰。
3.成果展示:每个小组将向全班展示他们的讨论成果和实验操作的结果。
(四)学生小组讨论(用时10分钟)
1.讨论主题:学生将围绕“正方形在实际生活中的应用”这一主题展开讨论。他们将被鼓励提出自己的观点和想法,并与其他小组成员进行交流。
2.引导与启发:在讨论过程中,我将作为一个引导者,帮助学生发现问题、分析问题并解决问题。我会提出一些开放性的问题来启发他们的思考。
四、教学流程
(一)导入新课(用时5分钟)
同学们,今天我们将要学习的是“1.3正方形的性质与判定”。在开始之前,我想先问大家一个问题:“你们在日常生活中是否见过哪些物体的形状是正方形?”(举例说明,如桌面、瓷砖等)这个问题与我们将要学习的内容密切相关。通过这个问题,我希望能够引起大家的兴趣和好奇心,让我们一同探索正方形的性质与判定的奥秘。
3.重点难点解析:在讲授过程中,我会特别强调正方形的性质和判定方法这两个重点。对于难点部分,如正方形性质的推导和判定方法的应用,我会通过举例和比较来帮助大家理解。
(三)实践活动(用时10分钟)
1.分组讨论:学生们将分成若干小组,每组讨论一个与正方形相关的实际问题。
2.实验操作:为了加深理解,我们将进行一个简单的实验操作,如用直角尺和尺子测量正方形的对角线,验证对角线互相垂直平分的性质。
正方形性质与判定复习

课 后 反 思
难点 正方形的性质和判定的综合运用
学 法
指 自主学习 导
合作探究
正方形定义:四条边都相等,四个角都是直角的四边形是正方 形。
有一组邻边相等并且有一个角是直角的平行四边形叫做正 方形。
正方形性质:(既有矩形的性质,又有菱形的性质) 1、对边平行且相等;2、四条边都相等;3、各角都是直角;
记忆 4、对角线相等且互相垂直平分;5、每一条对角线平分一组对 清单 角。
2、如图,正方形ABCD的边长为12 cm,在AB上有点P,且AP=5 cm,将正方形折叠,使点D与点P重合,折痕为EF,求△EAP的 周长.
3、如图,在AB上取一点C,以AC、BC为正方形的一边在同一 侧作正方形AEDC和BCFG连结AF、BD延长BD交AF于H。 求证:(1) △ACF≌△DCB
实验中学八年级数学教学通案
课 题
18.2.3正方形的性质与判定复习
课
型
新授 课
课时
主备 教师
审核 教师
使用教 师
上
备课
课
日期
日
期
1.掌握正方形的概念和性质、判定,并会用它们进行有关的论证和
学习 计算.
目标 2.熟练运用正方形性质和判定,进一步体会数学的数形结合思想,
提高学生的逻辑思维能力.
重点 正方形的性质和判定
1.正方形与平行四边形、矩形、菱形的关系图:
个案补充
2.正方形特征: 3.正方形的识别方法:
4.正方形还有许多有趣的性质.例如,如果要用给定长度
的篱笆围成一个最大面积的四边形区域,那么应当把这个区
域的形状选成Leabharlann 方形. 3、 练习巩固1、矩形、菱形、正方形都具有的性质是( )
1.3 正方形的性质与判定(二)

定理:对角线垂直的矩形是正方形
正方形的判定方法:
1、定义 判定没有固定方法, 2、对角线相等的菱形是正方形。 只要既是矩形又 3、有一个角是直角的菱形是正方形。 是菱形就可判定。 4、对角线垂直的矩形是正方形。 5、有一组邻边相等的矩形是正方形。
注意:正方形的
有一组邻边相等且 有一个角是直角
第二环节
E
F
A
C
H
D
G
第三环节 猜想结论,分组验证
如果四边形ABCD变为特殊的四边形,中点四边形 EFGH会有怎样的变化呢?先猜一猜,再证明。 原四边形可以是:
平行四边形
矩形
菱形
正方形
等腰梯形
直角梯形
梯形
第三环节 猜想结论,分组验证
特殊四边形的中点四边形:
平行四边形的中点四边形是平行四边形
矩形的中点四边形是菱形
证明:∵四边形ABCD是菱形 ∴四边形ABCD是平行四边形,AB=AD ∵ ∠ABC=90° ∴四边形ABCD是正方形(正方形定义 )
定理:有一个角是直角的菱形是正方形。
证明:对角线相等的菱形是正方形。
已知: 四边形ABCD是菱形, AC=BD
求证: 四边形ABCD是正方形
证明:∵四边形ABCD是菱形 ∴四边形ABCD是平行四边形 ∵AC=BD ∴四边形ABCD是矩形 ∴∠ABC=90° ∴四边形ABCD是正方形.(正方形的定义)
已知: 四边形ABCD是矩形, AB=AD 求证: 四边形ABCD是正方形
证明:∵四边形ABCD是矩形, ∴四边形ABCD是平行四边形, ∠ABC=90° ∵ AB=AD ∴四边形ABCD是正方形(正方形的定义)
定理:有一组邻边相等的矩形是正方形。
正方形的性质与判定(教案)

正方形的性质与判定教学目标:1. 理解正方形的定义及其性质。
2. 学会使用正方形的性质进行判定。
3. 培养学生的观察能力、推理能力和解决问题的能力。
教学重点:1. 正方形的性质。
2. 正方形的判定方法。
教学难点:1. 正方形性质的灵活运用。
2. 正方形判定方法的掌握。
教学准备:1. 教学课件或黑板。
2. 正方形模型或图片。
3. 练习题。
教学过程:第一章:正方形的定义1.1 引入:展示正方形模型或图片,引导学生观察并猜测正方形的定义。
1.2 讲解:正方形是四条边相等且四个角都是直角的四边形。
1.3 互动:让学生举例说明生活中常见的正方形,如棋盘、正方形纸等。
第二章:正方形的性质2.1 引入:展示正方形模型或图片,引导学生观察正方形的性质。
2.2 讲解:正方形的性质包括:四条边相等,四个角都是直角,对角线互相垂直平分且相等。
2.3 互动:让学生运用正方形的性质解决问题,如计算正方形对角线的长度。
第三章:正方形的判定3.1 引入:展示非正方形的模型或图片,引导学生思考如何判断一个四边形是否为正方形。
3.2 讲解:正方形的判定方法包括:四条边相等,四个角都是直角,对角线互相垂直平分且相等。
3.3 互动:让学生举例说明如何判断一个四边形是否为正方形。
第四章:正方形的应用4.1 引入:展示正方形应用的例子,如正方形图案设计、正方形桌面等。
4.2 讲解:正方形在实际生活中的应用,如建筑设计、电路板设计等。
4.3 互动:让学生举例说明正方形在实际生活中的应用。
第五章:总结与练习5.1 总结:回顾本节课所学的内容,强调正方形的定义、性质和判定。
5.2 练习:布置练习题,让学生巩固所学内容。
教学反思:本节课通过展示正方形模型或图片,引导学生观察和思考正方形的性质和判定。
通过互动和举例,让学生更好地理解和应用正方形的性质。
在教学过程中,要注意引导学生主动参与,培养他们的观察能力、推理能力和解决问题的能力。
第六章:正方形边的性质6.1 引入:通过正方形模型或图片,引导学生关注正方形边的性质。
《正方形的判定》 讲义

《正方形的判定》讲义一、正方形的定义在平面几何中,正方形是一种特殊的四边形。
它的定义为:四条边都相等,四个角都是直角的四边形叫做正方形。
要深刻理解正方形的定义,我们需要明确以下几个关键点:1、四条边相等:这意味着正方形的边长长度是完全一致的。
2、四个角都是直角:直角的度数为 90 度,所以正方形的四个角都是 90 度。
二、正方形的性质在探讨正方形的判定方法之前,我们先来了解一下正方形所具有的一些重要性质:1、边的性质四条边长度相等。
对边平行。
2、角的性质四个角均为直角(90 度)。
3、对角线的性质对角线相等。
对角线互相垂直平分。
对角线平分一组对角。
4、对称性正方形是中心对称图形,对称中心为两条对角线的交点。
正方形也是轴对称图形,有四条对称轴,分别是两条对角线所在的直线以及两组对边中点连线所在的直线。
三、正方形的判定方法1、有一组邻边相等且有一个角为直角的平行四边形是正方形若一个平行四边形满足邻边相等,那么它已经是菱形。
而如果在菱形的基础上,再有一个角是直角,那么根据矩形的定义(有一个角为直角的平行四边形是矩形),这个图形既是菱形又是矩形,所以它就是正方形。
例如,在平行四边形 ABCD 中,如果 AB = AD 且∠A = 90°,那么四边形 ABCD 就是正方形。
2、有一组邻边相等的矩形是正方形矩形的特点是四个角都是直角。
当矩形的一组邻边相等时,它就满足了正方形四条边相等的条件,从而成为正方形。
比如,矩形 ABCD 中,若 AB = AD ,那么它就是正方形。
3、有一个角为直角的菱形是正方形菱形的特点是四条边相等。
当菱形有一个角为直角时,它就满足了正方形四个角都是直角的条件,进而成为正方形。
例如,菱形 ABCD 中,若∠A = 90°,那么它就是正方形。
4、对角线互相垂直平分且相等的四边形是正方形如果一个四边形的对角线互相垂直平分,那么它是菱形;如果对角线还相等,那么它就同时满足了矩形的特征(对角线相等的平行四边形是矩形)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
正方形的性质及判定正方形的性质及判定板块名称 中考考试要求层次ABC正方形会识别正方形掌握正方形的概念、性质和判定,会用正方形的性质和判定解决简单问题会用正方形的知识解决有关问题1.正方形的定义:有一组邻边相等,并且有一个角是直角的平行四边形叫做正方形.2.正方形的性质正方形是特殊的平行四边形、矩形、菱形.它具有前三者的所有性质:① 边的性质:对边平行,四条边都相等. ② 角的性质:四个角都是直角.③ 对角线性质:两条对角线互相垂直平分且相等,•每条对角线平分一组对角. ④ 对称性:正方形是中心对称图形,也是轴对称图形. 平行四边形、矩形、菱形和正方形的关系:(如图)3.正方形的判定判定①:有一组邻边相等的矩形是正方形. 判定②:有一个角是直角的菱形是正方形.1. 掌握正方形的定义和性质,弄清正方形与平行四边形、菱形、矩形的关系2. 掌握正方形的判定方法并能在解题中选择恰当的方法。
3. 提高学生分析问题及解决问题的能力。
4. 通过分析概念之间的联系与区别,培养学生辨证唯物主义观点教学目标知识点睛中考要求正方形菱形矩形平行四边形重点:知晓正方形的性质和正方形的判定方法。
难点:正方形知识的灵活应用一、正方形的性质【铺垫】正方形有条对称轴.【例1】☆⑴已知正方形BDEF的边长是正方形ABCD的对角线,则:BDEF ABCDS S=正方形正方形⑵如图,已知正方形ABCD的面积为256,点F在CD上,点E在CB的延长线上,且20AE AF AF⊥=,,则BE的长为FEDCBA⑶如图,在正方形ABCD中,E为AB边的中点,G,F分别为AD,BC边上的点,若1AG=,2BF=,90GEF∠=︒,则GF的长为.【例2】☆将n个边长都为1cm的正方形按如图所示摆放,点12...nA A A,,,分别是正方形的中心,则n个正方形重叠形成的重叠部分的面积和为A5A4A3A2A1【例3】☆如图,正方形ABCD的边长为2cm,以B为圆心,BC长为半径画弧交对角线BD于点E,连接CE,P是CE上任意一点,PM BC⊥于M,PN BD⊥于N,则PM PN+的值为例题精讲重、难点PNME DCBA【铺垫】如图,E 是正方形ABCD 对角线BD 上的一点,求证:AE CE =.EDCBA【例4】 如图,P 为正方形ABCD 对角线上一点,PE BC ⊥于E ,PF CD ⊥于F .求证:AP EF =.F EPDCB A【巩固】 如图所示,正方形ABCD 对角线AC 与BD 相交于O ,MN ∥AB ,且分别与AO BO 、交于M N 、.试探讨BM 与CN 之间的关系,写出你所得到的结论的证明过程.M N CDO B A【巩固】 ☆如图,已知P 是正方形ABCD 内的一点,且ABP ∆为等边三角形,那么DCP ∠=PDCBA【例5】 已知正方形ABCD ,在AD 、AC 上分别取E 、F 两点,使2ED AD FC AC =∶∶,求证:BEF ∆是等腰直角三角形.GE H DFCBA【例6】 如图,已知E 、F 分别是正方形ABCD 的边BC 、CD 上的点,AE 、AF 分别与对角线BD 相交于M 、N ,若50EAF ∠=︒,则CME CNF ∠+∠= .NMFEDCBA【例7】 ☆如图,四边形ABCD 为正方形,以AB 为边向正方形外作正方形ABE ,CE 与BD 相交于点F ,则AFD ∠=FEDCBA【例8】 如图,正方形ABCD 中,在AD 的延长线上取点E ,F ,使DE AD =,DF BD =.连结BF 分别交CD ,CE 于H ,G .求证:GHD ∆是等腰三角形.3142FE GHCDBA【巩固】 如图,过正方形顶点A 引AE BD ∥,且BE BD =.若BE 与AD 的延长线的交点为F ,求证DF DE =.GFEBDA【例9】 如图所示,在正方形ABCD 中,AK 、AN 是A ∠内的两条射线,BK AK ⊥,BL AN ⊥,DM AK ⊥,DN AN ⊥,求证KL MN =,KL MN ⊥.K NMLDCBA【巩固】 如图,正方形ABCD 的边CD 在正方形ECGF 的边CE 上,连接,BE DG ,求证:BE DG =.GC FEDBA【例10】 (2007年三帆中学期中考试)如图,在正方形ABCD 中,E 为CD 边上的一点,F 为BC 延长线上的一点,CE CF =,30FDC ∠=︒,求BEF ∠的度数.BDCAEF【巩固】 ☆已知:如图,在正方形ABCD 中,G 是CD 上一点,延长BC 到E ,使CE CG =,连接BG 并延长交DE 于F . (1)求证:BCG DCE ∆∆≌;(2)将DCE △绕点D 顺时针旋转90︒得到DAE '∆,判断四边形E BGD '是什么特殊四边形?并说明理由.【例11】 若正方形ABCD 的边长为4,E 为BC 边上一点,3BE =,M 为线段AE 上一点,射线BM 交正方形的一边于点F ,且BF AE =,则BM 的长为 .【例12】 ☆如图1,在正方形ABCD 中,E 、F 、G 、H 分别为边AB 、BC 、CD 、DA 上的点,HA EB FC GD ===,连接EG 、FH ,交点为O .⑴ 如图2,连接EF FG GH HE ,,,,试判断四边形EFGH 的形状,并证明你的结论; ⑵ 将正方形ABCD 沿线段EG 、HF 剪开,再把得到的四个四边形按图3的方式拼接成一个ABCD EF E 'G四边形.若正方形ABCD 的边长为3cm ,1cm HA EB FC GD ====,则图3中阴影部分的面积为_________2cm .图3图1图2H DGC FEBAOH GFEDC BA【巩固】 如图,正方形ABCD 对角线相交于点O ,点P 、Q 分别是BC 、CD 上的点,AQ DP ⊥,求证:(1)OP OQ =;(2)OP OQ ⊥.BO D CAQP【例13】 如图,正方形ABCD 中,E F ,是AB BC ,边上两点,且EF AE FC DG EF =+⊥,于G ,求证: DG DA =G FEC DBA【巩固】 如图,点M N ,分别在正方形ABCD 的边BC CD ,上,已知MCN ∆的周长等于正方形ABCD 周长的一半,求MAN ∠的度数NMDCBA【巩固】 如图,设EF ∥正方形ABCD 的对角线AC ,在DA 延长线上取一点G ,使AG AD =,EG 与DF 交于H ,求证:AH =正方形的边长.HEGCDFBA【例14】 ☆把正方形ABCD 绕着点A ,按顺时针方向旋转得到正方形AEFG ,边FG 与BC 交于点H (如图).试问线段HG 与线段HB 相等吗?请先观察猜想,然后再证明你的猜想.GC HF EDB A【例15】 如图所示,在直角梯形ABCD 中,AD BC ∥,90ADC ∠=︒,l 是AD 的垂直平分线,交AD 于点M ,以腰AB 为边作正方形ABFE ,作EP l ⊥于点P ,求证22EP AD CD +=.lPM FE DC BA二、正方形的判定 【例16】 四边形ABCD 的四个内角的平分线两两相交又形成一个四边形EFGH ,求证:⑴四边形EFGH 对角互补;⑵若四边形ABCD 为平行四边形,则四边形EFGH 为矩形. ⑶四边形ABCD 为长方形,则四边形EFGH 为正方形.HEFG DCBA【巩固】 如图,已知平行四边形ABCD 中,对角线AC 、BD 交于点O ,E 是BD 延长线上的点,且ACE ∆是等边三角形.⑴ 求证:四边形ABCD 是菱形;⑵ 若2AED EAD ∠=∠,求证:四边形ABCD 是正方形.OEDCBA【巩固】 已知:如图,在ABC ∆中,AB AC =,AD BC ⊥,垂足为点D ,AN 是ABC ∆外角CAM ∠的平分线,CE AN ⊥,垂足为点E .⑴ 求证:四边形ADCE 为矩形;⑵ 当ABC ∆满足什么条件时,四边形ADCE 是一个正方形?并给出证明.M ENCDBA【例17】 ☆如图,点M 是矩形ABCD 边AD 的中点,2AB AD =,点P 是BC 边上一动点,PE MC ⊥,PF BM ⊥,垂足分别为E 、F ,求点P 运动到什么位置时,四边形PEMF为正方形.PMF EDC BA【例18】 ☆如图,ABCD 是边长为1的正方形,EFGH 是内接于ABCD 的正方形,AE a AF b ==,,若23EFGH S =,则b a -=H GFEDCBA【例19】 如图,A 在线段BG 上,ABCD 和DEFG 都是正方形,面积分别为27cm 和211cm ,则CDE ∆ 的面积为GFEDCB A【巩固】 ☆如图,在正方形ABCD 中,点1P P ,为正方形内的两点,且11PB PD PB AB CBP PBP ==∠=∠,,,则1BPP ∠=P 1PDCBA【例20】 如图,若在平行四边形ABCD 各边上向平行四边形的外侧作正方形,求证:以四个正方形中心为顶点组成一个正方形.PRQ S NMFEDCBA【例21】 ☆已知:2PA =,4PB =,以AB 为一边作正方形ABCD ,使P 、D 两点落在直线AB 的两侧.(1)如图,当∠APB=45°时,求AB 及PD 的长;(2)当∠APB 变化,且其它条件不变时,求PD 的最大值,及相应∠APB 的大小.PDCBA1.如图,正方形ABCD 中,O 是对角线AC BD ,的交点,过点O 作OE OF ⊥,分别交AB CD ,于E F ,,若43AE CF ==,,则EF = OFE DC BA课后练习2. 如图所示,ABCD 是正方形,E 为BF 上的一点,四边形AEFC 恰好是一个菱形,则EAB ∠=______.A BCD EF3. 如果点E 、F 是正方形ABCD 的对角线BD 上两点,且BE DF =,你能判断四边形AECF 的形状吗?并阐明理由.ECD F B A4. 如图,在正方形ABCD 中,E 、F 分别是AB 、BC 的中点,求证:AM AD =.MF ED CB A。
