线性空间与欧几里得空间
第九章欧几里得空间

xi 2
i 1
(4) , arccos
n
xi yi
i1
n
n
xi2
yi2
i1
i1
第九章欧几里得空间
12
首页 上页 下页 返回 结束
n
(5) d() (xi yi)2 i1
4. 标准正交基的存在性与正交化方法
设 1 ,2 , ,n 是 一 组 基 . 正 交 化 过 程 如i1aj1 ai2aj2 ainajn 0, i j A 是 正 交 矩 阵 A 的 列 向 量 组 和 行 向 量 组 都 构 成
R n 的 标 准 正 交 基 .
第九章欧几里得空间
15
首页 上页 下页 返回 结束
6. 对称变换与对称矩阵
设是n维欧氏空间V的一个线性变换. 是
长度: | | (,)
距离: d(,)||
夹角:,arccos|( |,|)|,0,.
第九章欧几里得空间
6
首页 上页 下页 返回 结束
(3) 度量矩阵
基 1 ,2 , ,n 的 度 量 矩 阵
(1,1) (1,2) A( aij)nn (2,1) (2,2)
(n,1) (n,2)
(1,n) (2,n)
对称变换的刻化:
矩阵是正交阵.
第九章欧几里得空间
14
首页 上页 下页 返回 结束
n 级 实 数 矩 阵 A 是 正 交 矩 阵 A A E . 标准正交基到标准正交基的过渡矩阵是正交矩阵; 设A (aij ),则A是正交矩阵
1, 当i j, a1ia1j a2ia2j anianj 0, 当i j.
3. 标准正交基下基本度量的表达式
设 1,2, ,n是 欧 氏 空 间 V的 一 个 标 准 正 交 基 ,
线性空间的基本内容

(3)线性变换将线性相关的向量组变为线性相关的向量组
注意:线性无关的向量组经过线性变换后可能会变成线性相关的向量组,如零变换
3、线性变换的矩阵
(1) 定义 教材P133定义3.11
(2) 求线性变换一组基下的矩阵 教材P134例8---例11。
(2) 正交基与标准正交基 教材P145定义3.17
对一组正交基进行单位化,就得到一组标准正交基
(3) 在标准正交基下,向量坐标可用内积简单表示:见教材P145 定理3.11
在标准正交基下,内积也有特别简单的表达式:设 ,在 的标准正交基 下,有 , ,则
(4)第二章中施密特正交化方法可以推广到一般的欧氏空间 教材P146定理3.12
② 两个等价的线性无关的向量组一定含有相同个数的向量。
(4)基 教材P122定义3.5
(5)坐标 教材P122定义3.6
注意:
① 若是 为 维线性空间 的一组基,则它们线性无关,并且对于任意 , 线性相关。
② 向量在一组基下的坐标唯一。
4、基变换与坐标变换 教材P125定理 3.4
本章小结
线性空间是线性代数最基本的概念之一,也是我们碰到的第一个抽象的概念。在线性空间中,元素之间的联系是通过映射来实现的,而通常将线性空间到自身的映射称为变换。线性变换是其中最基本也是最重要的变换,它是线性代数的主要研究对象之一。本章重点介绍了两方面的内容:线性空间的概念、性质,线性空间的基与坐标;线性变换的定义,线性变换的矩阵。最后简要介绍了欧氏空间。
(3) 线性变换的像 与 的坐标之间的关系 教材P137定理3.7
4、线性变换与矩阵的一一对应关系
《高等代数与解析几何》教学大纲
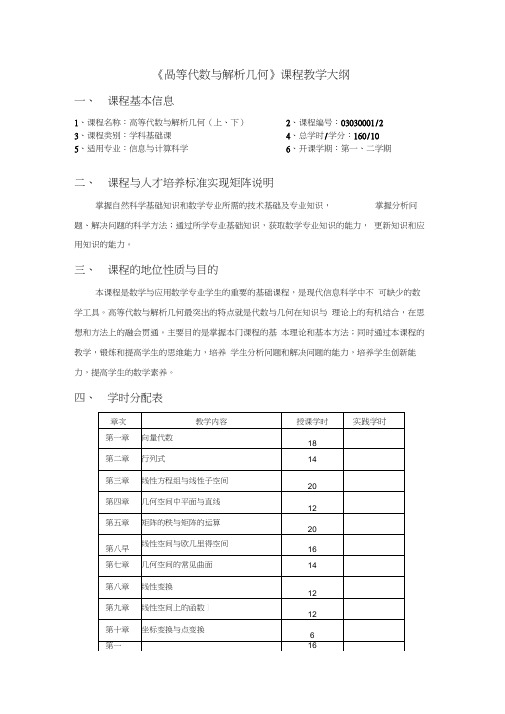
《咼等代数与解析几何》课程教学大纲一、课程基本信息1、课程名称:高等代数与解析几何(上、下)2、课程编号:03030001/23、课程类别:学科基础课4、总学时/学分:160/105、适用专业:信息与计算科学6、开课学期:第一、二学期二、课程与人才培养标准实现矩阵说明掌握自然科学基础知识和数学专业所需的技术基础及专业知识,掌握分析问题、解决问题的科学方法;通过所学专业基础知识,获取数学专业知识的能力,更新知识和应用知识的能力。
三、课程的地位性质与目的本课程是数学与应用数学专业学生的重要的基础课程,是现代信息科学中不可缺少的数学工具。
高等代数与解析几何最突出的特点就是代数与几何在知识与理论上的有机结合,在思想和方法上的融会贯通。
主要目的是掌握本门课程的基本理论和基本方法;同时通过本课程的教学,锻炼和提高学生的思维能力,培养学生分析问题和解决问题的能力,培养学生创新能力,提高学生的数学素养。
四、学时分配表五、课程教学内容和基本要求总的目标:通过本课程的学习要求学生对高等代数与解析几何的基本概念、基本定理有比较全面、系统认识,能把几何的观点与代数的方法结合起来,“代数为几何提供研究方法,几何为代数提供直观背景”,逐步培养学生运用几何与代数相结合的方法分析问题、解决问题的能力,培养学生抽象的思维能力及空间想象能力。
本课程各章的教学内容和基本要求如下:第一章向量代数【教学内容】1、向量的线性运算2、向量的共线与共面3、用坐标表示向量4、线性相关性与线性方程组5、n维向量空间6、几何空间向量的内积7、几何空间向量的外积8、几何空间向量的混合积【基本要求】理解向量的概念,掌握向量的线性运算、内积、外积、混合积运算;熟悉向量间垂直、共线、共面的条件;会用坐标进行向量的运算。
【教学重点及难点】重点:向量的概念,向量的线性运算、内积、外积、混合积运算;用坐标进行向量的运算。
难点:向量间垂直、共线、共面的条件。
第二章行列式【教学内容】1、映射与变换2、置换的奇偶性3、矩阵4、行列式的定义理解n阶行列式的概念及性质,掌握常见类型的行列式的计算;熟悉克拉默法则。
同构对线性空间和欧几里得空间的作用及推广

0 引言
线性空 间和欧几里 得空 间( 称 欧 氏空 间) 简
映射 来研 究欧氏空间 中线性 变换 的作 用 ,并 着重对对 称变换进行 了分析 。
关 键 词 :线 性 空 间 ;欧 几 里 得 空 间 ; 同构 映 射 ;对 称 变换 中 图分 类 号 :0 7 . 6 1 52 文 献 标 识 码 :A 文 章 编 号 :17 6 3—6 2 (0 0 3— 0 1 3 15 2 1 )0 0 6 一o
The Ro e a d Ex e i n o s m o p c M a l n t nso f I o r hi p
i ne r S c nd Euci e n S c n Li a pa e a ld a pa e
CA00 e .2 1
同构 对 线 性 空 间 和欧 几 里 得 空 间的 作 用 及 推 广
曲 、卓 日 言 l
( 内蒙古财经学院 统计数学学院 , 内蒙古 呼和浩特 007 ) 10 0
摘
要 :讨 论 了 同构 映 射 对 线 性 空 间及 欧 氏 空 间 的 作 用 , 同 构 的 线 性 空 间及 欧 氏 空 间 之 间 的 性 质 ;通 过 同 构
第 5卷
第 3期
贵 阳学院 学报 ( 自然科 学 版 ) ( 刊 ) 季
J OUR NAL O F GUI YANG COU GE E
V 1 5 No 3 0 _ . .
空间维度的概念是什么

空间维度的概念是什么空间维度指的是描述空间中位置的自由度,也是某个空间中的坐标轴的数量。
在数学和物理学中,我们常常用维度来描述一个空间的性质和特征。
维度的概念在不同的学科中有不同的定义和应用,下面我将从几个方面来详细介绍空间维度的概念。
1. 欧几里得空间维度欧几里得空间是指我们通常所了解的三维空间,即我们常常使用的三维坐标系来描述。
在欧几里得空间中,我们通常使用三个坐标轴(x,y,z)来描述物体或者位置的三个自由度。
这三个自由度可以分别看作是空间中的长度、宽度和高度。
因此,欧几里得空间的维度为3。
2. 线性代数中的维度在线性代数中,我们定义了向量空间的维度。
向量空间是指由一组向量所张成的空间。
在向量空间中,我们定义了线性独立性的概念。
一组向量中的任意一个向量都不能用其他向量的线性组合表示,那么我们称这组向量是线性独立的。
一个向量空间的维度是指能够张成该空间的最大线性无关的向量的数量。
例如,对于二维向量空间,我们可以用两个线性无关的向量来张成该空间,因此其维度为2。
同样地,对于三维向量空间,我们需要三个线性无关的向量来张成该空间,因此其维度为3。
3. 分形维度在分形几何学中,我们引入了分形维度的概念。
分形是指一个具有自相似性的几何形状,即这个几何形状的一部分看起来和整体是相似的。
分形维度是一种描述分形几何形状复杂性的度量,其概念是由数学家曼德博特提出的。
曼德博特通过计算某个几何形状的维数来刻画其自相似的特性。
一般来说,分形维度小于整数维度,因为分形形状的复杂性无法用整数维度来描述。
分形维度的计算方法有多种,比较常用的包括盒计数法、哈斯托夫维度法等。
4. 多维空间除了传统的三维空间,数学上还引入了多维空间的概念。
多维空间是指具有多个坐标轴的空间。
在多维空间中,我们可以用更多的坐标轴来描述物体或者位置的自由度。
多维空间的维度可以是任意的,不仅限于二维或者三维。
例如,四维空间常常在相对论中使用,其中一个维度是时间维度。
高代第9章讲义

(α,α) 第九章Euclid(欧几里得)空间知识点考点精要一、欧几里得空间的基本概念1、设V 是实数域 R 上的线性空间,在V上定义了一个二元实函数,称为内积,记作(α,β) ,它具有以下性质:(1) (α,β) = (β,α) ; (2) (k α,β) = k (α,β) ; (3) (α+ β,γ) = (α,γ) + (β,γ) ;(4) (α,α) ≥ 0, 当且仅当α= 0 时, (α,α) = 0 。
这里α,β,γ是V 中任意向量, k 是任意实数,这样的线性空间V 称为欧几里得空间。
2、向量的长度 α= 。
3、柯西 - 布涅柯夫斯基不等式对于欧氏空间V 中的任意向量α,β,有 (α,β) ≤ αβ。
当且仅当α,β线性相关时,等号成立。
4、非零向量α, β的夹角< α,β> 规定为 < α,β>= arccos (α,β),0 ≤< α,β>≤ π。
αβ5、如果(α,β) = 0, 称α与β正交,记为α⊥ β。
6、度量矩阵 设V 是 n 维欧氏空间,ε1 ,ε2 , ,εn 是⎨ V 的一组基,令 a ij= (εi ,εj )(i ,j = 1,2,.., n ) 矩阵 A= (a ij )n ⨯n 称为基ε1 ,ε2 , ,εn 的度量矩阵,⎛ (ε1 ,ε1 ) (ε1 ,ε2 ) (ε ,ε)(ε ,ε ) (ε1 ,εn ) ⎫ (ε ,ε ) ⎪A = 2 1222n⎪ ⎪ (ε ,ε) (ε ,ε )(ε ,ε ) ⎪⎝ n 1n2 n n ⎭1) 度量矩阵为正定矩阵; 2) 不同基的度量矩阵是合同的。
7、标准正交基1) ε1 ,ε2 , ,εn 是欧氏空间 V 的一组基,如果(ε,ε ) = ⎧1 (i = j )ij ⎩0 (i ≠ j ) ,那么称ε1 ,ε2 , ,εn 是V的一组标准正交基。
2) 标准正交基的度量阵是单位阵。
数学中的空间概念

数学中的空间概念
数学中的空间概念是指用数学语言和方法对空间进行描述和研究的概念。
1. 欧几里得空间(Euclidean space):欧几里得空间是数学中
最基本且最常见的空间概念,它以几何学为基础,通常用笛卡尔坐标系表示。
2. 向量空间(Vector space):向量空间是指一组向量构成的
集合,满足一系列定义的运算规则,常用于向量和矩阵的研究。
3. 坐标空间(Coordinate space):坐标空间是指通过一组坐标系,将点的位置表示为坐标的空间。
常见的坐标空间有二维平面、三维空间等。
4. 线性空间(Linear space):线性空间是指满足特定运算规
则的向量空间,其中向量的加法和数乘满足线性运算的性质。
5. 拓扑空间(Topological space):拓扑空间是指在集合上定
义了一种拓扑结构,用来研究集合中的连通性、收敛性以及极限等性质。
6. 测度空间(Measure space):测度空间是指在集合上定义了一种测度,用来度量集合中的大小或者衡量集合中的某种特性。
7. 平面几何(Plane geometry):平面几何是指研究二维平面
中图形的性质、关系和构造等内容。
8. 立体几何(Solid geometry):立体几何是指研究三维空间
中立体图形的性质、关系和构造等内容。
9. 代数拓扑(Algebraic topology):代数拓扑是将代数学方法
应用于拓扑空间研究的一个分支,研究空间的代数性质和变形等问题。
10. 同调论(Homology theory):同调论是数学中的一个分支,研究空间中的“洞”和“环”等代数特征,用于研究空间的性质和
分类。
线性空间和欧式空间

线性空间和欧式空间第六章线性空间和欧式空间§1线性空间及其同构一线性空间的定义设V是一个非空集合,K是一个数域,在集合V的元素之间定义了一种代数运算,叫做加法;这就是说,给出了一个法则,对于V中任意两个元素和,在V中都有唯一的一个元素与他们对应,成为与的和,记为在数域K与集合V的元素之间还定义了一种运算,叫做数量乘法,即对于数域K中任一数k与V中任一元素,在V中都有唯一的一个元素与他们对应,称为k与的数量乘积,记为k,如果加法与数量乘法满足下述规则,那么V称为数域K上的线性空间。
加法满足下面四条规则:1);交换律2)()();结合律3)在V中有一个元素0,对于V中任一元素都有0(具有这个性质的元素0称为V的零元素);存在零元4)对于V中每一个元素,都有V中的元素,使得0(称为的负元素).存在负元数量乘法满足下面两条规则:5)1;存在1元6)k(l)(kl).数的结合律数量乘法与加法满足下面两条规则:7)(kl)kl;数的分配律8)k()kk.元的分配律在以上规则中,k,l表示数域中的任意数;,,等表示集合V中任意元素。
例1.元素属于数域K的mn矩阵,按矩阵的加法和矩阵的与数的数量乘法,构成数域K上的一个线性空间,记为Mm,n(K)。
例2.全体实函数(连续实函数),按函数的加法和数与函数的数量乘法,构成一个实数域上的线性空间。
例3.n维向量空间K是线性空间。
n1例4.向量空间的线性映射的集合HomK(K,K)是线性空间。
二.简单性质1.零元素是唯一的。
2.负元素唯一。
3.00,k00,(1)4.若k0,则k0或者0。
三.同构映射定义:设V,V是数域K上的线性空间.AHomK(V,V)是一个线性映射.如果A 是一一映射,则称A是线性空间的同构映射,简称同构。
线性空间V与V'称为同构的线性空间。
定理数域P上两个有限维线性空间同构的充分必要条件是他们有相同的维数。
同构映射的逆映射以及两个同构映射的乘积还是同构映射。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
线性空间与欧几里得空间
自测题
一、填空题
1、对欧几里得空间V 中的任意向量βα,,有()βαβα≤
,,而且等号成立当且仅当 。
2、设1W 与2W 是V 的两个线性子空间,如果1W +2W 中的每个向量α都可唯一的被表示成21ααα+=,2211W W ∈∈αα,,则称1W +1W 为这两个子空间的 。
3、两个同构的线性空间的维数 。
4、第二类正交变换的行列式的值等于 。
5、如果A 是正交矩阵。
若k 为实数,使kA 为正交矩阵,则k 等于 。
二、选择题
6、下列n R 的子集是n R 的子空间的为( )
A :(){}n i Z a a a a a i n ...,3,2,1,.....,,,321=∈
B :(){}0.....,,,21321=a a a a a a n
C :(){}R a a a a n ∈211,,0,...,0, C :{}
1..)...,,(2222121≤+++n n a a a a a a 7、全体正实数的集合+R 对于下面定义的加法与标量乘法:k
a a k a
b b a ==⊕ ,构成R 上的线性空间,则+R 的零元素为( )
A :0 B: 1 C: 2 D: 3
8、若A 是正交矩阵,则下列矩阵中仍为正交矩阵的是(多重选择,其中k 是1±≠的整数)
A:kA B:k A C:交换A 的任两行所得的矩阵
D :把A 的某行k 倍加到另一行所得的矩阵
9、设A 是欧几里得空间V 关于基n ααα,,,...21的度量矩阵,则A 满足以下哪个条件时,n ααα,,,...21是规范正交基? ( )
A: A 是正交矩阵 B :A 为对称矩阵 C :1-A 为正交矩阵 D :A 为单位矩阵
10、以下哪个结论不是两个线性子空间1W 与2W 的和21W W +为直和的等价命题:( ) A :dim ()()()()221121dim dim dim dim W W W W W W >+>+且
B: 021=W W
C: ()2121dim dim dim W W W W +=+
D: 若m αα...,1,是1W 的一个基,n ββ...,1,是2W 的一个基,则m αα...,1,,n ββ...,1,线性无关。
三、判断题
11、欧几里得空间中任一基下的度量矩阵必为实对称矩阵 ( )
12、正交变换保持向量间的夹角不变 ( )
13、在3
R 中,对向量()()321321,,,,,b b b a a a ==βα规定()332211b a b a b a +-=βα,,则 3R 关于这一实函数成为欧几里得空间。
( )
14、当数域K 和非空集合V 固定时,只有惟一的一种方法定义线性空间。
( )
四、计算题
15、集合(){}0,,,432143211=-+-==
a a a a a a a a V α与(){}0,,,432143212=+++=a a a a a a a a V 是4R 的两个子空间,找出21V V 的一个基,并求21V V 的维数。
16、设U 与W 分别是4R 的由()()()()()()343,132,3,222,2,11,33,203,2,110,1,1321321-=-=-=-==-=,,,,,,,与,,,,,βββααα生成的子空间,求U+W 和U W 的基和维数。
17、在欧几里得空间中求以下各组向量的长度和夹角。
(1)()()2,1,011,1,1,3,,==βα (2)()()0,11,32,1,11-==,,,βα
18、求由欧几里得空间4
R 中的向量()()()78,2,33,51,112,2,1321-=-=-=,,,,,ααα所生成的子空间的规范正交基。
19、在标准欧几里得空间4R 中,求向量()2,53,3-=,β在由向量()3,21,21
--=,α, ()()1,32,22,32,132-=-=,,,αα生成的子空间上的正交投影*β。
20、设U 是n 维线性空间V 的非平凡子空间,证明:存在不止一个V 的子空间W ,使.W U V ⊕=
21、设()
()R M a A n ∈=ij 为正交矩阵,且1=A 。
证明:ij ij A a =,这里ij A 是ij a 的代数余子式。
22、设m m a a ββ,...,,,...11为欧几里得空间V 的两组向量。
证明如果
()(),,...,2,1,,,,m j i a a j i j i ==ββ,则子空间()m a a L V ,...,11=与()m L V ββ,...,12=同构。
23、设s V V V ,...,,21是欧几里得空间V 的子空间,s V V V W +++=...21.若s V V V ,...,,21两两正交,证明:s V V V W ⊕⊕⊕=...21。
