山东省2019年普通高校招生(春季)考试 数学试题-答案
(完整word版)2019年山东省春季高考数学真题

山东省2019级普通高校招生(春季)考试数学试题1、本试卷分卷一(选择题)和卷二(非选择题)两部分。
满分120分,考试时间120分钟。
考试请在答题卡上答题,考试结束后,请将本试卷和答题卡一并交回。
2、本次考试允许使用函数型计算器。
凡使用计算器的题目,除题目有具体要求外,最后结果精确到0.01。
卷一(选择题 共60分)一、选择题(本大题共20小题,每小题3分,共60分。
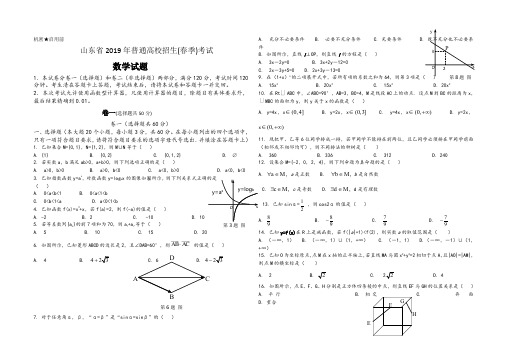
在每小题给出的四个选项中,只有一项是符合题目的要求,请将符合题目要求的选项字母代号选出,并涂在答题卡上)1. 已知集合{}{},2,1,1,0==N M 则N M 等于 A .{}1 B .{}2,0 C .{}2,1,0 D .∅ 2.若实数b a ,满足0,0>>b a ab +,则下列选项正确的是A .0,0>>b aB .0,0<>b aC .0,0><b aD .0,0<<b a3.已知指数函数,xa y =对数函数x y a log =的图像如图所示,则下列关系式成立的是( ).A .1b 0<<<aB .b 10<<<aC .a <<<1b 0D .b a <<<104.已知函数x x x f +=3)(,若2)(=a f ,则)(a f -的值是 A .-2 B .2 C .-10 D .10 5.若等差数列}{n a 的前7项和为70,则71a a +等于 A .5 B .10 C .15D .206.如图所示,已知菱形ABCD 的边长是2,且︒=∠60DAB ,则AC AB ⋅的值是A .4B .324+C .6D .324-7.对于任意角”的”是““βαβαβαsin sin ,,== ( ).A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件 8.如图所示,直线OP l ⊥,则直线l 的方程是A .023=-y xB .01223=-+y xC .0532=+-y xD .01332=-+y x9.在n x )1(+的二项展开式中,若所以项的系数之和为64,则第3项是.A .315xB .320xC .215xD .220x10.在ABC △Rt 中,M 4B C 3AB 90AB C ,,,==︒=∠是线段AC 上的动点,设点M 到BC 的距离为x,△MBC 的面积为y ,则y 关于x 的函数是( ).A .]4,0(,4∈=x x yB .]3,0(,2∈=x x yC .)+∞∈=,0(,4x x yD .)+∞∈=,0(,2x x y11. 线把甲、乙等6位同学排成一列,若甲同学不能排在前两位,且乙同学必须排在甲同学前面(相邻或不相邻均可),则不同的排法的种数是A .360B .336C .312D .240 12. 设集合},4,2,0,2{-=M 则下列命题为真命题的是A .是正数a M a ,∈∀B .是自然数b M b ,∈∀C .是奇数c M c ,∈∃D .是有理数d M d ,∈∃ 13. 已知31sin =α,则α2cos 的值是 A .98 B .98- C .97 D .97-14. 已知)(x f y =在R 上是减函数,若)2()1(f a f <+,则实数a 的取值范围是 A .)1,(-∞ B .),1()1,(+∞-∞C .)1,1(-D .),1()1,(+∞--∞15. 已知O 为坐标原点,点M 在x 轴的正半轴上,若直线MA 与圆222=+y x 相切于点A,且AM AO =,则点M 的横坐标是A .2B .2C .22D .416. 如图所示,点E,F,G ,H 分别是正方体四条棱的中点,则直线EF 与GH 的位置关系是A.平行 B .相交 C. 异面 D .重合17. 如图所示,若y x ,满足线性约束条件⎪⎩⎪⎨⎧≥≤≥+-1002y x y x 则线性目标函数y x z -=2取得最小值时的最优解是A .)1,0(B .)2,0(C .)1,1(-D .)2,1(-18. 箱子中放有6张黑色卡片和4张白色卡片,从中任取一张,恰好取到黑色卡片的概率是 A .61 B .31 C .52D .5319. 已知抛物线的顶点在坐标原点,对称轴为坐标轴,若该抛物线经过点)4,2(-M ,则其标准方程是A .x y 82-=B .y x y =-=22x 8或C .y x =2D .y x y -==22x 8或20. 已知△ABC 的内角A,B,C 的对边分别是a,b,c ,若C B A a sin cos 2sin ,6==,向量,m ),sin ,cos (),3,(n B A n b a m ∥且-==则△ABC 的面积是A .318B .39C .33D .3卷二(非选择题 共60分)二、填空题(本大题共5小题,每小题4分,共20分。
2019年高考数学真题及答案(含全国1卷,全国2卷,全国3卷共3套)

绝密★启用前 全国卷Ⅰ2019年普通高等学校招生全国统一考试理科数学本试卷共4页,23小题,满分150分,考试用时120分钟。
注意事项:1.答卷前,考生务必将自己的姓名、考生号、考场号和座位号填写在答题卡上。
用2B 铅笔将试卷类型(B )填涂在答题卡的相应位置上。
2.作答选择题时,选出每小题答案后,用2B 铅笔在答题卡上对应题目选项的答案信息点涂黑;如需改动,用橡皮擦干净后,再选涂其它答案。
答案不能答在试卷上。
3.非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新答案;不准使用铅笔和涂改液。
不按以上要求作答无效。
4.考生必须保证答题卡的整洁。
考试结束后,将试卷和答题卡一并交回。
一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合}242{60{}M x x N x x x =-<<=--<,,则M N =A .}{43x x -<<B .}42{x x -<<-C .}{22x x -<<D .}{23x x <<2.设复数z 满足=1i z -,z 在复平面内对应的点为(x ,y ),则A .22+11()x y +=B .221(1)x y +=-C .22(1)1y x +-=D .22(+1)1y x +=3.已知0.20.32log 0.220.2a b c ===,,,则 A .a b c <<B .a c b <<C .c a b <<D .b c a <<4.古希腊时期,人们认为最美人体的头顶至肚脐的长度与肚脐至足底的长度之比是512-(512-≈0.618,称为黄金分割比例),著名的“断臂维纳斯”便是如此.此外,最美人体的头顶至咽喉的长度与咽喉至肚脐的长度之比也是512-.若某人满足上述两个黄金分割比例,且腿长为105 cm ,头顶至脖子下端的长度为26 cm ,则其身高可能是A .165 cmB .175 cmC .185 cmD .190cm5.函数f (x )=2sin cos ++x xx x在[,]-ππ的图像大致为 A . B .C .D .6.我国古代典籍《周易》用“卦”描述万物的变化.每一“重卦”由从下到上排列的6个爻组成,爻分为阳爻“——”和阴爻“— —”,如图就是一重卦.在所有重卦中随机取一重卦,则该重卦恰有3个阳爻的概率是A .516B .1132C .2132D .11167.已知非零向量a ,b 满足||2||=a b ,且()-a b ⊥b ,则a 与b 的夹角为A .π6B .π3C .2π3D .5π68.如图是求112122++的程序框图,图中空白框中应填入A .A =12A+ B .A =12A+C .A =112A+D .A =112A+9.记n S 为等差数列{}n a 的前n 项和.已知4505S a ==,,则A .25n a n =-B . 310n a n =-C .228n S n n =-D .2122n S n n =- 10.已知椭圆C 的焦点为121,01,0F F -(),(),过F 2的直线与C 交于A ,B 两点.若22||2||AF F B =,1||||AB BF =,则C 的方程为A .2212x y += B .22132x y += C .22143x y += D .22154x y += 11.关于函数()sin |||sin |f x x x =+有下述四个结论:①f (x )是偶函数②f (x )在区间(2π,π)单调递增③f (x )在[,]-ππ有4个零点 ④f (x )的最大值为2其中所有正确结论的编号是 A .①②④B .②④C .①④D .①③12.已知三棱锥P -ABC 的四个顶点在球O 的球面上,P A =PB =PC ,△ABC 是边长为2的正三角形,E ,F分别是P A ,PB 的中点,∠CEF =90°,则球O 的体积为A .B .C . D二、填空题:本题共4小题,每小题5分,共20分。
2019年山东数学(理)高考试题(Word版,含答案解析)

高考数学精品复习资料2019.5绝密★启用前普通高等学校招生全国统一考试(山东卷)理科数学一、选择题:本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符号题目要求的.(1)设函数A ,函数y=ln(1-x)的定义域为B,则A B =(A )(1,2) (B )⎤⎦(1,2 (C )(-2,1) (D )[-2,1) 【答案】D【解析】由240x -≥得22x -≤≤,由10x ->得1x <,故A B={|22}{|1}{|21}x x x x x x -≤≤⋂<=-≤<,选D.(2)已知a R ∈,i 是虚数单位,若,4z a z z =⋅=,则a=(A )1或-1 (B (C ) (D 【答案】A【解析】由,4z a z z =⋅=得234a +=,所以1a =±,故选A.(3)已知命题p:()x x ∀+>0,ln 1>0;命题q :若a >b ,则a b 22>,下列命题为真命题的是 (A ) pq∧ (B )p q⌝∧ (C )p q ⌝∧ (D )p q ⌝⌝∧【答案】B(4)已知x,y 满足x y 3x y ⎧-+≤⎪+≤⎨⎪+≥⎩30+5030x ,则z=x+2y 的最大值是(A )0 (B ) 2 (C ) 5 (D )6【答案】C【解析】由x y 3x y ⎧-+≤⎪+≤⎨⎪+≥⎩30+5030x 画出可行域及直线20x y +=如图所示,平移20x y +=发现,当其经过直线3x +y 50=+与x -3=的交点(3,4)-时,2z x y =+最大为3245z =-+⨯=,选C. (5)为了研究某班学生的脚长x (单位:厘米)和身高y (单位:厘米)的关系,从该班随机抽取10名学生,根据测量数据的散点图可以看出y 与x 之间有线性相关关系,设其回归直线方程为ˆˆˆybx a =+.已知101225i i x ==∑,1011600i i y ==∑,ˆ4b =.该班某学生的脚长为24,据此估计其身高为(A )160 (B )163 (C )166 (D )170 【答案】C【解析】22.5,160,160422.570,42470166x y a y ==∴=-⨯==⨯+= ,选C.(6)执行学科#网两次右图所示的程序框图,若第一次输入的x 的值为7,第二次输入的x 的值为9,则第一次、第二次输出的a 的值分别为(A )0,0 (B )1,1 (C )0,1 (D )1,0【答案】D【解析】第一次227,27,3,37,1x b a =<=>= ;第二次229,29,3,39,0x b a =<===,选D. (7)若0a b >>,且1ab =,则下列不等式成立的是 (A )()21log 2a b a a b b +<<+ (B )()21log 2a b a b a b <+<+ (C )()21log 2a ba ab b +<+< (D )()21log 2a b a b a b +<+<【答案】B【解析】221,01,1,log ()log 1,2aba b a b ><<∴<+>= 12112log ()a ba ab a a b b b+>+>+⇒+>+ ,所以选B. (8)从分别标有1,2,,9的9张卡片中不放回地随机抽取2次,每次抽取1张.则抽到的2张卡片上的数奇偶性不同的概率是 (A )518 (B )49 (C )59(D )79 【答案】C【解析】125425989C C =⨯ ,选C. (9)在C ∆AB 中,角A ,B ,C 的对边分别为a ,b ,c .若C ∆AB 为锐角三角形,且满足()sin 12cosC 2sin cosC cos sinC B +=A +A ,则下列等式成立的是(A )2a b = (B )2b a = (C )2A =B (D )2B =A【答案】A【解析】sin()2sin cos 2sin cos cos sin A C B C A C A C ++=+ 所以2sin cos sin cos 2sin sin 2B C A C B A b a =⇒=⇒=,选A.(10)已知当[]0,1x ∈时,函数()21y mx =-的图象与y m =的图象有且只有一个交点,则正实数m 的取值范围是 (A )(])0,123,⎡+∞⎣(B )(][)0,13,+∞(C )()23,⎡+∞⎣(D )([)3,+∞【答案】B二、填空题:本大题共5小题,每小题5分,共25分(11)已知()13nx +的展开式中含有2x 项的系数是54,则n = . 【答案】4【解析】()1C 3C 3rr r r rr n n x x +T ==⋅⋅,令2r =得:22C 354n ⋅=,解得4n =.(12)已知12,e e 是互相垂直的单位向量,若12-e 与12λ+e e 的夹角为60,则实数λ的值是 .【解析】)()221212112122333e e e e e e e e e λλλλ-⋅+=+⋅-⋅-=,()2221233232e e e e e e e -=-=-⋅+=,()22221221e e e e e e e e λλλλ+=+=+⋅+=+∴2cos601λ==+,解得:3λ=. (13)由一个长方体和两个14圆柱体构成的几何体的三视图如右图,则该几何体的体积为 .【答案】22π+【解析】该几何体的体积为21V 112211242ππ=⨯⨯⨯+⨯⨯=+. (14)在平面直角坐标系xOy 中,双曲线()222210,0x y a b a b-=>>的右支与焦点为F 的抛物线()220x px p =>交于,A B 两点,若4AF BF OF +=,则该双曲线的渐近线方程为 .【答案】y x =(15)若函数()x e f x ( 2.71828e =是自然对数的底数)在()f x 的定义域上单调递增,则称函数()f x 具有M 性质.下列函数中所有具有M 性质的函数的序号为 .①()2x f x -=②()3x f x -=③()3f x x =④()22f x x =+【答案】①④【解析】①()22xxxxe ef x e -⎛⎫=⋅= ⎪⎝⎭在R 上单调递增,故()2xf x -=具有M 性质;②()33xx x x e e f x e -⎛⎫=⋅= ⎪⎝⎭在R 上单调递减,故()3xf x -=不具有M 性质;③()3xxe f x e x =⋅,令()3xg x e x =⋅,则()()32232xxxg x e x e x x ex '=⋅+⋅=+,∴当2x >-时,()0g x '>,当2x <-时,()0g x '<,∴()3x x e f x e x =⋅在(),2-∞-上单调递减,在()2,-+∞上单调递增,故()3f x x =不具有M 性质;④()()22x x e f x e x =+,令()()22xg xe x =+,则()()()2222110xxx g xe x e x e x ⎡⎤'=++⋅=++>⎣⎦,∴()()22x x e f x e x =+在R 上单调递增,故()22f x x =+具有M 性质.三、解答题:本大题共6小题,共75分。
2019山东高考理数真题[含答案已排版]
![2019山东高考理数真题[含答案已排版]](https://img.taocdn.com/s3/m/2adbac50647d27284b7351ce.png)
2019山东高考理数真题[含答案已排版]2019年普通高等学校招生全国统一考试(山东卷)理科数学本试卷分第I 卷和第II 卷两部分,共4页,满分150分。
考试用时120分钟。
考试结束后,将本试卷和答题卡一并交回。
一、选择题:本大题共12小题,每小题5分,满分60分. 在每小题给出的四个选项中,只有一项是符合题目要求的.1、复数z 满足(z -3)(2-i ) =5(i 为虚数单位),则z 的共轭复数z 为()(A )2+i (B )2-i (C )5+i (D )5-i2、已知集合A ={0, 1, 2},则集合B ={x -y |x ∈A , y ∈A }中元素的个数是()(A )1 (B )3 (C )5 (D )93、已知函数f (x ) 为奇函数,且当x >0时,f (x ) =x +2-1,则f (-1) =() x9,底面是边长为的正三角4(A )-2 (B )0 (C )1 (D )2 4、已知三棱柱ABC -A 1B 1C 1的侧棱与底面垂直,体积为形,若P 为底面A 1B 1C 1的中心,则PA 与平面ABC 所成角的大小为()(A )5ππππ (B )(C )(D ) 123465、若函数f (x ) =sin(2x +ϕ) 的图像沿x 轴向左平移则ϕ的一个可能取值为()(A )π个单位,得到一个偶函数的图像,83πππ (B )(C )0 (D )- 444⎧2x -y -2≥0⎧6、在平面直角坐标系x O y 中,M 为不等式组⎧x +2y -1≥0,所表示的区域上一动点,⎧3x +y -8≤0⎧则直线O M 斜率的最小值为(A )2 (B )1 (C )-11 (D )- 327、给定两个命题p 、q ,若⌝p 是q 的必要而不充分条件,则p 是⌝q 的(A )充分而不必要条件(B )必要而不充分条件(C )充要条件(D )既不充分也不必要条件 8、函数y =x cos x +sin x 的图象大致为y = f (x )(A) (B) (C)(D)9、过点(3,1)作圆(x -1) 2+y 2=1作圆的两条切线切点为A ,B ,则直线AB 的方程(A )2x +y -3=0 (B )2x -y -3=0 (C )4x -y -3=0 (D )4x +y -3=010、用0,1,,9十个数字可以组成有重复数字的三位数的个数为(A )243 (B )252 (C )261 (D )279212x C 1:y =x (p >0) C 2:-y 2=12p 311、抛物线的焦点与双曲线的右焦点的连线交C 1于第一象限的点M ,若C 1在点M 处的切线平行于C 2的一条渐近线,则p =33246 (B )8 (C )3 (D )3212xy +-22x , y , z x -3xy +4y -z =0x y z 的最大12、设正实数满足,则当z 取最大值时,值为9(A )0 (B )1 (C )4 (D )3二、填空题:本大题共4小题,每小题4分,共16分13、执行右面的程序框图,若输入的ε值为0.25,则输出的n 的值为______________x -≥1成立的概率为______________. 14、在区间[-3, 3]上随机取一个数x ,使得x +15、已知向量AB 与AC 的夹角120且|AB |=3,|AC |=2,若AP =λAB +AC ,且0,−−→−−→−−→−−→−−→−−→−−→−−→AP ⊥BC ,则实数λ的值为____________.−−→⎧0,016、定义“正对数”: ln x =⎧, 现有四个命题:ln x , x ≥1⎧++b +①若a >0, b >0, l n a =b l n a ;()n a b =l n a +l n b ; ②若a >0 , b >0, l ()+++③若a >0, b >0, l n + ⎧≥l n +a -l n +b ;⎧a ⎧⎧b ⎧n a +b ≤l n a +l n b +l n 2; ④若a >0 , b >0, l ()+++其中真命题有____________.(写出所有真命题的编号)三、解答题:本大题共6小题,共74分。
2019年山东春季高考数学真题(含答案)
机密★启用前山东省2019年普通高校招生(春季)考试数学试题1.本试卷分卷一(选择题)和卷二(非选择题)两部分,满分120分,考试时间120分钟。
考生清在答题卡上答题,考试结束后,请将本试卷和答题卡一并交回。
2.本次考试允许使用函数型计算器,凡使用计算器的题目,除题目有具体要求外,最后结果精确到0.01。
卷一(选择题共50分)卷一(选择题共60分)一、选择题(本大题20个小题,每小题3分,共60分。
在每小题列出的四个选项中,只有一项符合题目要求,请将符合题目要求的选项字母代号选出.并填涂在答题卡上)1. 已知集合M={0,1},N={1,2},则M ∪N 等于( )A. {1}B. {0,2}C. {0,1,2}D. ∅ 2. 若实数a ,b 满足ab>0,a+b>0,则下列选项正确的是( )A. a>0,b>0B. a>0,b<0C. a<0,b>0D. a<0,b<0 3. 已知指数函数y=a x,对数函数y=log b x 的图像如图所示,( )A. 0<a<b<1B. 0<a<1<bC. 0<b<1<aD. a<0<1<b4. 已知函数f(x)=x 3+x ,若f(a)=2,则f(-a)的值是( )5. 若等差数列{a n }的前7项和为70,则a1+a 7等于( )A. 5B. 10C. 15D. 20 6. 如图所示,已知菱形ABCD 的边长是2,且∠DAB =60°,则AB AC ⋅ 的值是( )A. 4B. 4+-7. 对于任意角α,β,“α=β”是“sinα=sin β”的( )A. 充分不必要条件B. 必要不充分条件C. 充要条件件 8. 如图所示,直线l ⊥OP ,则直线l 的方程是( ) A. 3x -2y=0 B. 3x+2y -12=0C. 2x -3y+5=0D. 2x+3y -13=09. 在(1+x )n的二项展开式中,若所有项的系数之和为64,则第3A. 15x 3 B. 20x 3 C. 15x 2 D. 20x 210. 在RtABC 中,∠ABC =90°,AB=3,BC=4,M 是线段AC 上的动点. 设点M 到BC 的距离为x ,MBC 的面积为y ,则y 关于x 的函数是( )A. y=4x ,x∈(0,4]B. y=2x ,x∈(0,3]C. y=4x ,x∈(0,)+∞D. y=2x ,x∈(0,)+∞11. 现把甲、乙等6位同学排成一排,若甲同学不能排在前两位,且乙同学必须排在甲同学前面(相邻或不相邻均可),则不同排法的种树是( )A. 360B. 336C. 312D. 240 12. 设集合M={-2,0,2,4},则下列命题为真命题的是( ) A. ,a M ∀∈ a 是正数 B. ,b M ∀∈ b 是自然数 C. ,c M ∃∈ c 是奇数 D. ,d M ∃∈ d 是有理数13. 已知sinα=12,则cos2α的值是( ) 89 B. 89- C.79 D. 79- 14. 已知y=f(x)在R 上是减函数,若f(|a |+1)<f(2),则实数a 的取值范围是( )A. (-∞,1)B. (-∞,1)∪(1,+∞)C. (-1,1)D.(-∞,-1)∪(1,+∞)15. 已知O 为坐标原点,点M 在x 轴的正半轴上,若直线MA 与圆x 2+y 2=2相切于点A ,且|AO|=|AM|,则点M 的横坐标是( )D. 416. 如图所示,点E 、F 、G 、H 分别是正方体四条棱的中点,则直线EF 与GH 的位置关系是( ) A. 平行 B. 相交 C. 异面 D. 重合y第3题 图B第6题 图EFGH17. 如图所示,若x ,y 满足线性约束条件 2 0 0 1x y x y -+⎧⎪⎨⎪⎩≥≤≥ , 则线性目标函数z=2x-y 取得最小值时的最优解是( ) A. (0,1) B. (0,2) C. (-1,1) D . (-1,2)18. 箱子中放有6张黑色卡片和4张白色卡片,从中任取一张,恰好取得黑色卡片的概率是( )A. 16B. 13C. 25D. 3519. 已知抛物线的顶点在坐标原点,对称轴为坐标轴,若该抛物线经过点M (-2,4),则其标准方程是( ) A. y 2=-8x B. y 2=-8x 或x 2=y C. x 2=y D. y 2=8x 或x 2=-y 20. 已知ABC 的内角A ,B ,C 的对边分别是a ,b ,c ,若a =6,sinA=2cosBsinC ,向量m=()a ,向量n =(-cosA ,sinB),且m ∥n ,则ABC 的面积是( )卷二(非选择题 共60分)二、填空题(本大题5个小题,每小题4分,共20分。
(完整版)2019年山东省春季高考数学试题及答案

山东省2019年普通高校招生(春季)考试数学试题1.本试卷分卷一(选择题)和卷二(非选择题)两部分,满分120分,考试时间120分钟。
考生清在答题卡上答题,考试结束后,请将本试卷和答题卡一并交回。
2.本次考试允许使用函数型计算器,凡使用计算器的题目,除题目有具体要求外,最后结果精确到0.01。
卷一(选择题共60分)一、选择题(本大题20个小题,每小题3分,共60分。
在每小题列出的四个选项中,只有一项符合题目要求,请将符合题目要求的选项字母代号选出.并填涂在答题卡上)1. 已知集合M={0,1},N={1,2},则M ∪N 等于( )A. {1}B. {0,2}C. {0,1,2}D. ∅ 2. 若实数a ,b 满足ab>0,a+b>0,则下列选项正确的是( )A. a>0,b>0B. a>0,b<0C. a<0,b>0D. a<0,b<03. 已知指数函数y=a x ,对数函数y=log b x 的图像如图所示,则下列关系式正确的是(A. 0<a<b<1B.0<a<1<b C. 0<b<1<a D. a<0<1<b4. 已知函数f(x)=x 3+x ,若f(a)=2,则f(-a)的值是( )A. -2B. 2C. -10D. 10 5. 若等差数列{a n }的前7项和为70,则a 1+a 7等于( )A. 5B. 10C. 15D. 206. 如图所示,已知菱形ABCD 的边长是2,且∠DAB =60°,则AB AC ⋅ 的值是( ) A. 4 B. 4+ C. 6 D. 4-y第3题 图B第6题 图7. 对于任意角α,β,“α=β”是“sin α=sin β”的( )A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件 8. 如图所示,直线l ⊥OP ,则直线l 的方程是( ) A. 3x -2y=0 B. 3x+2y -12=0 C. 2x -3y+5=0 D. 2x+3y -13=0 9.在(1+x )n 的二项展开式中,若所有项的系数之和为64,则第3项是( )A. 15x 3B. 20x 3C. 15x 2D. 20x 2 10. 在RtABC 中,∠ABC =90°,AB=3,BC=4,M 是线段AC 上的动点. 设点M 到BC 的距离为x ,MBC 的面积为y ,则y 关于x 的函数是( )A. y=4x ,x∈(0,4]B. y=2x ,x∈(0,3]C. y=4x ,x∈(0,)+∞D. y=2x ,x∈(0,)+∞ 11. 现把甲、乙等6位同学排成一排,若甲同学不能排在前两位,且乙同学必须排在甲同学前面(相邻或不相邻均可),则不同排法的种树是( )A. 360B. 336C. 312D. 240 12. 设集合M={-2,0,2,4},则下列命题为真命题的是( ) A. ,a M ∀∈ a 是正数 B. ,b M ∀∈ b 是自然数 C. ,c M ∃∈ c 是奇数 D. ,d M ∃∈ d 是有理数 13. 已知sinα=12,则cos2α的值是( ) A.89 B. 89- C. 79 D. 79- 14. 已知y=f(x)在R 上是减函数,若f(|a |+1)<f(2),则实数a 的取值范围是( )A. (-∞,1)B. (-∞,1)∪(1,+∞)C. (-1,1)D.(-∞,-1)∪(1,+∞) 15. 已知O 为坐标原点,点M 在x 轴的正半轴上,若直线MA 与圆x 2+y 2=2相切于点A ,且|AO|=|AM|,则点M 的横坐标是( ) A. 2B.C.D. 416. 如图所示,点E 、F 、G 、H 分别是正方体四条棱的中点,则直线EF 与GH 的位置关系是( ) A. 平行 B. 相交 C. 异面 D. 重合17. 如图所示,若x ,y 满足线性约束条件 2 01x y x y -+⎧⎪⎨⎪⎩≥≤≥ , 则线性目标函数z=2x-y 取得最小值时的最优解是( ) A. (0,1) B. (0,2) C. (-1,1) D . (-1,2)18. 箱子中放有6张黑色卡片和4张白色卡片,从中任取一张,恰好取得黑色卡片的概率是( ) A.16 B. 13 C. 25 D. 3519. 已知抛物线的顶点在坐标原点,对称轴为坐标轴,若该抛物线经过点M (-2,4),则其标准方程是( ) A. y 2=-8x B. y 2=-8x 或x 2=y C. x 2=y D. y 2=8x 或x 2=-y 20. 已知ABC 的内角A ,B ,C 的对边分别是a ,b ,c ,若a =6,sinA=2cosBsinC ,向量m =(,3)a b ,向量n =(-cosA ,sinB),且m ∥n ,则ABC 的面积是( )A. 183B. 93C. 33D. 3卷二(非选择题 共60分)二、填空题(本大题5个小题,每小题4分,共20分。
(完整word版)2019年山东省高考理科数学试卷及答案【word版】

2019年高考山东卷理科数学真题及参考答案一.选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,选择符合题目要求的选项。
1.已知i R b a ,,∈是虚数单位,若i a -与bi +2互为共轭复数,则=+2)(bi a (A )i 45- (B) i 45+ (C) i 43- (D) i 43+ 答案:D2.设集合},]2,0[,2{},21{∈==<-=x y y B x x A x 则=B A (A) [0,2] (B) (1,3) (C) [1,3) (D) (1,4) 答案:C3.函数1)(log 1)(22-=x x f 的定义域为(A))210(, (B) )2(∞+, (C) ),2()210(+∞ , (D) )2[]210(∞+,,答案:C4. 用反证法证明命题“设,,R b a ∈则方程02=++b ax x 至少有一个实根”时要做的假设是 (A)方程02=++b ax x 没有实根 (B)方程02=++b ax x 至多有一个实根 (C)方程02=++b ax x 至多有两个实根 (D)方程02=++b ax x 恰好有两个实根 答案:A5.已知实数y x ,满足)10(<<<a a a yx,则下列关系式恒成立的是 (A)111122+>+y x (B) )1ln()1ln(22+>+y x (C) y x sin sin > (D) 33y x > 答案:D6.直线x y 4=与曲线2x y =在第一象限内围成的封闭图形的面积为(A )22(B )24(C )2(D )4 答案:D7.为了研究某药厂的疗效,选取若干名志愿者进行临床试验,所有志愿者的舒张压数据(单位:kPa )的分组区间为[12,13),[13,14),[14,15),[15,16),[16,17],将其按从左到右的顺序分别编号为第一组,第二组,……,第五组,右图是根据试验数据制成的频率分布直方图,已知第一组与第二组共有20人,第三组中没有疗效的有6人,则第三组中有疗效的人数为舒张压/kPa(A )6 (B )8 (C ) 12(D )18 答案:C8.已知函数()12+-=x x f ,()kx x g =.若方程()()x g xf =有两个不相等的实根,则实数k 的取值范围是(A )),(210(B )),(121(C )),(21(D )),(∞+2答案:B9.已知y x,满足的约束条件⎩⎨⎧≥≤0,3-y -2x 0,1-y -x 当目标函数0)b 0,by(a ax z >>+=在该约束条件下取得最小值52时,22a b +的最小值为(A )5(B )4(C )5(D )2 答案:B10.已知0b 0,a >>,椭圆1C 的方程为1x 2222=+b y a ,双曲线2C 的方程为1x 2222=-by a ,1C 与2C 的离心率之积为23,则2C 的渐近线方程为 (A )02x =±y (B )02=±y x (C )02y x =±(D )0y 2x =± 答案:A二.填空题:本大题共5小题,每小题5分,共25分,答案须填在题中横线上。
2019春考数学答案

机密★启用前山东省2019年普通高校招生(春季)考试数学试题答案及评分标准 卷一(选择题共60分)题号 1 2 3 4 5 6 7 8 9 10 答案 C A B A D C A D C B 题号 11 12 13 14 15 16 17 18 19 20 答案 B D C D A B C D B C卷二(非选择题共60分)二、填空题(本大题5个小题,每小题4分,共20分) 21.36° 22.-4 23.5424.2[填1.41 亦可]25. y= ±26X 三、解答题(本大题5个小题,共40分) 26.(本小题7分)解:因为f(1)=-1, f(3)=-1, 所以二次函数f(x)的对称轴为x=231+=2,(2分) 又因为函数f(x)图像的顶点在直线y=2x -1上,则联立方程组⎩⎨⎧-==1x 2y 2x ,解得⎩⎨⎧==32y x ,(1分)故函数f(x)图像的顶点坐标为(2, 3)1分可设二次函数的解析式为f(x)=a(x -2)2+3,(1分) 因为f(1)=-1, 则a(1-2)2+3=-1,解得a=-4,(1分) 所以f(x)= -4(x -2)2+3,即f(x)=-4x2+16x -13 (1分 27. (本小题8分)解: (1)由图像可知,函数f(x)的最大值是2, 最小值是-2 ,A>0. 所以A=2 ,(1分)因为125π-6π=4π,4π最小正周期的41, 所以函数f(x) 的最小正周期T=4πX4=π,故ωπ2=π,解得ω=2,(1分)可得函数f(x)=2 sin(2x+φ),又因为函数f(x)图像经过点(6π,0), 所以2sin(2x 6π+φ)=0 ,即sin( 3π+φ)=0,(1分)因此3π+φ=2K π ,k ∈Z ,解得φ=2k π-3π,k ∈Z ,又因为|φ|<2π,所以φ=-3π(1分)所以该函数的解析式为f(x)=2 sin(2x -3π)(1分)(2)因为f(x)≥l ,所以2sin(2x -3π)≥l ,即sin(2x -3π)≥21,(1分) 所以6π+2k π≤2x -3π≤65π+2k π,k ∈Z ,(1分)即4π+k π≤x ≤127π+k π,k ∈Z , 故当f(x)≥1时,实数x 的取值范围是{x| 4π+k π≤x ≤127π+k π,k ∈Z}.(1分)注: x 的取值范围写为“[ 4π+k π,127π+k π],k ∈Z",亦可。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
山东省2019年普通高校招生(
春季)考试数学试题答案及评分标准
卷一(选择题 共60分)
一㊁选择题(本大题20个小题,每小题3分,共60分)
1.C
2.A
3.B
4.A
5.D
6.C
7.A
8.D
9.C 10.B 11.B 12.D 13.C 14.D
15.A 16.B 17.C 18.D 19.B 20.C 卷二(非选择题 共60分)
二㊁填空题(本大题5个小题,每小题4分,共20分)21.36ʎ 22.-4 23.54 24.2ʌ填1.41亦可ɔ 25.y =ʃ62x 三㊁解答题(本大题5个小题,共40分)26.(本小题7分)解:因为f (1)=-1,f (
3)=-1,所以二次函数f (x )的对称轴为x =1+32=2,2分 又因为函数f (x )图像的顶点在直线y =2x -1上,
则联立方程组x =2,y =2x -1,{解得x =2,y =3,{1分 故函数f (x )图像的顶点坐标为(2,3).1分 可设二次函数的解析式为f (x )=a (x -2)2+3,1分
因为f (1)=-1,则a (1-2)2+3=-1,解得a =-4,1分 所以f (x )=-4(x -2)2+3,
即f (x )=-4x 2+16x -13.1分 (第27题图)27.(本小题8分)解:(1)由图像可知,函数f (x )的最大值是2,最小值是-2,A >0,所以A =2.1分
因为5π12-π6=π4,π4是最小正周期的14
,所以函数f (x )的最小正周期T =π4ˑ4=π,故2πω
=π,解得ω=2,1分 东博文化传媒
可得函数f (x )=2s i n (2x +φ),又因为函数f (x )图像经过点π6,0æèçöø
÷,所以2s i n 2ˑπ6+φæèçöø÷=0,即s i n π3+φæèçöø÷=0,1分 因此
π3+φ=2k π,k ɪZ ,解得φ=2k π-π3,k ɪZ ,又因为|φ|<π2,所以φ=-π3
,1分 所以该函数的解析式为f (x )=2s i n 2x -π3æèçöø
÷.1分 (2)因为f (x )ȡ1,所以2s i n 2x -π3æèçöø÷ȡ1,即s i n 2x -π3æèçöø÷ȡ12
,1分 所以
π6+2k πɤ2x -π3ɤ5π6+2k π,k ɪZ ,1分 即π4+k πɤx ɤ7π12
+k π,k ɪZ ,故当f (x )ȡ1时,实数x 的取值范围是x π4+k πɤx ɤ7π12+k π,k ɪZ {}
.1分 注:x 的取值范围写为 π4+k π,7π12+k πéëêêùûúú,k ɪZ ,亦可
.(第28题图)
28.
(本小题8分)(1)证明:因为平面S A C ʅ平面A B C ,平面S A C ɘ平面A B C =A C ,且S A ʅA C ,所以S A ʅ平面A B C ,2分
又因为B C ⊂平面A B C ,所以S A ʅB C ,1分
又因为A B ʅB C ,S A ɘA B =A ,所以B C ʅ平面S A B .
1分 (2)解:由(1)知,S A ʅ平面A B C ,所以点S 到平面A B C 的距离即为线段S A 的长度.1分 并且可知,S B 在平面A B C 内的射影为A B ,1分
所以øS B A 即为S B 与平面A B C 所成角,即øS B A =30ʎ,1分 在R t әS A B 中,øS A B =90ʎ,øS B A =30ʎ,S B =2,所以S A =12S B =1,所以点S 到平面A B C 的距离是1.1分
东博文化
传媒
(第29题图)
29.
(本小题8分)解:(1)因为四边形F 1B 2F 2B 1为正方形,所以|F 1F 2|=|B 1B 2|.因为|F 1F 2|=2c ,|B 1B 2|=2b ,所以c =b ,1分 因为a 2=b 2+c 2,所以a =2b ,1分
因此椭圆的方程可化为x 22b 2+y 2b
2=1,因为椭圆经过点P 1,22æèçöø÷,所以12b 2+22æèçöø÷2b 2=1,解得b =1,故a =2b =2,1分
所以椭圆的标准方程是x 22
+y 2=1.1分 (2)由(1)可知c =1,1分 设双曲线的实半轴长为a ',
因为e =322,且双曲线与椭圆有公共的焦点,故c a '=322,即1a '=322,解得a '=23.1分 由椭圆和双曲线的定义可知
|M F 1|+|M F 2|=2a ,|M F 1|-|M F 2|=2a ',{即|M F 1|+|M F 2|=22,|M F 1|-|M F 2|=223,ìîíïïïï1分 解得|M F 1|=423,|M F 2|=223
,ìîíïïïïï所以线段M F 1,M F 2的长度分别是423,223.1分 注:线段M F 1,M F 2的长度分别写为 1.89,0.94
,亦可.30.(本小题9分)解:(1)由题意知,自2018年起,每年的人口总数构成等差数列{a n }
,其中首项a 1=50,公差d =1.5,1分
通项公式为a n =a 1+(n -1)d =50+(n -1)ˑ1.5,2分 设第n 项a n =
60,即50+(n -1)ˑ1.5=60,解得n =7.7,1分 因为n ɪN +,所以n =8,2018+8-1=2025.答:到2025年年底,该城市人口总数达到60万.1分 (2)由题意知,自2018年起,每年的绿化面积数构成数列{b 1}
,其中b 1是2018年年底的绿化面积数,b 1=35,b 2是2019年年底的绿化面积数,b 2=
35ˑ(1+5%)-0.1=35ˑ1.05-0.1,东博文化传媒
b 3是2
020年年底的绿化面积数,b 3=(
35ˑ1.05-0.1)ˑ1.05-0.1=35ˑ1.052-0.1ˑ1.05-0.1, b k 是(
2018+k -1)年年底的绿化面积数,b k =35ˑ1.05k -1-0.1ˑ1.05k -2-0.1ˑ1.05k -3- -0.1ˑ1.05-0.1,1分 =35ˑ1.05k -1-0.1ˑ(1-1.05k -1)1-1.05
.1分 设b k =
60ˑ0.9,即35ˑ1.05k -1
-0.1ˑ(1-1.05k -1)1-1.05=60ˑ0.9,解得k ʈ10.3,1分 因为k ɪN +,所以k =11,2018+11-1=2028.答:到2028年年底,该城市人均绿化面积达到0.9平方米.
1分 东
博文化传媒。
