三角形角平分线部分经典题型.docx
初一三角形角平分线经典例题

《角平分线》经典例题在直角三角形ABC中,∠A=90°,∠ABC的平分线BE交AC于E点,过E点作ED⊥BC于D点,已知AC=10cm,ΔCDE的周长为16cm,求CD的长.〔解析〕根据角平分线上的点到角的两边的距离相等可得AE=DE,从而求出DE+CE=AC,所以ΔCDE的周长=AC+CD,根据ΔCDE的周长及AC的长即可求得CD的长.解:∵BE为∠ABC的平分线,∠A=90°,DE⊥BC,∴AE=DE,∴DE+CE=AE+CE=AC=10cm,∵ΔCDE的周长为16cm,∴DE+CE+CD=16cm,∴CD=16-10=6(cm).如图(1)所示,已知∠ADC+∠ABC=180°,DC=BC.求证点C在∠DAB的平分线上.〔解析〕作CE⊥AB,CF⊥AD,垂足分别为E,F,利用∠ADC+∠ABC=180°,∠ADC+∠CDF=180°,得出∠ABC=∠CDF,进而证得ΔCBE≌ΔCDF,得出FC=EC,即可求得结论.证明:如图(2)所示,作CE⊥AB,CF⊥AD,垂足分别为E,F,∴∠BEC=∠DFC=90°,∵∠ADC+∠ABC=180°,∠ADC+∠CDF=180°,∴∠ABC=∠CDF,在ΔCBE和ΔCDF中,∴ΔCBE≌ΔCDF(AAS),∴FC=EC,∴点C在∠DAB的平分线上.如图(1)所示,已知点P 是ΔABC 三条角平分线的交点,PD ⊥AB ,若PD =5,ΔABC 的周长为20,求ΔABC 的面积.〔解析〕作PE ⊥BC 于E ,PF ⊥AC 于F ,根据角平分线的性质定理得PE =PF =PD =5,然后根据三角形面积公式和S ΔABC =S ΔPAB +S ΔPBC +S ΔPAC 得到S ΔABC =(AB +BC +AC ),再把ΔABC 的周长为20代入计算即可.解:作PE ⊥BC 于E ,PF ⊥AC 于F ,如图(2)所示,∵点P 是ΔABC 三条角平分线的交点,∴PE =PF =PD =5,∴S ΔABC =S ΔPAB +S ΔPBC +S ΔPAC=PD ·AB +PE ·BC +PF ·AC=(AB +BC +AC )=20=50.如图(1)所示,在RtΔABC 中,∠ACB =90°,且AC =b ,BC =a ,AB =c ,∠A 与∠B 的平分线交于点O ,O 到AB 的距离为OD.试探究OD 与a ,b ,c 的数量关系.〔解析〕过点O作OE⊥AC于E,OF⊥BC于F,然后根据角平分线上的点到角的两边的距离相等可得OD=OE=OF,然后证得四边形EOFC是正方形,从而证得OE=OF=FC=EC=OD,AE=AD,BD=BF,通过AB=AC-OD+BC-OD即可求解.解:如图(2)所示,过点O作OE⊥AC于E,OF⊥BC于F,∵∠BAC,∠ABC的平分线交于点O,OD⊥AB,∴OD=OE,OD=OF,∴OD=OE=OF,∵∠ACB=90°,∴四边形EOFC是正方形,∴OE=OF=FC=EC=OD,在RtΔOAE和RtΔOAD中,∴RtΔOAE≌RtΔOAD,∴AE=AD,同理BD=BF,∴AE+EC=AD+OD=AC=b,BF+CF=BD+OD=BC=a,∴AD=b-OD,BD=a-OD,∴AD+BD=a+b-2OD,即c=a+b-2OD,∴OD=(a+b-c).。
角平分线的性质练习题

角平分线的性质练习题一、选择题1. 在三角形ABC中,BD是角B的平分线,若AB=5,BC=7,AC=6,那么BD的长度为:A. 4B. 6C. 8D. 无法确定2. 如果角平分线将三角形分成两个面积相等的部分,那么这两个部分的底边分别是:A. 相等B. 不相等C. 一个底边是另一个的两倍D. 底边长度无法确定3. 在三角形ABC中,角A的平分线与BC相交于点D,若AD=4,AC=8,那么AB的长度可能是:A. 6B. 8C. 10D. 12二、填空题4. 在三角形ABC中,如果角A的平分线将BC分为BD和DC两段,BD=DC,那么三角形ABD与三角形ACD的面积之比为________。
5. 若角平分线定理告诉我们,在三角形ABC中,如果BD是角B的平分线,则AB:AC=______:______。
6. 在三角形ABC中,如果角A的平分线与BC相交于点D,且AD垂直于BC,那么角B和角C的度数之和为________。
三、简答题7. 描述角平分线定理的内容,并给出一个应用此定理的几何问题。
8. 解释为什么在三角形中,角平分线可以将对边分成的两段长度与相邻两边成比例。
四、计算题9. 在三角形ABC中,已知角A的平分线AD与BC相交于点D,且BD=3,DC=4,AB=6,求AC的长度。
10. 在三角形ABC中,角B的平分线BE与AC相交于点E,已知AE=4,EC=6,AB=5,求BC的长度。
五、证明题11. 证明:在三角形ABC中,如果BD是角B的平分线,那么AB/AC = BD/DC。
12. 证明:如果点D在三角形ABC的边BC上,且AD是角A的平分线,那么三角形ABD与三角形ACD的面积相等。
六、综合题13. 在三角形ABC中,已知角A的平分线AD与BC相交于点D,且AD=2,BD=3,DC=4,AB=5,求BC的长度,并证明你的结论。
14. 给定三角形ABC,其中角A的平分线AD与BC相交于点D,角B的平分线BE与AC相交于点E。
实用文库汇编之三角形 角平分线部分经典题型

*实用文库汇编之1.如图1所示,在△ABC中,∠A =90°,BD平分∠ABC,AD=2 cm,则点D到BC的距离为________cm.*图1图22.如图2所示,在RtΔABC中,∠C=90°,BD是∠ABC的平分线,交AC于D,若CD=n,AB=m,则ΔABD的面积是()A.mn31B.mn21C.mn D.2mn3.如图,在△ABC中,∠C=900,BC=40,AD是∠BAC的平分线交BC于D,且DC∶DB=3∶5,则点D到AB的距离是。
4.如图,已知BD是∠ABC的内角平分线,CD是∠ACB的外角平分线,由D出发,作点D到BC、AC和AB 的垂线DE、DF和DG,垂足分别为E、F、G,则DE、DF、DG的关系是。
5.如图,已知AB∥CD,O为∠A、∠C的角平分线的交点,OE⊥AC于E,且OE=2,则两平行线间AB、CD的距离等于。
6.AD是△BAC的角平分线,自D向AB、AC两边作垂线,垂足为E、F,那么下列结论中错误的是( )A、DE=DFB、AE=AFC、BD=CDD、∠ADE=∠ADF7.到三角形三条边的距离都相等的点是这个三角形的()A.三条中线的交点B.三条高的交点C.三条边的垂直平分线的交点D.三条角平分线的交点8.已知△ABC中,∠A=80°,∠B和∠C的角平分线交于O点,则∠BOC= 。
9.如图,已知相交直线AB和CD,及另一直线EF。
如果要在EF上找出与AB、CD距离相等的点,方法是,这样的点至少有个,最多有个。
第3题图DC BA10.如图所示,已知△ABC 中,∠C =90°,AC =BC ,AD 平分∠CAB ,交BC 于点D ,DE ⊥AB 于点E ,且AB =6 cm,则△DEB 的周长为( )。
A.9 cm B.5 cm C.6 cm D.不能确定11.如图,AB //CD ,CE 平分∠ACD ,若∠1=250,那么∠2的度数是 .12.如图,OP 平分AOB ∠,PA OA ⊥,PB OB ⊥,垂足分别为A ,B .下列结论中不一定成立的是( )A .PA PB = B .PO 平分APB ∠C .OA OB =D .AB 垂直平分OP13.如图,已知AC ∥BD 、EA 、EB 分别平分∠CAB 和∠ABD ,CD 过点E ,则AB 与AC+BD•相等吗?说明理由.14、如图所示,已知AD 为等腰三角形ABC 的底角的平分线,∠C =90° 求证:AB =AC +CD .15、如图,在四边形ABCD 中,BC>BA ,AD=DC,BD 平分∠ABC,求证:∠A+∠C=180°D16、如图,∠ACB=90°,AC=BC,BE⊥CE,AD⊥CE. 求证:△ACD≌△CBE.17.已知:如图,△ABC中,∠C=90°,试在AC上找一点P,使P到斜边的距离等于PC.(画出图形,并写出画法)18.已知:OD平分∠POQ,在OP、OQ边上取OA=OB,CM⊥AD于M,CN⊥BD于N.求证:CM=CN.19.已知:如图,ΔABC的外角∠CBD和∠BCE的平分线BF、CF交于点F.求证:一点F必在∠DAE的平分线上.20.已知:如图,A、B、C、D四点在∠MON的边上,AB=CD,P为∠MON内一点,并且△PAB的面积与△PCD的面积相等.求证:射线OP是∠MON的平分线.ABCDE21.如图,ΔABC中,∠C=90°,BD平分∠ABC,DE⊥AB于E,若△BCD与△BCA的面积比为3∶8,求△ADE与△BCA的面积之比.22.已知:如图,∠B=∠C=90°,M是BC的中点,DM平分∠ADC.(1)求证:AM平分∠DAB;(2)猜想AM与DM的位置关系如何?并证明你的结论.23.已知:如图,在ΔABC中,AD是△ABC的角平分线,E、F分别是AB、AC上一点,并且有∠EDF +∠EAF=180°.试判断DE和DF的大小关系并说明理由.24.如图1所示:AM∥DN,AE、DE分别平分∠MAD和∠AND,并交于E点.过点E的直线分别交AM、DN于B、C.(1)如图2,当点B、C分别位于点AD的同侧时,猜想AD、AB、CD之间的存在的数量关系:_______________________________.(2)试证明你的猜想.(3)若点B、C分别位于点AD的两侧时,试写出AD、AB、CD之间的关系,并选择一个写出证明过程。
解三角形(角平分线问题问题)(典型例题+题型归类练)(原卷版)

专题05 解三角形(角平分线问题问题)(典型例题+题型归类练) 一、必备秘籍角平分线如图,在ABC ∆中,AD 平分BAC ∠,角A ,B ,C 所对的边分别为a ,b ,c 核心技巧1:内角平分线定理:AB AC BD DC =或AB BDAC DC= 核心技巧2:等面积法(使用频率最高)ABC ABD ADC S S S ∆∆∆=+⇒111sin sin sin 22222A A AB AC A AB AD AC AD ⨯⨯=⨯⨯+⨯⨯ 核心技巧3:边与面积的比值:ABD ADCSAB AC S=核心技巧4:角互补:ADB ADC π∠+∠=⇒cos cos 0ADB ADC ∠+∠=在ADB ∆中有:222cos 2DA DB AB ADB DA DB +-∠=⨯;在ADC ∆中有:222cos 2DA DC AC ADC DA DC+-∠=⨯二、典型例题例题1.如图,已知AD 是ABC ∆中BAC ∠的角平分线,交BC 边于点D .(1)用正弦定理证明:AB BDAC DC=; (2)若120BAC ∠=︒,2AB =,1AC =,求AD 的长.第(2)问思路点拨:本小题已知,,,求的长.可利用第(1)问结论解答过程:根据余弦定理,,即,解得利用第(1)问结论由(1)知∴,得,;在与中,根据余弦定理得,且解得,即的长为.例题2.在ABC 中,内角,,A B C 所对的边分别为,,a b c 且πsin sin 3a B b A ⎛⎫=+ ⎪⎝⎭.(1)求角A 的大小;(2)若3AB =,1AC =,BAC ∠的内角平分线交BC 于点D ,求AD .第(2)问思路点拨:由(1)知,求角平分线长,,可优先考虑面积公式解答过程:由(1)知,由角平分线面积公式∴,∴.代入数据计算例题3.在ABC 中,3,AB =4,BC =线段BD 是B ∠的角平分线,且 6.ABDS =求BCD S △.思路点拨:已知在中,线段是的角平分线,且涉及角平分线问题,但是不知的大小,不适合直接用面积公式,但知,可考虑面积和边长的关系解答过程:平分由,代入代入例题4.在ABC中,D是BC的中点,1AB=,2AC=,32 AD=.(1)ABC的面积为________.(2)若AE为BAC∠的角平分线,E在线段BC上,则AE的长度为________.第(2)问思路点拨:由(1)知,可优先考虑面积公式解答过程:由可得即,从而.代入,计算例题5.在△ABC 中, AM 是BAC ∠的角平分线, 且交BC 于M . 已知23,2,3AM BM MC ===, 则AC = __________;思路点拨:在中,是的角平分线, 且交于. 已知,涉及到角平分线,又,可利用,得到的关系解答过程:由是的角平分线,又,得,设,则因为,则,利用余弦定理代入得:,整理得,解得或(舍).所以.利用角互补关系(不适合面积公式)三、题型归类练1.三角形内角平分线定理:三角形的内角平分线分对边所得的两条线段和这个角的两边对应成比例.请你认真思考,用三角形内角平分线定理解决问题:已知ABC 中,AD 为角平分线,3AB =,4AC =,5BC =,则AD =( )A .127B .157C .7D .72.在ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,已知,()(sin sin )(sin sin )a b A B c C B +-=+,若角A 的内角平分线AD 的长为2,则4b c +的最小值为( ) A .10B .12C .16D .183.在△ABC 中,内角A 、B 、C 所对的边分别为a 、b 、c ,若()sin sin sin a A c C b c B =+-,角A 的角平分线交BC 于点D ,且3AD c b ==,则a 的值为( )A .72BC .3D4.在ABC 中,CD 是ACB ∠的角平分线且4,||AB AD AD ==若||3CD =,则CDA ∠=__________,ABC的面积为__________.5.在ABC 中,60A ∠=,∠A 的角平分线与BC 边相交于D .AD =BC =AB 边的长度为___.6.已知△ABC 的内角A ,B ,C 所对的边分别为a ,b ,c ,tan tan tan 0B C B C +=. (1)求角A 的大小;(2)若2BD DC =,AD =2,且AD 平分∠BAC ,求△ABC 的面积.注:三角形的内角平分线定理:在△PQR 中,点M 在边QR 上,且PM 为∠QPR 的内角平分线,有PQ QMPR MR=.7.记ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,已知22cos cos (sin sin )sin 0C A A B B +-+=. (1)求C ;(2)若a ,b 为方程210200x x -+=的两个实数根,且C 的角平分线交AB 于点D ,求CD .8.已知△ABC 中,内角A 、B 、C 的对边分别为a 、b 、c ,BD 为∠ABC 的角平分线.(1)求证:::AD AB CD CB =;(2)若2BD =且26c a ==,求△ABC 的面积.9.已知△ABC 中,,,a b c 分别为内角,,A B C 的对边,且()()2sin 2sin 2sin a A b c B c b C =+++. (1)求角A 的大小;(2)设点D 为BC 上一点,AD 是ABC 的角平分线,且2AD =,3b =,求ABC 的面积.10.已知ABC 的内角A ,B ,C 的对边分别是a ,b ,c ,点D 在BC 边上,AD 是角平分线,222sin sin sin sin sin C B C B A ++⋅=,且ABC 的面积为(1)求A 的大小及AB AC ⋅的值; (2)若4c =,求BD 的长.11.在△ABC 中,角A ,B ,C 所对的边分别是a ,b ,c ,AD 为∠BAC 的角平分线,已知2c =且222223a c b cosA bc AD ⎛⎫+-=-= ⎪⎝⎭,(1)求△ABC 的面积;12.在ABC 中,角A 、B 、C 所对的边分别为a 、b 、c ,a =1b =,c =M 是BC 上的点. (1)若AM 是BAC ∠的角平分线,求BMCM的值; (2)若AM 是BC 边上的中线,求AM 的长.13.已知ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,点D 在AC 边上,BD 为ABC ∠的角平分线.32ABC ABD S S =△△.(1)求sin sin CA∠∠; (2)若BD b =,求cos ABC ∠的大小.。
(完整版)角平分线经典题型

全等三角形与角平分线1、如图所示,四边形ABCD中,AB=AD,AC平分∠BCD,AE⊥BC,AF⊥CD.求证:△ABE≌△ADF.2、如图,D为BC的中点,DE⊥DF,E、F分别在AB、AC边上,则BE+CF ()A.大于EF B.小于EFC.等于EF D.与EF的大小无法比较3、(12分)如图四边形ABCD中,AC平分∠BAD,CE⊥AB于E,∠D+∠B=180°,求证:AD+AB=2AE.4、已知:如图,在四边形ABCD中,AB>BC,BD平分.求证:AD=CD.5、如图,已知在△ABC中,∠B=60°,△ABC的角平分线AD、CE相交于O点,求证:AE+CD=AC.6、在△ABC,∠C=90°,BC=16cm,∠A的平分线AD交BC于D,且CD︰DB=3︰5,则D到AB的距离等于()A.6cm B.7cmC.8cm D.9cm2、如图,D是△ABC的一个外角的平分线上一点,求证:AB+AC<DB+DC.7、如图,在△ABC中,D为BC的中点,DE⊥BC,交∠BAC的平分线AE于E,EF⊥AB于F,EG⊥AC交AC的延长线于G,求证:BF=CG.8、如图,△ABC中,∠ABC=45°,CD⊥AB于D,BE平分∠ABC,且BE⊥AC 于E,与CD相交于点F.H是BC边的中点,连结DH与BE相交于点G.(1)求证:BF=AC;(2)求证:CE=BF;(3)CE与BG的大小关系如何?试证明你的结论.9、如图,已知∠1=∠2,P为BN上一点,且PD⊥BC于D,AB+BC=2BD,求证:∠BAP+∠BCP=180°10、如图,△ABC中,AM是BC边上的中线,求证:11、已知:如图,在Rt△ABC中,AB=AC,∠BAC=90°,∠1=∠2,CE⊥BD的延长线于E.求证:BD=2CE.。
角平分线的性质典型例题

【典型例题】例1. 已知:如图所示,∠C=∠C′=90°,AC=AC′.求证:(1)∠ABC=∠ABC′;(2)BC=BC′(要求:不用三角形全等判定).分析:由条件∠C=∠C′=90°,AC=AC′,可以把点A看作是∠CBC′平分线上的点,由此可打开思路.证明:(1)∵∠C=∠C′=90°(已知),∴AC⊥BC,AC′⊥BC′(垂直的定义).又∵AC=AC′(已知),∴点A在∠CBC′的角平分线上(到角的两边距离相等的点在这个角的平分线上).∴∠ABC=∠ABC′.(2)∵∠C=∠C′,∠ABC=∠ABC′,∴180°-(∠C+∠ABC)=180°-(∠C′+∠ABC′)(三角形内角和定理).即∠BAC=∠BAC′,∵AC⊥BC,AC′⊥BC′,∴BC=BC′(角平分线上的点到这个角两边的距离相等).评析:利用三角形全等进行问题证明对平面几何的学习有一定的积极作用,但也会产生消极作用,在解题时,要能打破思维定势,寻求解题方法的多样性.例2. 如图所示,已知△ABC中,PE∥AB交BC于E,PF∥AC交BC于F,P是AD上一点,且D点到PE的距离与到PF的距离相等,判断AD是否平分∠BAC,并说明理由.分析:判定一条射线是不是一个角的平分线,可用角平分线的定义和角平分线的判定定理.根据题意,首先由角平分线的判定定理推导出∠1=∠2,再利用平行线推得∠3=∠4,最后用角平分线的定义得证.解:AD平分∠BAC.∵D到PE的距离与到PF的距离相等,∴点D在∠EPF的平分线上.∴∠1=∠2.又∵PE∥AB,∴∠1=∠3.同理,∠2=∠4.∴∠3=∠4,∴AD平分∠BAC.评析:由角平分线的判定判断出PD平分∠EPF是解决本例的关键.“同理”是当推理过程相同,只是字母不同时为书写简便可以使用“同理”.例3. 如图所示,已知△ABC的角平分线BM,CN相交于点P,那么AP能否平分∠BAC?请说明理由.由此题你能得到一个什么结论?分析:由题中条件可知,本题可以采用角的平分线的性质及判定来解答,因此要作出点P到三边的垂线段.解:AP平分∠BAC.结论:三角形的三条角平分线相交于一点,并且这一点到三边的距离相等.理由:过点P分别作BC,AC,AB的垂线,垂足分别是E、F、D.∵BM是∠ABC的角平分线且点P在BM上,∴PD=PE(角平分线上的点到角的两边的距离相等).同理PF=PE,∴PD=PF.∴AP平分∠BAC(到角的两边的距离相等的点在这个角的平分线上).例4.如图所示的是互相垂直的一条公路与铁路,学校位于公路与铁路所夹角的平分线上的P点处,距公路400m,现分别以公路、铁路所在直线为x轴、y 轴建立平面直角坐标系.(1)学校距铁路的距离是多少?(2)请写出学校所在位置的坐标.分析:因为角平分线上的点到角的两边距离相等,所以点P到铁路的距离与到公路的距离相等,也是400m;点P在第四象限,求点P的坐标时要注意符号.解:(1)∵点P在公路与铁路所夹角的平分线上,∴点P到公路的距离与它到铁路的距离相等,又∵点P到公路的距离是400m,∴点P(学校)到铁路的距离是400m.(2)学校所在位置的坐标是(400,-400).评析:角平分线的性质的作用是通过角相等再结合垂直证明线段相等.例5.如图所示,在△ABC中,∠C=90°,AC=BC,DA平分∠CAB交BC于D,问能否在AB上确定一点E,使△BDE的周长等于AB的长?若能,请作出点E,并给出证明;若不能,请说明理由.分析:由于点D在∠CAB的平分线上,若过点D作DE⊥AB于E,则DE=DC.于是有BD+DE=BD+DC=BC=AC,只要知道AC与AE的关系即可得出结论.解:能.过点D作DE⊥AB于E,则△BDE的周长等于AB的长.理由如下:∵AD平分∠CAB,DC⊥AC,DE⊥AB,∴DC=DE.在R t△ACD和R t△AED中,,∴R t△ACD≌R t△AED(HL).∴AC=AE.又∵AC=BC,∴AE=BC.∴△BDE的周长=BD+DE+BE=BD+DC+BE=BC+BE=AE+BE=AB.评析:本题是一道探索题,要善于利用已知条件获得新结论,寻找与要解决的问题之间的联系.本题利用角平分线的性质将要探究的结论进行转化.这是初中几何中常用的一种数学思想.【方法总结】学过“角的平分线上的点到角的两边的距离相等”与“到角的两边的距离相等的点在角的平分线上”这两个结论后,许多涉及角的平分线的问题用这两个结论解决很方便,需要注意的是有许多同学对证明两个三角形全等的问题已经很熟悉了,所以证题时,不习惯直接应用这两个结论,仍然去找全等三角形,结果相当于重新证明了一次这两个结论.所以特别提醒大家,能用简单方法的,就不要绕远路.Welcome !!! 欢迎您的下载,资料仅供参考!。
角平分线的性质专项练习(含解析)
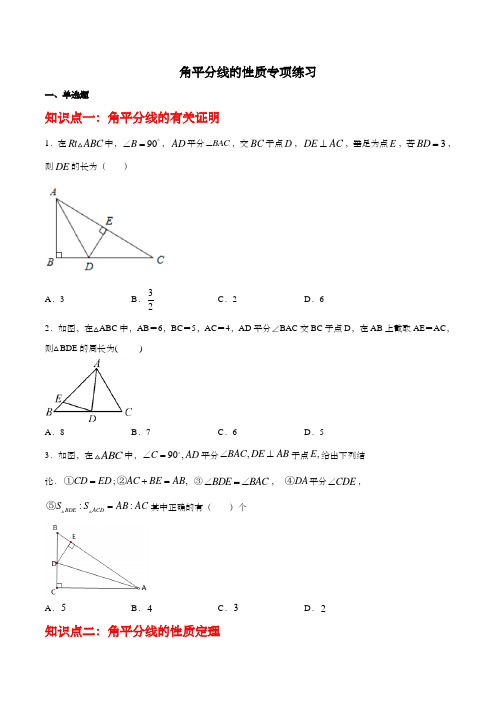
角平分线的性质专项练习一、单选题知识点一:角平分线的有关证明1.在Rt ABC 中,90B ︒∠=,AD 平分BAC ∠,交BC 于点D ,DE AC ⊥,垂足为点E ,若3BD =,则DE 的长为( )A .3B .32C .2D .62.如图,在△ABC 中,AB =6,BC =5,AC =4,AD 平分∠BAC 交BC 于点D ,在AB 上截取AE =AC ,则△BDE 的周长为( )A .8B .7C .6D .53.如图,在ABC 中,90,C AD ∠=平分,BAC DE AB ∠⊥于点,E 给出下列结论.CD ED =①;,AC BE AB +=② ③BDE BAC ∠=∠, DA ④平分CDE ∠,::BDE ACD S S AB AC =⑤其中正确的有( )个A .5B .4C .3D .2知识点二:角平分线的性质定理4.如图,在Rt ABC ∆中,90B =∠,以点A 为圆心,适当长为半径画弧,分别交AB AC 、于点,D E ,再分别以点D E 、为圆心,大于12DE 为半径画弧,两弧交于点F ,作射线AF 交边BC 于点1,4BG AC ==,则ACG ∆的面积是( )A .1B .32C .2D .525.如图,在△ABC 中,AB =AC ,AD 是中线,DE ⊥AB ,DF ⊥AC ,垂足分别为E ,F ,则下列四个结论中:①AB 上任一点与AC 上任一点到D 的距离相等;②AD 上任一点到AB ,AC 的距离相等;③∠BDE =∠CDF ;④∠1=∠2;其中正确的有( )A .1个B .2个C .3个D .4个6.如图,AB ∥CD ,BP 和CP 分别平分∠ABC 和∠DCB ,AD 过点P ,且与AB 垂直.若AD =8,则点P 到BC 的距离是( )A .8B .6C .4D .27.如图,已知在四边形ABCD 中,90BCD ∠=︒,BD 平分ABC ∠,6AB =,9BC =,4CD =,则四边形ABCD 的面积是( )A.24 B.30 C.36 D.42知识点三:角平分线判定定理=,则()8.如图,AC AD=,BC BDA.CD垂直平分AD B.AB垂直平分CDC.CD平分ACB∠D.以上结论均不对9.如图,已知AB∥CD,PE⊥AB,PF⊥BD,PG⊥CD,垂足分别E、F、G,且PF=PG=PE,则∠BPD=().A.60°B.70°C.80°D.90°10.如图所示,若DE⊥AB,DF⊥AC,则对于∠1和∠2的大小关系下列说法正确的是()A.一定相等B.一定不相等C.当BD=CD时相等D.当DE=DF时相等11.如图,在CD上求一点P,使它到OA,OB的距离相等,则P点是()A .线段CD 的中点B .OA 与OB 的中垂线的交点C .OA 与CD 的中垂线的交点 D .CD 与∠AOB 的平分线的交点知识点四:角平分线性质的实际应用12.如图,在ABC ∆中,90︒∠=C ,8AC =,13DC AD =,BD 平分ABC ∠,则点D 到AB 的距离等于( )A .4B .3C .2D .113.如图,Rt △ABC 中,∠C=90°,AD 平分∠BAC ,交BC 于点D ,若AB=14,S △ABD=14,则CD=( )A .4B .3C .2D .114.如图,AD 是△ABC 的角平分线,DE ⊥AB ,垂足为E ,S △ABC =7,DE =2,AB =4,则AC 长是( )A .6B .5C .4D .3知识点五:尺规作图-角平分线15.尺规作图作AOB ∠的平分线方法如下:以O 为圆心,任意长为半径画弧交OA 、OB 于C 、D ,再分别以点C 、D 为圆心,以大于12CD 长为半径画弧,两弧交于点P ,作射线OP ,由作法得OCP ODP ≌的根据是( )A .SASB .ASAC .AASD .SSS16.如图,在ABC ∆中,,40AC BC A =∠=︒,观察图中尺规作图的痕迹,可知BCG ∠的度数为()A .40︒B .45︒C .50︒D .60︒17.如图1,已知ABC ∠,用尺规作它的角平分线.如图2,步骤如下,第一步:以B 为圆心,以a 为半径画弧,分别交射线BA ,BC 于点D ,E ;第二步:分别以D ,E 为圆心,以b 为半径画弧,两弧在ABC ∠内部交于点P ;第三步:画射线BP .射线BP 即为所求.下列正确的是( )A .a ,b 均无限制B .0a >,12b DE >的长C .a 有最小限制,b 无限制D .0a ≥,12b DE <的长18.如图,观察图中尺规作图痕迹,下列说法错误的是( )A .OE 是AOB ∠的平分线B .OC OD =C .点C,D 到OE 的距离不相等D .AOE BOE ∠=∠二、填空题 知识点一:角平分线的有关证明19.如图,已知△ABC 的周长是21,OB ,OC 分别平分∠ABC 和∠ACB ,OD ⊥BC 于D ,且OD =4,△ABC 的面积是_____.20.如图,在平面直角坐标系xOy 中,点A 、B 分别在x 轴的正半轴、y 轴的正半轴上移动,点M 在第二象限,且MA 平分∠BAO ,做射线MB ,若∠1=∠2,则∠M 的度数是_______。
专题06 角平分线的性质与判定(五大类型)(题型专练)(原卷版)

专题06角平分线的性质与判定(五大类型)【题型1 角平分线的作法及应用】【题型2 角平分线性质的应用】【题型3 角平分线的性质与全等】【题型4 角平分线的判定】【题型5 角平分线的判定与性质综合】【题型1 角平分线的作法及应用】1.如图:已知OA和OB两条公路,以及C、D两个村庄,建立一个车站P,使车站到两个村庄距离相等即PC=PD,且P到OA,OB两条公路的距离相等.2.如图,l1、l2交于A点,请确定M点,使它到l1、l2的距离相等.(用直尺和圆规)【题型2 角平分线性质的应用】3.(2022春•本溪期中)如图,在△ABC中,∠C=90°,AD是∠BAC的角平分线,若CD=3,AB=8,则△ABD的面积是()A.24B.12C.15D.10 4.(2022秋•澄迈县期中)如图,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,DE=4,BC=9,则BE的长为()A.6B.5C.4D.3 5.(2023•城厢区校级模拟)如图,OP平分∠MON,点A在射线OP上,AB ⊥ON于点B,若OA=5,OB=4,则点A到射线OM的距离为.6.(2023春•通道县期中)如图,在Rt△ABC中,∠A=90°,BD平分∠ABC=12,BC=8,则AD=.交AC于点D,S△BDC7.(2023•门头沟区二模)如图,在△ABC中,CD是AB边上的高线,∠ABC 的平分线交CD于E,当BC=4,△BCE的面积为2时,DE的长为.8.(2022秋•大丰区期末)如图,地块△ABC中,边AB=40m,AC=30m,其中绿化带AD是该三角形地块的角平分线.若地块△ABD的面积为320m2,则地块△ACD的面积为m2.9.(2023•开福区校级一模)如图,BO平分∠ABC,OD⊥BC于点D,点E为射线BA上一动点,若OD=6,则OE的最小值为.10.(2022秋•藁城区期末)在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交AC,AB于点E,F;再分别以点E,F为圆心,大于的长为半径画弧,两弧交于点P,作射线AP交BC于点D.若CD=6,则点D到AB的距离是.11.(2022秋•交口县期末)如图,AC平分∠BAD,∠B+∠D=180°,CE⊥AD 于点E,AD=18cm,AB=11cm,那么DE的长度为cm.12.(2022秋•雨花区期末)如图所示,AC平分∠BAD,∠B+∠D=180°,CE ⊥AD于点E,AD=10cm,AB=7cm,那么DE的长度为cm.13.(2022秋•新华区校级期末)如图,已知OC平分∠AOB,P是OC上一点,PH⊥OB于点H,Q是射线OA上的一个动点,若PH=5,则PQ长的最小值为.14.(2022秋•云梦县期末)如图,已知△ABC的周长是22,OB、OC分别平分∠ABC和∠ACB,OD⊥BC于D,且OD=3,△ABC的面积是.15.(2022秋•和田市校级期末)如图,在△ABC中,∠BAC=90°,AD⊥BC 于点D,AE平分∠DAC.(1)当∠B=50°时,求∠AEC的度数.(2)DE=2,AC=6,求△ACE的面积.16.(2022秋•肇源县期末)如图,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB,如果DE=5cm,∠CAD=32°,求CD的长度及∠B的度数.17.(2023春•禅城区校级月考)如图,已知△ABC中,∠B=40°,∠C=76°,AD是△ABC的角平分线,DE⊥AB于E点.(1)求∠EDA的度数;.(2)若AB=20,AC=16,DE=6,求S△ABC【题型3 角平分线的性质与全等】18.如图,四边形ABCD中,∠B=∠C=90°,E是BC的中点,DE平分∠ADC.(1)求证:AE平分∠BAD;(2)判断AB、CD、AD之间的数量关系,并证明;(3)若AD=10,CB=8,求S.△ADE19.在△ABC中,已知∠A=90°,AB=AC,BD平分∠ABC,DE⊥BC于E,请解答下列问题:(1)若AD=2cm,则D点到BC边的距离是.(2)若BC=7cm,则△CDE的周长为.(3)连接AE,试判断线段AE与BD的位置关系,并说明理由.20.如图,已知△ABC中,∠C=90°,AD平分∠BAC交BC于D,DE⊥AB 于E,点F在AC上,且BD=FD,求证:AE﹣BE=AF.21.如图,DE⊥AB于E,DF⊥AC于F,AD平分∠BAC,若BE=CF,探索AB+AC 与AE的数量关系,并证明之.22.已知:如图,AC平分∠BAD,CE⊥AB于E,CF⊥AD于F,且BC=DC.(1)BE与DF是否相等?请说明理由.(2)若DF=1,AD=3,求AB的长.【题型4 角平分线的判定】23.(2022•南京模拟)如图,在△ABC中,∠ABC=60°,∠ACB=40°,点P为∠ABC、∠ACB的角平分线的交点.(1)∠BPC的度数是.(2)请问点P是否在∠BAC的角平分线上?请说明理由.(3)证明:AB=PC.24.(2023春•西安月考)如图,OC是∠AOB内的一条射线,D是OC上一点,过点D作DE⊥OA于点E,DF⊥OB于点F,已知OE=OF,求证:OC是∠AOB的平分线.25.如图,△ABC的外角∠MBC,∠NCB的平分线交于P,求证:点P在∠BAC的平分线上.26.如图,D、E、F分别是△ABC的三条边上的点,CE=BF,△DCE和△DBF 的面积相等.求证:AD平分∠BAC.27.如图,△ABC中,∠B的平分线与∠C的外角的平分线交于P点,PD⊥AC 于D,PH⊥BA于H,(1)若点P到直线BA的距离是5cm,求点P到直线BC的距离;(2)求证:点P在∠HAC的平分线上.【题型5 角平分线的判定与性质综合】28.已知:如图,在Rt△ABC中,∠C=90°,D是AC上一点,DE⊥AB于E,且DE=DC.(1)求证:BD平分∠ABC;(2)若∠A=36°,求∠DBC的度数.29.(2022秋•秦淮区期末)如图,在△ABC中,∠ACB、∠ABC的平分线l1、l2相交于点O.(1)求证:点O在∠BAC的平分线上;(2)连接OA,若AB=AC=5,BO=4,AO=2,则点O到三角形三条边的距离是.30.(2022秋•利川市期末)如图,四边形ABCD中,∠B=∠C=90°,点E 为BC的中点,且AE平分∠BAD.(1)求证:DE平分∠ADC;(2)求证:AB+CD=AD.31.如图,在△ABC中,D,E分别为BC,AC边上一点,连接AD,DE,BE,过点E向AB作垂线,交BA的延长线于点F.已知AE平分∠DAF.BE平分∠ABC,2AB=3AD.(1)求证:DE平分∠ADC;(2)若AD=3,CD=7,且S△ABE =,求S△ADC.32.如图,四边形ABDC中,∠D=∠ABD=90°,点O为BD的中点,且OA 平分∠BAC.(1)求证:OC平分∠ACD;(2)求证:OA⊥OC;(3)求证:AB+CD=AC.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1如图1所示,在△ ABC中,∠ A= 90°, BD平分∠ ABC AD= 2 Cm ,则点D到BC的距离为___________ cm.
2. 如图2所示,在Rt Δ ABC中,∠ C = 90°, BD是∠ ABC的平分线,交
AC于D,若CD = n, AB = m, 则Δ ABD的面积是()
1 1
A . -mn B. — mn C. mn D. 2mn
3 2
3. 如图,在△ ABC中,∠ C= 900, BC= 40, AD是∠ BAC的平分线交BC于D,且DC:
DB= 3 : 5,则点D到AB的距离是________ 。
4. 如图,已知BD是∠ ABC的内角平分线,CD是∠ ACB的外角平分线,由D出发,作点D到
BC3题题图和AB
的垂线DE DF和DG垂足分别为 E F、G贝U DE DF、DG的关系是__________________________
5. _________________________________ 如图,已知AB//
CD O为∠ A∠ C的角平分线的交点, 则两平行线间AB CD的
距离等于______________________________ 。
6. AD是厶BAC的角平分线,自D向AB AC两边作垂线,垂足为E、F,那么下列结论中错误的是
()
A DE=DF
B 、AE=AF C、BD=CD D∠ ADE玄ADF
7. 到三角形三条边的距离都相等的点
是这个三角形的()
A.三条中线的交点 E.三条高的交点
C.三条边的垂直平分线的交点
D.三条角平分线的交点
8. 已知△ ABC中,∠ A=80°,∠ B和∠ C的角平分线交于O点,则∠ BOC= ___ 。
9. 如图,已知相交直线AB和CD及另一直线EF。
如果要在EF上找出与AB CD距离相等的点,方
法
是___________ ,这样的点至少有________ 个,最多有___ 个。
OEL AC于E,且0E=2
10.如图所示,已知△ ABC中,∠ C=90°, AC=BC AD平分∠ CAB 交BC于点D,DELAB于点E,且AB=6 cm,则厶DEB勺周长为()。
A.9 Cm
B.5 Cm
C.6 Cm
D.不能确定
11.如图,
AB/ CDCE
D
平分∠ ACD
若∠ 1=250,
那么∠ 2的
12 .如图,
OP平分
AoB ,
PA OA ,
PB OB ,
垂足分别
为A, B.下
列结论中
不一定成
立的是()
A. PA PB B . PO 平分APB C. OA
CAB和∠ ABD CD过点E,则AB与AC+BD相等吗?说
明理由.
OB D . AB垂直平分OP
13.如图,已知AC// BD EA EB分别平分∠
14、如图所示,已知AD为等腰三角形ABC的底角的平分线,∠ C= 90°
求证:AB= AC+ CD
15、如图,在四边形ABCD中,BC>BA AD=DC,BD平分∠ ABC,求证:∠
A+∠
C=180°并写出画法)
18. 已知:OD平分∠ PoQ ,在OP、OQ边上取OA = OB, CM丄AD于M , CN丄BD于N. 求证:
CM = CN .
19. 已知:如图,ΔABC的外角∠ CBD和∠ BCE的平分线BF、CF交于点F.
求证:一点F必在∠ DAE的平分线上.
16、如图,∠ ACB=90 ,AC=BC BE⊥ CE AD⊥ CE.求证:△ACD^△ CBE.
17.已知:如图,△ ABC中,∠ C = 90° ,试在AC上找一点P,使P到斜边的距离等于
20. 已知:如图, A 、B 、C 、D 四点在∠ MON 的边上,AB = CD , P 为∠ MON 内一点,并且△ PAB 的面积 与厶
PCD 的面积相等.
求证:射线 OP 是∠ MON 的平分线.
21 .如图,Δ ABC 中,∠ C = 90°, BD 平分∠ ABC , DE 丄AB 于丘,若厶BCD 与厶BCA 的面积比为 3 : 8, 求
厶ADE 与厶BCA 的面积之比.
22.已知:如图,∠ B =∠ C = 90°, M 是BC 的中点,DM 平分∠ ADC .
(1) 求证:AM 平分∠ DAB ;
2)猜想AM 与DM 的位置关系如何?并证明你的结论.
23 .已知:如图,在Δ ABC 中,AD 是厶ABC 的角平分线,E 、F 分别是 + ∠ EAF = 180°.试判断 DE 和DF 的大小关系并说明理由.
24 .如图1所示:AMy DN AE DE 分别平分∠ MAD∏∠ AND 并交于E 点. 过点E 的直线分别交AM DNf B 、C.
(1 )如图2 ,当点 B 、C 分别位于点 AD 的同侧时,猜想 AD AB 、CD 之间的存在的数量关系
:
Af
EDF
(2) 试证明你的猜想
(3) 若点B、C分别位于点AD的两侧时,试写出AD AB CD之间的关系,并选择一个写出证明过程。
2 ,当点C在X轴正半轴上运动,点A在y轴正半轴上运动,点试判断°C―B D
OA
OA
结论: 证明:
26. 如图,△ ABC中,∠ ABC=42 ,D 是BC边上一点,DC=A D .且
工
(1 )△ ABC是 ___________ 三角形;
(2)证明你的结论。
27 .在△ ABC中,AB AC ,点D是直线BC上一点(不与B、C重合),以AD为一边在AD的右侧作
△ ADE ,使AD AE, DAE BAC ,连接CE .
(1)如图1 ,当点D在线段BC上,如果BAC 90°,则BCE _______________ 度;
(2)设BAC , BCE .
①如图2,当点D在线段BC上移动,贝U , 之间有怎样的数量关系?请说明理由;
②当点D在直线BC上移动,则之间有怎样的数量关系?请直接写出你的结论.
25. 已知:在平面直角坐标系中,△ABC的顶点A C分别在y轴、X 轴上,且∠ ACB=90 ,AC=BC.
(1)如图 1 ,当A(Q l 2),C(1,0),点B在第四象限时,则点B的坐标为*y
B在第四象限时,作BD⊥ y轴于点D,
与°C B D哪一个是定值,
并说明定值是多少?请证明你的结论
(2)如图
图1
图 2
Ay
A
B=27。
28.已知:如图,在△
∠ PCA=120 —
备用图
ABC中,AB=AC ∠ BAC= ,■且60° <
(1) 用含的代数式表示∠
(2) 求证:∠ BAPg PCB
(3) 求∠ PBC的度数.
证明:(2)
APq 得∠ APC =
备用图
<120 ° . P为厶ABC内部一点,且PC=AC。
