关于数论函数方程
2024年新高考版数学专题1_3.5 函数与方程及函数的综合应用(分层集训)

B.3
答案 B
C.4
D.5
)
3.(2022南京师范大学附中期中,7)用二分法研究函数f(x)=x3+2x-1的零点
时,第一次计算,得f(0)<0,f(0.5)>0,第二次应计算f(x1),则x1等于 (
A.1
B.-1
答案 C
C.0.25
D.0.75
)
4.(多选)(2022湖南师大附中三模,11)已知函数f(x)的定义域为R,且f(x)=f(x
1.(2023届长春六中月考,7)若函数f(x)=ln x+x2+a-1在区间(1,e)内有零点,则
实数a的取值范围是 (
A.(-e2,0)
C.(1,e)
答案 A
B.(-e2,1)
D.(1,e2)
)
2.(2017课标Ⅲ,文12,理11,5分)已知函数f(x)=x2-2x+a(ex-1+e-x+1)有唯一零点,
A型
0.4
3
B型
0.3
4
C型
0.5
3
D型
0.4
4
则保温效果最好的双层玻璃的型号是 (
A.A型
答案 D
B.B型
C.C型
D.D型
)
3.(2020课标Ⅲ理,4,5分)Logistic模型是常用数学模型之一,可应用于流行
病学领域.有学者根据公布数据建立了某地区新冠肺炎累计确诊病例数
I(t)(t的单位:天)的Logistic模型:I(t)=
1 e
K
0.23( t 53)
,其中K为最大确诊病例数.
当I(t*)=0.95K时,标志着已初步遏制疫情,则t*约为(ln 19≈3) (
数论知识点归纳总结

数论知识点归纳总结数论是数学的一个分支,研究整数及其性质的科学。
它是由数学中最古老的领域之一,也是最重要的领域之一。
数论大部分内容都集中在整数的性质和关系,包括数的性质、数的划分、数的因子、余数、等式、方程等。
数论在许多不同的领域有很多应用,如密码学、加密技术、算法设计、计算机科学等等。
下面将对数论的一些重要知识点进行归纳总结,以便更好地理解和掌握数论的基本概念和方法。
一、整数及其性质1. 整数的性质:整数是由自然数和其相反数构成的有理数。
整数的性质包括奇数和偶数的性质、质数和合数的性质、互质数和最大公约数的性质等等。
2. 除法定理:任意两个整数a和b中,存在唯一的一对整数q和r使得a=bq+r,其中0<=r<|b|。
3. 唯一分解定理:每一个大于1的自然数都可以写成一组素数的乘积。
而且,如果一个数有两种不同的素因数分解形式,那么这两种形式只差一个或若干个单位。
4. 有限整除原理:如果一个整数被另一个不等于0的整数整除,那么这两个整数中一定有一个是整数的最大公因子。
二、数的划分1. 除法和约数:一个整数能被另一个整数整除,那么这个整数就是另一个整数的约数。
2. 素数:只有1和它本身两个因子的自然数,称为素数。
3. 合数:大于1的除了1和它本身以外还有其他因子的数,称为合数。
4. 最大公因数和最小公倍数:两个整数a和b最大的公因数称为a和b的最大公因数,最小的公倍数称为a和b的最小公倍数。
5. 互质数:两个数的最大公因数是1,就称这两个数是互质数。
三、同余和模运算1. 同余性质:如果两个整数a和b除以正整数m所得的余数相等,就称a与b对模m同余。
2. 同余方程:形如ax≡b(mod m)的方程称为同余方程,其中a,b,m都是整数。
3. 欧拉函数:对于任意正整数n,欧拉函数φ(n)是小于或等于n且与n互质的正整数的个数。
4. 模反元素:在模n的情况下,如果一个数a与n互质,那么a关于模n的乘法逆元素x 就是属于[0, n-1]的一个整数,使得ax ≡ 1 (mod n)。
数论复习

⑴计算mi
设n=n1 *n2 *...*nk ; m1 =n/n1 =n2 *n3 ...*nk ; m2 =n/n2 =n1 *n3 *n4 ...*nk ; ...; mi =n/ni =n1 *..*ni-1 *ni+1 ...*nk ; ... mk =n/nk =n1 *...*nk-2 *nk-1 ;
初等数论
• 人们在对整数进行运算的应用和研究中,逐步 熟悉了整数的特性。比如,整数可分为两大 类—奇数和偶数等。利用整数的一些基本性质, 可以进一步探索许多有趣和复杂的数学规律, 正是这些特性的魅力,产生了整数论。后来整 数论又进一步发展,就叫做数论了。确切的说, 数论就是一门研究整数性质的学科。使用不超 过高中程度的初等代数处理的数论问题即为初 等数论,初等数论最主要的工具包括整数的 整除性与同余。
步骤2:证明ax≡b(mod m)只有 [x], [x+m/d],[x+2*m/d], …,[x+(d-1)*m/d]这d个不同 的解 从以上讨论知,可设x+t*m/d为ax≡b(mod m)的 一个解,由于t≡i(mod d),i∈{0,1,2,…,d-1}。在 t≡i(mod d)两边同乘m/d便有t*m/d≡i*m/d(mod m),这就是说,[x+tm/d]为 [x],[x+m/d],[x+2m/d],…,[x+(d-1)m/d]中之一。
建立模数方程
数字i和数字j在第1‥min{li,lj}次移动中共同移 动。它们能否在该期间相遇与空格数、相对位置 cab[i,j]和的相对速度pab[i,j]有关。设x为移动 次数,m为可能的空格数。显然,若pab [i,j]*x 和cab [i,j]对模m有相同的余数,则说明在第x次 移动中数字i和数字j处于同一个空格。我们的目 的就是要寻找最小的m,使得任何一对数字在移 动过程中不会相遇,即x在(1‥min{l[i],l[j]}) 范围内,pab[i,j]*x≡cab[i,j](mod m)无解 (1≤i≤n,i+1≤j≤n)。
欧拉定理及其在数论中的应用

欧拉定理及其在数论中的应用欧拉定理(Euler's theorem),也称为费马-欧拉定理(Fermat-Euler theorem)是数论中非常重要的定理之一。
该定理描述了整数的幂与模运算之间的关系,具体地说,它说明了如果正整数a与正整数n互质,那么a的欧拉函数值与n的模运算结果余数的幂是相等的。
欧拉函数φ(n)指的是小于或等于n且与n互质的正整数的个数。
欧拉定理的数学表达式如下:如果a与n互质,那么a^φ(n)与1对模n同余。
其中,^表示乘方运算,φ(n)表示欧拉函数的值。
欧拉定理具有广泛的应用,特别在密码学和安全领域中发挥重要作用。
例如,在RSA(一种非对称加密算法)中,欧拉定理用于实现密钥的生成和加密过程。
此外,它还在数学证明和计算机科学中有诸多应用。
让我们进一步深入探讨欧拉定理在数论中的应用。
首先,欧拉定理提供了一种有效的方法来计算整数的模逆元素。
模逆元素是指在模意义下乘法的逆元素。
根据欧拉定理,如果a与n互质,那么a的欧拉函数值与n的模运算结果余数的幂是相等的。
因此,我们可以使用欧拉定理来计算整数a模n的逆元素。
具体地说,如果a与n互质,那么a^φ(n)与1对模n同余;所以, a^(φ(n)-1)与a的乘法逆元素对模n同余。
这种方法在RSA算法以及其他需要计算模逆元素的情况下非常有用。
其次,欧拉定理在素数测试中也有重要的应用。
根据费马定理(Fermat's theorem),如果p是一个素数,那么对于任意整数a,a^(p-1)与1对模p同余。
然而,对于合数n,a^(n-1)与1对模n同余的性质不一定成立。
欧拉定理的推广版本,即欧拉-费马定理(Euler-Fermat theorem),描述了当a和n互质时,a的欧拉函数值与n的模运算结果余数的幂是相等的。
这一定理可以有效用于检验一个数是否为素数,从而在素数测试中起到重要的作用。
此外,欧拉定理在分解整数的质因数和求解同余方程中也有广泛应用。
数论的方法和技巧 03高斯函数
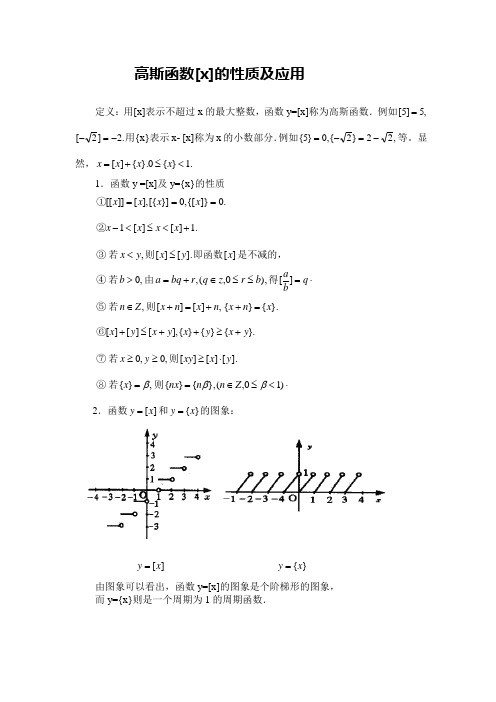
高斯函数[x]的性质及应用定义:用[x]表示不超过x 的最大整数,函数y=[x]称为高斯函数.例如,5]5[=.2]2[-=-用{x}表示x- [x]称为x 的小数部分.例如,22}2{,0}5{-=-=等。
显然,.1}{0}.{][<≤+=x x x x1.函数y =[x]及y={x}的性质.0]}{[,0}][{],[]][[===x x x x ① .1][][1+<≤<-x x x x ②③若,y x <则].[][y x ≤即函数][x 是不减的,④若,0>b 由),0,(,b r z q r bq a ≤≤∈+=得⋅=q ba][⑤若,Z n ∈则,][][n x n x +=+}.{}{x n x =+ }.{}{}{],[][][y x y x y x y x +≥++≤+⑥⑦若,0,0≥≥y x 则].[][][y x xy ⋅≥⑧若,}{β=x 则⋅<≤∈=)10,(},{}{ββZ n n nx2.函数][x y =和}{x y =的图象:][x y = }{x y =由图象可以看出,函数y=[x]的图象是个阶梯形的图象, 而y={x}则是一个周期为1的周期函数.在解与[x]有关的题目时,通常可以利用[x]性质把问题转化为不等式求解,因此限定x 的范围,使问题得解,(1)与 [x] 有关的计算 例1 求和式]10123[1001nn ∑=的值例2. (1993年亚太地区竞赛题)求函数[]]4[]3[]35[]2[)(x x x x x x f ++++=在0≤x≤100上所取的不同的整数值的个数.例3. (1993年全国高中联赛)试求正整数]31010[3193+的末两位数字.例4. 设,N n k ∈、,41212+++=k k α求n α的整数部分][n α除以k 所得的余数.(2)运用 [x ] 的性质证明含[f (n )]的恒等式和不等式 例5. 对于任意),1(>∈n N n 试证明:][log ][log ][log ][][][323n n n n n n n n +++=+++例6. 若),7()1(,][+⋅⋅+=∈n n n x N x n 求证:.67][24++=n n x例7. ,N n ∈求证:①].[][2]2[1][nx nnx x x ≤+++例8. 设有n 个小于1 000的正整数:⋅n a a a 、、21其中任意两个数j i a a 、的最小公倍数,1000],[≥j i a a 求证:①⋅<∑=2311i ni a(3)运用 [x ] 的性质解含[α]的恒等式和不等式 例9. 解方程02][lg lg 2=--x x例10.(1989年第二十三届全苏竞赛题)当n 是怎样的最小自然数时,方程1989]10[=x n有整数解?例11. (第三届美国邀请赛题)前1000个正整数中可以表示成]8[]6[]4[]2[x x x x +++ 的正整数有多少个?例12. ,N n ∈求证:].[][])[1(][][ny nx y x n y x +≤+-++(4)运用 [x ] 的性质解含[α]的杂题 例13. 设集合},,23|{2N n n n a a A n n ∈-==}.],213[)(|)({N n n n n f n f B ∈++==求证:.,N B A B A =∅=例14. 设,=x求[x]的末三位数.+5(1000)62例15. 令],2[n a n 求证:在数列}{n a 中有无穷多个项是2的整数次方幂,例16. (1992年四川高中竞赛题)设正实数a >1,自然数n ≥2.且方程[ax ]=x 恒有n 个不同的解.求a 的取值范围.练习题1.用<x> 表示不小于x 的最小整数,则方程024][82=++><x x 的解为( )A. -5 <x< -4 B . 一6<x< -5 C.x< -5 D. -5≤x≤-42.方程8082]310[3]310[31212-=+⨯-+⨯-++x x x x 的整数解的个数为( )A. 0B. 1C. 2D. 33.=++++]32[]32[]32[]31[10002 。
重庆高考文科数学知识点

重庆高考文科数学知识点在重庆高考文科数学中,有一些重要的知识点需要掌握。
这些知识点不仅在高考中扮演着重要角色,而且对于学生的数学素养的提高也具有重要意义。
下面将列举一些重要的数学知识点。
一、函数与方程在高考中,函数与方程是一个非常重要的部分。
在函数与方程的学习中,学生需要了解如何解一元二次方程,一元一次方程以及相关的图像特征和性质。
此外,学生还需要了解如何求解函数的零点、极限、导数等。
二、三角函数三角函数是数学中一个重要的分支,也是高考中的一个重要考点。
学生需要了解正弦、余弦、正切等三角函数的概念、性质以及相关的应用。
另外,学生还需要掌握如何求解三角函数的一些常用基本性质和公式。
三、排列组合与概率排列组合与概率是数学中的一个重要内容,也是高考文科数学中的考点之一。
在排列组合与概率的学习中,学生需要了解如何计算排列、组合、全排列和重复排列等问题。
此外,学生还需要了解概率的概念、性质以及如何计算概率。
四、数列与数列求和数列与数列求和是高考数学中的一个重要内容。
学生需要了解等差数列、等比数列等概念、性质以及相关的计算方法。
此外,学生还需要掌握如何计算等差数列、等比数列的前n项和以及无穷级数的和。
五、复数与复数平面复数与复数平面是高考文科数学中的一个重要考点。
学生需要了解复数的概念、性质以及如何进行复数的基本运算。
此外,学生还需要了解复数在平面几何中的应用,如平面向量等。
六、平面几何与立体几何平面几何与立体几何是高考数学中的重要内容。
学生需要了解如何计算平面图形的周长、面积等,并能够解决相关的计算问题。
在立体几何的学习中,学生需要了解如何计算立体图形的体积、表面积等,并能够解决一些相关的应用问题。
七、数论与逻辑数论与逻辑是高考数学中的一个重要部分。
在数论的学习中,学生需要了解质数、合数、约数等概念,并能够解决一些相关的问题。
在逻辑的学习中,学生需要了解命题、充分必要条件等概念,并能够运用逻辑进行推理。
八、统计与概率统计与概率是高考数学中的一个重要内容。
数论 欧拉定理

数论欧拉定理欧拉定理(euler theorem),也称费马-欧拉定理或欧拉函数定理,是一个关于同余的性质,得名于瑞士数学家莱昂哈德·欧拉。
该定理被认为是数学世界中最美妙的定理之一,在西方经济学中又称为产量分配净尽定理,指在完全竞争的条件下,假设长期中规模收益不变,则全部产品正好足够分配给各个要素。
欧拉定理指出:如果产品市场和要素市场都是完全竞争的,而且厂商生产的规模报酬不变,那么在市场均衡的条件下,所有生产要素实际所取得的报酬总量正好等于社会所生产的总产品。
该定理又叫做边际生产力分配理论,还被称为产品分配净尽定理。
如上所述,要素的价格是由于要素的市场供给和市场需求共同决定。
在完全竞争的条件下,厂商和消费者都被动地接受市场形成的价格。
定理推论在完全竞争的条件下,厂商使用要素的原则是:要素的边际产品价值等于要素价格。
即:p*mpl=w (1)p*mpk=r (2)由式1和2只须:mpl=w/p (3)mpk=r/p(4p为产品的价格,w/p和r/p分别表示了劳动和资本的实际报酬。
因为在完全竞争的条件下,单位劳动、单位资本的实际报酬分别等于劳动、资本的边际产量。
假定整个社会的劳动总量和资本总量为l和k,而社会总产品为q,由在市场均衡的条件下,所有生产要素实际所取得的报酬总量正好等于社会所生产的总产品,得:q=l*mpl+k*mpk(5)式5称为欧拉分配定理。
它是由于该定理的证明使用了数学上的欧拉定理而得名。
定理证明假设生产函数为:q=f(l.k)(即q为齐次生产函数),定义人均资本k=k/l方法1:根据齐次生产函数中相同类型的生产函数展开分类探讨(1)线性齐次生产函数n=1,规模报酬维持不变,因此存有:q/l=f(l/l,k/l)=f(1,k)=g(k)k为人均资本,q/l为人均产量,人均产量就是人均资本k的函数。
让q对l和k求偏导数,有:由上面两式,即可得欧拉分配定理:(2)非线性齐次生产函数1.当n〉1时,规模报酬递减,如果按照边际生产力分配,则产品比较分配给各个生产要素,即为:2.当n\uc1时,规模报酬递减,如果按边际生产力进行分配,则产品在分配给各个生产要素之后还有剩余,即:方法2:设立一个通常的齐次生产函数q=f(l,k)为n齐次(即n任一的齐次生产函数,既可以就是线性的,也可以就是非线性的),则存有:q=l *g(k)将该函数对k,对l谋略偏导数,得:综合上述两式,有:当n=1时,规模报酬维持不变,该式即为欧拉分配定理当n〉1时,规模报酬递增,故有:当n\uc1时,规模报酬递增,故存有:实例在技术经济学中,欧拉定理属一次齐次函数的一个关键性质,它就是说道一次齐次函数的数值都可以则表示为各自变量和因变量对适当自变量一阶偏导的乘积之和。
初等数论第五章同余方程

第五章同余方程本章主要介绍同余方程的基础知识,并介绍几类特殊的同余方程的解法。
第一节同余方程的基本概念本节要介绍同余方程的基本概念及一次同余方程。
在本章中,总假定m是正整数。
定义1设f(x) = a n x n a1x a0是整系数多项式,称f(x) 0 (mod m) (1)是关于未知数x的模m的同余方程,简称为模m的同余方程。
若a n≡/0 (mod m),则称为n次同余方程。
定义2设x0是整数,当x = x0时式(1)成立,则称x0是同余方程(1)的解。
凡对于模m同余的解,被视为同一个解。
同余方程(1)的解数是指它的关于模m互不同余的所有解的个数,也即在模m的一个完全剩余系中的解的个数。
由定义2,同余方程(1)的解数不超过m。
定理1下面的结论成立:(ⅰ) 设b(x)是整系数多项式,则同余方程(1)与f(x) b(x) b(x) (mod m)等价;(ⅱ) 设b是整数,(b, m) = 1,则同余方程(1)与bf(x) 0 (mod m)等价;(ⅲ) 设m是素数,f(x) = g(x)h(x),g(x)与h(x)都是整系数多项式,又设x0是同余方程(1)的解,则x0必是同余方程g(x) 0 (mod m) 或h(x) 0 (mod m)的解。
证明 留做习题。
下面,我们来研究一次同余方程的解。
定理2 设a ,b 是整数,a ≡/0 (mod m )。
则同余方程ax b (mod m ) (2)有解的充要条件是(a , m )b 。
若有解,则恰有d = (a , m )个解。
证明 显然,同余方程(2)等价于不定方程ax my = b , (3)因此,第一个结论可由第四章第一节定理1得出。
若同余方程(2)有解x 0,则存在y 0,使得x 0与y 0是方程(3)的解,此时,方程(3)的全部解是⎪⎪⎩⎪⎪⎨⎧-=+=t m a a y y t m a m x x ),(),(00,t Z 。
(4) 由式(4)所确定的x 都满足方程(2)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
关于数论函数方程()()2S n n ϕ=李宋宋(安徽师范大学 安徽芜湖 241000)摘要:对于任给的正整数n ,()n ϕ和()S n 分别是Euler 函数和Smarandache 函数,本文根据初等数论的理论以及分类讨论的方法,对数论方程()()2S n n ϕ=的解进行了讨论并给出了解的表达式以及解的判别条件。
关键词:Euler 函数;Smarandache 函数;阶乘;费马数;方程On the Arithmetic Functional Equation()()2S n n ϕ=Abstract: For any given positive integer n,()n ϕ and ()S n are Euler function and Smarandache functionrespectively, according to the elementary number theory and the method of classification discussion, this article has discussed the arithmetic functional equation ()()2S n n ϕ=and finally given the expression and thediscriminants of solution.Keywords: Euler function ;Smarandache function ;factorial ;Fermat number ;equations1 引言对于任意正整数n ,设()n ϕ和()S n 分别是Euler 函数和Smarandache 函数.其中,()n ϕ表示不大于n 且与n 互素的正整数的个数;()S n 定义为最小正整数m ,使得|!n m ,即:!}|,{()min m n m m Z S n +=∈.()S n 的各种性质是数论及其应用领域中一个十分引人关注的研究课题[1].关于这两个函数之间关系的讨论,一直也是很多学者研究的对象[2]-[4], 例如文献[2]中讨论了数论方程()()tn S n ϕ=的相关性质和求解过程,并且在很多学者努力下,此类型方程的求解结果已经很完善;文献[4]中讨论并给出了方程()()2n n ωϕ=的解.在诸多文章和结果的启发下,本文提出了一类数论方程()()2S n n ϕ=的求解问题,并通过分类讨论的方法,在现有的五个费马素数的基础上得到了此类方程解的表达式和部分解的判别条件.现将本文的主要结果列在下面:定理 对于任给的正整数n ,()n ϕ和()S n 分别是Euler 函数和Smarandache 函数,若n 为数论方程()()2S n n ϕ=的解,则n的标准分解式为:12m s n p p =,1(3,15)s p p s ≤<<≤≤为素数,其中221k ii p =+,{0,1,2,3,4},(1,,)i k i s ∈=,m 满足:(1)当1s =时,1121km p =-+,1{23,4}k ∈,,或者m 满足不等式组:11111(21)21(22)221k k k k a m a m m p ⎧+-≤-⎪+->-⎨⎪≥-⎩,1{12,3,4}k ∈, 特别地,当15p =时,21,3t m t =-≥.(2)当15s <≤时,121i sk s i m p ==-+∑,或者m 满足不等式组:1111(21)21(22)221i i i is sk k i i s s k k i i s a m a m m p ====⎧+-≤-⎪⎪⎪+->-⎨⎪⎪≥-⎪⎩∑∑∑∑ 其中{0,1,2,3,4}i k ∈.()a n 为n 的二进制表示的各数字之和.2 相关引理引理1[5]对任意互素的正整数a 和b ,Euler 函数为积性函数,即()()()ab a b ϕϕϕ=.引理2[5]如果1212ss n p p p ααα=是正整数n 的标准分解式,其中i p 为不同素数,iα为正整数=1,2,,s (i ),则有11(1)()isi i i p p n αϕ-=-=∏引理3[6] 如果1212ss n p p p ααα=是正整数n 的标准分解式,则有1212()max{(),(),,()}ss S n S p S p S p ααα=引理4[5]若12,,,s p p p 为不大于n的互不相同的正素数,则!n 的标准分解式为21!k i i i i in n n sp p p i n p⎡⎤⎡⎤⎡⎤+++⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦==∏其中1i i k k i i p n p +≤<.引理5 对任给的正整数k ,方程(2)m m k S +=的解m 满足:()(1)1a m k ka m k k +≤⎧⎨+->-⎩ 其中()a n 表示n 的二进制表示的各数字之和.证明 设()!m k +的标准分解式中,2的指数为2()!Ord mk +,首先证明2()!()()Ord m k m k a m k +=+-+.设()m k +的二进制表示为1(s s m k a a -+=102)a a ,其中0i a =或1,(0~)i s =,记()a m k +为二进制表示的数字之和,即110()s s a m k a a a a -+=++++则由引理4,2()!222m k m k m k Ord m k t ⎡⎤⎡⎤+++⎡⎤+=+++⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦其中12()2t t m k +≤+<,于是212121221112111210121010()!()()()(111)(111)++(11)(10001)(10001)++(1001)(101)(11)()()().s s s s s s sS S s s S S s s s s s s Ord m k a a a a a a a a a a a a a a a a a a a a a a a a a a a m k a m k ---------+=++++=++=-+--+-+-=-+++=+-+个个个个其次,若m 为方程(2)mm k S +=的解,由()S n 的定义知,min{:2!}mm k n n +=,也就是:22()!,(-1)!Ord m k m Ord m k m +≥+<且即()()(1)(1)().(1)1m k a m k m m k a m k m a m k k a m k k +-+≥⎧⎨+--+-<⎩+≤⎧⇒⎨+->-⎩引理6[7]若p 为21t+型的素数,则2k t =,即221kp =+为费马素数.目前知道的费马素数只有3,5,17,257, 65537,本文就在这些费马素数的范围内讨论所给方程的解.3 定理的证明分两部分证明,首先证明方程解的标准分解式为 12m s n p p =,1(3p ≤<<,15)s p s ≤≤;其次给出1,,,s p p m 应满足的条件。
第一部分:当1n =时,(1)(1)1,22S ϕ==,因此1n =不是方程的解;当n p α=时,代入方程有:1()()(1)2S n n p p αϕ-=-=因此要求(i) 当3p ≥时,1α=,即12pp -=,显然等式不成立,故此种情形无解;(ii) 当2p =,即1(2)22,S αα-=从而1(2)S αα-=.由于222111(!)()222222k k Ord αααααα⎡⎤⎡⎤⎡⎤=+++≤+++<⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦——(*)所以1(2)S ααα-<<,故此种情形无解;当1221ssp n p p ααα=时, 1(3p ≤<,2,1,,)s i p Z s i s α+<∈≥=为素数,此时方程为:1()1()(1)2i sS n i i i n p p αϕ-==-=∏要使方程有解,则1(1,,)i i s α==,方程可写为:1(1)2s sp i i p =-=∏.则(1,,)i p i s =必为21k+型的素数,由引理6知, (i p i =1,,)s 为Fermat 素数,本文仅考虑3,5,17,257,65537这5个费马素数.设为:221k ii p =+, {0,1,2,3,4}i k ∈,其中1,,,24i s s =≤≤根据引理知,s11222()=222sk ik k i n ϕ=∑=12()max{(),(),,()}s s S n S p S p S p p ==代入方程得:21221k si sk i ==+∑, 但是23211125222,(0)k sisssk k k s i k k ++=<⨯<<>=∑也即 ()()2S n n ϕ<.因此,此种情形方程无解.排除以上几种情况,并且由上面的分析可知,n 的标准分解式只能为:112(3),15m s s n p p p p s =≤<<≤≤——(**)第二部分:将(**)代入方程()()2S n n ϕ=有: 1()12(1)(1)2m S n s p p ---=如果方程有解,则(1,,)i p i s =必须为21t +形的素数,由引理6,(1,,)i p i s =为费马素数221kp =+.下面对s 进行分类讨论:(1)当1s =时,即2m n p =,其中221kp =+0,1,2,3,=(k ),根据引理2和引理3,有:11212()2(1)222k km m m n p ϕ---+=-==()(2)max{(2),}m m S n S p S p ==代入方程得:12(2)2,(2)22,(2)km p mm S mp S p S -+⎧≥⎪=⎨<⎪⎩① 当221(2)km p S +=≥时,若方程有解,则有:2122121kk k m m p -+=+⇒=-+对k 进行分类讨论:当0,3k p ==时,得3m =,但是3(2)43S =>,矛盾! 当1,5k p ==时, 521m =-+即4m =,但是4(2)65S =>,矛盾!当2,17k p ==时, 1741m =-+,即14m =,并且14(2)17S <,故14217n =⨯为方程的解;当3,257k p ==时,得m =250,并且250(2)257S <,故2502257n =⨯为方程的解;当4,65537k p ==时,得m =65522,并且65522(2)65537S <,故65522265537n =⨯为方程的解;②当221(2)km p S +=<时,若方程有解,则12(2)k m m S -+=,同样对k 进行分类讨论:当0,3k p ==时,有(2)m m S =,由(*)式知此种情形无解;当1,5k p ==时,有1(2)m m S +=,若方程有解,由引理5知m 应满足:(1)1(1)1()0a m a m a m +≤⎧⇒+=⎨>⎩12(3)21(3t tm t m t ⇒+=≥⇒=-≥ 因此,2125,(3)tn t -=⨯≥为方程的解.当2,17k p ==时,有3(2)mm S +=,若m 为方程的解,由引理5,当且仅当(3)3(2)2a m a m +≤⎧⎨+>⎩ 当3,257k p ==时,有7(2)m m S +=,若m 为方程的解,由引理5,当且仅当(7)7(6)6a m a m +≤⎧⎨+>⎩ 当4,65537k p ==时,有15(2)m m S +=,若m 为方程的解,由引理5,当且仅当(15)15(14)14a m a m +≤⎧⎨+>⎩综合起来,2mn p =型的解为:1121k m p =-+,12k ≥,或者m 满足不等式组:111111(21)21(22)22,11k k k ka m a m k m p ⎧+-≤-⎪+->-≥⎨⎪≥-⎩. 并且当15p =时,21,3t m t =-≥.解的具体表达式参见表格1.表格1 方程()()2S n n ϕ=的2mn p =型的解Table 12m n p = type of solution of the equation ()()2S n n ϕ=表格2 方程()()2S n n ϕ=的122m n p p =型的解Table 2122m n p p = type of solution of the equation ()()2S n n ϕ=(2)当2s =时,即122m n p p =,其中1222121221,21(04)k k p p k k =+=+≤<≤,根据引理2和引理3知:1212122122()2222k k k k m m n ϕ--++==22()(2)22,(2)22,(2)mp mS n S mp S p S ⎧≥⎪=⎨<⎪⎩ 代入方程()()2S n n ϕ=有:12222,(2)122(2),(2)mk k m mp p S m S p S ⎧≥⎪-++=⎨<⎪⎩1212222221,(2)122(2),(2)k k mk k m mm p p S m S p S ⎧=--+≥⎪⇒⎨-++=<⎪⎩ 同(1)中的讨论方法一样,不同的是,此时是对12(,)k k =(0,1),(0,2),(0,3),(0,4),(1,2),(1,3),(1,4),(2,3),(2,4),(3,4)进行分类讨论,具体步骤不再重复,最后得到对12(,)k k 的所有分类情况均存在方程的解.归纳起来有:122m n p p =型解中122221k k m p =-++,或者m 满足不等式组:121212122(221)221(222)2221k k k k k k k ka m a m m p ⎧++-≤+-⎪++->+-⎨⎪≥-⎩其中12,k k N ∈,且1204k k ≤<≤.解的具体表达式参见表格2.(3) 当3s =时,即1232mn p p p =,其中212321,1,2,3(04)k ii p i k k k =+=≤<<≤根据引理2和引理3知33121212221222()22222k k k k k k m m n ϕ--+++==33()(2)32,(2)22,(2)mp m S n S mp S p S ⎧≥⎪=⎨<⎪⎩ 代入方程有:33312322221,21(2)1222(2),21(2)kkk m k k k m m S m S S ⎧++≥⎪-+++=⎨+<⎪⎩333133121,(2)12(2),(2)i i k m i k m m i m p p S m S p S ==⎧=-+≥⎪⎪⇒⎨⎪-+=<⎪⎩∑∑ 同前面的讨论方法一样,对123(,,)k k k =(0,1,2),(0,1,3),(0,1,4),(0,2,3),(0,2,4),(0,3,4),(1,2,3),(1,2,4),(1,3,4),(2,3,4)的进行分类讨论,最后得到每种情况均存在方程的解,综合起来有: 1232m n p p p =型解中33121i k i m p ==-+∑或者m 满足不等式组:331133113(21)21(22)221i ii i k k i i k ki i a m a m m p ====⎧+-≤-⎪⎪⎪+->-⎨⎪⎪≥-⎪⎩∑∑∑∑ 其中123,,k k k N ∈,且12304k k k ≤<<≤.具体表达式参见表格3.(4) 当4s =时, 12342m n p p p p =,其中221k ii p =+,1,2,3,4i =,12(0k k ≤<34)k k <<,此时:312412222()22222k k k k m n ϕ-=31241222+22k k k k m -+++=44()(2)42,(2)22,(2)m p m S n S mp S p S ⎧≥⎪=⎨<⎪⎩若方程有解,则:31241222+2k k k k m -+++44422221,21(2)(2),21(2)kkk m m m S S S ⎧++≥⎪=⎨+<⎪⎩444144121,(2)12(2),(2)i i k m i k m m i m p p S m S p S ==⎧=-+≥⎪⎪⇒⎨⎪-+=<⎪⎩∑∑ 同前面的讨论方法一样,对1234(,,,)k k k k =(0,1,2,3),(0,1,2,4),(0,2,3,4),(1,2,3,4)进行分类讨论,最后也可得到每种情况均存在方程的解, 12342m n p p p p =型的解中44121i k i m p ==-+∑或者m 满足不等式组:441144114(21)21(22)221i i i i k k i i k ki i a m a m m p ====⎧+-≤-⎪⎪⎪+->-⎨⎪⎪≥-⎪⎩∑∑∑∑其中1234,,,k k k k N ∈,且1230k k k ≤<<<44k ≤.解的具体表达式参见表格4.表格3 方程()()2S n n ϕ=的1232m n p p p =型的解Table 31232m n p p p = type of solution of the equation ()()2S n n ϕ=满足:6)65)5+≤+> 35257nm 满足10)109)9+≤⎧⎪+>⎨3565537满足18)1817)17+≤+>满足12)1211)11+≤+>m 满足20)2019)19m m +≤⎧⎪+>⎨满足24)24+≤ 满足13)13+≤ 满足21)21+≤ 525765537满足25)25+≤ 1725765537满足27)27+≤表格4 方程()()2S n n ϕ=的12342m n p p p p =型的解Table 112342m n p p p p = type of solution of the equation ()()2S n n ϕ=(5)当5s =时,即23517m n =⨯⨯⨯⨯2565537⨯此时:112481630()2222222m m n ϕ-+=⋅⋅⋅⋅⋅=65537()(2)2,65537(2)22,65537(2)m m S n S mS S ⎧≥⎪=⎨<⎪⎩ 代入方程,若m 为方程的解,则m 满足:65537,65537(2)30(2),65537(2)mm mS m S S ⎧≥⎪+=⎨<⎪⎩ 若65537(2)m S ≥,则306553765507m m +=⇒=并且65507(2)65537S <,即6550723n =⨯51725765537⨯⨯⨯⨯为方程的解;若65537(2)mS <,有30(2)mm S +=,则由引理6, m 满足:(30)30(29)2965536a m a m m +≤⎧⎪+>⎨⎪≥⎩此时,2351725765537mn =⨯⨯⨯⨯⨯.也综上,在现有的五个Fermat 素数的基础上,对数论方程()()2S n n ϕ=的解进行了讨论,给出了部分解的表达式和解的判别条件.值得思考的是,本文没有总结出解的一般形式,但并不意味着不存在这样的表达式.比如根据二进制数码和组合数的相关性质,结合给出的解答判别条件,或许能得到更优的结论.参考文献:[1]Dubuc S.Interpolation through an iterative scheme. Mathematical Analysis and Applications,1986,114(1): 185—204[2] MA J P. An equation involving the Smarandache function [J]. Scientia Magna, 2005, 1( 2): 89- 90 [3] Y IY . An equation involving the Euler function and Smarandache function [J].Scientia Magna, 2005,1( 2):173- 175.[4]吕志宏.一个包含Euler 函数的方程[J]西北大学学报(自然科学版),2006(2)[5]闵嗣鹤、严士健.初等数论[M].北京:高等教育出版社,1979[6]FARRISM,MITCHELLP.BoundingtheSmarandach eFunction[J].SmarandacheNotions,2002,13:37-43 [7]于小秋、肖藻. Fermat 数的若干结论[J]. 佳木斯大学学报(自然科学版),2003(3):0290-03。
