定位误差计算
定位误差的分析与计算
定位误差的分析与计算一、定位误差的概念和原因定位误差是指定位系统测量结果与真实位置之间的差异或偏差。
在现代生活中，定位系统广泛应用于导航系统、无人驾驶、无人飞行器等领域，而定位误差对于系统的准确性和可靠性至关重要。
1.信号传播误差：这是由于信号在传播过程中受到大气中的影响，如电离层、大气湿度等所产生的误差。
这种误差对于GPS系统尤为明显，导致多径效应、钟差误差等。
2.接收机误差：接收机的硬件和软件系统可能存在不同程度的误差。
硬件方面，接收机的时钟精度、天线阻抗匹配等问题都可能导致定位误差。
软件方面，接收机的算法、数据处理等也可能引入误差。
3.观测误差：观测误差是指由于测量设备的精度或不完善性所导致的误差。
例如，测量设备的精度限制了对信号强度、TOA（Time of Arrival）等参数的准确测量。
4.环境因素：环境因素也是定位误差产生的原因之一、比如，建筑物、树木、走廊等物体会对信号传播产生阻碍和衍射，从而影响接收机的测量结果。
5.多径效应：多径效应是指信号传播过程中，信号除了直射到达接收机外，还经历了反射，导致信号的多个传播路径同时到达接收机。
多径效应会产生明显的信号干扰和测量误差。
二、定位误差的计算方法1.位置误差计算：位置误差是指实际测量位置与真实位置之间的距离差异。
一种常见的计算方法是通过比较GPS测量点与参考点之间的差异来计算位置误差。
通过收集多个测量点的数据，可以使用最小二乘法进行曲线拟合，从而计算出测量点与真实位置之间的距离差异。
2.时间误差计算：时间误差是指实际测量时间与真实时间之间的差异。
在GPS系统中，时间误差主要由于卫星钟的钟差所引起。
通过GPS接收机接收到的卫星信号的时间戳和GPS接收机内部的时间戳之间的差异，可以计算出时间误差。
4.误差修正算法：为了减小定位误差，可以使用一些误差修正算法来对测量结果进行修正。
一种常见的方法是差分GPS技术，通过使用两个或多个接收机接收同一卫星信号，对测量结果进行差分处理，从而减小定位误差。
定位误差的分析与计算_new
为保证加工要求，上述三项误差合成后应小于或等于
工件公差δ。
3
即：
△定+ △安-调+ △过 ≤ δ
在对定位方案进行分析时，可以假设上述三项误差各占工 件公差的1/3。
则有：
△定≤ δ/3
此就是夹具定位误差验算公式。
4
1. 造成定位误差的原因
造成定位误差的原因有两个。
⑴定位基准与设计基准不重合，产生基准不重合误 差△不。 ⑵定位基准与限位基准不重合，产生基准位移误差 △基（也叫定位副制造不准确误差）。
17
合成时，若设计基准不在定位基面上（设计基准 与定位基面为两个独立的表面），即基准不重合误 差与基准位移误差无相关公共变量。
△定＝△基＋△不 合成时，若设计基准在定位基面上，即基准不重 合误差与基准位移误差有相关的公共变量。
△定＝△基±△不
18
+ - 确定方法：
定位基面与限位基面接触，定位基面直径由小变 大（或由大变小），分析定位基准变动方向。
本例中∆定1 ＞ ∆定2 ＞ ∆定3 。
26
3．常见定位方式定位误差的计算
⑴工件以平面定位
平面为精基面
基准位移误差 △基＝0
定位误差
△定＝△不
注：若为毛坯面，则仍有△基
27
⑵工件以内孔定位
28
①工件孔与定位心轴（或销）采用间隙配合的定位误 差计算 △定 = △不 + △基
工件以内孔在圆柱心轴、圆柱销上定位。由于孔与轴有配 合间隙，有基准位移误差，分两种情况讨论：
a.心轴（或定位销）垂直放置，按最大孔和最销轴求得孔 中心线位置的变动量为：
△基 = δD + δd + △min = △max =孔Dmax-轴dmin (最大间隙） b.心轴（或定位销）水平放置，孔中心线的最大变动量
定位误差的分析与计算
华北航天工业学院教案教研室：机制工艺授课教师：陈明第十章机床夹具的设计原理第三节定位误差的分析与计算一批工件逐个在夹具上定位时，各个工件在夹具上所占据的位置不可能完全一致，以致使加工后各工件的加工尺寸存在误差，这种因工件定位而产生的工序基准在工序尺寸上的最大变动量，称为定位误差，用∆D表示。
一、定位误差的组成1．基准不重合误差如前所述，当定位基准与设计基准不重合时便产生基准不重合误差。
因此选择定位基准时应尽量与设计基准相重合。
当被加工工件的工艺过程确定以后，各工序的工序尺寸也就随之而定，此时在工艺文件上，设计基准便转化为工序基准。
设计夹具时，应当使定位基准与工序基准重合。
当定位基准与工序基准不重合时，也将产生基准不重合误差，其大小对于定位基准与工序基准之间尺寸的公差，用∆B表示。
工序基准与定位基准之间的尺寸就称为定位尺寸。
2．基准位移误差工件在夹具中定位时，由于工件定位基面与夹具上定位元件限位基面的制造公差和最小配合间隙的影响，从而使各个工件的位置不一致，给加工尺寸造成误差，这个误差称为基准位移误差，用∆Y表示。
基准位移误差的大小对应于因工件内孔轴线与心轴轴线不重合所造成的工序尺寸最大变动量。
当定位基准的变动方向与工序尺寸的方向相同时，基准位移误差等于定位基准的变动范围，即∆Y = ∆i当定位基准的变动方向与工序尺寸的方向不同时，基准位移误差等于定位基准的变动范围在加工尺寸方向上的投影，即∆Y = ∆i cos a二、各种定位方式下定位误差的计算1．定位误差的计算方法如上所述，定位误差由基准不重合误差与基准位移误差两项组合而成。
计算时，先分别算出∆B和∆Y，然后将两者组合而成∆D。
组合方法为：如果工序基准不在定位基面上：∆D =∆Y + ∆B如果工序基准在定位基面上：∆D = ∆Y±∆B式中“+”、“-”号的确定方法如下：1）1）分析定位基面直径由小变大（或由大变小）时，定位基准的变动方向。
常见定位方式定位误差的计算
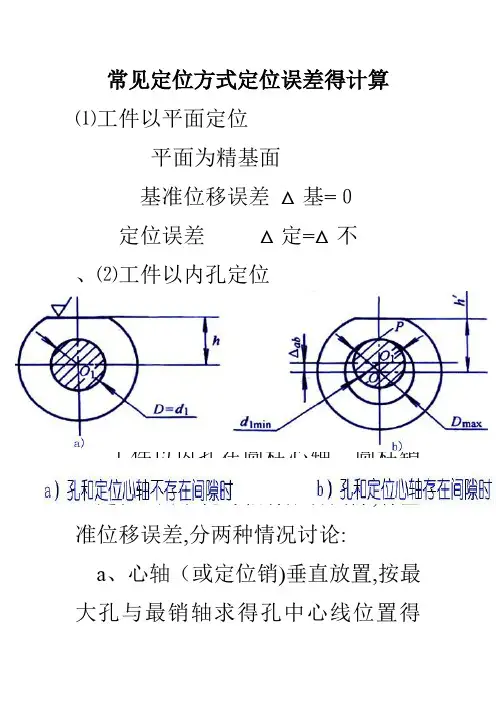
常见定位方式定位误差得计算⑴工件以平面定位平面为精基面基准位移误差△基=０定位误差△定=△不、⑵工件以内孔定位①工件孔与定位心轴（或销)采用间隙配合得定位误差计算△定= △不+ △基工件以内孔在圆柱心轴、圆柱销上定位。
由于孔与轴有配合间隙,有基准位移误差,分两种情况讨论:a、心轴（或定位销)垂直放置,按最大孔与最销轴求得孔中心线位置得变动量为:△基= δD+ δｄ＋△min = △max =孔Dmａｘ－轴dmin (最大间隙)b、心轴(或定位销）水平放置,孔中心线得最大变动量(在铅垂方向上）即为△定△基=OO'=1/2（δD+δｄ+△mi ｎ)=△max／2或△基＝(Dmax/２)-(ｄmin ／２)＝△mａx/2= (孔直径公差+轴直径公差) / ２②工件孔与定位心轴(销)过盈配合时(垂直或水平放置)时得定位误差此时,由于工件孔与心轴（销)为过盈配合,所以△基=0。
对Ｈ1尺寸:工序基准与定位基准重合,均为中心Ｏ，所以△不=0对H2尺寸：△不＝δd/2⑶工件以外圆表面定位Ａ、工件以外圆表面在V型块上定位由于V型块在水平方向有对中作用。
基准位移误差△基=0Ｂ.工件以外圆表面在定位套上定位定位误差得计算与工件以内孔在圆柱心轴、圆柱销上定位误差得计算相同。
⑷工件与"一面两孔"定位时得定位误差①“1”孔中心线在Ｘ,Y方向得最大位移为:△定（１x）=△定（1y)=δＤ１+δd １+△1mｉn=△1mａｘ(孔与销得最大间隙)②“2”孔中心线在X,Ｙ方向得最大位移分别为:△定（2ｘ)=△定(1ｘ)+2δLd(两孔中心距公差)△定(２y)=δD2＋δd2＋△2min=△2ｍaｘ③两孔中心连线对两销中心连线得最大转角误差：△定（α)=2α=2tan-１[(△1ｍax+△２max)/2Ｌ]（其中L为两孔中心距)以上定位误差都属于基准位置误差，因为△不＝０。
需要指出得就是定位误差一般总就是针对批量生产，并采用调整法加工得情况而言。
第2节 定位误差分析与计算.
（A3）=
2（H – h）tanΔα
（A1）
Δdw（A1） = Δjb（A1）+ Δjy
= δA2 + 2（H – h）tanΔα
2．定位误差的计算方法
1）极限位置法（几何作图法）
先根据工件的定位方案，画出工序（设计）基准
相对起始（调刀、限位）基准最大与最小的两个极限
位置，再根据几何关系求出这两个极限位置间的距离，
jy
4 ．如图车外圆，要求外圆对内孔有同轴度要求，已知心 0.009 轴直径为 30－ － 0.025 ，计算工件内外圆的同轴度的定位误差 △dw。
jy
5．钻孔O，a)为工序图，图b)~f)为不同定位方案，试分别 计算各种方案的定位误差。
求： Δdw（30）= ？
解：分析可知 Δjb（30）≠ 0 ； Δjy（30）≠ 0 得： Δjb （30）= 0.03/2 ＋ 0.02 = 0.035 0.02 Δjy（30）= = 0.014 0 2 sin 45 Δdw（30）= Δjb （30）＋ Δjy（30）= 0.049
已知：大圆直径公差为0.03，小圆直径公差为0.02，同轴度误差为0.02，
0.02，同轴度误差为0.02，定位套直径
公差为0.04。 解：分析得 Δjb （30） ≠ 0，Δjy （30） ≠ 0
Δjb （30） ＝ 0.03/2 ＋ 0.02 = 0.035
0.04 0.02 0.01 0.07
Δjy （30） ＝
Δdw （30）＝Δjb （30） + Δjy （30） ＝0.105
0.03
解：分析 Δjb （59） ≠ 0 ；Δjy （59） ≠ 0
0 . 12 Δjb （59） ＝ 0.04 0.1 2
2.5定位误差的分析与计算(二) 改
D2 min X 2 min 则 b 2a
式中
X 2 min—菱形销与孔之间的最小配合间隙，mm；
a—满足工件顺利装卸的补偿量，mm。
a TLD TLd 2
LOGO
2.5 定位误差的分析与计算（二）
菱形销圆柱部分的宽度b可查手册确定， 则由上式得
Y O 1O 2 δ d 2 sin( / 2)
LOGO
2.5 定位误差的分析与计算（二）
M1
d max /2
d min /2
工序尺寸A3的定位误差
δ d 2
M2 O
工件定位 外圆直径 由大变小
δ d
ΔY O 1O 2
δ d 2 sin( α/ 2)
ΔB与ΔY同向
δ 1 Δ D＝Δ Y＋Δ B＝ d [ ＋1] 2 sin(α/ 2)
LOGO
A3
M2
2.5 定位误差的分析与计算（二）
M1
d max /2
d m in /2
O
δ d 2
d max /2
d mi n /2
C1 C2
ΔY O 1O 2
δ d 2 sin( α/ 2)
工件定位 外圆直径 由大变小
δ d
δ 1 Δ D＝Δ Y－Δ B＝ d [ －1] 2 sin(α/ 2)
复习
1．定位误差的概念
（1）基准不重合误差 △ B （2）基准位移误差 △Y
2．工件以平面定位误差计算
精基准平面定位时，一般认定△Y=0， △D=△B
3．以圆孔定位时的定位误差计算
LOGO
Page 2
2.5 定位误差的分析与计算（二）
定位误差
工序基准：孔的轴线 定位基准：孔的轴线
d = jy
工序尺寸标注为H2
工序基准：孔上母线 定位基准：孔的轴线
基准不重合 有基准不重合误差jb
H'2 H O= O1 d/2 Y d -d O1 H O
H''2 (D+D)/2
D + D
孔最小、心轴最大
/
P
d(H2)= jy+ jb
工序尺寸标注为H3
d(H3)=H''3–H'3 H'3 =d/2 +H H''3=(d–d)/2 + H+ jy
H'3 H
O
jy
O'
H''3
d/2 (d–d)/2
δd 1 Δd H 1 3 α 2 sin 2
如果两者的变动方向相同，则取“ + ”号， 如果两者的变动方向相反，则取 “ - ”号。
H1
H2
工序尺寸不同的 标注方式
H3
d0 d0
工件在水平心轴上定位时的定位误差计算 工序尺寸标注为H1
当孔最大、心轴最小
H1min O O1 H1max
Dmax= D+ D ；
dmin= d – d
jy=(Dmax–dmin)/2 = (D +d)/2
Y
D +D
d -d
d = H1max – H1min = jy
基准不重合误差：工序基准相对于定位基准在加 工方向上的最大位置变动量。（用△jb表示可简化为
△B ）
定位误差分析计算
式中：
d2max——第2个定位销的最大直径； D2min——第2个定位孔的最小直径； X2min——两孔同时定位时， 在极限情况下， 第2个定位副
(1)正确处理过定位； (2) 控制各定位元件对定位误差的综合影响。
2. 解决一面两孔定位问题的有效方法
（1） 以两个圆柱销及平面支承定位。由上述分析可知， 工件以一面两孔在夹具平面支承和两个圆柱销上定位时，出现 过定位。当工件上第一个定位孔装上定位销后， 由于孔间距 和销间距有制造误差，第二个定位孔将有可能装不到第二个定 位销上。解决的方法是：通过减小第二个定位销的直径来增加 连心线方向上定位副的间隙，达到解决两孔装不进定位销的矛 盾。
ΔB2d
ΔY2s
d in(/2)
分析：当定位外圆直径由大变小时，定位基准下移，从而使
工序基准也下移，即Δ Y使工序尺寸H2增大；与此同时，假定定
位基准不动，当定位外圆直径仍由大变小时（注意：定位外圆 直径变化趋势要同前一致），工序基准上移，即Δ B使工序尺寸 H2减小。
因Δ B、Δ Y引起工序尺寸H2作反方向变化，故取“－”号。
0.0350.0250.0m 1 m
只占加工允差0.10的10%。
图1-39 以V形块定位时的定位误差分析计算
② 分析计算定位误差时，必然会遇到定位误差占工序允差 比例过大问题。究竟所占比例值多大才合适，要想确定这样一 个值来分析、比较是很困难的。因为加工工序的要求各不相同， 不同的加工方法所能达到的经济精度也各有差异。 这就要求 工艺设计人员有丰富的实际工艺经验知识， 并按实际加工情 况具体问题具体分析，根据从工序允差中扣除定位误差后余下 的允差部分大小，来判断具体加工方法能否经济地保证精度要 求。 在分析定位方案时，一般推荐在正常加工条件下， 定位 误差占工序允差的1/3以内比较合适。
定位误差计算
• 4）计算出的定位误差数值是指加工一批工件时某加工精度参 数可能产生的最大误差范围（加工精度参数最大值与最小值 之间的变动量）。它是个界限范围，而不是某一个工件定位 误差的具体值。 • 5）一批工件的工序基准（设计基准）相对定位基准、定位基 准相对对刀基准产生最大位置变动量是产生定位误差的原因， 而不一定就是定位误差的数值。
关键：找出同一批工件的工序基准在工序尺寸方向上可能的最大位移变动量
方法1—合成法：
先分别求出基准位移误差和基准不重 合误差，再求出其在加工尺寸方向上的矢 量合，即Δdw ＝Δjb ＋Δjw
•当 Δjb 和Δjw 由两个互不相关的变量引起时，用“+”；
•当Δjb 和Δjw 是同一变量引起时，要判断两者对Δdw 的影
响是否同向，方向相同时“+”，方向相反时“－”。
分析计算定位误差时应注意的问题：
• 1）定位误差是指工件某工序中某加工精度参数的定位误差。 它是该加工精度参数（尺寸、位置）的加工误差的一部分。 • 2）某工序的定位方案对本工序的多个不同加工精度参数产生 不同的定位误差，应分别逐一计算。 • 3）分析计算定位误差的前提是用夹具装夹加工一批工件，用 调整法保证加工要求。
定位误差计算实例
1. L1
Δdw= Δjw
2. L2
L2 的定位误差为两者的合成。两者都是由外圆直径的变化同时引 起的,所以要判断两者的方向特点。
要判断两者的方向特点。
当外圆直径从大到小时，工序基准M相对定位基准O是向O 方向即向下偏移的。 当放入V形块中后，当外圆直径由大变小时，定位基准相对 与理论也是向下偏移的。 综合起来两者合成方向相同。
dw T (d ) T (d ) jw jb 2 sin 2 2
定位误差的计算
差 范围±ΔH内波动），因而也就产生了定位误差（εA ）。
定位误差大小计算
（1） 画出被加工零件定位时的两个极限尺寸的位置 （2） 从图形中的几何关系，找出零件图上被加工尺寸方向上
• ① ∆jb≠0， ∆jw=0 时， ∆dw=∆jb； • ② ∆jb=0， ∆jw≠0时， ∆dw=∆jw； • ③ ∆jb≠0，∆jw≠0时： 如果工序基准不在定位基准面上（工序基准与定位基面
是两个独立的表面），即∆jb 与∆jw无关联时， ∆dw=∆jb+∆jw； 如果工序基准在定位基准面上，即∆jb 与∆jw有关联时， ∆dw=∆jb±∆jw。
总结
二、定位误差的计算
1、定位误差计算的方法
工件定位误差的实质是工件上被加工表面的工序基准相对 于定位元件工作表面在加工尺寸方向上的最大变动量，因此， 计算定位误差时， 首先要找出工序尺寸的工序基准； 然后求其在工序尺寸方向上的最大变动量。
极限法
定位误差计算的方法
合成法
微分法
1）极限法
2
2
O E
A
(a)
用微小增量代替微分，并将尺寸误差视为微小增量， 且考虑到尺寸误差可正可负，各项误差应取绝对值，故定 位误差为：
dh
1
d cosa
Td
2 Ta
2sina
4sin2(a )
2
2
若使用同一夹具进行加工，则Ta＝0
所以
H1
Td a
2 si n
2
同理：
CA
OA OC
定位误差分析计算
定位误差分析计算所谓定位误差，是指由于工件定位造成的加工面相对工序基准的位置误差。
因为对一批工件来说，刀具经调整后位置是不动的，即被加工表面的位置相对于定位基准是不变的，所以定位误差就是工序基准在加工尺寸方向上的最大变动量。
㈠引言①△总≤δ其中△总为多种原因产生的误差总和，δ是工件被加工尺寸的公差，△总包括夹具在机床上的装夹误差，工件在夹具中的定位误差和夹紧误差，机床调整误差，工艺系统的弹性变形和热变形误差，机床和刀具的制造误差及磨损误差等。
②△定+ω≤δ 其中，ω除定位误差外，其他因素引起的误差总和，可按加工经济精度查表确定。
所以由①和②知道：△定≤δ-ω（是验算加工工件合格与否的公式）或者：△定≤1/3δ（也是验算加工工件合格与否的公式）㈡定位误差的组成1、定义：定位误差是工件在夹具中定位，由于定位不准造成的加工面相对于工序基准沿加工要求方向上的最大位置变动量。
2、定位误差的组成：1) 定位基准与工序基准不一致所引起的定位误差，称基准不重合误差，即工序基准相对定位基准在加工尺寸方向上的最大变动量，以△不表示。
图示零件，设e面已加工好，今在铣床上用调整法加工f面和g面。
在加工f面时若选e面为定位基准，则f面的设计基准和定位基准都是e面，基准重合，没有基准不重合误差，尺寸A的制造公差为TA。
加工g 面时，定位基准有两种不同的选择方案，一种方案（方案Ⅰ）加工时选用f面作为定位基准，定位基准与设计基准重合，没有基准不重合误差，尺寸B的制造公差为TB；但这种定位方式的夹具结构复杂，夹紧力的作用方向与铣削力方向相反，不够合理，操作也不方便。
另一种方案（方案Ⅱ）是选用e面作为定位基准来加工g面，此时，工序尺寸C是直接得到的，尺寸B是间接得到的，由于定位基准e与设计基准f不重合而给g面加工带来的基准不重合误差等于设计基准f面相对于定位基准e面在尺寸B方向上的最大变动量TA。
定位基准与设计基准不重合时所产生的基准不重合误差，只有在采用调整法加工时才会产生，在试切法加工中不会产生。
定位误差的计算方法解析
定位误差的计算方法：（1）合成法为基准不重合误差和基准位移误差之和； （2）极限位置法工序基准相对于刀具（机床）的两个极限位置间的距离就是定位误差； （3）微分法先用几何方法找出工序基准到定位元件上某一固定点的距离，然后对其全微分，用微小增量代替微分，将尺寸误差视为微小增量代入，就可以得到某一加工尺寸的定位误差。
注：基准不重合误差和基准位移误差它们在工序尺寸方向上的投影之和即为定位误差。
例如：用V 型块定位铣键槽，键槽尺寸标注是轴的中心到键槽底面的尺寸H 。
T D 为工件定位外圆的公差；α为V 型块夹角。
1. 工序基准为圆柱体的中心线。
表示一批工件依次放到V 型块上定位时所处的两个极端位置情形，当工件外圆直径尺寸为极大和极小时，其工件外圆中心线分别出于点O '和点O ''。
因此工序基准的最大位置变动量O O '''，便是对加工尺寸H 1所产生的定位误差： 故得：OE O E H H O O 11DH1''-'='-''='''=ε O A E Rt 1''∆中： max 1D 21A O ='' 2sin A O O E 1α''='O A E Rt 1''''∆中：min 1D 21A O ='''' 2sin A O O E 1α''''=''2sin 2T 2sin 2T 2sin A O A O O E O E D D11DH1α=α=α''''-''=''-'=ε2. 工序基准为圆柱体的下母线：工件加工表面以下母线C 为其工序基准时，工序基准的极限位置变动量C C '''就是加工尺寸H2所产生的定位误差。
定位误差的分析与计算
位方案在实践中也可以采用。
201差△不。
基准不重合误差的大小应等于定位基准与设计
基准之间所有尺寸的公差和。
在工序图上寻找这些尺寸的公差。
2019-3
11
当设计基准的变动方向与加工尺寸的方向不一 致，存在一夹角时，基准不重合误差等于定位基准 与设计基准之间所有尺寸的公差和在加工尺寸方向 上的投影。
序尺寸方向上的最大变动量。
2019-3
7
加工顶面2，以底面和侧面定位，此时定位基准和 设计基准都是底面3，即基准重合。
定位误差： △定 = 0
2019-3
8
加工台阶面1，定位同工序一，此时定位基准为底面3，而 设计基准为顶面2，即基准不重合。
即使本工序刀具以底面为基准调整得绝对准确，且无其它
2019-3
36
2019-3
37
2019-3
38
2019-3
39
定位误差的计算（续）
微分方法
[例 ] 工件在V型块上定位铣键
槽（右图），试计算其定位误
差。
[解] 工件在V型块上定位
B
铣键槽时，需要保证的工序尺
寸和工序要求是：① 槽底至
工件外圆中心的距离H；② 键
槽对工件外圆中心的对称度。
2019-3
故安装后孔和轴的中心必 然不重合，使得两个基准 发生位置变动。
此时基准位移误差： △基=（ △D+ △d ）/2
2019-3
15
若定位基准与限位基准的最大变动量为Δi。
定位基准的变动方向与设计尺寸方向相同时：
△基 =Δi
定位基准的变动方向与加工尺寸的方向不一致，
定位误差的计算(平面定位)
定位误差分析计算 1、工件以平面定位（1）如图所示工件图样，底面已经加工完成，以工件底面定位铣加工台阶面，保证尺寸20±0.15，其定位误差是多少？该种定位方法是否满足工序的要求？工序分析工序内容：铣平面工序要求：20±0.15（T=0.3） 工序基准：顶面 定位基准：底面基准不重合误差：△B=0.14×2=0.28(两基准间尺寸公差在加工尺寸方向上的投影) 基准位移误差：△W=0(精基准平面定位，基准位移误差可以不考虑) 定位误差：△D=△B+△W=0.28（工序基准不在定位基面上△D=△B+△W ）定位质量评定：△D=0.28＞（T/3=0.1） 不满足工序要求 解决办法：（1）定位方案不变，提高定位尺寸的精度，以减少△D 的数值；（2）改变定位方案。
（2）如图所示箱体类工件图样，底面和中间通孔已经加工完成，以工件底面定位铣加工平面，保证尺寸28±0.1，其定位误差是多少？该种定位方法是否满足工序的要求？工序分析工序内容：铣平面工序要求：28±0.1（T=0.2） 工序基准：孔轴线 定位基准：底面基准不重合误差：△B=0.1×2×cos45°=0.1414 (两基准间尺寸公差在加工尺寸方向上的投影) 基准位移误差：△W=0(精基准平面定位，基准位移误差可以不考虑) 定位误差：△D=△B+△W=0.1414（工序基准不在定位基面上△D=△B+△W ）定位质量评定：△D=0.1414＞（T/3=0.0667） 不满足工序要求 解决办法：（1）定位方案不变，提高定位尺寸的精度，以减少△D 的数值；（2）改变定位方案。
（3）下图所示工件，A 、B 面已由前道工序加工完成。
本铣槽工序要求确保尺寸50±0.05mm ，宽度30±0.042mm 由铣刀尺寸保证，试检验本方案的定位精度是否满足加工要求。
若不能满足加工要求，可采用什么方案定位？工序分析工序内容：铣槽工序要求：50±0.05mm (T=0.1mm) 工序基准：B 面 定位基准：左端面 基准不重合误差：△B=0.065×2+0.055×2=0.24mm (两基准间尺寸公差在加工尺寸方向上的投影) 基准位移误差：△W=0(精基准平面定位，基准位移误差可以不考虑) 定位误差：△D=△B+△W=0.24mm（工序基准不在定位基面上△D=△B+△W ）定位质量评定：△D=0.24＞（T/3=0.033） 不满足工序要求（4）如下图所示，工件镗孔加工图样，孔1和孔2均已加工完成，以工件底面A 为基准镗削孔3，要求保证尺寸（15±0.055）mm ，试检验f 该方案的定位精度。
定位误差计算
定位误差专题一、工件以外圆Φd Td -0在V 型铁上定位，求尺寸L 的定位误差。
解：h jb δ2=∆45222Sin Td SinTd jw ==∆α则：)71.0(24522)(Td Th Sin Tdh L dw +=+=∆ δ二、已知ｄ１＝Φ2500210-.,ｄ2＝Φ4000250-.，两外圆同轴度Φ0.02，V 型块夹角α＝90°,试计算： (1)铣键槽时的定位误差。
(2)若键槽深度要求A=34.8-0170.，此定位方案可行否？解:(1)∆jb ＝0.025＋0.02＝0.045∆jw ＝2sin21αd ∆＝ 45sin 2021.0⨯≈0.015∆dw ＝∆jb ＋∆jw ＝0.045＋0.015＝0.060(2)3工∆＝3170．〈∆dw ＝0.06故不能满足加工要求，此方案不可行。
三、如图ａ所示一批零件，外圆已加工合格，今设计钻模加工2-Φ8孔。
除保证图ａ所示中心距要求外，还要求两孔连心线通过外圆中心，偏移量不得大于0.08。
试分别分析图ｂ和图ｃ两种定位方案的定位误差对各项精度的影响（1是钻模板，2是V 形块）。
解：中心距要求是由钻模板1的制造保证的，与工件定位无关。
两孔连心线通过外圆中心（偏移量不大于0.08）与工件定位有关，对图b:0=∆dw ;对图c:2sin2αd dw ∆=∆;为此应选用图b 的方案。
四、 某圆盘形工件外圆尺寸为Φ80-0150.；按尺寸30±0.07铣出一平面，然后用如图所示定位元件定位加工一孔Φ2000045+.；试计算孔加工后由于定位所产生的与外圆的最大同轴度误差。
解：jy jb dw ∆+∆=∆ 2465.0045sin 215.04514.0=+︒+︒⨯=tg五、(10分)如图所示零件已加工好Φ100005+.，40003+.，α＝45°，求尺寸L 的定位误差。
解：由40引起的定位误差：3.0453.01=︒=∆tg L 由100引起的定位误差：3535.045sin 125.02=⨯=∆LL 的定位误差为：ΔL =ΔL 1+ΔL 2=0.3+0.3535=0.6535(mm)六、如图所示，加工刨刀架拖板燕尾槽工序，需保证尺寸A ±ΔA 。
定位误差的分析和计算
⑵基准位移误差△基
定位基准与限位基准不重叠引起旳误差。 工件定位面与夹具定位元件共同构成定位 副，因为定位副制造得不精确和定位副间旳 配合间隙引起旳工件最大位置变动量，也称 为定位副制造不精确误差。 这是因为定位基面和限位基面旳制造公差 和间隙造成旳。
13
如图所示，工件以内孔中心O
为定位基准，套在心轴上，铣上
定位误差： △定 = 0
8
加工台阶面1，定位同工序一，此时定位基准为底面3，而设 计基准为顶面2，即基准不重叠。
虽然本工序刀具以底面为基准调整得绝对精确，且无其他加工 误差，仍会因为上一工序加工后顶面2在 H ± △H 范围内变 动，造成加工尺寸A ± △A 变为A ± △A ± △H，其误差为2 △H。
15
基准位移误差旳示例阐明
一批工件定位基准旳最大变动量应为
∆ = =OO -OO = i
Amax
Y
Amin
TD Td
2
Dmax d min
即
1 轴公差
2 孔公差
2
2
Dmin
d max
2
TD
Td
2
16
若定位基准与限位基准旳最大变动量为Δi。 定位基准旳变动方向与设计尺寸方向相同步：
△基 =Δi 定位基准旳变动方向与加工尺寸旳方向不一致， 两者之间成夹角时，基准位移误差等于定位基准旳 变动范围在加工尺寸方向上旳投影。
但若采用试切法进行加工，则一般不考虑定位误差。
38
[思索题] 工件以外圆表面在V型块上定位铣键槽，若工序尺寸
标注如图2-45所示，其定位误差为多少？
39
答案：
1）若工件旳工序基准为外圆旳下母线时（相应旳工序尺寸 为H1，参照图2-45a），C点至A点旳距离为：
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
考虑同轴度误差， ' 同 0.1 0.1 0.2
3．图示钻孔，已知条件和加工要求见图示，试分析a)、
b) 、 c ） 三 种 定 位 方 案 中 ， 工 序 尺 寸 L 的 定 位 误 差
(
40H
7
/
g6
4000.025
/－ 0.009
10．如图 在圆柱体 上铣台阶 面，采用 b)～h)定 位方案， 试分别进 行定位误 差分析。
a）
b）
C）
d）
T T b
d ( 1 1) 0.207 2 sin 45
0.207 0.08 0.01656
d
T c
1 2
0.04
d
T d
1 2
0.04
d
a）
e）
f）
g）
h）
e 0
T f
1 2
0.04
d
T g
1 2
0.04
d
T h
1 2
0.04
d
11．如图同时钻两孔，采用b)～c)两种钻模， 试分别进行定位误差分析。
T bo1
d ( 1 1) 2 sin 45
0.207 0.2 0.0414
T b02
d ( 1 1) 2 sin 45
1.207 0.2 0.2414
2
'
TD 2sin 450
Td
2
2
2
0.039
sin 450
0.025 2
0.0276 0.0125
0.04
考虑同轴度误差 ' 同 0.04 0.02) 0.06
6．钻孔O，a)为工序图，b)~f)为不同定位方案， 试分别计算各种方案的定位误差。
解：
T T 1
D 2
d 0.02 0.03 0.02 0.02 0.045
T co1
d 0.2 0.5 0.1 2
T co2
d 0.2 0.5 0.1 2
d
c 0
8．如图钻d孔，保 证同轴度要求，采 用a)～d) 四种定位 方式，试分别进行 定位误差分析。
T T a
d
2 sin 45
0.707
d
T T b
d
2 sin 45
0.707
d
c 0
T d 0.5 d
9．如图铣槽，保证对称度、m或n，采 用a)～c)三种定位方案，试分别进行定位 误差分析。
－ 0.025
)。
解：
D d 1
0.025 0.025 0.05
max
min
D d 2 (
max
)
m in
不
0.05
0.1 2
0.1
D d 3 (
max
)
min
不
同 0.1 0.02 0.12
4．钻直径为φ 10的孔，采用a）、b)两种 定位方案，试分别计算定位误差。
解：a)
习题课
1．如图钻φ12孔，试分析 90－0 0.1 工序尺寸的定
位误差分析。
解：由于夹紧力的作用，为右端点接触，故
1 2
(T
D
T d)
1 2
(0.1 0.02)
0.06
1T 3பைடு நூலகம்
0.1 3
不能满足
2．如图铣平面保证h，已知两圆的同轴度φ 0.1，
其它已知条件见图，试分析工序尺寸h的定位误差。
解：若不考虑同轴度误差，
1 0.1 0.025 0.125
45 b) 2
Td
2 s in
0.05 2 s in
0 0.707 0.05 0.03535
2
5．如图在工件上铣台阶面，保证工序尺寸 A，采用V形块定位，试进行定位误差分析。
o
D C B
解：若不考虑同轴度误差，
Dd
BD
微分
BO DO
2 sin
D 0.02 0.05 0.02 0.03 0.02 0.105
2
2
7．如图钻孔，保证A，采用a)～d)四种方案， 试分别进行定位误差分析（外圆d－△d）。
T T a
d
2 sin 45
0.707
d
T T b
d ( 1 1) 0.207 2 sin 45
d
T T d
d ( 1 1) 1.207 2 sin 45
2
2
2
T T 2
D
2
2
d
sin
0.02
0.03 0.02 0.707 0.02 0.049 2
2
T T 3
D
2
d
2sin
0.02
0.03 0.02 0.707 0.02 0.049 2
2
T 4
D 0.02 0.03 0.02 0.035
2
2
D T 5
套max dmin