广西科技大学线性代数试卷B
广西科技大学《高等数学B2》2019-2020-2模拟试卷4

).
x→0 2 − 4 + xy
y→0
( A) −4 ;
(B) 4 ;
(C) ;
(D) 0 .
4、以曲面 z = x2 + y2 为顶,以 xoy 平面上的区域 D = ( x, y) x2 + y2 1 为底,以 D 的边界曲
线为准线,母线平行于 z 轴的曲顶柱体体积为(
( A) ; 2
).
( A) e −P( x)dx Q( x)e P( x)dxdx + C
( B) e P( x)dx Q( x)e P( x)dxdx + C
(C ) e −P( x)dx Q( x)e −P( x)dxdx + C
( D) e P( x)dx Q( x)e −P(x)dxdx + C
(B) ;
5、数项级数
(−1)n
1
(
n=1
3n
).
( A) 发散
(C) 收敛而且是绝对收敛
). (C) 3 ;
2
( D) 2 .
(B) 收敛但是条件收敛 ( D) 敛散性无法确定
三(9
分)、求过点
P(0,
2,
5)
且与直线
x x
+ −
2y− y− z
z +1= 0 −1= 0
平行的直线方程.
第1页(共4页)
x y
第4页(共4页)
19-20-2 高数 B2 模拟题 4 一、填空题(每空 3 分,共 15 分) 1、一阶齐次线性微分方程 y − 2xy = 0 的通解为___________________________.
2、将 yoz 平面上的曲线 y2 + z2 = 1 绕 z 轴旋转一周所生成的旋转曲面的方程为 49
广西科技大学线性代数试卷B

广西工学院 2010 — 2011学年第 一学期课程考核试题考核课程 线性代数A ( A 卷)考核班级 学生数 印数 考核方式 闭卷 考核时间 120 分钟一.填空题(每空3分,共30分):1.在五阶行列式ij a 中,1523324451a a a a a 取 号.2.1112344916= .3.设矩阵A 为三阶方阵,若已知2A =,则2A -= .4.矩阵10001111A k ⎛⎫ ⎪= ⎪ ⎪-⎝⎭可逆,则k 满足 .5.已知123021003A ⎛⎫ ⎪= ⎪ ⎪⎝⎭,则()1A -*= .6.若123,,ααα都是齐次线性方程组0AX =的解向量,则123(352)A ααα-+= .7.设3阶矩阵A 的特征值为1,2-,3 ,则2A A -的特征值为 .8.设3阶矩阵A 的特征值为1,2-,3 ,则A = .9.对任意n 阶方阵A 、B ,必定成立的是( )(填写正确答案的序号)①AB BA = ②||||AB BA = ③()T T T AB A B =10. 设AX b =有无穷多组解,则0AX =( )(填写正确答案的序号)①必有唯一解 ②必定没有解 ③必有无穷多解二(10分):计算行列式110001100011D x y z w--=-三(10分):设1234012300120001A -⎛⎫ ⎪--⎪= ⎪ ⎪-⎝⎭,求1A -. 四(15分):已知向量组123451321311011,,,,1110213120ααααα⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪ ⎪ ⎪-- ⎪ ⎪ ⎪ ⎪ ⎪=====⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭(1)求该向量组的秩; (2)求该向量组的一个极大无关组,并将其余向量用此极大无关组来线性表示.五(15分):求解方程组123512345123451234531222423345382x x x x x x x x x x x x x x x x x x x --+=-⎧⎪--++=-⎪⎨--++=-⎪⎪--++=⎩六(14分):已知实对称矩阵200012021A ⎛⎫⎪= ⎪ ⎪⎝⎭(1)求A 的特征值与特征向量;(2)求一个正交矩阵P ,使T P AP 为对角矩阵,并写出T P AP .七(6分):设向量组123,,ααα线性无关, 而向量组1234,,,αααα 线性相关,证明向量4α可由向量组123,,ααα线性表示.2010-2011(二)线性代数(40学时)试题 一、填空题(每小题3分,共30分):1.设01200341ab=-,则a 、b 满足的关系是_______________.2.设1234123421232112D =,则1121314122A A A A +++=________________.3.设矩阵A 的逆矩阵1100220333A -⎛⎫ ⎪= ⎪ ⎪⎝⎭,则A 的伴随矩阵A *=________________.4.设A 、B 为3阶方阵,若1A =,2B =,则2AB -=________________.5.设A 、B 、C 为n 阶非零方阵,且AB AC =,则当____________时,有B C =.6.向量组1(1,2,3,4)T α=,2(1,2,3,0)T α=,3(1,2,0,0)T α=,4(1,0,0,0)T α=一定线性_ _关.7.设()3R A =,已知12,ηη是4元非齐次线性方程组AX b =的2个不同解,则AX b =的一般解为______ ___________________.8.设3阶矩阵A 的特征值为1,2,3,则22A A +的特征值为___ ______,且2|2|A A +=_____.9.设12312001A x ⎛⎫⎪=- ⎪ ⎪⎝⎭,A 的特征值为1,2,3,则x =__ ___.10.设A 为实对称矩阵,1,2,3为A 的三个特征值,α为1所对应的特征向量,β为2所对应的特征向量,γ为3所对应的特征向量,则[,]αβγ+=___ __.二(10分):计算行列式1211000200121123231042410D =. 三(12分):设矩阵2234022300220002A ⎛⎫ ⎪ ⎪= ⎪⎪⎝⎭,10211001B ⎛⎫⎪ ⎪=⎪- ⎪⎝⎭,若AX X B =+,求矩阵X . 四(14分):设有向量组:1(1,1,0,1)T α=,2(0,1,1,1)T α=--,3(1,0,2,0)T α=,4(3,1,0,1)T α=,5(0,1,1,1)T α=.(1)求向量组12345,,,,ααααα的秩r ;(2)求向量组12345,,,,ααααα的一个极大线性无关组,并将其余的向量用极大线性无关组线性表示.五(14分):求方程组12345123523451235213250242154756x x x x x x x x x x x x x x x x x ++++=⎧⎪++-=⎪⎨+++=⎪⎪++++=⎩的一般解.六(14分):设矩阵120210001⎛⎫ ⎪= ⎪ ⎪⎝⎭A .(1)求A 的特征值和特征向量;(2)求正交矩阵T ,使T T AT 为对角矩阵并求该对角阵.七(6分):设方阵A 满足2240A A E --=,证明A E +可逆,并求1()A E -+.模拟试题第一套题目年春(秋)学期期末考试试题(考试时间:120分钟 )一、填空题(每小题3分,共30分)1.三阶行列式=-410021321 13 .2. 排列42135的逆序数为 4 .3. 利用行列式的性质计算三阶行列式=-11026422375551321 .4. 矩阵,341021⎪⎪⎭⎫ ⎝⎛-=A 则=TA .5. 已知A 为2阶方阵,3=A ,则=A 2 .6. =⎪⎪⎪⎭⎫ ⎝⎛123)3,2,1( .7. 若二阶方阵,0231⎪⎪⎭⎫⎝⎛=A 则=A 2 .8. 矩阵,000710312⎪⎪⎪⎭⎫⎝⎛-=A 则该矩阵的秩=)(A R .9. n 元线性方程组b Ax =有惟一解的充分必要条件为 .10. 已知向量,120,342⎪⎪⎪⎭⎫⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛=βα则=-βα .二、计算题(每小题10分,共10分)2321260512131412-三、计算题(每小题10分,共10分)求矩阵A 的逆,其中⎪⎪⎭⎫⎝⎛=2174A四、计算题(每小题12分,共12分)求下列矩阵的秩⎪⎪⎪⎭⎫⎝⎛---=412431211013A五、计算题(每小题14分,共14分)求解线性方程组⎪⎩⎪⎨⎧-=+++-=-++=-+-6242163511325432143214321x x x x x x x x x x x x六、计算题(每小题12分,共12分)问a 取什么值时向量组123(,1,1),(1,,1),(1,1,)T T T a a a ααα==-=-线性相关?第二套题目年春(秋)学期期末考试试题(考试时间:120分钟 )一、填空题(每小题3分,共30分)1. 四阶行列式式中含有1123a a 的项是44322311a a a a -和 .2. 排列52413的逆序数为 .3.对于两个n 阶方阵,A B ,若 ,则称方阵A 与B 是可交换的 4. 方阵A 为可逆矩阵的充分必要条件是 . 5. 矩阵的转置运算中()T AB = .6. 行列式||A 的各个元素的代数余子式ij A 所构成的矩阵*A 为伴随矩阵,则**AA A A == .7. 若A 可逆,数0λ≠,则A λ可逆,且1()A λ-= .8.设向量组123(1,3,1),(2,1,0),(1,4,1)T T T ααα=-==,它们的相性相关性是 . 9.n 元齐次线性方程组0Ax =只有零解的充要条件为 .10.已知向量,120,342⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛=βα则=+βα2 .二、计算题(每小题12分,共12分)计算行列式x a a a x aa a x.三、计算题(每小题10分,共10分)求矩阵A 的逆,其中⎪⎪⎪⎪⎪⎭⎫⎝⎛=2500380000120025A四、计算题(每小题12分,共12分)求下列矩阵的秩⎪⎪⎪⎭⎫⎝⎛-------=831113507312123A五、计算题(每小题14分,共14分)求解线性方程组⎪⎩⎪⎨⎧=+++=-++=-++02220202432143214321x x x x x x x x x x x x六、计算题(每小题10分,共10分)判定下列向量组是线性相关还是线性无关: ,141,012,131⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫⎝⎛⎪⎪⎪⎭⎫ ⎝⎛-七、计算题(每小题12分,共12分)求下列向量组的秩:⎪⎪⎪⎪⎪⎭⎫ ⎝⎛---=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-=8242,4101009,4121321ααα。
广西科技大学-高等数学A2-往年试卷合集(含详解答案)
.
解 方程右端是 f ( x) = Pm ( x)eλx 型的函数,其中 Pm ( x) = 3x 是一次多项式, λ = −2 是特征方程
λ 2 − 4 =0 的单根,故二阶常系数非齐次线性微分方程 y′′ − 4 y = 3xe−2x 的特解形式
= y* xkQm ( x= )eλx x(ax + b)e−2x .
三、设二元函数 z = z( x, y) 由方程 x + y − z =e2z 所确定,求偏导数 ∂ z , ∂ z 及全微分 d z . ∂x ∂y
解 令 F ( x, yz) = x + y − z − e2z , 则
Fx ( x, y, z) =1, Fy ( x, y, z) =1, Fz ( x, y, z) =−1 − 2e2z
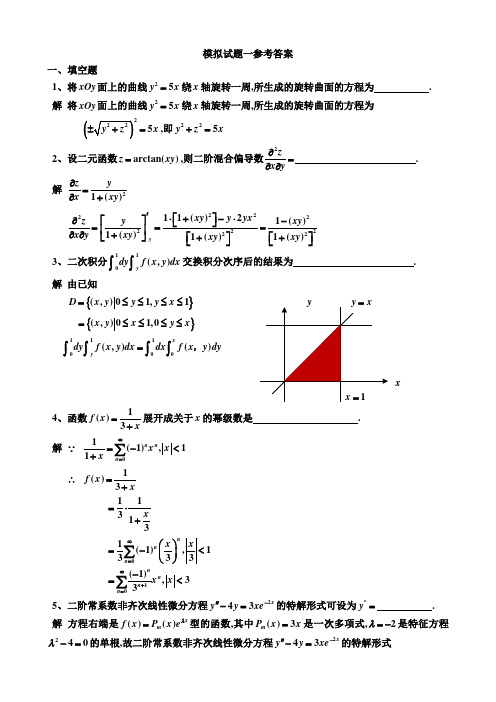
=D {( x, y) 0 ≤ y ≤ 1, y ≤ x ≤ 1}
y
y= x
= {( x, y) 0 ≤ x ≤ 1,0 ≤ y ≤ x}
1
1
1
x
∫ 0 dy∫ y f ( x, y)dx = ∫ 0 dx∫0 f ( x,y) dy
x
x =1
4、函数 f ( x) = 1 展开成关于 x 的幂级数是
.
∂x∂y
解
∂z ∂x
=
1+
y ( xy)2
= ∂∂x2∂zy = 1 + (yxy)2 ′y
1= ⋅ 1 +1( x+y()2xy)−2 y2⋅ 2 yx2
1 − ( xy)2 1 + ( xy)2 2
1
1
3、二次积分 ∫ 0 dy∫ y f ( x, y)dx 交换积分次序后的结果为
(完整版)广西科技大学线性代数试卷A及B

广西工学院 2010 — 2011学年第 一学期课程考核试题考核课程 线性代数A ( A 卷)考核班级 学生数 印数 考核方式 闭卷 考核时间 120 分钟一.填空题(每空3分,共30分):1.在五阶行列式ij a 中,1523324451a a a a a 取 号.2.1112344916= . 3.设矩阵A 为三阶方阵,若已知2A =,则2A -= .4.矩阵10001111A k ⎛⎫ ⎪= ⎪ ⎪-⎝⎭可逆,则k 满足 .5.已知123021003A ⎛⎫⎪= ⎪ ⎪⎝⎭,则()1A -*= .6.若123,,ααα都是齐次线性方程组0AX =的解向量,则123(352)A ααα-+= .7.设3阶矩阵A 的特征值为1,2-,3 ,则2A A -的特征值为 .8.设3阶矩阵A 的特征值为1,2-,3 ,则A = .9.对任意n 阶方阵A 、B ,必定成立的是( )(填写正确答案的序号) ①AB BA = ②||||AB BA = ③()T T T AB A B =10. 设AX b =有无穷多组解,则0AX =( )(填写正确答案的序号) ①必有唯一解 ②必定没有解 ③必有无穷多解二(10分):计算行列式110001100011D xyzw--=-三(10分):设1234012300120001A -⎛⎫ ⎪--⎪= ⎪ ⎪-⎝⎭,求1A -. 四(15分):已知向量组123451321311011,,,,1110213120ααααα⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪ ⎪-- ⎪ ⎪ ⎪ ⎪ ⎪===== ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭(1)求该向量组的秩; (2)求该向量组的一个极大无关组,并将其余向量用此极大无关组来线性表示.五(15分):求解方程组123512345123451234531222423345382x x x x x x x x x x x x x x x x x x x --+=-⎧⎪--++=-⎪⎨--++=-⎪⎪--++=⎩六(14分):已知实对称矩阵200012021A ⎛⎫⎪= ⎪ ⎪⎝⎭(1)求A 的特征值与特征向量;(2)求一个正交矩阵P ,使T P AP 为对角矩阵,并写出T P AP .七(6分):设向量组123,,ααα线性无关, 而向量组1234,,,αααα 线性相关,证明向量4α可由向量组123,,ααα线性表示.2010-2011(B)线性代数(40学时)试题一、填空题(每小题3分,共30分):1.设01200341ab=-,则a 、b 满足的关系是_______________.2.设1234123421232112D =,则1121314122A A A A +++=________________.3.设矩阵A 的逆矩阵1100220333A -⎛⎫ ⎪= ⎪ ⎪⎝⎭,则A 的伴随矩阵A *=________________.4.设A 、B 为3阶方阵,若1A =,2B =,则2AB -=________________.5.设A 、B 、C 为n 阶非零方阵,且AB AC =,则当____________时,有B C =.6.向量组1(1,2,3,4)T α=,2(1,2,3,0)T α=,3(1,2,0,0)T α=,4(1,0,0,0)T α=一定线性_ _关.7.设()3R A =,已知12,ηη是4元非齐次线性方程组AX b =的2个不同解,则AX b =的一般解为______ ___________________.8.设3阶矩阵A 的特征值为1,2,3,则22A A +的特征值为___ ______,且2|2|A A +=_____.9.设12312001A x ⎛⎫⎪=- ⎪ ⎪⎝⎭,A 的特征值为1,2,3,则x =__ ___.10.设A 为实对称矩阵,1,2,3为A 的三个特征值,α为1所对应的特征向量,β为2所对应的特征向量,γ为3所对应的特征向量,则[,]αβγ+=___ __.二(10分):计算行列式121100020012112323104241D =.三(12分):设矩阵2234022300220002A ⎛⎫ ⎪⎪= ⎪⎪⎝⎭,10211001B ⎛⎫⎪⎪= ⎪-⎪⎝⎭,若AX X B =+,求矩阵X . 四(14分):设有向量组:1(1,1,0,1)T α=,2(0,1,1,1)T α=--,3(1,0,2,0)T α=,4(3,1,0,1)T α=,5(0,1,1,1)T α=. (1)求向量组12345,,,,ααααα的秩r ;(2)求向量组12345,,,,ααααα的一个极大线性无关组,并将其余的向量用极大线性无关组线性表示.五(14分):求方程组12345123523451235213250242154756x x x x x x x x x x x x x x x x x ++++=⎧⎪++-=⎪⎨+++=⎪⎪++++=⎩的一般解.六(14分):设矩阵120210001⎛⎫ ⎪= ⎪ ⎪⎝⎭A .(1)求A 的特征值和特征向量;(2)求正交矩阵T ,使T T AT 为对角矩阵并求该对角阵.七(6分):设方阵A 满足2240A A E --=,证明A E +可逆,并求1()A E -+.。
线性代数第1章分类题解

x 1 例 5 已知 f ( x ) = 3 1
1 1 2 x 1 −1 3 ,求 x 的系数 2 x 1 1 2x 1
t 3
分析 由 n 阶行列式的定义知,四阶行列式的一般项为 ( −1) a1 p1 a2 p2 a3 p3 a4 p4 ,其中 t 为 p1 p2 p3 p4 的逆序 数. 要使四项的乘积含 x ,首先在第一列中选择 a11 = x ,此时 p1 = 1 ;接着第二个元素取第二列中的 a22 = x , 此时 p2 = 2 .由于 p1 = 1, p2 = 2 已固定, p1 p2 p3 p4 只能形如 12 □□,即 1234 或 1243.这两项都含 x ,它
3
们对应的 t 分别为 0 + 0 + 0 + 0 = 0 或 0 + 0 + 0 + 1 = 1 ,故它们的和为 x − 2 x = − x ,故 x 的系数为 −1 .
3 3 3 3
0 0 L 0 1 0 0 0 L 2 0 0 例 6 用行列式的定义计算 Dn = L L L L L L n −1 0 L 0 0 0 0 0 L 0 0 n
(6)在排列 13… (2n − 1) (2n ) (2n − 2) …42 中. 第 2 个元素前没有比它大的数,故第 2 个元素的逆序是 0; 同样,第 3,4,…, n , n + 1 个元素的逆序也为 0; 第 n + 2 个元素前有 2 比它大的数,故第 n + 2 个元素的逆序是 2; 第 n + 3 个元素前有 4 比它大的数,故第 n + 3 个元素的逆序是 4; ……; 第 2n − 1 个元素前有 2( n − 2) 比它大的数,故第 2n − 1 个元素的逆序是 2( n − 2) ; 第 2n 个元素 2( n − 1) 前没有比它大的数,故第 2n 个元素的逆序是 2( n − 1) . 故排列 13… (2n − 1) (2n ) (2n − 2) …42 的逆序数为 2 + 4 + L + 2( n − 1) = n ( n − 1) .
线性代数试题答案及评分细则B卷

0
1
1 1
0
0
0
0
1 0 0 1
0
1
0
3
0 0 1 2
0
0
0
0
所以, r(1,2,3,4 ) 3
(2)1,2,3 为向量组的一个极大无关组
且3 1 32 24
六、计算(12 分)
解:对方程组的增广矩阵施与初等变换,得
其导出组的基础解系为:
3
2
3 4
1
3 2
,
2
7 4
1
0
0
1
所以该方程组的通解为
x k11 k22 ( k1, k2 为任意常数) 七、计算(10 分)
解:因为 A2 A E 0
解: 设 k11 k2 2 k3 3
展开可得关于 k1 , k2 , k3 为未知量的线性方程组
k1 k2 k3 1 k1 2k2 k3 0 2k1 k2 4k3 3 2k1 3k2 1
不难发现,若方程组有解,则 可由1, 2 ,3 线性表示, 且其解就是组合系数。若方程组有唯一解,则表达式唯一;若 方程组有无穷多解,则表达式也有无穷多种形式,若方程组无 解,则 不可由1, 2 ,3 线性表示.
k1 3 2 于是解方程组得: k2 k 2 1
k3 1 0
( k 为任意常数)
广西科技大学考研题目及答案
广西科技大学考研题目及答案广西科技大学作为一所综合性大学,其考研题目及答案涵盖了多个学科领域。
以下是一些模拟的考研题目及答案,供参考:### 考研题目#### 1. 数学题目:设函数f(x) = 3x^2 - 2x + 5,求f(x)的极值点。
答案:首先求导数f'(x) = 6x - 2。
令导数等于零,解得x = 1/3。
将x = 1/3代入原函数,得到f(1/3) = 19 2/3。
由于导数在x = 1/3处由正变负,所以f(x)在x = 1/3处取得极大值。
#### 2. 英语题目:Translate the following sentence into English: “随着科技的发展,人们的生活质量得到了显著提高。
”答案:With the advancement of technology, the quality of people's lives has been significantly improved.#### 3. 计算机科学题目:简述什么是数据库的事务,并说明其四个基本属性(ACID)。
答案:数据库事务是一系列操作,它们作为一个整体被执行,以保证数据库的完整性。
事务的四个基本属性(ACID)包括原子性(Atomicity)、一致性(Consistency)、隔离性(Isolation)和持久性(Durability)。
#### 4. 物理题目:解释什么是光的折射现象,并给出一个生活中的例子。
答案:光的折射现象是指光从一种介质进入另一种介质时,其传播方向发生改变的现象。
生活中的例子包括:当你把一根棍子插入水中时,棍子看起来像是在水面处弯曲了。
#### 5. 化学题目:解释什么是化学平衡,并给出一个平衡反应的例子。
答案:化学平衡是指在一个可逆反应中,正向反应和反向反应进行的速度相等,反应物和生成物的浓度保持不变的状态。
一个平衡反应的例子是氮气和氢气合成氨的反应:N2(g) + 3H2(g) ⇌ 2NH3(g)。
(本科)线性代数期末考试题及答案AB卷
线性代数试题测试卷及答案2套一、填空题1.四阶行列式中含有因子112432a a a 的项为_________.2.行列式222111ab c a b c 的值为_________. 3.设矩阵1000010000210022⎛⎫⎪⎪= ⎪⎪⎝⎭A ,则1-=A _________.4.设四元齐次线性方程组的系数矩阵的秩为1,则其解空间的维数为_________.5.设矩阵1234(,,,)=A αααα,其中234,,ααα线性无关,12342=-+αααα,向量41i i ==∑βα,则方程=AX β的通解为_________.6.已知三阶矩阵A 的特征值为1,2,3,则32--=A A E _________.二、选择题1.若两个三阶行列式1D 与2D 有两列元素对应相同,且123,2D D ==-,则12D D +的值为( ).A.1B.6-C.5D.02.对任意的n 阶方阵,A B 总有 ( ). A.=AB BA B.=AB BA C.()111---=AB B A D.()222=AB A B3.若矩阵X 满足方程=AXB C ,则矩阵X 为( ).A.11--A B C B.11--A CB C.11--CA B D.条件不足,无法求解4.设矩阵A 为四阶方阵,且()3R =A ,则*()R =A ( ). A.4 B.3 C.2 D.15.下列说法与非齐次线性方程组=AX β有解不等价的命题是( ).A.向量β可由A 的列向量组线性表示B.矩阵A 的列向量组与(,)A β的列向量组等价C.矩阵A 的行向量组与(,)A β的行向量组等价D.(,)A β的列向量组可由A 的列向量组线性表示6.设n 阶矩阵A 和B 相似,则下列说法错误的是( ). A.=A B B.()()R R =A BC.A 与B 等价D.A 与B 具有相同的特征向量7.设222123121323()224f x x x x ax x x x x x =+++-+为正定二次型,则a 满足( ).A.11a a ><-或B.12a <<C.11a -<<D.21a -<<- 三、计算题1.已知12111111111n na a D a ++=+,其中120n a a a ≠,求12n n nn A A A +++.2.设矩阵022110123⎛⎫ ⎪= ⎪ ⎪-⎝⎭A ,且2=+AX A X ,求X .3.求矩阵123451122102151(,,,,)2031311041⎛⎫ ⎪-⎪== ⎪- ⎪-⎝⎭A ααααα的列向量组的一个最大无关组,并把其余列向量用最大无关组线性表示.4.求非齐次线性方程组12341234123431,3344,5980x x x x x x x x x x x x +--=⎧⎪--+=⎨⎪+--=⎩的通解.5.求一个正交变换=X PY ,将二次型123121323(,,)222f x x x x x x x x x =--化成标准形.四、证明题已知n 阶方阵A 和B 满足124-=-A B B E ,证明2不是A 的特征值。
线性代数考试试卷+答案超强合集
大学生校园网— 线性代数综合测试题共3页第1页×××大学线性代数期末考试题一、填空题(将正确答案填在题中横线上。
每小题2分,共10分)1. 1. 若若022150131=---x,则=c ____________________。
2.若齐次线性方程组ïîïíì=++=++=++000321321321x x x x x x x x x l l 只有零解,则l 应满足。
3 3.已知矩阵.已知矩阵n s ij c C B A ´=)(,,,满足CB AC =,则A 与B 分别是阶矩阵。
阶矩阵。
44.矩阵÷÷÷øöçççèæ=323122211211a a a a a a A 的行向量组线性。
5.n 阶方阵A 满足032=--E A A ,则=-1A。
二、判断正误(正确的在括号内填“√”,错误的在括号内填“×”。
每小题2分,共10分)1. 1. 若行列式若行列式D 中每个元素都大于零,则0ñD 。
()2. 2. 零向量一零向量一定可以表示成任意一组向量的线性组合。
() 3. 3. 向量组向量组m a a a ,,, 21中,如果1a 与m a 对应分量成比例,则向量组s a a a ,,, 21线性相关。
()4. úúúúûùêêêêëé=01100000010010A ,则A A =-1。
()5. 5. 若若l 为可逆矩阵A 的特征值,则1-A的特征值为l 。
( )三、单项选择题 (每小题仅有一个正确答案,将正确答案题号填入括号内。
每小题2分,共10分) 1. 1. 设设A 为n 阶矩阵,且2=A ,则=TA A ()。
(完整版),大一线性代数期末试题及答案,推荐文档
【 】
A. a1 a2 0 b2 b3
B. a1 a2 0 b1 b2
C. a1 a2 a3 b1 b2 b3
9.方程组
2x1 x2 x3 1 x1 2x2 x3 1
3 x1 3x2 2x3 a 1
有解的充分必要的条件是
D. a1 a3 0 b1 b2
【 】
A. a=-3
25. -2 4
0
4 0 1
19. 16 23. 1、2、3
20. 2
三、计算题(每小题 6 分,共 30 分)
0345
345
3 4 1 0
26. D
3 2 2 - 2 …………4 分 96. …………8 分
0 2 2 2
69 2
0 692
27. 解:由于 A2 AB E ,因此 AB A2 E ,又 A 1 0 ,故 A 可逆, ……2 分
101
101 002
a1 (1, 0,1), a2 (1,1, 0), a3 (0,1,1) 为 R3 的一组基,…………4 分
又设
x
x11
x2 2
x3 3
,得线性方程组
x1
x2
x2 x3
2 2
《线性代数》试卷第 6页x1共7x3页 2
解之得向量 x (2, 2, 2) 在该组基下的坐标为 x (1,1,1) 。…………8 分
6 -2 7 2
1 1 1
26.设 A
0
1
1 ,且 A2 AB E ,其中 E 是三阶单位矩阵,求矩阵 B。
0 0 1
27.a
取何值时,方程组 4x1
x1 2x2 7x2 x3
3 10 有解?在有解时求出方程组的通解。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
广西工学院 2010 — 2011学年第 一学期课程考核试题考核课程 线性代数A ( A 卷)考核班级 学生数 印数 考核方式 闭卷 考核时间 120 分钟一.填空题(每空3分,共30分):1.在五阶行列式ij a 中,1523324451a a a a a 取 号.2.1112344916= . 3.设矩阵A 为三阶方阵,若已知2A =,则2A -= .4.矩阵10001111A k ⎛⎫ ⎪= ⎪ ⎪-⎝⎭可逆,则k 满足 .5.已知123021003A ⎛⎫⎪= ⎪ ⎪⎝⎭,则()1A -*= .6.若123,,ααα都是齐次线性方程组0AX =的解向量,则123(352)A ααα-+= .7.设3阶矩阵A 的特征值为1,2-,3 ,则2A A -的特征值为 .8.设3阶矩阵A 的特征值为1,2-,3 ,则A = .9.对任意n 阶方阵A 、B ,必定成立的是( )(填写正确答案的序号) ①AB BA = ②||||AB BA = ③()T T T AB A B =10. 设AX b =有无穷多组解,则0AX =( )(填写正确答案的序号) ①必有唯一解 ②必定没有解 ③必有无穷多解二(10分):计算行列式110001100011D x y z w--=-三(10分):设1234012300120001A -⎛⎫ ⎪--⎪= ⎪ ⎪-⎝⎭,求1A -. 四(15分):已知向量组123451321311011,,,,1110213120ααααα⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪ ⎪ ⎪-- ⎪ ⎪ ⎪ ⎪ ⎪=====⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭(1)求该向量组的秩; (2)求该向量组的一个极大无关组,并将其余向量用此极大无关组来线性表示.五(15分):求解方程组123512345123451234531222423345382x x x x x x x x x x x x x x x x x x x --+=-⎧⎪--++=-⎪⎨--++=-⎪⎪--++=⎩六(14分):已知实对称矩阵200012021A ⎛⎫⎪= ⎪ ⎪⎝⎭(1)求A 的特征值与特征向量;(2)求一个正交矩阵P ,使T P AP 为对角矩阵,并写出T P AP .七(6分):设向量组123,,ααα线性无关, 而向量组1234,,,αααα 线性相关,证明向量4α可由向量组123,,ααα线性表示.2010-2011(二)线性代数(40学时)试题 一、填空题(每小题3分,共30分):1.设01200341ab=-,则a 、b 满足的关系是_______________.2.设1234123421232112D =,则1121314122A A A A +++=________________.3.设矩阵A 的逆矩阵1100220333A -⎛⎫ ⎪= ⎪ ⎪⎝⎭,则A 的伴随矩阵A *=________________.4.设A 、B 为3阶方阵,若1A =,2B =,则2AB -=________________.5.设A 、B 、C 为n 阶非零方阵,且AB AC =,则当____________时,有B C =.6.向量组1(1,2,3,4)T α=,2(1,2,3,0)T α=,3(1,2,0,0)T α=,4(1,0,0,0)T α=一定线性_ _关.7.设()3R A =,已知12,ηη是4元非齐次线性方程组AX b =的2个不同解,则AX b =的一般解为______ ___________________.8.设3阶矩阵A 的特征值为1,2,3,则22A A +的特征值为___ ______,且2|2|A A +=_____.9.设12312001A x ⎛⎫⎪=- ⎪ ⎪⎝⎭,A 的特征值为1,2,3,则x =__ ___.10.设A 为实对称矩阵,1,2,3为A 的三个特征值,α为1所对应的特征向量,β为2所对应的特征向量,γ为3所对应的特征向量,则[,]αβγ+=___ __.二(10分):计算行列式121100020012112323104241D =. 三(12分):设矩阵2234022300220002A ⎛⎫ ⎪⎪= ⎪⎪⎝⎭,10211001B ⎛⎫⎪⎪= ⎪- ⎪⎝⎭,若AX X B =+,求矩阵X . 四(14分):设有向量组:1(1,1,0,1)T α=,2(0,1,1,1)T α=--,3(1,0,2,0)T α=,4(3,1,0,1)T α=,5(0,1,1,1)T α=.(1)求向量组12345,,,,ααααα的秩r ;(2)求向量组12345,,,,ααααα的一个极大线性无关组,并将其余的向量用极大线性无关组线性表示.五(14分):求方程组12345123523451235213250242154756x x x x xx x x xx x x xx x x x++++=⎧⎪++-=⎪⎨+++=⎪⎪++++=⎩的一般解.六(14分):设矩阵120210001⎛⎫⎪= ⎪⎪⎝⎭A.(1)求A的特征值和特征向量;(2)求正交矩阵T,使T T AT为对角矩阵并求该对角阵.七(6分):设方阵A满足2240A A E--=,证明A E+可逆,并求1()A E-+.模拟试题第一套题目年春(秋)学期期末考试试题(考试时间:120分钟)一、填空题(每小题3分,共30分)1.三阶行列式=-410021321 13 .2. 排列42135的逆序数为 4 .3. 利用行列式的性质计算三阶行列式=-11026422375551321 .4. 矩阵,341021⎪⎪⎭⎫ ⎝⎛-=A 则=TA . 5. 已知A 为2阶方阵,3=A ,则=A 2 .6. =⎪⎪⎪⎭⎫ ⎝⎛123)3,2,1( .7. 若二阶方阵,0231⎪⎪⎭⎫⎝⎛=A 则=A 2 .8. 矩阵,000710312⎪⎪⎪⎭⎫⎝⎛-=A 则该矩阵的秩=)(A R .9. n 元线性方程组b Ax =有惟一解的充分必要条件为 .10. 已知向量,120,342⎪⎪⎪⎭⎫⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛=βα则=-βα .二、计算题(每小题10分,共10分)2321260512131412-三、计算题(每小题10分,共10分)求矩阵A 的逆,其中⎪⎪⎭⎫⎝⎛=2174A四、计算题(每小题12分,共12分)求下列矩阵的秩⎪⎪⎪⎭⎫⎝⎛---=412431211013A五、计算题(每小题14分,共14分)求解线性方程组⎪⎩⎪⎨⎧-=+++-=-++=-+-6242163511325432143214321x x x x x x x x x x x x六、计算题(每小题12分,共12分)问a 取什么值时向量组123(,1,1),(1,,1),(1,1,)T T T a a a ααα==-=-线性相关?第二套题目年春(秋)学期期末考试试题(考试时间:120分钟 )一、填空题(每小题3分,共30分)1. 四阶行列式式中含有1123a a 的项是44322311a a a a -和 .2. 排列52413的逆序数为 .3.对于两个n 阶方阵,A B ,若 ,则称方阵A 与B 是可交换的 4. 方阵A 为可逆矩阵的充分必要条件是 . 5. 矩阵的转置运算中()T AB = .6. 行列式||A 的各个元素的代数余子式ij A 所构成的矩阵*A 为伴随矩阵,则**AA A A == .7. 若A 可逆,数0λ≠,则A λ可逆,且1()A λ-= .8.设向量组123(1,3,1),(2,1,0),(1,4,1)T T T ααα=-==,它们的相性相关性是 . 9.n 元齐次线性方程组0Ax =只有零解的充要条件为 .10.已知向量,120,342⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛=βα则=+βα2 .二、计算题(每小题12分,共12分)计算行列式x a aa x a a ax.三、计算题(每小题10分,共10分)求矩阵A 的逆,其中⎪⎪⎪⎪⎪⎭⎫⎝⎛=2500380000120025A四、计算题(每小题12分,共12分)求下列矩阵的秩⎪⎪⎪⎭⎫⎝⎛-------=831113507312123A五、计算题(每小题14分,共14分)求解线性方程组⎪⎩⎪⎨⎧=+++=-++=-++02220202432143214321x x x x x x x x x x x x六、计算题(每小题10分,共10分)判定下列向量组是线性相关还是线性无关: ,141,012,131⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫⎝⎛⎪⎪⎪⎭⎫ ⎝⎛-七、计算题(每小题12分,共12分)求下列向量组的秩:⎪⎪⎪⎪⎪⎭⎫ ⎝⎛---=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-=8242,4101009,4121321ααα。
第三套题目年春(秋)学期期末考试试题(考试时间:120分钟 )一、填空题(每小题3分,共30分)1.对角行列式=400030000200001. 2. 排列52431的逆序数为 .3. 若行列式有两行(列)完全相同,则此行列式等于 .4. 矩阵,341021⎪⎪⎭⎫⎝⎛-=A 则=A 2 .5. =+T B A )( .6. 若A 可逆,则7. 若二阶方阵1221,,2505A B ⎛⎫⎛⎫== ⎪ ⎪⎝⎭⎝⎭则A B -= .8. 矩阵,000400351⎪⎪⎪⎭⎫ ⎝⎛=A 则该矩阵的秩=)(A R.9. n 元线性方程组b Ax =有无穷多解的充分必要条件为 .10. 已知向量,120,342⎪⎪⎪⎭⎫⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛=βα则=-βα32 .二、计算题(每小题10分,共10分)71100251020214214三、计算题(每小题10分,共10分)求矩阵A 的逆,其中5192A ⎛⎫= ⎪⎝⎭四、计算题(每小题12分,共12分)求下列矩阵的秩⎪⎪⎪⎭⎫⎝⎛---=412431211013A五、计算题(每小题14分,共14分)求解线性方程组⎪⎩⎪⎨⎧=+++=-++=-++02220202432143214321x x x x x x x x x x x x六、计算题(每小题12分,共12分)判定下列向量组是线性相关还是线性无关: 2103,4,0,002-⎛⎫⎛⎫⎛⎫ ⎪⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭七、计算题(每小题12分,共12分)设),(5)(2)(3321αααααα+=++-求α,其中.1114,105110,3152321⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=ααα第四套题目年春(秋)学期期末考试试题(考试时间:120分钟 )一、填空题(每小题3分,共30分)1. 下三角行列式=4095034200210001 .2. 排列52314的逆序数为 .3. 行列式中如果有两行(列)元素成比例,则此行列式等于 .4. 矩阵,6342,2142⎪⎪⎭⎫ ⎝⎛--=⎪⎪⎭⎫ ⎝⎛--=B A 则=+B A .5. =T A )(λ .6. =⎪⎪⎪⎭⎫ ⎝⎛423)1,0,2( .7. 若二阶方阵,1432⎪⎪⎭⎫⎝⎛=A 则=A 2 .8. 矩阵,000500311⎪⎪⎪⎭⎫⎝⎛=A 则该矩阵的秩=)(A R .9. n 元线性方程组b Ax =无解的充分必要条件为 .10. 已知向量,121,332⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛=βα则=+βα2 .二、计算题(每小题10分,共10分)efcfbfde cd bdae ac ab ---三、计算题(每小题10分,共10分)求矩阵A 的逆,其中⎪⎪⎭⎫⎝⎛=3275A四、计算题(每小题12分,共12分)求下列矩阵的秩⎪⎪⎪⎪⎪⎭⎫⎝⎛---=02301085235703273812A五、计算题(每小题14分,共14分)求解线性方程组⎪⎩⎪⎨⎧=-++=--+=-++05105036302432143214321x x x x x x x x x x x x六、计算题(每小题12分,共12分)问a 取什么值时向量组123(,1,1),(1,,1),(1,1,)T T T a a a ααα==-=-线性相关?七、计算题(每小题12分,共12分)求下列向量组的秩:⎪⎪⎪⎪⎪⎭⎫ ⎝⎛---=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-=8242,4101009,4121321ααα。
