运筹学 单纯形法应用问题
运筹学单纯形法

运筹学单纯形法
运筹学单纯形法,又称单纯性法,是一种用于求解线性规划问题的数学方法,它在运筹学中发挥着重要作用。
它主要应用于决策及资源分配问题,可以帮助决策者更好地把握资源的优化配置,并寻求最优解。
单纯性法是以线性规划问题作为理论基础,它是将该问题转化为一系列形如Ax=b的线性方程组的运筹学方法。
在这个方程组通过调整方程中的系数和右面常数而变换为形如Cx≤d的不等式形式,而这种不等式系统称为单纯性约束条件。
单纯性法从不等式中寻找一系列基向量,并通过改变基向量来实现改变不等式的求解方程之间的关系,从而求出最优解的问题。
传统的单纯性法分为有界单纯性和无界单纯性两种情形。
无界单纯性以简单费用曲线方法、扩展的简单费用曲线方法和增广次数法三大类。
有界单纯性主要是对对角单纯性和非对角单纯性这两类单纯性系统分别使用不同的方法进行求解。
单纯性求解方法在线性规划问题求解中具有重要应用,它能通过求解线性规划问题中的一系列互不相关的子问题来求出最优解。
使用该方法,可以以最少的成本达到最优的收益,它包括费用最低优化、网络流优化、全格研究和数学优化模型等。
运筹学 线性规划问题的单纯形法
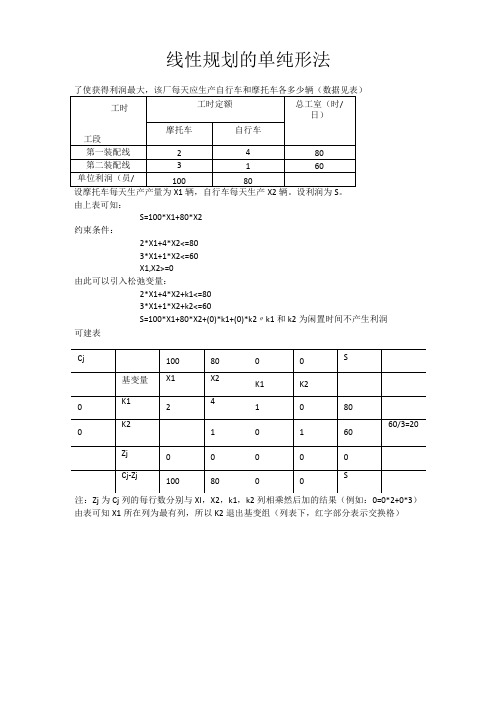
线性规划的单纯形法
由上表可知:
S=100*X1+80*X2
约束条件:
2*X1+4*X2<=80
3*X1+1*X2<=60
X1,X2>=0
由此可以引入松弛变量:
2*X1+4*X2+k1<=80
3*X1+1*X2+k2<=60
S=100*X1+80*X2+(0)*k1+(0)*k2〃k1和k2为闲置时间不产生利润
可建表
注:Zj为Cj列的每行数分别与XI,X2,k1,k2列相乘然后加的结果(例如:0=0*2+0*3)由表可知X1所在列为最有列,所以K2退出基变组(列表下,红字部分表示交换格)
而由表可知要消去图中绿字所在行必须是图中绿字所在行-2*红字所在行。
消去后的表的情
注:此时由上表可知X2所在列是最有解,切Cj-Zj依旧为正。
所以,此时K1出基(将k1行中各数据*3/10)得到如下表:
注:由表可知此时Cj-Zj为零,如果接续下去此值将会为负所以此时由最大利润为2560即:当摩托车生产16辆,自行车生产12辆是有最大利润。
本题只是为了让和我有一样迷惑的人有一个解题案例,如若真正搞懂线性规划问题的单纯形法还得去以参考书为准。
运筹学原理单纯形法练习题

四、把下列线性规划问题化成标准形式:2、minZ=2x1-x2+2x3五、按各题要求。
建立线性规划数学模型1、某工厂生产A、B、C三种产品,每种产品的原材料消耗量、机械台时消耗量以及这些资源的限量,单位产品的利润如下表所示:根据客户订货,三种产品的最低月需要量分别为200,250和100件,最大月销售量分别为250,280和120件。
月销售分别为250,280和120件。
问如何安排生产计划,使总利润最大。
2、某建筑工地有一批长度为10米的相同型号的钢筋,今要截成长度为3米的钢筋90根,长度为4米的钢筋60根,问怎样下料,才能使所使用的原材料最省?某运输公司在春运期间需要24小时昼夜加班工作,需要的人员数量如下表所示: 起运时间 服务员数 2—6 6—10 10一14 14—18 18—22 22—24 8 10 7 12 4每个工作人员连续工作八小时,且在时段开始时上班,问如何安排,使得既满足以上要求,又使上班人数最少?五、分别用图解法和单纯形法求解下列线性规划问题.并对照指出单纯形迭代的每一步相当于图解法可行域中的哪一个顶点。
六、用单纯形法求解下列线性规划问题:七、用大M法求解下列线性规划问题。
并指出问题的解属于哪一类。
八、下表为用单纯形法计算时某一步的表格。
已知该线性规划的目标函数为maxZ=5x1+3x2,约束形式为“≤”,X3,X4为松驰变量.表中解代入目标函数后得Z=10XlX2 X3 X4 —10 b-1 f g X3 2 C O 1 1/5 Xlade1(1)求表中a ~g 的值 (2)表中给出的解是否为最优解?(1)a=2 b=0 c=0 d=1 e=4/5 f=0 g=-5 (2) 表中给出的解为最优解 第四章 线性规划的对偶理论 五、写出下列线性规划问题的对偶问题 1.minZ=2x1+2x2+4x3六、已知线性规划问题应用对偶理论证明该问题最优解的目标函数值不大于25七、已知线性规划问题maxZ=2x1+x2+5x3+6x4其对偶问题的最优解为Yl﹡=4,Y2﹡=1,试应用对偶问题的性质求原问题的最优解。
运筹学 第二章 单纯形法

按最小非负比值规则:
5 0 1 1/ 3 1 1 2 1
x2 x3
5 0 1 1/ 3 0 2/3 0 1/ 3 1
0 15 0 1/ 6 0 4 0 1/ 6 1 1 0 1/ 3 0 8 0
至此,检验行已没有负数, 当前解即为最优解。
0
此时对应的LP问题为:
min S 0 x1 0 x2 x3 x4 0 x5 1
x4 1 x1 2 x2 2 x3 s.t 0 x1 3x2 3x3 x4 x5 5 x 0 (i 1,2,3,4,5) i
i 1, ,5
可行基{ x1 , x 2 , x 3 }
令非基变量 x4 , 最优值:
x 5为0,得到最优解
17 max Z 2
15
7 3 15 X 3 ( , , ,0,0)T 2 2 2
此基本可行解对应可行域的顶点(7 / 2, 3 / 2) 其结果与图解法一致。 总结:①在迭代过程中要保持常数列向量非负,这能保证基 可行解的非负性。最小比值能做到这一点。 ②主元素不能为0。因为行的初等变换不能把0变成1。
此时,
x4
已经从24降到了0,达到了非基的取值,变
成非基变量。从而得到新的可行基{x1 , x3 , x5 } 。 由此得到一个新的基本可行解: X 1 ( 4,0,15,0,1)T
8
此基本可行解对应可行域的顶点(4,0)
目标函数值: ( X1 ) 2 4 8 Z ( X 0 ) 0. Z
T
X 0 (0,0,15,24,5)
(对应可行域的 o(0,0) )
显然不是最优。 因为从经济意义上讲, x1 0, x2 0
运筹学单纯形法例题求解过程

运筹学单纯形法例题求解过程(原创版)目录一、运筹学单纯形法的基本概念二、运筹学单纯形法的求解步骤1.确定基变量和初始基本可行解2.编制初始单纯形表3.判断基本可行解是否为最优解4.迭代求解下一个使目标函数更优的基本可行解5.重新计算机会费用和检验数三、运筹学单纯形法的应用实例正文一、运筹学单纯形法的基本概念运筹学单纯形法是一种求解线性规划问题的方法,它是基于数学和统计学的理论基础,通过逐步优化算法,寻找线性规划问题中最优解的一种方法。
线性规划问题是指在一定约束条件下,寻求目标函数的最小值或最大值的问题。
而单纯形法是线性规划问题中最常用的求解方法之一,它通过迭代计算,不断优化基变量,从而得到问题的最优解。
二、运筹学单纯形法的求解步骤1.确定基变量和初始基本可行解在求解线性规划问题时,首先需要确定问题的基变量,即在所有变量中选择若干个变量作为基变量。
基变量的选取可以通过寻找单位矩阵的方法来确定。
确定基变量后,可以求出初始基本可行解,即满足所有约束条件的变量值组合。
2.编制初始单纯形表根据初始基本可行解和线性规划模型提供的信息,可以编制初始单纯形表。
单纯形表是一个包含基变量、非基变量、目标函数系数、约束条件常数项和检验数等元素的矩阵表。
3.判断基本可行解是否为最优解在求解过程中,需要判断基本可行解是否为最优解。
这可以通过检验数来进行。
检验数是指非基变量与对应约束条件的乘积,如果所有非基变量的检验数都小于等于 0,说明已经达到最优解。
否则,需要继续迭代求解。
4.迭代求解下一个使目标函数更优的基本可行解如果基本可行解不是最优解,需要通过迭代求解来寻找下一个使目标函数更优的基本可行解。
迭代过程中,需要确定换入变量和换出变量,然后根据换入变量和换出变量生成新的单纯形表,并重新计算机会费用和检验数。
5.重新计算机会费用和检验数在迭代过程中,需要重新计算机会费用和检验数,以便判断新的基本可行解是否更优。
如果新的基本可行解的检验数满足条件,说明已经找到最优解,可以结束迭代求解过程。
单纯形法原理及例题

单纯形法原理及例题
单纯形法原理:
单纯形法是求解线性规划问题的一种数学方法,它是由美国数学家卢克·单纯形于1947年发明的。
用单纯形法求解线性规划的过程,往往利用线性规划的对偶形式,将原问题变换为无约束极大化问题,逐步把极大化问题转换为标准型问题,最后利用单纯形法的搜索方法求解满足所有约束条件的最优解。
例题:
问题:求解最小化目标函数z=2x1+x2的线性规划问题,约束条件如下:
x1+2x2≥3
3x1+x2≥6
x1,x2≥0
解:将上述线性规划问题转换为无约束极大化问题,可得:
极大化问题:
Max z=-2x1-x2
s.t. x1+2x2≤3
3x1+x2≤6
x1,x2≥0
将极大化问题转换为标准型问题,可得:
Max z=-2x1-x2
s.t. x1+2x2+s1=3
3x1+x2+s2=6
x1,x2,s1,s2≥0
运用单纯形法的搜索方法求解:
令x1=0,x2=0,则可得s1=3,s2=6,即(0,0,3,6)是单纯形的初始解;
令z=-2x1-x2=0,代入约束条件,可得x1=3,x2=3,则可得s1=0,s2=0,即(3,3,0,0)是新的单纯形解。
由于s1=s2=0,说明x1=3,x2=3是线性规划问题的最优解,且最小值为z=2*3+3=9。
运筹学单纯形法的对偶问题

可以为负,即 y3 没有非负限制。
这样我们把原规划的对偶问题化为
min f 440 y1 100 y2 200 y3
s.t. 2 y1 6 y2 5y3 3,
3y1 4 y2 3y3 4,
6 y1 y2 y3 6,
y1, y2 0, y3 没有非负限制。
对照原线性规划问题,我们可以知道:
解:设x1为产品 的计划产量,x2 为产品Ⅱ的计划产量,则有
目标函数: 约束条件:
Max z=50 x1 + 100 x2
x1 x2 300
2x1 x2 400
x2 250
x1, x2 0
管理运筹学
1
§1 线性规划的对偶问题
现在我们从另一个角度来考虑这个问题。假如有另外一个工厂要求租用该厂的设备A、B、 c,那么该厂的厂长应该如何来确定合理的租金呢?
管理运筹学
14
§1 线性规划的对偶问题
首先在写对偶问题之前,我们先把第二个约束条件两边乘以-1得
2x1 3x2 x3 60
然后按照上面的规则,我们可以得到其对偶问题为
max z 180 y1 60 y2 240 y3;
y1 2 y2 5 y3 3
s.t.
2 y1 3y2 3y3 9
管理运筹学
16
§2 对偶规划的基本性质
3.最优性。如果 Xˆ是原问题的可行解,Yˆ 是对偶问题 的可行解,并且cXˆ bTYˆ,则 Xˆ 和 Yˆ分别为原问题和 对偶问题的最优解。
4.强对偶性。即若原问题及其对偶问题都有可行解,
则两者都有最优解,且它们的最优解的目标函数都 相等。
5.互补松弛性。在线性规划问题的最优解中,如果
决策变量都来源于原问题的第三个约束条件,记为
单纯形法求解线性规划问题例题

单纯形法求解线性规划问题例题线性规划问题(LinearProgrammingProblem,LPP)是指由一系列约束条件和优化目标函数组成的数学最优化模型,它可以用于解决各种单位时间内最高效率的分配问题。
在求解LPP的过程中,单纯形法(Simplex Method)是最主要的优化算法之一。
单纯形法的原理是采用一组基本变量的拿破仑表示法,一步步构造出线性规划问题的最优解。
下面我们来看一个例子:有公司向农户出售两种农药,甲和乙,每瓶甲农药售价3元,每瓶乙农药售价2元,公司每天有200瓶甲农药和150瓶乙农药,问该公司售出多少瓶甲农药和乙农药,能每天获得最大收益?该问题可表示为下述线性规划模型:最大化 $3x_1+2x_2$约束条件:$x_1+x_2le 200$$2x_1+x_2le 150$$x_1,x_2ge 0$由上述模型可知,有两个未知量$x_1$和$x_2$,它们分别代表出售的甲农药和乙农药的瓶数。
单纯形法的基本思想是采用一组基本变量表示未知量,将未知量$x_1$和$x_2$表示为由两个基本变量$y_1$和$y_2$组成的拉格朗日变换系数矩阵形式,即:$x_1+x_2=y_1+y_2$$2x_1+x_2=m(y_1+y_2)$其中,m是一个系数,根据上面的约束条件,m取200/150=4/3,则:$x_1=y_1+frac{1}{3}y_2$$x_2=y_2-frac{1}{3}y_2$由此可以得到该问题的新的线性规划模型:最大化 $3y_1+2(frac{4}{3})y_2$约束条件:$y_1+y_2le 200$$y_2le 150$$y_1,y_2ge 0$可以看出,该问题所构建出来的新的线性规划模型比原来的模型更加容易求解。
我们将建立单纯形表,以便求出最优解。
首先列出单纯形表:$begin{array}{|c|c|c|c|c|c|c|}hline& y_1 & y_2 & S_1 & S_2 & f & b hline1 & 1 & 1 & 1 & 0 & 3 & 200 hline2 & 0 & 1 & 0 & 1 & 4/3 & 150 hlineend{array}$其中,$y_1$和$y_2$是基本变量,$S_1$和$S_2$是可行解系数,$f$是目标函数系数,$b$是右端项。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
0 -2 0 1/4
1 0 B1b 4 1
0 0
-
1 2
8
2
2
16
8
1 4
12
3
注意:B 的列顺序 和 XB 的下标顺序 相同。
1 0 B1P2 4 1
0 0
-
1 2
2
0
2
出售,单价=16
=0.75,工 时=1.5
B=2M
出售B,单价=7
第三车间加工费用=4,
工资=0.5,工时=1
出售,单价=12
设 x1 =A出售的数量;x2=A在第2车间加工后的出售数量;x3=B的出售数 量 ;x4=B在第3车间加工后的出售数量;x5=第1车间所用原料数量
Max Z=8 X1+8.5 X2+7 X3+7.5 X4-2.75 X5
3 x2 3 0 1 0 0 1/4
-z -13 0 0 -2 0 1/4
1 0 2
第三张表:B 4 1
0
,
0 0 4
1 0
-
1 2
B-1 4 1
2
0 0
1 4
0.3
(5)
01
3 6.6
0.8
设按方案1、2、3、4、5各截取x1,x2,x3,x4 ,x5根原料,则
Min Z 0x1 0.1x2 0.2x3 0.3x4 0.8x5
x1 2x2 x4 ( ?)100
2x3 2x4 x5 ( ?)100
3x1 x2 2x3
4
3
令
y
min(
7
x1
6x2
8x3
,
5x1
9x2
4
x3 )
4
3
7x1 6x2 8x3 y 4
5x1 9x2 4x3 y 3
目标函数
max z y
9.城市间汽车运输问题
某汽车运输公司经营A、B、C三个城市之间的货物运 输业务,任两个城市间都有公路连通,货运量及每年 利润如下表。公司有汽车250辆,每周每辆车最多在两 个城市间单程运行4次,由于技术原因,全部汽车每周 末必须停留在A城。汽车回空没有利润,也不记成本, 建立最大利润的线性规划模型。
利润=收入-成本
原料用量约束(A )
原料用量约束(B ) 原料用量约束(C )
x1
x4
x7
2000
原料成本(元/千克)
2.00
x2 x5 x8 2500
1.50
x3 x6 x9 1200
1.00
Z=(3.4-0.5)(x1+x2+x3)+(2.85-0.40)(x4+x5+x6)+(2.25-0.30)(x7+x8+x9)
- [x1 x4 x7 *2.00 x2 x5 x8 * 1.50 x3 x6 x9 * 1]
4. 连续加工问题
某工厂在第1车间用1单位原料M加工成3单位产品A及2单 位产品B. A可以按单位售价8元出售,也可以在第2车间继续 加工,单位生产费用要增加6元,加工后单位售价为16元。 B可以按单位售价7元出售,也可以在第3车间继续加工,单 位生产费用要增加4元,加工后单位售价为12元。原料的单 位购入价为2元,上述生产费用均不包括工资在内。
2. 现要做100套钢架,每套用长为2.9m,2.1m和1.5m的元钢各一 根。已知原料长7.4m,问如何下料,使用的原材料最省?
可能的方案: 2.9m 2.1m 1.5m 用料长m 余料(m)
(1) 1
0
3 7.4
0
(2) 2 0
1 7.3
0.1
(3) 0 2
2 7.2
0.2
(4) 1 2
0 7.1
线性规划的应用
1. 生产2#岩石铵梯炸药和3#露天铵梯炸药,配比如下:
品种 配比(%) 原料
硝酸铵 梯恩梯 木粉 售价(元 / 吨)
2#岩石铵梯炸药
85
3#露天铵梯炸药
88
原料可用量(吨)
400
11 4
3
9
44 36
1200 800
该厂应如何规划下个月的生产,才能使产值最高。
品种 配比(%) 原料 2#岩石铵梯炸药
在哪里设厂,生产能力多大,使总费用(生产费、原料费 和运输费)最少?
地点 年原料产量(万t) 年成品销量(万t) 每万t成品加工费(千元)
A 30
7
5.5
B 26
13
4
C 24
0
3
7 .生产问题
某公司生产甲、乙、丙三种产品,都需要经过铸造、机加工
和装配三个车间。甲、乙两种产品的铸件既可以外包协作,也可
3#露天铵梯炸药 原料可用量(吨)
硝酸铵 梯恩梯 木粉 售价(元 / 吨)
85
11 4
1200
883Biblioteka 9800400
44 36
设下月生产两种产品分别为x1,x2吨,所获产值为Z,
max Z 1200x1 800x2
0.85x1 0.88x2 400 0.11x1 0.03x2 44 0.04x1 0.09x2 36 x1 ,x2 ,x3 0
3个车间每月最多有20万工时,每小时工资为0.5元。每 加工1单位M需1.5工时,如A继续加工,每单位需3工时, 如B继续加工,每单位需1工时。每月最多能够得到原料 M10万单位,问如何安排生产,使工厂获利最大?
出售A,单价=8
A=3M
第一车间加
第二车间加工费用=6,
M
工,购入费 用=2,工资
工资=1.5,工时=3
原料供应限制 X5 ≤ 100000 工时限制 3X2+X4+1.5X5 ≤200000 A产品数量的限制 X1+X2-3X5=0 B产品数量的限制 X3+X4-2X5=0
5.连续投资问题
某部门有现金10万元,在今后五年内考虑给下面项目投资,已知:
项目A,从第一年到第四年每年年初需要投资,并于次年末回收本利115% 项目B,第三年初需要投资,到第五年末回收本利125%,但最大投资额不 超过4万元 项目C,第二年初需要投资,到第五年末回收本利140%,但最大投资额不 超过3万元 项目D,五年内每年初可购买公债,于当年末归还,并加利息6%
0
0
1 4
4
1
CBB-1 称为单
纯形乘子向量。
1
3 c3 CBB1P3 0 [2 0 3] 4 2
0
cj
2
3
00
0
CB XB b
x1
x2
x3
x4
x5
2 x1 2 1 0 1 0 -1/2 0 x4 8 0 0 -4 1 [2]
X5:由外协铸造再由本公司机加工和装配的乙产品数; c5=18-(6+1+2)
8.非线性规划问题
某工厂有3个车间生产同一种产品。每件产品由4个零件1和 3个零件2组成。这两种零件需耗用两种原材料。已知这两种原 材料的供应量分别为300公斤和500公斤。由于3个车间拥有的 设备及工艺条件不同,每个工班原材料用量和零件产量也不同, 具体情况如下表。建立产量最多的线性规划模型。
以自行生产,但产品丙必须本厂铸造才能保证质量。有关的数据
如表。问公司为了获得最大利润,甲、乙、丙三种产品各生产多
少件?
甲乙丙
工时限制
单件铸造工时/h
5
10 7
单件机加工工时/h
6
4
8
单件装配工时/(元/件) 3
2
2
自产铸件成本/(元/件) 4
5
4
外协铸件成本/(元/件) 5
6
-
机加工成本/(元/件) 2
每月应生产这三种型号的糖果各多少千克,使该厂获利最大?
设每月生产三种糖果分别为x1,x2,x3 千克,所获利润为
Z 3.40 0.50x1 2.85 0.40x2 2.25 0.30x3
2.90x1 2.45x2 1.95x3
利润=收入-成本
产品 原料
货运量
ABC
A
150 250
B 100
200
C 500 100
利润
ABC
A
150 200
B 50
300
C 100 150
第二章 对偶理论和灵敏度分析
§1 单纯形法的矩阵描述
本节重点: 单纯形表各部分的数量关系
方程组中,非基变量为 0,基变量系数矩阵为 单位矩阵,故
XB=B-1b
z CB B1b
j c j CB B1Pj c j CB P'j
P'j B1Pj
可知,XS 的系数总对应B1 ;已知B1 ,就能求出 整个表。
单纯形表的矩阵形式
基变量
非基变量
XB
XN
XS
I
B-1 N
B-1
B-1b
0
CN-CBB-1N -CBB-1 -CBB-1b
如例1 的初始表和第三张表
X2C ≤ 30000
Max Z=1.15X4A+ 1.40X2C +1.25 X3B +1.06 X5D
6.工厂选址问题
有A、B、C三个原料产地,其原料要在工厂加工,制成成 品,再在销售地出售。A、B两地又是销售地。已知有关数据 如下表。4t原料制成1t成品。AB间距离150km,BC间距离 200km,CA间距离100km。原料运费为300元/万tkm,成品运 费为250元/万tkm。如在B地设厂,每年生产成品不能超过5万 t,在A、C设厂,生产规模不受限制。
