2019年深国交G1入学考试数学:二次函数的性质01(选择题)
2019年深国交G1入学考试数学:二次函数01(填空)

G1入学二次函数01(填空)一.填空题(共30小题)1.(2015•肥城市一模)已知抛物线y=x2+bx+c的对称轴为x=2,点A,B均在抛物线上,且AB与x轴平行,其中点A的坐标为(0,3),则点B的坐标为.2.(2015•杭州模拟)已知点P(5,n),点Q(m,n)是抛物线y=2x2+4x﹣c的两个不同的点,则m=.3.(2015•和平区一模)某飞机着陆滑行的路程s(米)与时间t(秒)的关系式为:s=60t ﹣1.5t2,那么飞机着陆后滑行米才能停止.4.(2015•杭州模拟)已知正整数a满足不等式组(x为未知数)无解,则a的值为;函数y=(3﹣a)x2﹣x﹣3图象与x轴的交点坐标为.5.(2015秋•潮州期末)抛物线y=﹣x2+bx+c的部分图象如图所示,则关于x的一元二次方程﹣x2+bx+c=0的解为.6.(2014•涪城区校级自主招生)一个函数的图象关于y轴成轴对称图形时,我们称该函数为“偶函数”.如果二次函数y=x2+bx﹣4是“偶函数”,该函数的图象与x轴交于点A和点B,顶点为P,那么△ABP的面积是.7.(2014•杨浦区二模)抛物线y=2x2+4x﹣2的顶点坐标是.8.(2014•上海一模)已知一个二次函数的图象具有以下特征:(1)经过原点;(2)在直线x=1左侧的部分,图象下降,在直线x=1右侧的部分,图象上升.试写出一个符合要求的二次函数解析式..9.(2014•丹东校级二模)已知二次函数y=ax2+bx+c(a≠0)的图象如图,则下列4个结论正确的有个①ac<0;②2a+b=0;③4a+2b+c>0;④对于任意x均有ax2+bx≥a+b.10.(2014•老河口市模拟)抛物线y=2x2+3上有两点A(x1,y1)、B(x2,y2),且x1≠x2,y1=y2,当x=x1+x2时,y=.11.(2014•独山县模拟)如图,抛物线y=x2沿直线y=x向上平移个单位后,顶点在直线y=x上的M处,则平移后抛物线的解析式为.12.(2014•工业园区一模)二次函数y=(x+3)(2﹣x)取得最大值时,x=.13.(2014•牡丹江一模)已知抛物线y=ax2+bx+c经过三个点(0,5),(4,5)(3,0)并且与x轴另一个交点为点P,若将抛物线先向左平移2个单位,再向下平移1个单位,则点P 的对应点的坐标为.14.(2014•天门模拟)抛物线y=kx2﹣5x+2的图象和x轴有交点,则k的取值范围是.15.(2014•乳山市二模)抛物线y=x2﹣(2m﹣1)x﹣2m与x轴的两交点坐标分别是A(x1,0),B(x2,0),且||=1,则m的值为.16.(2013秋•龙口市期末)已知抛物线y=x2﹣x﹣3与x轴的一个交点为(m,0),则代数式m2﹣m+2012的值为.17.(2013秋•开封县期末)将抛物线y=3x2﹣6x+4先向右平移3个单位,再向上平移2个单位后得到新的抛物线,则新抛物线的顶点坐标是.18.(2013秋•文登市期末)已知下列函数:①y=﹣(x﹣1)2;②y=x2+1;③y=﹣x2﹣1.其中,图象通过平移可以得到函数y=﹣(x﹣2)2﹣1的图象的有(填写所有正确选项的序号).19.(2013秋•日照期末)二次函数y=x2+4x+5(﹣3≤x≤0)的最大值和最小值分别是.20.(2014春•永定县校级期末)不论x取何值,二次函数y=﹣x2+6x+c的函数值总为负数,则c的取值范围为.21.(2013秋•南京期末)某公园草坪的防护栏形状是抛物线形.为了牢固起见,每段护栏需要间距0.4m加设一根不锈钢的支柱,防护栏的最高点距底部0.5m(如图),则其中防护栏支柱A3B3的长度为m.22.(2013秋•宜城市期末)向上发射一枚炮弹,经x秒后的高度为ym,且时间与高度关系为y=ax2+bx.若此炮弹在第7秒与第14秒时的高度相等,则炮弹飞行第秒时高度是最高的.23.(2013秋•宝安区期末)某服装店销售童装平均每天售出20件,每件赢利50元,根据销售经验:如果每件童装降价4元,那么平均每天就可以多售出4件.则每件童装应降价元时,每天能获得最大利润.24.(2013•鞍山一模)若二次函数y=(a+1)x2+2x+a2﹣1的图象经过原点,则a的值是.25.(2013•大港区一模)已知二次函数y=x2+bx+c中,函数y与自变量x的部分对应值如下则该二次函数的关系式为.26.(2013•黄陂区模拟)已知y=ax2﹣2x+1与x轴没有交点,那么该抛物线的顶点所在的象限是.27.(2013•灌云县模拟)根据下列表格中y=ax2+bx+c的自变量x与函数值y的对应值,判228.(2013•黄冈二模)如图,是y=x2、y=x、y=在同一直角坐标系中图象,请根据图象写出<x<x2时x的取值范围是.29.(2013秋•如皋市期中)已知点A(x1,y1)、B(x2,y2)在二次函数y=﹣(x﹣1)2+1的图象上,若﹣1<x1<0,3<x2<4,则y1y2(填“>”、“<”或“=”).30.(2013秋•工业园区期中)若二次函数y=(m+1)x2+m2﹣9有最小值,且图象经过原点,则m=.。
二次函数图像与性质总结含答案.
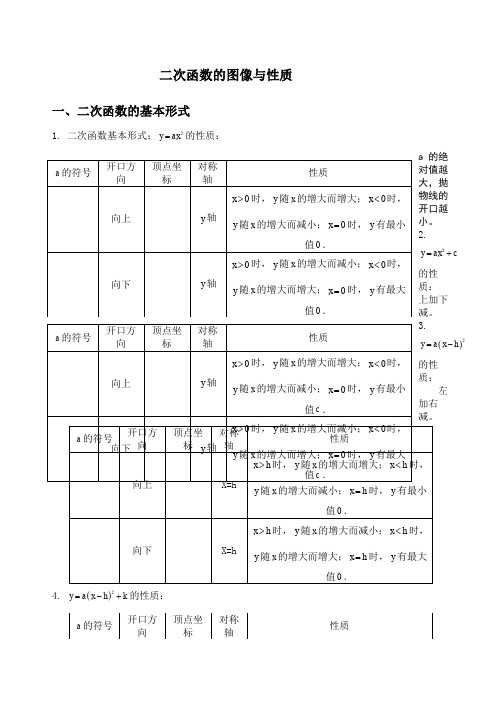
二次函数的图像与性质一、二次函数的基本形式1. 二次函数基本形式:2=的性质:y axa 的绝Array对值越大,抛物线的开口越小。
2.2=+y ax c的性质:上加下减。
()2x h-左4. ()2y a x h k=-+的性质:1. 平移步骤:方法一:⑴ 将抛物线解析式转化成顶点式()2y a x h k =-+,确定其顶点坐标()h k ,; ⑵ 保持抛物线2y ax =的形状不变,将其顶点平移到()h k ,处,具体平移方法如下: 2. 平移规律在原有函数的基础上“h 值正右移,负左移;k 值正上移,负下移”. 概括成八个字“左加右减,上加下减”. 方法二:⑴c bx ax y ++=2沿y 轴平移:向上(下)平移m 个单位,c bx ax y ++=2变成m c bx ax y +++=2(或m c bx ax y -++=2)⑵c bx ax y ++=2沿轴平移:向左(右)平移m 个单位,c bx ax y ++=2变成c m x b m x a y ++++=)()(2(或c m x b m x a y +-+-=)()(2)三、二次函数()2y a x h k =-+与2y ax bx c =++的比较从解析式上看,()2y a x h k =-+与2y ax bx c =++是两种不同的表达形式,后者通过配方可以得到前者,即22424b ac b y a x a a -⎛⎫=++ ⎪⎝⎭,其中2424b ac b h k a a -=-=,. 四、二次函数2y ax bx c =++图象的画法五点绘图法:利用配方法将二次函数2y ax bx c =++化为顶点式2()y a x h k =-+,确定其开口方向、对称轴及顶点坐标,然后在对称轴两侧,左右对称地描点画图.一般我们选取的五点为:顶点、与y 轴的交点()0c ,、以及()0c ,关于对称轴对称的点()2h c ,、与x 轴的交点()10x ,,()20x ,(若与x 轴没有交点,则取两组关于对称轴对称的点).画草图时应抓住以下几点:开口方向,对称轴,顶点,与x 轴的交点,与y 轴的交点.五、二次函数2y ax bx c =++的性质1. 当0a >时,抛物线开口向上,对称轴为2bx a =-,顶点坐标为2424b ac b a a ⎛⎫-- ⎪⎝⎭,. 当2b x a <-时,y 随x 的增大而减小;当2b x a >-时,y 随x 的增大而增大;当2bx a=-时,y 有最小值244ac b a-. 2. 当0a <时,抛物线开口向下,对称轴为2b x a =-,顶点坐标为2424b ac b aa ⎛⎫-- ⎪⎝⎭,.当2bx a <-时,y 随x 的增大而增大;当2b x a >-时,y 随x 的增大而减小;当2bx a=-时,y 有最大值244ac b a-. 六、二次函数解析式的表示方法1. 一般式:2y ax bx c =++(a ,b ,c 为常数,0a ≠);2. 顶点式:2()y a x h k =-+(a ,h ,k 为常数,0a ≠);3. 两根式:12()()y a x x x x =--(0a ≠,1x ,2x 是抛物线与x 轴两交点的横坐标).注意:任何二次函数的解析式都可以化成一般式或顶点式,但并非所有的二次函数都可以写成交点式,只有抛物线与x 轴有交点,即240b ac -≥时,抛物线的解析式才可以用交点式表示.二次函数解析式的这三种形式可以互化. 七、二次函数的图象与各项系数之间的关系 1. 二次项系数a二次函数2y ax bx c =++中,a 作为二次项系数,显然0a ≠.⑴ 当0a >时,抛物线开口向上,a 的值越大,开口越小,反之a 的值越小,开口越大; ⑵ 当0a <时,抛物线开口向下,a 的值越小,开口越小,反之a 的值越大,开口越大.总结起来,a 决定了抛物线开口的大小和方向,a 的正负决定开口方向,a 的大小决定开口的大小.2. 一次项系数b在二次项系数a 确定的前提下,b 决定了抛物线的对称轴. ⑴ 在0a >的前提下,当0b >时,02ba-<,即抛物线的对称轴在y 轴左侧; 当0b =时,02ba-=,即抛物线的对称轴就是y 轴; 当0b <时,02ba->,即抛物线对称轴在y 轴的右侧. ⑵ 在0a <的前提下,结论刚好与上述相反,即 当0b >时,02ba->,即抛物线的对称轴在y 轴右侧; 当0b =时,02ba-=,即抛物线的对称轴就是y 轴;当0b <时,02ba-<,即抛物线对称轴在y 轴的左侧. 总结起来,在a 确定的前提下,b 决定了抛物线对称轴的位置.ab 的符号的判定:对称轴abx 2-=在y 轴左边则0>ab ,在y 轴的右侧则0<ab ,概括的说就是“左同右异” 总结:3. 常数项c⑴ 当0c >时,抛物线与y 轴的交点在x 轴上方,即抛物线与y 轴交点的纵坐标为正; ⑵ 当0c =时,抛物线与y 轴的交点为坐标原点,即抛物线与y 轴交点的纵坐标为0; ⑶ 当0c <时,抛物线与y 轴的交点在x 轴下方,即抛物线与y 轴交点的纵坐标为负. 总结起来,c 决定了抛物线与y 轴交点的位置.总之,只要a b c ,,都确定,那么这条抛物线就是唯一确定的.二次函数解析式的确定:根据已知条件确定二次函数解析式,通常利用待定系数法.用待定系数法求二次函数的解析式必须根据题目的特点,选择适当的形式,才能使解题简便.一般来说,有如下几种情况:1. 已知抛物线上三点的坐标,一般选用一般式;2. 已知抛物线顶点或对称轴或最大(小)值,一般选用顶点式;3. 已知抛物线与x 轴的两个交点的横坐标,一般选用两根式;4. 已知抛物线上纵坐标相同的两点,常选用顶点式.八、二次函数图象的对称二次函数图象的对称一般有五种情况,可以用一般式或顶点式表达 1. 关于x 轴对称2y ax bx c =++关于x 轴对称后,得到的解析式是2y ax bx c =---;()2y a x h k =-+关于x 轴对称后,得到的解析式是()2y a x h k =---;2. 关于y 轴对称2y ax bx c =++关于y 轴对称后,得到的解析式是2y ax bx c =-+;()2y a x h k =-+关于y 轴对称后,得到的解析式是()2y a x h k =++;3. 关于原点对称2y ax bx c =++关于原点对称后,得到的解析式是2y ax bx c =-+-; ()2y a x h k =-+关于原点对称后,得到的解析式是()2y a x h k =-+-; 4. 关于顶点对称(即:抛物线绕顶点旋转180°)2y ax bx c =++关于顶点对称后,得到的解析式是222b y ax bx c a=--+-;()2y a x h k =-+关于顶点对称后,得到的解析式是()2y a x h k =--+.5. 关于点()m n ,对称 ()2y a x h k =-+关于点()m n ,对称后,得到的解析式是()222y a x h m n k =-+-+-根据对称的性质,显然无论作何种对称变换,抛物线的形状一定不会发生变化,因此a 永远不变.求抛物线的对称抛物线的表达式时,可以依据题意或方便运算的原则,选择合适的形式,习惯上是先确定原抛物线(或表达式已知的抛物线)的顶点坐标及开口方向,再确定其对称抛物线的顶点坐标及开口方向,然后再写出其对称抛物线的表达式.二次函数图像参考:十一、【例题精讲】一、一元二次函数的图象的画法【例1】求作函数64212++=x x y 的图象【解】 )128(21642122++=++=x x x x yx 【例2】求作函数342+--=x x y 的图象。
深国交招生考试真题

选择题下列函数中,是二次函数的是()。
A. y = x^2 + 1/xB. y = 3x^2 + 2x - 1C. y = √(x^2 + 1)D. y = (x + 1)^3若关于x的方程ax^2 + bx + c = 0 (a ≠ 0) 的两个根为x1 = 2, x2 = 3,则 b 的值为()。
A. 5B. -5C. 6D. -6钝角三角形的一个锐角为30°,则另一个锐角的取值范围是()。
A. 0° < α < 30°B. 30° < α < 60°C. 60° < α < 90°D. 0° < α < 90°一个扇形的圆心角为120°,半径为3cm,则这个扇形的面积是_______ cm²。
在直角坐标系中,点A(2, -3) 关于x 轴对称的点的坐标是_______。
已知数据x1, x2, ..., xn 的平均数为5,则数据3x1, 3x2, ..., 3xn 的平均数为_______。
填空题方程x^2 - 4x + _______ = 0 的一个根为2,则另一个根为_______。
已知直角三角形的两直角边分别为3 和4,则斜边上的中线长为_______。
函数y = 2x^2 的图象经过点(1, _______)。
若二次函数y = ax^2 + bx + c 的图象经过点(0, 1) 和(1, 0),则c = _______,a + b = _______。
在△ABC 中,△A = 45°,△B = 60°,则△C = _______°。
一个正n 边形的内角和为1080°,则n = _______。
简答题已知方程x^2 - 5x + 6 = 0 的两个根为x1 和x2,求x1^2 + x2^2 的值。
二次函数的图象与性质(三套带答案解析)

二次函数的图象与性质1一、选择题:1.把二次函数y=ax2+bx+c(a>0)的图象作关于x轴的对称变换,所得图象的解析式为y=﹣a(x﹣1)2+4a,若(m﹣1)a+b+c≤0,则m的最大值是()A. ﹣4B. 0C. 2D. 62.如图,二次函数y=ax2+bx+c(a≠0)的图象的对称轴是直线x=1,则以下四个结论中:① abc>0,② 2a+b=0,③ 4a+b2<4ac,④ 3a+c<0.正确的个数是()A. 1B. 2C. 3D. 43.已知二次函数y=−x2+2x+4,则下列关于这个函数图象和性质的说法,正确的是()A. 图象的开口向上B. 图象的顶点坐标是(1,3)C. 当x<1时,y随x的增大而增大D. 图象与x轴有唯一交点4.如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A,B两点,与y轴交于点C,点A坐标为(−1,0),点C在(0,2)与(0,3)之间(不包括这两点),抛物线的顶点为D,对称轴为直线x=2,有以下结论:① abc>0;②若点M(−12,y1),点N(72,y2)是函数图象上的两点,则y1<y2;③ −35<a<−25;④ ΔADB可以是等腰直角三形.其中正确的有()A. 1个B. 2个C. 3个D. 4个5.点P(m,n)在以y轴为对称轴的二次函数y=x2+ax+4的图象上.则m﹣n的最大值等于()A. 154B. 4 C. ﹣154D. ﹣1746.已知二次函数y=x2−2ax+a2−2a−4(a为常数)的图象与x轴有交点,且当x>3时,y随x的增大而增大,则a的取值范围是()A. a≥−2B. a<3C. −2≤a<3D. −2≤a≤3二、填空题7.抛物线y=(k−1)x2−x+1与x轴有交点,则k的取值范围是________.8.二次函数y=ax2+bx+c的图象如图所示,下列结论:①ab>0;②a+b﹣1=0;③a>1;④关于x.其中正确结论的序号是________.的一元二次方程ax2+bx+c=0的一个根为1,另一个根为﹣1a9.下表中y与x的数据满足我们初中学过的某种函数关系,其函数表达式为________.10.如果将抛物线y=x2向上平移3个单位,那么所得新抛物线的表达式是________.11.将抛物线y=(x-1)2-5关于y轴对称,再向右平移3个单位长度后顶点的坐标是________.三、解答题12.二次函数y=ax2+bx+c(a≠0)的图象过点A(﹣1,8)、B(2,﹣1),与y轴交于点C(0,3),求二次函数的表达式.13.已知二次函数y=ax2−2ax−3a的图象与x轴交于A、B两点,且经过C(1,-2),求点A、B的坐标和a的值.14.已知二次函数的顶点坐标为(2,−2),且其图象经过点(1,−1),求此二次函数的解析式.15.如图,抛物线y=-x2+bx+c与x轴负半轴交于点A,正半轴交于点B,OA=2OB=4.求抛物线的顶点坐标。
二次函数图像及性质总结包括答案.doc

二次函数的图像与性质一、二次函数的基本形式1.二次函数基本形式:y ax2的性质:a 的符号开口方向顶点坐标对称轴性质0 ,0 x 0 时, y 随x的增大而增大; x0时, y随a 0 向上y 轴x 0 时, y 有最小值 0 .x 的增大而减小;0 ,0 x 0 时, y 随x的增大而减小; x0时, y随a 0 向下y 轴x 0 时, y 有最大值 0 .x 的增大而增大;a的绝对值越大,抛物线的开口越小。
2.y ax2 c 的性质:上加下减。
a 的符号开口方向顶点坐标对称轴性质0 ,c x 0 时, y 随x的增大而增大; x0时, y随a 0 向上y 轴x 0 时, y 有最小值c.x 的增大而减小;0 ,c x 0 时, y 随x的增大而减小; x0时, y随a 0 向下y 轴x 0 时, y 有最大值c.x 的增大而增大;3. y a x h 2的性质:左加右减。
a 的符号开口方向顶点坐标对称轴性质h ,0 x h 时, y 随x的增大而增大;x h 时, ya 0 向上X=hx h 时, y 有最小值 0 .随 x 的增大而减小;h ,0 x h 时, y 随x的增大而减小;x h 时, ya 0 向下X=hx h 时, y 有最大值 0 .随 x 的增大而增大;4. y a x h 2k 的性质:a 的符号开口方向顶点坐标对称轴性质h ,k x h 时, y 随x的增大而增大;x h 时, ya 0 向上X=hx h 时, y 有最小值 k .随 x 的增大而减小;h ,k x h 时, y 随x的增大而减小; x h 时, ya 0 向下X=hx h 时, y 有最大值 k .随 x 的增大而增大;二、二次函数图象的平移1.平移步骤:方法一:⑴ 将抛物线解析式转化成顶点式y a2h ,k ;x hk ,确定其顶点坐标⑵保持抛物线 y ax2的形状不变,将其顶点平移到h ,k 处,具体平移方法如下:向上 (k>0)【或向下 (k<0)】平移 |k |个单位y=ax 2+ky=ax2向右 (h>0)【或左 ( h<0)】向右 (h>0) 【或左 (h<0) 】向右 (h>0)【或左 (h<0)】平移 |k|个单位平移 |k|个单位平移 |k|个单位向上 (k>0) 【或下 (k<0) 】平移 |k|个单位y=a(x-h)2|k|个单位y=a(x-h)2+k向上 (k>0) 【或下 (k<0)】平移2.平移规律在原有函数的基础上“h 值正右移,负左移;k 值正上移,负下移”.概括成八个字“左加右减,上加下减”.方法二:⑴ y ax2 bx c 沿y轴平移:向上(下)平移 m 个单位, y ax 2 bx c 变成y ax 2 bx c m (或 y ax 2 bx c m )⑵ y ax2 bx c 沿轴平移:向左(右)平移m 个单位, y ax 2 bx c 变成y a( x m) 2 b( x m) c (或 y a(x m) 2 b( x m) c )三、二次函数 y a x h 2 k 与 y ax2 bx c 的比较从解析式上看,y a x2k 与 y ax2 bx c是两种不同的表达形式,后者通过配h2b2b,k2方可以得到前者,即y a x b 4ac ,其中 h 4ac b .2a 4a 2a 4a 四、二次函数 y ax2 bx c 图象的画法五点绘图法:利用配方法将二次函数y ax 2bx c 化为顶点式 y a (x h)2 ,k 确定其开口方向、对称轴及顶点坐标,然后在对称轴两侧,左右对称地描点画图. 一般我们选取的五点为:顶点、与 y 轴的交点0 ,c 、以及0 ,c 关于对称轴对称的点2h ,c 、与 x 轴的交点x1,0 ,x2,0 (若与 x 轴没有交点,则取两组关于对称轴对称的点).画草图时应抓住以下几点:开口方向,对称轴,顶点,与x 轴的交点,与y 轴的交点.五、二次函数y ax2bx c 的性质1. 当 a 0 时,抛物线开口向上,对称轴为x b ,顶点坐标为 b ,4ac b 2 .2a 2a 4a当 x b时, y 随x的增大而减小;当x b 时, y 随x的增大而增大;当x b 2a 2a 2a 2时, y 有最小值4ac b.4a2. 当 a 0 时,抛物线开口向下,对称轴为x b ,顶点坐标为 b ,4ac b 2 .当2a 2a 4ax b时, y 随x的增大而增大;当xb时, y 随x的增大而减小;当x b 时, y 2a 2a 2a 2有最大值4ac b.4a六、二次函数解析式的表示方法1. 一般式:y ax2 bx c ( a ,b, c 为常数,a 0 );2. 顶点式:y a( x h) 2 k ( a ,h,k为常数,a 0 );3. 两根式:y a( x x1 )( x x2 ) (a 0, x1, x2是抛物线与 x 轴两交点的横坐标) .注意:任何二次函数的解析式都可以化成一般式或顶点式,但并非所有的二次函数都可以写成交点式,只有抛物线与x 轴有交点,即 b 2 4 ac0 时,抛物线的解析式才可以用交点式表示.二次函数解析式的这三种形式可以互化.七、二次函数的图象与各项系数之间的关系1.二次项系数 a二次函数y ax2 bx c 中, a 作为二次项系数,显然 a 0 .⑴当 a 0 时,抛物线开口向上, a 的值越大,开口越小,反之 a 的值越小,开口越大;⑵当 a 0 时,抛物线开口向下, a 的值越小,开口越小,反之 a 的值越大,开口越大.总结起来, a 决定了抛物线开口的大小和方向, a 的正负决定开口方向, a 的大小决定开口的大小.2.一次项系数 b在二次项系数 a 确定的前提下,b决定了抛物线的对称轴.⑴在 a 0 的前提下,当 b 0 时,b0 ,即抛物线的对称轴在y 轴左侧;2a当 b 0 时,b0 ,即抛物线的对称轴就是y 轴;2a当 b 0 时,b0 ,即抛物线对称轴在y 轴的右侧.2a⑵在 a 0 的前提下,结论刚好与上述相反,即当 b 0 时,b0 ,即抛物线的对称轴在y 轴右侧;2a当 b 0 时,b0 ,即抛物线的对称轴就是y 轴;2a当 b 0 时,b0 ,即抛物线对称轴在 y 轴的左侧.2a总结起来,在 a 确定的前提下, b 决定了抛物线对称轴的位置.ab 的符号的判定:对称轴xb0 ,在 y 轴左边则 ab 0 ,在 y 轴的右侧则 ab2a概括的说就是“左同右异”总结:3.常数项 c⑴当 c 0 时,抛物线与y 轴的交点在x轴上方,即抛物线与y 轴交点的纵坐标为正;⑵当 c 0 时,抛物线与y 轴的交点为坐标原点,即抛物线与y 轴交点的纵坐标为 0 ;⑶当 c 0 时,抛物线与y 轴的交点在x轴下方,即抛物线与y 轴交点的纵坐标为负.总结起来, c 决定了抛物线与y 轴交点的位置.总之,只要 a ,b ,c 都确定,那么这条抛物线就是唯一确定的.二次函数解析式的确定:根据已知条件确定二次函数解析式,通常利用待定系数法.用待定系数法求二次函数的解析式必须根据题目的特点,选择适当的形式,才能使解题简便.一般来说,有如下几种情况:1.已知抛物线上三点的坐标,一般选用一般式;2.已知抛物线顶点或对称轴或最大(小)值,一般选用顶点式;3.已知抛物线与 x 轴的两个交点的横坐标,一般选用两根式;4.已知抛物线上纵坐标相同的两点,常选用顶点式.八、二次函数图象的对称二次函数图象的对称一般有五种情况,可以用一般式或顶点式表达1.关于 x 轴对称y ax 2 bx c 关于 x 轴对称后,得到的解析式是y ax2 bx c ;y a x h 2y a x h2 k 关于 x 轴对称后,得到的解析式是k ;2.关于 y 轴对称y ax 2 bx c 关于y轴对称后,得到的解析式是y ax2 bx c ;y a x h 2y a x h2 k 关于y轴对称后,得到的解析式是k ;3.关于原点对称y ax2 bx c 关于原点对称后,得到的解析式是y ax2 bx c;y a x2k 关于原点对称后,得到的解析式是y a x h2k ;h4. 关于顶点对称(即:抛物线绕顶点旋转180°)2 y ax2 bx c 关于顶点对称后,得到的解析式是y ax 2 bx c b ;2ay a x2k 关于顶点对称后,得到的解析式是y a x h2k .h5. 关于点m,n 对称y a x2k 关于点 m,n 对称后,得到的解析式是y a x22n k h h 2m根据对称的性质,显然无论作何种对称变换,抛物线的形状一定不会发生变化,因此 a 永远不变.求抛物线的对称抛物线的表达式时,可以依据题意或方便运算的原则,选择合适的形式,习惯上是先确定原抛物线(或表达式已知的抛物线)的顶点坐标及开口方向,再确定其对称抛物线的顶点坐标及开口方向,然后再写出其对称抛物线的表达式.y=2x 2二次函数图像参考:y=3(x+4)2y=3x2y=x 2y=3(x-2)2x2 y=2y=2x 2y=2(x-4) 2十一、y=2(x-4) 2-3y=2 x 2+2y=2 x 2y=2 x 2-4x 2 y= -2y= -x 2y=-2(x+3)2【 例精y=-2x 2y=-2(x-3)2y=-2x 2】一、一元二次函数的 象的画法【例 1】求作函数 y1 x2 4x 6 的 象1 x 22 1( x 2【解】 y4x 68x 12)221[( x24) 2- 4]1( x 24) 2 - 222以 x4 中 ,取 x 的一些 ,列表如下:x⋯-7 -6 -5-4 -3-2 -1 ⋯y 5 03 -23 5 ⋯⋯222 02【例 2】求作函数 y x 24x 3 的 象。
2019年深国交G1入学考试复习专题:二次函数的最值(试题版)

2019年深国交G1入学考试复习专题:二次函数的最值一.选择题(共15小题)22或C或或2.已知二次函数的图象y=ax2+bx+c(0≤x≤3)如图.关于该函数在所给自变量取值范围内,下列说法正确的是()22﹣D﹣22225.二次函数y=﹣x2+6x﹣7,当x取值为t≤x≤t+2时,y最大值=﹣(t﹣3)2+2,则t的取值范27.如图,已知点A(4,0),O为坐标原点,P是线段OA上任意一点(不含端点O,A),过P、O两点的二次函数y1和过P、A两点的二次函数y2的图象开口均向下,它们的顶点分别为B、C,射线OB与AC相交于点D.当OD=AD=3时,这两个二次函数的最大值之和等于()C210.小聪、小明、小伶、小俐四人共同探究代数式2x2﹣4x+6的值的情况.他们作了如下分工:小聪负责找值为0时x的值,小明负责找值为4时x的值,小伶负责找最小值,小俐负11.y=x2+(1﹣a)x+1是关于x的二次函数,当x的取值范围是1≤x≤3时,y在x=1时取22222C15.正实数x,y满足xy=1,那么的最小值为()C二.填空题(共8小题)16.二次函数y=x2+2ax+a在﹣1≤x≤2上有最小值﹣4,则a的值为.17.已知实数x、y满足x2﹣2x+4y=5,则x+2y的最大值为.18.若的最大值为a,最小值为b,则a2+b2的值为.19.正方形ABCD的边长为4,M、N分别是BC、CD上的两个动点,且始终保持AM⊥MN.当BM=时,四边形ABCN的面积最大.20.如图,已知A,B两点的坐标分别为(2,0),(0,2),⊙C的圆心坐标为(﹣1,0),半径为1.若D是⊙C上的一个动点,线段DA与y轴交于点E,则△ABE面积的最小值是.21.若二次函数y=x2+2x﹣3(0≤x≤3)的最小值为,最大值为.22.函数y=﹣+的最大值为.23.已知二次函数y=(x﹣1)2+(x﹣3)2,当x=时,函数达到最小值.。
二次函数及函数的性质及答案

二次函数及函数的性质及答案一、选择题(每小题6分,共36分)1.关于函数y =-3x 的单调性的叙述正确的是( )(A)在(-∞,0)上是递增的,在(0,+∞)上是递减的 (B)在(-∞,0)∪(0,+∞)上递增 (C)在[0,+∞)上递增 (D)在(-∞,0)和(0,+∞)上都是递增的2.(2012·厦门模拟)函数f(x)=2x 2-mx +2当x∈[-2,+∞)时是增函数,则m 的取值范围是( )(A)(-∞,+∞) (B)[8,+∞) (C)(-∞,-8] (D)(-∞,8] 3.若函数f(x)=log a (x +1)(a>0,a≠1)的定义域和值域都是[0,1],则a 等 于( )(A)13 (B) 2 (C)22(D)2 4.函数f(x)=ln(4+3x -x 2)的单调递减区间是( )(A)(-∞,32] (B)[32,+∞) (C)(-1,32] (D)[32,4)5.(2012·杭州模拟)定义在R 上的函数f(x)在区间(-∞,2)上是增函数,且f(x +2)的图象关于x =0对称,则( )(A)f(-1)<f(3) (B)f(0)>f(3) (C)f(-1)=f(3) (D)f(0)=f(3)6.定义在R 上的函数f(x)满足f(x +y)=f(x)+f(y),当x<0时,f(x)>0,则函数f(x)在[a ,b]上有( )(A)最小值f(a) (B)最大值f(b) (C)最小值f(b) (D)最大值f(a +b2)二、填空题(每小题6分,共18分)7.如果二次函数f(x)=x 2-(a -1)x +5在区间(12,1)上是增函数,那么f(2)的取值范围是 .8.(预测题)已知定义在R 上的奇函数f(x),满足f(x -4)=-f(x),且在区间[0,2]上是增函数,若方程f(x)=m(m>0)在区间[-8,8]上有四个不同的根x 1,x 2,x 3,x 4,则x 1+x 2+x 3+x 4= .9.(2012·深圳模拟)f(x)=⎩⎪⎨⎪⎧a x (x<0)(a -3)x +4a (x≥0)满足对任意x 1≠x 2,都有f(x 1)-f(x 2)x 1-x 2<0成立,则a 的取值范围是 . 三、解答题(每小题15分,共30分) 10.(2012·青岛模拟)已知函数f(x)=|x|x +2,(1)判断函数f(x)在区间(0,+∞)上的单调性并加以证明; (2)求函数f(x)的值域.11.(易错题)函数f(x)=x 2+x -14.(1)若定义域为[0,3],求f(x)的值域;(2)若f(x)的值域为[-12,116],且定义域为[a ,b],求b -a 的最大值.【探究创新】(16分)定义:已知函数f(x)在[m ,n](m<n)上的最小值为t ,若t≤m 恒成立,则称函数f(x)在[m ,n](m<n)上具有“DK”性质.(1)判断函数f(x)=x 2-2x +2在[1,2]上是否具有“DK”性质,说明理由. (2)若f(x)=x 2-ax +2在[a ,a +1]上具有“DK”性质,求a 的取值范围. 一、选择题(每小题6分,共36分)1.(2012·揭阳模拟)若关于x 的方程2x 2-3x +m =0的两根满足x 1∈(-2,-1),x 2∈(2,3),则m 的取值范围是( )(A)(-∞,98) (B)(-9,-5) (C)(-14,98) (D)(-14,-2)2.如果函数f(x)=x 2+bx +c 对任意实数t 都有f(2+t)=f(2-t),那么( ) (A)f(2)<f(1)<f(4) (B)f(1)<f(2)<f(4) (C)f(2)<f(4)<f(1) (D)f(4)<f(2)<f(1)3.(预测题)设二次函数f(x)=ax 2+bx +c ,如果f(x 1)=f(x 2)( x 1≠x 2),则f(x 1+x 2)等于( )(A)-b 2a (B)-b a (C)c (D)4ac -b24a4.(2012·韶关模拟)若f(x)=x 2-x +a ,f(-m)<0,则f(m +1)的值为( ) (A)正数 (B)负数 (C)非负数 (D)与m 有关5.函数f(x)=ax 2+(a -3)x +1在区间[-1,+∞)上是递减的,则实数a 的取值范围是( )(A)[-3,0) (B)(-∞,-3] (C)[-2,0] (D)[-3,0]6.若不等式x 2+ax +1≥0对于一切x∈(0,12]恒成立,则a 的最小值是( )(A)0 (B)2 (C)-52 (D)-3二、填空题(每小题6分,共18分)7.(2011·南京模拟)已知函数f(x)=4x 2+kx -8在[-1,2]上具有单调性,则实数k 的取值范围是 .8.若函数f(x)=(x +a)(bx +2a)(a 、b∈R)是偶函数,且它的值域为(-∞,4],则该函数的解析式f(x)= .9.(2012·泉州模拟)若函数y =x 2-3x -4的定义域为[0,m],值域为[-254,-4],则m 的取值范围为 . 三、解答题(每小题15分,共30分)10.(易错题)设f(x)为定义在R 上的偶函数,当x≤-1时,y =f(x)的图象是经过点(-2,0),斜率为1的射线,又在y =f(x)的图象中的一部分是顶点在(0,2),且过点(-1,1)的一段抛物线,试写出函数f(x)的表达式,并作出其图象. 11.(2012·揭阳模拟)已知:函数f(x)=ax 2-2x +1.(1)若13≤a≤1,且f(x)在[1,3]上的最大值为M(a),最小值为N(a),令g(a)=M(a)-N(a),求g(a)的表达式;(2)在(1)的条件下,求证:g(a)≥12.【探究创新】(16分)已知直线AB 过x 轴上一点A(2,0)且与抛物线y =ax 2相交于B(1,-1)、C 两点. (1)求直线和抛物线对应的函数解析式.(2)问抛物线上是否存在一点D ,使S △OAD =S △OBC ?若存在,请求出D 点坐标,若不存在,请说明理由.答案解析1. 【解析】选D.由于函数y =1x 在(-≦,0)和(0,+≦)上是递减的,且-3<0,因此函数y =-3x 在(-≦,0)和(0,+≦)上都是递增的,这里特别注意两区间之间只能用“和”或“,”,一定不能用“∪”.2.【解析】选C.由已知得m4≤-2,解得:m ≤-8.3.【解析】选D.当0<a<1时,f(x)在[0,1]上为减函数,则其值域不可能为[0,1];当a>1时,f(x)在[0,1]上为增函数,由已知有⎩⎪⎨⎪⎧log a 1=0log a 2=1,得a =2,综上知a =2.4.【解题指南】本题为求复合函数单调区间问题,需先求定义域,再在定义域内判断t =4+3x -x 2的单调性,从而根据“同增异减”求解.【解析】选D.要使函数有意义需4+3x -x 2>0, 解得-1<x<4, ≨定义域为(-1,4). 令t =4+3x -x 2=-(x -32)2+254.则t 在(-1,32]上递增,在[32,4)上递减, 又y =lnt 在(0,254]上递增,≨f(x)=ln(4+3x -x 2)的单调递减区间为[32,4).5.【解析】选A.因为f(x +2)的图象关于x =0对称,所以f(x)的图象关于x =2对称,又f(x)在区间(-≦,2)上是增函数,则其在(2,+≦)上为减函数,作出其图象大致形状如图所示.由图象知,f(-1)<f(3),故选A. 6.【解析】选C.设x 1<x 2,由已知得f(x 1)=f[(x 1-x 2)+x 2]=f(x 1-x 2)+f(x 2).又x 1-x 2<0,≨f(x 1-x 2)>0.≨f(x 1)> f(x 2). 即f(x)在R 上为减函数. ≨f(x)在[a ,b]上亦为减函数.≨f(x)min =f(b) f(x)max =f(a),故选C.7.【解析】f(x)=x 2-(a -1)x +5在(a -12,+≦)上递增,由已知条件得a -12≤12,则a ≤2,f(2)=11-2a ≥7.答案:[7,+≦)8.【解析】≧f(x)是奇函数, ≨f(x -4)=-f(x)=f(-x),≨f(x)=f(-x -4), ≨f(x)的图象关于x =-2对称. 又f(x)在区间[0,2]上是增函数,≨f(x)在区间[-2,0]上是增函数.又f(x)=m(m>0)在区间 [-8,8]上有四个不同的根x 1,x 2,x 3,x 4,则数形结合知≨x 1+x 2+x 3+x 4=-8.答案:-89.【解析】由已知x 1≠x 2,都有f(x 1)-f(x 2)x 1-x 2<0,知f(x)在R 上为减函数,则需⎩⎪⎨⎪⎧0<a<1a 0≥(a -3)·0+4a a -3<0,解得0<a ≤14.答案:(0,14]10.【解析】(1)当x>0时,f(x)=|x|x +2=x +2-2x +2=1-2x +2.设0<x 1<x 2,f(x 1)-f(x 2)=(1-2x 1+2)-(1-2x 2+2)=2(x 1-x 2)(x 1+2)(x 2+2),由0<x 1<x 2可得f(x 1)-f(x 2)<0,即f(x 1)<f(x 2),因此f(x)在(0,+≦)上递增. (2)f(x)=⎩⎪⎨⎪⎧1-2x +2 x ≥0-1+2x +2 x<0且x ≠-2.可以证明f(x)在(-≦,-2)上递减,且f(x)在(-2,0)上递减,由反比例函数y =2x 通过平移、对称变换得 f(x)的图象如图所示,因此f(x)的值域为:(-≦,-1)∪[0,+≦). 11.【解析】≧f(x)=(x +12)2-12,≨对称轴为x =-12. (1)≧3≥x ≥0>-12,≨f(x)的值域为[f(0),f(3)],即[-14,474];(2)≧x =-12时,f(x)=-12是f(x)的最小值, ≨x =-12∈[a ,b],令x 2+x -14=116,得x 1=-54,x 2=14,根据f(x)的图象知b -a 的最大值是14-(-54)=32.【探究创新】 【解析】(1)≧f(x)=x 2-2x +2,x ∈[1,2], ≨f(x)min =1≤1, ≨函数f(x)在[1,2]上具有“DK ”性质.(2)f(x)=x 2-ax +2,x ∈[a ,a +1],其对称轴为x =a 2.①当a 2≤a ,即a ≥0时,函数f(x)min =f(a)=a 2-a 2+2=2.若函数f(x)具有“DK ”性质,则有2≤a 总成立,即a ≥2. ②当a<a2<a +1,即-2<a<0时,f(x)min =f (a 2)=-a24+2.若函数f(x)具有“DK ”性质,则有-a24+2≤a 总成立,解得a ∈∅.③当a2≥a +1,即a ≤-2时,函数f(x)的最小值为f(a +1)=a +3.若函数f(x)具有“DK ”性质,则有a +3≤a ,解得a ∈∅.综上所述,若f(x)在[a ,a +1]上具有“DK ”性质,则a 的取值范围为[2,+≦).答案解析1.【解析】选B.构造二次函数f(x)=2x 2-3x +m ,由二次函数f(x)的图象得:⎩⎪⎨⎪⎧f(-2)·f(-1)<0f(2)·f(3)<0得-9<m <-5.2.【解析】选A.依题意,函数f(x)=x 2+bx +c 的对称轴方程为x =2,且f(x)在[2,+≦)上为增函数,因为f(1)=f(2-1)=f(2+1)=f(3),2<3<4, ≨f(2)<f(3)<f(4),即f(2)<f(1)<f(4).3.【解析】选C.≧f(x 1)=f(x 2)(x 1≠x 2), ≨x 1+x 22=-b2a ,即x 1+x 2=-b a ,≨f(x 1+x 2)=f(-b a )=a(-b a )2+b ·(-ba )+c =c.4. 【解析】选B.由f(x)=x 2-x +a 的图象知f(x)=x 2-x +a 的图象关于x =12对称,设x 2-x +a =0的两根为x 1,x 2,且x 1<x 2,则f(-m)<0的解为x 1<-m<x 2,1-x 2<1+m<1-x 1,而x 1+x 2=1, ≨1-x 1=x 2,1-x 2=x 1,≨x 1<1+m<x 2,故f(1+m)<0,故选B. 5.【解析】选D.当a =0时,f (x)=-3x +1显然成立, 当a ≠0时,需⎩⎪⎨⎪⎧a <0-a -32a≤-1,解得-3≤a <0,综上可得-3≤a ≤0.6.【解析】选C.方法一:设g(a)=ax +x 2+1, ≧x ∈(0,12],≨g(a)为单调递增函数.当x =12时满足:12a +14+1≥0即可,解得a ≥-52.方法二:由x 2+ax +1≥0得a ≥-(x +1x )在(0,12]上恒成立,令g(x)=-(x +1x ),则知g(x)在(0,12]为增函数,≨g(x)max =g(12)=-52,≨a ≥-52.7.【解析】函数f(x)=4x 2+kx -8的对称轴为x =-k 8, 依题意有:-k 8≤-1或-k 8≥2,解得k ≥8或k ≤-16. 答案:k ≥8或k ≤-168.【解析】≧f(x)=(x +a)(bx +2a)=bx 2+(2a +ab)x +2a 2是偶函数,则其图象关于y 轴对称, ≨2a +ab =0,≨b =-2或a =0(舍去).又≧f(x)=-2x 2+2a 2且值域为(-≦,4], ≨2a 2=4,f(x)=-2x 2+4. 答案:-2x 2+4 9.【解析】y =x 2-3x -4=(x -32)2-254, 对称轴为x =32,当x =32时,y =-254,≨m ≥32,而当x =3时,y =-4,≨m ≤3. 综上:32≤m ≤3. 答案:32≤m ≤310.【解析】当x ≤-1时,设f(x)=x +b ,则由0=-2+b ,即b =2,得f(x)=x +2; 当-1<x <1时,设f(x)=ax 2+2,则由1=a(-1)2+2,即a =-1,得f(x)=-x 2+2; 当x ≥1时,f(x)=-x +2. 故f(x)=⎩⎪⎨⎪⎧x +2,x ≤-12-x 2,-1<x <1-x +2,x ≥1,其图象如图.11.【解析】(1)≧f(x)=a(x -1a )2+1-1a , 由13≤a ≤1得1≤1a ≤3,≨N(a)=f(1a )=1-1a .当1≤1a <2,即12<a ≤1时, M(a)=f(3)=9a -5,故g(a)=9a +1a -6,当2≤1a ≤3,即13≤a ≤12时, M(a)=f(1)=a -1,故g(a)=a +1a-2.≨g(a)=111a 2a []a 32119a 6a (,1]a 2⎧∈⎪⎪⎨⎪∈⎪⎩+-,,+-,(2)≧当a ∈11[]32,时,g ′(a)=1-21a <0,,≨函数g(a)在11[]32,上为减函数;当a ∈(12,1]时,g ′(a)=9-21a>0,,≨函数g(a)在(12,1]上为增函数, ≨当a =12时,g(a)取最小值,g(a)min =g(12)=12,故g(a)≥12.【探究创新】【解析】(1)设直线对应的函数解析式为y =kx +b ,由题知,直线过点A(2,0),B(1,-1), ≨2k b 0k b 1⎧⎨⎩+=+=-,解得k =1,b =-2. ≨直线的解析式为y =x -2,又抛物线y =ax 2过点B(1,-1),≨a =-1. ≨抛物线的解析式为y =-x 2. (2)直线与抛物线相交于B 、C 两点,故由方程组2y x 2y x⎧⎨⎩=-=-,解得B 、C 两点坐标为B(1,-1),C(-2,-4).由图象可知,S △OBC =S △OAC -S△OAB=12×|-4|×2-12×|-1|×2=3.假设抛物线上存在一点D ,使S △OAD =S △OBC ,可设D(t ,-t 2),≨S △OAD =12×2×t 2=t 2,,≨t 2=3,≨t或t即存在这样的点-3)或(3).。
二次函数的基本性质及习题.docx

二次函数的基木性质1二次函数即为形式为y=ax2+bx+c(a#:O),因为若a=0,且bH0时, 函数变为一次函数,若a二0,且b二0时,函数则变为常函数。
因此判断函数是否为二次函数,只需判断二次项系数不为0即可。
例]:若函数y二(5a2+3a-2) x2+ (a2-l) x+6 a-2 为二次函数,贝Ua 满足什么条件?解::•函数为二次丙数,则5a2+3a-2^0,(这里解方程需要用到二次函数求根公式),aH芈壬,即3工-3±号丁4空,得aHj或2/5。
2a2-5(引申:若函数为一次函数,则需要满足5a2+3a-2=0, a2-1^0, 解得a=2/5)2上面提到了求根公式,若二次函数为y=ax2+bx+c(a7^0), Va7^0, 就注定a只能有两种符号1)其中a>0时,二次函数开口向上2)aVO时,二次函数开口向下但不论a的符号如何,△二沪一4ac,即当厶〉。
吋,方程有两个不相等的实根,即图像与x轴有两个不同的交点;(方程有两个解)△二0时,方程有两个相等的实根,即图像与x轴有一个交点;(方程有一个解)△ V0时,方程没有实根,即图像与x轴无交点;(方程无解)二次函数乂叫抛物线(顾名思义是弧状图形),如下图所示,此函数y=x2-4x-5, 二次项系数为1,则开口向上,△二沪—4ac二「4)2—4 • 1 •(・5)二36 >0,故与x轴有两个交点,可以求得两根为丄5画出即可,其中图像与y轴的交点为常数项c的值(令x=0,代入方程,得y二c)当然,上述方程可以用到十字相乘法,所谓十字相乘就是在脑袋里把二次函数想成两个式了相乘,并且常数项相乘等于・5(此时想到1或J -5) 又一次项系数相加为・4(即-5+1)所以可以列成这种形式(x-5) <x+l), 与x轴交点即y二0,得-x=-l或5。
例2若二次函数为y=-x2+x+6,图像与x轴的两个交点坐标是什么?可以先变成-(X2-X-6),BP-(X-3)(X+2),故与x轴两个交点分别为(3,0),(・乙0)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二次函数的性质01
(选择题)
一.选择题(共30小题)
1.(2015•益阳)若抛物线y=(x﹣m)2+(m+1)的顶点在第一象限,则m的取值范围为()
A.m>1 B.m>0 C.m>﹣1 D.﹣1<m<0
2.(2015•常州)已知二次函数y=x2+(m﹣1)x+1,当x>1时,y随x的增大而增大,而m的取值范围是()
A.m=﹣1 B.m=3 C.m≤﹣1 D.m≥﹣1
3.(2015•南昌)已知抛物线y=ax2+bx+c(a>0)过(﹣2,0),(2,3)两点,那么抛物线的对称轴()
A.只能是x=﹣1
B.可能是y轴
C.可能在y轴右侧且在直线x=2的左侧
D.可能在y轴左侧且在直线x=﹣2的右侧
4.(2015•梅州)对于二次函数y=﹣x2+2x.有下列四个结论:①它的对称轴是直线x=1;
②设y1=﹣x12+2x1,y2=﹣x22+2x2,则当x2>x1时,有y2>y1;③它的图象与x轴的两个交点是(0,0)和(2,0);④当0<x<2时,y>0.其中正确的结论的个数为()A.1 B.2 C.3 D.4
5.(2015•甘孜州)二次函数y=x2+4x﹣5的图象的对称轴为()
A.x=4 B.x=﹣4 C.x=2 D.x=﹣2
6.(2015•新疆)抛物线y=(x﹣1)2+2的顶点坐标是()
A.(﹣1,2)B.(﹣1,﹣2)C.(1,﹣2)D.(1,2)
7.(2016•重庆模拟)在平面直角坐标系中,已知抛物线与直线的图象如图所示,当y1≠y2时,取y1,y2中的较大值记为N;当y1=y2时,N=y1=y2.则下列说法:①当0<x<2时,N=y1;②N随x的增大而增大的取值范围是x<0;③取y1,y2中的较小值记为M,则使得M大于4的x值不存在;④若N=2,则x=2﹣或x=1.其中正确的有()
A.1个B.2个C.3个D.4个
8.(2015•台州)设二次函数y=(x﹣3)2﹣4图象的对称轴为直线l,若点M在直线l上,则点M的坐标可能是()
A.(1,0)B.(3,0)C.(﹣3,0)D.(0,﹣4)
9.(2015•贵阳)已知二次函数y=﹣x2+2x+3,当x≥2时,y的取值范围是()
A.y≥3 B.y≤3 C.y>3 D.y<3
10.(2015•福州)已知一个函数图象经过(1,﹣4),(2,﹣2)两点,在自变量x的某个取值范围内,都有函数值y随x的增大而减小,则符合上述条件的函数可能是()A.正比例函数B.一次函数 C.反比例函数D.二次函数
11.(2015•玉林)如图,反比例函数y=的图象经过二次函数y=ax2+bx图象的顶点(﹣,m)(m>0),则有()
A.a=b+2k B.a=b﹣2k C.k<b<0 D.a<k<0
12.(2015•南开区二模)二次函数y=x2﹣x+m(m为常数)的图象如图所示,当x=a时,y <0;那么当x=a﹣1时,函数值()
A.y<0 B.0<y<m C.y>m D.y=m
13.(2015•深圳模拟)若(2,5)、(4,5)是抛物线y=ax2+bx+c上的两个点,则它的对称轴是()
A.x=﹣B.x=1 C.x=2 D.x=3
14.(2015•潍坊模拟)若函数y=的自变量x的取值范围是全体实数,则c的取
值范围是()
A.c<1 B.c=1 C.c>1 D.c≤1
15.(2015•巴中模拟)抛物线y=x2﹣8x+m的顶点在x轴上,则m等于()
A.﹣16 B.﹣4 C.8 D.16
16.(2015•大庆模拟)若点A(2,y1),B(﹣3,y2),C(﹣1,y3)三点在抛物线y=x2﹣4x﹣m的图象上,则y1、y2、y3的大小关系是()
A.y1>y2>y3B.y2>y1>y3C.y2>y3>y1D.y3>y1>y2
2
时,y随x的增大而增大;⑤方程ax2+bx+c=0有两个不相等的实数根.其中正确的是()A.①②③ B.①③⑤ C.①③④ D.①④⑤
18.(2015•巴中模拟)若直线y=ax+b(a≠0)在第二、四象限都无图象,则抛物线y=ax2+bx+c ()
A.开口向上,对称轴是y轴B.开口向下,对称轴平行于y轴
C.开口向上,对称轴平行于y轴D.开口向下,对称轴是y轴
19.(2015•鄄城县三模)关于二次函数y=3x2﹣kx+k﹣3,以下结论:
①抛物线交x轴有两个不同的交点;
②不论k取何值,抛物线总是经过一个定点;
③设抛物线交x轴于A、B两点,若AB=1,则k=9;
④抛物线的顶点在y=﹣3(x﹣1)2图象上.
中正确的序号是()
A.①②③④B.②③C.②④D.①②④
20.(2015•山西模拟)已知二次函数y1=﹣3x2,,,它们的图象开口
由小到大的顺序是()
A.y1<y2<y3B.y3<y2<y1C.y1<y3<y2D.y2<y3<y1
21.(2015•亭湖区校级模拟)若二次函数y=(x﹣k)2+m,当x≤2时,y随x的增大而减小,则k的取值范围是()
A.k=2 B.k>2 C.k≥2 D.k≤2
22.(2015•平阴县二模)下列函数中,在0≤x≤2上y随x的增大而增大的是()A.y=﹣x+1 B.y=x2﹣4x+5 C.y=x2D.y=
23.(2015•石家庄校级模拟)已知二次函数y=ax2+bx+c的x、y的部分对应值如表:则该二
)
y 5 1 ﹣1 ﹣1 1
A.y轴B.直线x= C.直线x=2 D.直线x=﹣2
24.(2015•海宁市模拟)二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中的x与y的部
+(b ﹣1)x+c=0的一个根;(4)当﹣1<x<3时,ax2+(b﹣1)x+c>0.其中正确的个数为()A.1个B.2个C.3个D.4个
25.(2015•岱岳区二模)已知Y1,Y2,Y3分别表示二次函数、反比例函数和一次函数的三个函数值,它们的交点分别是A(﹣1,﹣2)、B(2,1)和C(,3),规定M={Y1,Y2,Y3中最小的函数值},则下列结论错误的是()
A.当x<﹣1时,M=Y1
B.当﹣1<x<0时,Y2<Y3<Y1
C.当0≤x≤2时,M的最大值是1,无最小值
D.当x≥2时,M最大值是1,无最小值
26.(2015•牡丹江二模)抛物线y=ax2+bx+c经过点(4,﹣5)且对称轴是直线x=2,则代数式c﹣2的值为()
A.25 B.﹣25 C.D.﹣
27.(2015•彭州市校级模拟)已知二次函数y=x2+bx+c过点(0,﹣3)和(﹣1,2m﹣2)对于该二次函数有如下说法:
①它的图象与x轴有两个公共点;
②若存在一个正数x0,使得当x<x0时,函数值y随x的增大而减小,则m>0;若存在一个负数x0,使得当x>x0时,函数值y随x的增大而增大,则m<0;
③若将它的图象向左平移3个单位后过原点,则m=﹣1;
④若当x=2时的函数值与x=2012时的函数值相等,则当x=20时的函数值为﹣3.
其中正确的说法的个数是()
A.1 B.2 C.3 D.4
28.(2015•杭州模拟)如图,已知二次函数的解析式为y=x2﹣1,其图象上有一个动点P,连接OP(O为坐标原点),并以OP为半径作圆,则该圆的最小面积是()
A.πB.πC.πD.π
29.(2015•杭州模拟)如图,已知点A(﹣1,0),B(7,0),P是线段AB上任意一点(不含端点A,B),过A、P两点的二次函数y1和过P、B两点的二次函数y2的图象开口均向上,它们的顶点分别为C、D,射线BD与AC相交于点E.当AE=BE=5时,这两个二次函数的最小值之和等于()
A.﹣1 B.﹣2 C.﹣3 D.﹣4
30.(2015•岱岳区二模)若不等式组(x为未知数)无解,则对二次函数y=ax2﹣2x+1的图象的下列叙述:
(1)开口向上;(2)与x轴没有交点;(3)顶点在第二象限;(4)当x>﹣时,y随x的
增大而增大.
其中正确的有()
A.4个B.3个C.2个D.1个。
