三角形全等的判定专项练习题
12.2三角形全等的判定(ASA,AAS,HL)练习题
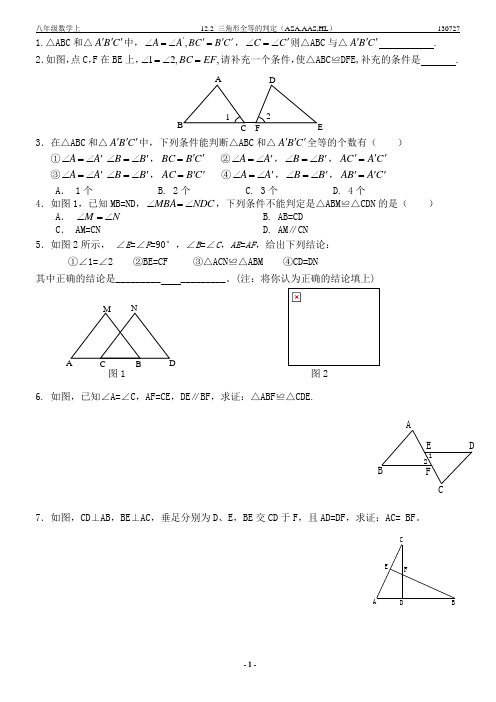
1.△ABC 和△C B A '''中,C B C B A A ''='∠=∠,',C C '∠=∠则△ABC 与△C B A ''' . 2.如图,点C ,F 在BE 上,,,21EF BC =∠=∠请补充一个条件,使△ABC ≌DFE,补充的条件是 .3.在△ABC 和△C B A '''中,下列条件能判断△ABC 和△C B A '''全等的个数有( )①A A '∠=∠ B B '∠=∠,C B BC ''= ②A A '∠=∠,B B '∠=∠,C A C A ''=' ③A A '∠=∠ B B '∠=∠,C B AC ''= ④A A '∠=∠,B B '∠=∠,C A B A ''='A . 1个 B. 2个 C. 3个 D. 4个4.如图1,已知MB=ND ,NDC MBA ∠=∠,下列条件不能判定是△ABM ≌△CDN 的是( )A . N M ∠=∠ B. AB=CD C . AM=CN D. AM ∥CN5.如图2所示, ∠E =∠F =90°,∠B =∠C ,AE =AF ,给出下列结论:①∠1=∠2 ②BE=CF ③△ACN ≌△ABM ④CD=DN其中正确的结论是_________ _________。
(注:将你认为正确的结论填上)图1图26. 如图,已知∠A=∠C ,AF=CE ,DE ∥BF ,求证:△ABF ≌△CDE.BAE21F CD7.如图,CD ⊥AB ,BE ⊥AC ,垂足分别为D 、E ,BE 交CD 于F ,且AD=DF ,求证:AC= BF 。
BA EFCDC1.如图,CE ⊥AB ,DF ⊥AB ,垂足为E 、F ,AC ∥DB ,且AC=BD ,那么Rt △AEC ≌Rt △BFC 的理由是( ).A .SSSB. AASC. SASD. HL2.下列说法正确的个数有( ).①有一角和一边对应相等的的两个直角三角形全等; ②有两边对应相等的两个直角三角形全等; ③有两边和一角对应相等的两个直角三角形全等; ④有两角和一边对应相等的两个直角三角形全等. A .1个B. 2个C. 3个D. 4个3.过等腰△ABC 的顶点A 作底面的垂线,就得到两个全等三角形,其理由是 .4.如图,△ABC 中,∠C=︒90,AM 平分∠CAB ,CM=20cm ,那么M 到AB 的距离是( )cm.5.在△ABC 和△C B A '''中,如果AB=B A '',∠B=∠B ',AC=C A '',那么这两个三角形( ). A .全等 B. 不一定全等 C. 不全等 D. 面积相等,但不全等6.如图,∠B=∠D=︒90,要证明△ABC 与△ADC 全等,还需要补充的条件是 .7.如图,在△ABC 中,∠ACB=︒90,AC=BC ,直线MN 经过点C ,且AD ⊥MN 于D ,BE ⊥MN 于E ,求证:DE=AD+BE.8.如图,△ABC 中,∠C=90°,AB=2AC ,M 是AB 的中点,点N 在BC 上,MN ⊥AB 。
全等三角形判定基础50题
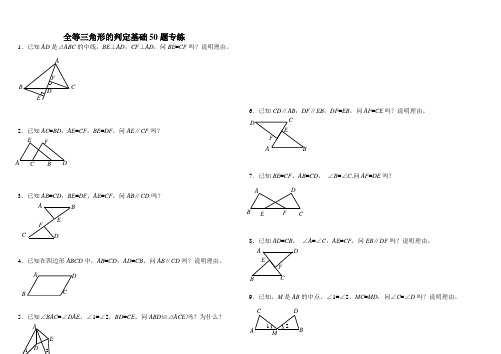
全等三角形的判定基础50题专练1.已知AD 是⊿ABC 的中线,BE ⊥AD ,CF ⊥AD ,问BE =CF 吗?说明理由。
2.已知AC =BD ,AE =CF ,BE =DF ,问AE ∥CF 吗?3.已知AB =CD ,BE =DF ,AE =CF ,问AB ∥CD 吗?4.已知在四边形ABCD 中,AB =CD ,AD =CB ,问AB ∥CD 吗?说明理由。
5.已知∠BAC =∠DAE ,∠1=∠2,BD =CE ,问ABD ≌⊿ACE .吗?为什么? 6.已知CD ∥AB ,DF ∥EB ,DF =EB ,问AF =CE 吗?说明理由。
7.已知BE =CF ,AB =CD , ∠B =∠C .问AF =DE 吗? 8.已知AD =CB , ∠A =∠C ,AE =CF ,问EB ∥DF 吗?说明理由。
9.已知,M 是AB 的中点,∠1=∠2,MC =MD ,问∠C =∠D 吗?说明理由。
AB CDFEA CB DE FDCF EA BAD E1 2 A D C E F B A C D B E F B A D F E C M A B C D 1 210.已知,AE =DF ,BF =CE ,AE ∥DF ,问AB =CD 吗?说明理由。
11.已知∠1=∠2,∠3=∠4,问AC =AD 吗?说明理由。
12.已知∠E =∠F ,∠1=∠2,AB =CD ,问AE =DF 吗?说明理由。
13.已知ED ⊥AB ,EF ⊥BC ,BD =EF ,问BM =ME 吗?说明理由。
14.在⊿ABC 中,高AD 与BE 相交于点H ,且AD =BD ,问⊿BHD ≌⊿ACD ,为什么? 15.已知∠A =∠D ,AC ∥FD ,AC =FD ,问AB ∥DE 吗?说明理由。
16.已知AC =AB ,AE =AD , ∠1=∠2,问∠3=∠4吗? 17.已知EF ∥BC ,AF =CD ,AB ⊥BC ,DE ⊥EF ,问⊿ABC ≌⊿DEF 吗?说明理由。
三角形全等的判定(SSS、SAS) 习题

1全等三角形(SSS 、SAS)例1:如图, CE=DE ,EA=EB ,CA=DB ,求证:∠CAB=∠DBA 证明∵CE=DE , EA=EB ( )∴________=________ 即:_______=________ 在△ABC 和△BAD .中,∵()()()⎪⎩⎪⎨⎧===___________________________________________已证已知∴△ABC ≌△BAD .( )∴∠CAB=∠DBA ( )练一练:1、如图,AC =BD ,BC =AD ,说明.∠C=∠D证明:在△ABC 与△BAD 中,()()()______________________________________________= ⎧⎪= ⎨⎪=⎩ ∴△ABC ≌△BAD ( )∴∠C=∠___ ( )2、如图,AB=DF ,AC=DE ,BE=FC ,问:(1)ΔABC 与ΔDFE 全等吗? (2)AB 与DF 平行吗?请说明你的理由。
AFDC E23、如图1所示,点C 、F 在直线AD 上,且AF=DC ,AB=DE ,BC=EF 。
(1)试说明AB ∥DE;(2)观察图2,图3,指出它们是怎样由图1变换得到的? (3)在满足已知条件的情况下根据图2,试证明BC ∥EF 。
4、已知AB ⊥BD ,ED ⊥BD ,AB=CD ,BC=DE ,点B 、C 、D 在一条直线上,求证:AC ⊥CE 。
5、(多变题)已知AB=CD ,AD=CB ,求证:∠A=∠C一变:已知AD ∥BC ,AD=CB ,试证明:△ADC ≌△CBA二变:已知AD ∥BC ,AD=CB ,AE=CF.试证:△AFD ≌△CEB图3图2图1F ED CB A E DB A E DC FA B D E B A C D C B A D CB A F E CBD A36、(实际运用)有一湖的湖岸在A 、B 之间呈不规则形状,A 、B 之间的距离不能直接测量,你能用已学过的知识或方法设计测量方案并求出A 、B 之间的距离吗?做一做:7、如图所示,有一块三角形的镜子,小明不小心弄破裂成1、2两块,现需配成同样 大小的一块.为了方便起见,需带上________块,其理由是__________.8、如图所示,AB ,CD 相交于O ,且AO =OB ,观察图形,图中已具备的另一相等 的条件是________,联想到SAS ,只需补充条件________,则有△AOC ≌△_______9、如图,已知CA=CB ,AD=BD ,E ,F 分别为CB ,CA 的中点,求证:DE=DF10、如图,已知AB =AE ,∠B =∠E ,BC =ED ,点F 是CD 的中点.求证:AF ⊥CD.FEBDB A E F C11、已知△ABE和三角形DEC均为等边三角形,连接BD,AC,求证:AC=BD4。
《全等三角形的判定》练习(含答案)

全等三角形的判定一、选择题1.小明不小心把一块三角形形状的玻璃打碎成了三块,如图①②③,他想要到玻璃店去配一块大小形状完全一样的玻璃,你认为应带( )A .①B .②C .③D .①和②【答案】C .【解析】解带③去可以利用“角边角”得到全等的三角形.故选C .2.如图,已知:∠A=∠D ,∠1=∠2,下列条件中能使△ABC ≌△DEF 的是()A .∠E=∠B B .ED=BC C .AB=EFD .AF=CD【答案】D .【解析】添加AF=CD ,∵AF=CD ,∴AF+FC=CD+FC ,∴AC=FD ,在△ABC 和△DEF 中12A DAC DF ∠=∠⎧⎪=⎨⎪∠=∠⎩,∴△ABC ≌△DEF (ASA ),故选D .3.下列关于两个三角形全等的说法:①三个角对应相等的两个三角形全等;②三条边对应相等的两个三角形全等;③有两角和其中一个角的对边对应相等的两个三角形全等;④有两边和一个角对应相等的两个三角形全等.正确的说法个数是( )A .1个B .2个C .3个D .4个【答案】B .【解析】①不正确,因为判定三角形全等必须有边的参与;②正确,符合判定方法SSS ;③正确,符合判定方法AAS ;④不正确,此角应该为两边的夹角才能符合SAS .所以正确的说法有两个.故选B .4.在△ABC 和△A ˊB ′C ′中,已知∠A=∠A ′,AB=A ′B ′,在下面判断中错误的是( )A .若添加条件AC=A ′C ′,则△ABC ≌△A ′B ′C ′B .若添加条件BC=B ′C ′,则△ABC ≌△A ′B ′C ′C .若添加条件∠B=∠B ′,则△ABC ≌△A ′B ′C ′D .若添加条件∠C=∠C ′,则△ABC ≌△A ′B ′C ′【答案】B.【解析】A ,正确,符合SAS 判定;B ,不正确,因为边BC 与B ′C ′不是∠A 与∠A ′的一边,所以不能推出两三角形全等;C ,正确,符合AAS 判定;D ,正确,符合ASA 判定;故选B .5.如图,在等腰△ABC 中,AB=AC ,∠A=20°,AB 上一点D 使AD=BC ,过点D 作DE ∥BC 且DE=AB ,连接EC ,则∠DCE 的度数为( )A .80°B .70°C .60°D .45°【答案】B.【解析】如图所示,连接AE .∵AE=DE,∴∠ADE=∠DAE,∵DE∥BC,∴∠DAE=∠ADE=∠B,∵AB=AC,∠BAC=20°,∴∠DAE=∠ADE=∠B=∠ACB=80°,在△ADE 与△CBA 中,DAE ACB AD BCADE B ∠=∠⎧⎪=⎨⎪∠=∠⎩,∴AE=AC,∠AED=∠BAC=20°,∵∠CAE=∠DAE﹣∠BAC=80°﹣20°=60°,∴△ACE 是等边三角形,∴CE=AC=AE=DE,∠AEC=∠ACE=60°,∴△DCE 是等腰三角形,∴∠CDE=∠DCE,∴∠DEC=∠AEC﹣∠AED=40°,∴∠DCE=∠CDE=(180﹣40°)÷2=70°.故选B .6.如图:AB=AC ,∠B=∠C,且AB=5,AE=2,则EC 的长为( )A .2B .3C .5D .2.5【答案】B.【解析】在△ABE 与△ACF 中,∵A AAB AC B C∠=∠⎧⎪=⎨⎪∠=∠⎩,∴△ABE≌△ACF(ASA ),∴AC=AB=5∴EC=AC﹣AE=5﹣2=3,故选B.二、填空题.7.如图,AB=AC ,要使△ABE≌△ACD,依据ASA ,应添加的一个条件是 .【答案】∠C=∠B .【解析】添加∠C=∠B,在△ACD 和△ABE 中,A AAB AC C B∠=∠⎧⎪=⎨⎪∠=∠⎩,8.如图,AB∥CF,E 为DF 中点,AB=20,CF=15,则BD= 5 .【答案】5.【解析】∵AB∥FC,∴∠ADE=∠EFC,∵E 是DF 的中点,∴DE=EF,在△ADE 与△CFE 中,ADE EFC DE EFAED CEF ∠=∠⎧⎪=⎨⎪∠=∠⎩, ∴△ADE≌△CFE,∴AD=CF,∵AB=20,CF=15,∴BD=AB﹣AD=20﹣15=5.9.如图,∠1=∠2,∠3=∠4,BC=5,则BD= .【答案】5. 【解析】∵∠ABD+∠3=180°∠ABC+∠4=180°,且∠3=∠4,∴∠ABD=∠ABC在△ADB 和△ACB 中,1=2AB ABABD ABC ∠∠⎧⎪=⎨⎪∠=∠⎩, ∴△ADB≌△ACB(ASA ),∴BD=BC=5.10.如图,要测量一条小河的宽度AB 的长,可以在小河的岸边作AB 的垂线 MN ,然后在MN 上取两点C ,D ,使BC=CD ,再画出MN 的垂线DE ,并使点E 与点A ,C 在一条直线上,这时测得DE 的长就是AB 的长,其中用到的数学原理是: .【答案】ASA ,全等三角形对应边相等 .【解析】∵AB⊥MN,DE⊥MN,∴∠ABC=∠EDC=90°,在△ABC 和△EDC 中,ABC EDC BC DCACB ECD ∠=∠⎧⎪=⎨⎪∠=∠⎩, ∴△ABC≌△EDC(ASA ),∴DE=AB.11.如图,在四边形ABCD 中,AB∥DC,AD∥BC,对角线AC 、BD 相交于点O ,则图中的一对全等三角形为 .(写出一对即可)【答案】△ABC ≌△ADC.【解析】△ABC≌△ADC,理由如下:∵AB∥DC,AD∥BC,∴∠BAC=∠DCA,∠DAC=∠BCA,在△ABC 与△ADC 中,BAC DCA AC CADAC BCA ∠=∠⎧⎪=⎨⎪∠=∠⎩, ∴△ABC≌△ADC(ASA ),∴AB=DC,BC=DA ,在△ABO 与△CDO 中,BAO DCO AOB COD AB CD ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△ABO≌△CDO(AAS ),同理可得:△BCO≌△DAO,三、解答题12.如图,点A ,B ,C ,D 在同一条直线上,AB=FC ,∠A=∠F,∠EBC=∠FCB.求证:BE=CD .【答案】证明见解析.【解析】∵∠EBC=∠FCB,∠EBC+∠ABE=180°,∠FCB+∠FCD=180°,∴∠ABE=∠FCD,在△ABE 与△FCD 中,A F AB FCABE FCD ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△ABE≌△FCD(ASA ),∴BE=CD.13.如图,点D 在AB 上,DF 交AC 于点E ,CF∥AB,AE=EC .求证:AD=CF .【答案】答案见解析.【解析】∵CF∥AB,∴∠A=∠ACF,∠ADE=∠CFE.在△ADE 和△CFE 中,A ACF ADE CFE AE EC ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△ADE≌△CFE(AAS ).∴AD=CF.14. 如图,锐角△ABC 中,∠BAC=60°,O 是BC 边上的一点,连接AO ,以AO 为边向两侧作等边△AOD 和等边△AOE,分别与边AB ,AC 交于点F ,G .求证:AF=AG .【答案】答案见解析.【解析】∵△AOD 和△AOE 是等边三角形,∴∠E=∠AOF=60°,AE=AO ,∠OAE=60°,∵∠BAC=60°,∴∠FAO=∠EAG=60°﹣∠CAO, 在△AFO 和△AGE 中, FAO EAG AO AEAOF E ∠=∠⎧⎪=⎨⎪∠=∠⎩, ∴△AFO≌△AGE(ASA ), ∴AF=AG.。
2022年《直角三角形全等的判定》专题练习(附答案)

1.3 直角三角形全等的判定一、选择题(本大题共8小题)1. 在以下条件中,不能判定两个直角三角形全等的是( )2. 如下图,AB=CD,AE⊥BD于点E,CF⊥BD于点F,AE=CF,那么图中全等的三角形有( )第2题图第5题图第6题图3.以下说法中正确的选项是〔〕A.a,b,c是三角形的三边长,那么a2+b2=c2B.在直角三角形中,两边长和的平方等于第三边长的平方C.在Rt△ABC中,假设∠C=90°,那么三角形对应的三边满足a2+b2=c2D.在Rt△ABC中,假设∠A=90°,那么三角形对应的三边满足a2+b2=c24. 在Rt△ABC和Rt△A′B′C′中,∠C=∠C′=90°,∠A=∠B′,AB=B′A,那么以下结论中正确的选项是〔〕A. AC=A′C′B.BC=B′C′C.AC=B′C′D.∠A=∠A′5. 如下图,△ABC中,AB=AC,AD⊥BC交D点,E、F分别是DB、DC的中点,那么图中全等三角形的对数是〔〕6. 如图,在△ABC中,CD是AB边上的高线,BE平分∠ABC,交CD于点E,BC=5,DE=2,那么△BCE的面积等于〔〕A.10 B.7 C.5 D. 47. 在△ABC和△DEF中,∠A=∠D=90°,那么以下条件中不能判定△ABC和△DEF全等的是( )A.AB=DE,AC=DFB.AC=EF,BC=DFC.AB=DE,BC=EFD.∠C=∠F,BC=EF8. 如图,在Rt△ABC的斜边BC上截取CD=CA,过点D作DE⊥BC交AB于点E,那么有( )A.DE=DBB.DE=AEC.AE=BED.AE=BD第8题图第9题图二、填空题(本大题共4小题)9. :如图,AE⊥BC,DF⊥BC,垂足分别为E、F,AE=DF,AB=DC,那么△ABE≌△__________.10. 如图,BD⊥AE于点B,C是BD上一点,且BC=BE,要使Rt△ABC≌Rt△DBE,应补充的条件是∠A=∠D或__________或__________或__________.第10题图第11题图11. 如图,△ABC中,AD⊥BC于点D,要使△ABD≌△ACD,假设根据“HL〞判定,还需要加一个条件__________.12. :如图,AB=CD,DE⊥AC于点E,BF⊥AC于点F,且DE=BF,∠D=60°,那么∠A=__________.三、计算题(本大题共4小题)13. :如图△ABC中,BD⊥AC,CE⊥AB,BD、CE交于O点,且BD=CE求证:OB=OC.14. :Rt△ABC中,∠ACB是直角,D是AB上一点,BD=BC,过D作AB的垂线交AC于E,求证:CD⊥BE15. 如图:在△ABC中,∠C=90° AD是∠BAC的平分线,DE⊥AB于E,F在AC上,BD=DF;说明:〔1〕CF=EB.〔2〕AB=AF+2EB.16. 如图,△ABC中,AB=BC,BE⊥AC于点E,AD⊥BC于点D,∠BAD=45°,AD与BE交于点F,连接CF.(1)求证:BF=2AE;(2)假设CD=2,求AD的长.参考答案:一、选择题(本大题共8小题)1.A2. D3. C4. C5. D6. B7. B8. C二、填空题(本大题共6小题)9.分析:根据直角三角形全等的条件HL判定即可。
全等三角形判定-专题复习50题(含答案解析)

全等三⾓形判定-专题复习50题(含答案解析)全等三⾓形判定⼀、选择题:1.如图所⽰,亮亮书上的三⾓形被墨迹污染了⼀部分,很快他就根据所学知识画出⼀个与书上完全⼀样的三⾓形,那么这两个三⾓形完全⼀样的依据是()A.SSS B.SAS C.AAS D.ASA2.⽅格纸中,每个⼩格顶点叫做⼀个格点,以格点连线为边的三⾓形叫做格点三⾓形.如图,在4×4的⽅格纸中,有两个格点三⾓形△ABC、△DEF,下列说法中成⽴的是()A.∠BCA=∠EDF B.∠BCA=∠EFDC.∠BAC=∠EFD D.这两个三⾓形中,没有相等的⾓3.如图所⽰,△ABD≌△CDB,下⾯四个结论中,不正确的是()A.△ABD和△C DB的⾯积相等B.△ABD和△CDB的周长相等C.∠A+∠ABD=∠C+∠CBD D.AD∥BC,且AD=BC4.下列判断中错误..的是()A.有两⾓和⼀边对应相等的两个三⾓形全等B.有两边和⼀⾓对应相等的两个三⾓形全等C.有两边和其中⼀边上的中线对应相等的两个三⾓形全等D.有⼀边对应相等的两个等边三⾓形全等5.使两个直⾓三⾓形全等的条件是()A.⼀个锐⾓对应相等B.两个锐⾓对应相等C.⼀条边对应相等D.两条边对应相等6.如图,在△ABC和△BDE中,点C在边BD上,边AC交边BE于点F.若AC=BD,AB=ED,BC=BE,则∠ACB等于()A.∠EDB B.∠BED C.∠AFB D.2∠ABF7.在△ABC和△A/B/C/中,已知∠A=∠A/,AB=A/B/,在下⾯判断中错误的是( )A.若添加条件AC=A/C/,则△ABC≌△△A/B/C/B.若添加条件BC=B/C/,则△ABC≌△△A/B/C/C.若添加条件∠B=∠B/,则△ABC≌△△A/B/C/D.若添加条件∠C=∠C/,则△ABC≌△△A/B/C/8.如图,△ABC和△DEF中,AB=DE、∠B=∠DEF,添加下列哪⼀个条件⽆法证明△ABC≌△DEF()A.AC∥DF B.∠A=∠D C.AC=DF D.∠ACB=∠F9.如图,在△ABC中,∠ABC=45°,AC=8cm,F是⾼AD和BE的交点,则BF的长是()A.4cm B.6cm C.8cm D.9cm10.在如图所⽰的5×5⽅格中,每个⼩⽅格都是边长为1的正⽅形,△ABC是格点三⾓形(即顶点恰好是正⽅形的顶点),则与△ABC有⼀条公共边且全等的所有格点三⾓形个数是()A.1 B.2 C.3 D.411.如图,点E在正⽅形ABCD的对⾓线AC上,且EC=2AE,直⾓三⾓形FEG的两直⾓边EF、EG分别交BC、DC于点M、N.若正⽅形ABCD的边长为a,则重叠部分四边形EMCN的⾯积为()A.a2B.a2C.a2D.a212.在连接A地与B地的线段上有四个不同的点D、G、K、Q,下列四幅图中的实线分别表⽰某⼈从A地到B地的不同⾏进路线(箭头表⽰⾏进的⽅向),则路程最长的⾏进路线图是()A.B.C.D.⼆、填空题:13.如图所⽰,有⼀块三⾓形的镜⼦,⼩明不⼩⼼弄破裂成1、2两块,现需配成同样⼤⼩的⼀块.为了⽅便起见,需带上块,其理由是.14.如图⽰,点B在AE上,∠CBE=∠DBE,要使ΔABC≌ΔABD, 还需添加⼀个条件是__________.(填上你认为适当的⼀个条件即可)15.如图,已知∠1=∠2,AC=AD,请增加⼀个条件,使△ABC≌△AED,你添加的条件是.16.如图,∠1=∠2,要使△ABD≌△ACD,需添加的⼀个条件是(只添⼀个条件即可).17.如图,在△ABC中,AB=AC,AD⊥BC于D点,E、F分别为DB、DC的中点,则图中共有全等三⾓形对.18.如图,△ABD≌△BAC,若AD=BC,则∠BAD的对应⾓是.19.如图,已知AB⊥BD,垂⾜为B,ED⊥BD,垂⾜为D,AB=CD,BC=DE,则∠ACE= 度.20.如图,如果两个三⾓形的两条边和其中⼀条边上的⾼对应相等,那么这两个三⾓形的第三边所对的⾓的关系是.三、解答题:21.如图,∠DCE=90°,CD=CE,AD⊥AC,BE⊥AC,垂⾜分别为A.B.试说明AD+AB=BE.22.如图,E、A.C三点共线,AB∥CD,∠B=∠E,,AC=CD。
三角形全等的判定专题训练50题

三角形全等的判定专题训练题1、如图(1):AD ⊥BC ,垂足为D ,BD=CD 。
求证:△ABD ≌△ACD 。
2、如图(2):AC ∥EF ,AC=EF ,AE=BD 。
求证:△ABC ≌△EDF 。
3、 如图(3):DF=CE ,AD=BC ,∠D=∠C 。
求证:△AED ≌△BFC 。
4、 如图(4):AB=AC ,AD=AE ,AB ⊥AC ,AD ⊥AE 。
求证:(1)∠B=∠C ,(2)BD=CE.(图1)D CBA F E (图2)DCB A F E (图3)DCB A E (图4)D C B A5、如图(5):AB ⊥BD ,ED ⊥BD ,AB=CD ,BC=DE 。
求证:AC ⊥CE 。
6、如图(6):CG=CF ,BC=DC ,AB=ED ,点A 、B 、C 、D 、E 在同一直线上。
求证:(1)AF=EG ,(2)BF ∥DG 。
7、如图(7):AC ⊥BC ,BM 平分∠ABC 且交AC 于点M ,N 是AB 的中点且BN=BC 。
求证:(1)MN 平分∠AMB ,(2)∠A=∠CBM 。
8、如图(8):A 、B 、C 、D 四点在同一直线上,AC=DB ,BE ∥CF ,AE ∥DF 。
求证:△ABE ≌△DCF 。
GF E(图6)D CBA N M(图7)CBA F E (图8)D CBA E (图5)DC B A9、如图(9)AE 、BC 交于点M ,F 点在AM 上,BE ∥CF ,BE=CF 。
求证:AM 是△ABC 的中线。
10、如图(10)∠BAC=∠DAE ,∠ABD=∠ACE ,BD=CE 。
求证:AB=AC 。
11、如图(11)在△ABC 和△DBC 中,∠1=∠2,∠3=∠4,P 是BC 上任一点。
求证:PA=PD 。
12、如图(12)AB ∥CD ,OA=OD ,点F 、D 、O 、A 、E 在同一直线上,AE=DF 。
求证:EB ∥CF 。
全等三角形的判定精选练习题(分SSS、SAS、AAS、ASA、HL分专题)

D CB A 全等三角形的判定(一)(SSS )1、如图1,AB=AD ,CB=CD ,∠B=30°,∠BAD=46°,则∠ACD 的度数是( )A.120°B.125°C.127°D.104°2、如图2,线段AD 与BC 交于点O ,且AC=BD ,AD=BC ,•则下面的结论中不正确的是( ) A.△ABC ≌△BAD B.∠CAB=∠DBA C.OB=OC D.∠C=∠D3、在△ABC 和△A 1B 1C 1中,已知AB=A 1B 1,BC=B 1C 1,则补充条件____________,可得到△ABC ≌△A 1B 1C 1.4、如图3,AB=CD ,BF=DE ,E 、F 是AC 上两点,且AE=CF .欲证∠B=∠D ,可先运用等式的性质证明AF=________,再用“SSS ”证明______≌_______得到结论.5、如图,已知AB=CD ,AC=BD ,求证:∠A=∠D .6、如图,AC 与BD 交于点O ,AD=CB ,E 、F 是BD 上两点,且AE=CF ,DE=BF.请推导下列结论:⑴∠D=∠B ;⑵AE ∥CF .7、已知如图,A 、E 、F 、C 四点共线,BF=DE ,AB=CD.⑴请你添加一个条件,使△DEC ≌△BFA ; ⑵在⑴的基础上,求证:DE ∥BF.全等三角形的判定(SAS)1、如图1,AB ∥CD ,AB=CD ,BE=DF ,则图中有多少对全等三角形( )A.3B.4C.5D.62、如图2,AB=AC ,AD=AE ,欲证△ABD ≌△ACE ,可补充条件( ) A.∠1=∠2 B.∠B=∠C C.∠D=∠E D.∠BAE=∠CAD3、如图3,AD=BC ,要得到△ABD 和△CDB 全等,可以添加的条件是( ) A.AB ∥CD B.AD ∥BC C.∠A=∠C D.∠ABC=∠CDA4、如图4,AB 与CD 交于点O ,OA=OC ,OD=OB ,∠AOD=________,•根据_________可得到△AOD ≌△COB ,从而可以得到AD=_________.5、如图5,已知△ABC 中,AB=AC ,AD 平分∠BAC ,请补充完整过程说明△ABD ≌△ACD 的理由. ∵AD 平分∠BAC , ∴∠________=∠_________(角平分线的定义). 在△ABD 和△ACD 中,∵____________________________, ∴△ABD ≌△ACD ( ) 6、如图6,已知AB=AD ,AC=AE ,∠1=∠2,求证∠ADE=∠B.7、如图,已知AB=AD ,若AC 平分∠BAD ,问AC 是否平分∠BCD ?为什么?8、如图,在△ABC 和△DEF 中,B 、E 、F 、C ,在同一直线上,下面有4个条件,请你在其中选3个作为题设,余下的一个作为结论,写一个真命题,并加以证明. ①AB=DE ;②AC=DF ;③∠ABC=∠DEF ;④BE=CF.9、如图⑴,AB ⊥BD ,DE ⊥BD ,点C 是BD 上一点,且BC=DE ,CD=AB .⑴试判断AC 与CE 的位置关系,并说明理由.⑵如图⑵,若把△CDE 沿直线BD 向左平移,使△CDE 的顶点C 与B 重合,此时第⑴问中AC 与BE 的位置关系还成立吗?(注意字母的变化)全等三角形(三)AAS 和ASA【知识要点】1.角边角定理(ASA ):有两角及其夹边对应相等的两个三角形全等.2.角角边定理(AAS ):有两角和其中一角的对边对应相等的两个三角形全等. 【典型例题】例1.如图,AB ∥CD ,AE=CF ,求证:AB=CD例2.如图,已知:AD=AE ,ABE ACD ∠=∠,求证:BD=CE.例3.如图,已知:ABD BAC D C ∠=∠∠=∠.,求证:例4.如图已知:AB=CD ,AD=BC ,O 是BD 中点,过O AE=CF.例5.如图,已知321∠=∠=∠,AB=AD.求证:BC=DE.例6.如图,已知四边形ABCD 中,AB=DC ,AD=BC ,点F 在AD 交于O ,请问O 点有何特征?【经典练习】 1.△ABC 和△C B A '''中,C B C B A A ''='∠=∠,',C C '∠=∠2.如图,点C ,F 在BE 上,,,21EF BC =∠=∠3.在△ABC 和△C B A ''' ) ①A A '∠=∠B B '∠=∠,BC =C A C A ''='③A A '∠=∠B B '∠=∠,AC =C A B A ''=' A . 1个B. 2个C. 3个D. 4个4.如图,已知MB=ND ,NDC MBA ∠=∠,下列条件不能判定是△ABM ≌△CDN 的是( )A . N M ∠=∠ B. AB=CD C . AM=CN D. AM ∥CN 5.如图2所示, ∠E =∠F =90°,∠B =∠C ,AE =AF ,给出下列结论:①∠1=∠2 ②BE=CF ③△ACN ≌△ABM ④CD=DN其中正确的结论是__________________。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
B
c
D
E
1
2
3
4
图2
A
图1
D
c
B
A
4
3F
B
c
D
E图3
A
第8题
三角形全等的判定专项练习题
一、填空题:
一、如图,已知∠3=∠4,要说明△ABC≌△DCB,
(1)若以“SAS”为依据,则需添加一个条件是;
(2)若以“AAS”为依据,则需添加一个条件是;
(3)若以“ASA”为依据,则需添加一个条件是。
二、如图,若∠1=∠2,,3=∠4,则图中共有全等三角形对,它们别离是
3F在一条直线上,AB∥DE,AC DF,AC=DE,若BE=3cm,则CF=
4、若DEF
ABC∆
≅
∆,△DEF周长为28 cm,DE=9 cm,EF=12 cm,则AB= ,BC=
五、已知DEF
ABC∆
≅
∆,∠A=52°,∠B=31°,ED=10,那么∠F= ,AB=
六、如图,在△ABC和△DEF中,AB∥DE,可以推出= ,然后加上条件AB=DE
和可取得DEF
ABC∆
≅
∆,按照是
7、如图,△ABD≌△ACD,AD、BC交于点D,则∠ABD= .
∠4,则△≌△,按照是
九、如图,∠xoy,别离在ox,oy上截取OA=OB,OC=OD。
连AD、BC相交于E点。
则射线OE与∠xoy
的关系为。
10、如图,AB=CD,AD=CB,O为AC上一点,过O任作直线EF别离交AD、BC于E、F,要使BE=FD,则
应知足的条件是。
11、等边△ABC中,D、E为BC、AC上两点,且BD=CE,连AD、BE交于O,则∠DOE= .
二、选择题:
1二、已知△ABC≌△DEF,若∠A=500,∠C=300,则∠E的度数为()
A、300
B、500
C、600
D、1000
第6题
C
D
E第7题
A
B C
D
第11题
第10题
第9题
第1题第2题第3题
O
6题
D
c
B
A
E F
A
13、如图,若AC=BD,AB=DC,则图中全等三角形的对数是()
A、1对
B、2对
C、3对
D、4对
14、如图,在△ABC中,AD是△BAC的角平分线,DE⊥AB,DF⊥AC,垂足别离为E、F,下面给出四个结论:
①DA平分∠EDF;②AE=AF;③AD⊥BC;④BD=CD,其中正确的结论有()
A、1个
B、2个
C、3个
D、4个
1五、下列说法正确的是()
⑴形状相同的两个图形是全等形⑵对应角相等的两个三角形是全等形
⑶全等三角形的面积相等⑷若DEF
ABC∆
≅
∆,MNP
DEF∆
≅
∆,则MNP
ABC∆
≅
∆
A、0个
B、1个
C、2个
D、3个
1六、若BCD
ABC∆
≅
∆,AB=6cm,BD=7cm,AD=4cm,那么BC的长为()
A、6 cm
B、5 cm
C、4cm
D、不能确定
17、若AD=BC,∠A=∠B,直接能利用“SAS”证得△ADF ≌△BCE的条件是()
A、AE=BF
B、DF=CE
C、AF=BE
D、∠CEB=∠DFA
1八、下列能够肯定△ABC的形状和大小的是()
A、AB=4,BC=5,∠C=60°
B、AB=6,∠C=60°,∠B=70°
C、∠C=60°,∠B=70°,∠A=50°
D、AB=4,BC=5,CA=10
1九、如图所示,已知OA=OB,则再加上下列哪个条件后,不能
..判断△AOC≌△BOD的是()
A、∠A=∠B
B、∠C=∠D
C、AC=BD
D、OC=OD
20、如图所示,已知AB=AC,BD=CE,
则图中共有()组全等三角形
A、4
B、5
C、6
D、7
2一、以下能够判定两个直角三角形全等的情况有()
⑴两个锐角和一个锐角的对边对应相等⑵
⑶一个锐角和它的对边对应相等⑷两条直角边对应相等
⑸两边对应相等⑹斜边和一条直角边相等
A、3
B、4
C、5
D、6
22、如图,A在DE上,F在DC上,且∠1=∠2=∠3,AC=CE,则DE的等于()
A.DC
B.BC
C.AB
D.1
23、下列几个命题中正确的个数有()
①全等三角形对应边高线相等②两边和其中一边上的高线对应的两个三角形全等
③两边和第三边上的高对应相等的两个三角形全等④两边上的高对应相等的两个三角形全等
A.1个
B.2个
C.3个
D.4个
C
A
O
D
第19题
D
E
O
第20题
第22题
第14题第13题
F O C
A B D E D E F
B
A C A
B
C
D
E
F E F H D A 图11
24、△ABC 中,AB =AC ,E 在BC 上,D 在AE 上。
则下列说法:
①若E 为BC 中点,则有BD =CD ; ②若BD =CD ,则E 为BC 中点; ③若AE ⊥BC ,则有BD =CD ; ④若BD =CD ,则AE ⊥BC 。
其中正确的有( )
A. ①③④
B. ②③④
C. ①②③
D. ①②③④
三、解答题
2五、三月三,放风筝,下图是小明制作的风筝,他按照DE =DF ,EH =FH ,不用气宇,就知道AF AE ,
请你用所学的知识给予证明。
2六、已知:如图,AB =CD ,BC =DA ,AO =CO ,求证:△AOE ≌△COF
27、如图,BE ⊥AC 于点E ,CF ⊥AB 于点F ,CF 、BE 相交于点D ,且BD =CD. 求证:AD 平分∠BAC
2八、已知:如图,∠AOD=∠BOC ,∠B=∠D ,O 是AC 的中点。
求证:OB=OD .
2九、如图,已知AB=DE ,且AB ∥DE ,BE=CF 。
求证: AC ∥DF
30、如图,已知BD=CE ,∠B=∠C ,求证:(1)AB=AC ,(2)BE=CD.
3一、如图,已知AM 是△ABC 的中线,CE ⊥AM 于E ,BF ⊥AM 于F 。
求证:CE=BF
A B B C
M E
C D A E F
第27题 第31题 第25题 第26题
第28题 第28题
3二、如图,在△ABC和△DEF中,AM和DN别离为高,而且AC=DF,AM=DN,∠BAC=∠EDF。
求证:△ABC≌△DEF
33、如图,AB=DC,AC=DB。
求证:OB=OC.
34、如图,AB=DC,AD=CB,AE=CF. 求证:∠E=∠F。
第33题第34题第32题
第30题。
