图论第一次作业
图论第一次作业

算法能否用来求:
(1)赋权连通图中的最大权的树 (2)赋权图中的最小权的最大森林如果可以,怎样实现 答:1、不能,由 Kruskal 算法得到的任何生成树一定是最小生成树。
2、能 a.选择边 e1 使其权值最小 b.若已经选定边 e1 e2 e3 ……ek,则从 E-{e1,e2,e3……ek},选择边 ek+1
习题一:
4.证明下面两图同构。
v1
u1
v2
v6
v10 v5
v7
v8 v9
v3
v4 (a)
u6 u5
u2
u8
u10
u3
u7
u9
u4
(b)
证明:作映射 f : vi ↔ ui (i=1,2….10) 容易证明,对 vi v j E ((a)),有 f (v i vj,), ,ui,uj, ,E,((b)) (1 i 由图的同构定义知,图(a)与(b)是同构的。
矛盾,推出 不是最长路。即说明 与 是树叶,则 与 均是一度的。所以非平凡
树的最长路的起点和终点均是 度的。 9.证明:顶点度数为偶数的连通图本身可构成一个包含所有边的闭迹。 证明:证明:由于 是连通非平凡的且每个顶点度数为偶数,所以 中至少存在
圈 ,从 中去掉 中的边,得到 的生成子图 ,若 没有边,则 的边集合能划分
(5,4,3,2,2,0)是图序列,然而(5,4,3,2,2,0)不是图序列,所以(6,6,5,4,3,3,1) 不是图序列。
12.证明:若 ,则 包含圈。 证明:下面仅对连通图的下的条件下进行证明,不连通的情形可以通过分成若干
个连通的情形来证明。设
,对于 中的路
若
与 邻接,则构成一个圈。若
是一条路,由于 ,因此,
第一次 图论 作业
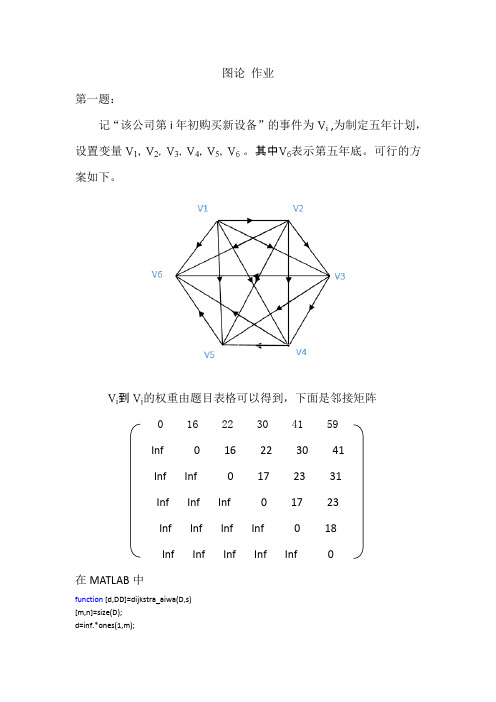
图论作业第一题:记“该公司第i年初购买新设备”的事件为,为制定五年计划,设置变量。
表示第五年底。
可行的方案如下。
的权重由题目表格可以得到,下面是邻接矩阵0 16 22 30 41 59Inf 0 16 22 30 41Inf Inf 0 17 23 31Inf Inf Inf 0 17 23Inf Inf Inf Inf 0 18Inf Inf Inf Inf Inf 0在MATLAB中function [d,DD]=dijkstra_aiwa(D,s)[m,n]=size(D);d=inf.*ones(1,m);d(1,s)=0;dd=zeros(1,m);dd(1,s)=1;y=s;DD=zeros(m,m);DD(y,y)=1;counter=1;while length(find(dd==1))<mfor i=1:mif dd(i)==0d(i)=min(d(i),d(y)+D(y,i));endendddd=inf;for i=1:mif dd(i)==0&&d(i)<dddddd=d(i);endendyy=find(d==ddd);counter=counter+1;DD(y,yy(1,1))=counter;DD(yy(1,1),y)=counter;y=yy(1,1);dd(1,y)=1;end最后得到,d =0 16 22 30 41 53当节点为6个时,最短路径53,可以看出V0到V3,V3到V5,即最开始买一台,第四年年初买可以最划算。
第二问:针对于第二问问题,定义四维状态向量(m,n,p,q),m、n、p、q分别为人、狼、羊和蔬菜的状态,当状态为0时,该物处在对岸,当状态为1时,该物在此岸。
由于题目要求,狼不能和羊一个状态,羊不能和蔬菜一个状态,穷举得可行状态(1,1,1,1),(1,1,1,0),(1,1,0,1),(1,0,1,1),(1,0,1,0),(0,1,0,1),(0,1,0,0),(0,0,1,0),(0,0,0,1),(0,0,0,0)。
图论第一次作业

图论第一次作业习题一:● 4.证明下面两图同构。
证明:作映射f : vi ? ui(i=1,2….10)容易证明,对?vi vj∈E ((a)),有f (vivj,),=,ui,uj,∈,E,((b)) (1≤ i ≤ 10,1≤j≤ 10 ) 由图的同构定义知,图(a)与(b)是同构的。
● 5.证明:四个顶点的非同构简单图有11个。
证明:设四个顶点中边的个数为m,则有:m=0:m=1 :m=2:m=3:m=4:m=5:m=6:因为四个顶点的简单图最多就是具有6条边,上面所列出的情形是在不同边的条件下的不同构的情形,则从上面穷举出的情况可以看出四个顶点的非同构简单图有11个。
● 11.证明:序列(7,6,5,4,3,3,2)和(6,6,5,4,3,3,1)不是图序列。
证明:由于7个顶点的简单图的最大度不会超过6,因此序列(7,6,5,4,3,3,2)不是图序列;(6,6,5,4,3,3,1)是图序列非负整数组12121(,,,),,2n n n i i d d d d d d d m π==≥≥≥=∑是图序列的充要条件是:1112312(1,1,,1,,,)d d n d d d d d π++=---是图序列(5,4,3,2,2,0)是图序列,然而(5,4,3,2,2,0)不是图序列,所以(6,6,5,4,3,3,1)不是图序列。
● 12.证明:若δ≥2,则G 包含圈。
证明:下面仅对连通图的下的条件下进行证明,不连通的情形可以通过分成若干个连通的情形来证明。
设V (G )={V 1,V 2,V 3,?V n },对于G 中的路V 1,V 2,V 3,?V n 若V k 与V 1邻接,则构成一个圈。
若V i1,V i2,V i3,?V in 是一条路,由于δ≥2,因此,对于V in ,存在V ik 与之邻接,则V ik ,,?V in V ik 构成一个圈。
● 17.证明:若G 不连通,则G ?连通。
电子科技大学-图论第一次作业-

课本习题一:
4. 证明下面两图同构。
v1
u1
v2
v6
v10 v5
v7
v8 v9
v3
v4 (a)
u6 u5
u2
u8
u10
u3
u7
u9
u4
(b)
证明:作映射 f : vi ↔ ui (i=1,2….10)
容易证明,对vi v j E ((a)),有 f (v i vj,),,ui,uj,,E,((b))
中不
3.设 G 是阶大于 2 的连通图,证明下列命题等价:
(1)
G 是块
(2)
G 无环且任意一个点和任意一条边都位于同一
个圈上;
(3)
G 无环且任意三个不同点都位于同一条路上。
: 是块,任取 的一点 ,一边 ,在 边插入一点 ,使得 成为两条边,由此 得到新图 ,显然 的是阶数大于 的块,由定理 4, 中的 u,v 位于同一个 圈上,于是 中 u 与边 都位于同一个圈上。
件下的不同构的情形,则从上面穷举出的情况可以看出四个顶点的非同构简单图
有 11 个。
11.证明:序列(7,6,5,4,3,3,2)和(6,6,5,4,3,3,1)
不是图序列。
证明:由于 7 个顶点的简单图的最大度不会超过 6,因此序列(7,6,5,4,3,3,2)不
是图序列;
(6,6,5,4,3,3,1)是图序列
(G1) 2 最小边割{(6,5),(8,5)} {(6,7),(8,7)}{(6,9),(8,9)}
1j 10 ) 由图的同构定义知,图(a)与(b)是同构的。
5.证明:四个顶点的非同构简单图有 11 个。
证明:设四个顶点中边的个数为 m,则有:
图论 王树禾 答案

图论第一次作业By byh|E(G)|,2|E(G)|2G υυ⎛⎫≤ ⎪⎝⎭⎛⎫ ⎪⎝⎭1.1 举出两个可以化成图论模型的实际问题略1.2 证明其中是单图证明:(思路)根据单图无环无重边的特点,所以 最大的情形为任意两个顶点间有一条边相连,即极端情况为。
•1.4 画出不同构的一切四顶单图•0条边:1条边:•2条边:3条边:•4条边:5条边:•6条边:1.10G≅H当且仅当存在可逆映射θ:V G→V H,使得uv∈E G⇔θuθv∈E H,其中G和H是单图。
(证明充分性和必要性)•必要性•若G≅H,由定义可得,存在可逆映射θ:V G→V Hφ:E G→E(H)当且仅当ψG e=uv时,ψHφe=θuθ(v),所以uv∈E G⇒θuθv∈E H•充分性•定义ϕ:E G→E(H),使得uv∈E G和θuθv∈E(H)一一对应,于是ϕ可逆,且ψe=uv的充要条件是ψHφe=θuθv,得G≅HG1.12求证(a)ϵK m,n =mn,(b)G是完全二分图,则ϵG≤14v G2•(a)对于K m,n ,将顶集分为X和Y,使得X∪Y=V Km,n,X∩Y=∅,X=m,Y=n,对于X中的每一顶点,都和Y中所有顶点相连,所以ϵKm,n=mn•(b)设G的顶划分为X,Y,X=m,Y=v−m,则ϵG≤•ϵK m,v-m =v−m m≤v24•证明:•(a)第一个序列考虑度数7,第二个序列考虑6,6,1•(b)将顶点v分成两部分v’和v’’•v’ = {v|v= v i, 1≤ i≤ k},•v’’ = {v|v= v i, k< i≤ n}•以v’点为顶的原图的导出子图度数之和小于•然后考虑剩下的点贡献给这k个点的度数之和最大可能为•1.37:证明无环图G 含二分生成子图H ,使得d H v ≥12d G v 对每个v ∈V(G)成立。
•证明:•任取X, Y 满足X U Y = V(G),X ∩ Y = ø,且令X,Y 中的顶两两不相邻,所得的图是H 且是二分子图,令H 是G 边数最多的二分生成子图,若存在v ϵV(G),使得d H (v) < d G (v),不妨设v ϵX ,则将v 所连的边取消,换成d G (v) -d H (v) 条边,且将v 加入Y 中,于是H 的边数增加了d G (v) -2d H (v)条,与H 边数最多矛盾,故原命题成立。
图论作业(1)

第三章1.证明: 必要性:v 是连通图G 的割边, 则, 至少有两个连通分支。
设其中一个连通分支顶点集合为V1,另外连通分支顶点集合为V2,即V1与V2构成V 的划分。
对于任意的u ∈V1, v ∈V2,如果割边e 不在某一条(u ,v )路上,那么,该路也是连接G-e 中的u 与v 的路,这与u,v 处于G-v 的不同分支矛盾。
“充分性”若e 不是图G 的割边,那么G-v 连通,因此在G-v 中存在u,v 路,当然也是G 中一条没有经过边e 的u,v 路。
矛盾。
7.证明: v 是单图G 的割点,则G-v 至少两个连通分支。
现任取 , 如果x,y 在G-v 的同一分支中,令u 是与x,y 处于不同分支的点,那么,通过u ,可说明,x 与y 在G-v 的补图中连通。
若x,y 在G-v 的不同分支中,则它们在G-v 的补图中邻接。
所以,若v 是G 的割点,则v 不是其补图的割点。
9.连通图G 的一个子图B 称为是G 的一个块,如果(1), 它本身是块;(2), 若没有真包含B 的G 的块存在。
又由于对于阶数至少是3的()()G e G ωω->图G是块当且仅当G无环并且任意两点都位于同一圈上。
根据题意,对于阶数至少是3的图G,由于G没有偶圈,所以G的每个块的点可以在奇圈上,如果不在奇圈上,则块只能是K2,否则如果不是K2的话,该子图将存在割点,该子图就不是块。
得证。
16.(1)(2)(3)第四章3. (1)既是欧拉闭迹又是哈密尔顿圈(2)(3)(4)7.由于图没有奇度顶点,所以是欧拉图,又定理1可得,图G的边集可以划分为圈C1,C2,。
Cm,所以E(G)可以表示成C1,C2.。
Cm的并。
10.若图不是二连通,则存在割点,由于哈密尔顿图不存在割点,因而G是非哈密尔顿图。
若G是具有二分类(X,Y)的偶图,且|X|不等于|Y|,设X中所有点为x1,x2.。
xm,Y中的所有点为y1,y2.。
yn,若存在哈密尔顿图,则在哈密尔顿圈中必然存在X中的点与Y中的点相互交替出现,但是|X|不等于|Y|,则必然出现某两个点同属于|X|或者|Y|,但是G是偶图,属于同一集合的这样的两个点不可以相连,所以存在哈密尔顿圈矛盾,因而不存在哈密尔顿圈。
图论第一次作业答案(201099)

图论第一次作业答案(2010.9.9):1:证明 ()|E G |2v ⎛⎫≤ ⎪⎝⎭,其中G 是单图。
证:因为G 是单图,所以|()||()|v E G E K ≤又因为v |()|2v E K ⎛⎫≤⎪⎝⎭ ,所以()|E G |2v ⎛⎫≤ ⎪⎝⎭5:若N 个人的人群中至少有一个人未与每个人握手,求可能与每个人握手的最多有几个人?解:假设每个人为一个顶点,共有N 个顶点(V 1,V 2,。
V N ),俩人握手可看做两顶点相连,从而构成图G不是一般性,假设V i 与V j 没有握手,则V i 与V j 均未与所有人握手,所以至多有N-2个人与每个人握手。
4:画出不同构的一切四顶点图。
解:20: 证明每个顶皆2次的连通图是圈。
证:设P=v 0v 1v 2…. v n 为最长轨,由于()d v 2≡,所以v i (0<i<n )只能与v i -1和v i +1相连v 0除了与v 1相连,还与v x 相连,若v x 不P 上,则P 还可以加长,与最长轨定义矛盾,所以v x 在P 上。
对于P 上的任一顶点v i (0<i<n ),已经存在d (v i )=2,每个顶不可能有与之关联的第三条边,又因为此图是连通图,所以v x就是v n,此时原图为圈。
29,证明二分图的子图是二分图。
证明:设S是二分图G的子图。
且有,。
因,不妨设包含X中顶点子集和Y中顶点子集。
(1)若和都不为空。
又因,且X中任二顶不相邻,Y中任二顶不相邻,所以,中任二顶不相邻,中任二顶不相邻。
因此,S是二分图。
(2)若不为空,为空。
因X中任二顶不相邻,所以,中任二顶不相邻。
将分为,中任二顶不相邻,中任二顶不相邻。
因此,S是二分图。
(3)若为空,为空。
同(2)。
命题得证。
32,证明。
证明:对任意顶点有:。
(i=1,2, (v)因此,v,即,。
由Euler定理,得:。
命题得证。
中科院研究生院图论讲义习题1

第一章习题1. 对任何简单图G ,(1) 证明:(1)()2G υυε−≤;(2)(1)()2G υυε−=当且仅当G K ν≅。
2. 证明:(1),()m n K mn ε=;(2) 若G 是完全二部图,则2()4G υε≤。
3. 图G 有21条边,12个3度顶点,其余顶点的度均为2,求图G 的阶数。
4. 证明:任何简单图必有至少两个顶点具有相等的度。
5. 设G 是简单图,求G 的所有不同的生成子图的个数(包括G 本身和空图)。
6. 证明:任何图中,奇度顶点的个数总是偶数(包括0)。
并由此证明:在任一次聚会上握过奇数次手的人必为偶数个。
7. 证明或反证:如果u 和v 是图G 中仅有的具有奇数度的顶点,则G 包含一条u , v 路。
8. 证明:若4υ≥且1+=νε,则存在)(G V v ∈使得3)(≥v d 。
由此证明: n 个球队比赛(4n ≥),已赛完n +1场,则必定有一个球队已参加过至少3场比赛。
9. 在一个运动联盟中,将所有运动队组织成两个赛区,每个赛区有13个队,能否恰当安排比赛使得每个队在其所在赛区中进行9场比赛而与另一个赛区中的运动队进行4场比赛?10. 在平面上有n 个点12{,,,}n S x x x =⋅⋅⋅,其中任两个点之间的距离至少是1。
证明在这n 个点中,距离为1 的点对数不超过3n 。
11. 某次会议有n 人参加,其中有些人互相认识,但每两个互相认识的人,都没有共同的熟人,每两个互不认识的人都恰好有两个共同的熟人。
证明每一个参加者都有同样数目的熟人。
12. 在一个化学实验室里,有n 个药箱,其中每两个不同的药箱恰有一种相同的化学品,而且每种化学品恰好在两个药箱中出现,问:(1)每个药箱有几种化学品?(2)这n 个药箱中共有几种不同的化学品?13. 在一次舞会中,A 、B 两国留学生各(2)n n >人,A 国每个学生都与B 国一些(不是所有)学生跳过舞,B 国每个学生至少与A 国一个学生跳过舞。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
习题一:
●。
证明:作映射f : v i ↔ u i (i=1,2….10)
容易证明,对∀v i v j ∈E ((a)),有f (v i v j,),=,u i,u j,∈,E,((b)) (1≤ i ≤ 10,
1≤j ≤ 10 ) 由图的同构定义知,图(a)与(b)是同构的。
● 5.证明:四个顶点的非同构简单图有11个。
证明:设四个顶点中边的个数为m ,则有:
m=0:
m=1 :
m=2:
m=3:
m=4:
(a) v (b)
m=5:
m=6:
因为四个顶点的简单图最多就是具有6条边,上面所列出的情形是在不同边的条件下的不同构的情形,则从上面穷举出的情况可以看出四个顶点的非同构简单图有11个。
● 11.证明:序列(7,6,5,4,3,3,2)和(6,6,5,4,3,3,1)不是图序列。
证明:由于7个顶点的简单图的最大度不会超过6,因此序列(7,6,5,4,3,3,2)不是图序列;
(6,6,5,4,3,3,1)是图序列
非负整数组12121(,,,),,2n n n i i d d d d d d d m π==≥≥≥=∑是图序列的充要条件是:
⇔
11
12312(1,1,,1,,,)d d n d d d d d π++=---是图序列 (5,4,3,2,2,0)是图序列,然而(5,4,3,2,2,0)不是图序列,所以(6,6,5,4,3,3,1)不是图序列。
● 12.证明:若δ≥2,则G 包含圈。
证明:下面仅对连通图的下的条件下进行证明,不连通的情形可以通过分成若干个连通的情形来证明。
设V (G )={V 1,V 2,V 3,⋯V n },对于G 中的路V 1,V 2,V 3,⋯V n 若V k 与V 1邻接,则构成一个圈。
若V i1,V i2,V i3,⋯V in 是一条路,由于δ≥2,因此,对于V in ,存在V ik 与之邻接,则V ik ,,⋯V in V ik 构成一个圈。
● 17.证明:若G 不连通,则G ̅连通。
证明:对于任意的u,v ∈(G
̅),若u 与v 属于G 的不同连通分支,显然u 与v 在G ̅中连通;若u 与v 属于g 的同一连通分支,设w 为G 的另一个连通分支中的一个顶点,
则u 与w ,v 与w 分别在G
̅中连通,因此,u 与v 在G ̅中连通。
● 18.证明:若e ∈E(G),则w (G )≤w (G −e )≤w (G )+1.
证明:若e 为G 的割边,则w (G −e )= w (G )+1,若e 为G 的非割边,则w (G −e )=w (G ),所以,若e ∈E(G),则有w (G )≤w (G −e )≤w (G )+1.
习题二:
1.证明:非平凡树的最长路的起点和终点均是1度的。
证明设P =v 1v 2…v k 是非平凡树T 中一条最长路,若d(v 1)≥2则v 1与v k 在T 中的邻接点只能有一个,否则,若v 1与除了P 中顶点之外的其他顶点相连,则P 可以继续延长,这与P 是最长路是相矛盾的。
若v 1与P 上的某顶点相连,则就构成了圈,这与数相矛盾,推出P 不是最长路。
即说明v 1与v k 是树叶,则v 1与v k 均是一度的。
所以非平凡树的最长路的起点和终点均是1度的。
9.证明:顶点度数为偶数的连通图本身可构成一个包含所有边的闭迹。
证明:证明:由于G 是连通非平凡的且每个顶点度数为偶数,所以G 中至少存在圈C 1,从G 中去掉C 1中的边,得到G 的生成子图G 1,若G 1没有边,则G 的边集合能划分为圈。
否则,G 1的每个非平凡分支是度数为偶数的连通图,于是又可以抽取一个圈。
反复这样抽取,E(G)最终划分为若干圈。
设C 1是G 的边划分中的一个圈。
若G 仅由此圈组成,则G 显然是闭迹。
否则,由于G 连通,所以,必然存在圈C 2,它和C 1有公共顶点。
于是,C 1∪C 2是一条含有C 1与C 2的边的欧拉闭迹,如此拼接下去,得到包含G 的所有边的一条闭迹.
16.Kruskal 算法能否用来求:
(1)赋权连通图中的最大权的树?
(2)赋权图中的最小权的最大森林?如果可以,怎样实现?
答:1、不能,由Kruskal 算法得到的任何生成树一定是最小生成树。
2、能
a.选择边e1使其权值最小
b.若已经选定边e1 e2 e3 ……ek ,则从E-{e1,e2,e3……ek},选择边ek+1 c .G[e1,e2,e3……ek]为无圈图,且可以不连通
d .ek+1的权值w (eK+1)尽可能小
e .当a 、b 、c 不能进行时,停止。
习题三:
1.证明:e 是连通图G 的割边当且仅当V(G)可划分为两个子集V1和V2,使对任意u ∈V 1及v ∈V 2, G 中的路(u ,v )必含e .
证明:必要性: e 是G 的割边,故G −e 至少含有两个连通分支,设V 1是其中一个连通分支的顶点集,V 2是其余分支的顶点集,对12,u V v V ∀∈∀∈,因为G −e
中的u,v 不连通,而在G 中u 与v 连通,所以e 在每一条(u,v)路上,G 中的(u,v)必含e 。
充分性:取12,u V v V ∈∈,由假设G 中所有(u,v)路均含有边e ,从而在G −e 中
不存在从u 与到v 的路,这表明G −e 不连通,所以e 是割边。
3.设G 是阶大于2的连通图,证明下列命题等价:
(1) G 是块
(2) G 无环且任意一个点和任意一条边都位于同一个圈上;
(3) G 无环且任意三个不同点都位于同一条路上。
(1)→(2):
G 是块,任取G 的一点u ,一边e ,在e 边插入一点v ,使得e 成为两条边,由此得到新图G 1,显然G 1的是阶数大于2的块,由定理4,G 1中的u,v 位于同一个圈上,于是G 中u 与边e 都位于同一个圈上。
(2)→(3):
G 无环,且任意一点和任意一条边都位于同一个圈上,任取G 的点u ,边e ,若u 不在e 上,则三个不同点位于同一个圈,即位于同一条路,如u 在e 上,由定理e 的两点在同一个圈上,在e 边插入一个点v ,使得e 成为2条边,由此得到新图G 1,显然G 1的是阶数大于2的块,则两条边的三个不同点在同一条路上。
(3)→(1):
G 连通,若G 不是块,则G 中存在着割点u ,划分为不同的子集块V 1, V 2, V 1, V 2无环,12,x v y v ∈∈,点u 在每一条(x,y)的路上,由于x,y 的任意性,则三个不同点不能位于同一条路上,则与已知矛盾,G 是块。
7.证明:若v 是简单图G 的一个割点,则v 不是补图G
̅的割点。
证明:v 是单图G 的割点,则G −v 至少两个连通分支。
现任取x,y ∈V(G −v), 如果x,y 在G −v 的同一分支中,令u 是与x,y 处于不同分支的点,那么,通过u ,可说明,x,与y 在G −v 的补图中连通。
若x,y 在G −v 的不同分支中,则它们在G −v 的补图中邻接。
所以,若v 是G 的割点,则v 不是其补图的割点。
12.对图3——20给出的图G1和G2,求其连通度和边连通度,给出相应的最小点割和最小边割。
解:()12G κ= 最小点割 {6,8}
1()2G λ= 最小边割{(6,5),(8,5)} {(6,7),(8,7)}{(6,9),(8,9)}
()25G κ= 最小点割{6,7,8,9,10}
2()5G λ= 最小边割{(2,7),(1,6),(5,10),(4,9),(3,8)}
13.设H 是连通图G 的子图,举例说明:有可能k(H)> k(G).
解:
通常k (H )<k(G).
e
H
整个图为G,割点e左边的图H为G的的子图,k(H)=3k(G)=1,则k(H)>k(G).。
