【2019年整理】电桥灵敏度与线性度比较
电桥灵敏度研究
电桥灵敏度研究张云义广东省惠州市一中(516001)一、惠斯登电桥惠斯登电桥是准确测量电阻的一种重要方法。
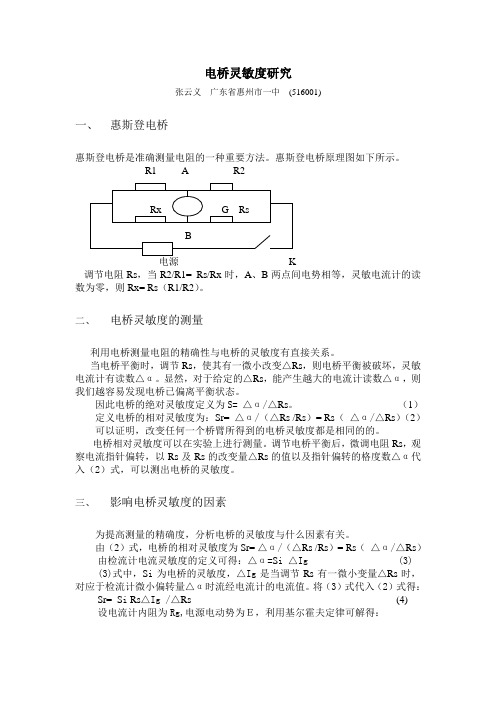
惠斯登电桥原理图如下所示。
R1 A R2调节电阻Rs,当R2/R1= Rs/Rx时,A、B两点间电势相等,灵敏电流计的读数为零,则Rx= Rs(R1/R2)。
二、电桥灵敏度的测量利用电桥测量电阻的精确性与电桥的灵敏度有直接关系。
当电桥平衡时,调节Rs,使其有一微小改变△Rs,则电桥平衡被破坏,灵敏电流计有读数△α。
显然,对于给定的△Rs,能产生越大的电流计读数△α,则我们越容易发现电桥已偏离平衡状态。
因此电桥的绝对灵敏度定义为S= △α/△Rs。
(1)定义电桥的相对灵敏度为:Sr=△α/(△Rs /Rs)= Rs(△α/△Rs)(2)可以证明,改变任何一个桥臂所得到的电桥灵敏度都是相同的的。
电桥相对灵敏度可以在实验上进行测量。
调节电桥平衡后,微调电阻Rs,观察电流指针偏转,以Rs及Rs的改变量△Rs的值以及指针偏转的格度数△α代入(2)式,可以测出电桥的灵敏度。
三、影响电桥灵敏度的因素为提高测量的精确度,分析电桥的灵敏度与什么因素有关。
由(2)式,电桥的相对灵敏度为Sr=△α/(△Rs /Rs)= Rs(△α/△Rs)由检流计电流灵敏度的定义可得:△α=S i △Ig (3)(3)式中,S i为电桥的灵敏度,△Ig是当调节Rs有一微小变量△Rs时,对应于检流计微小偏转量△α时流经电流计的电流值。
将(3)式代入(2)式得:Sr=S i Rs△Ig /△Rs (4)设电流计内阻为Rg,电源电动势为E,利用基尔霍夫定律可解得:-R1E△Rs△Ig=(5) R1Rx(R2+Rs)+R2Rs(R1+Rx)+Rg(R1+Rx)(R2+Rs)由(5)式代入(4)式可得S iESr= (6) (R1++R2+Rx+Rs)+Rg(1+Rx/R1)(1+Rs/R2)(6)式说明了电桥的灵敏度与电流计的灵敏度Si,电源电动势E,电流计的内阻Rg,四条臂上的总电阻,以及对应臂的电阻比值Rx/R1、Rs/R2有关。
2020年智慧树知道网课《机械工程测试技术基础(黑龙江联盟)》课后章节测试满分答案12

绪论单元测试【单选题】(2 分)仪器结构不完善所引起的误差属于()A.过失误差过失误差过失误差引用误差引用误差引用误差引用误差C. 系统误差D. 随机误差2【单选题】(2 分)判断下列语句正确的是()A.精度就是指精密度B.准确度高则正确度不一定高C.精确度高则正确度一定高D.正确度高而精密度不一定高3【单选题】(2 分)现有0~300°C、0.5 级和0 ~120°C 、1 级的两支温度计,预测两量精度高的是()A.A 、B 均可A 、B 都不对C. 用0~300° C、 0.5 级D.用 0~120°C、 1 级4【单选题】(2 分)通常用来表征仪器本身精度、而不是测量的精度。
()A.相对误差B.量化误差C.引用误差绝对误差100°C 左右的温度,测D.【单选题】(2 分)系统误差具有的性质是()A.偶然性B.不可消除或减弱性C.规律性D.随机性【判断题】(2 分)测量结果不可避免地存在误差,任何观测值都存在误差()错B.【判断题】(2 分)观测条件好,则成果精度就高;观测条件差,则成果精度就低()A.错B.对8【判断题】(2 分)观测误差与观测成果精度成反比()A.错B.对9【判断题】(2 分)产生系统误差的主要原因是测量仪器和工具构造不完善或校正不完全准确()A.对B.错10【判断题】(2 分)系统误差和偶然误差通常是同时产生的,是偶然误差()当系统误差消除或减弱后,决定观测精度的主要A.错B.对第一章测试1【单选题】(2 分)周期信号的频谱是()A.离散的,个频率成分的频率比不是有理数B. 离散的,只发生在基频整数倍的频率C.连续的,只在有限区间有非零值D.连续的,随着频率的增大而减小2【单选题】(2 分)瞬变信号的频谱是()A.离散的,个频率成分的频率比不是有理数B.连续的,随着频率的增大而减小C.离散的,只发生在基频整数倍的频率D.连续的,只在有限区间有非零值3【单选题】(2 分)对于x (t)=2sin (2πt+0.5 )+cos (πt+0.2 )和y(t)= sin(πt+0.5)两个信号,下面描述正确的是()A.都是瞬变信号B.x(t)是周期信号, y(t)是瞬变信号C.y(t)是周期信号, x(t)是瞬变信号D.都是周期信号4【单选题】(2 分)若F[x(t)]=X(f),k 为大于零的常数,则有A.1/kx ( kf)B.x(f/k)1/kx ( f/k )5【单选题】(2 分)描述周期信号的数学工具是()A.傅氏变换相关函数C.傅氏级数拉氏级数kx(kf)D.F[x(kt)]=B.6【判断题】(2 分)非周期变化的信号就是随机信号()A.错B.对7【判断题】(2 分)脉冲信号的频谱等于常数()A.对B.错8【判断题】(2 分)单边频谱和双边频谱是信号等价的描述方法()A.对B.9【判断题】(2 分)非周期信号的幅值谱表示的是其幅值谱密度与时间的函数关系()A.错B.对10 【判断题】(2 分)周期单位脉冲序列的频谱仍为周期单位脉冲()A.对B.错第二章测试1【单选题】(2 分)在一测试系统中,被测信号的频率为1000HZ ,幅值为5V ,另有两干扰信号分别为2000 HZ ,7V 和800HZ ,4V ,则利用()提取有用信息A.比例性B.频率保持性C.幅值保持性D.叠加性2【单选题】(2 分)信噪比越大,则()A.有用信号成分越大,噪声的影响越大B.有用信号成分越小,噪声影响越小C.有用信号成分越大,噪声的影响越小D.有用信号成分越小,噪声影响越大3【单选题】(2 分)传感器的输出量对于随时间变化的输入量的响应特性称为传感器的(A.静态B.幅频4【单选题】(2 分)传感器的静态特性中,输出量的变化量与引起此变化的输入量的变化量之比为(A.稳定性C.线性度回程误差5【单选题】(2 分)下列哪个参数反映测试系统的随机误差的大小?(C.输入输出相频)特性D.灵敏度A.灵敏度B. 线性度C. 滞后量D. 重复性判断题】 (2 分 )用一阶系统做测试系统,为了获得较佳的工作性能,其时间常数 A.7【判断题】 (2 分 )用二阶系统作测量装置时,为获得较宽的工作频率范围,系统的阻尼比应接近于A.错对B. τ应尽量大()0.707 对错8【判断题】(2 分)二阶系统中,当降频特性中φ(ω)=90°所对应的频率ω 作为系统固有频率该值与系统阻尼比的大小略有关系。
《机械工程测试技术基础》期末试题及答案

第一章 信号及其描述(一)填空题1、 测试的基本任务是获取有用的信息,而信息总是蕴涵在某些物理量之中,并依靠它们来传输的。
这些物理量就是 信号 ,其中目前应用最广泛的是电信号。
2、 信号的时域描述,以 时间 为独立变量;而信号的频域描述,以 频率 为独立变量。
3、 周期信号的频谱具有三个特点: 离散性 , 谐波性 , 收敛性 。
4、 非周期信号包括 准周期 信号和 瞬变周期 信号。
5、 描述随机信号的时域特征参数有 均值 、 均方值 、 方差 。
6、 对信号的双边谱而言,实频谱(幅频谱)总是 关于Y 轴 (偶) 对称,虚频谱(相频谱)总是 关于原点(奇) 对称。
(二)判断对错题(用√或×表示)1、 各态历经随机过程一定是平稳随机过程。
( √ )2、 信号的时域描述与频域描述包含相同的信息量。
( √ )3、 非周期信号的频谱一定是连续的。
( × )4、 非周期信号幅频谱与周期信号幅值谱的量纲一样。
( × )5、 随机信号的频域描述为功率谱。
( √ )(三)简答和计算题1、 求正弦信号t x t x ωsin )(0=的绝对均值μ|x|和均方根值x rms 。
2、 求正弦信号)sin()(0ϕω+=t x t x 的均值x μ,均方值2x ψ,和概率密度函数p(x)。
3、 求指数函数)0,0()(≥>=-t a Ae t x at 的频谱。
4、 求被截断的余弦函数⎩⎨⎧≥<=T t T t t t x ||0||cos )(0ω的傅立叶变换。
5、 求指数衰减振荡信号)0,0(sin )(0≥>=-t a t e t x at ω的频谱。
第二章 测试装置的基本特性(一)填空题1、 某一阶系统的频率响应函数为121)(+=ωωj j H ,输入信号2sin )(t t x =,则输出信号)(t y 的频率为=ω ,幅值=y ,相位=φ 。
2、 试求传递函数分别为5.05.35.1+s 和2224.141n n ns s ωωω++的两个环节串联后组成的系统的总灵敏度。
电桥灵敏度定义式

电桥灵敏度定义式电桥灵敏度是指电桥对于被测量物理量的变化的敏感程度。
电桥是一种用来测量电阻、电容或电感等被测量物理量的仪器,其基本原理是通过比较电桥两边的电势差来确定被测量物理量的大小。
电桥灵敏度是评价电桥的重要指标之一,它描述了电桥输出信号相对于被测量物理量变化的响应程度。
在电桥中,通过调节电桥的元件,可以使电桥平衡,即电桥两边的电势差为零。
当被测量物理量发生变化时,电桥就会失去平衡,产生一个不为零的电势差。
电桥灵敏度就是描述这个电势差与被测量物理量变化之间的关系。
电桥灵敏度的定义式为:S = ΔV/ΔX其中,S表示电桥的灵敏度,ΔV表示电桥输出信号的变化,ΔX表示被测量物理量的变化。
电桥灵敏度的单位通常为V/m或V/Ω,其中m表示被测量物理量的单位,Ω表示电阻的单位。
电桥灵敏度的大小取决于电桥的设计和元件的选择。
一般来说,电桥灵敏度越大,电桥对于被测量物理量的变化越敏感。
对于一些精密测量,需要选择灵敏度较高的电桥。
为了提高电桥的灵敏度,可以采取以下几种措施:1. 选择合适的电桥元件:不同的电桥元件对于不同的被测量物理量具有不同的灵敏度。
在实际应用中,应根据具体的测量要求选择合适的电桥元件。
2. 提高电桥元件的灵敏度:可以通过增加电桥元件的长度、面积或导电性来提高其灵敏度。
例如,对于电阻片,可以选择细丝电阻片或薄膜电阻片,以提高电桥的灵敏度。
3. 优化电桥电路:可以采用差分放大器等电路来增强电桥的输出信号,并降低噪声干扰,从而提高灵敏度。
4. 降低电桥的噪声:可以通过选择低噪声元件、优化接线和屏蔽来降低电桥的噪声,提高灵敏度。
需要注意的是,虽然电桥灵敏度越大越好,但过高的灵敏度也会增加电桥的噪声和误差。
因此,在实际应用中,需要根据具体的测量要求和条件,选择合适的电桥灵敏度。
电桥灵敏度是评价电桥性能的重要指标之一,它描述了电桥对于被测量物理量变化的响应程度。
通过选择合适的电桥元件、优化电桥电路和降低噪声,可以提高电桥的灵敏度,从而实现更精确的测量。
线性度实验报告

线性度实验报告篇一:传感器实验报告传感器实验报告(二)自动化1204班蔡华轩 UXX13712 吴昊 UXX14545实验七:一、实验目的:了解电容式传感器结构及其特点。
二、基本原理:利用平板电容C=εA/d 和其它结构的关系式通过相应的结构和测量电路可以选择ε、A、d 中三个参数中,保持二个参数不变,而只改变其中一个参数,则可以有测谷物干燥度(ε变)测微小位移(变d)和测量液位(变A)等多种电容传感器。
三、需用器件与单元:电容传感器、电容传感器实验模板、测微头、相敏检波、滤波模板、数显单元、直流稳压源。
四、实验步骤:1、按图6-4 安装示意图将电容传感器装于电容传感器实验模板上。
2、将电容传感器连线插入电容传感器实验模板,实验线路见图7-1。
图 7-1 电容传感器位移实验接线图3、将电容传感器实验模板的输出端V01 与数显表单元Vi 相接(插入主控箱Vi 孔),Rw 调节到中间位置。
4、接入±15V 电源,旋动测微头推进电容传感器动极板位置,每间隔0.2mm图(7-1)五、思考题:试设计利用ε的变化测谷物湿度的传感器原理及结构,并叙述一下在此设计中应考虑哪些因素?答:原理:通过湿度对介电常数的影响从而影响电容的大小通过电压表现出来,建立起电压变化与湿度的关系从而起到湿度传感器的作用;结构:与电容传感器的结构答大体相同不同之处在于电容面板的面积应适当增大使测量灵敏度更好;设计时应考虑的因素还应包括测量误差,温度对测量的影响等六:实验数据处理由excle处理后得图线可知:系统灵敏度S=58.179非线性误差δf=21.053/353=6.1%实验八直流激励时霍尔式传感器位移特性实验一、实验目的:了解霍尔式传感器原理与应用。
二、基本原理:霍尔式传感器是一种磁敏传感器,基于霍尔效应原理工作。
它将被测量的磁场变化(或以磁场为媒体)转换成电动势输出。
根据霍尔效应,霍尔电势UH=KHIB,当霍尔元件处在梯度磁场中运动时,它就可以进行位移测量。
电桥灵敏度与线性度比较

闽江学院本科毕业论文(设计)题目电桥的灵敏度和线性度比较研究学生姓名欧爱华学号 120031001051系别物理学与电子信息工程系年级 2003级专业物理学指导教师苏启录职称副教授完成日期 2006.12.01-2007.5.20目录摘要、关键词 (1)1.引言 (1)2.惠斯登电桥原理 (2)3.惠斯登电桥非平衡工作状态下线性度和灵敏度的理论探讨 (4)3.1单桥 (4)3.2半桥 (5)3.3 全桥 (5)4.惠斯登电桥非平衡工作状态下线性度和灵敏度的实验研究 (6)4.1单桥实验研究 (6)4.2半桥实验研究 (9)4.3全桥实验研究 (14)4.4总结 (15)5.结束语 (16)6.参考文献 (16)电桥线性度和灵敏度的比较研究欧爱华闽江学院物理学与电子信息工程系03级物理教育学号:120031001051指导老师:苏启录副教授摘要:灵敏度和线性度是惠斯登电桥的两个重要性能。
本文就单桥、半桥、全桥等惠斯登电桥不同桥路形态下的灵敏度和线性度进行比较研究,以便实践中更好地应用惠斯登电桥。
关键词:惠斯登电桥;电阻;灵敏度;线性度Abstract: The sensitivity and linear are the wheatstone bridge twoimportant performance. This article on Shan Qiao, half bridge, theentire bridge and so on under the wheatstone bridge different bridgeconnection shape sensitivity and linear conducts the comparisonresearch, in order to practices applies the wheatstone bridge well.Key word: Wheatstone bridge; Resistance; Sensitivity; Linear1.引言:电桥的桥路形式多种多样,特性千差万别。
电气与电子测量技术(罗利文)课后习题答案
由此可见,等效阻抗与电阻率、磁导率以及几何形状有关,还与线圈的几何数、线圈中激磁电流频率f有关,同时还与线圈与导体间的距离x有关。
由此可知
M与距离x相关,可用于测量位移、振幅,厚度等。
R1、R2与传感线圈、金属导体的电导率有关,且电导率是温度函数,可用于测量表面温度、材质判别等。
设输入交流电压 为正半周,即A点为正,B点为负,则二极管 、 导通, 、 截止。在A→E→C→B支路中,C点电位由于 的增大而比平衡时低;在A→F→D→B支路中,D点电位由于 的减小而比平衡时高,即D点电位高于C点电位,此时直流电压表正向偏转。
设输入交流电压 为负半周,即A点为负,B点为正,则二极管 、 导通, 、 截止。在B→C→F→A支路中,C点电位由于 的减小而比平衡时低。在B→D→E→A支路中,D点电位由于 的增加而比平衡时的电位高。所以仍然是D点电位高于C点电位,直流电压表正向偏转。因此只要衔铁上移,不论输入电压是正半周还是负半周,电压表总是正向偏转,即输出电压 总为下正上负。
解:
图3-7变压器式交流电桥
图3-7的交流电桥图中,当衔铁向上移动和向下移动相同距离时,其输出大小相等,方向பைடு நூலகம்反。由于电源电压是交流,所以尽管式中有正负号,还是无法加以分辨。可采用带有相敏整流的交流电路,如图3-8所示。
图3-8相敏整流交流电路
当衔铁处于中间位置时,Z1=Z2=Z0,电桥处于平衡状态,输出电压 ;当衔铁上移,使上线圈阻抗增大,Z1=Z0+Z,而下线圈阻抗减少,Z2=Z0Z。
图3.1压电传感器的等效电路
由于外力作用而在压电材料上产生的电荷只有在无泄漏的情况下才能保存,即需要测量回路具有无限大的输入阻抗,这实际上是不可能的,因此压电式传感器不能用于静态测量。压电材料在交变力的作用下,电荷可以不断补充,以供给测量回路一定的电流,故适用于动态测量。
电气与电子测量技术罗利文课后习题答案
电气与电子测量技术罗利文课后习题答案集团标准化工作小组 [Q8QX9QT-X8QQB8Q8-NQ8QJ8-M8QMN]第3章常用传感器及其调理电路3-1 从使用材料、测温范围、线性度、响应时间几个方面比较,Pt100、K 型热电偶、热敏电阻有什么不同 解(1)电气设备的过载保护或热保护电路;(2)温度范围为?100~800℃,温度变化缓慢;(3)温度范围为?100~800℃,温度波动周期在每秒5~10次; 解:(1)热敏电阻;测量范围满足电力设备过载时温度范围,并且热敏电阻对温度变化响应快,适合电气设备过载保护,以减少经济措施(2)Pt 热电阻;测温范围符合要求,并且对响应速度要求不高(3)用热电偶;测温范围符合要求,并且响应时间适应温度波动周期为100ms 到200ms 的情况3-3 热电偶测温为什么一定做冷端温度补偿冷端补偿的方法有哪几种解:热电偶输出的电动势是两结点温度差的函数。
T 为被测端温度,0T 为参考端温度,热电偶特性分度表中只给出了0T 为0℃时热电偶的静态特性,但在实际中做到这一点很困难,于是产生了热电偶冷端补偿问题。
目前常用的冷端温度补偿法包括:0℃恒温法;冷端温度实时测量计算修正法; 补偿导线法; 自动补偿法。
3-4 采用Pt100的测温调理电路如图3-5所示,设Pt100的静态特性为:R t =R 0(1+At ),A =℃,三运放构成的仪表放大电路输出送0~3V 的10位ADC ,恒流源电流I 0= 1mA ,如测温电路的测温范围为0~512℃,放大电路的放大倍数应为多少可分辨的最小温度是多少度解:V AT R I u R 19968.05120039.010*******=⨯⨯⨯⨯==∆-024.1519968.03==∆=VVu u k R out ,放大倍数应为15倍。
可分辨的最小温度为3-5 霍尔电流传感器有直测式和磁平衡式两种,为什么说后者的测量精度更高解:霍尔直测式电流传感器按照安培环路定理,只要有电流I C 流过导线,导线周围会产生磁场,磁场的大小与流过的电流I C 成正比,由电流I C 产生的磁场可以通过软磁材料来聚磁产生磁通?=BS ,那么加有激励电流的霍尔片会产生霍尔电压U H 。
自动化检测实验指导
自动化检测实验指导实验一应变片单臂、半桥、全桥特性比较一、实验目的:了解电阻应变片的工作原理与应用并掌握应变片测量电路。
二、基本原理:电阻应变式传感器是在弹性元件上通过特定工艺粘贴电阻应变片来组成,一种利用电阻材料的应变效应将工程结构件的内部变形转换为电阻变化的传感器,此类传感器主要是通过一定的机械装置将被测量转化成弹性元件的变形,然后由电阻应变片将变形转换成电阻的变化,再通过测量电路将电阻的变化转换成电压或电流变化信号输出。
可用于能转化成变形的各种非电物理量的检测,如力、压力、加速度、力矩、重量等,在机械加工、计量、建筑测量等行业应用十分广泛。
三、需用器件与单元:机头中的应变梁的应变片、测微头;显示面板中的F/V表(或电压表)、±2V~±10V步进可调直流稳压电源;调理电路面板中传感器输出单元中的箔式应变片、调理电1位数显万用表(自备)。
路单元中的电桥、差动放大器;42五、实验步骤:1位数显万用表2kΩ电阻档测量所有在应变梁自然状态(不受力)的情况下,用42应变片阻值;在应变梁受力状态(用手压、提梁的自由端)的情况下,测应变片阻值,观察一下应变片阻值变化情况(标有上下箭头的4片应变片纵向受力阻值有变化;标有左右箭头的2片应变片横向不受力阻值无变化,是温度补偿片)。
如下图1—7所示。
图1—7观察应变片阻值变化情况示意图差动放大器调零点:按下图1—8示意接线。
将F/V表(或电压表)的量程切换开关切换到2V档,合上主、副电源开关,将差动放大器的增益电位器按顺时针方向轻轻转到底后再逆向回转一点点(放大器的增益为最大,回转一点点的目的:电位器触点在根部估计会接触不良),调节差动放大器的调零电位器,使电压表显示电压为零。
差动放大器的零点调节完成,关闭主电源。
图1—8差放调零接线图3、应变片单臂电桥特性实验:⑴将±2V~±10V步进可调直流稳压电源切换到4V档,将主板上传感器输出单元中的箔式应变片(标有上下箭头的4片应变片中任意一片为工作片)与电桥单元中R1、R2、R3组成电桥电路,电桥的一对角接±4V直流电源,另一对角作为电桥的输出接差动放大器的二输入端,将W1电位器、r电阻直流调节平衡网络接入电桥中(W1电位器二固定端接电桥的±4V电源端、W1的活动端r电阻接电桥的输出端),如图1—9示意接线(粗细曲线为连接线)。
《检测与传感技术》思考题答案
答:直流电桥是测量小电阻的一种电路,分为单臂电桥、半桥和全桥。半桥输出电压为单臂电桥的2倍,全桥输出电压为半桥的2倍。
2-4拟在等截面的悬臂梁上粘贴4个完全相同的电阻应变片,并组成差动全桥电路,试问:
①4个应变片应怎样粘贴在悬臂梁上?
4.4根据螺管型差动变压器的基本特性,说明其灵敏度和线性度的主要特点。
答:差动变压器的结构如图所示,主要由一个初级线圈、两个次级线圈和插入线圈中央的圆柱形铁芯等组成。
差动变压器传感器中的两个次级线圈反相串联,并且在忽略铁损、导磁体磁阻和线圈分布电容的理想条件下,当衔铁位于中心位置时,两个次级线圈感应电压大小相等、方向相反,差动输出电压为零,但实际情况是差动变压器输出电压往往并不等于零。差动变压器在零位移时的输出电压称为零点残余电压,它的存在使传感器的输出特性不经过零点,造成实际特性与理论特性不完全一致,使传感器的灵敏度降低,分辨率变差和测量误差增大。
解:
3-7简述差动式电容测厚传感器系统的工作原理。
答:电容测厚传感器是用来对金属带材在轧制过程中厚度的检测,其工作原理是在被测带材的上下两侧各置放一块面积相等,与带材距离相等的极板,这样极板与带材就构成了两个电容器C1、C2。把两块极板用导线连接起来成为一个极,而带材就是电容的另一个极,其总电容为C1+C2,如果带材的厚度发生变化,将引起电容量的变化,用交流电桥将电容的变化测出来,经过放大即可由电表指示测量结果。
4.5概述差动变压器的应用范围,并说明用差动变压器式传感器检测振动的基本原理。
答:差动变压器式传感器可以直接用于位移测量,也可以测量与位移有关的任何机械量,如振动、加速度、应变、比重、张力和厚度等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
闽江学院本科毕业论文(设计)题目电桥的灵敏度和线性度比较研究学生姓名欧爱华学号 120031001051系别物理学与电子信息工程系年级 2003级专业物理学指导教师苏启录职称副教授完成日期 2006.12.01-2007.5.20目录摘要、关键词 (1)1.引言 (1)2.惠斯登电桥原理 (2)3.惠斯登电桥非平衡工作状态下线性度和灵敏度的理论探讨 (4)3.1单桥 (4)3.2半桥 (5)3.3 全桥 (5)4.惠斯登电桥非平衡工作状态下线性度和灵敏度的实验研究 (6)4.1单桥实验研究 (6)4.2半桥实验研究 (9)4.3全桥实验研究 (14)4.4总结 (15)5.结束语 (16)6.参考文献 (16)电桥线性度和灵敏度的比较研究欧爱华闽江学院物理学与电子信息工程系03级物理教育学号:120031001051指导老师:苏启录副教授摘要:灵敏度和线性度是惠斯登电桥的两个重要性能。
本文就单桥、半桥、全桥等惠斯登电桥不同桥路形态下的灵敏度和线性度进行比较研究,以便实践中更好地应用惠斯登电桥。
关键词:惠斯登电桥;电阻;灵敏度;线性度Abstract: The sensitivity and linear are the wheatstone bridge twoimportant performance. This article on Shan Qiao, half bridge, theentire bridge and so on under the wheatstone bridge different bridgeconnection shape sensitivity and linear conducts the comparisonresearch, in order to practices applies the wheatstone bridge well.Key word: Wheatstone bridge; Resistance; Sensitivity; Linear1.引言:电桥的桥路形式多种多样,特性千差万别。
总的可以把电桥可分为直流电桥、交流电桥。
直流电桥可以用于测电阻,交流电桥可用于测电容、电感。
我们所研究的是直流电桥即惠斯登电桥。
惠斯登电桥的原理在许多方面得到广泛应用,比如工业、农业、军事、医学、传感器等方面。
通过传感器可以将压力、温度等非电学量转化为传感器阻抗的变化进行测量。
惠斯登电桥的灵敏度的高低又关系到测量的结果的精确。
影响惠斯登电桥的灵敏度的因素又是各种各样的,本文中主要是从桥臂电阻方面研究电桥的灵敏度和线性度。
在惠斯登电桥中,我们对三种桥路(即:单桥、半桥和全桥)进行研究,主要是研究在不同桥臂下电桥的灵敏度和线性度。
通过对电桥的线性度和灵敏度的研究,可以更好的把惠斯登电桥特性运用到当代的测量技术中去。
2. 惠斯登电桥原理电桥是一种可以精确测量电阻的仪器。
如图1所示是一个通用的惠斯登电桥。
电阻1R ,2R ,3R ,X R 叫做电桥的四个臂,在C 、D 两端可以接检流计,用以检查它所在的支路有无电流。
当无电流通过时,称电桥达到平衡。
平衡时,四个臂的阻值满足一个简单的关系,利用这一关系就可测量电阻。
平衡时,检流计所在支路电流为零,则有:(1)流过1R 和3R 的电流相同(记作1I ),流过2R 和X R 的电流相同(记作2I )。
(2)C ,D 两点电位相等,即C U =D U 。
因而有1I 1R =2I 2R ;三个阻值已知,便可求得第四个电阻。
测量时,选择适当的电阻作为1R 和2R ,用一个可变电阻作为3R ,令被测电阻充当X R ,调节3R 使电桥平衡,电阻而且可利用高灵敏度的检流计来测零。
当电桥平衡时:Rx=21R R 3R (1) 当Rx 电桥偏离平衡阻值变化时△Rx 时,电桥可能偏离平衡,C 、D 两点不再等电位。
如C 、D 间接毫伏表,则毫伏表电压值为ΔU ;如C 、D 间接电流计,则电流计示值为ΔI 。
平衡监测仪选用电流计时,电桥测量灵敏度为:I S = XXI R R ∆∆ (2)平衡检测仪表选用毫伏表时,电桥测量灵敏度为:V S =X XUR R ∆∆ (3) 电桥测量灵敏度反映了电桥平衡监测仪表示值变化对待测电阻阻值相对变化的反映灵敏程度。
电路图1中,根据基尔霍夫定律可得惠斯登电桥测量灵敏度数学表达式为:I S =X X IR R ∆∆ = ()212322ab X a X X V R R R R R R R R R ⎛⎫++++++ ⎪⎝⎭(4) 其中A R 为电流表内阻。
V S =X X UR R ∆∆ =()123222ab X X X V V R R R R R R R R R +++⎛⎫+++ ⎪⎝⎭(5) 其中V R 为毫伏表内阻。
令:Rz=1R +2R +3R +X R ,表示桥臂电阻阻值总和;X=2XR R ,表示桥臂电阻率;K= 2XR R + 2X R R +2,表示桥臂电阻比率相关的量。
则有:V S = abZ vV R K R +(6) I S =aba ZV KR R + (7)与电桥灵敏度S 相关的物理量有:电桥端电压Vab 、桥臂电阻阻值总和Rz 、桥臂电阻比率X 、检测仪表的灵敏度和内阻。
本文是通过桥臂电阻阻值总和来研究电桥的灵敏度和线性度。
3. 惠斯登电桥非平衡工作状态下线性度和灵敏度的理论探讨自组惠斯登电桥原理与惠斯登电桥原理相同。
本实验中通过研究在不同桥路电桥灵敏度和线性度,来比较电桥的性能。
实验中通过三种桥路的比较,即单桥(通过改变其中一个电阻的变化,并且研究当电阻增大、减小的情况)、半桥(同时改变二个电阻的大小,相邻电阻一个增大一个减小,相对电阻同时增大或减小)、全桥(四个电阻同时改变,相邻的一个增大一个减小,相对的同时增或减小)。
通过这三种桥路的比较,研究电桥非平衡工作状态下线性度和灵敏度。
本实验的电路图如图1所示,图中通过四个电阻箱的连接,并在电阻1R 3R 和2R 4R 中间接数字毫伏表,通过测量在不同桥路下(单桥、半桥、全桥)的阻值变化与输出电压变化之间的关系。
通过实验数据分析在不同情况下电桥的灵敏度和线性度。
通过灵敏度和线性度的分析,把这些知识更好的运用到实际中去。
3.1 单桥:如图1所示当电桥平衡时,13R R =24R R ,电路C 、D 两点间的电势差D Uc =0。
若此时使一个桥臂的电阻(4R )增加上一个很小的电阻R ∆,则电桥失去平衡,电路中C 、D 两点间存在一定的电势差D Uc 。
该电势差为电桥不平衡时输出的电压。
若电桥的稳压电源电压为U ,根据串联电阻分压原理,A 点为零电势参考点,则电桥输出电压为:=C U -D U =434231R RR U R R R R R +∆⎛⎫- ⎪+∆++⎝⎭=()()12413R RU R R R R R ∆+∆++ =23444111RU R R R R R R R ∆∆⎛⎫⎛⎫+++ ⎪⎪⎝⎭⎝⎭ (8) 令电桥比率K=13R R ,根据电桥平衡条件,13R R =24R R ,且当△R4R 时,略去分母中的微小项4RR ∆,有: =4U R R∆ (9)若4RR ∆不能略去,则: =4411R KR U R K K K R ∆∆+⎛⎫++ ⎪⎝⎭(10)定义V S =X XUR R ∆∆为电压输出的电桥灵敏度,则有: V S =()21KUK + (11)由(9)式可知, 当1RR∆时,非平衡电桥的输出电压与R ∆成线性关系。
由(11)式可知,电桥的电压灵敏度由选择的电桥比率K 及供电电源电压所决定。
如果,电桥供电电压一定,当K=1时,电桥输出电压灵敏度最大,且为:=4U(12) 3.2 半桥:在惠斯登电桥电路中,若相邻臂内接入两个变化量相同,而变化量符号相反的两个电阻,或者是相对的两个电阻变化量相同且变化量符号也相同的电阻,这样的电路就叫做半桥电路。
对于半桥电路 ,若电桥开始是平衡的,则13R R =24R R 。
在对称情况下1R =3R =2R =4R =R ,Δ2R =Δ4R =△R ,则半桥电路输出电压为:=2U RR∆ (13) 电桥的输出电压灵敏度:S =2U(14)可见,半桥电路的输出电压灵敏度比单臂输入时的最大电桥电压灵敏度提高了一倍。
3.3 全桥:在惠斯登电桥电路中,若电桥的四个臂都发生变化。
即相邻臂的两个电阻变化量相同但符号相反,相对的两个臂变化量和符号都相同,这样的电路就叫做全桥电路。
对于全桥电路,若电桥开始是平衡的,则13R R =24R R 。
在对称情况下1R =3R =2R =4R =R ,Δ1R =Δ2R =Δ3R =Δ4R =△R ,则全桥电路输出电压为:=U RR∆ (15) 电桥的输出电压灵敏度:S =U(16)4. 惠斯登电桥非平衡工作状态下线性度和灵敏度的实验研究在本文选用自组惠斯登电桥来测量电桥的灵敏度和线性度,实验原理图如图1所示,平衡监测仪表选用数字毫伏表。
图中的电阻1R 、2R 、3R 、4R 选用ZX21A 电阻箱。
图中的电压选用直流电压。
实验设备:QJ3005S 直流稳压电源、ZX21A 电阻箱、GDM-8135台式数字万用表。
4.1 单桥实验研究1R =2R =3R =4R =1K Ω不变 V=4伏 改变1R ,测量出对应的输出电压ΔU ,并且计算出对应的灵敏度 ,实验数据如下表1:表1=2R=3R=4R=1KΩ不变 V=4伏改变2R,测量出对应的输出电压ΔU,并且计算出对应的灵敏度,实验数据如下表2:表2=2R=3R=4R=1KΩ不变 V=4伏改变3R,测量出对应的输出电压ΔU,并且计算出对应的灵敏度,实验数据如下表3:表3=2R=3R=4R=1KΩ不变 V=4伏改变4R,测量出对应的输出电压ΔU,并且计算出对应的灵敏度,实验数据如下表4:表4根据以上数据做电阻变化与输出电压的关系图,如图2所示:图2单桥情况下电桥电阻与电压变化关系图根据最小二乘法进行线性拟合,U a b R ∆=+∆,其中:222..R R U R Ua R R∆∆∆-∆∆=∆-∆ (17)22.R U R U b R R∆∆-∆∆=∆-∆ (18)根据以上实验所得的数据,我们可以求出a 和b ,并且求出最佳线性关系U a b R ∆=+∆。
两个变量的关系不能确定是否为线性关系的情况下,先假设其为线性关系,测得一系列数据,根据以上方法求得线性参数量。
必须判别线性关系的合理性。
线性相关系数:2222()()r R R U U =∆-∆∆-∆(19)可以证明:-1≤r ≤1,︱r ︱的值越接近1说明假设其为线性关系越合理。
根据以上数据求得:(1)改变1R 时: a =-76.19 b =1.247 r =0.931 76.19 1.247U R ∆=-+∆ (2)改变2R 时: a =78.12 b =1.255 r =0.930 78.12 1.255U R ∆=+∆ (3)改变时: a =78.26 b =1.255 r =0.930 78.26 1.255U R ∆=+∆(4)改变4R时: a=-82.57 b=1.252 r=0.931 82.57 1.252∆=-+∆U R 从图中我们可以看出当电阻变化量很小时,线性度比较好,呈直线。
