电桥灵敏度研究
自组惠斯通电桥灵敏度分析

自组惠斯通电桥灵敏度分析作者:张可欣来源:《科学与财富》2015年第33期摘要:惠斯通电桥是一种广泛应用于电阻测量的电桥电路。
它具有灵敏度高、测量准确和使用方便等特征。
本文是对自组惠斯通电桥的灵敏度进行了分析研究,首先阐述了惠斯通电桥的工作原理,其次通过实验分析了惠斯通电桥的比例系数和电压对其灵敏度影响,并且给出了详细的论述。
关键词:惠斯通电桥;灵敏度分析;自组电路一、引言电桥在电测技术中应用非常广泛。
利用桥式电路制成的电桥是一种用比较方法进行测量的仪器。
惠斯通电桥是英国物理学家惠斯通在1843年首先提出来的。
电桥主要是四个桥臂电阻,电源和检流计组成。
在实际应用中,电桥可以被用于实验应力分析,测试计量和自动检测与控制等诸多领域;能够进行各种机械和工程结构强度及寿命的诊断和评估;用于多种物理量的检测和控制,实现生产过程和科学实验过程的测量和控制。
因此研究电路灵敏度的相关因素,是理论研究和各种技术应用中设计电路的关键。
而当前利用成品箱式电桥不能够分析检测具体部分对于整个电桥的灵敏度影响,故本文运用相关知识自行组装了惠斯通电桥,并通过自主改变参数来检测比例系数与电压对电桥灵敏度的影响。
二、惠斯通电桥的工作原理图1是惠斯通电桥的工作原理图。
四个电阻R1、R2、R3、Rx连成一个四边形,每一条边称作电桥的一个臂,其中:R1、R2组成比例臂,Rx为待测臂,R3为比较臂,四边形中一条对角线AB接电源E,另一条对角线CD中接检流计G。
所谓的“桥”就是指CD这条对角线。
当接通电源时,每个支路上都有电流通过,电桥没有平衡时,“桥”上有电流通过检流计,适当调节各臂电阻值,可使“桥”上无电流,即C、D两点电位相等,电桥达到了平衡,时的等效电路图如图2所示。
此时很容易证明:(1-1)此式即电桥的平衡条件。
如果已知R1、R2、R3,则待测电阻Rx可求得。
设,R1/ R2=K 则有Rx=K R3式中K称为比例系数。
三、惠斯通电桥的灵敏度及相关因素电桥测量电阻,仅在电桥平衡时才成立的,而电桥的平衡是依据检流计的偏转来判断的,由于判断时受到眼睛分辨能力的限制而存在差异,会给测量结果带来误差,影响测量的准确性。
惠斯通电桥灵敏度与检测毫伏表内阻的关系研究

惠斯通电桥是一种用于测量电阻、电感和电容的仪器。
而在这个仪器的使用中,对于毫伏表内阻的检测尤为重要。
本文将探讨惠斯通电桥的灵敏度与检测毫伏表内阻的关系,并深入分析这一关系对于电子测量领域的重要意义。
**一、惠斯通电桥的基本原理与概念**让我们简单回顾一下惠斯通电桥的基本原理与概念。
惠斯通电桥由英国物理学家惠斯通于1833年发明,是一种用来测量未知电阻值的仪器。
其基本结构包括四个电阻,分别为R1、R2、R3和未知电阻Rx,它们构成了一个平衡的电桥电路。
当电桥平衡时,滑动变阻器位于中点,则滑动变阻器两端的电压为零。
而当电桥出现不平衡时,滑动变阻器两端会产生电压差。
**二、电桥灵敏度与内阻检测的关系**接下来,我们将重点讨论电桥的灵敏度与内阻检测的关系。
在电桥测量中,灵敏度是一个重要的参数,它决定了电桥能够测量的电阻变化范围。
而对于毫伏表内阻的检测来说,灵敏度则成为了一个关键因素。
当我们希望测量的电阻值较小时,需要较高的灵敏度。
惠斯通电桥的灵敏度与电桥的电阻值有关。
在惠斯通电桥中,灵敏度可以用下式表示:S = R3 / (R1 + R2)其中,S是灵敏度,R1、R2和R3分别为电桥中的三个已知电阻。
从这个公式可以看出,当R1和R2的数值接近时,电桥的灵敏度就会变得非常高。
因此在实际测量中,为了提高惠斯通电桥的灵敏度,我们通常会采用比较接近的电阻值。
**三、惠斯通电桥在毫伏表内阻检测中的应用**那么,惠斯通电桥的灵敏度与检测毫伏表内阻有何关系呢?事实上,毫伏表是一种用于测量电压的仪器,而其内阻则会影响到其测量的准确性。
当我们使用惠斯通电桥来检测毫伏表的内阻时,灵敏度的高低将直接影响到检测结果的精确度。
高灵敏度的电桥可以更精确地检测出毫伏表的内阻值。
因为当电桥的灵敏度较低时,对于内阻的微小变化可能无法被准确地检测出来,从而影响了测量的精度。
而高灵敏度的电桥则能够更加灵敏地发现内阻的变化,从而提高了内阻检测的准确性。
惠斯通电桥灵敏度的讨论

惠斯通电桥灵敏度的讨论
惠斯通电桥是一种用于测量电阻的电路,也被称为惠斯通电桥电路。
在实际应用中,我们经常需要测量电阻的值,例如在电子元器件的测试中。
而惠斯通电桥正是一种常用的测量电阻的方法。
惠斯通电桥由四个电阻组成,其中两个电阻相等,另外两个电阻也相等。
这四个电阻按照一定的方式连接起来,形成一个平衡电桥。
当平衡电桥中的电流达到平衡状态时,我们就可以通过调节其中一个电阻的值,来测量另一个未知电阻的值。
惠斯通电桥的灵敏度是指测量结果对未知电阻变化的敏感程度。
灵敏度越高,意味着我们可以更准确地测量未知电阻的值。
而灵敏度的大小取决于惠斯通电桥中各个电阻的比例关系。
具体来说,惠斯通电桥的灵敏度可以通过以下公式计算:
灵敏度 = ΔR / R
其中,ΔR表示未知电阻变化的大小,R表示惠斯通电桥中已
知电阻的值。
从公式中可以看出,灵敏度与已知电阻的值成反比。
因此,在设计惠斯通电桥时,我们需要根据需要确定已知电阻的值,以达到所需的灵敏度。
需要注意的是,惠斯通电桥的灵敏度并不是越高越好。
如果灵敏度过高,就会导致测量结果对环境因素的影响过大,从而影响测量精度。
因此,在实际应用中,我们需要根据具体情况来确定所需的灵敏度。
总之,惠斯通电桥是一种常用的测量电阻的方法,其灵敏度取决于已知电阻的值和未知电阻变化的大小。
在设计惠斯通电桥时,需要根据具体情况来确定所需的灵敏度。
实验三 用惠斯通电桥测电阻

实验三用惠斯通电桥测电阻【实验目的】1.掌握惠斯通电桥测电阻的原理和方法;2.理解电桥灵敏度的概念;3.研究惠斯通电桥测量灵敏度。
【实验原理】1.惠斯通电桥测电阻原理惠斯通电桥的原理图如图3-1所示,它由比例臂电阻R1、R2和调节臂电阻R以及待测电阻R X用导线连成的封闭四边形ABCDA组成,在对角线AC两端接电源,在对角线BD两端接灵敏度较高的检流计。
通常将BD端称为桥路,四个电阻R1、R2、R和R X称为桥臂。
若适当调节R1、R2或R阻值,使桥路两端的电位相等,即检流计示值为零,这时称为电桥平衡。
图3-1 惠斯通电桥的原理图电桥平衡时(V=0),得到:U AB=U AD,U BC=U DC即I1R1=I2R2,I X R X=I R R(1)同时有I1=I X,I2=I R(2)由式(1)、(2)得到R X=R(R1R2⁄)(3)当知道R 1R 2⁄的比值及电阻R 的数值后,由式(3)可算出R X 。
R1R 2⁄称为比率系数或倍率,R 称为比较臂。
式(3)称为电桥平衡条件。
惠斯通电桥适用于测量中值电阻(1Ω~1MΩ)。
2.惠斯通电桥灵敏度当BD 端接毫伏表,毫伏表显示为零时认为电桥平衡,但现实的问题是毫伏表的灵敏度是有限的,毫伏表所示电压为零不等于实际电压一定为零。
同样的道理,R X =R (R 1R 2⁄)为电桥平衡条件,由于毫伏表的灵敏度所限,R X (或R 1、R 2、R )有一定的偏差时毫伏表仍可能指示电桥平衡。
当电桥平衡时,保持3个桥臂电阻不变,1个电阻改变(假设R X 、R 1、R 2不变,R 改变ΔR ),则电桥输出电压偏离平衡为ΔU 0,电桥输出电压对桥臂电阻的相对变化反应灵敏度(简称电桥相对灵敏度)S 为:S =ΔU 0ΔR R ×100%与电桥灵敏度相关的物理量有:电源电压U AC 、桥臂电阻R 1+R 2+R +R X 、桥臂电阻分配比例R R 2⁄、检测仪表的灵敏度和内阻R V 。
基础物理实验研究性报告 惠斯通电桥测量中电阻及灵敏度的分析与探究

①平衡电桥采用了零示法——根据示零器的“零”或“非零”的指标,即可判断电桥是否平衡而不涉及数值的大小。因此,只需示零器足够灵敏,就可以使电桥达到很高的灵敏度,从而为提高它的测量精度提供了条件。
用平衡电桥测量电阻的实质是拿已知的电阻和未知的电阻进行比较,这种比较测量法简单而精确,如果采用精确电阻作为桥臂,则可以使测量的结果达到很高的精确度。
.读数过程中出现的误差。
6.电桥灵敏度的分析研究
6.1电桥灵敏度的物理意义
与课本上所学习到的绝对灵敏度不同,电桥(相对)灵敏度的定义为
表示当电桥平衡后桥臂电阻 的相对改变 引起检流计的偏转格数为 ,一定的 所引起 愈大,电桥灵敏度越大。
例如, ,它表示电桥平衡后,某一桥臂电阻改变万分之一,检流计就会显示 的偏转,这恰恰是通常情况下,人眼所能判断的最大偏转。所以该电桥灵敏度限制所带来的测量误差小于万分之一。
基础物理实验研究性报告
惠斯通电桥法测量中电阻及灵敏度的分析与探究
第一作者
胡子晗14131088
院系
交通科学与工程学院
第二作者
张彤昊14131082
院系
交通科学与工程学院
第三作者
张鸿曜14131031
院系
交通科学与工程学院
2015年12月15日
摘要:
本报告以惠斯通电桥法测量中等数值电阻的实验为出发点,在测量中电阻的过程中深入思考了电桥平衡条件以及实验操作中的一些问题。同时对电桥灵敏度进行了较为透彻的分析与研究,对该实验的正确操作与严格的数据处理具有重要的意义。并根据操作实验的经历对本实验的实验仪器和操作提出了自己的想法。
2.实验仪器
电阻箱、 型电子检流计、固定电阻两个(标称值相同,但不知准确值)、直流稳压电源、滑线变阻器( )、待测中电阻、开关等、 型箱式电桥。
探究惠斯通电桥灵敏的影响因素

探究惠斯通电桥灵敏的影响因素郭 超200802050234 08物理(2)班 红河学院摘要:电阻的测量是电磁学中的重要实验,测量方法很多其中以电桥发通常采用惠斯通电桥法,因为该方法从根本上消除了采用伏安法测电阻时由于电表内阻的接入而带来的系统误差,从而提高了准确度。
而“电桥”是很重要的电磁学基本测量仪器之一,它主要用来测量电阻器的阻值,线圈的电感和电容器的电容及其损耗,电桥的灵敏度直接影响测电阻的精确值,其灵敏读与诸多因素有关。
关键词:惠斯通电桥;灵敏度;因素一. 电桥原理惠斯通电桥的原理如(图一)所示,图中ab.bc.cd 和da 四条支路分别由电阻1R )(X R .2R .3R 和4R 组成,称为电桥的桥臂。
通常,桥臂ab 接待侧)(X R 电阻,其余各比电阻都市可以调节的标准电阻。
在ab 对角线之间连接检流计、开关、和限流电阻GR 。
在ac 两对角见连接电池、开关和限流电阻E R ,当接通开关E S 和GS 后,各支路中军有电流通过,检流计支路起了沟通abd 和adc 两条之路的作用,可以使比较bd 两点的电势,点桥之名由此而来。
适当调整各支臂的电阻阻值,可以使流过检流计的电流为零,即=G I 。
这时,称电桥达到了平衡。
平衡时 b.d两点的电势相等。
根据分压器原理可知:212R R R U U abbc += (1)433R R R U U acdb += (2)平衡时,dc bc U U =即433212R R R R R R +=+ (3)整理化简后得到 X R R R R R ==4321 (4)由(3)式可知:待测电阻1R )(X R 等于32R R 与4R 的乘积。
通常,称2R 、3R 为比例臂,与此相应的4R 为比较臂。
所以电桥由四臂(测量臂、比较臂、和比例臂)、检流计和电源三部分组成。
电桥灵敏度的引入及由于电桥灵敏度引入的被测量的相对系统误差2.1电桥灵敏度的引入在用天平秤称质量是已知,测得质量的精度住要取决于天平的灵敏度。
电桥灵敏度与桥臂阻值关系的研究
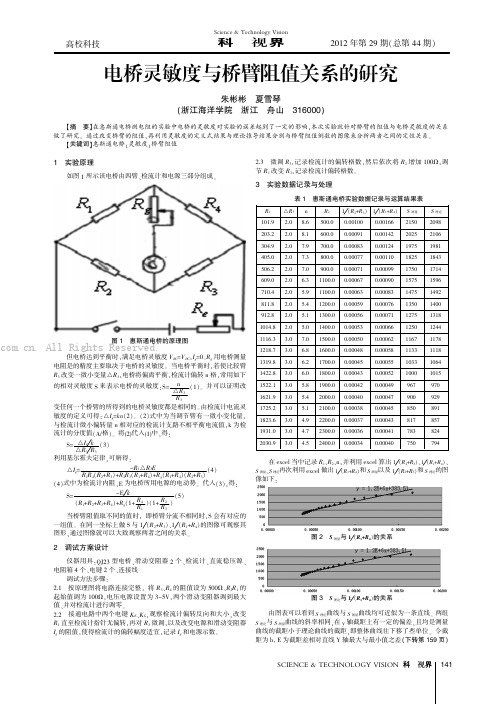
1实验原理如图1所示该电桥由四臂、检流计和电源三部分组成。
图1惠斯通电桥的原理图但电桥达到平衡时,满足电桥灵敏度V BC =V DC ,I g =0。
R g 用电桥测量电阻是的精度主要取决于电桥的灵敏度。
当电桥平衡时,若使比较臂R 3改变一微小变量△R 3,电桥将偏离平衡,检流计偏转n 格,常用如下的相对灵敏度S 来表示电桥的灵敏度:S=n △R 3R 3(1)。
并可以证明改变任何一个桥臂的所得到的电桥灵敏度都是相同的。
由检流计电流灵敏度的定义可得:△I g =kn (2)。
(2)式中为当调节臂有一微小变化量,与检流计微小偏转量n 相对应的检流计支路不相平衡电流值,k 为检流计的分度值(A/格)。
将(2)代入(1)中,得:S=△I g k △R 3R 3(3)利用基尔霍夫定律,可解得:△I g =-R 1△R 3E R 1R 4(R 2+R 3)+R 2R 3(R 1+R 4)+R g (R 1+R 4)(R 2+R 3)(4)(4)式中为检流计内阻,E 为电桥所用电源的电动势。
代入(3),得:S=-E k 1+R 2+R 3+R 4g R 4R 1R 2R 3(5)当桥臂阻值取不同的值时,即桥臂分流不相同时,S 会有对应的一组值。
在同一坐标上做S 与1(R 2+R 3)、1(R 1+R 4)的图像可观察其图形,通过图像就可以大致观察两者之间的关系。
2调试方案设计仪器用具:QJ23型电桥、滑动变阻器2个、检流计、直流稳压源、电阻箱4个、电键2个、连接线调试方法步骤:2.1按原理图将电路连接完整,将R 3、R 4的阻值设为500Ω、R 2R 1的起始值调为100Ω,电压电源设置为3~5V,两个滑动变阻器调到最大值、并对检流计进行调零。
2.2接通电路中两个电键K E 、K G ,观察检流计偏转反向和大小,改变R 1直至检流计指针无偏转,再对R 3微调,以及改变电源和滑动变阻器I g 的阻值,使得检流计的偏转幅度适宜,记录I g 和电源示数。
探究惠斯通电桥灵敏度的影响因素

探究惠斯通电桥灵敏度的影响因素实验者: 同组实验者: 指导教师:【摘要】用惠斯通电桥测电阻时,其精度主要取决于电桥的灵敏度。
电桥的灵敏度S 越大,由电桥灵敏度引入的误差越小。
要提高测量电阻的精度,就应该从电桥灵敏度的影响因素中入手。
该实验基于此思想,通过调试改变试验中的各相关数据和仪器,探究影响电桥灵敏度的几个具体因素,从而设法找出提高电桥灵敏度的方法。
【关键词】惠斯通电桥 灵敏度 因素 【实验原理】惠斯通电桥的原理图如右图所示,其中1R 、2R 、3R 和4R )(X R 组成了电桥的桥壁。
当满足0==g DC BC I V V ,时,电桥处于平衡,使调节3R 有一微小变化量3R δ,从而会引起检流计指针有一微小偏转n 。
通常定义电桥的绝对灵敏度S 为3R nS δ=(1) 电桥的相对灵敏度为:33R R nS δ=相 (2)可以证明,改变任何一个桥壁,其所得的电桥灵敏度都相同。
由检流计电流灵敏度的定义很容易导出:G I I S n ∆= (3)其中,I S 为检流计的电流灵敏度,G I ∆为改变桥壁3R 一个微小变化量3R δ时,检流计微小偏转n 格相对应的检流计支路的不平衡电流。
再利用基尔霍夫定理解得))(()()(32414132324131R R R R R R R R R R R R R ER R I G G ++++++-=∆δ (4)将(4)式带入(2)式,可得:)1)(1()(k/32144321R RR R R R R R R E S g ++++++-=(5)由(2)式可知,如果检流计的最小可辨偏转量为n ∆(一般认为0.2n ∆=格),则由电桥灵敏度引入的被测电阻值的相对不确定度为:R nR S∆∆=(6) 表明电桥的灵敏度S 越大,由电桥灵敏度引入的误差越小。
【调试方案设计】1、 仪器用品:直流稳压电源1个、检流计1个、滑动变阻器1个、万用表1个、电阻箱5个、电键1个、连接线若干 2、 调试方法步骤:2.1 按原理图连接电路,先使50G R =Ω,设置桥臂比为1:1,电源电压在3~5V 之间取值,滑动变阻器取最大值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
电桥灵敏度研究
张云义广东省惠州市一中(516001)
一、惠斯登电桥
惠斯登电桥是准确测量电阻的一种重要方法。
惠斯登电桥原理图如下所示。
R1 A R2
调节电阻Rs,当R2/R1= Rs/Rx时,A、B两点间电势相等,灵敏电流计的读数为零,则Rx= Rs(R1/R2)。
二、电桥灵敏度的测量
利用电桥测量电阻的精确性与电桥的灵敏度有直接关系。
当电桥平衡时,调节Rs,使其有一微小改变△Rs,则电桥平衡被破坏,灵敏电流计有读数△α。
显然,对于给定的△Rs,能产生越大的电流计读数△α,则我们越容易发现电桥已偏离平衡状态。
因此电桥的绝对灵敏度定义为S= △α/△Rs。
(1)定义电桥的相对灵敏度为:Sr=△α/(△Rs /Rs)= Rs(△α/△Rs)(2)可以证明,改变任何一个桥臂所得到的电桥灵敏度都是相同的的。
电桥相对灵敏度可以在实验上进行测量。
调节电桥平衡后,微调电阻Rs,观察电流指针偏转,以Rs及Rs的改变量△Rs的值以及指针偏转的格度数△α代入(2)式,可以测出电桥的灵敏度。
三、影响电桥灵敏度的因素
为提高测量的精确度,分析电桥的灵敏度与什么因素有关。
由(2)式,电桥的相对灵敏度为Sr=△α/(△Rs /Rs)= Rs(△α/△Rs)由检流计电流灵敏度的定义可得:△α=S i △Ig (3)
(3)式中,S i为电桥的灵敏度,△Ig是当调节Rs有一微小变量△Rs时,对应于检流计微小偏转量△α时流经电流计的电流值。
将(3)式代入(2)式得:Sr=S i Rs△Ig /△Rs (4)
设电流计内阻为Rg,电源电动势为E,利用基尔霍夫定律可解得:
-R1E△Rs
△Ig=(5) R1Rx(R2+Rs)+R2Rs(R1+Rx)+Rg(R1+Rx)(R2+Rs)
由(5)式代入(4)式可得
S iE
Sr= (6) (R1++R2+Rx+Rs)+Rg(1+Rx/R1)(1+Rs/R2)
(6)式说明了电桥的灵敏度与电流计的灵敏度Si,电源电动势E,电流计的内阻Rg,四条臂上的总电阻,以及对应臂的电阻比值Rx/R1、Rs/R2有关。
因此,为提高电桥的灵敏度,可以采取如下措施:
(1)所用直流电源的电动势E越大越好,但不能超出任一臂所允许的电流值,(2)所用检流计的灵敏度Si越高越好,
(3)对应臂的阻值之比Rx/R1、R2/Rs越小,电桥的灵敏度越高。
在给定的Rx,保持比例臂R1/R2比值不变的条件下,比率臂的电阻越大,灵敏度越高,(4)电流计的内阻越小,灵敏度越高。
(5)同一电桥,在比率臂电阻一定的情况下,待测电阻越大,电桥灵敏度越高。
四、电桥测量误差与电桥灵敏度
由电桥测量原理Rx= Rs(R1/R2)(6)得
△Rx=△Rs(R1/R2) (7)
由(6)/(7)得:
△Rx/Rx=△Rs/Rs (8)
将(8)式代入(2)式Sr=△α/(△Rs /Rs)得
Sr=△α/(△Rx/Rx)
因此,要想实验测量的相对误差越小,则需要电桥的灵敏度越高。
测量结果的相对误差与电桥灵敏度成反比。
举例说明,若要求被测电阻的相对误差(△Rx/Rx)小于万分之五,△α最小分辨率为1个单位,那么电桥灵敏度Sr应为
Sr=△α/(△Rx/Rx)=1/(5/10000)=2000.。
