【哈工大 结构动力学】SD 第10章 多自由度体系2020
合集下载
结构力学课后答案第10章结构动力学
\
解:
若 为静力荷载,弹簧中反力为 。
已知图示体系为静定结构,具有一个自由度。设为B点处顺时针方向转角 为坐标。建立动力方程:
则弹簧支座的最大动反力为 。
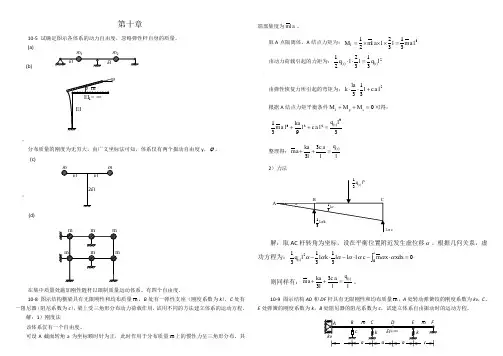
10-21设图a所示排架在横梁处受图b所示水平脉冲荷载作用,试求各柱所受的最大动剪力。已知EI=6×106Nm2,t1=,FP0=8×104N。
(a)
则同样有: 。
10-9图示结构AD和DF杆具有无限刚性和均布质量 ,A处转动弹簧铰的刚度系数为kθ,C、E处弹簧的刚度系数为k,B处阻尼器的阻尼系数为c,试建立体系自由振动时的运动方程。
*
解:
取DF隔离体, :
取AE隔离体:
将R代入,整理得:
/
10-10试建立图示各体系的运动方程。
(a)
解:(1)以支座B处转角作为坐标,绘出梁的位移和受力图如下所示。图中惯性力为三角形分布,方向与运动方向相反。
图 图
(1)求结构运动方程
如所示弯矩图,图乘后,
其中 ,稳态解:
所示结构的运动方程为 ,C点最大动位移幅值为
(2)求B点的动位移反应
,
!
B点的动位移幅值为
(3)绘制最大动力弯矩图
图 图
最大动力弯矩图
10-20试求图示集中质量体系在均布简谐荷载作用下弹簧支座的最大动反力。设杆件为无限刚性,弹簧的刚度系数为k。
(2)画出 和 图(在B点处作用一附加约束)
…
(3)列出刚度法方程
, ,
代入 、 的值,整理得:
(b)
解:
图 图
】
试用柔度法解题
此体系自由度为1 。设质量集中处的竖向位移y为坐标。
y是由动力荷载 和惯性力矩 共同引起的。
解:
若 为静力荷载,弹簧中反力为 。
已知图示体系为静定结构,具有一个自由度。设为B点处顺时针方向转角 为坐标。建立动力方程:
则弹簧支座的最大动反力为 。
10-21设图a所示排架在横梁处受图b所示水平脉冲荷载作用,试求各柱所受的最大动剪力。已知EI=6×106Nm2,t1=,FP0=8×104N。
(a)
则同样有: 。
10-9图示结构AD和DF杆具有无限刚性和均布质量 ,A处转动弹簧铰的刚度系数为kθ,C、E处弹簧的刚度系数为k,B处阻尼器的阻尼系数为c,试建立体系自由振动时的运动方程。
*
解:
取DF隔离体, :
取AE隔离体:
将R代入,整理得:
/
10-10试建立图示各体系的运动方程。
(a)
解:(1)以支座B处转角作为坐标,绘出梁的位移和受力图如下所示。图中惯性力为三角形分布,方向与运动方向相反。
图 图
(1)求结构运动方程
如所示弯矩图,图乘后,
其中 ,稳态解:
所示结构的运动方程为 ,C点最大动位移幅值为
(2)求B点的动位移反应
,
!
B点的动位移幅值为
(3)绘制最大动力弯矩图
图 图
最大动力弯矩图
10-20试求图示集中质量体系在均布简谐荷载作用下弹簧支座的最大动反力。设杆件为无限刚性,弹簧的刚度系数为k。
(2)画出 和 图(在B点处作用一附加约束)
…
(3)列出刚度法方程
, ,
代入 、 的值,整理得:
(b)
解:
图 图
】
试用柔度法解题
此体系自由度为1 。设质量集中处的竖向位移y为坐标。
y是由动力荷载 和惯性力矩 共同引起的。
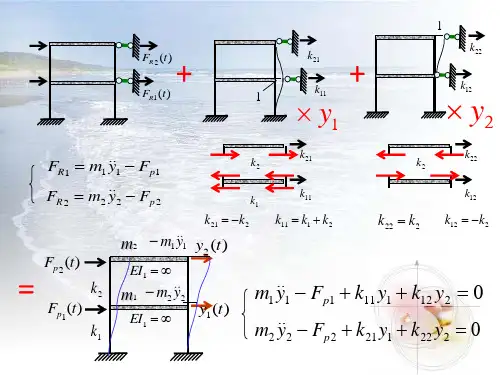
多自由度体系自由振动

KN
振动方程
y2 (t )
y1 (t )
质点在任何时刻要受力平衡
竖向
1 (t ) m y
FEK1
水平方向:
2 (t ) FEK 2 m y
问题转化为求质点在任意时刻 t 在2 个方向上受到的 恢复力
恢复力的求法
B
D
y2 (t )
y1 (t )
竖向
VDB
FEK1
A
C
弹簧反力
y1 (t )
1 (t )11 m2 212 y1 (t ) m1 y y
1 (t ) 21 m2 2 22 y2 (t ) m1 y y
y2 (t )
方程中各个系数意义如下:
P=1 L/4 L L/4 L/2 L/2 L/4
P=1
L/4
M1
L/4
A1 A11
与A1的比值,记为
A21
T
同理,把λ=λ2 代入振型方程中的任意一个方程,得到A2
A22 2 m1 11 A12 m2 12
y1(t)= A12sin(ω2t + φ) y2(t)= A22sin(ω2t + φ) 同样,称 A2 A 12
A22 为第二振型
-----频率方程
3. 柔度矩阵与刚度矩阵的关系
K 1
[计算举例]
,杆长都是L,列振动方程
m EI EI EI1=∞
13 EI 图示结构弹簧的刚度 KN= 3 2L
解:1)2个动力自由度,质点的 水平位移和竖向位移,如图
并求振动频率和振型,作出振型图
y 2 (t )
y1 (t )
振动方程
y2 (t )
y1 (t )
质点在任何时刻要受力平衡
竖向
1 (t ) m y
FEK1
水平方向:
2 (t ) FEK 2 m y
问题转化为求质点在任意时刻 t 在2 个方向上受到的 恢复力
恢复力的求法
B
D
y2 (t )
y1 (t )
竖向
VDB
FEK1
A
C
弹簧反力
y1 (t )
1 (t )11 m2 212 y1 (t ) m1 y y
1 (t ) 21 m2 2 22 y2 (t ) m1 y y
y2 (t )
方程中各个系数意义如下:
P=1 L/4 L L/4 L/2 L/2 L/4
P=1
L/4
M1
L/4
A1 A11
与A1的比值,记为
A21
T
同理,把λ=λ2 代入振型方程中的任意一个方程,得到A2
A22 2 m1 11 A12 m2 12
y1(t)= A12sin(ω2t + φ) y2(t)= A22sin(ω2t + φ) 同样,称 A2 A 12
A22 为第二振型
-----频率方程
3. 柔度矩阵与刚度矩阵的关系
K 1
[计算举例]
,杆长都是L,列振动方程
m EI EI EI1=∞
13 EI 图示结构弹簧的刚度 KN= 3 2L
解:1)2个动力自由度,质点的 水平位移和竖向位移,如图
并求振动频率和振型,作出振型图
y 2 (t )
y1 (t )
1005多自由度体系自由振动(力学)

FI 2 (t ) FS 2 (t ) FE 2 (t ) 0
其中
FIi mi i y
FSi kij y j
j 1
2
( i 1,2)
m1 1 k11 y1 k12 y2 FE1 (t ) y
m2 2 k 21 y1 k 22 y2 FE2 (t ) y
主振型的位移幅值等于 主振型惯性力幅值作用下产 生的静力位移。
(2)振型方程
( 11 m1 2 ) A1 12 m2 A2 0 1 21 m1 A1 ( 22 m2 2 ) A2 0 1
A1=A2= 0 ?
(3)频率方程
D
11m1
y 11 12 m1 0 1 y1 Δ1P (t ) 0 m y Δ (t ) 2 y2 21 22 2 2P
m1 0 0 1 k11 y k m2 y 2 21 k12 y1 FE1 (t ) y F ( t ) k 22 2 E 2
1
2
12m2 22m2
1
21m1
0
令
1
2
2
2 (11m1 22 m2 ) (11 22 m1m2 12 21m1m2 ) 0
1 1 ( 11m1 22 m2 ) ( 11m1 22 m2 ) 2 4( 11 22 12 21 )m1m2 2 2
y2 (t ) m1 1 (t ) 21 m2 2 (t ) 22 y y
设解为 y1 (t ) A1 sin(t )
其中
FIi mi i y
FSi kij y j
j 1
2
( i 1,2)
m1 1 k11 y1 k12 y2 FE1 (t ) y
m2 2 k 21 y1 k 22 y2 FE2 (t ) y
主振型的位移幅值等于 主振型惯性力幅值作用下产 生的静力位移。
(2)振型方程
( 11 m1 2 ) A1 12 m2 A2 0 1 21 m1 A1 ( 22 m2 2 ) A2 0 1
A1=A2= 0 ?
(3)频率方程
D
11m1
y 11 12 m1 0 1 y1 Δ1P (t ) 0 m y Δ (t ) 2 y2 21 22 2 2P
m1 0 0 1 k11 y k m2 y 2 21 k12 y1 FE1 (t ) y F ( t ) k 22 2 E 2
1
2
12m2 22m2
1
21m1
0
令
1
2
2
2 (11m1 22 m2 ) (11 22 m1m2 12 21m1m2 ) 0
1 1 ( 11m1 22 m2 ) ( 11m1 22 m2 ) 2 4( 11 22 12 21 )m1m2 2 2
y2 (t ) m1 1 (t ) 21 m2 2 (t ) 22 y y
设解为 y1 (t ) A1 sin(t )
结构动力学多自由度

▪ 振型方程:
(K i2M)ji 0 (i 1, 2, 3, n)
▪∵
K 2i M 0
▪ ∴ 第i 个振型方程中的n 个方程中只有n-1个是独立的! ▪ ——无法得到j1i、 j2i、 … 、 jni 的确定值, ▪ 但可以确定各质点振幅之间的相对比值: ▪ —— 振型的幅值是任意的,但形状是惟一的。
一致质量矩阵:
L
pava m13v1 0 fI ( x)v( x)dx
L
0
m( x) 3( x)v3
L
1( x)v1dx
mij 0 EI ( x)i ( x) j ( x)dx
L
cij 0 c( x) i ( x) j ( x)dx
其中,c(x)表示分布的粘滞阻尼特性。
一致节点荷载
L
vˆ 表示体系的形状,不随时间变化。
v 2vˆ sin(t ) 2v 2mvˆ sin(t ) kvˆ sin(t ) 0
k 2m vˆ 0
k 2m vˆ 0
即: k 2m 0
上式的N个根,表述体系可能存在的N个振型的频率。
1
2
3
N
2)
2
)
y32
(t
)
jˆ
32
s
in
(
2
t
2
)
1
jˆ
2i
yi
(t
)
jˆ3i
s
in(i
t
i
)
jˆ ni
1
jˆ 21
jˆ 31
jˆ 32
1
jˆ 22
将N个振型中的每一振型形式,用F表示N个振型所组成的方阵。
11 12 13 1N
结构动力学多自由度体系的自由振动
l/3 l/3 l/3 1
11
21
1
Y 1
1 1
Y
2
1 1
12
22
对称体系的振型分 成两组: 一组为对称振型
一组为反对称振型
按对称振型振动
m
l/3 l/6
=1 l/3
11
5 162
l3 EI
2 1 m11
5.692 EI / ml3
按反对称振型振动
m1 m m2 m EI
l/3 l/3 l/3 1
三.求多自由度体系频率、振型例题
例1.求图示体系的频率、振型
解
11
22
4 243
l3 EI
12
21
7 486
l3 EI
I 2 m 0
m1 m m2 m EI
l/3 l/3 l/3 1
11
21
1
11m1 1/ 2
m212
0
m1 21
22m2 1/ 2
令
1
11m1
2
1 12 / 11 0 21 / 11 1
(I 2 m)Y 0
频率方程
I 2 m 0
6。求振型、频率可列幅值方程.
按振型振动时
y1 y2
Y1 sin( t ) Y2 sin( t )
yy21
Y1 2 Y2 2
sin( t sin( t
) )
FI
1
(t
)
FI 2 (t)
m1Y12 sin( t ) m2Y22 sin( t )
YY1222
s
in(2t
2)
通解
yy12((tt))
A1
YY1211
11
21
1
Y 1
1 1
Y
2
1 1
12
22
对称体系的振型分 成两组: 一组为对称振型
一组为反对称振型
按对称振型振动
m
l/3 l/6
=1 l/3
11
5 162
l3 EI
2 1 m11
5.692 EI / ml3
按反对称振型振动
m1 m m2 m EI
l/3 l/3 l/3 1
三.求多自由度体系频率、振型例题
例1.求图示体系的频率、振型
解
11
22
4 243
l3 EI
12
21
7 486
l3 EI
I 2 m 0
m1 m m2 m EI
l/3 l/3 l/3 1
11
21
1
11m1 1/ 2
m212
0
m1 21
22m2 1/ 2
令
1
11m1
2
1 12 / 11 0 21 / 11 1
(I 2 m)Y 0
频率方程
I 2 m 0
6。求振型、频率可列幅值方程.
按振型振动时
y1 y2
Y1 sin( t ) Y2 sin( t )
yy21
Y1 2 Y2 2
sin( t sin( t
) )
FI
1
(t
)
FI 2 (t)
m1Y12 sin( t ) m2Y22 sin( t )
YY1222
s
in(2t
2)
通解
yy12((tt))
A1
YY1211
计算结构动力学 多自由度体系的振动

tgi=2i/i(1-i2)
(36)
将式(34)代回
{u}=ii(t){A}i , 得
{u(t)}=[iisin(it-i)/i2]{A}i
(37)
无阻尼情况自然可以当作有阻尼情况的特例,在上
述结果中令i=0得到。
4.3 多自由度的受迫振动
4.3.3 简谐荷载受迫振动反应分析步骤
左乘{A}jT、后一式左乘{A}iT,再将两式相减,由于质 量、刚度的对称性,可得
由此可得
(i2-j2){A}jT[M]{A}i=0
(11)
{A}jT[M]{A}i=0
(12)
上式乘j2,考虑到j2[M]{A}j物理意义是第j振型对应
的惯性力幅值,因此式(12)表明第j振型对应的惯性
力在第i振型位移上不做功,反之亦然。
(e)
方程两边同时左乘{A}jT,根据正交性则有
Mj*ÿj(t)+Kj*yi(t)=0
(20)
从式(20)可得(根据单自由度自由振动结果)
yi(t)=aisin(it+ci)
(f)
代回多自由度所假设的解,即可得
{u(t)}=aisin(it+ci){A}i
(21)
5)式(21)中的待定常数ai、ci可由初始条件确定。如何
22求无阻尼自由振动的振型求无阻尼自由振动的振型aaii频率频率ii33用阻尼比用阻尼比1122和频率和频率1122求瑞利阻尼的求瑞利阻尼的00和和44求求ii振型振型参与系数振型振型参与系数iiaaiittppaaiittmmaa55求求ii振型阻尼比振型阻尼比12120066求求ii振型动力系数振型动力系数iiii222244ii22ii22121277求求ii振型相位角振型相位角iiarctg2arctg2iiii2288求求ii振型广义位移振型广义位移iittiisinsiniittiiii2299将各振型广义位移代回将各振型广义位移代回uuiittaaii则得最终则得最终结果结果uuttiisinsiniittiiii2237374444441441基本原理基本原理对动力问题设单元位移场仍表示成对动力问题设单元位移场仍表示成ddnnddee只是现在只是现在ddddxtddee设杆单元的密度为设杆单元的密度为将微段惯性力将微段惯性力aaaaddxx作为作为体积力则这一单元荷载的总虚功为体积力则这一单元荷载的总虚功为dxdx3838引入单元一致质量矩阵引入单元一致质量矩阵mmeedx39394444由式3939代入形函数并积分对质量均匀分布的平代入形函数并积分对质量均匀分布的平面弯曲单元其单元一致质量矩阵面弯曲单元其单元一致质量矩阵mmee13221561354221354221564204040作业
【结构动力学】第10章 多自由度体系2020
0
0
N
其中,ωn— 第n阶自振频率,{φ}n—第 n阶振型。
[Φ]和[Ω]也分别称为振型矩阵和谱矩阵。
13
5 DOF with uniform mass and stiffness
5 DOF Base Isolated 14
15
5 DOF with uniform mass and stiffness
k22 2m22 k2N 2m2n 0
k N1 2mN1 k N 2 2mN 2 k NN 2mNN
10
对于N个自由度的稳定结构体系,频率方程是关于ω2的 N次方程,
a N ( 2 ) N a N 1 ( 2 ) N 1 a1 2 a 0 0
由此可以解得N个正实根(ω12<ω22<ω32…<ωN2)。 ωn(n=1, 2, …, N)即为体系的自振频率。其中量值最小的 频率ω1叫基本频率(相应的周期T1=2π/ω1叫基本周期)。 从以上分析可知,多自由度体系只能按一些特定的频 率即按自振频率做自由振动。按某一自振频率振动时,结 构将保持一固定的形状,称为自振振型,或简称振型。
上述齐次方程组有非零解条件为:系数行列式为零
A [I ] 0
N×N矩阵[A]一般将有N个特征值,对应N个特征向量
6
§10-2 多自由度体系的自由振动
多自由度体系无阻尼自由振动的方程为:
M u K u 0
其中:[M]、[K]为N×N阶的质量和刚度矩阵 {u}和{ü}是N阶位移和加速度向量 {0}是N阶零向量
11
把相应的自振频率ωn代入运动方程的特征方程得到振型
K n 2 M n 0
{φ}n={φ1n, φ2n , …, φNn }T—体系的第n阶振型 。 ➢ 由于特征方程的齐次性(线性方程组是线性相关的),振型向量 是不定的,只有人为给定向量中的某一值,例如令φ1n=1,才能确 定其余的值。 ➢ 实际求解时就是令振型向量中的某一分量取定值后才能求解。 虽然令不同的分量等于不同的量,得到的振型在量值上会不一样, 但其比例关系是不变的。
结构力学结构动力计算基础
解:自振频率是系统的固有特性,与荷载无关。可先求出柔度
系数11 ,再求固有频率
。由结构的 M
图, ,则 1
11E1IM12dx3E 4I
1 3EI m11 4m
当静荷载撤除后,梁的运动为单自由度体系的无阻尼自由
振动。初始时刻质点速度为零,即 y&0 0,y 0 可由图乘法计算得到,
y0E 1IM1MPdx1 E1I ,则质点m的位移
§10-1 概述
3)结构的振动自由度
⑴概念:结构振动时,确定某一时刻全部质量的位置所需要的
独立几何参数的数目,称为结构的振动自由度。
⑵集中质量法:这种方法是将连续分布的质量集中到结构的
若干点上,即结构动力计算简图为有限质点体系。
(a)
(b)
(a) 一个质量点 (b) 若干质量点
§10-1 概述
3)结构的振动自由度
将荷载幅值F作用在结构上,其跨中弯矩和位移为
M sF t 1 4F l1 410410kN m
结构的自振频率为
ysFt
F11
10 103 43 48 1.848 107
0.722 103 m
1 g g m11 mg11 yQ
9.8 2.53 103
62.2S1
动荷载的频率为
2πn 2 3.14 400 41.9S1
对于无阻尼自由振动,质点在惯性力FI和弹性恢复力FS作用下处于 动力平衡状态,则有 FI +Fs =0,即m & y & (t)+k11y(t)=0,此式可改写为
& y&(t)+k11 y(t)=0 m
此式为单自由度体系无阻尼自由振动的运动方程,这种由力系平 衡条件建立运动微分方程的方法称为刚度法。
多自由度体系
最后求第三主振型。将将3和3代入式(a),得
-6.054
K
32M
=
k 15
5
0
5 -5.027
3
0
3
-10.027
代入式(4-3-4),后两个方程为
-5Y13 5.027Y23 +3Y33 0 3Y23 +10.027Y33 0
令Y33 1,故式(f)的解为
Y (3) = Y13,Y23,Y33 T 2.760, 3.342,1T
M
M
kn1
kn2
L
k1n
k2n
0
M
knn -2mn
(4-3-3b)
n个根12,22, n2
Y (i)表示与频率i相应的主振型:
Y (i)T =(Y1i Y2i Yni )
将i和Y (i)代入式(4-3-2)得
(K i2M)Y (i) 0
(4-3-4)
令,i 1, 2,, n,可得n个向量方程,由此可求的n个主振型向量 Y (1),Y (2),,Y (n)
(1)验算正交关系式(4-3-8)
2 0 0 0.924
Y (1)T MY (2) =(0.163, 0.569,1) 0 1 0 1.227 m
0 0 1 1
m0.163 2 (0.924) 0.5691 (1.227) 111
0.0006m 0
同理,
Y (1)T MY (3) 0.002m 0,Y (2)T MY (3) 0.002m 0
3
0
3
1.707
代入式(4-3-4)中并展开,保留后两个方程,得
-5Y11 6.707Y21 3Y31 3Y21 1.707Y31 0
-6.054
K
32M
=
k 15
5
0
5 -5.027
3
0
3
-10.027
代入式(4-3-4),后两个方程为
-5Y13 5.027Y23 +3Y33 0 3Y23 +10.027Y33 0
令Y33 1,故式(f)的解为
Y (3) = Y13,Y23,Y33 T 2.760, 3.342,1T
M
M
kn1
kn2
L
k1n
k2n
0
M
knn -2mn
(4-3-3b)
n个根12,22, n2
Y (i)表示与频率i相应的主振型:
Y (i)T =(Y1i Y2i Yni )
将i和Y (i)代入式(4-3-2)得
(K i2M)Y (i) 0
(4-3-4)
令,i 1, 2,, n,可得n个向量方程,由此可求的n个主振型向量 Y (1),Y (2),,Y (n)
(1)验算正交关系式(4-3-8)
2 0 0 0.924
Y (1)T MY (2) =(0.163, 0.569,1) 0 1 0 1.227 m
0 0 1 1
m0.163 2 (0.924) 0.5691 (1.227) 111
0.0006m 0
同理,
Y (1)T MY (3) 0.002m 0,Y (2)T MY (3) 0.002m 0
3
0
3
1.707
代入式(4-3-4)中并展开,保留后两个方程,得
-5Y11 6.707Y21 3Y31 3Y21 1.707Y31 0
哈尔滨工业大学结构动力学PPT课件
x0 x0 , x0 x0 xt c1n cosnt c2n sinnt
c1 x0 n , c2 x0
第36页/共42页
x
t
x0
n
sin nt
x0
cos nt
令
x0 cos n
, x0 sin
则可化为
其中:
xt sinnt
2
x02
x0
n
tg x0n arctg x0n
T1
1 2
l 0
d
l
2
x2
1 2
(1 3
l)x2
1 m1 23
x2TΒιβλιοθήκη T1Tm1 2
m1 3
m
x2
1 2
meq x2
又因为: 弹簧的势能与弹簧质量无关, 则
V 1 kx2 2
由能量法,可得
meq x kx 0 弹性元件质量不能忽略时,利用等
效质量,将质量折算到质量块上, 弹性元件仍看作无质量的。
• 18世纪线性振动理论成熟期。
第11页/共42页
• 19世纪非线性振动理论,各种工程实际结构振动的近似 求解方法。
• 20世纪50年代初由于航空航天工程的发展,原本确定性 理论无法解释包含随机变化的工程问题,发展了随机振 动理论。
• 20世纪后期计算机技术的飞速发展,数值计算方法和理 论成为主要研究方法之一。
第7页/共42页
三、结构动力学研究的内容
结构动力学就是研究结构系统在激励力作用下产生的响 应规律的科学,研究激励力、结构和响应三者关系的科 学。
现代结构动力学主要研究以下三个方面的内容 第一类问题:响应分析(结构动力计算)
输入 (动力荷载)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
➢ 所谓振型就是结构不同点(自由度)变化时的比例关系。
11
以上分析方法就是代数方程中的特征值分析,自振频率相应 于特征值,而振型即是特征向量。
得到体系的N 个自振频率和振型后,可以把振型和自振频率
分别写成矩阵的形式,
1 2 N
1 0 0
0
2
0
或
1,2,3
T
n
15
算例10-1 如图(a)所示三层框架结构,各楼层的质量和层 间刚度示于图中,确定结构的自振频率和振型。
(统一单位制:质量:吨,力:千牛,长度:米) 结构模型及各刚度元素:
16
算例10-1 结构的质量阵、刚度阵:
2.0 0 0
M
0
1.5
0
0 0 1.0
k11 k12 k13 3000 1200 0
多自由度体系:
{惯性力}+{阻尼力}+{恢复力}={外荷载}
f I f D fs p(t)
M u C u K u p (t )
4
预备知识
若矩阵[A]存在常数λ满足:
[A]x x
则称λ为矩阵[A]的特征值,{x}为矩阵对应特征值λ 的特征向量。
问题求解:转化为线性代数方程
([A] [I ])x 0
得到三个根 :
B1 0.3515, B2 1.6066, B3 3.5420
k22 2m22 k2N 2m2n 0
k N1 2mN1 k N 2 2mN 2 k NN 2mNN
9
对于N个自由度的稳定结构体系,频率方程是关于ω2的 N次方程,
a N ( 2 ) N a N 1 ( 2 ) N 1 a1 2 a 0 0
由此可以解得N个正实根(ω12<ω22<ω32…<ωN2)。 ωn(n=1, 2, …, N)即为体系的自振频率。其中量值最小的 频率ω1叫基本频率(相应的周期T1=2π/ω1叫基本周期)。 从以上分析可知,多自由度体系只能按一些特定的频 率即按自振频率做自由振动。按某一自振频率振动时,结 构将保持一固定的形状,称为自振振型,或简称振型。
7
将位移向量{u}和加速度向量{ü}代入无阻尼自由振动方程:
u 2 sin( t ) u s in ( t )
M u K u 0
( 2 M K ) sin( t ) 0
因为sin(ωt+θ)为任意的,可以消去,因此,
(K 2 M ) 0
上式是关于{φ}的N阶齐次线性方程组,表征了振型和自振
6
设多自由度体系在进行自由振动时也是在作简谐振 动,多自由度体系的振动形式可写为:
u u (t ) s in ( t )
{φ}—表示体系位移形状向量,它仅与坐标位置有关, 不随时间变化,称为振型。
ω —简谐振动的频率, θ —相位角。
上式对时间求两次导数可得:
u u(t ) 2 sin( t )
(K
2
M
)
1200
0
1200
1800 1.5 2
600
0
600
600
2
5 2B
600 2
频率方程:
0
B 2 600
2 3 1.5B
1
0 0
1 0
1 B 0
K 2 M 0
B 3 5.5B 2 7.5B 2 0
18
算例10-1 由频率方程
B 3 5.5 B 2 7.5 B 2 0
上述齐次方程组有非零解条件为:系数行列式为零
A [I ] 0
N×N矩阵[A]一般将有N个特征值,对应N个特征向量
5
§10-2 多自由度体系的自由振动
多自由度体系无阻尼自由振动的方程为:
M u K u 0
其中:[M]、[K]为N×N阶的质量和刚度矩阵 {u}和{ü}是N阶位移和加速度向量 {0}是N阶零向量
K k 21
k 22
k
23
1200
1800
600
k 31 k 32 k 33 0
600 600
17
算例10-1 运动方程的广义特征值问题:
2.0 0 0
M
0
1.5
0
0 0 1.0
3000 1200 0
K 1200
1800
600
0 600 600
什么是多自由度体系?
工程中所涉及的结构一般都是多自由度的,例如多层建筑结 构、大跨桥梁结构、空间网架结构等等。
为合理反映振动过程中惯性力的影响,需要采用更多的自由 度描述结构体系的质量分布并确定体系的变形。
3
单自由度体系:
惯性力+阻尼力+恢复力=外荷载
m u c u k u p ( t )
10
把相应的自振频率ωn代入运动方程的特征方程得到振型
K n 2 M n 0
{φ}n={φ1n, φ2n , …, φNn }T—体系的第n阶振型 。 ➢ 由于特征方程的齐次性(线性方程组是线性相关的),振型向量 是不定的,只有人为给定向量中的某一值,例如令φ1n=1,才能确 定其余的值。 ➢ 实际求解时就是令振型向量中的某一分量取定值后才能求解。 虽然令不同的分量等于不同的量,得到的振型在量值上会不一样, 但其比例关系是不变的。
结构动力学
第10章 多自由度运动方程
wo
Chapter10 Formulation of the MDOF Equations of Motion
本章提要
➢ §10-1 多自由度体系运动方程 ➢ §10-2 多自由度体系自由振动 ➢ §10-3 多自由度体系动力特性 ➢ §10-4 模态分析注意事项
0
0
N
其中,ωn— 第n阶自振频率,{φ}n—第 n阶振型。
[Φ]和[Ω]也分别称为振型矩阵和谱矩阵。
12
5 DOF with uniform mass and stiffness
5 DOF Base Isolated 13
14
5 DOF with uniform mass and stiffness
频率的关系 ,称为运动方程广义特征值问题。
由广义特征值可解得ω和{φ}。
8
(K 2 M ) 0
方程存在非零解的充分必要条件是系数行列式等
于零 :
K 2 M 0
是一关于ω的多项式,称为频率方程。
将刚度阵和质量阵代入得频率方程的具体形式:
k11 2m11 k21 2m21
k12 2m12 k1N 2m1N
11
以上分析方法就是代数方程中的特征值分析,自振频率相应 于特征值,而振型即是特征向量。
得到体系的N 个自振频率和振型后,可以把振型和自振频率
分别写成矩阵的形式,
1 2 N
1 0 0
0
2
0
或
1,2,3
T
n
15
算例10-1 如图(a)所示三层框架结构,各楼层的质量和层 间刚度示于图中,确定结构的自振频率和振型。
(统一单位制:质量:吨,力:千牛,长度:米) 结构模型及各刚度元素:
16
算例10-1 结构的质量阵、刚度阵:
2.0 0 0
M
0
1.5
0
0 0 1.0
k11 k12 k13 3000 1200 0
多自由度体系:
{惯性力}+{阻尼力}+{恢复力}={外荷载}
f I f D fs p(t)
M u C u K u p (t )
4
预备知识
若矩阵[A]存在常数λ满足:
[A]x x
则称λ为矩阵[A]的特征值,{x}为矩阵对应特征值λ 的特征向量。
问题求解:转化为线性代数方程
([A] [I ])x 0
得到三个根 :
B1 0.3515, B2 1.6066, B3 3.5420
k22 2m22 k2N 2m2n 0
k N1 2mN1 k N 2 2mN 2 k NN 2mNN
9
对于N个自由度的稳定结构体系,频率方程是关于ω2的 N次方程,
a N ( 2 ) N a N 1 ( 2 ) N 1 a1 2 a 0 0
由此可以解得N个正实根(ω12<ω22<ω32…<ωN2)。 ωn(n=1, 2, …, N)即为体系的自振频率。其中量值最小的 频率ω1叫基本频率(相应的周期T1=2π/ω1叫基本周期)。 从以上分析可知,多自由度体系只能按一些特定的频 率即按自振频率做自由振动。按某一自振频率振动时,结 构将保持一固定的形状,称为自振振型,或简称振型。
7
将位移向量{u}和加速度向量{ü}代入无阻尼自由振动方程:
u 2 sin( t ) u s in ( t )
M u K u 0
( 2 M K ) sin( t ) 0
因为sin(ωt+θ)为任意的,可以消去,因此,
(K 2 M ) 0
上式是关于{φ}的N阶齐次线性方程组,表征了振型和自振
6
设多自由度体系在进行自由振动时也是在作简谐振 动,多自由度体系的振动形式可写为:
u u (t ) s in ( t )
{φ}—表示体系位移形状向量,它仅与坐标位置有关, 不随时间变化,称为振型。
ω —简谐振动的频率, θ —相位角。
上式对时间求两次导数可得:
u u(t ) 2 sin( t )
(K
2
M
)
1200
0
1200
1800 1.5 2
600
0
600
600
2
5 2B
600 2
频率方程:
0
B 2 600
2 3 1.5B
1
0 0
1 0
1 B 0
K 2 M 0
B 3 5.5B 2 7.5B 2 0
18
算例10-1 由频率方程
B 3 5.5 B 2 7.5 B 2 0
上述齐次方程组有非零解条件为:系数行列式为零
A [I ] 0
N×N矩阵[A]一般将有N个特征值,对应N个特征向量
5
§10-2 多自由度体系的自由振动
多自由度体系无阻尼自由振动的方程为:
M u K u 0
其中:[M]、[K]为N×N阶的质量和刚度矩阵 {u}和{ü}是N阶位移和加速度向量 {0}是N阶零向量
K k 21
k 22
k
23
1200
1800
600
k 31 k 32 k 33 0
600 600
17
算例10-1 运动方程的广义特征值问题:
2.0 0 0
M
0
1.5
0
0 0 1.0
3000 1200 0
K 1200
1800
600
0 600 600
什么是多自由度体系?
工程中所涉及的结构一般都是多自由度的,例如多层建筑结 构、大跨桥梁结构、空间网架结构等等。
为合理反映振动过程中惯性力的影响,需要采用更多的自由 度描述结构体系的质量分布并确定体系的变形。
3
单自由度体系:
惯性力+阻尼力+恢复力=外荷载
m u c u k u p ( t )
10
把相应的自振频率ωn代入运动方程的特征方程得到振型
K n 2 M n 0
{φ}n={φ1n, φ2n , …, φNn }T—体系的第n阶振型 。 ➢ 由于特征方程的齐次性(线性方程组是线性相关的),振型向量 是不定的,只有人为给定向量中的某一值,例如令φ1n=1,才能确 定其余的值。 ➢ 实际求解时就是令振型向量中的某一分量取定值后才能求解。 虽然令不同的分量等于不同的量,得到的振型在量值上会不一样, 但其比例关系是不变的。
结构动力学
第10章 多自由度运动方程
wo
Chapter10 Formulation of the MDOF Equations of Motion
本章提要
➢ §10-1 多自由度体系运动方程 ➢ §10-2 多自由度体系自由振动 ➢ §10-3 多自由度体系动力特性 ➢ §10-4 模态分析注意事项
0
0
N
其中,ωn— 第n阶自振频率,{φ}n—第 n阶振型。
[Φ]和[Ω]也分别称为振型矩阵和谱矩阵。
12
5 DOF with uniform mass and stiffness
5 DOF Base Isolated 13
14
5 DOF with uniform mass and stiffness
频率的关系 ,称为运动方程广义特征值问题。
由广义特征值可解得ω和{φ}。
8
(K 2 M ) 0
方程存在非零解的充分必要条件是系数行列式等
于零 :
K 2 M 0
是一关于ω的多项式,称为频率方程。
将刚度阵和质量阵代入得频率方程的具体形式:
k11 2m11 k21 2m21
k12 2m12 k1N 2m1N
