第一讲(五年级奥数)
小学五年级奥数第一讲和倍问题

第一讲:和倍问题【知识点】已知两个数的和与它们之间的倍数关系,求这两个数各是多少的应用题,叫做和倍应用题。
基本数量关系:和÷倍数和=较小数【例1】学校有科技书和故事书共480本,科技书是故事书的3倍,两种书各有多少本?【思路导航】把故事书的本数看作1份,那么科技书的本数就是这样的3份,两种书的本数就是1+3=4份。
把480本书平均分成4份,1份就是故事书的本数,3份就是科技书的本数。
【练习1】用锡和铝制成的合金是720千克,其中铝的质量是锡的5倍,铝和锡各用了多少千克?【练习2】一块长方形黑板的周长是96分米,长是宽的3倍,这块长方形黑板的长和宽各是多少分米?【例2】果园里有梨树、桃树和苹果树共1200棵,其中梨树的棵树是苹果树的3倍,桃树的棵树是苹果树的4倍。
求梨树、桃树和苹果树各有多少棵?【思路导航】如果把苹果树的棵树看作1份,三种树的总棵树是1+3+4=8份。
所以,苹果树有1200÷8=150(棵),梨树有150×3=450(棵),桃树有150×4=600(棵)【练习1】专业户李大伯养鸭、鸡、鹅共960只,养鸡的只数是鹅的3倍,养鸭的只数是鹅的4倍。
鸡、鸭、鹅各养了多少只?【练习2】商店有铅笔、钢笔、圆珠笔共560支,圆珠笔的支数是钢笔的3倍,铅笔的支数和圆珠笔的支数同样多。
铅笔、钢笔、圆珠笔各有多少支?【例3】少先队员种柳树和杨树共216棵,杨树的棵树比柳树的棵树的3倍多20棵,两种树各种了多少棵?【思路导航】如果杨树少种20棵,那么杨树和柳树的总棵树是216-20=196棵,这时杨树的棵树恰好是柳树的3倍,柳树的棵树是196÷(3+1)=49棵,杨树的棵树是216-49=167(棵)。
【练习1】小华和小明两人参加数学竞赛,两人共得168分,小华的得分比小明的2倍少42分,两人各得了多少分?【练习2】学校购买了720本图书分给高、中、低三个年级段,高年级段分得的比低年级段的3倍多8本,中年级段分得的比低年级段的2倍多4本。
五年级奥数第一讲:整除初步

五年级奥数第一讲:整除初步例题1,判断下面12个数的整除性。
23487,3568,8875,6765,5880,7538,198954,6512,93625,864,407,91301301。
(1)哪些数能被4整除?--末尾2位数。
分析:3568、5880、198954、6512、864都是4的倍数,因为末尾2位数都是4的倍数。
(2)哪些数能被8整除?--末尾3位数。
分析:3568、5880、6512、864都是8的倍数,末尾三位数是8的倍数即可。
(3)哪些数能被25整除?---末尾2位数。
分析:8875、93625都是25的倍数,因为末尾2位数是25倍数。
(4)哪些数能被125整除?---末尾3位数。
分析:8875、93625,末尾三位数都是125的倍数。
(5)哪些数能被3整除?-----数字和是3的倍数。
分析:23487、6765、5880、198954、864、91301301都是3的倍数,因为数字和都是3的倍数。
(6)哪些数能被9整除?---数字和是9的倍数。
分析:198954、864,因为数字和是9的倍数。
(7)哪些数能被11整除?--截位判别法或奇偶位和差分析法。
分析:6765、6512、407是11的倍数。
(8)哪些数能被13整除?-截位判别法。
分析:91301301,末尾三位数和末尾三位数之前的数的差是13的倍数。
练习1:在数列3124,312,3823,45235,5289,5588,661,7314中。
(1)哪些数能被4整除?--末尾2位数。
分析:3124、312、5588的末尾两位数都是4的倍数,所以是4的倍数。
(2)哪些数能被3整除?---数字和。
分析:312、5289、7314都是3的倍数,因为数字和是3的倍数。
(3)哪些数能11整除?--截位判别法或奇偶位和差分析法。
分析:3124、5588是11的倍数。
例题2,173()是一个四位数,在括号内依次输入三个数字,分别得到三个四位数,依次分别能被9,11,8整除。
五年级第一讲第一节 奥数课件

3、妈妈要将3.2千克的油分装在几个瓶子里,每个瓶子最多装0.5
千克,问至少准备几个瓶子? 解:3.2÷0.5=6.4(个)≈7(个) 答:至少准备7个瓶子。
4、一堆煤重18.5吨,平均每次运2.5吨,一共需运多少次才能运完?
解:18.5÷2.8≈6.61≈7(次) 答:一共需运7次 才能运完。
《西游记》里倒数诗
(2) 小多多的准确体重范围是大于或等于48.45千克,而小
于48.55千克。
【小结】在我们的日常生活中,经常会对两个人的身高与体重进行比较,
实际上在比较中就用到求近似数“四舍五入法”的有关知识。这种最常 用的求近似数的方法,主要是看它省略的尾数是4或比4小时,就把尾数
舍去;如果省略的尾数最高位上的数是5或比5大时,把尾数省略去掉后,
一、下列叙述中的各数,哪些是准确数?哪些是近似数?分别在括号中标出。 1、小红的班级里有53位同学 。( 准确数 ) 2、我国的国土面积大约是960万平方千米。( 近似数) 3、数学课本的定价是 9.70元。( 准确数 ) 4、月球与地球之间的 平均距离大约是38万千米。( 近似数) 5、鹏程的身高接近1.57米。( 近似数 ) 6、一只苹果的质量约为200克。( 近似数 )
快 乐 轻 在 松 海 学 卫 数 学
解:由于数10吨的实际范围是大于或等于9.5吨而小于10.5吨,而 一桶黄沙不可能有0.5吨左右重,所以还应认为是10吨。
4、小精灵与小多多在讨论问题
小精灵:如果你把7498近似到千位数,你就会得到7000. 小多多:不,我有另一种解答方法,可以得到不同的答案。首先,将7498近似到
百位,得到7500,接着把7500近似到千位,就得到8000。
解:老张测得的水管长度范围是大于或等于3.75米而小于3.85米;
(完整版)小学五年级奥数第一讲__定义新运算及作业

第一讲定义新运算一、a、b是自然数,规定a※b=(a+b)÷2,求:3※(4※6)的值。
二、对于任意两个自然数a、b,定义一种新运算“*”:a*b=ab+a÷b,求75*5=?,12*4=?三、定义运算符“◎”:a◎b=3a+4b-5,求6◎9=?9◎6=?四、定义两种运算“○+”和“○×”,对于任意两个整数a、b规定:a○+b=a+b-1,a○×b=a×b-1,那么8○× [(6○+10)○+(5○×3)]等于多少?五、定义运算“○+”=(a+b)÷3,那么(3○+6)○+12与3○+(6○+12)哪一个大?大的比小的大多少?六、a、b是自然数,规定a⊙b= ab-a-b-10,求8⊙8=?七、如果1*2=1+2,2*3=2+3+4,3*4=3+4+5+6,……,请按照此规则计算3*7=?八、规定运算a@b=(a+b)÷2,且3@(x@2)=2,求x=?九、规定a△b=ab+2a, a▽b=2b-a,求(8△3)▽(9△5)的值。
第二讲定义新运算作业十、定义新运算“*”:a*b=3a+4b-2,求(1)10*11;(2)11*10。
十一、定义新运算“△”:a△b= a÷b×3,求(1)24△6;(2)36△9。
十二、规定a○+b,表示自然数a到b的各个数之和,例如:3 ○+10=3+4+5+6+7+8+9+10=52,求1○+200的值。
十三、定义新运算“○×”,a○×b=10a+20b,求(3○×7)+(4○×8)。
十四、定义新运算“△”:a△b=6a+3b+7,那么5△6和6△5哪个大?大的比小的大多少?十五、规定a*b=(a+b)÷2,求[(1*9)*9]*3的值。
十六、规定a☆b=3a-2b,如果x☆(4☆1)=7,求x的值。
十七、规定X○+Y=(X+Y)÷4求:(1)2○+(3○+5),(2)如果X○+16=10,求X的值。
五年级奥数(教案)第1讲:速算与巧算(二)

=2×3×3
=18
练习2:[8分]
计算:
[1]16÷3.2÷2.5
[2]12.5×36.8÷3.68
[3][7.5×5.1×8.4]÷[1.7×4.2×2.5]
[4]9.3×3.2÷3.23×6.46÷1.6÷3.1
分析:
[1][2]两个题目主要是利用除法的性质来解题。[3][4]两个题目跟例题的类型也是一样的,先变成有倍数关系的两个数相除,然后再把结果相乘,最后得出结果。
是不是也需要花相当长的时间呢?那么对于这种类型的题目有没有更简便
的方法呢?思考一下。
生:老师我发现,被除数里数字与除数里的数字存在着倍数关系。
师:谁和谁存在倍数关系?
生:4.8与2.4,7.5与2.5,8.1与2.7。
师:是的,正好存在三对倍数关系的数。从这里出发,我们可以怎么去思考呢?
生:我们可以分别相除,然后再把结果相乘,这样和原来的结果是一样的。
一、复习导入[3分]
师:同学们,上节课我们学了什么?
生:速算与巧算。
师:是的,主要学了哪些速算的方法呢?
生:特殊的数字相乘能够凑整。
师:是的,特殊的数字,比如说25和4相乘等于100,125和8相乘等于1000。
这些特殊的数字,其实在小数里也是适用的。所以当看到特殊数字的时候,
我们可以直接将它们凑在一起,使计算变得简便,如果没有这样的两个数,
师:这个就是解题的关键。现在会做了吗?
生:最后我们可以利用乘法分配律的逆运算来解答,[7.2+2.8]×11.11=10×
11.11=111.1。
师:这是第一小题,接下来看第二小题,不仅有乘法,加法,还有减法,对吗?
五年级奥数专题第一讲 数阵
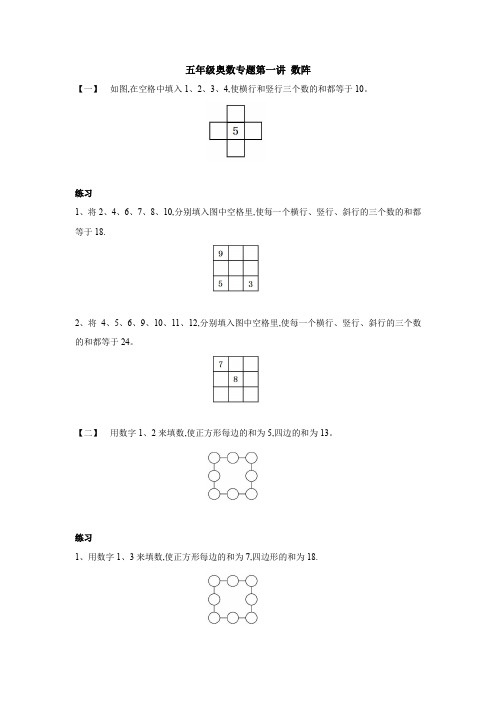
五年级奥数专题第一讲数阵【一】如图,在空格中填入1、2、3、4,使横行和竖行三个数的和都等于10。
练习1、将2、4、6、7、8、10,分别填入图中空格里,使每一个横行、竖行、斜行的三个数的和都等于18.2、将4、5、6、9、10、11、12,分别填入图中空格里,使每一个横行、竖行、斜行的三个数的和都等于24。
【二】用数字1、2来填数,使正方形每边的和为5,四边的和为13。
练习1、用数字1、3来填数,使正方形每边的和为7,四边形的和为18.2、用数字2、5来填数,使长方形每边的和为12,四边的和为31。
【三】把4、5、6、7、8五个数分别填入右图的五个方格里,使横行三个数的和与竖行三个数的和都是18。
练习1、把1~10各填入“六一”的10个空格里,使在同一直线的各数的和都是12。
2、把1~9各数填入“七一”的9个空格里,使在同一直线的各数的和都是13。
【四】将6~15这十个自然数填入下图的○中,使每个○上六个数的和是60。
练习1、把1~10这十个数分别填入下图的○内,使每个大圆上六个○内数的和相等。
2、把1~10这十个数分别填入下图的○内,,使每个四边形顶点的○内四个数的和都相等,且和最大。
【五】将2~7这六个数分别填入图中的圆中,使每条直线上三个圆内数的和相等、最大。
练习1、将3~8六个数分别填入下图的○内,使每边上的三个○内数的和相等。
2、将1~9九个数分别填入下图的○内,使每边上的三个○内数的和相等。
【六】将2~8分别填入下图的7个○内,使每条线段上的三个○内数的和相等。
练习1、将1~9填入下图的○中,使横、竖行五个数相加的和都等于26。
2、将1~11十一个数分别填入下图○里,使每条线上3个○内的数的和相等。
【七】如下图,四个小三角形的顶点处有六个圆圈。
如果在这些圆圈中分别填上六个质数,它们的和是20,而且每个小三角形三个顶点上的数的和相等。
问这个六个质数的积是多少?练习1、将九个不同的自然数填入下面方格中,使每行、每列、每条对角线上三个数的积都相等。
五年级奥数专题第一讲 尾数和余数

五年级奥数专题第一讲 尾数和余数【一】 写出除85后余1的数有哪些?练习1、写出除98余2的数有哪些?2、写出除105后余3的数有哪些?【二】 2×2×2×2×2×2×2×2积的尾数是几?练习1、5×5×5×5×5×5×5积的尾数是几?2、16×16×16×16×16×16积的尾数是几?【三】 写出除214后余4的全部两位数。
练习1、写出除111后余6的全部两位数。
2、180除以一个两位数后余数是5,适合条件的两位数有哪些?【四】 ”个“125100125125125125⨯⨯⨯⨯积的尾数是几?练习1、)个()()262110026212621()2621(⨯⨯⨯⨯⨯⨯⨯积的尾数是几?2、”个“45044444⨯⨯⨯⨯的积的个位数字是几?【五】”个“41004444÷6当商是整数时,余数是几?练习1、”个“5200855555÷13当商是整数时,余数是几?2、当商是整数时,余数是几?(1) ”个“6506666÷4 (2)”个“8808888÷7(3) ”个“410004444÷74 (4)”个“110001111÷5【六】 有一列数,前两个数是3与4,从第3个数开始,每一个数都是前两个数的和。
这一串数中第2000个数除以4,余数是多少?练习1、有一串数排成一行,其中第一个数是3,第二个数是10,从第三个数起,每个数恰好是前两个数的和。
在这一串数中,第2006个数被3除,所得的余数是几?2、一列数1、2、4、7、11、16、22、29……这一列数的规律是第二个数比第一个数多1;第三个数比第二个数多2;第四个数比第三个数多3,依次类推。
这列数左起第1000个数被5除余数是几?【七】 甲数除以11余9,乙数除以11余7。
五年级奥数第一讲:因数与倍数

五年级奥数第一讲:因数与倍数知识点拨1、因数和倍数:如果a×b=c(a,b,c都是不为零的整数),那么a,b就是c的因数,c就是a,b的倍数。
例如6×2=12,所以6和2是12的因数,12是6和2的倍数。
如果整数a能被b整除,那么a就是b的倍数,b就是a的因数。
例如10能被5整除,那么10就是5的倍数,5就是10的因数。
2、一个数的因数的求法:(1)列乘法算式找(2)列除法算式找一个数的因数的个数是有限的,最小的是1,最大的是它本身,方法是成对地按顺序找。
例如:15的因数有哪些?方法一:1×15=15,3×5=15(一般从自然数1开始,一对一对的找)方法二:15÷1=15,15÷3=5(计算时从除数1开始找,直到重复为止)所以15的因数就是1,3, 5, 15。
最大的因数就是15,也就是它本身!最小的是1。
3、一个数的倍数的求法:一个数的倍数的个数是无限的,最小的是它本身,没有最大的,方法是依次乘以自然数。
例如:3的倍数 3 6 9 12 15 。
...。
.。
3是3最小的倍数,也就是它本身倍数特征:最小的倍数是本身,没有最大的倍数如果两个数都是一个数的倍数,那么这两个数的和、差、积也是这个数的倍数.4、2、5、3的倍数的特征:①个位上是0、2、4、6、8的数,都是2的倍数。
②个位上是0或5的数,是5的倍数.③一个数各个数位上的数字之和是3的倍数,这个数就是3的倍数。
5、常见数字的整除判定方法:(1)2:个位是偶数的自然数(2)5:个位是0或5的自然数注:若一个数同时是2和5的倍数,则此数的个位一定为0(3)4、25:末两位能被4、25整除(4)8、125:末三位能被8、125整除(5)3、9:各个数位上的数之和能被3、9整除(6)7、11、13通用性质:①一个数如果是1001的倍数,即能被7、11、13整除。
如201201=201×1001,则其必能被7、11、13整除②从末三位开始三位一段,奇数段之和与偶数段之和的差如果是7、11、13的倍数,则其为7、11、13的倍数③末三位一段,前后均为一段,用较大的减去较小的,如果差为7、11、13的倍数,则其为7、11、13的倍数(7)11:奇数位数字之和与偶数位数字之和的差能被11整除(8)99:两位一段(从右往左),各段的和能被99整除(9)999:三位一段(从右往左),各段的和能被999整除6、在自然数中,是2的倍数的数叫做偶数(0也是偶数),不是2的倍数的数叫做奇数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一讲 初等数论1-最小公倍数和最大公约数
〖知识点〗
1、整数a 能被整数b(b ≠0)整除,称a 是b 的倍数,b 是a 的约数,记作: b/a 。
2、几个数公有的约数叫做这几个数的公约数,公约数的个数是有限的,其中最大的一个叫做这几个数的最大公约数。
若,1a 2a ,…n a 这几个数的最大公约数是d ,可记作:(1a ,2a ,…n a )=d
3、几个数公有的倍数叫做这几个数的公倍数,公倍数的个数是无限的,其中最小的一个叫做这几个数的最小公倍数。
若,1a 2a ,…n a 这几个数的最小公倍数是m ,可记作:[1a ,2a ,…n a ]=m
4、性质:
①(a,b)=d,c/d, 则c/a,c/b;
②(a,b)=d,则(d a ,d
b )=1; ③若(a,b)=d,[a,b]=m,则dm=ab,且d/m;
④[,1a 2a ,…n a ]=m,而1a /N,2a /N,…,n a /N,那么m/N;
⑤若b/a,则(a,b)=b,[a,b]=a
⑥若a 与b 互质,则(a,b)=1,[a,b]=ab
5、求最大公约数与最小公倍数的常见方法:列举法,短除法,分解质因数法,辗转相除法
〖典型例题〗
例1. 用短除法求42,168,252的最大公约数和最小公倍数。
例2.用分解质因数法求2520,14850,819的最大公约数和最小公倍数。
〖辗转相除法〗
定理:对于正整数a,b,成立带余除法式:a=mb+r, 0≤r<b,则(a,b)=(b,r).
例3.利用辗转相除法求:63677与5957的最大公约数。
例4. 如图所示,街道ABC在B处拐弯,在街道的一侧等距离装路灯,要求A、B、C处各装一盏路灯,这条街道最少要装多少盏灯?
1625米
A B
1170米
C
例5.有两个100以内的两位数,这两个两位数的最大公约数是16,这两个数分别是多少?
例6.三个连续自然数的最小公倍数是9828,这三个自然数的和是多少?
例7.甲每13天去公园一次,乙每15天去公园一次,今年甲在3月30日曾去公园,乙在4月1日曾去公园,他们可能在这公园第一次相遇的日期将是几月几日?
例8.培训学校给优秀学生发放奖品,奖品共有本297个,笔383枝。
将这些奖品等分给若干个优秀学生,最后多出3个本和5枝笔。
已知每个学生得到的本和笔的总数不超过20,那么优秀学生有几个?
例9.两个数的和是70,它们的最大公约数是7,求这两个数的差是多少?
例10.在除13511,13903,14589时能剩下相同余数的最大整数是多少?
例11.一个小于200的数,它除以11余8,除以13余10,那么这个数是多少?
例12.下面两个算式中,的书较大的是哪一个?
(1)(241+291)×30 (2)(311+37
1)×40
例13.有甲乙丙三个人在操场跑道上步行,甲每分钟走80米,乙每分钟走120米,丙每分钟走70米,已知操场跑道每周长400米,如果的三个人同时同一地点出发,问几分钟后三人可以相聚?
例14.已知两个自然数的差为2,它们的最小公倍数和最大公约数之差为142,求这两个自然数各是多少?
例15.已知两个自然数的和是60,它们的最小公倍数和最大公约数之和是84,求这两个自然数各是多少?
例16.在一根长木棍上,有三种刻度线,第一种刻度线将木棍等分成10等份,第二种刻度线把木棍等分成12等份,第三种刻度线把木棍等分成15等份,如果沿每条刻度线把木棍锯断,木棍总共被锯成多少段?
例17.设a与b为两个不相等的自然数,如果它们的最小公倍数是72,那么a 与b之和可以有多少种不同的值?
例18.已知a与b 的最大公约数是12,a与c的最小公倍数是300,b与c的最小公倍数是300,那么满足上述条件的自然数a,b,c共有多少组?(例如:a=12,b=13,c=300与a=300,b=12,c=300是不同的两个自然数组)
〖巩固练习〗
1.已知a=440,b=126,c=825,求(a,b,c)和[a,b,c]。
2.写出三个小于10的自然数,使它们三个数中有两个数的最大公约数为1,其余的最大公约数大于1。
3.甲数为24,甲、乙两数的最小公倍数是168,最大公约数是4,乙数是多少?
4.现有4个自然数,它们的和是1111,如果要求这4个数的公约数尽可能地大,那么这4个数的最大公约数是多少?
5.设A,B两个数都只含有质因数3和5,它们的最大公约数是75,已知A有12个约数,B有10个约数,那么A、B两数的和等于多少?
6.已知两个自然数的差为3,它们的最大公约数与最小公倍数之积为180,求这两个自然数。
7.写出小于20的三个自然数,使它们的最大公约数是1,但其中任两数都不互补。
8.所有形如abcabc的六位数,它们的最大公约数是多少?
9.两个自然数的和是50,它们的最大公约数是5,则这两个数的差是多少?
10.动物园的饲养员给三群猴子分花生,每群猴子的数量相等,如只分给第一群,则每只猴子可得12粒;如只分给第二群,则每只猴子可得15粒,如只分给第三群,则每只猴子可得20粒,那么平均分给三群猴子,每只猴子可得多少粒花生?
11.两个整数A,B 的最大公约数是C ,最小公倍数是D,且C+D=187,已知C不等于1,也不等于A或B,求A+B的值。
12.三条圆形跑道,圆心都在旗杆的中心处,甲、乙、丙3人分别在里圏、中圏、外圈沿同样的方向跑步,开始时,3人都在旗杆的正东方向,里圏跑道长5
1千米,中圈跑道长41千米,外圈跑道长83千米,甲每小时跑2
7千米,乙每小时跑4千米,丙每小时跑5千米,问他们同时出发,几小时后3人第一次同时回到出发点?。
