基于matlab的霍夫变换精品-讲义
霍夫变换(详解)

给定具体的五个点:
(a)image space
(b)hough space
选择由尽可能多直线汇成的点,如A和B。
y=x-1 y=1 (a)image space (b)hough translation
A,B确定了两组参数(k,q),代入直线方程y=kx+q, 可以描述图像空间中对应的直线。
特殊情况,
hough translation 霍夫变换检测直线
基本原理
霍夫变换利用点和线之间的对偶性,将 图像空间中直线上离散的 像素点 通过参数方 程映射为霍夫空间中的 曲线 ,并将霍夫空间 中多条曲线的 交点 作为直线方程的参数 映射 为图像空间中的 直线。 给定直线的参数方程,可以利用霍夫变 换来检测图像中的直线。
原图
二值化
canny边缘检测
霍夫变换直线检测
谢谢!
给定具体的三个点:
y=x-1
(1,-1) (a)image space 图像空间中共线的点, 在霍夫空间对应的直线相交于一点。 (b)hough space
点和线的对偶性
(1)图像空间中的点,对应霍夫空间中的直 线。 (2)图像中的直线,对应霍夫空间中的点。 (3)共点的直线,在霍夫空间中对应的点在 一条直线上。 (4)共线的点,在霍夫空间中对应的直线交 与一点。
(b)hough space
过同一点的直线,在霍夫空间中所对应的点在一条直线上。
两个点的情况:
y=kx+q
(k,q)
(a)image space 霍夫空间中的交点,确定了一组参数(k,q) 。 将(k,q)代入直线方程 y=kx+q , 可以描述图像空间中过A,B两点的直线。
(b)hough space
霍夫变换(hough transform)

一、概述霍夫变换是一种常用的图像处理技术,它可以用于检测图像中的直线、圆或者其他形状。
它具有很好的鲁棒性,可以应对图像中存在的噪声和其他干扰。
霍夫变换在计算机视觉、图像处理和模式识别领域有着广泛的应用,成为了处理图像中几何形状的重要工具。
二、霍夫变换的原理霍夫变换最初是由美国科学家保罗·霍夫在1962年提出的,用于检测图像中的直线。
后来,霍夫变换被扩展到检测圆或者其他形状。
霍夫变换的基本原理是将空间域中的坐标转换到参数域中,在参数域中对应的曲线经过的点在空间域中具有共线的特点。
通过累加空间域中的点的参数,可以找到曲线或者形状的参数方程,从而实现对图像中形状的检测。
具体来说,对于检测直线来说,可以通过霍夫变换将直线表示为参数空间中的斜率和截距,从而可以在参数空间中进行累加,最终找到直线的参数方程。
三、霍夫变换在直线检测中的应用1. 边缘检测在使用霍夫变换检测直线之前,通常需要对图像进行边缘检测。
边缘检测可以帮助找到图像中明显的过渡区域,这些过渡区域通常对应着直线的轮廓。
常用的边缘检测算法包括Sobel算子、Canny算子等。
2. 参数空间的设置为了使用霍夫变换来检测直线,需要设定参数空间的范围。
对于直线检测来说,一般可以设定直线的斜率和截距的取值范围。
3. 累加过程在设定好参数空间后,需要对图像中的边缘点进行霍夫变换的累加过程。
对于每一个边缘点,都可以在参数空间中找到对应的直线,通过对参数空间的累加,可以找到参数空间中的峰值,这些峰值对应着图像中的直线。
4. 直线检测可以根据参数空间中的峰值来确定图像中的直线。
通常可以设定一个阈值来筛选参数空间中的峰值,从而得到最终的直线检测结果。
四、霍夫变换在圆检测中的应用除了直线检测,霍夫变换也可以用于检测图像中的圆。
与直线检测类似,圆检测也需要进行边缘检测和参数空间的设定。
不同的是,在圆检测中,需要设定圆心和半径的参数空间范围。
五、霍夫变换的改进和应用1. 累加数组的优化在传统的霍夫变换中,需要对参数空间进行离散化,这会导致计算量较大。
matlabcanny边缘检测代码接霍夫变换-概述说明以及解释

matlabcanny边缘检测代码接霍夫变换-概述说明以及解释1.引言1.1 概述边缘检测是图像处理中的一个重要任务,它广泛应用于计算机视觉、图像分析和模式识别等领域。
边缘检测的目标是找到图像中不同区域之间的边界,并将其表示为像素强度的变化。
Canny边缘检测算法是一种经典且常用的边缘检测方法。
它通过一系列的图像处理步骤来提取图像中的边缘信息。
Canny算法的特点是能够检测出细且准确的边缘,并且对于图像中的噪声具有较好的抵抗能力。
Matlab是一种功能强大的数学软件,广泛应用于科学计算、数据可视化和图像处理等领域。
Matlab提供了丰富的图像处理函数和工具箱,其中包括了Canny边缘检测的实现代码。
本文的主要目的是介绍Matlab中Canny边缘检测的代码实现,并结合Hough变换算法进行边缘检测的应用。
通过使用Matlab中的相关函数和工具,我们可以有效地实现Canny边缘检测,并结合Hough变换来进一步处理和分析图像中的边缘特征。
本文将首先回顾Canny边缘检测算法的原理和步骤,然后介绍Matlab中的Canny边缘检测代码的使用方法。
接着,我们将介绍Hough 变换算法的原理和应用,并展示如何将Canny边缘检测与Hough变换相结合来实现更精确的边缘检测。
最后,我们将对Canny边缘检测和Hough变换的优缺点进行讨论,总结这两种方法在边缘检测中的应用。
同时,我们也将展望未来的研究方向,探讨如何进一步改进和优化边缘检测算法,以满足不断发展的图像处理需求。
通过阅读本文,读者将能够理解Canny边缘检测算法和Hough变换算法的原理,掌握Matlab中相关代码的使用方法,并了解边缘检测在实际应用中的优势和局限性。
希望本文能为读者在图像处理领域的学习和研究提供一定的帮助和启示。
文章结构是指文章的整体框架和组织形式。
一个良好的文章结构可以使读者更好地理解和领会文章的内容,同时也有助于文章的逻辑性和条理性。
霍夫变换(详解)

基本原理
霍夫变换利用点和线之间的对偶性,将 图像空间中直线上离散的 像素点 通过参数方 程映射为霍夫空间中的 曲线 ,并将霍夫空间 中多条曲线的 交点 作为直线方程的参数 映射 为图像空间中的 直线。 给定直线的参数方程,可以利用霍夫变 换来检测图像中的直线。
原图
二值化
canny边缘检测
霍夫变换直线检测
谢谢!
给定具体的五个点:
(a)image space
(b)hough space
选择由尽可能多直线汇成的点,如A和B。
y=x-1 y=1 (a)image space (b)hough translation
A,B确定了两组参数(k,q),代入直线方程y=kx+q,况,
q q=-2k+4 q=-2k+3 q=-2k+1
(a)Image space q = -xk+y 无法确定图像空间中的垂线。
(b) hough space
k
转化为极坐标下的参数方程:
x1cosθ+y1sinθ=ρ
x1cosθ=ρcos2θ y1sinθ=ρsin2θ
图像空间中的点,对应了霍夫空间中的曲线。 曲线的交点确定了一组参数,能够描述图像空间中的特定直线。
给定具体的三个点:
y=x-1
(1,-1) (a)image space 图像空间中共线的点, 在霍夫空间对应的直线相交于一点。 (b)hough space
点和线的对偶性
(1)图像空间中的点,对应霍夫空间中的直 线。 (2)图像中的直线,对应霍夫空间中的点。 (3)共点的直线,在霍夫空间中对应的点在 一条直线上。 (4)共线的点,在霍夫空间中对应的直线交 与一点。
MATLAB在复变函数中的应用 ppt课件

0.9501 + 0.4565i 0.4860 + 0.4447i 0.2311 + 0.0185i 0.8913 + 0.6154i 0.6068 + 0.8214i 0.7621 + 0.7919i
4
2 复数的运算
2.1 复数实部和虚部、共轭复数、复数的模和辐角
1.复数实部和虚部
real(X) 返回复数X的实部
fourier(f,v)=F(v)=int(f(x)*exp(-i*v*x),x,-inf,inf) ➢ F=fourier(f,u,v): 以v代替x且对u积分。且有
fourier(f,u,v)=F(v)=int(f(u)*exp(-i*v*u),u,-inf,inf)
% complex08.m syms s v w x F1=fourier(1/t) F2=fourier(exp(-x^2),x,t) F3=fourier(exp(-t)*sym(‘Heaviside(t)’),v) F4=fourier(diff(sym(‘F(x)’)),x,w)
基于matlab的直线检测原理

基于matlab的直线检测原理
基于Matlab的直线检测原理涉及到一种称为霍夫变换的方法。
霍夫变换是一种在图像处理中常用的方法,用于检测图像中的直线。
下面是基于Matlab的直线检测原理的具体步骤:
1. 读取图像:首先,在Matlab中读取需要进行直线检测的图像。
2. 边缘检测:使用Matlab提供的边缘检测算法(例如Canny
算法)来检测图像中的边缘。
这可以通过调用Matlab中的imedge函数来实现。
3. 霍夫变换:使用Matlab中的hough函数来执行霍夫变换。
霍夫变换将边缘图像转换为霍夫空间,其中每个点对应于直线在原始图像中的参数。
通过设置适当的阈值和其他参数,可以控制检测到的直线的数量和质量。
4. 直线提取:通过分析霍夫变换的结果,在霍夫空间中找到具有最高数量的交点,这些交点对应于图像中的直线。
可以使用Matlab的houghpeaks函数来找到霍夫空间中的交点。
5. 直线可视化:使用Matlab中的houghlines函数来提取直线
的位置和角度,并在原始图像上绘制检测到的直线。
这将帮助用户看到直线检测的结果。
需要注意的是,直线检测的结果可能会受到图像质量、边缘检
测算法的选择和参数设置的影响。
因此,在实际应用中,可能需要不断调整参数以获得更好的直线检测结果。
matlabcanny边缘检测代码接霍夫变换

matlabcanny边缘检测代码接霍夫变换全文共四篇示例,供读者参考第一篇示例:Matlab是一个强大的数学软件工具,其图像处理工具箱可以帮助我们进行各种图像处理操作,比如边缘检测和霍夫变换。
本文将分享如何使用Matlab进行Canny边缘检测,并结合霍夫变换进行线检测。
Canny边缘检测是一种经典的边缘检测算法,它的优点是能够检测到边缘的细节,并且对噪声具有一定的鲁棒性。
在Matlab中,我们可以通过一行简单的代码来实现Canny边缘检测:```edgeImage = edge(rgb2gray(image), 'canny');```以上代码中,我们首先将原始图像转换为灰度图像,然后调用Matlab的'edge'函数,并指定边缘检测算法为Canny,最后我们将得到的边缘图像存储在edgeImage中。
接下来,我们可以将边缘图像显示出来,以便进行进一步的处理和分析。
```imshow(edgeImage);通过上述代码,我们可以看到Canny边缘检测算法的效果,边缘比较清晰,同时也保留了边缘的细节信息。
接下来,我们将介绍如何使用霍夫变换来进行线检测。
霍夫变换是一种经典的图像处理算法,其主要应用是检测直线和圆等几何形状。
在Matlab中,我们可以通过一行代码来实现霍夫变换的线检测:```[H,theta,rho] = hough(edgeImage);peaks = houghpeaks(H, 10);lines = houghlines(edgeImage, theta, rho, peaks);imshow(image);hold on;for k = 1 : length(lines)xy = [lines(k).point1; lines(k).point2];plot(xy(:,1),xy(:,2),'LineWidth',2,'Color','green');endhold off;以上代码中,我们首先调用Matlab的'hough'函数来计算霍夫变换的极坐标空间。
RADON变换说明及MATLAB例子
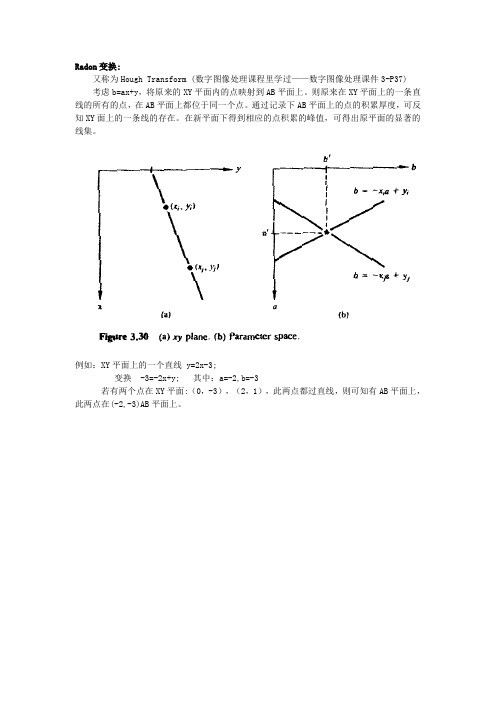
Radon变换:又称为Hough Transform(数字图像处理课程里学过——数字图像处理课件3-P37)考虑b=ax+y,将原来的XY平面内的点映射到AB平面上。
则原来在XY平面上的一条直线的所有的点,在AB平面上都位于同一个点。
通过记录下AB平面上的点的积累厚度,可反知XY面上的一条线的存在。
在新平面下得到相应的点积累的峰值,可得出原平面的显著的线集。
例如:XY平面上的一个直线y=2x-3;变换-3=-2x+y;其中:a=-2,b=-3若有两个点在XY平面:(0,-3),(2,1),此两点都过直线,则可知有AB平面上,此两点在(-2,-3)AB平面上。
一种更好的表示方法是用ρ和θ来代替ab。
即:xcosθ+ysinθ=ρ以图像的中心为极坐标原点,直线X`即为新的投影坐标,θ为角度。
我们所要求的原坐标上的一条直线,是一条垂直于上图X`的一条直线,而非X`本身。
如下例:function radontestI=zeros(200,200);%I(100:170,100:170)=1;A=eye(100,100);I(101:200,1:100)=A;figure,imshow(I);title('orginal image');orginal imagetheta=0:180;[R,xp]=radon(I,theta);%R是点的数量多少%xp是R对应的坐标位置,即为X`,另一解释为直线跟原点间距离%0-180代表0到180度%此变换是以图像的中心点为原点的变换figure,imagesc(theta,xp,R);title('R_theta X');xlabel('theta(degree)');ylabel('X\prime');colormap(hot);colorbar;即所求 =45度,X`=-75左右。
意思是在原XY坐标下的45度的直线X`上,距离原点75的位置有条与X`垂直的直线。
