系统辨识大作业论文Use
学生作业管理系统论文

目录摘要 (2)1课题的可行性与需求分析 (3)1.1系统功能需求 (3)1.1.1管理员部分的主要功能要求 (3)1.1.2教师部分的主要功能要求 (3)1.1.3学生部分的主要功能要求 (3)1.1.3 决定可行性的主要因素 (4)1.2性能分析 (5)1.2.1系统性能需求 (5)1.2.2主要功能要求 (5)1.3系统技术需求: (6)1.4系统数据需求 (6)1.5需求分析 (8)1.5.1 设计目标 (8)1.5.2 开发意图 (8)1.5.3 功能需求分析 (8)1.5.4 总结 (8)2总体设计 (9)2.1处理流程和数据流程 (9)3 详细设计 (12)3.1下面以结构图来描述 (12)3.2用户数据表 (13)4 结果分析 (17)参考文献 (18)摘要随着信息技术的迅速发展、电脑化教学与远程的网络化教学的普及,给传统的教学方式带来了重大的革命,也给教学改革的实施者们提出了很多新的课题。
如何有效进行作业管理就是一个让很多老师头痛的问题。
目前,国内外作业管理一般采用两种方法:一种将作业存在软盘上交;另一种者存放到教师电脑上的一个共享目录内。
但这两种方法都有各自的弊端:前一种方法不方便携带、速度慢、容量小、易损坏;后一种方法虽然解决了软盘容量小、容易坏的问题。
但却存在一个更致命的缺点:学生可以随意查看、更改和删除其它同学的作业,造成大量如抄袭作业、恶意删除或修改其他同学作业的事情发生;老师在帮学生修改作业时,也很容易弄不清楚作业批改与否;作业是谁的或是旧作业没删除掉,跟新作业搞混了等情况,虽然有些可以用严格的纪律来实现管理,但仍然会给学校和老师带来很多的麻烦。
在当前的信息化时代中,任何学校,都需要一个实用的作业管理系统来规范作业管理,这将会大大提高学校的管理水平,优化资源,实现效益的最大化。
关键词:ADO技术,JSP1课题的可行性与需求分析1.1系统功能需求学生作业管理系统主要提供网上的作业管理平台,主要分为管理员、教师、学生三个部分的功能。
系统辨识实验报告
i=1:800; figure(1) plot(i,Theta(1,:),i,Theta(2,:),i,Theta(3,:),i,Theta(4,:),i,Theta(5,:),i,T title('待估参数过渡过程') figure(2) plot(i,Pstore(1,:),i,Pstore(2,:),i,Pstore(3,:),i,Pstore(4,:),i,Pstore(5,: title('估计方差变化过程')
最小二乘法建模:
二、三次实验 本次实验要完成的内容: 1.参照index2,设计对象,从workspace空间获取数据,取二阶,三阶 对象实现最小二乘法的一次完成算法和最小二乘法的递推算法(LS and RLS); 2.对设计好的对象,在时间为200-300之间,设计一个阶跃扰动,用最 小二乘法和带遗忘因子的最小二乘法实现,对这两种算法的特点进行说 明; 实验内容结果与程序代码: 利用LS和RLS得到的二阶,三阶参数 算法 阶次 A1 A2 A3 B0 B1 B2 B3 LS 二阶 -0.78420.1373 -0.00360.5668 0.3157 RLS 二阶 -0.78240.1373 -0.00360.5668 0.3157 LS 三阶 -0.4381-0.12280.0407 -0.00780.5652 0.5106 0.1160
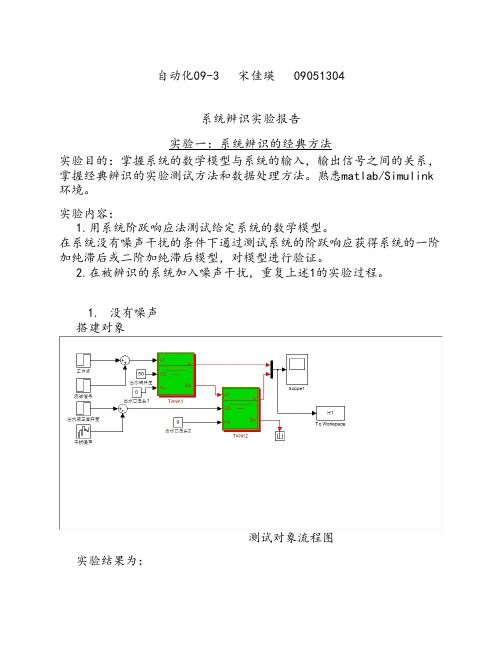
测试对象流程图 实验结果为:
2、加入噪声干扰 搭建对象
实验结果:
加入噪声干扰之后水箱输出不平稳,有波动。
实验二:相关分析法 搭建对象:
处理程序: for i=1:15 m(i,:)=UY(32-i:46-i,1);
end y=UY(31:45,2); gg=ones(15)+eye(15); g=1/(25*16*2)*gg*m*y; plot(g); hold on; stem(g); 实验结果: 相关分析法
系统辨识最小二乘法大作业

系统辨识最小二乘法大作业系统辨识大作业最小二乘法及其相关估值方法应用学号:2012302259姓名:王家琦基于最小二乘法的多种系统辨识方法研究1.最小二乘法的引出在系统辨识中用得最广泛的估计方法是最小二乘法(LS)。
设单输入-单输出线性定长系统的差分方程为x(k)+a1x(k−1)+⋯+a n(k−n)=b0u(k)+⋯+b n u(k−n),k=1,2,3,⋯式中: u(k)为随机干扰;x(k)为理论上的输出值。
x(k)只有通过观测才能得到,在观测过程中往往附加有随机干扰。
x(k)的观测值y(k)可表示为y(k)=x(k)+n(k)式中: n(k)为随机干扰。
由式得x(k)=y(k)−n(k)将式带入式得y(k)+a1y(k−1)+⋯+a n y(k−n)=b0u(k)+b1u(k−1)+⋯n+b n u(k−n)+n(k)+∑a i(k−i)i=1我们可能不知道n(k)的统计特性,在这种情况下,往往把n(k)看做均值为0的白噪声。
设nξ(k)=n(k)+∑a i(k−i)i=1则式可写成y(k)=−a1y(k−1)−a2y(k−2)−⋯−a n y(k−n)+b0u(k)+b1u(k−1)+⋯+b n u(k−n)+ξ(k)在观测u(k)时也有测量误差,系统内部也可能有噪声,应当考虑它们的影响。
因此假定ξ(k)不仅包含了x(k)的测量误差,而且包含了u(k)的测量误差和系统内部噪声。
假定ξ(k)是不相关随机序列(实际上ξ(k)是相关随机序列)。
现分别测出n+N个随机输入值y(1),y(2),⋯,y(n+N),u(1),u(2),⋯,u(n+N),则可写成N个方程,即y(n+1)=−a1y(n)−a2y(n−1)−⋯−a n y(1)+b0u(n+1)+b1u(n)+⋯+b n u(1)+ξ(n+1)y(n+2)=−a1y(n+1)−a2y(n)−⋯−a n y(2)+b0u(n+2)+b1u(n+1)+⋯+b n u(2)+ξ(n+2)⋮y(n+N)=−a1y(n+N−1)−a2y(n+N−2)−⋯−a n y(N)+b0u(n+N)+b1u(n+N−1)+⋯+b n u(N)+ξ(n+N)上述N个方程可写成向量-矩阵形式[y(n+1) y(n+2)⋮y(n+N)]=[−y(n)−y(n +1)⋯⋯−y(1)u(n +1)⋯u(1)−y(2)u(n +2)⋯u(2)⋮⋮ ⋮ ⋮ ⋮−y(n +N −1)⋯−y(N)u(n +N)⋯u(N)]×[ a1⋮a n b 0⋮b n ]+[ξ(n +1)ξ(n +2)⋮ξ(n +3)]设y =[y(n +1)y(n +2)⋮y(n +N)],θ=[ a 1⋮a n b 0⋮b n ],ξ=[ξ(n +1)ξ(n +2)⋮ξ(n +N)]Φ=[−y(n)−y(n +1)⋯⋯−y(1)u(n +1)⋯u(1)−y(2)u(n +2)⋯u(2)⋮⋮⋮ ⋮ ⋮−y(n +N −1)⋯−y(N)u(n +N)⋯u(N)]则式可写为y =Φθ+ξ式中:y为N维输出向量;ξ为N维噪声向量;θ为(2n+1)维参数向量;Φ为N×(2n+1)测量矩阵。
系统辨识论文

系统辨识摘要对现有的系统辨识方法进行了介绍。
首先说明了系统辨识的传统方法及其不足, 进一步引出了把神经网络、遗传算法、模糊逻辑、小波网络等知识应用于系统辨识得到的一些新型辨识方法, 最后介绍了系统辨识未来的发展方向。
Abstract: T he current methods for system identification arepresented. The traditional system identification methods andtheir shortcomings are summarized. Some new methods basedon neural network, genetic algorithms, fuzzy logic, waveletnetwork etc are introduced. Finally research trends of systemidentification are given.前言系统辨识是建模的一种方法。
不同的学科领域, 对应着不同的数学模型, 从某种意义上讲, 不同学科的发展过程就是建立它的数学模型的过程。
建立数学模型有两种方法: 即解析法和系统辨识。
L.A.Zadeh于 1962 年曾对“辨识”给出定义: 系统辨识是在对输入和输出观测的基础上, 在指定的一类系统中, 确定一个与被识别的系统等价的系统。
但是,实际上我们不可能找到一个与实际系统完全等价的模型。
从实用的角度来看, 系统辨识就是从一组模型中选择一个模型, 按照某种准则,使之能最好地拟合由系统的输入输出观测数据体现出的实际系统的动态或静态特性。
经典的系统辨识方法的发展已经比较成熟和完善, 他包括阶跃响应法、脉冲响应法、频率响应法、相关分析法、谱分析法、最小二乘法和极大似然法等。
其中最小二乘法( LS) 是一种经典的和最基本的, 也是应用最广泛的方法。
但是, 最小二乘估计是非一致的, 是有偏差的, 所以为了克服他的缺陷, 而形成了一些以最小二乘法为基础的系统辨识方法: 广义最小二乘法( GLS) 、辅助变量法( IV)、增广最小二乘法( ELS) 和广义最小二乘法( GLS) ,以及将一般的最小二乘法与其他方法相结合的方法, 有最小二乘两步法( COR- LS)和随机逼近算法等。
系统辨识大作业.

系统辨识大作业
已知一系统为两输入单输出系统,观测数据受有色噪声污染,噪信比为N/S=0.1。
系统经2000次采样,存放于文件T3T.TXT中。
系统输入u1为7级M序列,u2为u1的63步移位序列。
模型类可选为:A(q-1)y(k)=B1(q)u1(k)+ B2(q)u2(k)+w(k)/C(q-1)。
要求编制程序,辨识出该模型的结构及参数。
作业文档要求:
描述问题;
选择辨识方法并简单说明所选方法中的结构辨识原理和参数估计原理;
程序流程图及程序清单;
说明程序中用到的一些技术,如数据标准化、UD分解、稳定性判断等;
结构搜索路线及各结构下的参数、残差;
给出最终结果:A(q-1)=
B1(q)=
B2(q)=
C(q-1)=
并给出选择此最终结果的理由;
用你的辨识结果来预报系统输出误差e(k)=y(k)-y(k),并画出e(101)-e(400)的曲线图。
系统工程论文(共5篇)

系统工程论文(共5篇)第一篇:系统工程论文工程论文是指工程师论文,工程管理论文与工程论文发表的工程论文。
对于论文应该怎么写?一起来看看!公路建设中公路工程检测技术的应用【摘要】公路建设作为我国基础设施建设的重要组成内容,受到社会各界以及国家的广为重视,促使我国公路建设无论是在建设规模还是在建设范围方面都在不断扩大。
随着我国公路建设的不断扩大,存在诸多影响公路工程质量的因素,对公路工程的质量造成极大的威胁,因此,科学地应用公路工程检测十分必要。
为此,论文从公路建设入手来探讨公路工程试验以及检测技术实际应用的相关方面。
【关键词】公路;检测技术;公路工程试验1公路工程的试验检测内容分析公路工程的试验检测是控制工程质量的重要手段,也是公路工程质量验收评定的一个主要环节,通过试验检测活动客观、及时、准确地记录公路工程在开展过程中所涉及的真实记录,在充分利用资源的基础上采取科学方法实现工程质量提高的目标。
因此,加强公路工程试验检测工作,充分发挥这一工作的实际作用,对于提高工程质量、加快工程进度和降低工程成本具有重要的意义。
因此,本文对公路工程的检测试验活动进行分析。
1.1工前试验工前试验主要分为以下几个环节(1)材料检测,建筑材料是公路建设的物质基础,合理地使用材料关系到工程的整体开展,因此,对于工程所需要的材料都应该按照试验检测流程进行检验,检验合格后方能使用,检验不合格的产品一律禁用;(2)参数确定,正确、合理的参数对于公路工程的开展具有重要作用,因此,要认真对待这一环节,严格按照试验检测规程,最大程度上规避试验误差,提高试验的精确度,为工程的良好开展奠定基础;(3)标准试验,标准试验的结果是施工质量跟踪检测的依据,因此,要按照规程在工程开展之前进行基本性能试验,在进行各种混合材料的配合比试验,从而促进公路工程的良好开展。
1.2跟踪检测和验收检测在施工工程中,控制工程质量的因素主要涉及施工单位自检、监理抽检及监督等方面,因此,为了做好公路工程试验检测活动,一方面需要施工方从制度入手,建立一套符合实际发展情况的试验检测制度,并且配备专业的检测人员来进行有效的开展,另一方面需要从监督方面入手,充分发挥监督机构的作用,严格地进行考核、审批和检测,为公路工程检测试验活动的良好开展奠定基础。
系统辨识最小二乘法大作业 (2)

系统辨识大作业最小二乘法及其相关估值方法应用学院:自动化学院学号:姓名:日期:基于最小二乘法的多种系统辨识方法研究一、实验原理1.最小二乘法在系统辨识中用得最广泛的估计方法是最小二乘法(LS)。
设单输入-单输出线性定长系统的差分方程为(5.1.1)式中:为随机干扰;为理论上的输出值。
只有通过观测才能得到,在观测过程中往往附加有随机干扰。
的观测值可表示为(5.1.2)式中:为随机干扰。
由式(5.1.2)得(5.1.3)将式(5.1.3)带入式(5.1.1)得(5.1.4)我们可能不知道的统计特性,在这种情况下,往往把看做均值为0的白噪声。
设(5.1.5)则式(5.1.4)可写成(5.1.6)在观测时也有测量误差,系统内部也可能有噪声,应当考虑它们的影响。
因此假定不仅包含了的测量误差,而且包含了的测量误差和系统内部噪声。
假定是不相关随机序列(实际上是相关随机序列)。
现分别测出个随机输入值,则可写成个方程,即上述个方程可写成向量-矩阵形式(5.1.7) 设则式(5.1.7)可写为(5.1.8)式中:为维输出向量;为维噪声向量;为维参数向量;为测量矩阵。
因此式(5.1.8)是一个含有个未知参数,由个方程组成的联立方程组。
如果,方程数少于未知数数目,则方程组的解是不定的,不能唯一地确定参数向量。
如果,方程组正好与未知数数目相等,当噪声时,就能准确地解出(5.1.9)如果噪声,则(5.1.10)从上式可以看出噪声对参数估计是有影响的,为了尽量较小噪声对估值的影响。
在给定输出向量和测量矩阵的条件下求系统参数的估值,这就是系统辨识问题。
可用最小二乘法来求的估值,以下讨论最小二乘法估计。
2.最小二乘法估计算法设表示的最优估值,表示的最优估值,则有(5.1.11)写出式(5.1.11)的某一行,则有(5.1.12) 设表示与之差,即-(5.1.13)式中成为残差。
把分别代入式(5.1.13)可得残差。
设则有(5.1.14) 最小二乘估计要求残差的平方和为最小,即按照指数函数(5.1.15) 为最小来确定估值。
系统辨识大作业1201张青

《系统辨识》大作业学号:********班级:自动化1班姓名:**信息与控制工程学院自动化系2015-07-11第一题模仿index2,搭建对象,由相关分析法,获得脉冲响应序列ˆ()g k,由ˆ()g k,参照讲义,获得系统的脉冲传递函数()G z和传递函数()G s;应用最小二乘辨识,获得脉冲响应序列ˆ()g k;同图显示两种方法的辨识效果图;应用相关最小二乘法,拟合对象的差分方程模型;构建时变对象,用最小二乘法和带遗忘因子的最小二乘法,(可以用辨识工具箱) 辨识模型的参数,比较两种方法的辨识效果差异;答:根据index2搭建结构框图:相关分析法:利用结构框图得到UY 和tout其中的U就是题目中要求得出的M序列,根据结构框图可知序列的周期是1512124=-=-=npN。
在command window中输入下列指令,既可以得到脉冲相应序列()g k:aa=5;NNPP=15;ts=2; RR=ones(15)+eye(15); for i=15:-1:1UU(16-i,:)=UY(16+i:30+i,1)'; endYY=[UY(31:45,2)];GG=RR*UU*YY/[aa*aa*(NNPP+1)*ts]; plot(0:2:29,GG) hold onstem(0:2:29,GG,'filled') Grid;title('脉冲序列g(τ)')最小二乘法建模的响应序列由于是二阶水箱系统,可以假设系统的传递函数为221101)(sa s a sb b s G +++=,已知)(τg ,求2110,,,a a b b已知G (s )的结构,用长除法求得G(s)的s 展开式,其系数等于从 )( g 求得的各阶矩,然后求G(s)的参数。
得到结果: a1 =-1.1561 a2 =0.4283 b0 =-0.0028 b1=0.2961在command window 中输入下列指令得到传递函数:最小二乘一次算法相关参数%最小二乘法一次完成算法 M=UY(:,1); z=UY(:,2); H=zeros(100,4); for i=1:100 H(i,1)=-z(i+1); H(i,2)=-z(i); H(i,3)=M(i+1); H(i,4)=M(i); endEstimate=inv(H'*H)*H'*(z(3:102)) %结束得到相关系数为:Estimate =-0.7866 0.1388 0.5707 0.3115带遗忘因子最小二乘法:%带遗忘因子最小二乘法程序M=UY(:,1);z=UY(:,2);P=1000*eye(5); %Theta=zeros(5,200); %Theta(:,1)=[0;0;0;0;0];K=zeros(4,400); %K=[10;10;10;10;10];lamda=0.99;%遗忘因数for i=3:201h=[-z(i-1);-z(i-2);M(i);M(i-1);M(i-2)];K=P*h*inv(h'*P*h+lamda);Theta(:,i-1)=Theta(:,i-2)+K*(z(i)-h'*Theta(:,i-2));P=(eye(5)-K*h')*P/lamda;endi=1:200;figure(1)plot(i,Theta(1,:),i,Theta(2,:),i,Theta(3,:),i,Theta(4,:),i,Theta(5,:) )title('带遗忘因子最小二乘法')grid%结束Estimate 可由仿真图得出,可知两种方法参数确定十分接近。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
中南大学系统辨识大作业学院:信息科学与工程学院专业:控制科学与工程学生姓名:龚晓辉学号:134611066指导老师:韩华教授完成时间:2014年6月基于随机逼近算法的系统辨识设计龚晓辉1, 21. 中南大学信息科学与工程学院,长沙4100832. 轨道交通安全运行控制与通信研究所, 长沙410083E-mail: csugxh@摘要:本文对系统辨识的基本原理和要素进行了详细阐述,介绍和分析了系统辨识中常用的最小二乘算法,极大似然法,神经网络算法和随机逼近算法。
随机逼近算法只需利用输入输出的观测来辨识系统参数,在实际中有重要运用。
本文对随机逼近算法进行了详细说明。
同时,针对一个三阶系统设计了KW随机逼近算法进行了参数辨识,并且和递推最小二乘法进行了对比。
实验证明在实际辨识过程中两种算法各有优缺点。
关键词: 系统辨识, 随机逼近法, 递推最小二乘法1.引言在我们所学的线性系统理论中,都是在系统模型已知的情况来设计控制率,使系统达到稳定性,准确性和快速性的要求。
然而,在实际系统中,对象的模型往往是未知的。
而且,非线性是普遍存在的,线性系统只是对非线性系统的一种近似。
因此,了解对象准确的模型,对设计控制器及其重要。
在一些实际对象中,如导弹,化学过程,生物规律,药物反应,以及社会经济等,这些对象使用机理分析法比较困难,但是通过使用辨识技术可以建立系统精确的模型,确定最优控制率[1]。
如今,系统辨识技术已经在航空航天,海洋工程,生物学等各个领域获得了广泛运用。
2.系统辨识的基本思想与常用方法辨识的目的是为了获得对象模型。
对象的模型有多种表现形式,它包括直觉模型,图表模型,数学模型,解析模型,程序模型和语言模型。
这些模型之间可以相互转换。
我们在建立系统模型时,需要遵循目的性,实在性,可辨识性,悭吝性的基本原则。
目的性指的是建模的目的要明确,实在性指的是模型的物理概念要明确。
可辨识性指的是模型结构合理,输入信号持续激励,数据量充足。
悭吝性指的是被辨识参数的个数要尽量少。
辨识对象模型要遵循上面的基本原则。
它是将对象看成一个黑箱。
从含有噪声的输入输出数据中,按照一个准则,运用辨识理论,从一组给定的模型中,确定一个与所测系统等价的模型,是现代控制理论的一个分支。
系统辨识由数据、模型类和准则三要素组成。
数据是由观测实体而得,它不是唯一的,受观测时间、观测目的、观测手段等影响。
模型类就是模型结构,它也不是唯一的,受辨识目的、辨识方法等影响。
而准则是辨识的优化目标,用来衡量模型接近实际系统的标准。
它也不是唯一的,受辨识目的、辨识方法的影响。
由于存在多种数据拟合方法,要评价各种方法的优劣,只有在相同的三要素下才有意义。
由于被控系统受各种内外环境因素的影响,实际测量到的输入输出数据都含有一定的扰动和误差,因此辨识建模实际上是一种实验统计的方法,它所获得的模型仅仅是实际系统的外部特性等价的一种近似描述。
在确定了准则函数之后,如果不考虑测量数据的扰动和误差,问题实际上就变成了方程求解、函数优化、函数逼近、或数据拟合问题。
但是实际中会存在大量的噪声与扰动。
因此,输入输出数据中隐含的扰动和误差,是进行辨识困难性的关键。
在系统辨识的类别中,主要有在线辨识与离线辨识,线性辨识与非线性辨识,集中参数与分布参数辨识,开环辨识与闭环辨识这四种。
而对于误差准则,有常用的输出误差准则,广义误差准则等。
这些准则受模型结构和采样间隔的影响。
在确定了这三要素之后,可以对系统进行辨识,从而确定被控对象的模型。
在实际辨识一个对象的模型参数时,最关注的是辨识方法的选择。
最常用的系统辨识法主要有最小二乘法、极大似然法、神经网络法和随机逼近法。
最小二乘法是一种经典的有效的数据处理方法。
它是1795年高斯(K.E.Guass)在预测行星和彗星运动的轨道时,提出并实际使用的。
它的原理简单,不需要随机变量的任何统计特性,是动态系统辨识的主要手段。
其基本思想就是它使各次实际观测和计算值之间的差值的平方乘以度量其精确度的数值以后的和为最小。
因此,最小二乘法使用计算值与实测值误差的平方和函数作为准则函数,通过对准则函数求导求取其最小值来获得参数的估计值,由于准则函数是二次型函数,它的解是唯一的,其估计的结果是无偏的、收敛的和有效的。
在这个原理之上,最小二乘法有很多衍生的算法,如递推最小二乘法,广义最小二乘法等。
另外一种常用的参数辨识法是极大似然法。
它不仅适用于线性模型也适用于非线性模型,对最小二乘法而言,它不要求任何关于数据概率分布的假设,而极大似然法属于一种概率参数估计。
它需要构造一个以数据和未知参数为自变量的似然函数,并通过求这个似然函数的最大值,获得模型的参数估计值。
模型输出的概率分布将最大可能地逼近实际过程输出的概率分布。
但是,这种方法需要知道输出量的条件概率密度函数的先验知识。
而神经网络辨识方法是通过引入人工神经网络来辨识系统参数的方法。
人工神经网络是模拟人脑细胞的分布式工作特点和自组织功能,且能实现并行处理、自学习和非线性映射等能力的一种系统模型,它由连接权,求和单元和激活函数三个基本要素组成。
常用的人工神经网络有感知机神经网络,BP神经网络,径向基神经网络,竞争学习神经网络,Hopfield神经网络,Boltzmann神经网络等。
其辨识原理也是运用神经网络模型,在输入和输出数据的基础上,从一组给定的模型类中确定一个与所测系统等价的模型。
但是,神经网络辨识方法是以大规模的数据为依据,进行多次训练,确定系统的权值,在系统实时性要求高的地方不太适用,需要进行离线计算。
随机逼近算法是一般随机逼近算法和最小二乘法相结合的一种简便且很有实用价值的参数估计方法。
它主要用来求解准则函数的极值。
在系统辨识中,还有很多其它方法,如预报误差法,闭环辨识法,时变辨识法以及相关的递推算法。
这里限于篇幅,不再详细说明。
本文采用随机逼近算法对系统参数进行辨识。
随机逼近算法是一种递推算法,随机逼近法是由统计学中通过连续逼近而获得估计参数发展而来的,是随机问题的梯度法应用于观测数据被噪声污染而对此噪声的统计特性不够充分了解的情况,可用于任何一个可用反复观测值构成的回归方程式的问题。
3. 随机逼近算法1951年,Robbins 和Monro 提出随机逼近思想,是一个著名的在存在量测噪声的情况下寻找回归方程根的回归算法[2]。
1952年,Kiefer 和Wolfowitz 将随机逼近的思想应用于寻找函数极值的问题,称为KW 算法。
它是一种只利用输入随机变量1,2x x ,及对应的输出随机变量(1),(2),y x y x ,通过迭代运算逐步逼近方程的解的方法。
随机逼近算法在寻找函数极值问题中有非常重要的应用。
下面详细说明随机逼近算法的原理。
考虑模型参数辨识问题(1)。
T y(k)=(k)+e(k)ψθ(1)其中e(k)是均值为0的噪声,选择准则函数11222T J()=E[e (k)]=E{[y(k)-y (k)q]}θ,求^θ,使()J θ的值最小。
在{()}e k 为零均值的独立随机序列的情况下,只需求出()J θ的导数,并令其为0,即()()[]{[]}TT J x E (k)y(k)-(k)θϕψψθθ∂=-=∂ (2)利用(2)可求出使()J θ最小的^θ。
但是,由于表达式中()y k 与e(k)有关,在e(k )统计特性未知情况下,无法求解上面的表达式。
在上面的表达式中,如果用平均值来近似数学期望,那么上面表达式中^θ的解成了最小二乘问题。
但是,为了在e(k)统计特性未知的情况下,求解式(2),使获准则函数()J θ最小[3]。
随机逼近算法是可以解决这类问题。
3.1 随机逼近常用的迭代算法随机逼近算法中是一种迭代算法。
常用的迭代算法有Robbins-Monro 算法和Keifer-Wolfowitz 算法和同时扰动随机逼近算法(SPSA 算法)1. Robbins-Monro 算法 算法的递推表达式如(3)所示(1)()()[y()]x k x k k x(k)ρα+=+-(3)式中,(())y x k 是对应于()x k 的值,()k ρ为算法的收敛因子,且满足(4)。
211()0,lim ()0(),()k k k k k k k ρρρρ→∞∞∞==>==∞<∞∑∑ (4)则()x k 是在均方意义下收敛方程的解。
一般,式(5)中的收敛因子可以满足收敛条件(5)。
1(),[0.5,1]()vbk v k k a k ρρ=∈=+或者 (5)2. Keifer-Wolfowitz 算法Robbins-Monro 算法的出发点是求(){}x E y |x ϕα==的根,而Keifer-Wolfowitz (KW )算法则是用(){}x E y |x ϕα==来确定()x ϕ的极值。
迭代算法的表达式见(6)。
()(1)()()|x k dyx k x k k dxρ+=- (6)如果()k ρ满足(4),则KW 算法最终可以收敛到(())x k ϕ的极值。
3. 同时扰动随机逼近算法随机逼近算法主要是利用输入输出量值来估计未知函数的极值,在Keifer 和 Wolfowitz 提出KW 算法之后,又有有限微分随机逼近算法,随机方向的随机逼近算法,同时扰动随机逼近算法[4]。
其中,同时扰动随机逼近算法是三种算法中效率最好的。
该算法只用标准KW 方法的1p的数据就能得到其它方法相同精度水平的估计准确度(p 是自变量维数)。
令:',L →L为可微损失函数,为求()()0L g θθθ∂==∂的根,同时扰动随机逼近算法的递推表达式见(7)。
^^^^1(),0,1,2k k k a g k θθθ+=-=(7)^k θ是第k 次θ的估计值,^^()k g θ是()()Lg θθθ∂=∂在^k θ的同时扰动值,k a 为增益序列。
'k ∆∈是p 维相互独立零均值的随机的矢量12{,,}k k kp ∆∆∆,则在噪声情况下L 的测量值如式(8)所示。
()()()()()()k k k k k kk k k ky L c y L c θεθε++--=+∆+=-∆+ (8)其中,()(),k k εε+-为系统噪声,ki ∆由对称1Bernouli ±分布获得。
()g ⋅在第k 步后的估计为式(9)。
()()1^^()()2()2k k k k k k k k k kp y y c g y y c θ+-+-⎡⎤-⎢⎥∆⎢⎥⎢⎥=⎢⎥⎢⎥-⎢⎥∆⎣⎦^^11111()()[,,,]2T k k k k k k kp k y c y c c θθ---+∆--∆=∆∆∆ (9)在该算法中,存在{},{},{}k k k a c ∆参数需要选择,它们有一套规则遵循,许多文献都对该规则进行了详细说明。
