第18讲：巧求面积(一)
求面积的方法
求面积的方法面积是几何学中一个重要的概念，在日常生活和各个领域的应用中都有广泛的使用。
无论是计算一个平面图形的面积，还是确定一个地区的面积，掌握求解面积的方法都非常重要。
在本文中，我将介绍几种常见的求解面积的方法，并对其原理和应用进行详细阐述。
一、平面图形的面积计算方法1. 矩形、正方形和长方形的面积计算方法矩形、正方形和长方形是最常见的几何图形，计算它们的面积非常简单。
对于一个矩形，只需要将它的长和宽相乘即可得到面积；对于一个正方形，边长平方就是它的面积；对于一个长方形，长乘以宽也可以得到面积。
2. 三角形的面积计算方法三角形的面积计算相对复杂一些，常见的有以下两种方法：(1) 高度法：如果已知三角形的底和高，可以直接将底乘以高再除以2，即可得到面积。
(2) 海伦公式：对于任意三角形，可以利用三边的边长来计算面积。
根据海伦公式：面积= √(s(s-a)(s-b)(s-c))，其中s是半周长，a、b、c分别是三角形的三个边长。
3. 圆的面积计算方法圆的面积计算需要使用圆周率π。
圆的面积公式为：面积= πr²，其中r为圆的半径。
将半径的值代入公式中，即可计算得到圆的面积。
二、在实际应用中求解面积的方法1. 地理测量中的面积计算方法在地理测量中，求解地区的面积是一项重要任务。
常见的求解地区面积的方法有：(1) 多边形面积计算：将地区按照多边形的边界划分为多个三角形，然后使用三角形的面积计算方法计算每个三角形的面积，最后将所有三角形的面积相加，即可得到地区的总面积。
(2) 其他方法：对于特定形状的地区，如圆形、椭圆形等，可以使用相应的面积计算公式进行求解。
2. 建筑工程中的面积计算方法在建筑工程中，求解建筑物的面积是进行设计和施工的基础步骤。
常见的求解建筑物面积的方法有：(1) 平面图测量法：根据建筑物的平面图，通过测量各个分区域的长度和宽度，再将这些区域的面积相加，即可得到建筑物总面积。
(2) 激光测距法：利用激光测距仪对建筑物的各个部分进行扫描和测量，然后计算每个部分的面积，最后将这些部分的面积相加得到建筑物总面积。
图形求解面积技巧
图形求解面积技巧图形求解面积是几何学中的基本内容，根据不同的图形形状，求解面积的方法也不同。
在解题过程中，我们可以利用一些技巧来更快地求解面积。
以下是一些常见的图形求解面积的技巧。
一、矩形和正方形的面积求解技巧矩形和正方形是最简单的图形，其面积求解公式是直接应用的，即面积等于长度乘以宽度。
如果给定的是边长，可以根据给定的边长求解面积。
二、三角形的面积求解技巧三角形的面积求解有多种方法。
常见的方法有：1. 正直角三角形的面积求解：对于直角三角形，可以利用两条直角边的长度来求解面积，公式为面积等于直角边乘以直角边除以2。
2. 任意三角形的面积求解：根据三角形的海伦公式，可以利用三条边长来求解面积，公式为面积等于根号下（p * (p - a) * (p - b) * (p - c)），其中 p 为半周长，p = (a +b + c) / 2。
三、圆的面积求解技巧圆的面积求解需要用到圆周率π。
常见的圆的面积求解方法有：1. 根据半径求解圆的面积：对于给定半径的圆，可以直接用公式面积等于π乘以半径的平方来求解。
2. 根据直径求解圆的面积：如果给定的是圆的直径，可以先将直径除以2得到半径的长度，然后利用公式面积等于π乘以半径的平方来求解面积。
四、梯形的面积求解技巧梯形的面积求解需要利用梯形的上底、下底和高。
常见的梯形的面积求解方法有：1. 根据上底和下底求解梯形的面积：对于给定上底、下底和高的梯形，可以利用公式面积等于上底加下底乘以高除以2来求解面积。
2. 根据对角线和高求解梯形的面积：如果给定的是梯形的对角线和高的长度，可以利用公式面积等于对角线之和乘以高除以2来求解面积。
五、平行四边形的面积求解技巧平行四边形的面积求解需要利用平行四边形的底和高。
常见的平行四边形的面积求解方法有：1. 根据底和高求解平行四边形的面积：对于给定底和高的平行四边形，可以利用公式面积等于底乘以高来求解面积。
2. 根据对角线和夹角求解平行四边形的面积：如果给定的是平行四边形的对角线和夹角，可以利用公式面积等于对角线之积乘以夹角的正弦值来求解面积。
四年级秋季第五讲《巧求面积》(一)
7. 水池的面积是 8 3 24 ，铺完之后水池加上地砖的面积是 176 16 11 ．由于每铺一圈 都会是边长增加 2 ，所以铺了 8 2 4 (圈)． 8. 通过对图形进行分割， 可以发现 C 的长与宽分别是 5cm 和 2cm ， 则它的面积是 5 2 10 2 2 ( cm )，那么 A B 的面积是 31 10 21 ( cm )，如给 B 移到 A 的旁边，则知正方形的 边长：( cm )，正方形的面积是 3 3 9 ( cm2 )，原长方形的面积是 31 9 40 ( cm2 )．
图1
图2
图3
2. 方法一：如果求出长方形的宽及正方形的边长，则图形 ABEFGD 的周长和面积可以求 出．而正方形的边长 GC DC DG AB DG 10 4 6 (厘米)，长方形的 宽 BE CE 10 6 4 (厘米)， 所求图形的周长 10 2 6 2 4 4 40 (厘 米)，面积 S长方形ABCD S正方形CEFG 10 4 6 6 76 (平方厘米) 方法二：可以将线段 GF 、 DG 向外平移，得一个新的图形 ABEH ，因为 DG HF ， 所以图形 ABEH 的周长就是图形 ABEFGD 的周长． 而 AB BE 10 GF DH ， (厘米)，所以图形 ABEH 是边长为 10 厘米的正方形．所求图形的周长 正方形 ABEH 的周长 10 4 40 (厘米)， 面积 S正方形ABEH S长方形DGFH 10 10 6 4 76 (平方厘米)
A D 4 10
H F E
G
C
B
10
3. 方法一：可以直接求出每小块菜地的长和宽，从而求出每小块菜地的面积； 每一块地的面积是：（ [ 16 2） 2] （ [ 8 2） 2] 7 3 21 (平方米) 方法二：也可以求出这块地的总面积，再减去道路的面积，然后把剩余的面积四等分求 出每小块菜地的面积；每一块地的面积是： [16 8 （2 16 8 2 2 2） ]4 （ 128 44） 4 21 (平方米) 4. 根据题意，可以用下图表示增减变化的情况，从图中可以看出，原来长方形的长为 (2720 680) (60 50) 340 (米)，宽为 680 340 50 52 (米)．
巧求图形的面积和周长-教师版
巧求图形的面积和周长第一部分：知识介绍巧求图形的面积和周长的方法：1、平移法2、差不变3、旋转法4、图形的切割拼第二部分：例题精讲【例1】下图中标出的数表示每边长，单位是厘米．它的周长是多少厘米?【考点】巧求图形的周长。
【解析】长方形的长5+6=11(厘米)，宽1+3=4(厘米)，周长(11+4)×2=30(厘米)。
【答案】30厘米【例2】有9个小长方形，它们的长和宽分别相等，用这9个小长方形拼成的大长方形(如图)的面积是45平方厘米，求这个大长方形的周长。
【考点】巧求图形的周长【解析】从图上可以知道，小长方形的长的4倍等于宽的5倍，所以长是宽的54 1.25÷=倍。
每个小长方形的面积为4595=，所以宽为2厘米，÷=平方厘米，所以1.25⨯宽⨯宽5长为2.5厘米。
大长方形的周长为(2.542 2.5)229⨯++⨯=厘米。
【答案】29厘米【例3】如右图，计算这个格点三角形的面积。
【考点】巧求图形的面积【解析】这个三角形是处在长是6、宽是4的矩形内，除此之外还有其他三个直角三角形，如下右图（b），这三个直角三角形面积很容易求出，再用矩形面积减去这三个直角三角形面积,就是所要求的三角形面积。
矩形面积是6×4=24 ；直角三角形Ｉ的面积是：6×2÷2＝6 ；直角三角形Ⅱ的面积是：4×2÷2=4 ；直角三角形Ⅲ的面积是：4×2÷2=4 ；所求三角形的面积是：24-（6＋4＋4）=10（面积单位）。
【答案】10【例4】如右图，ABFE和CDEF都是矩形，AB的长是4厘米，BC的长是3厘米，那么图中阴影部分的面积是平方厘米．【考点】巧求图形的面积、一半模型EC【解析】图中阴影部分的面积等于长方形ABCD面积的一半，即4326⨯÷=(平方厘米)。
【答案】10【例 5】(2005年口试真题)右图中甲的面积比乙的面积大 __________ 平方厘米。
(完整word版)小学奥数模块教程四年级杯赛备战讲义——巧求面积
上课日期： 上课时间： 教师姓名：知识点一：格点面积 一、正方形格点问题在一张纸上，先画出一些水平直线和一些竖直直线，并使任意两条相邻的平行线的距离都相等(通常规定是1个单位)，这样在纸上就形成了一个方格网，其中的每个交点就叫做一个格点．在方格网中，以格点为顶点画出的多边形叫做格点多边形，例如，右图中的乡村小屋图形就是一个格点多边形．那么，格点多边形的面积如何计算？它与格点数目有没有关系？如果有，这两者之间的关系能否用计算公式来表达？下面就让我们一起来探讨这些问题吧！用N 表示多边形内部格点，L 表示多边形周界上的格点，S 表示多边形面积，请同学们分析前几个例题的格点数．我们能发现如下规律：12LS N =+-．这个规律就是毕克定理．二、 三角形格点问题1、定义：所谓三角形格点多边形是指：每相邻三点成“∵”或“∴”，所形成的三角形都是等边三角形．规定它的面积为1，以这样的点为顶点画出的多边形为三角形格点多边形．2、公式：关于三角形格点多边形的面积同样有它的计算公式：如果用S 表示面积，N 表示图形内包含的格点数，L 表示图形周界上的格点数，那么有22S N L =⨯+-，就是格点多边形面积等于图形内部所包含格点数的2倍与周界上格点数的和减去2．知识点二：图形剪拼巧求面积知识框架毕克定理若一个格点多边形内部有N 个格点，它的边界上有L 个格点，则它的面积为12LS N =+-．本讲中很多类型的题目还要求同学们去动手尝试．通过本讲知识的学习，让同学们了解不同图形的分割、拼合、剪拼的方法，锻炼同学们的平面想象能力以及增强学生的动手操作能力．（1）把一个几何图形按某种要求分成几个图形，就叫做图形的分割．（2）反过来，按一定的要求也可以把几个图形拼成一个完美的图形，就叫做图形的拼合．（3）将一个或者多个图形先分割开，再拼成一种指定的图形，则叫做图形的剪拼．我们在图形的分割、拼合和剪拼的过程中，都要结合所提供的图形特点来思考．（1）如果把一个图形分割成若干个大小、形状相等的部分，那么就要想办法找图形的对称点，把图形先分少，再分多．（2）图形中，如果有数量方面的要求，可以先从数量入手，找出平分后每块上所含数量的多少，再结合数量来分割图形．（3）如果是要把几个图形拼合成一个大图形，要特别注意每条边的长度，把相等的边长拼合在一起，先拼少的，再拼多的．（4）如果是剪拼图形，要抓住“剪、拼前后图形的面积相等”这个关键，根据已知条件和图形的特点，通过分析推理和必要的计算，确定剪拼的方法．一、解题关键：分割其实就是运用特殊的三角形（等角直角三角形、等边三角形等）、正方形、等边图形的特殊性质进行分割而得，所以分割的关键是利用了特殊图形的关系解题。
奥数-巧求面积
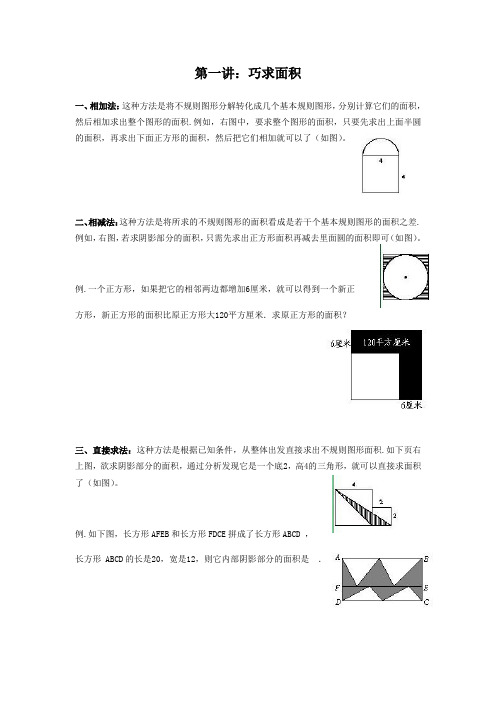
第一讲：巧求面积一、相加法：这种方法是将不规则图形分解转化成几个基本规则图形，分别计算它们的面积，然后相加求出整个图形的面积.例如，右图中，要求整个图形的面积，只要先求出上面半圆的面积，再求出下面正方形的面积，然后把它们相加就可以了（如图）。
二、相减法：这种方法是将所求的不规则图形的面积看成是若干个基本规则图形的面积之差.例如，右图，若求阴影部分的面积，只需先求出正方形面积再减去里面圆的面积即可（如图）。
例.一个正方形，如果把它的相邻两边都增加6厘米，就可以得到一个新正方形，新正方形的面积比原正方形大120平方厘米．求原正方形的面积？三、直接求法：这种方法是根据已知条件，从整体出发直接求出不规则图形面积.如下页右上图，欲求阴影部分的面积，通过分析发现它是一个底2，高4的三角形，就可以直接求面积了（如图）。
例.如下图，长方形AFEB和长方形FDCE拼成了长方形ABCD ，长方形 ABCD的长是20，宽是12，则它内部阴影部分的面积是．四、重新组合法：这种方法是将不规则图形拆开，根据具体情况和计算上的需要，重新组合成一个新的图形，设法求出这个新图形面积即可.例如，欲求右图中阴影部分面积，可以把它拆开使阴影部分分布在正方形的4个角处，这时采用相减法就可求出其面积了（如图）。
例.已知大正方形边长是7厘米，小正方形边长5厘米，求阴影部分的面积。
五、辅助线法：这种方法是根据具体情况在图形中添一条或若干条辅助线，使不规则图形转化成若干个基本规则图形，然后再采用相加、相减法解决即可.如右图，求两个正方形中阴影部分的面积.此题虽然可以用相减法解决，但不如添加一条辅助线后用直接法作更简便（如图）。
六、割补法：这种方法是把原图形的一部分切割下来补在图形中的另一部分使之成为基本规则图形，从而使问题得到解决.例如，如右图，欲求阴影部分的面积，只需把右边弓形切割下来补在左边，这样整个阴影部分面积恰是正方形面积的一半（如图）.例.求阴影部分的面积。
数学北师大版六年级下册巧求图形面积
巧求图形的面积教学目标：1、通过自主探究、合作交流，学会计算不规则图形的面积。
2、掌握把不规则图形转化成规则图形巧解图形面积的解题策略，渗透转化思想。
3、激发学生学习数学的兴趣，并从学习过程中获得成功的体验。
教学重点：通过自主探究、合作交流，学会计算不规则图形的面积。
教学难点：掌握把不规则图形转化成规则图形巧解图形面积的解题策略，渗透转化思想。
（一）、创设情景，提出问题。
每年的三、四月份，是我们进行绿化的最佳时节，在绿化过程中，造型独特的花坛是不可缺少的。
（出示：一个花坛平面图）园艺师设计了这样一个花坛造型，其中阴影部分表示种花的面积，种花的面积是多少呢？(二)、自主探究，寻求策略。
1、提问：请你仔细观察、认真分析，用自己喜欢的方法独立解题。
学生独立思考2、把自己的解题思路和小组同学交流3、集体反馈交流，学生拿着自己做的题在投影上讲解预设：A、S大– S小（去空求差）※同学们他的解题方法你们听明白了吗？监控：他这种方法主要是用什么方法来解答的？预设：大面积-小面积教师：我们把这样的方法叫做去空求差法B、（8÷2）×（8÷2）÷2×2——转化成两个小三角形※同学们他的解题方法你们听明白了吗？监控：谁能说说他是通过什么方法把这个几部分阴影面积转化成两个小三角形的？预设：割补、旋转8×（8÷2）÷2 ——转化成大三角形（学生出来就处理，不出来就最后处理）监控：谁能说说他是通过什么方法把这个几部分阴影面积转化成大三角形的？预设：割补、旋转、平移8÷2）2——转化成小正方形监控：谁能说说他是通过什么方法把这几个阴影部分的面积转化成小正方形的？预设：割补、旋转、平移……4、没有一个同学是直接求阴影部分的面积？为什么呀？预设：不是基本图形5、为了求这个不规则图形的面积，同学们都用了哪些方法？监控：割补、平移、旋转……（板书）6、板书小结：刚才同学运用割补、旋转等方法把不规则图形转化成了规则图形，巧妙求出阴影部分的面积，今天这节课我们就一起来巧求图形面积。
第18讲四年级数学图形的周长和面积学案
精锐教育学科教师辅导讲义学员编号：年级：课时数：学员姓名：辅导科目：学科教师：授课C-长方形正方形的周长C- 巧求面积（综合）T-周长与面积拓展类型授课日期时段教学内容1、上节学习了几何计数问题，利用上节课学到的知识和技能解答下面题目：（1）数一数下图中，各有多少条线段？各有多少个三角形？（2）如下图数一数图中长方形的个数。
一、专题导入同学们都知道，长方形的周长=（长＋宽）×2，正方形的周长=边长×4。
长方形、正方形的周长公式只能用来计算标准的长方形和正方形的周长。
如何应用所学知识巧求表面上看起来不是长方形或正方形的图形的周长，还需同学们灵活应用已学知识，掌握转化的思考方法，把复杂的问题转化为标准的图形，以便计算它们的周长。
二、专题精讲【例1】有5张同样大小的纸如下图（a）重叠着，每张纸都是边长6厘米的正方形，重叠的部分为边长的一半，求重叠后图形的周长。
【例2 】一块长方形木板，沿着它的长度不同的两条边各截去4厘米，截掉的面积为192平方厘米。
现在这块木板的周长是多少厘米？【例3 】已知下图中，甲是正方形，乙是长方形，整个图形的周长是多少？【例4 】下图是边长为4厘米的正方形，求正方形中阴影部分的周长。
【例5】右图中的阴影部分BCGF是正方形，线段FH长18厘米，线段AC长24厘米，则长方形ADHE的周长是多少厘米？三、专题过关1、小华和小兵玩打仗的游戏，每个人占据了一块，请问他们谁的边界线长？为什么？乙丙甲JIFEHGD CBA第1题2、如图是“环球戏探险”的地道的平面图，一儿童沿地道边周游一周，他走了多少米？第2题3、图（1）（2）都是由完全相同的小正方形拼成的，并且图（1）的周长是22厘米，那么图（2）的周长是多少厘米？第3题4、求所示图形的周长。
（单位：厘米）第4题5、求所示图形的周长（部位：厘米）第5题6、求所示图形的周长（单位：厘米）第6题三、学法提炼1、专题特点：以上专题以教材内容为基础拓展加深，体现转化，分割等解决图形周长问题的常用方法。
浅谈巧求平面图形面积的几种特殊解法
浅谈巧求平面图形面积的几种特殊解法巧求平面图形面积的几种特殊解法平面图形的面积是我们数学学习中常常遇到的一个问题。
人们对于这一问题的解法也有很多种不同的方法。
今天，我们就来浅谈一下巧求平面图形面积的几种特殊解法。
1.在坐标系中解决第一种解决方法是在坐标系中解决。
此方法适用于最基础的平面图形：矩形。
我们可以把矩形框进一个方格，将每个方格看作1，而每行和每列的方块数目就是矩形的长和宽。
于是矩形的面积就可以用长乘宽求出。
对于不规则图形，我们可以用坐标系来求解。
首先，我们需要将图形用坐标系表示出来，然后再对图形进行分割，将其分割为几个我们容易求解的部分，再把这些部分的面积求出来相加即可得到所求的答案。
2.运用三角形的性质解决第二种解决方法是运用三角形的性质解决。
我们可以把一个不规则图形分割成许多小三角形，并将其用勾股定理计算。
这种方法适用于图形的边缘是直线或者射线的情况。
在这种情况下，我们可以将不规则图形分割成多个三角形，根据勾股定理计算每个三角形的面积，再将它们相加就可以得到所求的答案。
3.极坐标解决第三种解决方法是运用极坐标解决。
极坐标是表示平面上任一点坐标的一种坐标系。
在极坐标系中，我们可以用极角和半径分别表示图形的各个部分。
由于这种坐标系适用于各种形状的图形，我们可以用它来解决许多复杂的问题。
4.向外引伸最后一种解决方法是将图形向外引伸，构造出一个大的矩形，然后再将不规则图形分割成若干个小矩形。
用整个大矩形的面积减去这些小矩形的面积即可求出所求的答案。
总之，巧求平面图形面积的几种特殊解法并不是一成不变的，我们需要根据不同的情况选择不同的方法。
这种方法不仅可以帮助我们更好地理解平面图形的面积计算，而且还能够提高我们的数学思维能力。
浅谈巧求平面图形面积的几种特殊解法
浅谈巧求平面图形面积的几种特殊解法韶关市吴礼和中心小学 倪韶武平面图形是小学数学教学的一个重要内容。
它更贴近学生的生活，很多数学问题都是从生活实际出发，所以在教学中，教师应该侧重从实际出发，注重操作实践、直观演示，让学生对知识真正达到理解，从而能够灵活运用，解决实际问题。
在解答求平面图形面积的各种解题方法中，我结合在实际教学，尤其是在多年的奥数教学中，浅谈巧解平面图形面积的几种特殊方法。
一、善于观察，运用等量代换解题。
在解平面几何题时，观察是很重要的。
一个不善于观察的学生，是不可能把数学知识学好并灵活运用的。
教师在教学过程中要注重培养学生的观察力，通过观察，找出题中是否具有等量关系，能否运用等量代换的方法来解答，从而起到特殊而又有效的效果。
例如，如右图，长方形长10厘米，宽8厘米。
梯形ABFD 的面积比梯形CGEF 的面积多20平方厘米，AB=EG ，求CG 的长度。
如果把梯形ABFD 看作①，把梯形CGEF 看作②，把三角形BCF 看作③，这题乍看，①的面积比③的面积多20平方厘米，这三者好像没有什么联系，但通过仔细观察，却发现①和③旁边有个公共的部分②，通过等量代换，用①的面积+②的面积比③的面积+②的面积还是多20平方厘米，这样就得到长方形的面积比三角形BGE 的面积多20平方厘米，而长方形的面积是可求的，进而把三角形BGE 的面积求出来，再把BG 的长求出，最后就可以把CG 的长解答出来。
具体解法如下：10×8=80（平方厘米），80-20=60（平方厘米），60×2÷10=12（厘米），12-8=4（厘米）。
又如：大小正方形边长分别长6厘米和10厘米。
求三角形AGE 的面积。
此题学生很容易用填补法解答：C DA B GB E（6+10）×6÷2+10×10÷2-（6+10）×6÷2=50（平方厘米）如果把小正方体边长6厘米这个条件去掉，又应该怎样解呢？通过上题的解答，发现梯形ABCG 的面积和三角形ABE 的面积是相等的，用梯形ABCG 的面积减去公共的部分梯形ABCO 的面积和用三角形ABE 的面积减去公共的部分梯形ABCO 的面积，剩下的两个三角形AOG 和COE 的面积也应该相等。
《巧求面积》培优课件
20米 米
练习： 练习： 1. 爷爷靠墙用篱笆围成一个鸡舍， 爷爷靠墙用篱笆围成一个鸡舍， 已知篱笆长是14米 鸡舍宽4米 已知篱笆长是 米，鸡舍宽 米， 鸡舍的面积是多少？ 鸡舍的面积是多少？
练习： 练习： 2. 把一根长 厘米的铁丝围成一 把一根长24厘米的铁丝围成一 个长方形，什么情况下面积最大？ 个长方形，什么情况下面积最大？ 最大的面积是多少？ 最大的面积是多少？
练习： 练习：
2. 图中阴影部分是正方形，面 图中阴影部分是正方形， 积是64平方厘米 平方厘米， 积是 平方厘米，大长方形的 周长是52厘米 厘米， 周长是 厘米，大长方形的面 积是多如图，图中的数代表数所在矩 如图， 形的面积， 形的面积，阴影部分面积是多少 平方厘米？ 平方厘米？
巧求面积
作者 熊红安
巧求面积
例1：求下面图形的面积。 ：求下面图形的面积。 1 2 4 3 2 8
2
练习： 练习： 计算下列图形的面积.(单位： 计算下列图形的面积 单位：厘米)
9 8 20 4 18 1 1 2 1 6 8 5 16
12
例2： ：
两边长是6厘米的正方形纸， 两边长是 厘米的正方形纸，一部 厘米的正方形纸 分叠在一起放在桌面上(如图 如图)， 分叠在一起放在桌面上 如图 ， 桌子被盖住的面积是多少？ 桌子被盖住的面积是多少？
4 2 2 6 2 2 2
整合集训： 整合集训： 7.如图，一个长方形与一个正方 形部分重合，求没有重合的阴影 部分面积相差多少？
8 6
整合集训： 整合集训： 8.下图中，大正方形的边长是20 厘米，顺次连接正方形各边上的 中点得到第二个正方形，再这样 连下去，阴影部分的面积是多少 平方厘米？
整合集训： 整合集训： 9.已知下图中每个小正方形的边 长都是2厘米，阴影部分的面积是 多少平方厘米？
面积口诀的应用
面积口诀的应用面积是我们在日常生活中经常会用到的概念，它用来描述一个平面图形所占据的空间大小。
在计算面积时，我们可以运用面积口诀来快速而准确地求解。
面积口诀是一种简单的策略，通过记忆一些常见图形的面积公式，并灵活运用这些公式的特点，可以帮助我们更加高效地计算面积。
下面是一些常见图形的面积公式和面积口诀的应用：1. 矩形的面积公式是：面积 = 长 ×宽。
这是最简单的面积公式，我们可以直接将矩形的长和宽相乘来求解面积。
2. 正方形的面积公式是：面积 = 边长 ×边长。
由于正方形的边长相等，我们可以将边长平方来求解面积，这样会更加方便。
3. 三角形的面积公式是：面积 = 底边长 ×高 ÷ 2。
在计算三角形的面积时，我们需要知道底边长和对应的高，然后将底边长乘以高再除以2即可得到面积。
4. 圆的面积公式是：面积= π × 半径 ×半径。
π是一个常数，约等于3.14，我们可以直接将半径的平方与π相乘来求解圆的面积。
除了这些常见的图形，还有许多其他的图形，它们的面积公式也可以通过面积口诀来求解。
通过记忆和熟练运用这些公式，我们可以在计算面积时节省时间和精力。
在使用面积口诀时，我们需要注意以下几点：1. 熟记常见图形的面积公式，并理解公式的含义和计算方法。
2. 灵活应用面积公式的特点，例如利用正方形的边长平方和三角形的底边长乘以高再除以2的公式特点。
3. 在计算面积时，要注意单位统一，确保长、宽、边长、半径等量的单位相同。
总之，面积口诀是一种简单但有效的策略，可以帮助我们快速而准确地计算各种图形的面积。
通过熟练掌握面积公式和灵活运用口诀，我们可以在日常生活和工作中更好地应用面积概念，解决与面积相关的问题。
巧用面积法 妙解几何题ppt课件
E
得证。 证明：∵ BF⊥AC于F ∴S △ABC=1/2AC·BF
B
P
C
∵ PD⊥AB于D，PE⊥AC于E
∴S △ABP=1/2AB·PD， S△ACP=1/2AC·PE ∵ S △ABC= S △ABP+ S△ACP ∴1/2AC·BF=1/2AB·PD+1/2AC·PE
∵AB=AC ∴PD+PE=BF
巧用面积法 妙解几何题
人教版八年级数学 上册 映山中学 严正霞
最新版整理ppt
1
何谓面积法
• 在求解平面几何问题的时候，根据有关几 何量与涉及的有关图形面积之间的内在联 系，用面积或面积之间的关系表示有关线 段间的关系，从而把要论证的线段之间的 关系转化为面积的关系，并通过图形面积 的等积变换对所论问题来进行求解的方法， 称之为面积法。
DO Q
P
有 S△ACE =S△DCB 且AE=BD，可 A 得CP=CQ。
C
B
证明：过点C作CP⊥AE于P，CQ⊥BD于Q，
∵△ACD、△BCE是等边三角形 ∴AC=DC，EC=BC，
∠ACD=∠ECB=60° ∴∠ACE=∠DCB=120° ∴△ACE≌△DCB
• 抓住面积不但能把平面几何知识变得更容 易学，而且使几何问题变得更简捷，更有 趣味。
最新版整理ppt
2
温故知新
填空：
1.若△ABC≌△DEF，且△ABC的面积为25，则△DEF的面积
为 25。
2.已为知AD为S△△AABBDC=的S△中。A线CD，则S △ABD与S △ACD的大小关系
3.(1)平行四边形ABCD的一条对角线AC把它分成两个三角形
∴ S△ABC=1/2AB·CE=1/2AC·BD 又AB=AC
3分钟·数学讲堂：巧算面积专题
启智数学·巧算面积与周长专题讲义课题：图形的周长和面积备注一、教学目标：掌握长方形、正方形的周长和面积并能灵活应用，巧算周长和面积二、教学重难点：灵活使用公式，计算周长和面积三、教学内容及过程：【知识梳理】正方形：周长=边长×4 面积=边长×边长长方形：周长=（长+宽）×2 面积=长×宽【融知于题】【典型例题分析】例1、如下图，一个长方形土地里面有一块正方形花坛，这个花坛的周长是200米，它的各边和长方形的各边恰好平行，和长方形各边的距离如图所示（单位：米），那么这个长方形的周长是多少？这样做正方形的边长是200÷4＝50（米）所以长方形的长＝50＋40＋60＝150（米）宽＝50＋20＋30＝100（米）因此长方形的周长是：（150＋100）×2＝500（米）答：这个长方形的周长是500米。
例2、下图是四个一样的长方形和一个小正方形拼成了一个大正方形，大正方形的面积为121平方米，小正方形的面积是25平方米。
求长方形的长和宽。
这样做由题意可知大正方形的面积是121平方米，所以它的边长为11米。
小正方形的面积是25平方米，所以它的边长是5米。
大正方形的边长恰等于长方形的长、宽的和，或者等于小正方形的边长再加上长方形的两个宽。
由第二个条件可以得到长方形的宽是：（11－5）÷2＝3（米）再由第一个条件可以得到长方形的长是：11－3＝8（米）答：长方形的边长是8米，宽是3米。
例3、如下图是一个长22米，宽18米的迷宫，其中道路的宽为2米，从A 点出发，沿道路的中心线向里走去，一直到B点（到迷宫的尽头，挨到墙）。
所走过的路线的长度是多少米？这样做将长方形的迷宫割补平移为宽1米的路，路的总面积和以前迷宫的面积一样，那么路有多长在迷宫里就走了多远， 22×18÷2=198（米）答：在迷宫里所走的路线的长度是198米。
小学四年级奥数竞赛班作业第18讲：巧求面积(一)
巧求面积练习题一．夯实基础：1. 如图是学校操场一角，请计算它的面积(单位：米)2. 一块长方形铁板，长15分米，宽12分米，如果长和宽各减少2分米，面积比原来减少多少平方分米？3. 一块长方形纸片，在长边剪去5cm ，宽边剪去2cm 后(如图)，得到的正方形面积比原长方形面积少231cm ．求原长方形纸片的面积．4. 一个边长为20厘米的正方形，依次连接四边中点得到第二个正方形，这样继续下去可得到第三个、第四个、第五个正方形．求第五个正方形的面积？30203040525. 如图所示，把一个正方形各边中点顺次相连，可得一个新的较小的正方形；把这个小正方形的各边中点顺次相连，又可以得到一个新的更小一些的正方形……如此依次连下去，一直连到第三个新正方形为止。
如果图中阴影的面积等于1，那么图中最大的正方形面积等于多少？二． 拓展提高：6. 甲、乙、丙三个正方形，它们的边长分别是6、8、10厘米，乙的一个顶点在甲的中心上，丙的一个顶点在乙的中心上．这三个正方形的覆盖面积是多少平方厘米？7. 如图，四边形ABCD 的周长是60厘米，点M 到各边的距离都是4.5厘米，这个四边形的面积是 平方厘米.8. 有一个长方形，如果宽减少2米，或长减少3米，则面积均减少24平方米，求这个长方形的面积？1086丙乙甲9. 有大、小两个长方形(如图)，对应边的距离均为1cm ，已知两个长方形之间部分的面积是216cm ，且小长方形的长是宽的2倍，求大长方形的面积．10. 空白处每个方格都是边长为4厘米的正方形，黑条的宽度为2厘米，求阴影部分的面积和周长。
11. 如图，一块正方形地砖，上面印有四周对称的花纹，正中心红色小正方形面积是8，四块绿色等腰直角三角形均相同，面积总和是36，那么图中阴影部分的面积是多少？三．超常挑战：12. 下图(单位：厘米)是两个相同的直角梯形重叠在一起，求阴影部分的面积.13. 两个相同的直角三角形如下图所示(单位：厘米)重叠在一起，求阴影部分的面积.四．杯赛演练：14. (2008年第七届”小机灵杯”数学竞赛决赛)如图是由5个大小不同的正方形叠放而成的，如果最小的正方形(阴影部分)的周长是8，那么最大的正方形的边长是 ．15. (2008年全国小学生”我爱数学夏令营”数学竞赛)如图，边长为 10的正方形中有一等宽的十字，其面积(阴影部分)为36，则十字中央的小正方形面积为 ．16. （武汉明心奥数挑战赛）如图所示，四个相叠的正方形，边长分别是5、7、9、11.问灰色区与黑色区的面积的差是多少？FBA第6题第2题1017.（第四届《小数报》数学竞赛决赛试题）有一大一小两个正方形，它们的周长相差20厘米，面积相差55平方厘米．小正方形的面积是多少平方厘米？18.(第五届”祖冲之杯”数学邀请赛)如右图所示，在长方形ABCD中，放入六个形状大小相同的长方形(尺寸如图)，图中阴影部分的面积是__________．B答案：1. 这是一个不规则图形，怎样使它能转化为我们熟悉的基本图形呢？可以在图中添上一条辅助线，把多边形切割成上下两个长方形或左右两个长方形；也可以把多边形补充完整，成为一个长方形；图一 图二 图三方法一：如图一，3040203040120014002600⨯+⨯+=+=（）(平方米) 方法二：如图二，203040203060020002600⨯+⨯+=+=（）(平方米) 方法三：如图三，40302030303035009002600+⨯+-⨯=-=（）（）(平方米)2. (方法一)如图，铁板面积比原来减少的面积就是阴影部分的面积，阴影部分的面积是用原长方形 的面积减去空白部分的面积．即: 1512(152)(122)⨯--⨯-180130=-=50(平方分米).(方法二)也可把阴影部分分割成两个长方形，求两个长方形的面积．3. 通过对图形进行分割，可以发现C 的长与宽分别是5cm 和2cm ，则它的面积是5210⨯=(2cm )，那么A B +的面积是311021-=(2cm )，如给B 移到A 的旁边，则知正方形的边长：(cm )，正方形的面积是339⨯=(2cm )，原长方形的面积是31940+=(2cm )．4. 第一个正方形的面积是2020400⨯=(平方厘米)，第二个正方形的面积如图，实际上是第一个正方形面积的一半．依次类推，第五个正方形的面积为：400222225÷÷÷÷=(平方厘米)．5. 最小的正方形面积等于2，每往外扩一层，面积就会增加一倍。
小学奥数面积计算(综合题型)
第十八周面积计算（一）专题简析：计算平面图形的面积时，有些问题乍一看，在已知条件与所求问题之间找不到任何联系，会使你感到无从下手。
这时，如果我们能认真观察图形，分析、研究已知条件，并加以深化，再运用我们已有的基本几何知识，适当添加辅助线，搭一座连通已知条件与所求问题的小“桥”，就会使你顺利达到目的。
有些平面图形的面积计算必须借助于图形本身的特征，添加一些辅助线，运用平移旋转、剪拼组合等方法，对图形进行恰当合理的变形，再经过分析推导，方能寻求出解题的途径。
图形面积）简单的面积计算是小学数学的一项重要内容.要会计算面积，首先要能识别一些特别的图形：正方形、三角形、平行四边形、梯形等等，然后会计算这些图形的面积.如果我们把这些图形画在方格纸上，不但容易识别，而且容易计算.上面左图是边长为4的正方形，它的面积是4×4＝16（格）；右图是3×5的长方形，它的面积是3×5＝15（格）.上面左图是一个锐角三角形，它的底是5，高是4，面积是5×4÷2＝10（格）；右图是一个钝角三角形，底是4，高也是4，它的面积是4×4÷2＝8（格）.这里特别说明，这两个三角形的高线一样长，钝角三角形的高线有可能在三角形的外面.上面左图是一个平行四边形，底是5，高是3，它的面积是5×3＝15（格）；右图是一个梯形，上底是4，下底是7，高是4，它的面积是（4+7）×4÷2＝22（格）.上面面积计算的单位用“格”，一格就是一个小正方形.如果小正方形边长是1厘米，1格就是1平方厘米；如果小正方形边长是1米，1格就是1平方米.也就是说我们设定一个方格的边长是1个长度单位，1格就是一个面积单位.在这一讲中，我们直接用数表示长度或面积，省略了相应的长度单位和面积单位.一、三角形的面积用直线组成的图形，都可以划分成若干个三角形来计算面积.三角形面积的计算公式是：三角形面积= 底×高÷2.这个公式是许多面积计算的基础.因此我们不仅要掌握这一公式，而且要会灵活运用.例1 右图中BD长是4，DC长是2，那么三角形ABD的面积是三角形ADC面积的多少倍呢？解：三角形ABD与三角形ADC的高相同.三角形ABD面积=4×高÷2.三角形ADC面积=2×高÷2.因此三角形ABD的面积是三角形ADC面积的2倍.注意：三角形的任意一边都可以看作是底，这条边上的高就是三角形的高，所以每个三角形都可看成有三个底，和相应的三条高.例2右图中，BD，DE，EC的长分别是2，4，2.F是线段AE的中点，三角形ABC的高为4.求三角形DFE的面积.解：BC＝2＋4＋2＝8.三角形ABC面积= 8×4÷2＝16.我们把A和D连成线段，组成三角形ADE，它与三角形ABC的高相同，而DE长是4，也是BC的一半，因此三角形ADE面积是三角形ABC面积的一半.同样道理，EF是AE的一半，三角形DFE面积是三角形ADE面积的一半.三角形DFE面积= 16÷4＝4.例3右图中长方形的长是20，宽是12，求它的内部阴影部分面积.解：ABEF也是一个长方形，它内部的三个三角形阴影部分高都与BE一样长.而三个三角形底边的长加起来，就是FE的长.因此这三个三角形的面积之和是FE×BE÷2，它恰好是长方形ABEF面积的一半.同样道理，FECD也是长方形，它内部三个三角形（阴影部分）面积之和是它的面积的一半.因此所有阴影的面积是长方形ABCD面积的一半，也就是20×12÷2＝120.通过方格纸，我们还可以从另一个途径来求解.当我们画出中间两个三角形的高线，把每个三角形分成两个直角三角形后，图中每个直角三角形都是某个长方形的一半，而长方形ABCD是由这若干个长方形拼成.因此所有这些直角三角形（阴影部分）的面积之和是长方形ABCD面积的的一半.例4 右图中，有四条线段的长度已经知道，还有两个角是直角，那么四边形ABCD（阴影部分）的面积是多少？解：把A和C连成线段，四边形ABCD就分成了两个，三角形ABC和三角形ADC.对三角形ABC来说，AB是底边，高是10，因此面积=4×10÷2＝20.对三角形ADC来说，DC是底边，高是8，因此面积=7×8÷2＝28.四边形ABCD面积= 20＋28＝48.这一例题再一次告诉我们，钝角三角形的高线有可能是在三角形的外面.例5在边长为6的正方形内有一个三角形BEF，线段AE＝3，DF＝2，求三角形BEF 的面积.解：要直接求出三角形BEF的面积是困难的，但容易求出下面列的三个直角三角形的面积三角形ABE面积=3×6×2＝9.三角形BCF面积= 6×（6-2）÷2＝12.三角形DEF面积=2×（6-3）÷2＝3.我们只要用正方形面积减去这三个直角三角形的面积就能算出：三角形BEF面积=6×6-9-12-3＝12.例6 在右图中，ABCD是长方形，三条线段的长度如图所示，M是线段DE的中点，求四边形ABMD（阴影部分）的面积.解：四边形ABMD中，已知的太少，直接求它面积是不可能的，我们设法求出三角形DCE与三角形MBE的面积，然后用长方形ABCD的面积减去它们，由此就可以求得四边形ABMD的面积.把M与C用线段连起来，将三角形DCE分成两个三角形.三角形DCE的面积是7×2÷2＝7.因为M是线段DE的中点，三角形DMC与三角形MCE面积相等，所以三角形MCE 面积是7÷2＝3.5.因为BE＝8是CE＝2的4倍，三角形MBE与三角形MCE高一样，因此三角形MBE面积是3.5×4＝14.长方形ABCD面积=7×（8＋2）=70.四边形ABMD面积=70-7- 14＝49.二、有关正方形的问题先从等腰直角三角形讲起.一个直角三角形，它的两条直角边一样长，这样的直角三角形，就叫做等腰直角三角形.它有一个直角（90度），还有两个角都是45度，通常在一副三角尺中.有一个就是等腰直角三角形.两个一样的等腰直角三角形，可以拼成一个正方形，如图（a）.四个一样的等腰直角三角形，也可以拼成一个正方形，如图（b）.一个等腰直角三角形，当知道它的直角边长，从图（a）知，它的面积是直角边长的平方÷2.当知道它的斜边长，从图（b）知，它的面积是斜边的平方÷4例7 右图由六个等腰直角三角形组成.第一个三角形两条直角边长是8.后一个三角形的直角边长，恰好是前一个斜边长的一半，求这个图形的面积.解：从前面的图形上可以知道，前一个等腰直角三角形的两个拼成的正方形，等于后一个等腰直角三角形四个拼成的正方形.因此后一个三角形面积是前一个三角形面积的一半，第一个等腰直角三角形的面积是8×8÷2＝32.这一个图形的面积是32＋16＋8＋ 4 ＋2＋1＝63.例8 如右图，两个长方形叠放在一起，小长形的宽是2，A点是大长方形一边的中点，并且三角形ABC是等腰直角三角形，那么图中阴影部分的总面积是多少？解：为了说明的方便，在图上标上英文字母D，E，F，G.三角形ABC的面积=2×2÷2＝2.三角形ABC，ADE，EFG都是等腰直角三角形.三角形ABC的斜边，与三角形ADE的直角边一样长，因此三角形ADE面积=ABC面积×2＝4.三角形EFG的斜边与三角形ABC的直角边一样长.因此三角形EFG面积=ABC面积÷2＝1.阴影部分的总面积是4＋1＝5.例9如右图，已知一个四边形ABCD的两条边的长度AD＝7，BC＝3，三个角的度数：角B和D是直角，角A是45°.求这个四边形的面积.解：这个图形可以看作是一个等腰直角三角形ADE，切掉一个等腰直角三角形BCE.因为A是45°，角D是90°，角E是180°-45°-90°＝45°，所以ADE是等腰直角三角形，BCE也是等腰直角三角形.四边形ABCD的面积，是这两个等腰直角三角形面积之差，即7×7÷2-3×3÷2＝20.这是1994小学数学奥林匹克决赛试题.原来试题图上并没有画出虚线三角形.参赛同学是不大容易想到把图形补全成为等腰直角三角形.因此做对这道题的人数不多.但是有一些同学，用直线AC把图形分成两个直角三角形，并认为这两个直角三角形是一样的，这就大错特错了.这样做，角A是45°，这一条件还用得上吗？图形上线段相等，两个三角形相等，是不能靠眼睛来测定的，必须从几何学上找出根据，小学同学尚未学过几何，千万不要随便对图形下结论.我们应该从题目中已有的条件作为思考的线索.有45°和直角，你应首先考虑等腰直角三角形.现在我们转向正方形的问题.例10 在右图11×15的长方形内，有四对正方形（标号相同的两个正方形为一对），每一对是相同的正方形，那么中间这个小正方形（阴影部分）面积是多少？解：长方形的宽，是“一”与“二”两个正方形的边长之和，长方形的长，是“一”、“三”与“二”三个正方形的边长之和.长-宽=15-11＝4是“三”正方形的边长.宽又是两个“三”正方形与中间小正方形的边长之和，因此中间小正方形边长=11-4×2＝3.中间小正方形面积=3×3＝9.如果把这一图形，画在方格纸上，就一目了然了.例11从一块正方形土地中，划出一块宽为1米的长方形土地（见图），剩下的长方形土地面积是15.75平方米.求划出的长方形土地的面积.解：剩下的长方形土地，我们已知道长-宽=1（米）.还知道它的面积是15.75平方米，那么能否从这一面积求出长与宽之和呢？如果能求出，那么与上面“差”的算式就形成和差问题了.我们把长和宽拼在一起，如右图.从这个图形还不能算出长与宽之和，但是再拼上同样的两个正方形，如下图就拼成一个大正方形，这个正方形的边长，恰好是长方形的长与宽之和.可是这个大正方形的中间还有一个空洞.它也是一个正方形，仔细观察一下，就会发现，它的边长，恰好是长方形的长与宽之差，等于1米.现在，我们就可以算出大正方形面积：15.75×4+1×1＝64（平方米）.64是8×8，大正方形边长是8米，也就是说长方形的长+宽=8（米）.因此长=（8＋1）÷2＝4.5（米）.宽=8-4.5＝3.5（米）.那么划出的长方形面积是4.5×1＝4. 5（平方米）.例12 如右图.正方形ABCD与正方形EFGC并放在一起.已知小正方形EFGC的边长是6，求三角形AEG（阴影部分）的面积.解：四边形AECD是一个梯形.它的下底是AD，上底是EC，高是CD，因此四边形AECD面积=（小正方形边长+大正方形边长）×大正方形边长÷2三角形ADG是直角三角形，它的一条直角边长DG=（小正方形边长+大正方形边长），因此三角形ADG面积=（小正方形边长+大正方形边长）×大正方形边长÷2.四边形AECD与三角形ADG面积一样大.四边形AHCD是它们两者共有，因此，三角形AEH与三角形HCG面积相等，都加上三角形EHG面积后，就有阴影部分面积=三角形ECG面积=小正方形面积的一半= 6×6÷2＝18.十分有趣的是，影阴部分面积，只与小正方形边长有关，而与大正方形边长却没有关系.三、其他的面积这一节将着重介绍求面积的常用思路和技巧.有些例题看起来不难，但可以给你启发的内容不少，请读者仔细体会.例13 画在方格纸上的一个用粗线围成的图形（如右图），求它的面积.解：直接计算粗线围成的面积是困难的，我们通过扣除周围正方形和直角三角形来计算.周围小正方形有3个，面积为1的三角形有5个，面积为1.5的三角形有1个，因此围成面积是4×4-3-5-1.5＝6.5.例6与本题在解题思路上是完全类同的.例14 下图中ABCD是6×8的长方形，AF长是4，求阴影部分三角形AEF的面积.解：三角形AEF中，我们知道一边AF，但是不知道它的高多长，直接求它的面积是困难的.如果把它扩大到三角形AEB，底边AB，就是长方形的长，高是长方形的宽，即BC 的长，面积就可以求出.三角形AEB的面积是长方形面积的一半，而扩大的三角形AFB是直角三角形，它的两条直角边的长是知道的，很容易算出它的面积.因此三角形AEF面积＝（三角形AEB面积）-（三角形AFB面积）＝8×6÷2-4×8÷2＝8.这一例题告诉我们，有时我们把难求的图形扩大成易求的图形，当然扩大的部分也要容易求出，从而间接地解决了问题.前面例9的解法，也是这种思路.例15 下左图是一块长方形草地，长方形的长是16，宽是10.中间有两条道路，一条是长方形，一条是平行四边形，那么有草部分的面积（阴影部分）有多大？解：我们首先要弄清楚，平行四边形面积有多大.平行四边形的面积是底×高.从图上可以看出，底是2，高恰好是长方形的宽度.因此这个平行四边形的面积与10×2的长方形面积相等.可以设想，把这个平行四边形换成10×2的长方形，再把横竖两条都移至边上（如前页右图），草地部分面积（阴影部分）还是与原来一样大小，因此草地面积=（16-2）×（10-2）＝112.例16 右图是两个相同的直角三角形叠在一起，求阴影部分的面积.解：实际上，阴影部分是一个梯形，可是它的上底、下底和高都不知道，不能直接来求它的面积.阴影部分与三角形BCE合在一起，就是原直角三角形.你是否看出，ABCD也是梯形，它和三角形BCE合在一起，也是原直角三角形.因此，梯形ABCD的面积与阴影部分面积一样大.梯形ABCD的上底BC，是直角边AD的长减去3，高就是DC的长.因此阴影部分面积等于梯形ABCD面积=（8＋8-3）×5÷2＝32.5.上面两个例子都启发我们，如何把不容易算的面积，换成容易算的面积，数学上这叫等积变形.要想有这种“换”的本领，首先要提高对图形的观察能力.例17 下图是两个直角三角形叠放在一起形成的图形.已知AF，FE，EC都等于3，CB，BD都等于4.求这个图形的面积.解：两个直角三角形的面积是很容易求出的.三角形ABC面积=（3＋3＋3）×4÷2＝18.三角形CDE面积=（4＋4）×3÷2＝12.这两个直角三角形有一个重叠部分--四边形BCEG，只要减去这个重叠部分，所求图形的面积立即可以得出.因为AF＝FE＝EC＝3，所以AGF，FGE，EGC是三个面积相等的三角形.因为CB＝BD＝4，所以CGB，BGD是两个面积相等的三角形.2×三角形DEC面积= 2×2×（三角形GBC面积）＋2×（三角形GCE面积）.三角形ABC面积= （三角形GBC面积）＋3×（三角形GCE面积）.四边形BCEG面积=（三角形GBC面积）＋（三角形GCE面积）=（2×12＋18）÷5＝8.4.所求图形面积=12＋18- 8.4＝21.6.例18 如下页左图，ABCG是4×7长方形，DEFG是2×10长方形.求三角形BCM与三角形DEM面积之差.解：三角形BCM与非阴影部分合起来是梯形ABEF.三角形DEM与非阴影部分合起来是两个长方形的和.（三角形BCM面积）-（三角形DEM面积）=（梯形ABEF面积）-（两个长方形面积之和=（7＋10）×（4＋2）÷2-（4×7 ＋2×10）=3.例19 上右图中，在长方形内画了一些直线，已知边上有三块面积分别是13，35，49.那么图中阴影部分的面积是多少？解：所求的影阴部分，恰好是三角形ABC 与三角形CDE 的公共部分，而面积为13，49，35这三块是长方形中没有被三角形ABC 与三角形CDE 盖住的部分，因此（三角形 ABC 面积）+（三角形CDE 面积）＋（13＋49＋35）＝（长方形面积）＋（阴影部分面积）.三角形ABC ，底是长方形的长，高是长方形的宽；三角形CDE ，底是长方形的宽，高是长方形的长.因此，三角形ABC 面积，与三角形CDE 面积，都是长方形面积的一半，就有阴影部分面积=13 ＋ 49＋ 35＝ 97.例题1。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
12
15
22
2
巧求面积练习题
一．夯实基础：
1.如图是学校操场一角，请计算它的面积(单位：米)
40
20
2.一块长方形铁板，长15分米，宽12分米，如果长和宽各减少2分米，面积比原来减少
多少平方分米？
3.一块长方形纸片，在长边剪去5cm，宽边剪去2cm后(如图)，得到的正方形面积比原
长方形面积少31cm2．求原长方形纸片的面积．
5
2
4.一个边长为20厘米的正方形，依次连接四边中点得到第二个正方形，这样继续下去可
得到第三个、第四个、第五个正方形．求第五个正方形的面积？
30
30
甲
6
乙
8
丙5.
如图所示，把一个正方形各边中点顺次相连，可得一个新的较小的正方形；把这个小正方形的各边中点顺次相连，又可以得到一个新的更小一些的正方形……如此依次连下去，一直连到第三个新正方形为止。
如果图中阴影的面积等于1，那么图中最大的正方形面积等于多少？
二．拓展提高：
6.
甲、乙、丙三个正方形，它们的边长分别是6、8、10厘米，乙的一个顶点在甲的中心上，丙的一个顶点在乙的中心上．这三个正方形的覆盖面积是多少平方厘米？
10
7.如图，四边形ABCD 的周长是60厘米，点M 到各边的距离都是4.5厘米，这个四边形的面积是
平方厘米.
8.
有一个长方形，如果宽减少2米，或长减少3米，则面积均减少24平方米，求这个长
方形的面积？
绿
红绿绿
绿58
9.
有大、小两个长方形(如图)，对应边的距离均为1cm ，已知两个长方形之间部分的面积是16cm 2，且小长方形的长是宽的2倍，求大长方形的面积．
10.空白处每个方格都是边长为4厘米的正方形，黑条的宽度为2厘米，求阴影部分的面积
和周长。
11.如图，一块正方形地砖，上面印有四周对称的花纹，正中心红色小正方形面积是
8，四
块绿色等腰直角三角形均相同，面积总和是36，那么图中阴影部分的面积是多少？
A
C B
D E
三．超常挑战：
12.下图(单位：厘米)是两个相同的直角梯形重叠在一起，求阴影部分的面积.
20
D
O C
3
2E
11
97
5
13.两个相同的直角三角形如下图所示(单位：厘米)重叠在一起，求阴影部分的面积.
A
B
F
10
14.如图是由5个大小不同的正方形叠放而成的，如果最小的正方形(阴影部分)的周长是8，
那么最大的正方形的边长是．
15.如图，边长为10的正方形中有一等宽的十字，其面积(阴影部分)为36，则十字中央的小正方形面积为．
16.如图所示，四个相叠的正方形，边长分别是5、7、9、11.问灰色区与黑色区的面积的差是多少？
17.有一大一小两个正方形，它们的周长相差20厘米，面积相差55平方厘米．小正方形的
面积是多少平方厘米？
18.如右图所示，在长方形ABCD中，放入六个形状大小相同的长方形(尺寸如图)，图中
阴影部分的面积是．
B
303030
30
答案：
1.这是一个不规则图形，怎样使它能转化为我们熟悉的基本图形呢？可以在图中添上一条辅助
线，把多边形切割成上下两个长方形或左右两个长方形；也可以把多边形补充完整，成为一个长方形；
40
40
40
20
20
20
图一图二图三
方法一：如图一，30⨯40+20⨯（30+40）=1200+1400=2600(平方米)方法二：如图二，20⨯30+40⨯（20+30）=600+2000=2600(平方米)方法三：如图三，（40+30）⨯（20+30）-30⨯30=3500-900=2600(平方米)
2.
(方法一)如图，铁板面积比原来减少的面积就是阴影部分的面积，阴影部分的面积是用原长方形的面积减去空白部分的面积．即:15⨯12-(15-2)⨯(12-2)=180-130=50(平方分米).
(方法二)也可把阴影部分分割成两个长方形，求两个长方形的面积．3.
通过对图形进行分割，可以发现C 的长与宽分别是5cm 和2cm ，则它的面积是5⨯2=10(cm 2)，那么A +B 的面积是31-10=21(cm 2)，如给B 移到A 的旁边，则知正方形的边长：(cm )，正方形的面积是3⨯3=9(cm 2)，原长方形的面积是31+9=40(cm 2)．
5
2
24.
第一个正方形的面积是20⨯20=400(平方厘米)，第二个正方形的面积如图，实际上是第一个正方形面积的一半．依次类推，第五个正方形的面积为：400÷2÷2÷2÷2=25(平方厘米)．
5.
最小的正方形面积等于2，每往外扩一层，面积就会增加一倍。
所以最大正方形面积等于2×2×2×2=16。
6.
如右图添加辅助线割补，如果甲的面积为4份量，则甲与乙的重合部分是1份量．同理，如果乙的面积为4份量，则乙与丙的重合部分是1份量．
所以这三个正方形覆盖面积是：10⨯10+8⨯8+6⨯6-6⨯6÷4-8⨯8÷4=175(平方厘米)．
30
30
C
B
A
C
M
甲
6
乙
8
丙10
7.
本题考查整体思维.下面中四个三角形的高都是4.5厘米，底的和是60厘米，所求四边形的面积为60⨯4.5÷2=135平方厘米
D
A B
8.
长方形宽减少2米，面积减少24平方米．说明长方形长：24÷2=12(米)．
长方形长减少3米，面积减少24平方米．说明长方形宽：24÷3=8(米)．所以这个长方形的面积为：12⨯8=96(平方米)．
9.
由于长方形之间的部分是不规则的，所以可以进行分割，这样分割后，A +B 的面积是16÷2=8(cm 2)，则知小长方形的长与宽之和是8÷1-1-1=6(cm )，小长方形的宽是6÷（2+1）=2(cm )，长是2⨯2=4(cm )，那么有大长方形的长是6(cm )，宽是4(cm )，面积是4⨯6=24(cm 2)．
10.阴影部分面积为大正方形面积减去8个小正方形面积：
(4⨯3+2⨯2)2-42⨯8=128cm 2；阴影部分周长利用平移为大正方形周长加上两个
小正方形周长：(4⨯3+2⨯2)⨯4+4⨯4⨯2=96cm 。
11.48。
空白部分面积为36＋8＋8＝52。
由边上的三角形面积为2，绿三角形面积为9，可
得BC＝2，BD＝6，所以正方形面积为100，阴影面积为48。
12.所求面积等于图中阴影部分的面积，为(20-5+20)⨯8÷2=140(平方厘米)．
B
A
正
13.阴影部分是一个高为3厘米的直角梯形，然而它的上底与下底都不知道，因而不能直接
求出它的面积.因为三角形ABC 与三角形DEF 完全相同，都减去三角形DOC 后，根据差不变性质，差应相等，即阴影部分与直角梯形OEFC 面积相等，所以求阴影部分的面积就转化为求直角梯形OEFC 的面积.直角梯形OEFC 的上底为10-3=7(厘米)，面积
为(7+10)⨯2÷2=17(厘米2
).
所以，阴影部分的面积是17平方厘米。
14.最小正方形的面积是2⨯2=4(平方厘米)，最大的正方形的面积是4⨯2⨯2⨯2⨯2=64
(平方厘米)，那么最大的正方形的边长是8厘米．15.题目中的空白部分可以组成一个如右图的正方形，正方形面积为100-36=64，右图中
的正方形边长为8，四角小等腰直角三角形的直角边长度为（10－8）÷2＝1，中间正方形面积为四角四个小等腰直角三角形的面积和，为S =12÷2⨯4=2．
16.灰色和白色区域形成一边长为11的正方形和一边长为7的正方形，它们的总面积是112+72=170；类似地，黑色和白色区域组成一边长为9的正方形和一边长为5的正方形，它们的总面积是92+52=106．
由于白色区域在这两种组合中都被计算了，根据差不变原理，可知灰色区域与黑色区域的面积之差就等于170-106=64．
17.大正方形的边长比小正方形的边长多20÷4=5（厘米）．
B 的面积是5×5＝25（平方厘米），A 的面积是（55－25）÷2＝15（平方厘米）左下角小正方形边长是15÷5＝3（厘米），面积是3×3＝9（平方厘米）18.由图中可以看出
小长方形的长+3⨯小长方形的宽=14，小长方形的长-小长方形的宽=6．第二式乘以3再与第一式相加得4⨯小长方形的长=14+6⨯3=32．
所以小长方形的长=8，小长方形的宽=2，
小长方形的面积8⨯2=16，大长方形的面积=14⨯(6+2⨯2)=140，
阴影面积=140-6⨯16=44
．。