16-17年沈阳自动化所博士入学考试理论力学试卷真题
(完整版)理论力学试卷4及答案
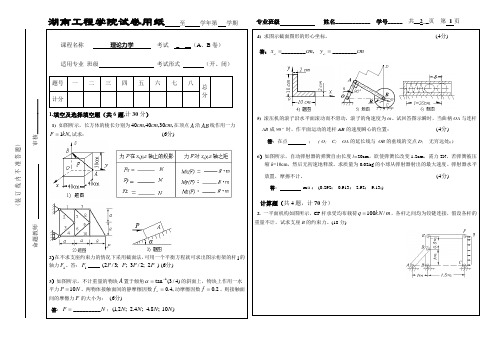
湖南工程学院试卷用纸 至 学年第 学期(装 订 线 内 不 准 答 题)命题教师 审核____________课程名称 理论力学 考试 _ __(A 、B 卷)适用专业 班级 考试形式 (开、闭) 题号一 二 三 四 五 六 七 八 总分计分1.填空及选择填空题(共6题,计30分)1) 如图所示,长方体的棱长分别为,30,40,40cm cm cm 在顶点A 沿AB 线作用一力 ,1kN F =试求: )6(分2)在不求支座约束力的情况下采用截面法,可用一个平衡方程就可求出图示桁架的杆1的轴力1F 。
答:____1F )2;2/3;;3/2(P P P P )6(分3)如图所示,不计重量的物块A 置于倾角)4/3(tan 1-=α的斜面上,物块上作用一水平力N P 10=。
两物体接触面间的静摩檫因数,4.0=S f 动摩檫因数2.0=f 。
则接触面间的摩檫力F 的大小为: )6(分 答:N F _________=;)10;8.4;4.2;2,1(N N N N专业班级 姓名____________ 学号_____ 共__2__页 第 1页4) 求图示截面图形的形心坐标。
)4(分 答:cm y cm x C C ________,________==5) 滚压机的滚子沿水平面滚动而不滑动,滚子的角速度为ω。
试回答图示瞬时,当曲柄OA 与连杆AB 成90 o 时,作平面运动的连杆AB 的速度瞬心的位置: )4(分 答:在点 ; ( O; C; OA 的延长线与 OB 的垂线的交点D; 无穷远处; )6)如图所示,自动弹射器的弹簧自由长度l=20cm ,欲使弹簧长改变1.2cm ,需力2N 。
若弹簧被压缩δ=10cm ,然后无初速地释放。
求质量为0.02kg 的小球从弹射器射出的最大速度。
弹射器水平放置,摩擦不计。
)4(分 答: m/s ; (0.292; 0.913; 2.92; 9.13;)计算题(共4题,计70分)2. 一平面机构如图所示,CF 杆承受均布载荷m kN q /100=,各杆之间均为铰链连接,假设各杆的重量不计,试求支座B 的约束力。
理论力学试题库

《理论力学》试题库第一部分 填空题:第一类:1,已知某质点运动方程为x=2bcoskt,y=2bsinkt,其中b 、k 均为常量,则其运动轨迹方程为————————————,速度的大小为————————————,加速度的大小为————————————。
2、已知某质点运动方程为x=2cos3t,y=2sin3t,z=4t 则其运动速度的大小为 ,加速度的大小为 。
3、已知某质点运动方程为r=e ct ,θ=bt,其中b 、c 是常数,则其运动轨道方程为——————————————————————,其运动速度的大小为——————————,加速度的大小为————————————。
4、已知某质点的运动方程为x=2bcos 2kt ,y=bsin2kt ,则其运动轨道方程为 ;速度大小为 ;加速度大小为 。
5、已知质点运动的参数方程为y=bt ,θ=at ,其中a 、b 为常数,则此质点在极坐标系中的轨道方程式为 ,在直角坐标系中的轨道方程式为 。
6、已知某质点的运动方程为r=at,θ=bt,其中a 、b 是常数,则其运动轨道方程为——————————————————————,其运动速度的大小为——————————,加速度的大小为————————————。
7、已知某质点运动方程为r=at,θ=b/t,其中a 、b 是常数,则其运动轨道方程为———————————————,其运动速度的大小为——————————,加速度的大小为—————————。
8、已知某质点的运动方程为x=at,y=a(e t -e -t )/2,其中a 为常数,则其运动轨道方程为——————————————————————,曲率半径为——————————。
第二类:9、质点在有心力作用下,其————————————————————均守恒,其运动轨道的微分方程为——————————————————————,通常称此轨道微分方程为比耐公式。
理论力学2017期末试卷及答案

姓名:__________大 连 理 工 大 学 学号:__________课 程 名 称: 理论力学 试卷: A 考试形式: 闭卷院系:__________ 授课院(系):__力学系_____ 考试日期:2017年1月9 日 试卷共 6 页 班级:__________装 一.简答题 (共30分, 每题5分)1. 图示机构中均质杆OA 、AB 完全相同,质量为m ,长度为l ,图示瞬时OA 杆角速度为1ω,角加速度为1α,AB 杆角速度为2ω,角加速度为2α。
根据达朗贝尔原理,试将AB 杆的惯性力向其质心简化。
(求惯性力和力偶的大小,方向标在右图上)订2. 图示构件由圆盘和两杆铰接而成,均质圆盘质量为2m ,半径为4l /,两根相同的均质杆长为l ,质量为m ,构件绕O 轴定轴转动,求该构件对O 轴的转动惯量O J 。
线得分 题一.2图601ω1603. 图示机构中均质杆OA 的质量为m ,长度为l ,绕O 轴匀速转动,角速度为ω,通过均质AB 杆带动均质圆轮A 的在地面上纯滚动,AB 杆质量为2m ,长度为2l ,圆轮质量为m ,半径为l/3,当OA 杆处于铅直位置时,求系统对O 轴的动量矩。
4. 图示桁架各夹角均为60,求AB 杆内力。
5. 图示机构中杆AB 以角速度ω绕A 轴匀速转动,由CB 杆带动滑块C 在滑槽中运动,已知AB 杆长为l ,CB 杆长为4l ,求滑块C 的运动方程和速度方程。
题一.3图题一.4图 题一.5图x6. 滑块A 和滑块B 与杆由铰链连接,分别在水平面和铅直面内滑动,在图示位置平衡,滑块质量均为m ,不计杆的自重。
试利用虚位移原理求滑块A 、B 所受摩擦力间的关系。
二.(15分)图示结构由直角折杆ABC 及杆CD 、EG 铰接而成,受集中力和线性分布力作用,求A 、D 处约束力和EG 杆的内力。
得分题一.6图三.(15分)图示起重机简图,机身重W = 80kN ,重力作用线通过E 点;三个轮子A ,B ,C与地面接触点的连线ABC 为等边三角形。
2017年中国科学院自动化研究所考博试题 神经解剖

中国科学院自动化研究所
2017年招收攻读博士学位研究生入学统一考试试卷
科目名称:神经解剖学
考试须知:本试卷满分为100分,全部考试时间总计180分钟——————————————————————————————————
I. Explain terms:(10×2分= 20分)
1.脊髓节段, 2.(脊髓)中间外侧核, 3.新小脑, 4.锥体交叉,5.外侧豆纹动脉, 6. 内侧纵束, 7.脑池, 8半卵圆中心,9.后丘脑 1 0. 丘脑髓纹,
II. Answer questions:(5×10分= 50分)
1.第10胸脊髓节段右侧半损伤,可出现那些感觉和运动障碍?为什么?
2.脑干内有哪些副交感神经核?各核发出的节前纤维参与哪几对脑神经?
节后纤维如何走行与管理?
3. 颈内动脉(颅内段)的分段名称、行程及主要分支名称;
在MRA / CTA正、侧位图像上如何识别?
4.下丘脑的外形、主要神经核团的名称及其纤维联系。
5.解释一侧内囊出血后,临床所谓的“三偏综合征”。
Ⅲ. Completion of drawing:(30×1分= 30分)
1 - 6 、海马结构; 7 – 12、间脑(后面观);
13 – 18、脑(经海马头的冠状切面);
19 - 24 、延髓(经舌下神经核的横断面);
25 – 30、脑底的动脉。
2016-2017年沈阳自动化所博士入学考试试卷真题

科目名称:机器人学
第 1页 共 3页
四、(20 分)设有一个旋转关节的单自由度操作臂处于静止状态,0 15o ,要在 3s 之内平稳运动到达终止位置: f 75o ,并且在终止点的速度为零。试用三次多项 式插值求 (t) ,(t) ,(t) 。
二、(14 分)试写出齐次变换阵 BAH ,它表示坐标系{B}连续相对固定坐标系{A} 作以下变换: (1)绕 Z A 轴旋转 90 。 (2)绕 X A 轴旋转-90 。
(3)移动 3 7 9T 。
三、(20 分)如图所示的三自由度机械手(两个旋转关节加一个平移关节,简称 RPR 机械手),三个关节的运动参数分别为θ1,d2 和θ3,连杆长度分别为 L1,L2 和 L3。
三、(20 分)如图所示,均质杆 AB 和 OD,质量均为 m,长度均为 l,垂直的固接 成 T 字型,且 D 为 AB 杆的中点,置于铅垂平面内,该 T 字杆可绕光滑固定轴 O 转动。开始时系统静止,OD 杆铅垂。在一常值力偶 M =(20/π)∙mgl 作用下转动。 求 OD 杆至水平位置时,(1)OD 杆角速度和角加速度;(2)支座 O 处的反力。
P
A
C
B
M D
二、(20 分)图示机构中,杆 AB 上的销钉 E 可在构件 CD 的滑槽内滑动。当机构 运动到图示位置时,滑块 A 的速度为 40cm/s,加速度为 140cm/s2。试求构件 CD 在铅垂位置时的角加速度。
B D
200mm
E
A
vA
C
aA
75mm
75mm
理论力学--期末考试试题(题库-带答案)

理论力学 期末考试试题1-1、自重为P=100kN 的T 字形钢架ABD,置于铅垂面内,载荷如图所示。
其中转矩M=20kN.m ,拉力F=400kN,分布力q=20kN/m,长度l=1m 。
试求固定端A 的约束力。
解:取T 型刚架为受力对象,画受力图.1-2 如图所示,飞机机翼上安装一台发动机,作用在机翼OA 上的气动力按梯形分布:1q =60kN/m ,2q =40kN/m ,机翼重1p =45kN ,发动机重2p =20kN ,发动机螺旋桨的反作用力偶矩M=18kN.m 。
求机翼处于平衡状态时,机翼根部固定端O 所受的力。
解:1-3图示构件由直角弯杆EBD以及直杆AB组成,不计各杆自重,已知q=10kN/m,F=50kN,M=6kN.m,各尺寸如图。
求固定端A处及支座C的约束力。
1-4 已知:如图所示结构,a, M=Fa, 12F F F ==, 求:A ,D 处约束力.解:1-5、平面桁架受力如图所示。
ABC 为等边三角形,且AD=DB 。
求杆CD 的内力。
1-6、如图所示的平面桁架,A 端采用铰链约束,B 端采用滚动支座约束,各杆件长度为1m 。
在节点E 和G 上分别作用载荷E F =10kN ,G F =7 kN 。
试计算杆1、2和3的内力。
解:2-1 图示空间力系由6根桁架构成。
在节点A上作用力F,此力在矩形ABDC平面内,且与铅直线成45º角。
ΔEAK=ΔFBM。
等腰三角形EAK,FBM和NDB在顶点A,B和D处均为直角,又EC=CK=FD=DM。
若F=10kN,求各杆的内力。
2-2 杆系由铰链连接,位于正方形的边和对角线上,如图所示。
在节点D沿对角线LD方向F。
在节点C沿CH边铅直向下作用力F。
如铰链B,L和H是固定的,杆重不计,作用力D求各杆的内力。
2-3 重为1P =980 N ,半径为r =100mm 的滚子A 与重为2P =490 N 的板B 由通过定滑轮C 的柔绳相连。
理论力学试题及参考答案

3、在图示系统中,A、B两物块的质量皆为1m,均质轮的质量为2m,半径为R。
若已知A物的速度大小为v,则系统动量大小=P12cos2m vθ,对O轴的动量矩=OL121(2)2m m Rv+。
四、图示平台车沿水平直线行驶,均质细杆AB用水平绳维持在铅直位置。
已知:杆长ml2=,杆质量kgm20=,平台车的加速度大小2/16sma=,重力加速度大小2/8.9smg=。
试用动静法求:(1)绳CD的张力;(2)支座A的约束力。
(本题15分)第 4 页解:选AB为研究对象,受力分析如图所示。
应有动静法列平衡方程,有xF=∑0Ax T IgF F F+-=yF=∑0AyF mg-=()0AM=∑F31042T IgF l F l-⨯+⨯=其中:2016320()IgF ma N==⨯=,联立求解,可得图三--2 图三--3l3 / 3水平线上。
在图示位置时,OA 垂直于OB ,试求该瞬时连杆AB 的角速度、角加速度和滚轮的角速度、角加速度。
(本题15分)解:(1)先进行速度分析。
在图示位置时,AB 杆作瞬时平动。
杆连杆AB 的角速度为0AB ω=滚轮的角速度为0B A B r v vR R Rωω=== (6分)(2)再进行加速度分析。
以A 为基点分析B 点的加速度。
由nB A BA τ=+a a a 作B 点的加速度合成图如图所示。
由图可知 (3分)o 20tan 30nB A a a ω==o20/cos30n BA A a a τω==(4分) 故连杆AB 的角加速度为202BA AB a r τε== 滚轮的角加速度为23B B r a R Rωε==(2分)第6页七、在图示机构中,滚子C 沿楔块D 的斜面向下滚动而不滑动,斜面与水平面成θ角,滚子借一跨过滑轮B 的绳提升重物A ,同时滑轮B 绕O 轴转动。
滚子C 与滑轮B 的质量均为1m 。
半径为r ,且同为均质圆盘。
物A 的质量为2m ,放在光滑基础上的楔块D 的质量为3m ,求滚子质心的加速度和楔块D 作用于基础凸出部分的水平压力。
理论力学模拟试题及答案---精品管理资料

理论力学模拟试题及答案一、是非题(每题2分。
正确用√,错误用×,填入括号内。
)1、作用在一个物体上有三个力,当这三个力的作用线汇交于一点时,则此力系必然平衡。
()2、力对于一点的矩不因力沿其作用线移动而改变。
( )3、在自然坐标系中,如果速度υ= 常数,则加速度α= 0。
()4、虚位移是偶想的,极微小的位移,它与时间,主动力以及运动的初始条件无关。
()5、设一质点的质量为m,其速度 与x轴的夹角为α,则其动量在x轴上的投影为mv x =mvcos a。
()二、选择题(每题3分.请将答案的序号填入划线内。
)1、正立方体的顶角上作用着六个大小相等的力,此力系向任一点简化的结果是.①主矢等于零,主矩不等于零;②主矢不等于零,主矩也不等于零;③主矢不等于零,主矩等于零;④主矢等于零,主矩也等于零。
2、重P的均质圆柱放在V型槽里,考虑摩擦柱上作用一力偶,其矩为M时(如图),圆柱处于极限平衡状态。
此时按触点处的法向反力N A与N B的关系为。
①N A = N B; ②N A > N B; ③N A < N B。
3、边长为L 的均质正方形平板,位于铅垂平面内并置于光滑水平面上,如图示,若给平板一微小扰动,使其从图示位置开始倾倒,平板在倾倒过程中,其质心C 点的运动轨迹是 。
①半径为L/2的圆弧; ②抛物线; ③椭圆曲线; ④铅垂直线。
4、在图示机构中,杆O 1 A //O 2 B ,杆O 2 C //O 3 D,且O 1 A = 20cm ,O 2 C = 40cm,CM = MD = 30cm ,若杆AO 1 以角速度 ω = 3 rad / s 匀速转动,则D 点的速度的大小为 cm/s ,M 点的加速度的大小为 cm/s 2。
① 60; ②120; ③150; ④360。
5、曲柄OA 以匀角速度转动,当系统运动到图示位置(OA//O 1 B 。
AB |OA)时,有A V B V ,A αB α,ωAB 0,εAB 0。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
中国科学院沈阳自动化研究所
2016年招收攻读博士学位研究生入学统一考试试题
(秋季)科目名称:理论力学
考生须知:
1.本试卷满分为100分,全部考试时间总计180分钟。
2.所有答案必须写在答题纸上,写在试题纸上或草稿纸上一律无效。
3.可以使用无字典存储和编程功能的电子计算器。
一、(20分)如图所示,杆AB 与杆CD 接触点C 的静摩擦系数f s =0.1,P =20kN ,AC=CB =5m ,AD =4m ,杆AB 处于水平位置。
不计各杆自重,试求系统在该位置平衡时的力偶矩M 的大小。
A B
C
D
P M
二、(20分)图示机构中,杆AB 上的销钉E 可在构件CD 的滑槽内滑动。
当机构运动到图示位置时,滑块A 的速度为40cm/s ,加速度为140cm/s 2。
试求构件CD 在铅垂位置时的角加速度。
A
B
C
D
E
v A a A
75mm
75mm
200m m
三、(20分)如图所示,均质杆AB 和OD ,质量均为m ,长度均为l ,垂直的固接成T 字型,且D 为AB 杆的中点,置于铅垂平面内,该T 字杆可绕光滑固定轴O 转动。
开始时系统静止,OD 杆铅垂。
在一常值力偶M =(20/π)∙mgl 作用下转动。
求OD 杆至水平位置时,(1)OD 杆角速度和角加速度;(2)支座O 处的反力。
O
M
A
D B
四、(20分)如图所示,三根均质直杆OA 、AB 、O 1B 的长度均为l ,质量为m ,用光滑的铰链连接,静止地悬挂在相距为l 的固定铰支座O 及O 1上。
若在水平直杆的A 端铰链处作用一水平向左的冲量S ,试求杆OA 及O 1B 的最大偏角。
A
O
B
S
O 1
φ
φ
l
(第五题、第六题任选其一,如果两题都作答,按第五题计分)
五、(20分)如图所示平面结构,有三根刚杆AC 、CE 和ED 铰接而成。
在力偶矩M 和力P 的作用下平衡,尺寸如图。
不计各杆重量及摩擦,试用虚位移原理求活动铰支座B 处的反力。
A
M a
2a
3a
a
a a
B
C
D
E
P
H 六、(20分)质量为m ,半径为r 的两均质圆轮A 、B ,轮心用刚度系数为k ,长度为l 的弹簧相连,在水平面上作纯滚动。
试用拉格朗日方程推导出系统运动的微分方程。
(提示:选两轮轮心水平位移x 1,x 2为广义坐标)
B
r A
r k
x 1x 2
中国科学院沈阳自动化研究所
2017年招收攻读博士学位研究生入学统一考试试题
(秋季)科目名称:理论力学
考生须知:
1.本试卷满分为100分,全部考试时间总计180分钟。
2.所有答案必须写在答题纸上,写在试题纸上或草稿纸上一律无效。
3.可以使用无字典存储和编程功能的电子计算器。
一、(20分)均质水平梁AB 重为P ,长为l ,两端搁于两平行的水平轨道上;AB 与轨道垂直,如图所示。
设梁与轨道间的摩擦系数均为f s 。
现以垂直于梁的力F 在C 处拉AB 梁,AC=(2l /3),F 与平行于轨道的直线夹角为α。
求能使AB 杆保持静止的力F 的最大值及A 、B 处的摩擦力。
αA
B
C
F 二、(20分)滚压机构的滚子沿水平面滚动而不滑动。
曲柄的半径为r =10cm ,以等转速n =30转/分绕O 轴转动。
如滚子半径R =10cm ,连杆AB 长为17.3cm ,求当曲柄与水平面交角为60°时,滚子的角速度和角加速度。
A
B O 60°
n R
r
C
三、(20分)匀质杆OA 长为l ,重为G ,圆柱A 半径为r ,重为Q ,圆柱质心用铰链与杆相连,开始时系统用绳悬挂在铅垂面内,且OA 为水平方向。
不计O 处及A 处摩擦,求切断绳索时OA 杆的角加速度及O 处反力。
A O
r Y O X O
G Q l
y x
绳索
四、(20分)如图所示,做铅直平动的匀质细杆AB 长l ,与铅直线成β角。
当杆下端碰到光滑水平面时,杆具有铅直速度v 0。
试求:(1)若接触点A 碰撞是完全弹性的,碰撞结束时杆的角速度;(2)若碰撞是完全塑性的,则解答如何?
βA
B
v 0
(第五题、第六题任选其一,如果两题都作答,按第五题计分)
五、(20分)杆OA 和AB 以铰链相连,O 端悬挂于圆柱铰链上,如图所示。
杆长OA=a ,AB=b 杆重和铰链的摩擦都忽略不计。
今在点A 和B 分别作用向下的铅垂力F A ,F B ,又在点B 作用一水平力F 。
试应用虚位移原理和广义力的概念求平衡时φ1,φ2与F A ,F B ,F 之间的关系。
O
φ1
F A B
A
x
y
φ2
F B
F
六、(20分)质量为m的均质圆盘,在三角块斜边上作纯滚动,如图所示。
三角块的质量也为m,置于光滑水平面上,其上有刚性系数为k的弹簧平行于斜面系在圆盘轴心O上。
设α=30°。
试用拉格朗日方程建立系统的运动微分方程。
x1。
