结构力学(零杆的判断)
简谈结构力学桁架零杆问题Word版

简谈结构力学桁架零杆问题姓名(楷体四号)单位(宋体小五)摘要:本文粗略讲解一下桁架结构中关于零杆的问题,包括零杆的判断,以及零杆在求解桁架结构的用处。
关键词:结构力学、桁架、零杆引言学习了结构力学,个人对于桁架印象较深,特别是桁架中我们认为约定出来的零杆印象很深,因为当初个人在学习的时候,对于零杆并未掌握,充其量只是知道有这么回事,其内在含义并不清楚。
但它的存在对于求解桁架结构非常重要,有时候可以让复杂的桁架变为几根杆件的简单桁架,非常实用。
通过后来的学习,网上查找资料,和同学探讨,现在虽不说精通,但也有些个人见解。
1零杆的含义在结构力学关于静定平面桁架的内力的计算中,当桁架的一些结点没有荷载时,并由于桁架形式所导致,桁架中一些杆件不产生内力,这些内力为零的杆件称为“零杆”。
零杆是在理论计算中为了便于计算才提出来的,实际生活中是很少见到的,只是我们为了计算桁架内力图时为了简化的方便,或者说忽略它的一点点受力对于整个求解结果影响并不是很大,我们就将其定义为零杆。
2零杆的作用桁架中的零杆虽然不受力,但却是保持结构坚固性所必需的。
因为桁架中的载荷往往是变化的。
在一种载荷工况下的零杆,在另种载荷工况下就有可能承载。
如果缺少了它,就不能保证桁架的坚固性。
掌握了判断出零杆的方法,在分析桁架内力时,如果首先确定其中的零杆,这对后续分析往往有利,会给计算带来很大的方便。
3零杆的判定1、无荷载的三杆结点,若两杆在同一直线上,则第三杆为零杆。
(如下图a)2、不在同一条直线上的两杆节点上若没有荷载作用,两杆均为零杆。
(如下图b)3、不共线的两杆结点,若荷载沿一杆作用,则另一杆为零杆。
(如下图c)4、对称桁架在对称荷载作用下,对称轴上的K形结点若无荷载,则该结点上的两根斜杆为零杆。
(如下图d)5、对称桁架在反对称荷载作用下,与对称轴重合或者垂直相交的杆件为零杆。
(如下图e)图示:值得注意的是,d,e中结构的支座不是对称的,但是只有竖向力的作用,铰支座的水平约束其实不起作用,因此可以忽略,这才可以把结构看成是对称的结构。
理论力学零杆判断方法
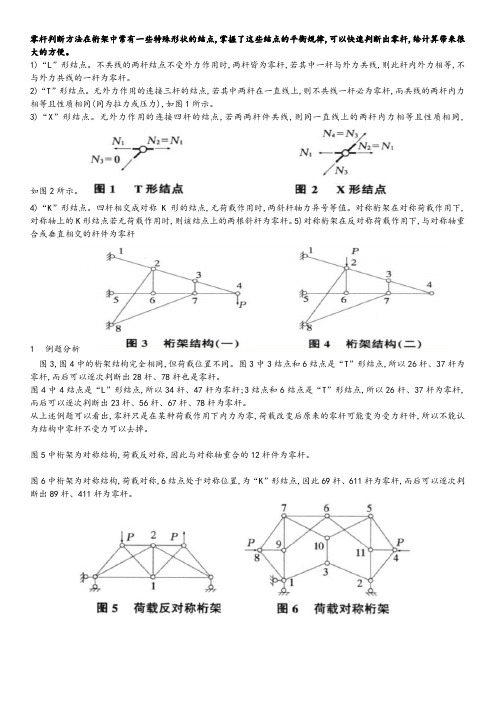
4)“K”形结点。四杆相交成对称K形的结点,无荷载作用时,两斜杆轴力异号等值。对称桁架在对称荷载作用下,对称轴上的K形结点若无荷载作用下,与对称轴重合或垂直相交的杆件为零杆
从上述例题可以看出,零杆只是在某种荷载作用下内力为零,荷载改变后原来的零杆可能变为受力杆件,所以不能认为结构中零杆不受力可以去掉。
图5中桁架为对称结构,荷载反对称,因此与对称轴重合的12杆件为零杆。
图6中桁架为对称结构,荷载对称,6结点处于对称位置,为“K”形结点,因此69杆、611杆为零杆,而后可以逐次判断出89杆、411杆为零杆。
零杆判断方法在桁架中常有一些特殊形状的结点,掌握了这些结点的平衡规律,可以快速判断出零杆,给计算带来很大的方便。
1)“L”形结点。不共线的两杆结点不受外力作用时,两杆皆为零杆,若其中一杆与外力共线,则此杆内外力相等,不与外力共线的一杆为零杆。
2)“T”形结点。无外力作用的连接三杆的结点,若其中两杆在一直线上,则不共线一杆必为零杆,而共线的两杆内力相等且性质相同(同为拉力或压力),如图1所示。
1例题分析
图3,图4中的桁架结构完全相同,但荷载位置不同。图3中3结点和6结点是“T”形结点,所以26杆、37杆为零杆,而后可以逐次判断出28杆、78杆也是零杆。
图4中4结点是“L”形结点,所以34杆、47杆为零杆;3结点和6结点是“T”形结点,所以26杆、37杆为零杆,而后可以逐次判断出23杆、56杆、67杆、78杆为零杆。
零杆的判断规则

零杆的判断规则
零杆是指一个数字中的最高位为0的数位,例如数值为104的数字中,百位就是零杆。
判断一个数字中是否存在零杆,可以根据以下规则:
1. 数字中只含有0和1的情况下,不存在零杆。
2. 数字中含有2及以上的数位,且最高位不为0的情况下,不存在零杆。
3. 数字中含有2及以上的数位,且最高位为0的情况下,最高位为零杆。
4. 对于一个多位数,从高位开始,若当前数位为0,则它前面的所有数位均为零杆。
例如,数字103400的百位为零杆,千位为非零杆,万位及其以上的数位均为零杆。
- 1 -。
结构力学第2章习题及参考答案
解悬臂刚架,梁部分先求杆端控制弯矩,再区段叠加。柱剪力为零,弯矩图为常数。
2-21(b)
解两刚片三支杆组成单体刚架,先求支座反力,再作弯矩图。注意二杆结点有外力偶作用时,杆端弯矩将产生突变,突变值等于力偶值。
2-21(c)
解(1)铰附近截面作用有集中力偶时,弯矩值等于力偶值,据此,可知顶铰左右两侧截面的弯矩为M,上侧受拉。又因为横梁上没有竖向集中力作用,弯矩图应是一条直线。考虑本题结构对称,荷载也对称,则横梁上的弯矩图为一条水平线。
2-14试作图示多跨静定梁内力图。
解:(1)确定求解顺序:EF→CDE→ABC
(2)求支座反力及各部分之间的相互作用力。结果如图(b)所示。
(3)分别画出每一部分的内力图,组合在一起就是原结构的内力图,如图(c)和(d)所示。
2-15试作图示多跨静定梁弯矩图。
解:(1)确定求解顺序。DEF→DCB→AB。
(2)二杆刚结点上,若无集中力偶作用时,则两个杆的杆端弯矩应该相等,且同时外侧受拉。这样就可以画出两个柱子的弯矩图了。
2-21(d)
解本题为基——附型结构,先算上部、后算下部。两个部分均三铰刚架,分别求解即可。
2-21(e)
2-22试作图示组合结构的弯矩图和轴力图。
FN12= -75kN,FN34=75kN
100kn100kn50kn2520251875knm202550kn截面内力5mcos3025sincos187525295kncossin5050188knsincos5050683kn5m305m5m213求图示三铰拱结构的支座反力链杆轴力并求指定截面k1求支座反力10kn10kn取ceb部分为隔离体截面的弯矩取kad部分为隔离体40knayed20kn4m4m4m4m214试作图示多跨静定梁内力图
零杆

零杆
1. 不在同一条直线上的两杆节点上若没有荷载作用,两杆均为零杆。
2. 不共线的两杆结点,若荷载沿一杆作用,则另一杆为零杆。
3. 无荷载的三杆结点,若两杆在一直线上,则第三杆为零杆。
4. 对称桁架在对称荷载作用下,对称轴上的k形结点若无荷载,则该结点上的两根斜杆为零杆。
5. 对称桁架在反对称荷载作用下,与对称轴重合或者垂直相交的杆件为零杆。
判别方法:
一节点上有三根杆件,如果节点上无外力的作用,其中两根共线,则另一杆为零杆
一节点上只有两根不共线杆件,如果节点上无外力的作用,则两杆件均为零杆
一节点上只有两根不共线杆件,如果作用在节点上的外力沿其中一杆,则另一杆为零杆
桁架中的零杆虽然不受力,但却是保持结构坚固性所必需的。
因为桁架中的载荷往往是变化的。
在一种载荷工况下的零杆,在另种载荷工况下就有可能承载。
如果缺少了它,就不能保证桁架的坚固性。
分析桁架内力时,如首先确定其中的零杆,这对后续分析往往有利。
结构力学第2章习题及参考答案

(2)BC部分(图(c-2)):
: ; :
:
(3)可以很方便地画出整个结构的弯矩图。
2-19(d)
解D结点(图(d-1)):
(考虑对称性):
AD杆(图(d-2)):
(考虑对称性):
取整体为隔离体
:
这样,ECF部分为一个顶铰作用集中荷载2FP的三铰刚架。整个结构的弯矩图就可以画了。
2-20试作图示结构的弯矩图。
第2章习题
2-1试判断图示桁架中的零杆。
2-1(a)
解静定结构受局部平衡力作用,平衡力作用区域以外的构件均不受力。所有零杆如图(a-1)所示。
2-1 (b)
解从A点开始,可以依次判断AB杆、BC杆、CD杆均为无结点荷载作用的结点单杆,都是零杆。同理,从H点开始,也可以依次判断HI杆、IF杆、FD杆为零杆。最后,DE杆也变成了无结点荷载作用的结点D的单杆,也是零杆。所有零杆如图(b-1)所示。
,
,
2-12图示圆弧三饺拱,求支座反力及截面D的M、FQ、FN值。
解(1)求支座反力。
, ,
(2)求等代梁D截面内力
(3)求三铰拱D截面内力
,
2-13求图示三铰拱结构的支座反力,链杆轴力,并求指定截面K的弯矩。
解(1)求支座反力
, ,
(2)链杆轴力
取CEB部分为隔离体
(3)求K截面的弯矩
取KAD部分为隔离体
由式(a)、(b)和(c)得
FNOG=FNGH=FNOH=0
同理,可判断在TRE三角形中
FNSK=FNKL=FNSL=0
D结点也是“K”结点,且处于对称荷载作用下的对称轴上,故ID、JD杆都是零杆。所有零杆如图(c-1)所示。
零杆判断典型例题

零杆判断典型例题
以下是一个典型的零杆判断例题:
问题:设有一根20cm长的细杆,在距杆左端4cm处有一力F
作用,斜向上方作用的力的大小为10N,方向与杆成30°角。
另有一力矩大小为15N·m作用在杆的右端点,方向指向杆的
左侧。
求杆的平衡条件。
解析:我们可以先将题目中的信息整理一下:
杆的长度:L = 20cm = 0.2m
作用力F的大小:F = 10N
作用力F与杆的夹角:θ = 30°
作用力F距杆左端的距离:d = 4cm = 0.04m
作用力矩的大小:M = 15N·m
作用力矩的方向:指向杆的左侧
首先,我们需要进行力的平衡条件的分析。
根据力的平衡条件,杆的平衡要求合外力的合力等于零。
合外力是指跟着杆发生平衡关系的所有外力。
设合外力的合力为F_R,根据题目中的信息可以得到:
F_R = Fsinθ - F_R' (式1)
其中,Fsinθ为斜向上方作用力在竖直方向上的分力,F_R'为
作用力矩所产生的阻力。
然后,我们还需要进行力矩平衡条件的分析。
根据力矩平衡条件,杆的平衡要求合外力的力矩等于零。
设合外力的力矩为M_R,根据题目中的信息可以得到:
M_R = (Fcosθ) * d - M (式2)
其中,Fcosθ为斜向上方作用力在水平方向上的分力。
将方程1和方程2联立求解,即可得到杆的平衡条件。
注:在计算过程中,注意单位的统一和角度值的正负问题。
结构力学(零杆的判断)

结构力学(零杆的判断)
零杆概念起源于20世纪80年代末在建筑结构工程领域的实用设计理论。
零杆理论被广泛应用于桥梁和其他建筑物的结构力学设计,旨在消除结构形状中只有柔性而没有刚性成分的可能存在,即“零杆”。
零杆是指某个结构组成部分本身受力状态下,其受力或受拉长程度可以抵消受力元件对其余未受力部分所起到的作用,从而使结构整体仅在节点处存在非零受力,而不构成结构受力系统。
零杆指的是一个结构在它自身受力的情况下,可以抵消其余部分的受力,从而使整个结构仅在节点出存在非零受力,不构成结构受力系统的情况。
零杆的判断主要依据实际问题中对结构运动特性(有限变形)和承载能力(稳定弹性范围)的评估结果(通过有限元计算),辅助用外力及支座控制试验,以及根据材料弹性及约束增强等实验结果,结合总体结构分析过程。
来确定结构中是否存在零杆。
由此可见,确定结构中是否存在零杆,需要从结构设计、材料处理、力学分析及实验结果上考量,系统的进行判断。
零杆的判断可以帮助结构工程师正确评估结构受力状态,进考虑结构改造和加固措施,从而提高结构的安全性和使用寿命。
