信号与系统_2017_第3章_习题课
西安交通大学_信号与系统A课后习题(第3、4章)

ω
31
(a) 证明下面三个不同单位冲激响应的 LTI 系统:
h1 (t ) = u (t )
h2 (t ) = −2δ (t ) + 5e −2t u (t )
和
8
h3 (t ) = 2te − t u (t )
对输入为 x(t ) = cos t 的响应全都一样。 (b) 求另一个 LTI 系统的单位冲激响应,它对 cos t 的响应也相同。 (这道题说明,对 cos t 的响应不能唯一用来标定一个 LTI 系统) 32 考虑一个 LTI 系统 S ,其单位冲激响应为
和
(t ) = x
k =−∞
∑ x(t − kT )
∞
(t ) 的傅里叶级数系数, X ( jω ) 为 x(t ) 的傅里叶变换。 式中 T > 2 。令 ak 记作 x
(a) 求 X ( jω ) 的闭式表达式。
7
(b) 求傅里叶级数 ak 的表达式,并验证 ak =
1 2π k ) X (j T T
2
∞
k
sin(4(t + 1)) (c) x3 (t ) = π (t + 1)
10
《第三次课后作业》 (a) 借助于表 4.1(P.233—傅里叶变换性质)和表 4.2(P.234—基本傅里叶变换对) ,求 下列信号的傅里叶变换:
⎛ sin t ⎞ x(t ) = t ⎜ ⎟ ⎝ πt ⎠
x(t ) =
k =−∞
∑ae
k
+∞
jk (2π / T ) t
中,对全部非零的偶数 k ,有 ak = 0 ,则称 x(t ) 是奇谐(odd-harmonic)的。 (i) 证明:若 x(t ) 是奇谐的,则有
信号与系统(习题课)

∴ y(t) = e-3t + t e-3t = (1+ t) e-3t
by wky
习题 3-6 (1)
已知系统的微分方程为 y’’(t) +5 y’(t) + 4 y(t) =2 f ’(t) + 5f(t), t >0; 初始状态y(0-) =1,y’(0-) =5, 求系统的零输入响应yx(t)。 解:系统特征方程为 s2+5s+4=0 , 解得特征根 s1=-1, s2=-4
特解 (强迫响应)
比较:完全响应=零输入响应 + 零状态响应 = e-t + (1 - 1/2e-t -1/2e-3t)
by wky
习题 3-4
已知微分方程为 y’(t) + 3 y (t) = f(t),t >0; y(0) =1,
求系统的固有响应(齐次解) yh(t)、强迫响应 (特解) yp(t)和完全响应(全解) y(t) 解:系统特征方程为 s+3=0,
f(t)
f(-t)
2
2
1
1
-3 -2 -1 0 1 2 3 t -3 -2 -1 0 1 2 3 t
2 f(t+2)
f(-3t)
2
1
1
-3 -2 -1 0 1 2 3 t -3 -2 -1 0 1 2 3 t by wky
2-10 已知信号波形, 绘出下列信号波形
f(t)
f(-t)
2
2
1
1
-3 -2 -1 0 1 2 3 t -3 -2 -1 0 1 2 3 t
信号与线性系统分析习题答案
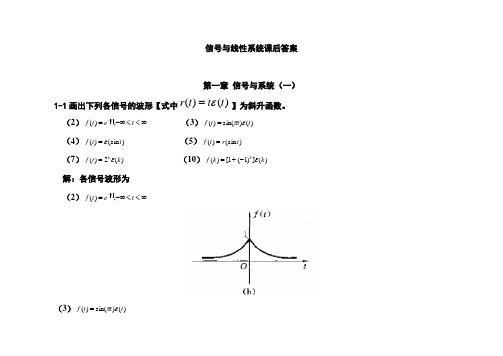
信号与线性系统课后答案第一章 信号与系统(一)1-1画出下列各信号的波形【式中)()(t t t r ε=】为斜升函数。
(2)∞<<-∞=-t e t f t ,)( (3))()sin()(t t t f επ= (4))(sin )(t t f ε= (5))(sin )(t r t f = (7))(2)(k t f k ε= (10))(])1(1[)(k k f k ε-+= 解:各信号波形为 (2)∞<<-∞=-t e t f t ,)((3))()sin()(t t t f επ=(4))fεt=(sin)(t (5))tf=r(sin)(t(7))tf kε(k=(2)(10))f kεk-=(k+]()1(1[)1-2 画出下列各信号的波形[式中)()(t t t r ε=为斜升函数]。
(1))2()1(3)1(2)(-+--+=t t t t f εεε (2))2()1(2)()(-+--=t r t r t r t f(5))2()2()(t t r t f -=ε (8))]5()([)(--=k k k k f εε(11))]7()()[6sin()(--=k k k k f εεπ (12))]()3([2)(k k k f k---=εε 解:各信号波形为 (1))2()1(3)1(2)(-+--+=t t t t f εεε(2))2()1(2)()(-+--=t rt rt rtf(5))2()2()(ttrtf-=ε(8))]5()([)(--=k k k k f εε(11))]7()()[6sin()(--=k k k k f εεπ(12))]()3([2)(kkkf k---=εε1-3 写出图1-3所示各波形的表达式。
1-4 写出图1-4所示各序列的闭合形式表达式。
1-5 判别下列各序列是否为周期性的。
如果是,确定其周期。
【信号与系统(郑君里)课后答案】第三章习题解答

3-1 解题过程:(1)三角形式的傅立叶级数(Fourier Series ,以下简称 FS )f ( t ) = a ++∞cos ( n ω t) + b sin ( n ω t ) a 0 ∑ n 1n 1 n =1式中ω1 =2π,n 为正整数,T 1 为信号周期T 11 t +T(a )直流分量a 0 = 0 ∫ 1 f ( t ) dtT1 t2 t +T(b )余弦分量的幅度a n = 0∫ 1f ( t ) cos ( n ω1t ) dtT1 t 02 t +T(c )正弦分量的幅度b n = 0 ∫ 1f ( t ) sin ( n ω1t ) dtT 1 t(2)指数形式的傅立叶级数+∞f ( t ) = ∑ F ( n ω1 )e jn ω1tn =其中复数频谱F n= F ( n ω1 ) = 1 ∫t 0 +T 1f ( t ) e − jn ω1t dt T 1 t 0F n =1( a n − jb n ) F − n = 1 ( a n + jb n ) 2 2由图 3-1 可知, f ( t ) 为奇函数,因而a 0 = a n = 04 Tb n = T ∫02= 2Eπ n4TE−2EEf (t ) sin ( n ω t ) dt =sin ( n ω t ) dt = cos ( n ω t = 1 − cos ( n π2T 1 ∫0 2 1 n t 1 n ) 1n = 2, 4,n = 1, 3,所以,三角形式的 FS 为2 E1 12π f ( t ) =sin ( ω1t ) +sin ( 3ω1t ) +sin ( 5ω1t ) +ω1 =π 3 5T指数形式的 FS 的系数为1n = 0, ±2, ±4,F n = − jb n jE=2 n = 0,−± 1, ±3,n π1所以,指数形式的 FS 为f ( t ) = − jE π ej ω1t+ πjE e − j ω1t − 3jE π e j 3ω1t + 3jEπ e − j 3ω1t +3-15 分析:半波余弦脉冲的表达式 f ( t ) =πτ E cos t u t+ τ 2求 f ( t ) 的傅立叶变换有如下两种方法。
信号与线性系统复习课用习题

第三、四章自测题解答一、 填空题:1、(1))(1t f 的参数为VA s T s 1,1,5.0===μμτ,则谱线间隔为__1000__kHz, 带宽为___2000__kHz 。
(2))(2t f 的参数为V A s T s 3,3,5.1===μμτ,则谱线间隔为___333__kHz, 带宽为_666__kHz 。
(3))(1t f 与)(2t f 的基波幅度之比为___1:3____。
(4))(1t f 的基波幅度与)(2t f 的三次谐波幅度之比为__1:1___。
2、由于周期锯齿脉冲信号的傅里叶级数的系数具有收敛性,因此,当k →∞时,k a =0。
3、信号x (t)的频带宽度为B ,x(2t)的频带宽度为 ,x(t/2)的频带宽度为 .3、根据尺度变化性质,可得x(2t)的频带宽度为2B ,可得x(t/2)的带宽为B/2。
6、设f (t)的傅里叶变换为)(ωj F ,则)(jt F 的傅里叶变换为2f ()πω-。
7、单个矩形脉冲的频谱宽度一般与其脉宽τ有关,τ越大,则频谱宽度 越窄 。
8、矩形脉冲通过RC 低通网络时,波形的前沿和后沿都将产生失真,这种失真的一个主要的原因是RC 低通网络不是理想低通滤波器,脉冲中的高频成分被削弱 。
9、为满足信号无失真,传输系统应该具有的特性(1)H(j )ω=;(2)h(t)= 。
9、(1)0j t Ke ω-(K 为常数),(2)0K (t-t )δ(0t 为常数) 10、已知某个因果连续时间LTI 系统的频率响应为H(j )ω,则该系统对输入信号tj t j e a e a E t x 0011)(ωω--++=的响应为 . 10、系统对输入信号t j t j e a e a E t x 0011)(ωω--++=的响应为)()()0()(010100ωωωωj H e a j H e a j EH t y t j t j -++=--。
信号与系统习题课(傅里叶变换

才有
F
(ω
)
=
(
1 jω
)2
F
⎡ d2
⎢ ⎣
dt
2
f
( t ) ⎤⎥
⎦
Signals and Systems, Tsinghua University
7
强调
由
F
⎡d ⎢⎣ dt
f
( t )⎤⎥⎦
= Φ(ω)
得到
F
⎡⎣
f
(t )⎤⎦
=
1 jω
Φ (ω )
实际上是引用了FT的积分性质.
因此要考虑 f (−∞) = 0
法二,频移
F(ω) = F0(ω +ω0)+ F(ω −ω0)
求出f0(t)后,
1 F0(ω)
ω
−ω1 0 ω1
[ ] f (t) = f0(t) ejωt +e−jωt =2f0(t)cosω0t
如何求f0S(igt)na?ls
and
定义、对称性、查表。
Systems, Tsinghua University
−2
−1
1
( ) ejω −e−jω ejω +e−jω − ej2ω +e−j2ω
=2
+
jω
ω2
= ......
(1)计算量大;(2)一些函数积分不收敛。
Signals and Systems, Tsinghua University
法二,利用FT的微积分性质
4 1 f(t)
思路:
f
(t
)
d
⎯⎯dt→δ
Φ(0) = 0
Signals and Systems, Tsinghua University
信号与系统课后习题答案

习 题 一 第一章习题解答基本练习题1-1 解 (a) 基频 =0f GCD (15,6)=3 Hz 。
因此,公共周期3110==f T s 。
(b) )30cos 10(cos 5.0)20cos()10cos()(t t t t t f ππππ+==基频 =0f GCD (5, 15)=5 Hz 。
因此,公共周期5110==f T s 。
(c) 由于两个分量的频率1ω=10π rad/s 、1ω=20 rad/s 的比值是无理数,因此无法找出公共周期。
所以是非周期的。
(d) 两个分量是同频率的,基频 =0f 1/π Hz 。
因此,公共周期π==01f T s 。
1-2 解 (a) 波形如图1-2(a)所示。
显然是功率信号。
t d t f TP T TT ⎰-∞→=2)(21lim16163611lim 22110=⎥⎦⎤⎢⎣⎡++=⎰⎰⎰∞→t d t d t d T T T W(b) 波形如图1.2(b)所示。
显然是能量信号。
3716112=⨯+⨯=E J (c) 能量信号 1.0101)(lim101025=-===⎰⎰∞∞---∞→T t ttT e dt edt eE J(d) 功率信号,显然有 1=P W1-3 解 周期T=7 ,一个周期的能量为 5624316=⨯+⨯=E J 信号的功率为 8756===T E P W 1-5 解 (a) )(4)2()23(2t tt δδ=+; (b) )5.2(5.0)5.2(5.0)25(5.733-=-=----t e t e t et tδδδ(c) )2(23)2()3sin()2()32sin(πδπδπππδπ+-=++-=++t t t t 题解图1-2(a) 21题解图1-2(b) 21(d) )3()3()(1)2(-=----t e t t et δδε。
1-6 解 (a) 5)3()94()3()4(2-=+-=+-⎰⎰∞∞-∞∞-dt t dt t t δδ(b) 0)4()4(632=+-⎰-dt t t δ(c) 2)]2(2)4(10[)]42(2)4()[6(63632=+++-=+++-⎰⎰--dt t t dt t t t δδδδ(d)3)3(3)(3sin )(1010=⋅=⎰⎰∞-∞-dt t Sa t dt ttt δδ。
【信号与系统(郑君里)课后答案】第三章习题解答

【信号与系统(郑君⾥)课后答案】第三章习题解答3-1 解题过程:(1)三⾓形式的傅⽴叶级数(Fourier Series ,以下简称 FS )f ( t ) = a ++∞cos ( n ω t) + b sin ( n ω t ) a 0 ∑ n 1n 1 n =1式中ω1 =2π,n 为正整数,T 1 为信号周期T 11 t +T(a )直流分量a 0 = 0 ∫ 1 f ( t ) dtT1 t2 t +T(b )余弦分量的幅度a n = 0∫ 1f ( t ) cos ( n ω1t ) dtT1 t 02 t +T(c )正弦分量的幅度b n = 0 ∫ 1f ( t ) sin ( n ω1t ) dtT 1 t(2)指数形式的傅⽴叶级数+∞f ( t ) = ∑ F ( n ω1 )e jn ω1tn == F ( n ω1 ) = 1 ∫t 0 +T 1f ( t ) e ? jn ω1t dt T 1 t 0F n =1( a n ? jb n ) F ? n = 1 ( a n + jb n ) 2 2由图 3-1 可知, f ( t ) 为奇函数,因⽽a 0 = a n = 0 4 Tb n = T ∫02= 2Eπ n4TE2EEf (t ) sin ( n ω t ) dt =sin ( n ω t ) dt = cos ( n ω t = 1 ? cos ( n π2T 1 ∫0 2 1 n t 1 n ) 1n = 2, 4,n = 1, 3,所以,三⾓形式的 FS 为2 E1 12π f ( t ) =sin ( ω1t ) +sin ( 3ω1t ) +sin ( 5ω1t ) +ω1 =π 3 5Tn = 0, ±2, ±4,F n = ? jb n jE=2 n = 0,± 1, ±3,n π1所以,指数形式的 FS 为f ( t ) = ? jE π ej ω1t+ πjE e ? j ω1t ? 3jE π e j 3ω1t + 3jEπ e ? j 3ω1t +3-15 分析:半波余弦脉冲的表达式 f ( t ) =πτ E cos t u t+ τ 2求 f ( t ) 的傅⽴叶变换有如下两种⽅法。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
ω0 , ω ω0 (3) F (ω) π 0, 其他
(2)F (ω) ε(ω ω0 ) ε(ω ω0 )
1 (4) F (ω) ( jω α ) 2
解: (1) 冲激函数的傅里叶变换有 δ(t ) 1
0 0 0 0
0
0
根据对称性,有 2πG (ω) 2ω Sa(ω t )
2 ω0 0 0
第13页
电气工程系平台课 《信号处理技术》
HITPEED
HIT_Prof. Liu X.S.
ω0 根据线性性质,即有 G2ω (ω) Sa(ω0t ) π 2 ω0 ω0 所以 F (ω) G2ω (ω) 的原函数是 f (t ) Sa(ω0t ) π π 1 1 1 (4) F (ω) 2 ( jω α ) jω α jω α
HITPEED
HIT_Prof. Liu X.S.
例9(3.17) 求
解 :令
ωτ 因有 Gτ (t ) τSa 2
sin 2πt sin 8πt 。 2πt 8πt sin 8πt sin 2πt f 2 (t ) f1 (t ) 8πt 2πt
,根据对称性,有
温馨提示:傅里叶变换频移性质
HITPEED
sin t 。求其傅里叶变换 F (ω) 。 例4 已知函数 f (t ) t
解: 根据常用函数——门信号的傅里叶变换,可知,
2
HIT_Prof. Liu X.S.
g2 (t ) 2Sa(ω)
根据傅里叶变换的线性性,有
1 Sa(ω) g 2 (t ) 2
第 2页
电气工程系平台课 《信号处理技术》
HITPEED
HIT_Prof. Liu X.S.
7. 熟练利用傅里叶变换对称特性、部分分时展开法
、傅里叶变换性质和常见变换对,求傅里叶反变 换。 8. 深刻理解频域系统函数H(ω)的定义、物理意义, 会求解并应用。 9. 掌握系统零状态响应、零输入响应和全响应的频 域求解方法;连续周期信号响应的频域分析方法 。 10.理解无失真传输系统级无失真传输条件; 11.了解抽样信号的频谱及其求解方法,理解抽样定 理。 12.了解调制与解调的基本定义域应用。 13.理解理想滤波器的定义、传输特性等。
根据傅里叶变换的对称性,有
2 ω 2πe 2 1 t 1 ω 2πe 2 1 t
电气工程系平台课 《信号处理技术》
根据傅里叶变换的线性性,有
温馨提示:傅里叶变换对称性质
第 6页
HITPEED
HIT_Prof. Liu X.S.
例3 已知函数 变换 F (ω) 。
f (t ) Ae
HITPEED
HIT_Prof. Liu X.S.
哈尔滨工业大学电气工程系专业技术基础课
第3章 连续时间信号与系统的频域分析 (习题课)
第 1页
电气工程系平台课 《信号处理技术》
HITPEED
HIT_Prof. Liu X.S.
本章学习重点
1. 了解函数正交的条件及完备正交函数集的概念。 2. 能用傅里叶级数的定义式、基本性质求解周期信
1 ε (t ) πδ(ω) jω
根据频域微分性质,有
d 1 jt ε (t ) πδ(ω) dω jω
即
1 tε(t ) jπδ(ω) 2 ω
第10页
电气工程系平台课 《信号处理技术》
温馨提示:频域微分和积分性质
HITPEED
HIT_Prof. Liu X.S.
2 T /2 2 τ /2 2Eτ a0 f t dt Edt T T / 2 T τ / 2 T
2 T /2 2 τ /2 an f t cos nω0tdt A cos nω0tdt T T / 2 T τ / 2 nω τ nω τ τ 2 2 sin 0 sin 0 2 A sin nω0t 2A 2 Aτ 2 2 nω0 τ T nω0 τ 2 T nω0 T 2 第 4页 温馨提示:傅里叶级数的定义
电气工程系平台课 《信号处理技术》
HITPEED
HIT_Prof. Liu X.S.
2 T /2 2 τ /2 2 Aτ a0 f t dt Adt T T / 2 T τ / 2 T
2 Aτ nω0 τ 2 Aτ nπτ an Sa( ) Sa T 2 T T
1 1 1 f ( t ) f ( t ) G ( ω ) G ( ω ) G4 π (ω) 根据卷积定理,有 1 2 4π 16 π 2 8 16 sin 2πt sin 8πt 1 1 1 4πSa(2πt ) Sa(2πt ) 取反变换,有 2πt 8πt 16 2π 8
n N
上式代入下式
a0 f t an cosnω0t 2 n1
Aτ 2 Aτ nπτ Sa cosnω0t 得 f t T n1 T T
第 5页
电气工程系平台课 《信号处理技术》
HITPEED
1 例2 已知函数 f (t ) ,求其傅里叶变换 F (ω) 。 2 1 t
HIT_Prof. Liu X.S.
解: 设 f 1 (t ) e a t , a 0
F1 (ω) f1 (t )e
jωt
则
at jωt
dt e e
t
0
dt 0 e e
at
jωt
令 a 1
2 则 e 2 1 ω
2a dt 2 2 a ω
0 0
因 e ε (t )
αt
1 jω α
根据卷积定理,有
f (t ) e αt ε(t ) e αt ε(t ) e ατ ε( τ )e α ( t τ ) ε(t τ )dτ 0e αt dτ teαt ε(t )
t
第14页
电气工程系平台课 《信号处理技术》
温馨提示:傅里叶反变换及性质
第12页
jt
电气工程系平台课 《信号处理技术》
HITPEED
HIT_Prof. Liu X.S.
根据线性性即有 ε (ω) 1 πδ(t ) 1
2
0
j 2πt
0
F (ω) ε(ω ω ) ε(ω ω ) 的原函数是 根据频移特性,
1 jω t 1 jω t f (t ) δ (t ) e δ (t ) e j 2πt j 2πt 1 jω t 1 jω t 2 j e e 2 j δ (t ) δ (t ) sin ω0t j 2πt 2j j 2πt 1 sin ω0t πt ω0 F ( ω ) G2ω (ω) (3) 门信号可以表示为 π ωτ 因有 Gτ (t ) τSa , τ 2ω0 即 G2 ω (t ) 2ω0 Sa(ωω0 ) 2
根据傅里叶变换的对称性,有
1 Sa(t ) 2π g 2 (ω) 2
根据傅里叶变换的卷积性质,有 2 1 sin t 2πg 2 (ω) 2πg 2 (ω) 2πg 2 (ω) g 2 (ω) 2π t
温馨提示:傅里叶变换卷积性质
第 8页
电气工程系平台课 《信号处理技术》
例7 某系统的微分方程为 y(t ) 2 y(t ) f (t ) t 求 f (t ) e ε(t ) 时的响应 y(t ) 。 解: 对微分方程两边取傅里叶变换,
,
jωY (ω) 2Y (ω) F (ω)
Y (ω) 1 则 H (ω) F (ω) jω 2
1 f (t ) 的傅里叶变换为 f (t ) e ε (t ) F (ω) jω 1
第15页
温馨提示:傅里叶变换卷积性质
电气工程系平台课 《信号处理技术》
HITPEED
HIT_Prof. Liu X.S.
例10(3.20) 设f(t)为限带信号,频带宽度为 ωM ,其 频谱F(ω)如图所示。 (1) 求f(2t), f(t/2)的带宽、奈奎斯特抽样频率 ΩN ,fN fN与奈奎斯特间隔TN。 (2) 设用抽样序列 δ (t ) δ(t nT ) 对信号f(t)进行抽样, 得抽样信号fs(t) ,求的频谱Fs(ω) ,画出频谱图。 (3)若用同一个δT(t)对f(2t), f(t/2)分别进行抽样,试画 出两个抽样信号fs(2t), fs (t/2)的频谱图。
3.
4. 5. 6.
号的频谱,会画频谱图,理解连续周期信号频谱 的特点,相位谱的作用。 能用傅里叶变换的定义式、基本性质求解非周期 信号的频谱,会画频谱图。 掌握常用周期信号的傅里叶变换和非周期信号的 傅里叶变换;理解周期信号与非周期信号之间的 关系。 熟练掌握傅里叶变换的性质,并会灵活应用。 理解功率信号与功率谱、能量信号与能量谱的概 念;
HITPEED
HIT_Prof. Liu X.S.
例5 已知函数 f (t ) 1 / t 2 。求其傅里叶变换 F (ω) 。 解: 根据常用函数——符号函数的傅里叶变换,可知 2 2 sgn(t ) 根据对称性,有 jt 2π sgn(ω) jω 根据傅里叶变换的线性性,有
根据时域微分性质,有
第 3页
电气工程系平台课 《信号处理技术》
HITPEED
HIT_Prof. Liu X.S.
例1 将下图的周期 矩形脉冲信号展开为三角函数形式 的傅里叶级数。
解:该信号为偶函数, 三角形式的傅里叶级数 无正弦项,只有直流和 余弦分量,为
