静定梁习题
重点_结构力学复习题

《结构力学I》期末复习题1.试画出图示静定梁的弯矩图和剪力图。
Pa aaa a2.试画出图示刚架的弯矩图、剪力图和轴力图。
各杆长均为l。
DA C4kN/mB10kNDC48m34kN/m3.试求图示桁架各指定杆的轴力。
已知F= 30kN。
三、静定结构的位移计算1.用图乘法计算图示荷载作用下外伸梁C点的竖向位移Δcy。
3×4=12m3F2313m3m4bacFF2×2=4m2×3=6m2F 3Fbac4m4×3=12m2.试画出 图示结构的弯距图。
并求C 点的水平位移和D 点转角。
已知三杆长均为l ,EI 为常数。
3.试绘制图示静定结构的弯矩图,并求A 点的垂直位移和B 点转角。
已知三杆长均为3m 。
各杆EI 均为10000kNm 2。
4.试绘制图示静定结构的弯矩图,并求A 点的垂直位移。
各杆EI 均为5000kNm 2。
5kN四.力法1.试用力法计算图示结构,绘制弯矩图。
已知二杆长均为l,EI为常数。
q2.试用力法计算图示结构,绘制弯矩图。
已知两杆长均为l,EI为常数。
3.试用力法计算图示结构,绘制弯矩图。
已知三杆长均为l,EI为常数。
4.用力法计算并作图示结构M图。
已知二杆长均为l,E I= 常数。
五、位移法1.建立图示结构的方程,求出方程的系数和自由项。
已知三杆长均为l,EI为常数。
2.试用位移法计算图示结构,绘制弯矩图。
已知两杆长均为l,EI为常数。
q3.试用位移法计算图示结构,绘制弯矩图。
已知三杆长均为6米 ,EI 为常数。
4. 位移法作图示刚架的M 图(EI﹦常数)。
5.试 用 最 简 捷 的 方 法 求 图 示 结 构 的 弯 矩 图 , 各 杆 的 长 度 l 均 相同 。
PEIEIEIEI EI 1=ACBD12kN/m6.用位移法作图示结构M 图,EI 常数。
l /2l /2六.力矩分配法1.试用力矩分配法计算图示连续梁,绘制弯矩图。
EI 为常数。
03静定梁

3 静定梁
3kN m
A
【例3.4】作图示伸臂梁的弯矩图。 【解】 (1)计算控制截面弯矩
M A 3kN m (上侧受拉)
4kN
C B
1kN/m
D
2.5m
3
(5)
2.5m
2
2m
M B 1 2 1 2kN m
(上侧受拉)
(0.5) 0.5
MD 0
(2)用分段叠加法作弯矩图
6 16 m) M (kN·
结构力学电子教程
3 静定梁
4kN m
【例】试求图示梁的弯矩图。 【解】 1、求支反力
RA 11kN( ) RD 23kN( )
10kN
B C
5kN/m
D E
4kN
A
2m
RA 11kN
4
2m
4m
2m
RD 23kN
8
2、定弯矩值
M A 4kN m (下侧受拉)
求支座反力:
ql M A 0, VB 2 ql M B 0, VA 2 X 0, H A 0
求内力:
结构力学电子教程
3 静定梁
结构力学电子教程
3 静定梁
1. 静定多跨梁的组成 承载的部分。
附属部分--不能独 立承载的部分。
3.4 静定多跨梁约束力计算与几何组成 基本部分--能独立
A
2.5
m) M (kN·
4kN
C
B
1kN/m
B D
1 M 4 5 5kN m 4
1 M 1 22 8 0.5kN m
结构力学电子教程
3 静定梁
16kN
工程力学习题集(二)
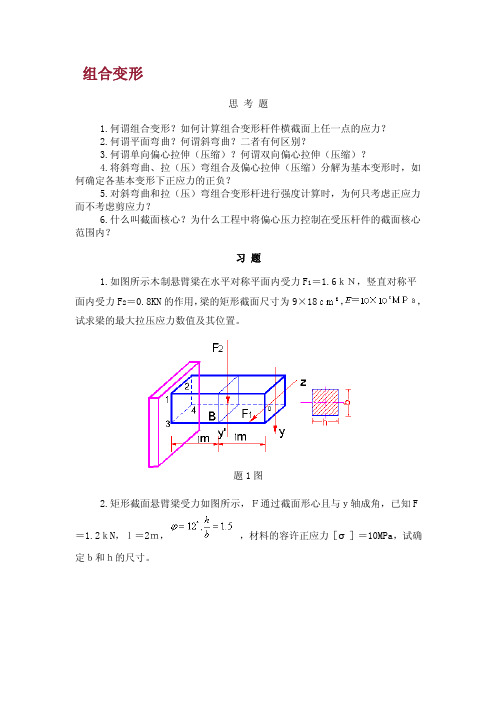
组合变形思考题1.何谓组合变形?如何计算组合变形杆件横截面上任一点的应力?2.何谓平面弯曲?何谓斜弯曲?二者有何区别?3.何谓单向偏心拉伸(压缩)?何谓双向偏心拉伸(压缩)?4.将斜弯曲、拉(压)弯组合及偏心拉伸(压缩)分解为基本变形时,如何确定各基本变形下正应力的正负?5.对斜弯曲和拉(压)弯组合变形杆进行强度计算时,为何只考虑正应力而不考虑剪应力?6.什么叫截面核心?为什么工程中将偏心压力控制在受压杆件的截面核心范围内?习题1.如图所示木制悬臂梁在水平对称平面内受力F1=1.6kN,竖直对称平面内受力F2=0.8KN的作用,梁的矩形截面尺寸为9×18,,试求梁的最大拉压应力数值及其位置。
题1图2.矩形截面悬臂梁受力如图所示,F通过截面形心且与y轴成角,已知F =1.2kN,l=2m,,材料的容许正应力[σ]=10MPa,试确定b和h的尺寸。
题2图3.承受均布荷载作用的矩形截面简支梁如图所示,q与y轴成角且通过形心,已知l=4m,b=10cm,h=15cm,材料的容许应力[σ]=10MPa,试求梁能承受的最大分布荷载。
题3图4.如图所示斜梁横截面为正方形,a=10cm,F=3kN作用在梁纵向对称平面内且为铅垂方向,试求斜梁最大拉压应力大小及其位置。
题4图5.柱截面为正方形,边长为a,顶端受轴向压力F作用,在右侧中部挖一个槽(如图),槽深。
求开槽前后柱内的最大压应力值。
题5图6.砖墙及其基础截面如图,设在1m长的墙上有偏心力F=40kN的作用,试求截面1-1和2-2上的应力分布图。
题6图7.矩形截面偏心受拉木杆,偏心力F=160kN,e=5cm,[σ]=10MPa,矩形截面宽度b=16cm,试确定木杆的截面高度h。
题7图8.一混凝土重力坝,坝高H=30m,底宽B=19m,受水压力和自重作用。
已知坝前水深H=30m,坝体材料容重,许用应力[]=10MPa,坝体底面不允许出现拉应力,试校核该截面正应力强度。
结构力学习题及答案(武汉大学)

结构力学习题第2章平面体系的几何组成分析2-1~2-6 试确定图示体系的计算自由度。
题2-1图题2-2图题2-3图题2-4图题2-5图题2-6图2-7~2-15 试对图示体系进行几何组成分析。
若是具有多余约束的几何不变体系,则需指明多余约束的数目。
题2-7图题2-8图题2-9图题2-10图题2-11图题2-12图题2-13图题2-14图题2-15图题2-16图题2-17图题2-18图题2-19图题2-20图题2-21图2-1 1=W 2-1 9-=W 2-3 3-=W 2-4 2-=W 2-5 1-=W 2-6 4-=W2-7、2-8、2-12、2-16、2-17无多余约束的几何不变体系 2-9、2-10、2-15具有一个多余约束的几何不变体系 2-11具有六个多余约束的几何不变体系2-13、2-14几何可变体系为2-18、2-19 瞬变体系2-20、2-21具有三个多余约束的几何不变体系第3章静定梁和静定平面刚架的内力分析3-1 试作图示静定梁的内力图。
(a)(b)(c) (d)习题3-1图3-2 试作图示多跨静定梁的内力图。
(a)(b)(c)习题3-2图3-3~3-9 试作图示静定刚架的内力图。
习题3-3图习题3-4图习题3-5图习题3-6图习题3-7图习题3-8图习题3-9图3-10 试判断图示静定结构的弯矩图是否正确。
(a)(b)(c) (d)部分习题答案3-1 (a )m kN M B ⋅=80(上侧受拉),kN F RQB 60=,kN F L QB 60-=(b )m kN M A ⋅=20(上侧受拉),m kN M B ⋅=40(上侧受拉),kN F RQA 5.32=,kN F L QA 20-=,kN F LQB 5.47-=,kN F R QB 20=(c) 4Fl M C =(下侧受拉),θcos 2F F L QC =3-2 (a) 0=E M ,m kN M F ⋅-=40(上侧受拉),m kN M B ⋅-=120(上侧受拉)(b )m kN M RH ⋅-=15(上侧受拉),m kN M E ⋅=25.11(下侧受拉)(c )m kN M G ⋅=29(下侧受拉),m kN M D ⋅-=5.8(上侧受拉),m kN M H ⋅=15(下侧受拉) 3-3 m kN M CB ⋅=10(左侧受拉),m kN M DF ⋅=8(上侧受拉),m kN M DE ⋅=20(右侧受拉) 3-4 m kN M BA ⋅=120(左侧受拉)3-5 m kN M F ⋅=40(左侧受拉),m kN M DC ⋅=160(上侧受拉),m kN M EB ⋅=80(右侧受拉)3-6 m kN M BA ⋅=60(右侧受拉),m kN M BD ⋅=45(上侧受拉),kN F QBD 46.28=3-7 m kN M C ⋅=70下(左侧受拉),m kN M DE ⋅=150(上侧受拉),m kN M EB ⋅=70(右侧受拉) 3-8 m kN M CB ⋅=36.0(上侧受拉),m kN M BA ⋅=36.0(右侧受拉) 3-9 m kN M AB ⋅=10(左侧受拉),m kN M BC ⋅=10(上侧受拉) 3-10 (a )错误 (b )错误 (c )错误 (d )正确第4章 静定平面桁架和组合结构的内力分析4-1 试判别习题4-1图所示桁架中的零杆。
结构力学--超静定问题典型习题解析

3
代入变形协调方程 wB = wC + ∆BC ,得
3 F a3 F a q(2a )4 FN (2a ) − = N + N 8EI 3EI 3EI EA
解得 FN =
2 qa 2 qa 3 A = 2 1 3a A + I 3+ 2 Aa
4
图示梁的右端为弹性转动约束,设弹簧常量为 k。AB 段可视为刚性,并与梁刚性连接。
()
3 结构如图示,设梁 AB 和 CD 的弯曲刚度 EI 相同。拉杆 BC 的拉压刚度 EA 已知,求拉杆 BC 的轴力。
C
a q A 2a B FN FN B FN C a FN a D a D
解题分析:将杆 CB 移除,则 AB、CD 均为静 定结构。杆 CB 的未知轴力 FN 作用在 AB,CD 梁上。为一度静不定问题。 解: 1、写出变形协调方程
2⎡
2
=
FR 3 EI
⎛ 3π 2 − 8 π − 4 ⎞ ⎜ ⎟ ⎜ ⎟ 8π ⎝ ⎠
6 结构如图 a 所示, AC = AD = BC = BD = a ,已知各杆弯曲刚度 EI 相同。A、B 点为刚 性连接,C、D 点为铰连接。将 C、D 点用一弹簧相连,弹簧常数为 2k。但由于弹簧短了 ∆ , 强行相连后,在 A、B 点加力 F。试问:当 F 为多大时,弹簧回复到其原长?
C
D
A
B
A
B
(c-1) 题 1 图(c)
1
(c-2)
大家论坛
(d) 解:图示结构为一封闭的圆圈,在任意截面截开后,有三个未知内力分量,故为三 度静不定。沿对称轴将圆环截开,由于对称性,轴力等于
F ,剪力等于零,只剩 2
静力学习题课答案

【1】 梁AB 一端为固定端支座,另一端无约束,这样的梁称为悬臂梁。
它承受均布荷载q 和一集中力P 的作用,如图4-9(a )所示。
已知P =10kN , q =2kN/m ,l =4m ,︒=45α,梁的自重不计,求支座A 的反力。
【解】:取梁AB 为研究对象,其受力图如图4-9(b )所示。
支座反力的指向是假定的,梁上所受的荷载和支座反力组成平面一般力系。
在计算中可将线荷载q 用作用其中心的集中力2qlQ =来代替。
选取坐标系,列平衡方程。
)(kN 07.7707.010cos 0cos - 0A A →=⨯====∑ααP X P X X)(kN 07.11707.010242sin 2 0sin 2 0A A ↑=⨯+⨯=+==--=∑ααP ql Y P qlY Y )( m kN 28.404707.0108423sin 83 0sin 422ql 022A A ⋅=⨯⨯+⨯⨯=⋅+==⋅-⎪⎭⎫⎝⎛+-=∑l P ql m l P l l m M A αα力系既然平衡,则力系中各力在任一轴上的投影代数和必然等于零,力系中各力对任一点之矩的代数和也必然为零。
因此,我们可以列出其它的平衡方程,用来校核计算有无错误。
校核028.40407.114424242A A B =+⨯-⨯⨯=+⋅-⨯=∑m l Y l ql M 可见,Y A 和m A 计算无误。
【2】 钢筋混凝土刚架,所受荷载及支承情况如图4-12(a )所示。
已知kN 20 m,kN 2 kN,10 kN/m,4=⋅===Q m P q ,试求支座处的反力。
【解】:取刚架为研究对象,画其受力图如图4-12(b )所示,图中各支座反力指向都是假设的。
本题有一个力偶荷载,由于力偶在任一轴上投影为零,故写投影方程时不必考虑力偶,由于力偶对平面内任一点的矩都等于力偶矩,故写力矩方程时,可直接将力偶矩m 列入。
设坐标系如图4-12(b )所示,列三个平衡方程)(kN 3446106 06 0A A ←-=⨯--=--==++=∑q P X q P X X)(kN 296418220310461834 036346 0B B A ↑=⨯++⨯+⨯=+++==⨯--⨯-⨯-⨯=∑q m Q P Y q m Q P Y M)(kN 92920 00B A B A ↓-=-=-==-+=∑Y Q Y Q Y Y Y校核3462203102)9(6)34(6363266 C=⨯⨯+-⨯+⨯+-⨯--⨯=⨯+-++-=∑qmQPYXMAA说明计算无误。
结构力学 静定梁与静定刚架习题

M BC 2kNm
3、取AB为研究对象
MBA
或 取B节点为研究对象
2 kNm 2 kNm MBA
MBA=0
-4 kN
练习题
2
M
2
B
A 2m 1m
D
2m L P L L L L L
P
练习题
L
P L
P
L
P L
练习题
C
1kN/m
VC A VA 4m D
3、取AD为研究对象 B 4m
4m
VA
MDA VDA
3 kNm
3、取BCD为研究对象
2 kN
B
A 2m
C
D
1m
1m
MBC
1m
MBC= -1 kNm,上侧 1
MBA
1、取整体为研究对象
VC=4 kN
HA=2 kN 2、取AB为研究对象 MBA= - 2 kNm ,右侧受拉
B
2 A
C
D
练习题 2kN/m
C
8kN
20kNm 2m
3、BC为悬臂部分 MBC= 4 kNm,左侧
20 kN/m
4m
VB
MCB
MCD=90
MCF=135
VF
3.基本部分的计算,为悬臂杆。
VB=135
ME=135×3=405 kNm,左侧受拉
4. 作出弯矩图。
90 90
405
135
45
[习题3] 作弯矩图,剪力图,轴力图。
1.取整体为研究对象, ∑MA=0 ,VC×94×5-2×5×2.5=0 , 解得VC= 5 kN , ∑Y=0,VA=5 kN ∑X=0,HA=8 kN 8 kN 4 kN 2 kN/m HA VA VC
结构力学第三章习题参考解答

FAy 6 FAx 2 0
1 ql 2A
1 ql 4
取整体:M A 0
Fy 0
取AC: MC 0
取整体: Fx 0
l
l
0.45ql
FBy
1 2l
ql 3l 2
3 ql 4
FAy
ql
3 4
ql
1 4
ql
FAx
2 ql 2 l4
1 ql 2
FBx
1 ql 2
l 2
1 ql B2 3 ql 4
取左段
FNK
ql cos
3l 4
1 q 3 l 2 2 4
9 ql 2 32
D
C
q
3 ql
4
A
1 ql
l
4
1 ql
4
1 ql 4
3 ql
4
FQ KN
1 ql 2
E
4
1 ql 2 4
9 ql2 32
1 ql
B
4
ql 2 8
M KNm
l
1 ql
4
1 ql
4
1 ql
4
FN KN
1 ql2 4
1 ql 4
3-12解:
q C
q
3 ql
4
A
l
1 ql
B
4
Fy 0
FAy
1 ql 4
1 ql 4
l
l
1 ql
4
取BC:
MC 0
FBx
1 4
ql
取整体:
Fx 0
FAx
ql
1 ql 4
3 ql 4
AD段的最大弯矩 M x 3 qlx 1 qx2 dM 3 ql qx 0
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
0
D
10kN
E
15kN
结构力学电子教程
10kN
5kN/m
A B
3 静定梁
20kN m
C F
10kN
D E
2m
2m
2m
2m
2m
2m
0
2m
20kN m
10kN
0
5kN/m
A 25kN
(2.5)
5kN F
C B 10kN 12
5kN
0
30kN.m
D
3、作弯矩图
20 m) M (kN·
10kN 15kN
2m
6 Q (kN) 38 18 6 m) M (kN·
结构力学电子教程
3 静定梁
10kN m
C
3.4
4kN m
A
2kN/m
8kN
D B
2m
2m
YB 8.75kN
【解】
YA 7.25kN
7.25
0.75
Q (kN) 8.75 m) M (kN·
3.625m
4
9.14 9 19 17.5
30
E
7.5 A B 10 C F
10 D E
4、作剪力图
Q
(kN) 10
15
5
10
A
B
5
C
F
D
15
E
结构力学电子教程
3 静定梁
3.28 根据静定多跨梁的受力特点和荷载与内力微分关系,直 接画出M图。 P
B A C D E
F
【解】
a
a
a
Pa
a
a
a
Pa
a
B
A
C
D Pa
E
结构力学电子教程
3 静定梁
结构力学(第二版)
结构力学电子教程
3 静定梁
本章小结
基本内容是静定单跨梁和多跨梁的支座反力、内力的计算 及内力图的绘制。学习时应强调多做练习,提高熟练程度。 要点如下: (1)计算步骤:支座反力、内力、内力图。 对静定多跨梁,要注意其几何组成特点,求支座反力的次 序应与组成次序相反。 (2)截面内力有弯矩、剪力、轴力;应注意其定义及正负 号规定。 (3)计算截面内力的基本方法是截面法。在此基础上,也 应能熟练地列出截面法算式,直接计算截面内力。 (4)绘制弯矩图的基本方法是分段叠加法。 (5)内力图的纵坐标垂直于杆轴线。弯矩图画在杆件受拉 纤维一侧,不注正负号;剪力图和轴力图注明正负号。
A
4 D C
结构力学电子教程
q
3 静定梁 【解】
RB 1.6q
3m
3.24 试作斜梁的内力图,并计算C、D截面的内力值。 (b)
B
M
(1)求支反力
A
0: q 4 2 RB 5 0
RB 1.6q
C
D A
0.96q
XA
x
1m 1m
3 X 0 : X R 0 A B 5
ND 1.2q
QD 0
Q 0.96q 0.6 2.72q 0.8 qx 0.8 1.6q 0.8qx
M 0.96q 0.75x 2.72qx qx 0.5x 2qx 0.5qx2
M C 1.5q
M D 2q
结构力学电子教程
结构力学电子教程
3 静定梁
10kN
A C B E
3.20 用分段叠加法作图示梁的弯矩图,并计算C点的弯矩值。
2kN/m
D
3kN
2m
2m
4
(10)
2m
6
2m
【解】
∴MC=5kN· m
m) M (kN·
3.22 【解】
5
2kN A
D
2kN/m
B C
2m2m(4)2m Nhomakorabea28
12
B
∴MC=-12kN· m
m) M (kN·
包世华 主编
结构力学电子教程
3 静定梁
Pl / 2
Pl / 4
3.1 用叠加法作图示单跨静定梁的弯矩图。 (a)
A C l/2 l/2 P B Pl/4 M
Pl / 4
【解】
Pl / 4
A C
B
Pl/4
P A C B
Pl / 2
结构力学电子教程
3 静定梁
3.2 作图示单跨梁的M图与Q图。 (a)
40
Q
(kN) 40 40
(40) (40)
92.5 80
m) M (kN· 55 70 130 65
结构力学电子教程
3 静定梁
课外作业
P39-41
第一次 3.20, 3.22
第二次 3.25, 3.26
建议尽量多作章后各习题。
结构力学电子教程
3 静定梁
3.1~3.6 绘制静定单跨梁或柱的弯矩图和剪力图。 3.2
MA
38kN m
A
4kN
3kN/m
B D
C
【解】
2m
YA 10kN
10
2m
20kN m
F
10kN
D E
【解】
2m
10kN
2m
5kN/m
A
2m
2m
2m
F
2m
2m
10kN
D E
20kN m
B
1、画层叠图
C
10kN
5kN/m
A B C
20kN m
F
10kN
D E
2、求支反力
10kN
0
20kN m
0
5kN 30kN.m
5kN/m
A 25kN
5kN F
C B 10kN
q
3 静定梁
(4)绘内力图
B
RB 1.6q
C
D A 3m
N
1m
(m)
XA 1m 0.96q YA 2.72q
2m
M (m2)
Q
(m)
结构力学电子教程
20kN
3 静定梁
2kN/m
B C D E F
3.25 计算静定多跨梁的支座反力,并画出梁的内力图。
A
【解】 1、画层叠图
3m
3m
1.5m
X A 0.96q
2m
YA 2.72q
Y 0: Y
4 RB q 4 0 5 YA 2.72q
A
(2)求内力方程
N 0.96q 0.8 2.72q 0.6 qx 0.6 2.4q 0.6qx
(3)C、D截面的内力
NC 1.8q QC 0.8q
20kN
0
A 9.28kN
C 13.61kN
4.32
12
3、作弯矩图
m) M (kN· A
B
C 5.78
D E 4
F
4、作剪力图
A (kN)
27.84 9.28
B C 2.89 D E 10.72 7.11 8 F 4
Q
结构力学电子教程
3 静定梁
10kN
5kN/m
A B C
3.26 计算静定多跨梁的支座反力,并画出梁的内力图。
8kN m
A C D E
4kN
4kN
2kN/m
B
【解】
VA 8kN
8
2m
2m
2m
VB 8kN
4
Q (kN) 8 8
8 9 16 16
m) M (kN·
结构力学电子教程
3 静定梁
20kN/m 60kN m
D B
(c)
40kN
E
【解】
C
A
2m
VA 101.5kN
67.5
2m
VB 132.5kN
2m
2.5m
2m
2kN/m
4m
2kN/m
20kN
B A C
F
D
E
2kN/m
0
F
2、求支反力
20kN
0
A 9.28kN
0
2.89kN
B
C 13.61kN D
2kN/m
E 15.11kN
4kN
4kN
结构力学电子教程
3 静定梁
2kN/m
0 0
2kN/m 2.89kN
B D E 15.11kN
F
4kN
4kN
