金属热防护系统多层隔热材料的稳态传热分析
传热过程中稳态与非稳态的传热性能研究

传热过程中稳态与非稳态的传热性能研究热传导是物体内部或物体之间通过分子间碰撞来传递热量的过程。
在传热过程中,往往会涉及到稳态和非稳态传热性能的研究。
稳态传热是指系统内部的温度分布和热流密度保持不变的传热过程,而非稳态传热则是指系统内部的温度分布和热流密度随时间变化的传热过程。
本文将探讨传热过程中稳态与非稳态的传热性能研究。
一、传热过程中的稳态传热性能研究稳态传热是热传导的一种重要情况,其特点是温度分布和热流密度在系统内部保持不变。
在稳态传热过程中,可以通过一系列的实验和数学模型来研究传热性能。
1. 实验方法稳态传热性能的研究通常需要通过实验来获得数据。
实验中需要测量物体的温度和热流密度等参数,并利用传热方程来计算传热速率。
同时,还可以进行不同条件下的对比实验,以研究传热性能随温度差、材料特性等因素的变化。
2. 数学模型在稳态传热性能研究中,数学模型起到了重要作用。
通过分析热传导方程、输运方程以及边界条件等,可以建立物体的温度分布模型,从而计算热流密度和传热速率。
常见的数学方法包括有限元法、有限差分法等,这些方法可以通过计算机模拟和数值计算来得到稳态传热性能的结果。
二、传热过程中的非稳态传热性能研究非稳态传热是热传导的另一种情况,其特点是温度分布和热流密度随时间变化。
非稳态传热性能的研究对于理解瞬态过程、优化传热设备等具有重要意义。
1. 实验方法对于非稳态传热性能的研究,实验方法同样起到了关键作用。
实验中需要测量物体的温度随时间的变化,并利用实验得到的数据建立传热模型。
此外,还可以通过改变传热边界条件、加热方式等来研究传热性能的变化。
2. 数学模型非稳态传热性能的研究同样离不开数学模型的建立。
根据热传导方程和边界条件,可以建立非稳态传热模型。
此外,还可以利用转换方法将非稳态问题转化为稳态问题进行求解。
例如,可以采用拉普拉斯变换等数学方法来分析非稳态传热性能。
三、稳态与非稳态传热性能的比较与应用稳态传热性能和非稳态传热性能在实际应用中都具有重要意义。
多层隔热装备的热防护性能与优化设计
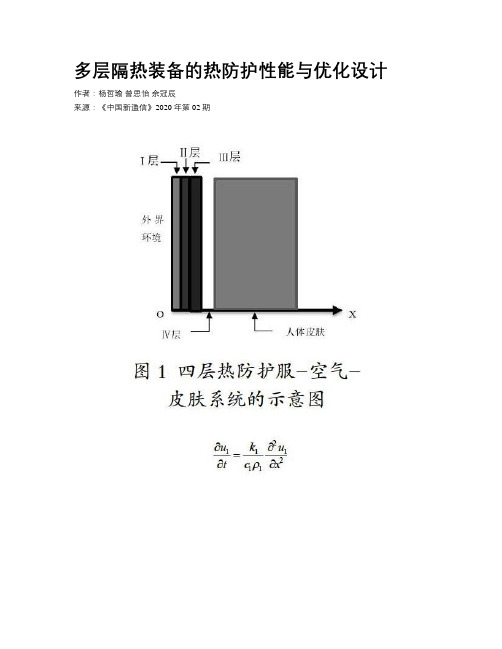
多层隔热装备的热防护性能与优化设计作者:杨哲瑜曾思怡余冠辰来源:《中国新通信》2020年第02期摘要:本文建立了热防护服的四层热传导模型,利用古典显式差分法对工况1进行MATLAB求解,研究其热防护性能;同时采用粒子群算法对工况2下防护服的厚度进行优化设计。
研究得到工况1下各层的温度分布并绘制温度分布图,工况2下防护服第三层的最优厚度。
本文研究内容对于热防护服的设计具有一定借鉴意义。
关键词:热传导模型;古典显式差分法;粒子群优化算法一、引言近年来,森林火灾发生频率激增,不断吞噬消防员的生命,因此对于高温作业下热防护服的优化设计显得尤为重要。
关于热防护服的设计,国内外许多的学者做了大量的研究。
不同于以往研究,本文主要用假人的体温变化来研究在特定边界条件下防护服的的热防护性能,利用有限差分法求解抛物型偏微分方程并得到温度分布三维图;采用粒子群算法优化算法来计算体温条件下的 II 层的最优厚度。
二、工况设定与模型建立2.1 工况设定本文工况测试选取专业服装材料及假人皮肤外侧温度变化。
专用服装通常由三层织物材料构成,记为第 I、II、III 层,其中 I 层与外界环境接触,III 层与皮肤之间存在空隙,将此空隙记为 IV 层。
工况 1:对环境温度为 75ºC、人体温度 37ºC、第 II 层厚度为 6mm、IV 层厚度为 5mm、工作时间为 90 分钟的情形开展实验,得到假人皮肤外侧的温度。
工况 2:当环境温度为 65ºC、IV 层的厚度为 5.5mm,假人皮肤外侧温度不超过 47ºC,且超过 44ºC 的时间不超过 5 分钟。
2.2 模型设定2.2.1 熱传导模型的建立首先建立四层热防护服-空气-皮肤系统的示意图如下:现在要模拟热量通过高温作业服的过程。
参考一维热传导方程的推导,可得Ⅰ层织物的热传导方程为:同理,将上式推广到i 层织物材料,得到各层的热传导方程:我们设定:相邻两层材料之间,左侧材料的右底面与右侧材料的左底面温度相等。
多层热防护结构烧蚀传热模型研究

2021年第1期 导 弹 与 航 天 运 载 技 术 No.1 2021 总第378期 MISSILES AND SPACE VEHICLES Sum No.378收稿日期:2020-11-20;修回日期:2020-12-14 基金项目:国家自然科学基金(11902364)文章编号:1004-7182(2021)01-0024-05 DOI :10.7654/j.issn.1004-7182.20210105多层热防护结构烧蚀传热模型研究丁 晨,牛智玲,单亦姣,张子骏,王 尧(中国运载火箭技术研究院,北京,100076)摘要:多层热防护结构由防热层与隔热层等多层热防护材料组成,在气动热作用下存在复杂的烧蚀与传热过程。
为准确预示多层热防护结构温度响应特性,建立了气动热环境下防热材料烧蚀模型,提出了烧蚀导致的变厚度多层结构传热数值计算方法,研究了气动热环境下多层热防护结构温度分布随时间变化规律,分析了多层热防护结构厚度分布对防热效果的影响。
研究表明,提出的模型能准确预示多层热防护结构烧蚀与传热过程,热量传导至承力结构后,隔热层内温度梯度大于防热层内温度梯度,在满足隔热层温度、烧蚀裕度以及工艺要求前提下,增大隔热层厚度能提高热防护性能。
关键词:热防护;烧蚀;多层热防护结构中图分类号:TB332 文献标识码:AHeat Transfer and Ablation Model for Multi-layer Thermal Protection SystemDing Chen, Niu Zhi-ling, Shan Yi-jiao, Zhang Zi-jun, Wang Yao(China Academy of Launch Vehicle Technology, Beijing, 100076)Abstract: Multi-layer thermal protection system is consisting of thermal protection layer and thermal insulation layer. Thereexists complex process of ablation and heat transfer under the effect of aerodynamic heating. In order to predict the temperature response for the multi-layer thermal protection system, the ablation model and the thermal conduction model for variable thickness caused by the ablation were proposed. Moreover, the temperature response for the multi-layer thermal protection system and the effect of the thickness distribution for different layers were discussed. It shows that the developed model can predict the ablation process and the heat transfer. As the heat is transferred to the structure, the temperature gradient in the insulation layer is higher than that in the thermal protection layer, and increasing the thickness of insulation layer can improve the thermal performance of the thermal protection system under the premise of temperature requirements, ablation margin and the technical requirements.Key words: thermal protection; ablation; multi-layer thermal protection structure0 引 言航天飞行器在大气层内长时间高速飞行时,飞行器表面与大气剧烈摩擦,形成了对飞行器严重的气动加热与气流剪切力,可能导致结构性能下降、设备功能失效,影响飞行器可靠性与安全性,甚至导致飞行失利。
多孔金属材料的高效隔热性能分析与优化

多孔金属材料的高效隔热性能分析与优化概述多孔金属材料被广泛应用于航空航天、汽车、能源等领域,其独特的结构和特性使其具备较好的隔热性能。
本文将对多孔金属材料的隔热性能进行分析与优化,探究其在工程上的应用潜力。
1. 多孔金属材料的热传导机制多孔金属材料的隔热性能取决于其热传导机制。
主要包括固体导热、辐射传热和对流传热。
固体导热是指热能通过金属材料固体颗粒之间的接触面传递。
辐射传热是指由于材料自身温度导致的辐射传热效应。
对流传热是指通过气体或液体流动导致的热能传递。
了解多孔金属材料的热传导机制是分析其隔热性能的基础。
2. 多孔金属材料的隔热性能测试方法为了准确评估多孔金属材料的隔热性能,我们需要合适的测试方法。
常用的方法包括热导率测试、热阻测试和热模拟分析。
热导率测试可以测量多孔金属材料的热导率,从而评估其热传导能力。
热阻测试可以测量多孔金属材料的热阻,即热能通过材料的能力。
热模拟分析通过建立数值模型,模拟多孔金属材料在实际工况下的热传导情况,为优化设计提供依据。
3. 多孔金属材料的隔热性能优化方法为了提高多孔金属材料的隔热性能,可以采用以下优化方法。
首先,优化多孔金属材料的孔隙率和孔径分布,可以控制材料的导热路径,降低热传导效率。
其次,可以设计导热屏障,例如在多孔金属材料的孔隙内填充绝热层,以阻止热能传递。
还可以改变多孔金属材料的表面形态,增加表面散热面积,促进辐射传热。
此外,引入气体或液体介质,通过对流传热来增强隔热效果。
通过优化多孔金属材料的结构和表面特性,可以显著提高其隔热性能。
4. 多孔金属材料在工程应用中的潜力多孔金属材料在航空航天、汽车、能源等领域具有广阔的应用潜力。
在航空航天领域,多孔金属材料的轻质高强性和隔热优势,可以应用于发动机的隔热罩和热交换器等部件中。
在汽车领域,多孔金属材料可以用于车辆的隔热垫和排气系统的隔热罩等部件中,提高车辆的燃油效率和节能性能。
在能源领域,多孔金属材料可以应用于太阳能电池板的隔热层,提高能量转化效率。
隔热层材料性能优化设计与热保护分析

隔热层材料性能优化设计与热保护分析随着科技的进步和空间探索的不断深入,隔热层材料的性能优化设计和热保护分析成为了航天工程中的重要问题。
隔热层材料的作用是在高温环境中减少传热,从而保护航天器的结构和仪器设备。
本文将探讨隔热层材料性能的优化设计以及热保护分析的相关内容。
一、隔热层材料性能的优化设计隔热层材料的性能设计需要综合考虑多个因素,包括传导热阻、辐射反射率、质量和耐久性等。
在传导热阻方面,降低热传导是减少传热的有效手段。
可以通过选择导热系数低的材料、增加材料的厚度或者设计多层隔热层来降低热传导。
而辐射反射率则影响材料对太阳辐射的吸收能力,因此优化设计中需要选用辐射反射率高的材料。
此外,材料的质量和耐久性也是优化设计的关键考虑因素。
二、隔热层材料的热保护分析隔热层材料的热保护分析是在航天器进入大气层时的重要工作。
当航天器从太空进入大气层时,由于高速运动和摩擦产生的热量,会使航天器表面温度迅速升高。
因此,热保护分析旨在确定隔热层材料在高温环境下的热响应和热保护性能。
在热保护分析中,首先需要对进入大气层时的热流密度进行计算和预测。
然后,根据航天器的热保护需求,选择合适的隔热材料和结构。
接下来,通过数值模拟和实验测试,评估所选材料在高温环境下的热响应和保护性能。
最后,根据分析结果对隔热层材料进行改进和优化。
三、隔热层材料的应用案例隔热层材料在航天工程中的应用非常广泛。
例如,热防护涂层是一种常见的隔热层材料,可以应用于航天器表面。
这种涂层一般由陶瓷颗粒、金属氧化物和聚合物等组成,具有优异的隔热性能和辐射反射能力。
此外,陶瓷纤维、泡沫材料和多层膜结构等也是常见的隔热层材料。
隔热层材料的性能优化设计和热保护分析在火星探测任务中发挥了重要作用。
由于火星表面温度极低且大气层较为稀薄,航天器需要有效的隔热层材料来提供热保护。
科学家们根据火星表面温度和大气层压力的数据,进行了多种材料的热保护分析和优化设计。
例如,火星车的隔热层材料采用了多层膜结构和陶瓷纤维,可以有效减少热传导和辐射热。
RLV金属热防护系统热分析方法进展

况。在厚度方向上划分单元和节点, 面积上的热短路。蜂窝结构、毡垫圈、
当然,在作金属热防护系统板的
一维导热单元连接热防护板厚度方向 绝热物质、缝隙中的空气也用二维热 热分析时,也不一定只采用一种模
上的各个节点。用各个节点温度值的 传导单元来模拟。这种二维模型可以 型,应该根据需要来建立相应的模
插值来近似模拟热防护板内的温度场 用来模拟三维热防护板的变形。
的。笔者推导出了三维层状壳元传热 步的研究。
公式,应用于热分析中得到了很好的
(责编 依然)
40 航空制造技术 2 0 0 6 年第1 1 期
但是,一维模型不能精确地模拟 建立模型。例如,美国 N A S A 2 国内情况
2 0 0 6 年第1 1 期 航空制造技术 39
封面文章 COVER STORY
在国内,可重复使用运载器的预 研工作刚刚起步,大多数研究工作为 工程计算,缺乏精确的理论依据、设 计与计算分析基础,缺乏对具体部位 的精确热分析和热应力与结构耦合计 算分析,缺乏具体部位的细节设计和 理论依据,特别在复杂结构体的热耦 合分析和热力耦合数值计算方法上缺 少研究及细致的分析技术与手段。目 前,根据我国“863 计划”的部署,国 内有几家科研单位正在进行这些热分 析与热应力的工程算法验证,但是也 只是初步研究,还没有足够的理论依 据和精确的算法。
统本身结构复杂,由几部分构成,以 布。一维单元模型最大的缺点是忽略 于四方的热防护板来说,三维模型可
美国在“X-33”航天飞机研制时期 了与板平行的板缘和板间缝隙的热短 以用板的1/8来代表整块板,这有赖
提出的超合金蜂窝结构热防护系统为 路现象。于是提出了二维和三维有限 于板几何形状的对称性以及结构和边
存在很小的缝隙。
多层热防护服装的热传递模型及参数最优决定
多层热防护服装的热传递模型及参数最优决定一、本文概述随着现代工业技术的快速发展,高温环境作业已成为许多行业不可避免的工作场景。
因此,对高温防护服装的研究显得尤为重要。
多层热防护服装作为一种有效的个人防护装备,在保护工作人员免受高温伤害方面起着至关重要的作用。
本文旨在深入探讨多层热防护服装的热传递模型,并通过参数优化决定,为高温防护服装的设计和优化提供理论支持和实践指导。
本文将首先介绍多层热防护服装的基本原理和构造,包括各层材料的热学性能和结构特点。
在此基础上,将详细阐述热传递模型的理论框架,包括热传导、热对流和热辐射等基本传热方式在多层结构中的综合作用。
通过构建热传递模型,可以更准确地预测多层热防护服装在不同高温环境下的热防护性能。
接下来,本文将探讨多层热防护服装参数的最优决定方法。
通过对影响服装热防护性能的关键因素进行分析,如材料导热系数、服装厚度、服装层数等,我们将建立参数优化模型,以寻求在给定条件下最佳的服装设计方案。
通过参数优化,可以进一步提高多层热防护服装的热防护效果,降低高温环境对工作人员的潜在威胁。
本文将总结多层热防护服装热传递模型及参数最优决定的研究意义和应用前景。
随着科技的不断进步,多层热防护服装的性能将不断优化,为保障高温环境作业人员的安全和健康发挥更加重要的作用。
本文的研究成果将为相关领域的科研人员和企业提供有益的参考和借鉴,推动多层热防护服装技术的持续发展和创新。
二、多层热防护服装的热传递模型多层热防护服装的设计初衷在于通过多层次的材料结构来抵抗外界热源的侵害,保护穿着者免受高温环境的伤害。
为了深入理解这种防护机制,需要构建一个能够准确描述多层热防护服装内部热传递过程的数学模型。
在构建模型时,我们首先需要考虑服装各层材料的热传导性能,包括导热系数、热容和密度等参数。
这些参数将直接影响热量在材料间的传递效率。
我们还需要考虑服装层间的接触热阻,这是由于层间空气和不完全接触导致的热传递阻碍。
导体和金属屏蔽热稳定计算书
导体和金属屏蔽热稳定计算书电缆导体及金属护套的短路热稳定性主要通过热稳定性短路电流和短路时间来进行校验,主要校验方法如下:一、允许短路电流的计算电缆中任何载流元件,其额定短路电流的计算方法都采用绝热方法,即在短路时间内,热量保留在在流体内。
实际上在短路时,一些热量会传入相邻的材料中去,并非是绝热的,但按极端条件计算,其结果是偏于安全的。
IEC-986(1989)标准推荐的短路电流计算公式中忽略热损失。
采用绝热方法导出的公式对大多数情况是准确的。
任何误差都是偏于安全的。
对任何初始温度从绝热温升方程中导出短路电流计算公式如下:式中:S—载流体截面积,mm²,对于导体和金属套而言,使用标称截面足够了(如果是屏蔽,此值需仔细考虑):I AD——短路电流(短路期间内电流有效值),A:t——短路时间,s,自动合闸情况下,t是短路电流持续时间的集合,最大到5s,二次短路之间任何冷却作用均忽略:K——与载流体材料有关的常数,As½/mm²,见表1。
θr——最终温度,℃;θi——起始温度,℃;β——0℃时载流体电阻温度系数的倒数,K,见附表1;σc——20℃时载流体比热,J/K·m³,见附表1;ρ20——导体20℃时电阻率,Ω·m,见附表1;二、短路电流计算简化式短路电流的实际过度过程是比较复杂的。
短路电流从产生瞬间时电流到衰变为暂态电流,最后达到稳定电流。
短路过程中载流导体的热效应正比于短路电流的平方并截止于切断故障的实际动作时间t。
一般情况下,短路电流作用时间很短,可以认为导体短路是个绝热过程。
通过分析和换算,可以将公式1化简为:式中:S——载流体截面积,mm²,对于导体和金属套而言,使用标称截面足够了(如果是屏蔽,此值需仔细考虑);I AD——短路电流(短路期间内电流有效值),A:t——短路时间,s,自动合闸情况下,t是短路电流持续时间的集合,最大到5s,二次短路之间任何冷却作用均忽略:C——热稳定系数,见附表2。
应用三层热防护服热传递改进模型的皮肤烧伤度预测
应用三层热防护服热传递改进模型的皮肤烧伤度预测一、本文概述随着工业技术的快速发展,高温环境下的作业越来越普遍,这无疑增加了工作人员遭受皮肤烧伤的风险。
传统的热防护服虽然在一定程度上能够降低这种风险,但由于其设计往往基于经验而非科学模型,因此其防护效果往往难以达到预期。
针对这一问题,本文提出了一种应用三层热防护服热传递改进模型的皮肤烧伤度预测方法。
该模型基于热传递理论,通过对热防护服各层材料的热传递性能进行深入研究,构建了一个能够准确预测皮肤烧伤度的数学模型。
这一模型不仅可以用于优化热防护服的设计,提高其在高温环境下的防护效果,还可以为相关行业的安全生产提供有力保障。
本文首先介绍了三层热防护服的基本原理和结构,然后详细阐述了热传递改进模型的建立过程,最后通过实验验证了模型的准确性和有效性。
希望通过本文的研究,能够为热防护服的设计和生产提供新的思路和方法,进一步降低高温环境下工作人员的皮肤烧伤风险。
二、三层热防护服热传递模型的建立随着工业的发展,高温环境作业变得日益普遍,热防护服在保护作业人员免受高温伤害方面发挥着重要作用。
然而,传统的热防护服设计往往基于单层或多层材料的热阻性能,缺乏对实际热传递过程的全面考虑。
因此,本文旨在建立一种三层热防护服热传递模型,以更准确地预测皮肤烧伤度。
该模型基于热传导、热对流和热辐射三种基本传热方式,综合考虑了防护服各层材料的热物性、服装结构、环境温度、湿度以及人体活动等因素。
模型将防护服分为内层、中层和外层,每层材料都具有不同的热阻、热容和导热系数等热物性参数。
同时,模型还考虑了服装结构对热传递的影响,如缝合处、袖口和领口等部位的热量泄漏。
在模型建立过程中,我们采用了有限差分法、有限元法等数值计算方法,对热传递过程进行离散化处理,并通过迭代计算求解各层材料的温度分布和热量传递情况。
同时,我们还结合了实验数据,对模型进行了验证和修正,以确保其准确性和可靠性。
通过该模型的建立,我们可以更全面地了解三层热防护服在实际使用过程中的热传递情况,为优化防护服设计、提高防护性能提供科学依据。
航天器热防护材料研究现状与发展趋势
*西北工业大学博士论文创新基金资助(CX200405)石振海:1960年生,博士研究生,主要从事热防护材料的研究 T el:029 ******** E mail:shizhenhai9307@航天器热防护材料研究现状与发展趋势*石振海,李克智,李贺军,田 卓(西北工业大学材料学院,西安710072)摘要 热防护系统中所采用的多层复合热防护材料的层间界面结合和小块材料之间的连接对航天器的可靠性有很大影响,目前二者都存在一定的缺陷。
依据功能梯度材料和C/C 复合材料的理论,将高导热率碳泡沫和低导热率碳微球设计成密度和热导率功能梯度热防护碳泡沫材料,使其具备组分之间无层间界面和小块材料间易于连接等特点。
关键词 热防护材料 碳泡沫 功能梯度材料 C/C 复合材料Research Status and Application Advance of Heat ResistantMaterials for Space VehiclesSH I Zhenhai,LI Kezhi,LI Hejun,T IAN Zhuo(Schoo l of M aterials Science,N o rthwester n P olytechnical U niver sity,Xi an 710072)Abstract T he reliability o f space v ehicles is much affected by the inter face bonding of multilayer heat resist ant mater ials and t he joining of smaller mater ials in the ther mal prot ection sy st em.Ho wev er,ther e ar e defect s in bothaspects.Based on the theo ries concerning funct ional g radient mater ials and C/C composit es,a way is desig ned to pre par e a functional gr adient carbon foam w ith density and heat conductiv ity for ther mal pr otection from the car bon foam with hig h heat conductivity and the carbon microsphere with low heat conductivity.T he advantag es of the newly designed material lie in that there are no interfaces between layers of materials and smaller pieces of materials ar e easy to join.Key words heat r esistant mater ial,carbon foam,functio nal gr adient mater ial,C/C composites1 航天器的热防护系统和热防护材料热防护系统(T her mal pr otectio n sy st em,简称T PS)是各国正在研制的可重复使用于航天(空天)飞行器上的关键部件之一[1,2]。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Steady heat transfer analysis of multilayer thermal insulations for metallic thermal protection system
YAN Chang-hai , M ENG Song-he , CH EN Gui-qing , Q U Wei , L IU Guo-qian
DO I 牶牨牥牣牨牫牪牪牬牤j牣cnki牣jasp牣牪牥牥牰牣牥牭牣牥牥牫
第 21 卷 第 5 期 2006 年 10 月
文章编号 :1000-8055(2006)05-0800-05
航空动力学报
Journal of Aerospace Power
Vol. 21 No. 5 Oct . 2006
金属热防护系统多层隔热材料的 稳态传热分析
(Resea rch Cent er o f Co mposit e M aterials , H arbin Instit ute of T echnology , H arbi n 150080 , China) Abstract :Com bined energy equi librium equat ion and t w o thermal flux approxim ation methods we re used to est ablish the steady heat transfe r mat hema tic model of t he multi-lay er thermal i nsulat ions in t he met alli c prot ectio n system. Radiat ion att enuatio n index o f f ibrous thermal i nsulat ions and emissivity of heat insulati on screen w ere optimized by genet ic alg ori thm and ex periment that m easured the ef fective conduct ivity of the multi lay er thermal insula tion element. T he experim ent ally measured eff ect ive conductivit y data of the multi-lay er thermal insulatio ns v alidate steady heat t ransfer m odel of the multi-layer t herm al insulatio ns , w hich adopt optimized thermal phy sical parame ters.
KB T
2
πd
2 g
P
(6)
式中 , K B 为玻尔兹曼常数(1. 38 ×10- 23 J / K), T
和 P 分别为气体的温度和压力 , dg 为气体的碰撞 直径 。 公式(5)中 LC 为纤维隔热材料中的气体 热传导的特征长度 , 可用下式表示 :
LC
=
π 4
Df m
(7)
式中 :m 为固体致密度 , 它是隔热材料的密度和隔 热材料母材密度的比率 ;D f 为隔热材料的纤维直
基础 。
法对传热模型参数进行优化 。
1 计算模型
要建立多层隔热材料传热的数学模型就要了
解其工作环境 。 飞船在再入过程中 , 主要的加热
时间为再入后 200 ~ 1 500 s 这一区间 , 这时外界
压力 的变 化为 103 ~ 104 P a , 温 度在 1 000 ℃。 K am ran[ 5] 通 过 实 验 发 现 , 当 外 界 压 力 大 于
闫长海 , 孟松鹤 , 陈贵清 , 曲 伟 , 刘国仟
(哈尔滨工业大学 复合材料与结构研究所 , 黑龙江 哈尔滨 150080)
摘 要 :采用能量平衡方程和两热流密度近似法建立了 金属热防护 系统多层 隔热材料的 稳态传热 的数 学模型 , 并利用测量多层隔热材料单元 的有效 导热系 数的实 验和遗 传算法 对纤维隔 热材料 的辐射 衰减系 数 和隔热屏表面辐射发射系数这两个热物 参数进 行了优 化 , 最 后用实 验测得 的多层隔 热材料 的有效 导热系 数 验证了采用优化后参数的多层隔热材料的稳态传热模型的正确性 。 关 键 词 :航空 、航天推进系统 ;金属热防护系统 ;稳态传热 ;多层隔热材料 ;遗传算法 ;优化 中图分类号 :V231. 1 文献标识码 :A
制成 , 所以 ks 为固体二氧化硅的导热系数 , k g 为
气体的导热系数 , 采用下式[ 4] :
kg
= 1
+8
k
* g
γλm
(γ+1)PrL C
(5)
式中
,
k
* g
为一个大气压下常温的气体导热系数
;γ
为气体比热比 ;P r 为普朗特数 ;气体分子的平均 自由程 λm 由公式(6)给出 :
λm
=
式中 :q 为再入过程中多层隔热材料内总的热流
密度 ;qc 为固体 和气体的 热传导的 热流密度 ;qr
为多层隔热材料内热辐射的热流密度 。
图 1 多层隔热材料的示意图 F ig . 1 M ultilayer the rmal insula tion
多层隔热材料是由纤维隔热材料与隔热屏组 成的 。 当温度大于 800 ℃时 , 热辐射是纤维隔热 材料内的主导传热方式 , 隔热屏的作用是降低高 温情况下热辐射在纤维隔热材料内的传递 。 国外 已对多 层 隔热 材 料的 传 热 进行 了 研 究 , Kamran[ 5] 采用两热流密度方法对多层隔热材料建立 了传热模型 , Ma rkur Spinnler[ 6 , 7] 采用 scaling 模 型对辐射传热进行求解 。 但是他们只是建立了传 热模型 , 并没有对传热模型所用到的参数进行优 化 , 而且认为隔热屏的表面辐射发射系数是常数 , 但是隔热屏的辐射系数实际是随温度的升高而增 加的 , 所以得到隔热屏的辐射系数随温度变化的 函数对于多层隔热材料传热模型的准确性是很重 要的 。由于两热流密度法精度较高 , 所以本文采 用能量方程和两热流密度法建立了多层隔热材料 传热的数学模型 , 并利用稳态传热实验与遗传算
要想建立多层隔热材料的稳态传热模型 , 还需(n
- 2)个方程来和以上方程联立才能得到多层隔热 材料的总的热流密度 q 。由于 是稳态传热 , 各个
单元得出的总热流密度是相同的 , 这样我们就可
图 2 多层隔热材 料单元传热示意图 Fig . 2 Hea t transfe r of cell of multilay er insula tion
多层隔热材料是由隔热屏和纤维隔热材料堆
栈而成 , 每个单元内的传热方式是相同的 , 所以取
出一个单元来建立多 层隔热材料传 热模型如图
2 。由于纤维隔热材料内的传热为热传导和热辐 射联合热传递问题 , 所以要想建立稳态传热模型 ,
103 P a , 纤维隔热材料的导热系数随压力的变化
很小 , 所以为了简化计算 , 设工作压力为 103 P a ,
温度为 1 000 ℃。在这种条件下 , 多层隔热材料内
的热传递是由气体和 固体的热传导 和热辐射组
成 , 气体的对流可以忽略不计[ 3] , 如公式(1):
q =qc +qr源自(1)件如下 :-
2 3(K eρ)
2
ε1 - ε1
G x
+G
=
4
σT
4 1
x =0
-
2 3(K eρ)
2
ε2 - ε2
G x
+G
=
4
σT
4 2
x =L
(12)
式中 :ε1 和 ε2 为隔热屏 上下表面的辐射 发射系 数。
公式(1)~ (12)给出了能量平衡方程 , 随温度
压力变化的纤维隔热材料的导热系数的求解方程
究.
第 5 期
闫长海等 :金属热防护系统多层隔热材料的稳态传热分析
80 1
到下一代可重复使用航天器上[ 1] 。 以 X-33 金属 热防护系统为例[ 2] , 金属热防护系统是由表面的 高温合金蜂窝盖板 、隔热材料和内部钛合金蜂窝 板三层结构组成 。表面为高温合金蜂窝盖板 , 用 于抵挡在发射和飞行中外来物体的撞击 。在飞行 器重返大气时 , 表面盖板由于受到严重的气动加 热 , 温度最高达 1 000 ℃, 而由于机身是铝合金制 成的 , 最高设计温度为 176 ℃[ 3] , 中间隔热材料的 作用就是减少进入机体内的热量 。在 X-33 改进 的 “A RM O R”[ 4] 金属热防护系统的设计过程中 , 中间的隔热材料采用纤维隔热材料 , 目前美国 , 欧 洲和日本的可重复使用航天器的验证机都采用隔 热效果更好 , 重量更轻的多层隔热材料(如图 1)。 可见要想设计出隔热性能更好 , 重量更轻的金属 热防护系统 , 对多层隔热材料的稳态传热过程进 行准确的分析是金属热防护系统进行防热设计的
就要从能量平衡方程和辐射传递方程出发 , 利用 边界条件对传热模型进行求解 。多层隔热材料的
稳态传热模型的能量方程可用公式(2)表示 :
qc + x
qr x
=0
(2)
把傅立叶公式带入公式(2)可得到下式 :
x kc
T x
-
qr x
=0
(3)
式中 , kc 是纤 维隔热 材料 固体 和气体 的导 热系
径。
公式(3)中的辐射热流密度 qr 可通过纤维隔
热材料内的辐射传递方程(8)来求解 :
1 Ke
dI ds
+I(s) =(1
