第六届江苏省大学生力学竞赛(专科组)试卷
第六届全国周培源大学生力学竞赛初试试题参考答案

第六届全国周培源大学生力学竞赛初试试题参考答案
高云峰
【期刊名称】《力学与实践》
【年(卷),期】2007(029)003
【摘要】无
【总页数】2页(P95,93)
【作者】高云峰
【作者单位】无
【正文语种】中文
【相关文献】
1.浅析第六届全国周培源大学生力学竞赛初试题型及参赛大学生应注意的问题 [J], 李道奎;丛广年;雷勇军
2.第六届全国周培源大学生力学竞赛初试试题 [J], 竞赛组委会
3.第六届全国周培源大学生力学竞赛各地方力学学会联系人名单 [J],
4.第十届全国周培源大学生力学竞赛(个人赛)试题参考答案 [J],
5.第九届全国周培源大学生力学竞赛(个人赛)试题参考答案 [J],
因版权原因,仅展示原文概要,查看原文内容请购买。
江苏大学生力学竞赛模拟11答案

江苏大学生力学竞赛模拟11答案校内编号________班级_________姓名_________成绩_________1、求图示梁支座B 左右两侧截面的相对转角。
EI =常数。
M i (c)(b)M P解:(1)荷载作用的实状态,其弯矩图如图(b )所示。
(2)建立虚设单位力状态, 其弯矩图如图(c )所示。
(3)图乘梁(b )、(c )求自由端的竖向位移VB ? 223121115()38224248i i B y ql ql ql l l EI EI EIω??==--=-∑(??) 2、求简支梁中点K 的竖向位移。
EI =常数。
M i M P 题6-64解:(1)荷载作用的实状态,其弯矩图如图(b )所示。
(2)建立虚设单位力状态, 其弯矩图如图(c )所示。
(3)图乘梁(b )、(c )求自由端的竖向位移V K ? 22241311122()()()3164222883232848Vi i k y ql l l l ql l l ql l ql EI EI EI EI EIω??==++=↓∑ 3、试计算如图所示桁架结点C 的竖向位移。
设各杆EA 为同一常数。
解:实际位移状态如图4.9(a)所示,并求内力NP F ,设立虚拟单位力状态如图4.9(b)所示,并求内力N F ,代入(4-8)式有11))(1)131(2)22224242Cy N NP F F l EAEA F F d F d d Fd EA ?==??+?? ? ? ? ????+?+?+-?? ?? ?????????-?+??+?? ? ? ? ? ???????????=∑ 2.71()Fd EA ?+≈↓ ??4、试求如图 (a)所示组合结构D 端的竖向位移Dy ?。
1122.110N m E ==?/,受弯杆件截面惯性矩543.210m I -=?,拉杆BE 的截面面积421610m A -=?。
(a) (b) (c) 解:作出实际荷载作用下的弯矩图P M ,并求出BE 杆轴力,如图4.16(b)所示,在D 端加一竖向单位力,作出M 图和BE 杆轴力,如图4.16(c)所示按(4-11)式图乘及运算。
第六届江苏省大学生力学竞赛(专科组)试卷试题答案

参考答案及评分标准第Ⅰ部分(共7题,每题4分)1. 1 0.5 【每 2分】 2. 0Fa 【每 2分】 3. 7.125o 【4分】 4.2Fl EAF EA Fl EA FEA 【每 1分】5. b e f g 【每 1分】 6.零杆见图示1N F F =(拉)【零杆共10根,答对41N 大小1分,表明拉的1分】 7.【剪力图2分,荷载图2分】4kN4kN或第Ⅱ部分(共6题,每题7分)1.由整体0A M ∑=,得/2250kN B F F == 再由杆BD 0C M ∑=,得/2433kN DE F == 故选用能承受500kN 张力的绳①。
【计算5分,结论2分】 2.设重心距AB 线右端D 之距离为C x ,则0.3m i Ci C ix A =∑设板重为W ,由平衡条件可求得:A 处吊杆受力0.9A F W =,B 处吊杆受力0.1B F W =设AB 杆长均为l ,材料弹性模量均为E ,A 杆面积为A A ,B 杆面积为A B ,则0.9A A A AF l Wl l EA EA ∆==,0.1B B B B F l Wll EA EA ∆== AB 边保持水平,则A B l l ∆∆=,计算得9A B A A =,A 、B 杆均为圆截面,故3A Bdd = 【求板重心位置2分,求二杆作用力1分,二杆变形1分,保持AB 水平条件1分,二杆直径比计算2分】3.在C 节点沿CA(图a ),或在节点沿x 、y 方向各作用一个拉力x y F F F ==(图b )以上两种情况均满足题意要求,且各杆内力均为0AD AB CD CB F F F F ====,AC F由各杆所受内力知,AD 、AB 、CD 、CB 均不变形,只有AC 杆沿AC 方向伸长2AC Fll CC EA EA∆''===(图c ) 由小变形,作垂线代替圆弧得C 节点位移至C′,则AC CC l EA'==D 节点有x方向的刚性位移DD CC ''==【主动力3分,其中:作用点位置、主动力方向及大小各1分;各杆内力2分,各节点位移2分】F =A C ′图a图b图c4.图a 33(a)0.098232d W d π==, 图b33(b)(/0.05896d W d ==图c o o 23(c)(cos 60)(sin 60)0.06256d d W d ==图a 22(a)0.7854d A d π==, 图b22(b)0.50A d == 图c o o 2(c)(cos60)(sin60)0.433A d d d ==由[]M W σ=计算梁所能承受的最大弯矩3max max (a)[][]0.0982[]M W W d σσσ===,为圆截面梁由max min MW σ=计算梁所能承受的最大工作应力max 33(b)170.0589M M M W d d σ===,为方截面梁由min min G A γ=计算梁的最轻自重2min (c)0.433G A d γγ==,为矩形截面梁 【max M 2分, max σ2分; 自重最轻3分】5.设材料单位体积重为γ,则实心圆梁自重集度24q D πγ=空心圆管梁 22(1)4q D παγ'=-,0.5dDα== 实心梁 2m a x 34M q l W D σπ== 空心圆管梁 2m a x 344(1)M q l W D σπα'''=='- 由于210.75q q α'=-=,故max 42max 10.8(1)1q q σσαα''===-+ 实心梁 44max45320384384ql ql w EI ED π== 空心圆管梁 44max445320384384(1)q l q l w EI ED πα'''=='- 故max 4max 0.8(1)w q w q α''==- 【/q q '比值1分,二梁max σ各1分,比值1分;二梁max w 各1分,比值1分】6.顺风:θθαθcos )cos(cos -==F F F N y)]sin ()cos(cos )1()sin([θθαθθαθ-⋅-+⋅-⋅--=F d dF y]sin )cos(cos )[sin(θθαθθα⋅--⋅-=F 0=)tan(tan θαθ-=,2αθ=逆风:如右图,帆画在角α′内即可。
2007-力学竞赛-理力(专科)解答讨论稿
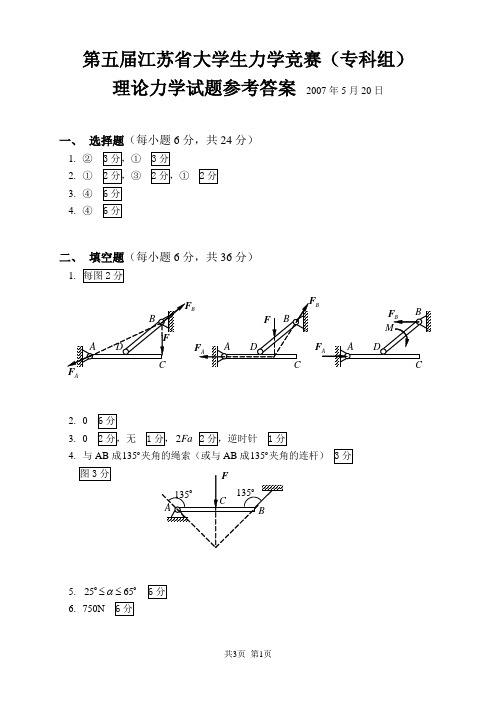
第五届江苏省大学生力学竞赛(专科组)理论力学试题参考答案 2007年5月20日一、 选择题(每小题6分,共24分)1. ②2. ①3. ④4. ④二、 填空题(每小题6分,共36分)1.2. 03. 02Fa4. 与AB 成135夹角的绳索(或与AB 成135夹角的连杆)5. 2565α≤≤6. 750NBA BB135三、 计算题(20分)解:取整体:0DM=∑ 0C Fl F b M -+-=C Fl MF b+=取AB :0AM=∑0G M Fl F b --+=G Fl M F b+=取AB 及AC :0EM=∑()02222G C AD bb b M F l F F F ---+++=AD F F =- (压)四、 计算题(15分)解:取AB :0AM=∑B 2600N DN F F == 取圆轮C :1)假设D 处达到临界而E 处未达到临界0EM=∑ 120DC F R F R '-= 1220.4600480N C DF F '==⨯⨯= 2)假设E 处达到临界而D 处未达到临界0yF =∑ 1000N ENDN F P F '=+=0D M =∑ 220EC F R F R -+= 2220.21000400N C E F F ==⨯⨯= 综上,使圆轮C 由静止开始运动时作用在轮心C 的水平拉力C F 的最小值为400N 。
B AyF DNBFD'ENE五、 计算题(5分)解:由节点D 可知DE 杆为零力杆。
作一截面将杆AE 、CE 及CG 截断并取右半部分研究0BM=∑CE F F = (压)。
大学生力学竞赛试题及答案
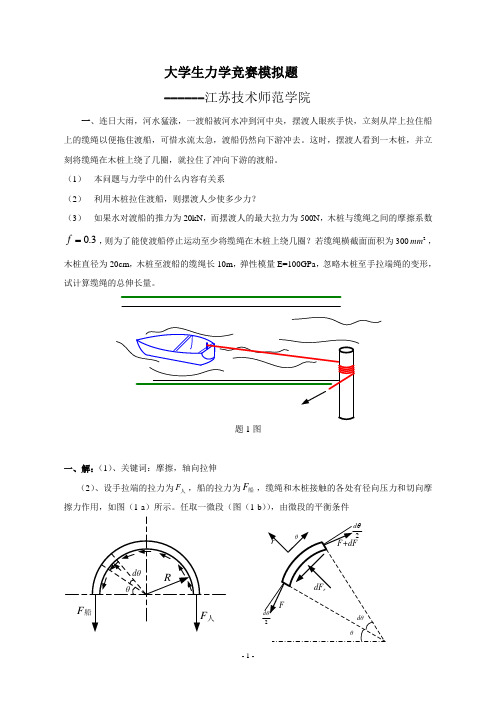
大学生力学竞赛模拟题 ------江苏技术师范学院一、连日大雨,河水猛涨,一渡船被河水冲到河中央,摆渡人眼疾手快,立刻从岸上拉住船上的缆绳以便拖住渡船,可惜水流太急,渡船仍然向下游冲去。
这时,摆渡人看到一木桩,并立刻将缆绳在木桩上绕了几圈,就拉住了冲向下游的渡船。
(1) 本问题与力学中的什么内容有关系 (2) 利用木桩拉住渡船,则摆渡人少使多少力?(3) 如果水对渡船的推力为20kN ,而摆渡人的最大拉力为500N ,木桩与缆绳之间的摩擦系数3.0=f ,则为了能使渡船停止运动至少将缆绳在木桩上绕几圈?若缆绳横截面面积为3002mm ,木桩直径为20cm ,木桩至渡船的缆绳长10m ,弹性模量E=100GPa ,忽略木桩至手拉端绳的变形,试计算缆绳的总伸长量。
题1图一、解:(1)、关键词:摩擦,轴向拉伸(2)、设手拉端的拉力为人F ,船的拉力为船F ,缆绳和木桩接触的各处有径向压力和切向摩擦力作用,如图(1-a )所示。
任取一微段(图(1-b )),由微段的平衡条件(1-a ) (1-b )0=∑r F 02sin 2sin )(=-+-θθd F d dF F dF r (1) 0=∑θF ()02cos 2cos=--+r fdF d F d dF F θθ (2) 对于微小角度θd ,可令 22sinθθd d ≈,12cos ≈θd ,并略去高阶微量2θd dF ⨯,即得fF d dF=θ(3) 分离变量,积分得θf Ae F = (4)其中积分常数由缆绳两端的边界条件确定,有0=θ, 船F F =; 船F A =所以,绕在木桩上缆绳任一截面的拉力为θf e F F 船= (5)所以θf e F F =船人,其中θ为缆绳绕过木桩的角度。
(3)、将N F 500=人,kN F 20=船,f = 0.3代入式(5),得θ3.031020500e ⨯=解得 3.12≈θ rad 所以至少将缆绳绕两圈。
第6届周培源全国大学生力学竞赛(样题)

第6届周培源全国大学生力学竞赛(样题)时间 3 小时,满分 120分一、奇怪的独木桥(25分)一位游客在某处发现有座独木桥,上面写着:禁止独自一人过桥。
他发现当地居民的确都是成双结队并且好像以某种相互配合的方式过桥。
他觉得很奇怪,为什么 2 个人可以过桥而 1 个人却不能。
等周围没有其它人时他想独自试试,结果没走到半程,就把独木桥压断了而掉入水中。
根据事后他的调查,小河宽 4 米,独木桥长 6米,如图 1所示横跨在小河上(支撑点可以认为是铰链约束)。
独木桥采用当地的轻质木材做成,等截面,允许最大弯矩为[M]=600N.m 。
为方便假设每人的体重均为 800N,而独木桥的重量不计。
请你分析一下:(1)本问题与力学中的什么内容有关系?(2)如果一个人想过桥,最多能走多远?(3)当地居民过桥时两人需要进行配合,你认为两人应如何配合才能安全过桥?图 1 奇怪的独木桥二、模特儿与新型舞台(35 分)有位模特儿在一种新型舞台上练习走台步。
该舞台类似长方形桌子,长为,宽为,有 6 条等长的桌腿(图 2)。
每条桌腿都与水平地面有接触开关,如果接触处有压力就会使对应的一盏灯亮起来。
该模特儿发现,站到舞台不同的位置会有不同数目的灯亮起来,如图2,她站在舞台右上角附近时,左下角的灯就不亮。
如果把模特儿的重量认为是集中载荷,把舞台认为是刚体且不计质量,则(1)本问题与力学中的什么内容有关系?(2)如果模特儿站在舞台的正中央,会有几盏灯亮起来?(3)模特儿在不同区域时会有不同数目的灯亮起来,请在长方形舞台上确定各区域的边界并画出示意图,然后在该区域内写上亮灯的数目(提示,亮灯的数目有可能为 6、5、4、3、2、1)。
图 2 模特儿的新舞台三、魔术师的表演(25分)魔术师要表演一个节目。
其中一个道具是边长为a的不透明立方体箱子,质量为M1;另一个道具是长为L的均质刚性板 AB,质量为 M2 ,可绕光滑的 A铰转动;最后一个道具是半径为R的刚性球,质量为 M3 ,放在刚性的水平面上。
江苏省大学生力学竞赛(专科组)模拟试题参考答案

由 s f
F
解之,
2 fEI WS 2 2lS S 2
由题意
F
2 fEI WS 2 2lS S 2 为所求.
16. ( 1 )组合 截面形 心的位 置: yc =0.592h1 ( 2) 使梁 B 端下表面刚好接触 D 台面所需的力 Fp
P A
P 1 6 0
4
900 1 k1 N 3
(2)由曲柄杠杆平衡确定 Q
m F 0
B
Q 200 P 250 0
5 Q 113 141KN 4
(3)作用在销钉处的合力
R P 2 Q 2 180.7 KN
(4)由销钉强度确定销钉直径
x
yE1 I z1 E2 I z2
x2
ME 2 y E1 I z1 E2 I z2
共 5页 第2页
11.解:
考虑先满足 M D = 0,计算模型如下图 为满足 D = 0 , 则令 则
2 1 qx3 2 qa x D 0 24EI 6EI
力 F 使轴弯曲,M 使轴扭转,此电动机轴是弯扭转组合变形 (2) 内力分析 , 作扭矩图 T= M = 120.2 N· mm 作弯矩图最大弯矩 Mmax =-3F× l =-3× 800× 0.1=-240 N· m
(3) 强度校核 ,危险面为轴的最左端, 按第三强度理论校核:
(240 000) 2 120 2002 M 2 T 2 r3 503 Wz 32 21.88MPa [ ]
所以强度足够
共 5页 第4页
15.(1) 求梁 S 处的转角
第六届周培源力学竞赛试题

第6届周培源全国大学生力学竞赛初赛(样题)时间3小时,满分120分一、奇怪的独木桥(25分)一位游客在某处发现有座独木桥,上面写着:禁止独自一人过桥。
他发现当地居民的确都是成双结队并且好像以某种相互配合的方式过桥。
他觉得很奇怪,为什么2个人可以过桥而1个人却不能。
等周围没有其它人时他想独自试试,结果没走到半程,就把独木桥压断了而掉入水中。
根据事后他的调查,小河宽4米,独木桥长6米,如图1所示横跨在小河上(支撑点可以认为是铰链约束)。
独木桥采用当地的轻质木材做成,等截面,允许最大弯矩为[]600N mM=⋅。
为方便假设每人的体重均为800N,而独木桥的重量不计。
请你分析一下:(1)本问题与力学中的什么内容有关系?(2)如果一个人想过桥,最多能走多远?(3)当地居民过桥时两人需要进行配合,你认为两人应如何配合才能安全过桥?图1 奇怪的独木桥二、模特儿与新型舞台(35分)2a a 有位模特儿在一种新型舞台上练习走台步。
该舞台类似长方形桌子,长为,宽为,有6条等长的桌腿(图2)。
每条桌腿都与水平地面有接触开关,如果接触处有压力就会使对应的一盏灯亮起来。
该模特儿发现,站到舞台不同的位置会有不同数目的灯亮起来,如图2,她站在舞台右上角附近时,左下角的灯就不亮。
如果把模特儿的重量认为是集中载荷,把舞台认为是刚体且不计质量,则(1)本问题与力学中的什么内容有关系?(2)如果模特儿站在舞台的正中央,会有几盏灯亮起来?(3)模特儿在不同区域时会有不同数目的灯亮起来,请在长方形舞台上确定各区域的边界并画出示意图,然后在该区域内写上亮灯的数目(提示,亮灯的数目有可能为6、5、4、3、2、1)。
aaaa图2 模特儿的新舞台三、魔术师的表演(25分)魔术师要表演一个节目。
其中一个道具是边长为的不透明立方体箱子,质量为a 1M;另一个道具是长为L 的均质刚性板AB ,质量为2M ,可绕光滑的A 铰转动;最后一个道具是半径为R 的刚性球,质量为3M ,放在刚性的水平面上。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1、,准考证号 考生姓名 考生所在学校
3.图示吊架ABC 中,已知l AB =2l AC ,杆
AB 的自重P =200N ,B 端挂重W =300N ,则铰A 的支反力F A 的倾角θ= 。
】
4.图a 和图b 为横截面面积A 相同、材料E 相同之受拉杆,则图a 所示的杆C 截面之位移 a C ∆= ,该杆BC 段之线
应变a
BC ε= ;图b 所示的杆C
截面之位移 b
C ∆= ,该杆
BC 段之线应变b
BC ε= 。
5.下列结构中, 、 、 、 是超静定结构。
】
~
W
B
l AC
图a
图b
F
F F
(a ) (b )
(c )
)
(e ) (f )
!
6.图示结构受F1=F2=F的二力作用,请在图中画出(或标注)内力为零的杆件,并计算杆①的内力F N 1。
—
7.图a所示简支梁AB之弯矩图(图中只画出弯矩的大小,符号可自行规定)如图b所示,试画出梁的剪力图和受力图。
)
a a
a
图a
图b
12kN·m
@
第Ⅱ部分(共6题,每题7分)
*
~
^
》
【
2.图中阴影线所示形状之均质钢板,尺寸如图示。
在A、B处用长度相同之圆截面钢杆吊住,若要求钢板AB边保持水平,试求两圆杆直径之
比。
,
【
{
】
3.由五根横截面面积、弹性模量均相同的杆件制成的ABCD正方形桁架如图所示,已知约束点A、B不受主动力作用,且桁架A支座的
约束反力F Ax=F Ay= -F,B支座的约束反力F By=0,试求该桁架所受主动力的作用点、作用方向和大小,以及各杆内力和各节点的位移。
{
、
封线
<
.
4.由直径为d 的圆截面材料制成圆形、正方形、对角线与底边成60o 的矩形等三个受竖向荷载作用的实心梁(图a 、b 、c 所示)。
在长度、支座、受载、材料相同的情况下,试比较三个梁中哪一个梁能承受的弯矩最大;哪一个梁能承受的工作应力最大;哪一个梁的重量最轻
…
图a 图b 图c
)
(
…
;
、
5.直径为D 的等截面圆柱简支梁,若将梁截面改为内径为d 、外径不变、且d /D =的等截面圆管,而梁长、材料、约束均不变。
试求二梁仅在
各自自重作用下最大正应力之比和最大挠度之比。
》
…
"
-
6.帆船航行时,受到与前进方向y成α角的风力F作用(见图a)。
试问调整帆与横向x的夹角θ至多大时,可使帆船获得最大的前进力。
又若遇逆风F'(见图b),应如何调整帆和船的位置,使船能继续前进。
(只需用示意图表示)
~
图a 图b ¥
¥
\
第Ⅲ部分(共3题,每题10分)
1.一混凝土挡水坝高5m,坝前水深4.5m。
取单位长度(1m)的坝段进行分析,坝前受按三角形规律分布的水压力作用(见图),已知水压力的合力F=,作用点在B。
混凝土的单位体积重γ=24kN/m3。
·
(1)若要求坝基A 处不出现拉应力,则坝宽b 至少应为多少
(2)若坝底与基础的滑动摩擦因数f =,该坝是否会滑动如不允许滑动,则b 最小又应为多少
!
;
/
》
2.在厂房内A 处(见平面图)有两部件,一重
厂房立剖面图
100kN ,另一重50kN ,该两部件必须在地面装配好后整体安放于B 处(见图)之高台基座上。
该厂房中仅有一额定吊重为120kN 、由两根40a 号工字钢并排组成的桥式吊车,该桥式吊车跨长8m ,允许正应力σ允=110MPa 。
试分析此吊放任务能否安全进行,并提出工作方案。
已知单根40a 号工字钢I z =21720cm 4,W z =1090cm 3。
3.架线工人用脚套钩攀登直径D =50cm 的电线杆,脚套钩仅在A 、B 两点与电线杆接触,两点垂直方向相距h =40cm ,见图。
已知脚套钩与电线杆之间的摩擦因数
z
f=,工人体重F=600kN,踩脚点C至电线杆中心的距离为s=85cm。
试问该工人能否用此脚套钩安全攀登而不至滑落。
