控制工程基础第2章答案
控制工程基础第二章参考答案

第二章 参考答案2-1 (1) 不是 (2) 是 (3) 不是 (4) 不是 2-2 (a))()()(3)(2222t u t u dtt du RC dt t u d C R i o o o =++ (b) )()()()()()()()(2211222121222111222121t u dtt du C R C R dt t u d C C R R t u dt t du C R C R C R dt t u d C C R R i i i o o o +++=++++ (c ) )()()()()()(33221312221t u R dtt du C R R t u R R dt t du C R R R R R i i o o +=++++(d))()()()()()()()(1211222121211211222121t u dtt du C R C R dt t u d C C R R t u dt t du C R C R C R dt t u d C C R R i i i o o o +++=++++ (e))()()()()()()()(221222121211222222121t u dtt du R C C dt t u d C C R R t u dt t du C R C R C R dt t u d C C R R i i i o o o +++=++++ (f) )()()()()()()(22121221t u R dtt du L t u R R dt t du L C R R dt t u d CL R i i oo o +=++++ 2-3 (a) )]()([)()()(23213121t u R dtt du C R R t u R dt t du C R R R R i i o o +=++-(b) )()()()(4141232022213210t u R R t u R R dt t du C R R R dt t u d C C R R R R i o o o -=++ (c))]()()([)(32321t u R R dtt du C R R t u R i i o ++=-(d) )()()()()(221122212121t u dt t du C R C R dt t u d C C R R dt t du C R i i i o +++=- (e) )()()()(2412222142t u dtt du C R C R dt t u d C C R R o o o +++ )}()(])([)({21213224223221432132t u dtt du R R C C R R C R dt t u d R R C C R R R R R R i i i +++++++=- 2-4 (a) dt t dx f dt t dx f f dt t x d m i o o )()()()(12122=++ (b) dt t dx f k t x k k dt t dx f k k i o o )()()()(12121=++ (c) )()()()()(121t x k dt t dx f t x k k dt t dx f i i o o +=++ (d) )()()()()()(112121t x k dtt dx f t x k k dt t dx f f i i o o +=+++2-5 (a))(1)()()()(1)()()(2112212221211*********t u C C dt t du C R C R dt t u d R R t u C C dt t du C R C R C R dt t u d R R i i i o o o +++=++++ (b))()()()()()()()(2112212221211211212221t x k k dtt dx k f k f dt t x d f f t x k k dt t dx k f k f k f dt t x d f f i i i o o o +++=++++ 由(a)(b)两式可以看出两系统具有相同形式的微分方程,所以(a)和(b)是相似系统。
控制工程基础第2章答案

第2章系统的数学模型(习题答案)2.1什么是系统的数学模型?常用的数学模型有哪些?解:数学模型就是根据系统运动过程的物理、化学等规律,所写出的描述系统运动规律、特性、输出与输入关系的数学表达式。
常用的数学模型有微分方程、传递函数、状态空间模型等。
2.2 什么是线性系统?其最重要的特性是什么?解:凡是能用线性微分方程描述的系统就是线性系统。
线性系统的一个最重要的特性就是它满足叠加原理。
2.3 图( 题2.3) 中三图分别表示了三个机械系统。
求出它们各自的微分方程, 图中x i表示输入位移, x o表示输出位移, 假设输出端无负载效应。
题图2.3解:①图(a):由牛顿第二运动定律,在不计重力时,可得整理得将上式进行拉氏变换,并注意到运动由静止开始,即初始条件全部为零,可得[]于是传递函数为②图(b):其上半部弹簧与阻尼器之间,取辅助点A,并设A点位移为x,方向朝下;而在其下半部工。
引出点处取为辅助点B。
则由弹簧力与阻尼力平衡的原则,从A和B两点可以分别列出如下原始方程:消去中间变量x,可得系统微分方程对上式取拉氏变换,并记其初始条件为零,得系统传递函数为③图(c):以的引出点作为辅助点,根据力的平衡原则,可列出如下原始方程:移项整理得系统微分方程对上式进行拉氏变换,并注意到运动由静止开始,即则系统传递函数为2.4试建立下图(题图2.4)所示各系统的微分方程并说明这些微分方程之间有什么特点,其中电压)(t u r 和位移)(t x r 为输入量;电压)(t u c 和位移)(t x c 为输出量;1,k k 和2k 为弹簧弹性系数;f 为阻尼系数。
+-+-u )tfC)+-+-f)(a )(b )(c )(d R题图2.4【解】:)(a方法一:设回路电流为i ,根据克希霍夫定律,可写出下列方程组:⎪⎩⎪⎨⎧=+=⎰i R u u dt i C u cc r 1消去中间变量,整理得:dtdu RC u dt du RCrc c =+方法二:dtdu RC u dt du RCRCs RCs CsR R s U s U rc c r c =+⇒+=+=11)()( 由于无质量,各受力点任何时刻均满足∑=0F ,则有:cc r kx dt dxdt dx f =-)(dtdx k f x dt dx k f rc c =+⇒()r r c c r c u dtduC R u dt du C R R Cs R R Cs R Cs R R CsR s U s U +=++⇒+++=+++=221212212)(1111)()( 设阻尼器输入位移为a x ,根据牛顿运动定律,可写出该系统运动方程r rc c aa c a r c r x dtdx k f x dt dx f k k k k dt dx f x x k x x k x x k +=++⇒⎪⎩⎪⎨⎧=--=-22121221)()()( 结论:)(a 、)(b 互为相似系统,)(c 、)(d 互为相似系统。
控制工程基础习题解答

第二章习题解
2-13:证明题图2-13中(a)与(b)表示的系统是相似系统。 (a )解:
1 u t R i ( t ) R i ( t ) i t dt 11 2 i C2 1 u t R i ( t ) it dt 2 0 C2 ui t u0 t R1i1 t 1 ui t u0 t i2 t dt C1 i (t ) i t i t 1 2
1 I 2 s C1s
联立上述方程可求得 : 1 R1C1s 1 R2C2 s U s G s 0 U i s R1C2 s 1 R1C1s 1 R2C2 s
R1 R2C1C2 s 2 R1C1 R2C2 s 1 R1 R2C1C2 s 2 R1C1 R2C2 R1C2 s 1
第二章习题解
(c)解:关键是确定 i1 t 和ic t 的方向 U i s u A t U A s ui t R R R1 R2 1 2 1 1 U A s I c s u A t ic t dt C Cs u0 t u A t R2i1 t U 0 s U A s U A s I c s R2 R2 U 0 s 2 R2Cs U A s
+
E
-
G1
Y +
+
G2
X0
B
H
X 0 ( s) G1G 2 X i ( s) 1 G1G 2 H X 0 ( s) H B( s ) G1G 2 H X i ( s) 1 G1G 2 H X i ( s)
2 0 t Dy 0 t 3ky0 0y0 t Fi t M y
机械控制工程基础第二章的答案及解析
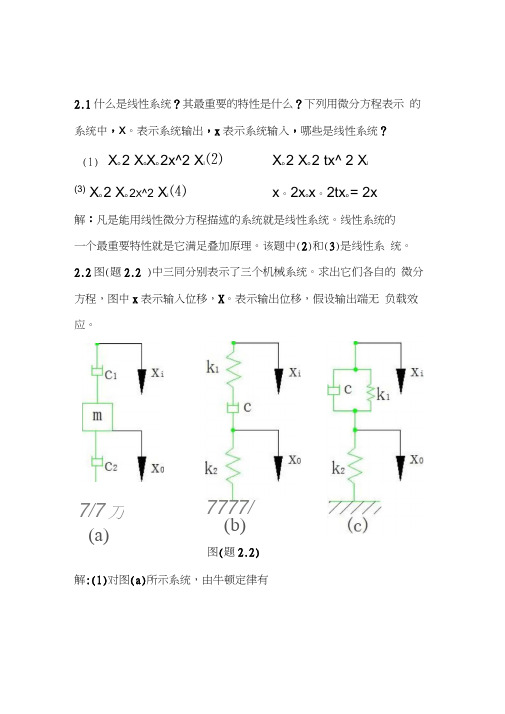
2.1什么是线性系统?其最重要的特性是什么?下列用微分方程表示 的系统中,x 。
表示系统输出,x 表示系统输入,哪些是线性系统? (1)X o2 X oX o2x^2 X i⑵X o2 X o 2 tx^ 2 Xi(3)X o2 X o2X ^2 X i⑷x 。
2x ox 。
2tx o= 2x解:凡是能用线性微分方程描述的系统就是线性系统。
线性系统的 一个最重要特性就是它满足叠加原理。
该题中(2)和(3)是线性系 统。
2.2图(题2.2 )中三同分别表示了三个机械系统。
求出它们各自的 微分方程,图中x 表示输入位移,X 。
表示输出位移,假设输出端无 负载效应。
图(题2.2)解:(1)对图(a)所示系统,由牛顿定律有7/7刀 (a)7777/ (b)c i( x —x 。
) —C 2X 。
二 mx 。
mx 。
( c iC 2)x 。
二 c iXi(X j-x)k i= c(x-x 。
)c(xx °) = k 2x 。
(1) (2)消除中间变量有c (总- k 2)x 。
- k ik zx 。
二 ckix(3) 对图(c)所示系统,由牛顿定律有c ( X - x 。
) k i( X - x 。
)= k zx 。
1c x°+ ( ki+ k 2)x °=cx+ kix2.3 求出图(题2.3)所示电系统的微分方程。
(a)图(题2.3)解:(1)对图⑻ 所示系统,设j 1为流过R 的电流,j 为总电流,则有1 u 厂 R ?iidtC2□ 一 u 。
二 R i j i对图(b)所示系统,引入一中间变量 x,并由牛顿定律有RiCiUiUnR解:设系统输入为M (即),输出二(即),分别对圆盘和质块进行动 力学分析,列写动力学方程如下:1U i-U 。
(i-i i)dtC1消除中间变量,并化简有C 1R 2U(1RC ) U 。
-= 0^+(肯+ C2)⑵ 对图(b )所示系统,设i 为电流,则有1CR 2U 。
机械控制工程基础第二章的答案及解析

2.1什么是线性系统?其最重要的特性是什么?下列用微分方程表示 的系统中,x 。
表示系统输出,x 表示系统输入,哪些是线性系统? (1)X o2 X oX o2x^2 X i⑵X o2 X o 2 tx^ 2 Xi(3)X o2 X o2X ^2 X i⑷x 。
2x ox 。
2tx o= 2x解:凡是能用线性微分方程描述的系统就是线性系统。
线性系统的 一个最重要特性就是它满足叠加原理。
该题中(2)和(3)是线性系 统。
2.2图(题2.2 )中三同分别表示了三个机械系统。
求出它们各自的 微分方程,图中x 表示输入位移,X 。
表示输出位移,假设输出端无 负载效应。
图(题2.2)解:(1)对图(a)所示系统,由牛顿定律有7/7刀 (a)7777/ (b)c i( x —x 。
) —C 2X 。
二 mx 。
mx 。
( c iC 2)x 。
二 c iXi(X j-x)k i= c(x-x 。
)c(xx °) = k 2x 。
(1) (2)消除中间变量有c (总- k 2)x 。
- k ik zx 。
二 ckix(3) 对图(c)所示系统,由牛顿定律有c ( X - x 。
) k i( X - x 。
)= k zx 。
1c x°+ ( ki+ k 2)x °=cx+ kix2.3 求出图(题2.3)所示电系统的微分方程。
(a)图(题2.3)解:(1)对图⑻ 所示系统,设j 1为流过R 的电流,j 为总电流,则有1 u 厂 R ?iidtC2□ 一 u 。
二 R i j i对图(b)所示系统,引入一中间变量 x,并由牛顿定律有RiCiUiUnR解:设系统输入为M (即),输出二(即),分别对圆盘和质块进行动 力学分析,列写动力学方程如下:1U i-U 。
(i-i i)dtC1消除中间变量,并化简有C 1R 2U(1RC ) U 。
-= 0^+(肯+ C2)⑵ 对图(b )所示系统,设i 为电流,则有1CR 2U 。
《控制工程基础》第3版-课后答案解析

lim e(t)
s0
lim
s0
sE(s)
lim s s0 1
G(s)
Xi (s)
所以,输入为 xi2 sin 6t 1(t), ess2 0.8
(对此题来说,还有一种办法:如果记得对于一阶惯性环节, 当输入为阶跃函数,t=4T时输出为输入的98%,则由放入水 中1min时为输入的98%可直接得出: T=1/4=0.25(min)
uo (30) 1 e 4 1V
arctan 1 2 arccos , cos
arctan 1 2 arccos , cos
3—19单位阶跃输人情况下测得某伺服机构的响应为
试求:(1)系统的闭环传递函数; (2)系统的无阻尼自振角频率及阻尼比。
解:ui (t) i(t)R1 uo (t)
uo (t)
1 c
i(t)dt i(t)R2
对方程式进行拉氏变换得:
U
i
(
s)
I (s)R1
UO (s)
UO (s)
1 Cs
I (s)
I (s)R2
Uo (s) R2Cs 1
消去I(s),得:Ui (s) (R1 R2 )Cs 1
Ds( x2 xo ) k2 xo
x2
Ds k2 Ds
xo
k1 x1
k1Ds k1k2 Ds
xo
k2 xo
(k1Ds k2 Ds k1k2 ) xo k1Dsxi
X o (s)
k1Ds
X i (s) (k1 k2 )Ds k1k2
《控制工程基础》第二版课后习题答案
第二章习题解答a) b)c——II— -------------- oC、1 i\Ro J pa)1必)=i(t)RRC _ %(" + u0(if = RC—曲(f) dt dt- ■Bb)M)=冲务甜("7 G)】} Mf)=fK(t) = Kx o(t)~iR o-i = 1R +4— f/?r二R严肖"吗=心站+u o C)R\R2C ~~ U n(^)+(^1 + R Z)U O0)= R&H 亍气Q) + R/i Q) at atKi f\({\ Bf dXj dx o、dt dt > Mld) d d临也吸临⑷+W)―吋2-^^^_]]_ 纟K (曲= A?2 (X 0 一 X } = B仗严心怡£陀©+“K 州(0=曲Q”K]K 円⑴dtdt10G02町 _9_-cLPQd 一%二遢十汕 itj =也十迢2dxdt17 G(5) =+ 5S 7 + 9$+ 7(Z l)(g +2)加]州2 £早+ (刚裙2 +旳坷+朋2*1 +砒2厉)今¥t/N+ (料《2 + 粮[K \ + BjS 》+ 〃1虽 + B2B3) &三川r+ (隔 + K 岛 + K 2B { + K% 爭 + K 、K 血 di二严 3dtJ + c@+Q )M +卯G(»E + 2捉£+1)? (£+3)3 辭 +25^8占(& +X| X 3")一3 一场鲁办J dt j83 GM )={$+□)($+帶E _a 1 c —b= ------------------ H ------(a-b)2 s + a a-b (5+6)2 (m —方尸 £+方8&⑷—用◎十2)(2十2f 十4)g(t) = £"[G<s)] = 1-2e~^ 十 e~x casVif, i H 0的4[G (帕和一遇型za~c 1g(z)=£-1[G(i)] = -_小+ -_ +- (d -by L@ ~^r a7 G(s) = ——5(x¥ + l)2 (-S + 3)_ 2 1 J 113 1 ~ 3 S 12 5 + 32(£ + l)2 45 + 1 <31 \—+ —/ e 就2丿2 ig ⑴=£T[G(9]=T 年号e _3r- 丸r>0■< />o 54 1i-2^—-F s £+ 2 s 1 +4\2士十(卄1乎+?1 1~2~ 13(恥吊P 血再1 s<D 2 S 2十血'= £+2 + ———{盼如2)g (t )= A _1[Gf5)] = 4s (r )+ 28(0+ 2k-&亠,r>oat242 x\t) - x(f) = 4sin/ + 5cos2r s x(0) = 1, x*(0) =-2h{7) + 2^(O+5X(0 = 3, X (0) = 0. /(0) = 01V2 2-肮(0)-玖 0) - X(f) = 4—^ + 5—^Z + l E+4 ^-2+4—!—+ 5^—M-U 2+4 s^i(s-2)(s 7 +1)(v 2 十4)十4(2 十4)+5$(W +1)-lXW+l)(/+4)X0)=丄--2 --誉亠l s —1K ?2 +1 Q+4x(f)=L ,+e r -2sin/—cos2/» t>0 3 Q X(s)+2sX(s) + 5X(s)=- s217OV+l)(A+2)0.6--0.6 1S'^ s ($ + 1尸+4M/)=(L6—OWL cos1^0.3e_f sin2c t>0*叫+2$+疔sI M +1= 0,6--0.6—二——03 _s (s+1)' 4 4 G+l”+4fl^+(l+b l^)(一+H Ish (I十 b 賀)(1—fl +^1嘗) ——® O S 丄A)ao3涉十朋+ KJ益(的-§誠⑻=(月弭+ KjXf ($)⑷=(伽+ KjX(R(恥+KXd”K』(s + K^)(B^ s + KJ + K\ R、s6b叱(4予(f)-怎(0-禹(0 .农⑴二恥(f)I馆(0二心比⑴-艾⑴]!如皆加)=陀)xz=乔二耳⑶-%⑸-压戈㈤F K^)=K{X O(S)同=忑[兀(町-*(舟]_ffl$Cl 2-0血⑴1Bs念(f)Rib)o-^附(f)o—1CG021mv2血(f)IId)讹f)-o/脚(f)二浙go-尤;(f)]办⑴二忌⑴-入⑹ 齐2(彳)=屍竝⑴儿⑴二丄[為㈤+耳㈤ms>耳(刀=銅心)-儿(创&©)=司尤⑷—血⑴]伦㈤=竝A31.心)—*2-10Cl-HI—R\ &RiC,必)o—b)卞C:就f)-------------- od)>□—+= i 护!z jy/7(^f+ b)J —+ 切”=(l)°n31~~|__H[—o―[J G)1?衍i"+ (T + ^3^)(1+訓。
《控制工程基础》第二版课后习题答案
第一章习题解笞U]>U2 U\ U2第二章习题解答2-1a) b)d)f)L^f| 忙d)f\ — fl =^2X O严(f)=$(M+E ⑴虑 如(f) =iQ)RRC^-u o (t)^u o (t) = RC^-u^t) at at fs (r)=B 低[xi (f) -曲(幼 j/B (t)=fK (t) = KXo(t) B dB d 『八10602斤不%()+%©二斤击可()占dR^c —% (0+ (*i + 心)% ⑴=邛应 ~u i (0+ R 2u t (0 atati =i R +,C u o =IR?:R R 严冃3宙 % =gR\ +u oa)=K ](旳一兀)+」:dx o ](J?l + J?2)C —«c (!)+ %("■ R Q C — Wj(O + tti (Oat at(K[ + K2)B — x o (t)+ K\K2X o (t)= K\R 〒曲(f)+ 琦心再(f)dt at10602a) b) c) Q © f)U Q —1/?2 + — j icit— Z/?| + iR-f H —J idte)dxK\% K i (兀 _ %) = K 》(兀)—x)=号二dtoB 2+ (®K° ++ B'B? + 场*3 + 水2〃?)& 2+ (K }B 2+K }B 3 + 心汝 + KM 巴2 + K }K 2X 2 dt3J S + 2用 + 8S-丘($ + 2)($戈+2$十4)广、■炉+ 5,2+9用+7E ($+恥 + 2)乡一rn\fU2K 2rdx { dx 2< dt dt ;/(O™-坷罕~_叭 dtdxj … 一 —- - K?x^ = m dtdx l dx 2dt dt护d 2x 2 2~d^ k,用典2+ (的+创坷+用2创+加2*3);?7皿乔对)13173 G($)= --------------- —(£+。
控制工程基础第三版习题答案_清华大学出版社
第二章2-1 解:(1): )](12[)](1[)](5[)]()4[()(t L t t L t L t t L S F ⋅+⋅++=δδ SS S S 215215022++=+++= (2): )25(253)(2++=s s S F (3): 11)(2++=-s e S F sπ(4): )}(1)6(1)]6(2cos 4{[)(5t e t t L S F t ⋅+-⋅-=-ππ5144512426226+++=+++=--S s Se S s Se ss ππ(5): Se S e S F ss 226600)(--+=+++= (6): )]4(1)90453cos(6[)(π-⋅--=t t L S F9636)]4(1)4(3cos 6[24224+=+=-⋅-=--S SeS Se t t L S Sππππ(7): )](18sin 25.0)(18cos [)(66t t e t t e L S F t t ⋅+⋅=--1001288)6(28)6(622222+++=++++++=S S S S S S (8): 99)20(52022)(262++++++=-s es s S F s π2-2解:(1): )(1)2()3221()(321t e e S S L t f t t ⋅+-=+++-=--- (2): )(12sin 21)(t t t f ⋅=(3): )(1)2sin 212(cos )(t t t e t f t ⋅+=(4): )1(1)1()(11-⋅=-=---t e S e L t f t s(5): )(1)22()(2t e e te t f t t t ⋅-+-=---(6): )(1215sin 15158))215()21(21515158()(2221t t e S L t f t⋅=++⋅=-- (7): )(1)3sin 313(cos )(t t t t f ⋅+=2-3 解:(1) 对原方程取拉氏变换,得:SS X x S SX x Sx S X S 1)(8)]0()([6)0()0()(2=+-+--⋅∙ 将初始条件代入,得:61)()86(1)(86)(6)(22++=++=+-+-S SS X S S SS X S SX S S X S48724781)86(16)(22+-++=++++=S S S S S S S S S X 取拉氏反变换,得:t t e e t x 42874781)(---+=(2) 当t=0时,将初始条件50)0(=∙x 代入方程,得:50+100x(0)=300 则x(0)=2.5对原方程取拉氏变换,得: sx(s)-x(0)+100x(s)=300/s 将x(0)=2.5代入,得:S300100X(S)2.5-SX(S)=+1005.03100)S(S 3002.5S X(S)+-=++=s s取拉氏反变换,得:-100t 0.5e -3x(t)=2-4解:该曲线表示的函数为:)0002.0(16)(-⋅=t t u则其拉氏变换为:se s U s 0002.06)(-=2-5 解:)0()0()(3)(2)(2)(30100==+=+i i x y t x dtt dx t y dt t dy 将上式拉氏变换,得:2332)()()()32()()23()(3)(2)(2)(30000++=+=++=+S S S X S Y S X S S Y S S X S SX S Y S SY i i i i23-S 32-S Z p ==∴零点极点又当 时)(1)(t t x i =S S X i 1)(=SS S S X S X S Y S Y i i 12332)()()()(00⋅++=⋅= 3212332)()0(2312332)()(limlim lim lim 000000=⋅++⋅=⋅=∴=⋅++⋅=⋅=∞∴∞→∞→→→S S S S S Y S y S S S S S Y S y s s s s2-6 解:(a )传递函数:132123233321123233321232333211111H G G G H G G H G G G G H H G G H G G G G H G G H G G G G R C+++=⋅++⋅+++⋅=(b )传递函数:(c)传递函数:(d)传递函数:32121212211211H G G H H G G H G H G G G R C++++=2-7 解:通过方块图的变换,系统可等价为下图:2-8 解:2-9解:(a)(b)(c)(d)(e)(f)(g)2-10解:(a)(b)(c)2-11解:(a)(b)(c)(d)2-12解:(a)(b)2-13 解:(a)(b)2-14 解:2-15 解:(1(2)2-16解:2-17解:2-18解:以题可画出方块图如下:2-19 解:2-20 解:2-21 解:(1)(2、3、4)缺第三章3-1解:3-23-33-4解:3-53-6解:3-7 解:3-8 解:3-9 解:3-103-113-12 解:3-13 解:3-14解:3-153-163-17 解:3-183-193-203-21 解:3-223-23 解:3-243-25 解:3-26、3-27 缺3-28解:3-29、3-30 缺3-31解:3-32、3-33缺第四章4-1解:4-3 解:4-4 解:4-6解:(a)(b)(c)(d)(e)4-74-8、4-9 缺4-10解:4-11解:4-12解:4-16解:4-17 缺4-18解:4-19、4-20、4-21 缺第五章5-15-2、5-3、5-4 缺5-55-6 缺5-75-85-115-125-13 缺5-145-15 缺5-16解:5-17 缺5-18 5-19解:5-20 5-25解:5-26 缺附题:设单位反馈的开环传递函数为)10)(2()5.0(10)(2+++=S S S S K S G试用乃氏判据确定该系统在K=1和K=10时的稳定性。
控制工程基础(董景新第2版)课后习题答案
第二章习题解
2-8: 对于题图2-8所示系统,分别求出
X 01 (s) ,X 02 (s) ,X 01 (s) ,X 02 (s)
X i1(s) X i2 (s) X i2 (s) X i1(s)
-
Xi1 + G1
G2
G3
X01
+
H2
H1
Xi2
+ +
+
G4
G5
G6
X02
-
1):求出 X 01 (s) X i1(s)
G(s)
=
1+
G1H
1
+
G
2H
2
G 1G 2 + G 1G 2 H
3
+
G 1G
2H
1H
2
第二章习题解
2-7:
求X0(s) 和Xi2(s)之间的闭环传递函数; 求X0(s) 和Xi1(s)之间的闭环传递函数;
Xi1 +
-
+
H3
② + Xi2
+
+
X0
G1
G2
G3
-
①
H2
③ H1
(1)解:第一步,回路 ② 后移
解:3 sY 0 (s ) − 3 y 0 (0 ) − 2Y0 (s ) = 2 sX i (s ) − 2 xi (0 ) + 3 X i (s )
又: y 0 (0 ) = xi (0 ) = 0
X i (s ) =
1 s
代入上式,得:
Y0 (s ) =
2s + 3s +
3 2
X
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Xt X0
k
题图
解:
1)求系统的传递函数 活塞的力平衡方程式为
经拉氏变换后有
k
xo
(t)
c
d dt
[
xi
(t)
xo
(t)]
解得传递函数为
kXo (s) cs[ X i (s) X o (s)]
G(s) X o (s) Ts X i (s) Ts 1
式中,T RC为时间常数。
由运算放大器组成的控制系统模拟电路图如图(题图所示,试求闭环传递函数Uc (s) / Ur (s)
题图 问题 2 质点振动系统。这是一个单轮汽车支撑系统的简化模型。 代表汽车质量,B 代表振动阻尼器, 为弹簧, 为轮子的质量, 为轮胎的弹性,建立质点平移系统数学
模型。 解答: 拉氏变换:
液压阻尼器原理如图(题图所示。其中,弹簧与活塞刚性联接,忽略运动件的惯性力,且 设 xi 为输入位移, xo 为输出位移,k 弹簧刚度,c 为粘性阻尼系数,求输出与输入之间的
R1R2C1C2s2 (R1C1 R2C2 R1C2 )s 1
(c)
Uc (s) Ur (s)
1 Cs
//( R2
Ls)
R1
1 Cs
//( R2
Ls)
R1LCs 2
R2 (R1R2C
Ls L)s
R1
R2
1
(R 1 ) // R
(d) Uc (s)
C2s
C1s
R
Ur (s) (R 1 ) // R 1 (R 1 ) // R 1 R 1
传递函数。
(2) 以N(s)为输入,当R(s) = 0 时,分别以C(s),Y(s),B(s),E(s) 为输出的闭环 传递函数。
(3) 比较以上各传递函数的分母,从中可以得出什么结论。
题图 解(1)以 为输入,当 N( )=0 时: 若以 C( )为输出,有
题图
若以 Y( )为输出,有
若以 B( )为输出,有
K0 θ
+15V -15V 10k
10k
30k — K1
20k
10k
10k
+ — K2
功放
+
K3
SM
TG
解: (1) (2)
题图 位置随动系统原理图
K0 θ
+15V -15V
=3
=2
系统结构图如下: (3)系统传递函数
设直流电动机双闭环调速系统的原理图如图(题图所示,要求: (1)分别求速度调节器和电流调节器的传递函数; (2)画出系统结构图(设可控电路传递函数为 K2 /(3s 1) ;电流互感器和测速发电机的
-
-
H3 G2
H1 H3
G4 G3 1+G3G4H4
H1
H3 -H3G4
G1G2G3 1+G3G4H4-G2G3H3
H3 -H3G4
解方法一:利用公式(),可得
X0(s) G4
X0(s) G4
X0(s) G4
方法二:利用方框图简化规则,有图(题)
求出图( 题图2 .11) 所示系统的传递函数 X o (S) / Xi (S) 。 解根据方框图简化的规则,有图(题)
题图 解:①图(a):由牛顿第二运动定律,在不计重力时,可得
整理得
将上式进行拉氏变换,并注意到运动由静止开始,即初始条件全部为零,可得
[
]
于是传递函数为
②图(b):其上半部弹簧与阻尼器之间,取辅助点 A,并设 A 点位移为 x,方向朝下;
而在其下半部工。引出点处取为辅助点 B。则由弹簧力与阻尼力平衡的原则,从 A 和 B 两 点可以分别列出如下原始方程:
C1
R1
C2
R2
R0
R0
R0
u
U
—K R0
—K
—K
解:
题图
式(1)(2)(3)左右两边分别相乘得 即
所以:
某位置随动系统原理方块图如图(题图所示。已知电位器最大工作角度max 330 0 ,功率 放大级放大系数为 K3 ,要求:
(1) 分别求出电位器传递系数 K0 、第一级和第二级放大器的比例系数 K1 和 K2 ; (2) 画出系统结构图; (3) 简化结构图,求系统传递函数o (s) /i (s) ;
若以 E( )为输出,有 (2)以 为输入,当 R( )=0 时:
若以 C( )为输出,有
若以 Y( )为输出,有
若以 B( )为输出,有
若以 E( )为输出,有 (3)从上可知:对于同一个闭环系统,当输入的取法不同时,前向通道的传递函数 不同,反馈回路的传递函数不同,系统的传递函数也不同,但系统的传递函数分母保持不 变,这是因为这一分母反映了系统的固有特性,而与外界无关。
消去中间变量 x,可得系统微分方程 对上式取拉氏变换,并记其初始条件为零,得系统传递函数为 ③图(c):以 的引出点作为辅助点,根据力的平衡原则,可列出如下原始方程: 移项整理得系统微分方程 对上式进行拉氏变换,并注意到运动由静止开始,即 则系统传递函数为
试建立下图(题图)所示各系统的微分方程并说明这些微分方程之间有什么特点,其中电
C1s
C2s
C1s
C2s
C1s
R 2C1C2 s 2 2RC1s 1
R 2C1C2 s 2 (2RC1 RC2 )s 1
求图( 题图 所示两系统的微分方程。
题图 解(1)对图(a)所示系统,由牛顿定律有
即
(2)对图(b)所示系统,由牛顿定律有 其中
求图( 题图 所示机械系统的微分方程。图中 M 为输入转矩,Cm 为圆周阻尼,J 为转动惯 量。圆周半径为 R,设系统输入为 M(即 M(t)),输出为 (即 ),
xc (t) (d )
题图
【解】: (a)
方法一:设回路电流为 i ,根据克希霍夫定律,可写出下列方程组:
消去中间变量,整理得:
ur
1 C
i dt
uc
uc R i
RC duc dt
uc
RC
dur dt
方法二:
U c(s ) U r(s )
R
R 1
Cs
RCs RCs 1
RC duc dt
求出图( 题图2 .10) 所示系统的传递函数 X o (S) / Xi (S) 。
Xi(s) +
题图Байду номын сангаас
H4G4
-
G1 -
G2
G3
+
H1
H3
-
H3
G4
H4G4
G1 + +
-
-
G2
G3
H1 H3 -H3G4
X0(s) G4
X0(s) G4
H4G4
Xi(s) -
Xi(s) -
-
G1 -
G2
G3
+
-
G1
压 ur (t) 和位移 xr (t) 为输入量;电压 uc (t) 和位移 xc (t) 为输出量;k, k1 和 k2 为弹簧弹性系数; f 为阻尼系数。
ur (t)
C R
(a)
uc (t)
xr (t)
f
k
xc (t) (b)
u r (t)
R1 R2 C
(c)
uc (t)
f
k1
k2
xr (t)
dur dt
ur
(d) 设阻尼器输入位移为 xa ,根据牛顿运动定律,可写出该系统运动方程
k1(xr xc ) k2 (xr xa )
k2 (xc
xa )
f
dxa dt
k1 k2 k1k2
f dxc dt
xc
f k2
dxr dt
xr
结论: (a) 、 (b) 互为相似系统, (c) 、 (d) 互为相似系统。四个系统均为一阶系统。
uc
RC
du r dt
(b) 由于无质量,各受力点任何时刻均满足 F 0 ,则有:
f(dxr dt
dxc ) dt
kxc
f k
dxc dt
xc
f k
dxr dt
(c)
Uc (s) Ur (s)
R2
1 Cs
R1
R2
1 Cs
R2Cs 1
R1 R2 Cs 1
(R1
R2 )C
duc dt
uc
R2C
题图 解:分别对圆盘和质块进行动力学分析,列写动力学方程如下:
消除中间变量 x,即可得到系统动力学方程
+k(c
)
求图( 题图 所示系统的传递函数(f(t)为输入,y2(t)为输出)。 解分别对 , 进行受力分析,列写其动力学方程有
对上两式分别进行拉氏变换有
消除 得
若系统传递函数方框图如图(题图 所示, 求: (1) 以R(s)为输入,当N(s) = 0 时,分别以C(s),Y(s), B(s),E(s) 为输出的闭环
试求下图(题图)所示各电路的传递函数。
ur (t)
_
ur (t)
_
R1
C
L
(a)
R1
R2 C
L
R2
uc (t)
_
uc (t)
_ (c)
ur (t)
_
ur (t)
_
R1
C1
R2
C2
(b)
uc (t)
_
C1
R
R C2
uc (t)
_
(d )
题图
【解】:可利用复阻抗的概念及其分压定理直接求传递函数。
1
