MATLAB实验六图形绘制
matlab实验指导2019-11-12

实验1 熟悉软件环境和基本的操作一、实验目的熟悉MATLAB运行环境和了解基本操作。
二、实验内容MATLAB的启动、操作界面组成1.熟悉MATLAB图形界面打开MATLAB,单击命令窗口菜单栏中的各个下拉菜单按钮,试使用各个按钮引出的选项;把光标移动到工具栏中各个图标上(不要按下),查看它们与菜单选项的对应情况。
2.熟悉MATLAB的基本命令。
在命令窗口中分别键入以下内容,以建立若干变量:A=[1 2;3 4;5 6]B=[7,8,9;10,11,12]C=[5 6 7;1 8 3];D=B+C问题1:如何输入一个矩阵变量的行元素和列元素?问题2:观察每行命令后是否加“;”,对显示执行结果有什么区别?键入以下命令或执行操作,查看效果,并体会命令功能:(1)工作空间管理。
whowhosclear A(2)路径编辑。
试用菜单File/Set Path将D盘根目录及其下的所有子目录和文件夹包含进来,设为搜索路径。
问题3:当前路径是什么?问题4:搜索路径是什么意思?(3)联机帮助help pausehelpwin(4)窗口清理。
先画出正弦函数在0-2π之间的图形,再用以下各种窗口清理命令,看每项命令都清除了什么。
figureplot(sin(0:0.1:6.28))claclfclose注意:figure为打开一幅图形图像窗口close为关闭当前图形图像窗口,而close all为关闭所有已打开的图形图像窗口。
(5)MATLAB基本矩阵操作演示playshow intro(6)MATLAB图形绘制演示playshow buckydem(7)MATLAB数学功能演示(快速傅氏变换)playshow fftdemo(8)MATLAB三维造型演示(茶壶演)playshow teapotdemo3.打开MATLAB命令窗口,键入demos,观看演示程序。
三、思考题1.将pi分别用15位数字格式、分数格式、十六进制格式、5位数字的科学计数法显示。
Matlab绘制图像

第一种方法 在Workspace中绘制
绘图基本线型和颜色
符号 y m c r g b w k 颜色 黄色 紫红 青色 红色 绿色 蓝色 白色 黑色 符号 . 。 x + * : -. -线型 点 圆圈 x 标记 加号 星号 实线 点线 点划线 虚线
绘图命令
绘图命令plot 主要是在数值计算中绘制函数图像。 绘制反函数图像非常容易。
绘图命令plot
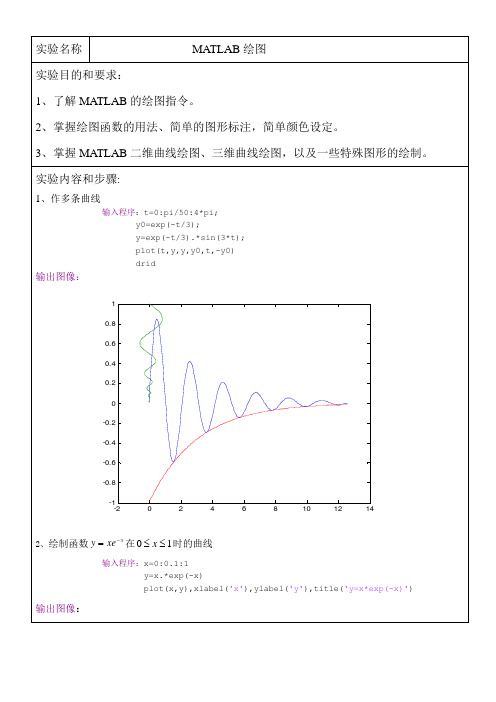
调用格式1:plot(x,y)
1. 首先定义自变量X的取值向量(横坐标) 2. 再定义函数Y的取值向量(纵坐标) 3. 用plot(x,y)命令给出平面曲线图。 在绘图参数中可以给出绘制图形的线型和颜 色的参数。例:plot(x,y,’r*’) 就是用红色的 ****线型绘图。
技巧
x=0:0.1:2*pi; y1=sin(x); y2=exp(-x); plot(x,y1,'--*',x,y2,':o'); xlabel('t=0 to 2\pi'); ylabel('value of sin(t) and e^{-x}') title('Function sin(t) and e^{-x}'); legend('sin(t)','e^{-x}') 后期的制作
ቤተ መጻሕፍቲ ባይዱ
绘出下面函数及其反函数的图像
1 1 y (x ) 2 x (1 x )
程序如下: x=1:0.001:5; %定义横坐标 y=1/2*(x+1./x); %定义纵坐标 plot(x,y,'r',y,x,'b') %红色画f(x) 蓝色画f(y).
Matlab实验

MATLAB实验报告学校:湖北文理学院学院:物理与电子工程学院专业:电子信息工程学号: 2013128182 姓名:张冲指导教师:宋立新实验一 MATLAB环境的熟悉与基本运算一、实验目的:1.熟悉MATLAB开发环境2.掌握矩阵、变量、表达式的各种基本运算二、实验内容1、学习使用help命令,例如在命令窗口输入help eye,然后根据帮助说明,学习使用指令eye(其它不会用的指令,依照此方法类推)2、学习使用clc、clear,观察command window、command history和workspace等窗口的变化结果。
3、初步程序的编写练习,新建M-file,保存(自己设定文件名,例如exerc1、exerc2、exerc3……),学习使用MATLAB的基本运算符。
三、练习1)help rand,然后随机生成一个2×6的数组,观察command window、command history和workspace等窗口的变化结果。
2)学习使用clc、clear,了解其功能和作用。
3)用逻辑表达式求下列分段函数的值4)求[100,999]之间能被21整除的数的个数。
(提示:rem,sum的用法)四、实验结果1)2)clc:清除命令窗口所有内容,数值不变;clear:初始化变量的值。
3)4)实验二 MATLAB数值运算一、实验目的1、掌握矩阵的基本运算2、掌握矩阵的数组运算二、实验内容1)输入C=1:2:20,则C(i)表示什么?其中i=1,2,3, (10)2)输入A=[7 1 5;2 5 6;3 1 5],B=[1 1 1; 2 2 2; 3 3 3],在命令窗口中执行下列表达式,掌握其含义:A(2, 3) A(:,2) A(3,:) A(:,1:2:3) A(:,3).*B(:,2)A(:,3)*B(2,:) A*B A.*B A^2 A.^2 B/A B./A3)二维数组的创建和寻访,创建一个二维数组(4×8)A,查询数组A第2行、第3列的元素,查询数组A第2行的所有元素,查询数组A第6列的所有元素。
MATLAB)课后实验答案-精简版.do

实验一1. 先求下列表达式的值,然后显示MATLAB 工作空间的使用情况并保存全部变量。
(1) 0122sin851z e =+(2) 21ln(2z x =,其中2120.455i x +⎡⎤=⎢⎥-⎣⎦(3) 0.30.330.3sin(0.3)ln , 3.0, 2.9,,2.9,3.022a a e e az a a --+=++=--(4)2242011122123t t z t t t t t ⎧≤<⎪=-≤<⎨⎪-+≤<⎩,其中t =0:0.5:2.52. 已知:34787,2033657327A B ⎡⎤⎡⎤⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦求下列表达式的值:(1) A+6*B 和A-B+I (其中I 为单位矩阵) (2) A*B 和A.*B (3) A^3和A.^3 (4) A/B 及B\A(5) [A,B]和[A([1,3],:);B^2] 3.设有矩阵A 和 B123453166789101769,111213141502341617181920970212223242541311A B ⎡⎤⎡⎤⎢⎥⎢⎥-⎢⎥⎢⎥⎢⎥⎢⎥==-⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦(1) 求它们的乘积C 。
(2) 将矩阵C 的右下角3×2子矩阵赋给D 。
(3) 查看MATLAB 工作空间的使用情况。
(1) 求[100,999]之间能被21整除的数的个数。
(2) 建立一个字符串向量,删除其中的大写字母。
ch='ABC123d4e56Fg9';则要求结果是:实验二1. 设有分块矩阵33322322E R A O S ⨯⨯⨯⨯⎡⎤=⎢⎥⎣⎦,其中E 、R 、O 、S 分别为单位矩阵、随机矩阵、零矩阵和对角阵,试通过数值计算验证22E R RS A O S +⎡⎤=⎢⎥⎣⎦。
解: M 文件如下;E=eye(3); R=rand(3,2); O=zeros(2,3);S=diag([1 2]);A=[E R a=[E,R+R*SO S] O ,S^2] A^2=a 2. 产生5阶希尔伯特矩阵H 和5阶帕斯卡矩阵P ,且求其行列式的值Hh 和Hp 以及它们的条件数Th 和Tp ,判断哪个矩阵性能更好。
MATLAB实验

MATLAB实验一:MATLAB语言基本概念实验实验目的:1. 熟悉MATLAB语言及使用环境;2.掌握MATLAB的常用命令;3.掌握MATLAB的工作空间的使用;4.掌握MATLAB的获得帮助的途径。
5.掌握科学计算的有关方法,熟悉MATLAB语言及其在科学计算中的运用;6.掌握MATLAB的命令运行方式和M文件运行方式;7.掌握矩阵在MATLAB中的运用。
实验方案分析及设计:本次实验主要目的是了解MATLAB的使用环境,以及常用的一些命令的使用;了解矩阵在MATLAB实验中的具体运用,以及相关的一些符号命令的使用。
实验器材:电脑一台,MATLAB软件实验步骤:打开MATLAB程序,将实验内容中的题目依次输入MATLAB中,运行得到并记录结果,最后再对所得结果进行验证。
实验内容及要求:1.熟悉MATLAB的菜单和快捷键的功能2.熟悉MATLAB的命令窗口的使用3.熟悉常用指令的使用format clc clear help lookfor who whos 4.熟悉命令历史窗口的使用5. 熟悉MATLAB工作空间的功能将工作空间中的变量保存为M文件,并提取该文件中的变量6.熟悉MATLAB获取帮助的途径将所有plot开头的函数列出来,并详细给出plotfis函数的使用方法1. 输入 A=[7 1 5;2 5 6;3 1 5],B=[1 1 1; 2 2 2;3 3 3],在命令窗口中执行下列表达式,掌握其含义:A(2, 3) A(:,2) A(3,:) A(:,1:2:3)A(:,3).*B(:,2) A(:,3)*B(2,:) A*BA.*BA^2 A.^2 B/A B./AA=[7 1 5;2 5 6;3 1 5]7 1 52 5 63 1 5>> B=[1 1 1; 2 2 2;3 3 3]1 1 12 2 23 3 3>> A(2, 3)6>> A(:,2)151>> A(3,:)3 1 5>> A(:,1:2:3)7 52 63 5>> A(:,3).*B(:,2)51215>> A(:,3)*B(2,:)10 10 1012 12 1210 10 10>> A*B24 24 2430 30 3020 20 20>> A.*B7 1 54 10 129 3 15>> A^266 17 6642 33 7038 13 46>> A.^249 1 254 25 369 1 25>> B/A0.1842 0.2105 -0.23680.3684 0.4211 -0.47370.5526 0.6316 -0.7105>> B./A0.1429 1.0000 0.20001.0000 0.4000 0.33331.0000 3.0000 0.60002.输入 C=1:2:20,则 C (i )表示什么?其中 i=1,2,3, (10)1到19差为2,i 代表公差3. 试用 help 命令理解下面程序各指令的含义:cleart =0:0.001:2*pi;subplot(2,2,1);polar(t, 1+cos(t))subplot(2,2,2);plot(cos(t).^3,sin(t).^3)subplot(2,2,3);polar(t,abs(sin(t).*cos(t)))subplot(2,2,4);polar(t,(cos(2*t)).^0.5)4计算矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡897473535与⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡638976242之和。
matlab--函数图形绘制实验报告1

实验报告课程名称: 数学实验学院名称: 数学与统计学院班级:姓名:学号:2012-2013 学年第学期数学与统计学院制(二)参数方程作图例2: 画出星形线{ 及旋轮线{ 的图形解: 输入以下命令:%星形线作图t=linspace(0,2*pi,5000);x=2*(cos(t)).^3;y=2*(sin(t)).^3;plot(x,y),grid;结果:%旋轮线作图t=linspace(0,4*pi,5000); x=2*(t-sin(t));y=2*(1-cos(t));plot(x,y),axis equal; axis(0,8*pi,0,5);grid;结果:(三)极坐标方程图形例3:画出四叶玫瑰线的图形。
知其极坐标方程: ρ=acos(2 )。
解: 取a=5做图。
在命令窗口输入下命令theta=linspace(0,2*pi);r=2*cos(2*theta);polar(theta,r)结果:(四)空间曲面(线)的绘制例4: 绘制双曲抛物面z= 。
解:将其化为参数方程:{ , 编写m文件运行以下命令r=linspace(-4,4,30);s=r;[u,v]=meshgrid(r,s);x=u;y=v;z=(u.^2-v.^2)./4;surf(x,y,z);bix on;结果:(五)空间曲线在坐标平面上的投影曲面和投影柱面例5: 画出螺旋线{ , 在xOz面上的正投影曲线的图形。
解:化为参数方程{ , 运行下列程序t=linspace(-2*pi,2*pi);x=10*cos(t);z=2*t;h=plot(x,z);grid;xlabel('x');ylabel('z');set(h,'linewidth',2);结果:(一)实验分析:(二)在本次实验中我们初步了解了matlab。
(三)学会了一些简单绘图。
(四)在编制中我们要很明确“点乘的重要性”。
MATLAB图形绘制

18
【例6-4】 在图形中添加文本字符串。 x=0:0.1:10; y=sin(x); plot(x,y) xlabel('x') ylabel('y=sinx') text(0,sin(0),‘\leftarrowsin(x)=0’) % 在指定位置添
加左箭头及字符串
text(3*pi/4,sin(3*pi/4),'\rightarrowsin(x)=0.707') text(7*pi/4,sin(7*pi/4),'\leftarrowsin(x)=-0.707')
x=x+(x==0)*eps; % 用一个“机器0”小数代替0
y=sin(x)./x; % 用可逻辑运算的sin(esp)/esp近似代替sin(0)/0的极限
plot(x,y)
xlabel('x')
% 在x轴上标注x
ylabel('y=sinx/x')
% 在y轴上标注y=sinx/x
title('门函数的频谱') % 在图形上方添加标题
9
④plotyy指令的常用调用格式 plotyy(x1,y1,x2,y2) plotyy(x1,y1,x2,y2,'f') plotyy(x1,y1,x2,y2,'f1','f2')
指令中出现的参数f、f1、f2等代表绘制数据的 方式,可选择plot、semilogx、semilogy、 loglog等不同的形式。
28
⑤二维区域图的绘制 区域图的绘制使用area指令,该指令用于
在图形窗口中显示一段曲线,该曲线可由一 个矢量生成,也可由矩阵中的列生成(其实 在MATLAB中,矢量是矩阵的一种特殊形式 ,即列数为1的矩阵就是矢量)。如果矩阵的 列数大于1,则area指令将矩阵中每一列的 值都绘制为独立的曲线,并且对曲线之间和 曲线与x轴之间的区域进行填充。这种图形 在MATLAB中就称为区域图。
MATLAB实验报告绘图
68 54 35;
45 25 12;
48 68 45;
68 54 69];
x=sum(t);
h=pie(x);
textobjs=findobj(h,'type','text');
str1=get(textobjs,{'string'});
val1=get(textobjs,{'extent'});
运行图像
4、采用模型 画一组椭圆
输入程序:th = [0:pi/50:2*pi]';
a = [0.5:.5:4.5];
X = cos(th)*a;
Y = sin(th)*sqrt(25-a.^2);
plot(X,Y),axis('equal'),xlabel('x'), ylabel('y')
title('A set of Ellipses')
oldext=cat(1,val1{:});
names={'商品一;'商品二';'商品三'};
str2=strcat(names,str1);
set(textobjs,{'string'},str2)
val2=get(textobjs,{'extent'});
newext=cat(1,val2{:});
xlable('sin(t)'),ylable('cos(t)'),zlable('t');
gridon;
输出图像
9、用MATLAB绘制饼图
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验6 图形绘制(3)
报告人: 王业成 年级: 机电131 学号: 2013012496 实验日期: 2015.4.27 报告完成日期: 2015.4.27 一、实验名称
图形绘制
二、实验目的:
熟悉MATLAB 的三维图形绘制函数。
三、实验内容:
subplot(2,2,1),sphere(3); title('n=3'),axis equal subplot(2,2,2), sphere(6); title('n=6'),axis equal subplot(2,2,3), sphere(10) title('n=10'),axis equal subplot(2,2,4), sphere(15); title('n=15'),axis equal
n=3
n=6
n=10
n=15
t=linspace(pi/2,3.5*pi,50);R=cos(t)+2; subplot(2,2,1);
cylinder(R,3), title('n=3'); subplot(2,2,2)
cylinder(R,6),title('n=6'); subplot(2,2,3)
cylinder(R),title('n=20') subplot(2,2,4)
cylinder(R,50),title('n=50')
[x,y]=meshgrid(-8:0.5:8,-10:0.5:10); R=sqrt(x.^2+y.^2)+eps; z=sin(R)./R; mesh(x,y,z);
n=3
n=6
n=20
n=50
x=-pi:0.15:pi; y=sin(x); subplot(2,1,1), H=bar(x,y); xx=get(H,'xdata'); yy=get(H,'ydata');
subplot(2,1,2),plot(xx,yy);
四、回答问题:
(回答实验指导书中提出的问题)
五、思考题:
1.试绘制出 2
2
2
2
)1(1)11)y ,x (f z y
x y
x +++
+-==的三维曲面图
和三视图
[x,y]=meshgrid(-1:0.1:1,-1:0.1:1); R=sqrt((1-x.^2)+y.^2)+eps; P=sqrt((1+x.^2)+y.^2)+eps; z=1./R+1./P; subplot(4,1,1) surf(x,y,z);
angle=[0,0;-90,0;0,90]; subplot(4,1,2) surf(x,y,z); z=1./R+1./P; view(angle(1,:)) title('主视图'); subplot(4,1,3) surf(x,y,z); z=1./R+1./P; view(angle(2,:)) title('左视图'); subplot(4,1,4) z=1./R+1./P; surf(x,y,z); view(angle(3,:)) title('俯视图');
2.绘出函数t
2
e t y ,sint x +==的慧星效果图。
x 1015
三维曲线
15主视图
-1
-0.8-0.6-0.4-0.200.2
0.40.60.8115
左视
图
-1
-0.8-0.6-0.4-0.200.20.40.60.81
俯视图
x=sin(t);
y=t.^2+exp(t);
figure(1)
comet(x,y);
figure(2)
plot(t,x,'k-',t,y,'k--');
title('The curves of x and y')
The curves of x and y
六、遇到的问题及解决:
三视图函数不知道,画有函数分析的图形时,不能确定函数变量的取值范围,在老师的指导下,知道了三视图函数是view,还有视角的情况,对于函数变量的取值范围,多练习多知识积累就可以学好的。
七、体会:
函数很多,但只要多看,多积累就可以很快学到很多知识,在写函数是也可以很快的调用自己想要的函数,还可以相互嵌套使用。
