离散系统数学模型
合集下载
离散时间系统的数学模型—差分方程
?用差分方程描述线性时不变离散系统?由实际问题直接得到差分方程?由微分方程导出差分方程?由系统框图写差分方程?差分方程的特点一
一．用差分方程描述线性时不变离散系统
线性：均匀性、可加性均成立；
x (n) 1
离散时间系统
y (n) 1
x 2 ( n ) 离散时间系统
c x (n ) + c x (n )
x1n+ x2n
x2 n
乘法器：
x1n x1n+ x2n
x2 n
x1 n
x1n x2 n
x2 n
系统框图
乘法器
xn
延时器
axn
a
yn
1
yn 1
E
xn a axn
yn
yn 1
z 1
五．差分方程的特点
(1)输出序列的第n个值不仅决定同一瞬间的输入样值， 而且还与前面输出值有关，每个输出值必须依次保留。
11
22
离散时间系统
y2 (n )
c y (n ) + c y (n )
11
22
时不变性
xn yn，xn N yn N 整个序列右移 N位
x(n)
y(n)
1 1 0 1 2 3 n
1
系统
1 o 1 2 3 4 n
x(n N )
y(n N )
1
1
系统
1 0 1 2 3
yt ynT yn
f t f nT f n
yn yn 1 ayn+ f n
T
yn 1 yn 1+ T f n
1 aT
1 aT
当前输出 前一个输出 输入
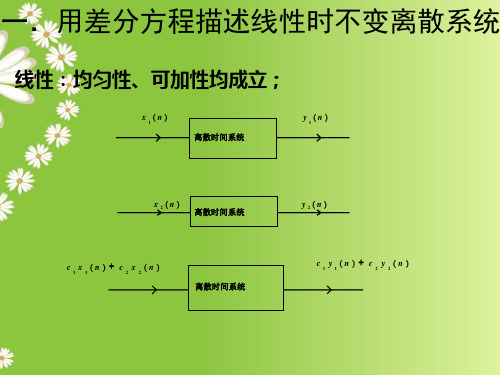
一．用差分方程描述线性时不变离散系统
线性：均匀性、可加性均成立；
x (n) 1
离散时间系统
y (n) 1
x 2 ( n ) 离散时间系统
c x (n ) + c x (n )
x1n+ x2n
x2 n
乘法器：
x1n x1n+ x2n
x2 n
x1 n
x1n x2 n
x2 n
系统框图
乘法器
xn
延时器
axn
a
yn
1
yn 1
E
xn a axn
yn
yn 1
z 1
五．差分方程的特点
(1)输出序列的第n个值不仅决定同一瞬间的输入样值， 而且还与前面输出值有关，每个输出值必须依次保留。
11
22
离散时间系统
y2 (n )
c y (n ) + c y (n )
11
22
时不变性
xn yn，xn N yn N 整个序列右移 N位
x(n)
y(n)
1 1 0 1 2 3 n
1
系统
1 o 1 2 3 4 n
x(n N )
y(n N )
1
1
系统
1 0 1 2 3
yt ynT yn
f t f nT f n
yn yn 1 ayn+ f n
T
yn 1 yn 1+ T f n
1 aT
1 aT
当前输出 前一个输出 输入
离散系统的数学模型
信号与系统
离散系统的数学模型
1.1 离散时间系统的数学模型
为激励信号,
为响应信号
离散时间系统 将激励序列转换为响应序列的系统，其 输入输出都是离散信号。在数学上，离 散系统的输入-输出关系可表示为
离散系统可以用差分方程来描述 差分方程 由输入序列、输出序列以及它们的差分所组
成的方程。 例如:
无反馈差分方程 某ຫໍສະໝຸດ 时刻的输出只与输入有关，而余 ，月利率为1%。写出结余 与净存款
的
关系式。
解： 当月的净存款
月末结余
月末利息
所以有
或
例5.3.2 试写出第k 节点电压 的数学模型。
解： 整理得
例5.3.3 假设离散时间系统的差分方程为 求其传输算子
解：算子方程为 即
所以
离散系统的模拟框图表示
差分方程的基本元算符号
例5.3.4 某离散系统的差分方程为
与该时刻之前的输出无关 。
有反馈差分方程 某一时刻的输出不仅与输入有关，还 与该时刻之前的输出有关。
系统的差分方程的一般形式 ：
前向差分方程
后向差分方程
差分算子 离散系统的传输算子
差分方程 算子方程
传输算子
系统的输入-输出模型
1.2离散时间系统数学模型的建立
例5.3.1 某一银行按月结余。设第 个月末的结
试用模拟框图表示此系统。 解：系统的差分方程可化为 框图来表示为
信号与系统
离散系统的数学模型
1.1 离散时间系统的数学模型
为激励信号,
为响应信号
离散时间系统 将激励序列转换为响应序列的系统，其 输入输出都是离散信号。在数学上，离 散系统的输入-输出关系可表示为
离散系统可以用差分方程来描述 差分方程 由输入序列、输出序列以及它们的差分所组
成的方程。 例如:
无反馈差分方程 某ຫໍສະໝຸດ 时刻的输出只与输入有关，而余 ，月利率为1%。写出结余 与净存款
的
关系式。
解： 当月的净存款
月末结余
月末利息
所以有
或
例5.3.2 试写出第k 节点电压 的数学模型。
解： 整理得
例5.3.3 假设离散时间系统的差分方程为 求其传输算子
解：算子方程为 即
所以
离散系统的模拟框图表示
差分方程的基本元算符号
例5.3.4 某离散系统的差分方程为
与该时刻之前的输出无关 。
有反馈差分方程 某一时刻的输出不仅与输入有关，还 与该时刻之前的输出有关。
系统的差分方程的一般形式 ：
前向差分方程
后向差分方程
差分算子 离散系统的传输算子
差分方程 算子方程
传输算子
系统的输入-输出模型
1.2离散时间系统数学模型的建立
例5.3.1 某一银行按月结余。设第 个月末的结
试用模拟框图表示此系统。 解：系统的差分方程可化为 框图来表示为
信号与系统
7-4离散系统的数学模型全篇
如何建立采样系统的差分方程，将在“脉冲 传递函数”小节中讨论。
2. 线性常系数差分方程及其解法
c(k
)
a1c(k b1r(k
11))ba22rc((kk22))bamnrc((kk
n) m)；
n
m
c(k) aic(k i) bjr(k j)；
i 1
j 1
后向差分方程：时间概念清楚，便于编制程序。
c(kn) a1c(kn 1) a2c(kn 2) anc(k) b1r(kn 1) b2r(kn 2) bmr(kn m)；
n
m
c(k n) aic(k n i) bjr(k n j)；
i 1
j 1
前向差分方程：便于讨论系统阶次、使用Z变换 法计算初始条件不为零的解。
上述几个差分方程在书写上都很烦琐，为书 写简便可采用时间移动算子。
0.1 0.4 16k 0.3 81k
c(nT
)
0.1 0.8 16k 0.1 1.6 16k
0.9 81k 2.7 81k
0.1 3.2 16k 8.1 81k
k 0, 1, 2, 3, 4, ；
n 4k
n 4k 1 ； n 4k 2
n 4k 3
3. 脉冲传递函数(定义、意义) 使用 脉冲传递函数，便于分析和校正线性离
c(k) 0.5c(k 1) 0.5c(k 2) r(k)； r(k) 1(k)； c(k) 0, k 0；
试用递推法计算输出序列c(k)，k= 0,1,2,…。
解例7采-16用-1递续推关系 c(k) = 1+0.5c(k-1)– 0.5c(k-2)；
c(0) 1； c(1) 1 0.5 1.5；
c(2) 1 0.51.5 0.5 1.25； c(3) 1 0.51.25 0.51.5 0.875；
2. 线性常系数差分方程及其解法
c(k
)
a1c(k b1r(k
11))ba22rc((kk22))bamnrc((kk
n) m)；
n
m
c(k) aic(k i) bjr(k j)；
i 1
j 1
后向差分方程：时间概念清楚，便于编制程序。
c(kn) a1c(kn 1) a2c(kn 2) anc(k) b1r(kn 1) b2r(kn 2) bmr(kn m)；
n
m
c(k n) aic(k n i) bjr(k n j)；
i 1
j 1
前向差分方程：便于讨论系统阶次、使用Z变换 法计算初始条件不为零的解。
上述几个差分方程在书写上都很烦琐，为书 写简便可采用时间移动算子。
0.1 0.4 16k 0.3 81k
c(nT
)
0.1 0.8 16k 0.1 1.6 16k
0.9 81k 2.7 81k
0.1 3.2 16k 8.1 81k
k 0, 1, 2, 3, 4, ；
n 4k
n 4k 1 ； n 4k 2
n 4k 3
3. 脉冲传递函数(定义、意义) 使用 脉冲传递函数，便于分析和校正线性离
c(k) 0.5c(k 1) 0.5c(k 2) r(k)； r(k) 1(k)； c(k) 0, k 0；
试用递推法计算输出序列c(k)，k= 0,1,2,…。
解例7采-16用-1递续推关系 c(k) = 1+0.5c(k-1)– 0.5c(k-2)；
c(0) 1； c(1) 1 0.5 1.5；
c(2) 1 0.51.5 0.5 1.25； c(3) 1 0.51.25 0.51.5 0.875；
第03章线性离散系统的数学模型
3.2.2 差分方程解 =通解+特解
➢ 通解是齐次方程的解，为零输入解，代表系统在无外力 作用下的自由运动，反映了离散系统自身的特性。
➢ 特解是由非零输入产生的解，对应于非齐次方程的特解， 反映了系统在外作用下的强迫运动。
差分方程求解有两种方法：解析法与递推法。
解法一：递推法——从初始值递推求解
相似变换 初值定理 终值定理 实卷积定理 复卷积定理
L[ x(at )] 1 X ( s )
aa
lim x (t ) lim sX ( s )
t0
s
lim x (t ) lim sX ( s )
t
s0
L[ x1 (t ) x 2 (t )] X 1 ( s ) X 2 ( s )
L[ x1 (t ) x 2 (t )]
例 y(k2)2y(k1)5y(k)0,求通解。 解：特征方r程 2 2r50， 有一对共轭 1复 j2根 5ejarc2t， g 则通解为y(k)c1(1j2)k c2(1j2)k。
例y(k2)4y(k1)4y(k)0,求通解。 解：特征方 r2程 4r40，有二重 2，根 则通解为 y(k)c1(2)k c2k(2)k。
它的y ( 齐 k n ) a 1 次 y ( k n 1 方 ) a n 程 y ( k ) 0 为 它 的 特 rn a 1 征 rn 1 a 方 2 rn 2 程 a n 为 0 有n个特征根： （1）若解为 n个单根 r1 , r2 ,, rn ,则方程通解为：
y(k) c1r1k c2r2k cnrnk； （2）若解有m重根，则m重根的解的形式为
1 2
X1(s) X 2(s)
3.4.4 Z反变换
1、 长 除 法
➢ 通解是齐次方程的解，为零输入解，代表系统在无外力 作用下的自由运动，反映了离散系统自身的特性。
➢ 特解是由非零输入产生的解，对应于非齐次方程的特解， 反映了系统在外作用下的强迫运动。
差分方程求解有两种方法：解析法与递推法。
解法一：递推法——从初始值递推求解
相似变换 初值定理 终值定理 实卷积定理 复卷积定理
L[ x(at )] 1 X ( s )
aa
lim x (t ) lim sX ( s )
t0
s
lim x (t ) lim sX ( s )
t
s0
L[ x1 (t ) x 2 (t )] X 1 ( s ) X 2 ( s )
L[ x1 (t ) x 2 (t )]
例 y(k2)2y(k1)5y(k)0,求通解。 解：特征方r程 2 2r50， 有一对共轭 1复 j2根 5ejarc2t， g 则通解为y(k)c1(1j2)k c2(1j2)k。
例y(k2)4y(k1)4y(k)0,求通解。 解：特征方 r2程 4r40，有二重 2，根 则通解为 y(k)c1(2)k c2k(2)k。
它的y ( 齐 k n ) a 1 次 y ( k n 1 方 ) a n 程 y ( k ) 0 为 它 的 特 rn a 1 征 rn 1 a 方 2 rn 2 程 a n 为 0 有n个特征根： （1）若解为 n个单根 r1 , r2 ,, rn ,则方程通解为：
y(k) c1r1k c2r2k cnrnk； （2）若解有m重根，则m重根的解的形式为
1 2
X1(s) X 2(s)
3.4.4 Z反变换
1、 长 除 法
离散系统的数学模型
2326.4 离散系统的数学模型为研究离散系统的性能，需要建立离散系统的数学模型。
线性离散系统的数学模型有差分方程、脉冲传递函数和离散状态空间表达式三种。
本节主要介绍差分方程及其解法，脉冲传递函数的定义，以及求开环脉冲传递函数和闭环脉冲传递函数的方法。
有关离散状态空表达式及其求解，将在第8章介绍。
6.4.1 线性常系数差分方程及其解法对于线性定常离散系统，k 时刻的输出)(k c ，不但与k 时刻的输入)(k r 有关，而且与k 时刻以前的输入 ),2(),1(--k r k r 有关，同时还与k 时刻以前的输出 ),2(),1(--k c k c 有关。
这种关系一般可以用n 阶后向差分方程来描述，即∑∑==-+--=mj jni i j k r bi k c a k c 01)()()( (6-34)式中，i a ，i =1，2，…，n 和j b ，j ＝0，1，…，m 为常系数，n m ≤。
式(6-34)称为n 阶线性常系数差分方程。
线性定常离散系统也可以用n 阶前向差分方程来描述,即∑∑==-++-+-=+mj jni i j m k r bi n k c a n k c 01)()()( (6-35)工程上求解常系数差分方程通常采用迭代法和z 变换法。
1. 迭代法若已知差分方程式(6-34)或式(6-35)，并且给定输出序列的初值，则可以利用递推关系，在计算机上通过迭代一步一步地算出输出序列。
例6-10 已知二阶差分方程)2(6)1(5)()(---+=k c k c k r k c输入序列1)(=k r ，初始条件为1)1(,0)0(==c c ，试用迭代法求输出序列)(k c ， ,5,4,3,2,1,0=k 。
解 根据初始条件及递推关系，得0)0(=c 1)1(=c6)0(6)1(5)2()2(=-+=c c r c 25)1(6)2(5)3()3(=-+=c c r c 90)2(6)3(5)4()4(=-+=c c r c301)3(6)4(5)5()5(=-+=c c r c2. z 变换法233设差分方程如式(6-34)所示，对差分方程两端取z 变换，并利用z 变换的实数位移定理，得到以z 为变量的代数方程，然后对代数方程的解)(z C 取z 反变换，可求得输出序列)(k c 。
离散系统的数学模型与分析
2.2.3 系统的脉冲传递函数
e( z )
H1 ( z)
u( z)
e( z )
H1 ( z ) H 2 ( z )
H1 ( z ) H 2 ( z )
u( z)
H 2 ( z)
e( z )
H1 ( z)
H 2 ( z)
H1 ( z)
u( z)
e( z )
u( z)
e( z )
u( z)
e( z )
2.6 离散系统时域响应特性分析
2. 极点为复数
R( z ) 1
ci 1 z ci z G( z) z pi z pi 1
k
pi,i 1 pi e ji
ci,i 1 ci e ji
脉冲响应
c(k ) Z [G( z ) R( z )] ci pi (e j ( ki i ) e j ( ki i ) ) 2 ci pi cos(
u( z) H1 ( z ) 1 H1 ( z ) H 2 ( z )
H 2 ( z)
2.3 状态空间描述
2.3.1 离散系统的状态方程
连续系统的状态空间描述来自X (k 1) FX (k ) GU (k ) Y (k ) CX (k ) DU (k )
X (k ) x1 (k ) x2 (k ) xn (k )
2. w变换与劳斯稳定性判据 w变换
z w 1 z 1 或 w w 1 z 1
－－双线性变换
2.5 离散系统稳态误差分析
2.5.1 稳态误差的定义
r(k) e(k)
D(z)
u(k)
G(z)
c(k)
2.5.2 稳态误差的计算
§7.3 离散时间系统的数学模型—差分方程
i =−∞ n
2n − 1 ∇ sin nω = sin nω − sin(n − 1)ω = 2 sin cos ω 2 2
ω
∑δ (i ) = u(n)
n
i =−∞ n
∑ u(i ) = (n + 1)u(n)
2
n
1 ∑ iu(i ) = 2 n(n + 1)u(n) i =−∞
i =−∞
1 ∑ i u(i ) = 6 n(n + 1)(2n + 1)u(n) i =−∞
n代表序号
注意：微分方程近似写作差分方程的条件是样值间隔T 注意：微分方程近似写作差分方程的条件是样值间隔T 要足够小， 越小，近似程度越好。实际上， 要足够小， T越小，近似程度越好。实际上，利用计算 机来求解微分方程时，就是根据这一原理完成的。 机来求解微分方程时，就是根据这一原理完成的。 返回
返回
(四）稳定系统
有界输入、产生有界输出的系统称为稳定系统。 称为稳定系统 有界输入、产生有界输出的系统称为稳定系统。 稳定系统的充要条件：∑ h (n ) < ∞ 稳定系统的充要条件：
n = −∞ ∞
即：单位脉冲响应绝对可和。 单位脉冲响应绝对可和。
lim 注意： 注意： h( n ) = 0，只是系统稳定的必要条件， 只是系统稳定的必要条件，
n→∞
而非充分条件 而非充分条件。 充分条件。
返回
二、差分方程
在连续时间系统中， 在连续时间系统中，系统内部的数学运算关系可归结 为微分（积分）、乘系数、相加的关系， ）、乘系数 微分方程。 为微分（积分）、乘系数、相加的关系，即：微分方程。 在离散时间系统中，基本运算关系是延时（移位）、 在离散时间系统中，基本运算关系是延时（移位）、 乘系数、相加的关系， 差分方程。 乘系数、相加的关系，即：差分方程。 这是由于系统的组成以及所处理的信号的性质不同， 这是由于系统的组成以及所处理的信号的性质不同， 因此描述系统的数学手段也不同。 因此描述系统的数学手段也不同。 （一）数学模型的基本单元 数学模型的基本单元 （二）差分 （三）差分方程 （四）差分方程的建立 （五）差分方程的特点
2n − 1 ∇ sin nω = sin nω − sin(n − 1)ω = 2 sin cos ω 2 2
ω
∑δ (i ) = u(n)
n
i =−∞ n
∑ u(i ) = (n + 1)u(n)
2
n
1 ∑ iu(i ) = 2 n(n + 1)u(n) i =−∞
i =−∞
1 ∑ i u(i ) = 6 n(n + 1)(2n + 1)u(n) i =−∞
n代表序号
注意：微分方程近似写作差分方程的条件是样值间隔T 注意：微分方程近似写作差分方程的条件是样值间隔T 要足够小， 越小，近似程度越好。实际上， 要足够小， T越小，近似程度越好。实际上，利用计算 机来求解微分方程时，就是根据这一原理完成的。 机来求解微分方程时，就是根据这一原理完成的。 返回
返回
(四）稳定系统
有界输入、产生有界输出的系统称为稳定系统。 称为稳定系统 有界输入、产生有界输出的系统称为稳定系统。 稳定系统的充要条件：∑ h (n ) < ∞ 稳定系统的充要条件：
n = −∞ ∞
即：单位脉冲响应绝对可和。 单位脉冲响应绝对可和。
lim 注意： 注意： h( n ) = 0，只是系统稳定的必要条件， 只是系统稳定的必要条件，
n→∞
而非充分条件 而非充分条件。 充分条件。
返回
二、差分方程
在连续时间系统中， 在连续时间系统中，系统内部的数学运算关系可归结 为微分（积分）、乘系数、相加的关系， ）、乘系数 微分方程。 为微分（积分）、乘系数、相加的关系，即：微分方程。 在离散时间系统中，基本运算关系是延时（移位）、 在离散时间系统中，基本运算关系是延时（移位）、 乘系数、相加的关系， 差分方程。 乘系数、相加的关系，即：差分方程。 这是由于系统的组成以及所处理的信号的性质不同， 这是由于系统的组成以及所处理的信号的性质不同， 因此描述系统的数学手段也不同。 因此描述系统的数学手段也不同。 （一）数学模型的基本单元 数学模型的基本单元 （二）差分 （三）差分方程 （四）差分方程的建立 （五）差分方程的特点
数学模型之离散模型
离散模型的应用领域
计算机科学
离散模型在计算机科学中广泛 应用于算法设计、数据结构、
网络流量分析等领域。
统计学
离散模型在统计学中用于描述 和分析离散数据，如人口普查 、市场调查等。
经济学
离散模型在经济学中用于描述 和分析离散的经济现象，如市 场交易、人口流动等。
生物学
离散模型在生物学中用于描述 和分析生物种群的增长、疾病
强化学习与离散模型
强化学习通过与环境的交互来学习最优策略。离散模型可以用于描述环境状态和行为，为 强化学习提供有效的建模工具。
离散模型在人工智能中的应用
1 2
决策支持系统
离散模型在决策支持系统中发挥着重要作用，通 过建立预测和优化模型，为决策者提供科学依据 和解决方案。
推荐系统
离散模型常用于构建推荐系统，通过分析用户行 为和偏好，为用户提供个性化的推荐服务。
03
分布式计算与并行化
为了处理大规模数据集，离散模型需要结合分布式计算和并行化技术，
以提高计算效率和可扩展性。
机器学习与离散模型的结合
集成学习与离散模型
集成学习通过结合多个基础模型来提高预测精度。离散模型可以作为集成学习的一部分， 与其他模型进行组合，以实现更准确的预测。
深度学习与离散模型
深度学习具有强大的特征学习和抽象能力。将深度学习技术与离散模型相结合，可以进一 步优化模型的性能，并提高对复杂数据的处且依赖于过去误差项的平方。
GARCH模型
定义
广义自回归条件异方差模型（Generalized AutoRegressive Conditional Heteroskedasticity Model）的简称，是ARCH模型的扩展。
特点
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
s si
例4 已知 F ( s ) 12 ，求 F ( z ) 。 s 解:
N 1 , l 2 ， s1 0
2016/8/2
2 1 s 2 z 1 d s F (z) sT ( 2 1)! ds z e
查表得
y(kT) (1)k (2)k
(k 0,1,2,)
为了书写方便，通常将 kT 写成 k 。
第2章 线性离散系统 的数学描述和分析方法
本章主要内容
1.信号变换理论
2.线性离散系统的数学描述方法
3.线性离散系统的Z变换分析法
4.脉冲传递函数
5.线性离散系统的性能分析
2016/8/2 1
2．1 信号变换理论
1. 连续信号的采样和量化 采样过程
f (t )
f (t )
T
f (t )
f (t )
2016/8/2 14
留数法
若 F ( s ) 已知，具有N个不同的极点，有 l 个重极点
（ l =1，为单极点），则
1 d l 1 F (z) ds l 1 ( l 1 )! i 1
N
( s si ) l F ( s ) z sT z e
由线性定理: Z[ y(k 2)] Z[3 y(k 1)] Z[2 y(k )] 0 由超前定理: [z 2Y ( z ) z 2 y(0) zy(1)] 3[ zY ( z ) zy(0)] 2Y ( z ) 0
2016/8/2 19
代入初始条件，解得
Y (z) z z z z z 2 3 z 2 ( z 1)(z 2) z 1 z 2
k 0
令： 则：
2016/8/2
ze
Ts
F ( z ) Z[ f * ( t )] f ( kT ) z k
k 0
11
注意：
（1）只有采样函数 f * ( t )才能定义Z变换； （2）比较下面两式
f * (t ) f (0) (t ) f (1) (t T ) f (2) (t 2T )
f1 为 t 1T 时刻的单脉冲，脉冲的幅值为 f (1T ) ；……； 。
f k 为 t kT 时刻的单脉冲，脉冲的幅值为 f ( kT ) 。
则：
f k f (kT) (t kT)
只有在 t kT 时刻，才有 ( t kT ) 0，而在的 所有 t kT时刻，都有 ( t kT ) 0 。
f * (t ) 0.6 (t T ) 0.84 (t 2T ) 0.936 (t 3T )
2016/8/2
16
部分分式法
例6 用部分分式法求 F ( z ) 解：
F (z) A A2 1 z z 1 z 0.4
A1 ( z 1) 0.6 z 2 1.4 z 0.4
0
2016/8/2
T 2T 3T 4T 5T 6T 7T 8T
t /T
0
T 2T 3T
4T
5T 6T 7T 8T
t /T
2
图1
采样过程
在计算机控制系统中，采样信号 f * (t ) 是一数 字序列，可分解成一系列单脉冲之和。
f * (t ) f 0 f1 ＋f k
f 0 为 t 0T 时刻的单脉冲，脉冲的幅值为 f (0T ) ； 式中，
z pi
f (kT ) lim( z p )F ( z )z
k 1 i 1 z pi i
n 2, p1 1, p2 0.4
0.6 z k 0.6 z k f ( kT ) lim ( z 1) 2 lim( z 0.4) 2 z 1 z 1.4 z 0.4 z 0.4 z 1.4 z 0.4 1 (0.4)k
2．2
线性离散系统的数学描述方法
1. 差分方程
y(kT ) a1 y(kT T ) a2 y(kT 2T ) an y(kT nT ) b0 r (kT ) b1r (kT T ) b2 r (kT 2T ) bm r (kT mT )
t2
t3
t4
t5
t6
t7
t8
t
6 5 4 3
A4
A3
'
'
A5
'
A6
'
A7 A8
'
'
A2 A1
'
'
2 1
0
为量化过程。
2016/8/2
t1
t2
t3
t4
t5
t6
t7
t8
t
图3
量化过程
5
2. 采样定理
F ( j )
F ( j )
*
s / 2
0
s / 2
2 s
s
0
s
2 s
输入信号
k , r(kT) 0, k0 k0
初始条件 y(0) 2 ，试求解差分方程。 解：令：k 1,2,3 ，代入差分方程，得
y(0) 2, y(T ) 1, y(2T ) 3, y(3t ) 2, y(4T ) 6,
2016/8/2
10
2． 3
0.6 z 的Z反变换。 2 z 1.4 z 0.4
z 1
1
1
A2 ( z 0.4)
0.6 z 2 1.4 z 0.4
z 0.4
F (z)
z z z 1 z 0.4
2016/8/2
f (kT) Z 1[F ( z )] 1 (0.4)k
kT t
图2
对单位脉冲序列的调制
因此：
2016/8/2
f * ( t ) f ( kT ) ( t kT )
k 0
4
量化过程
6 5 4 3
f (t )
A4
A3
A2 A1
A5
A6 A7 A8
所谓量化，就是采用 一组数码（如二进制
2 1
0
q
t1
f (t )
*
码）来逼近离散模拟
信号的幅值，将其转 换成数字信号。这个 经量化使采样信号成 为数字信号的过程称
2016/8/2 18
3.用变换解差分方程
用变换求解差分方程主要用到变换的平移定理。 例8 用Z变换解下列差分方程：
y(k 2) 3 y(k 1) 2 y(k ) 0
初始条件为： y(0) 0, y(1) 1 解： 对上式进行Z变换得
Z[ y(k 2) 3 y(k 1) 2 y(k )] 0
将上式两端同时乘以 z 1 ,有
z 1F ( z ) z 1 z 2 z 3
①
②
①式减②式 (1 z 1 )F ( z ) 1
1 则： Z [1( t )] F ( z ) 1 1 z 2016/8/2
13
部分分式法 例3 已知
解: F ( s )
——线性离散系统的差分方程
r (t )
(s)
y (t )
r (k )
T
(s)
y (k )
T
（a）连续系统 图6
（b）离散系统 连续系统和离散系统
2016/8/2
9
2 . 差分方程的求解
例1 已知一个数字系统的差分方程为
y(kT ) y(kT T ) r (kT ) 2r (kT 2T )
s 2max
采样定理奠定了选择采样频率的理论基础，但对于 连续对象的离散控制，不易确定连续信号的最高频率。 因此，采样定理给出了选择频率的准则，在实际应用中 还要根据系统的实际情况综合考虑。
2016/8/2 7
3.采样信号的复现和采样保持器
保持器
保持器是一种基于时域外推原理、把采样信号转换成连 续信号，实现采样点之间的插值的元件。
(a)
G1 ( j )
(b)
C ( j )
F ( j )
F ( j )
*
C ( j ) F ( j )
s / 2
0
s / 2
s /2
0
s /2
(c )
(d )
图4
f (t ) 、 f * ( t ) 的频谱 F ( j ) 及从 F * ( j ) 恢复 F ( j )
零阶保持器
* e (t )
e * (t )
零阶保持器 (b)
e h (t )
eh ( t )
。
0
T
2T
t /T
0
T
(a)
2
T
2T
t /T
(c)
图5
零阶保持器的功能
零阶保持器采用恒值外推原理，把每个采样值 e(kT )一直 * 保持到下一个采样时刻 ( k 1)T ,从而把采样信号 e ( kT )变成 2016/8/2 8 了阶梯连续信号 eh ( t ) 。
（查表2—1 ）
17
留数计算法
0.6 z 例7 用留数计算法求 F ( z ) 2 的Z反变换。 z 1.4 z 0.4
根据留数定理 f ( kT ) Re s [ F ( z ) z k 1 ]z p
i 1
n
i
Re sF ( z )z k 1
n
z pi