arch_model函数的返回值
使用ARCH模型进行金融计算

使用ARCH模型进行金融计算ARCH模型是金融领域中常用的一种计量经济学方法,用于分析和预测金融时间序列数据的波动性。
ARCH模型的全称是自回归条件异方差模型(Autoregressive Conditional Heteroskedasticity Model),它能够捕捉到金融市场中的波动性聚集现象,帮助投资者更好地理解和应对市场风险。
首先,ARCH模型的基本思想是,金融市场中的价格和收益率并不是随机波动的,而是存在一定的波动性聚集现象。
也就是说,市场的波动性在某个时期内可能会比其他时期更高或更低。
ARCH模型通过引入条件异方差的概念,能够对这种波动性聚集进行建模。
ARCH模型的核心是条件异方差,即波动性的方差是与过去的波动性有关的。
在ARCH模型中,通过引入滞后期的平方误差项来捕捉波动性的变化。
具体来说,ARCH模型可以表示为:σt^2 = α0 + α1ε(t-1)^2 + α2ε(t-2)^2 + ... + αpε(t-p)^2其中,σt^2表示第t期的条件异方差,ε(t-i)表示第t-i期的误差项,α0、α1、α2...αp是模型的参数,p是滞后期数。
ARCH模型的核心思想是,过去的波动性会对当前的波动性产生影响,通过对过去波动性的建模,可以更好地预测未来的波动性。
ARCH模型的应用范围非常广泛,包括股票、债券、汇率、商品等金融市场中的各种时间序列数据。
例如,在股票市场中,投资者可以利用ARCH模型对股票的波动性进行建模,从而制定更合理的投资策略。
在外汇市场中,投资者可以利用ARCH模型对汇率的波动性进行预测,从而进行有效的风险管理。
此外,ARCH模型还可以与其他模型相结合,进行更复杂的金融计算。
例如,可以将ARCH模型与随机游走模型相结合,构建GARCH模型(GeneralizedARCH Model),从而更准确地描述金融市场中的波动性聚集现象。
GARCH模型在金融风险管理、期权定价等领域有着广泛的应用。
数学建模EViews中估计ARCH模型

(EViews4.0)的对话框
第15页/共75页
(EViews5)的对话框
第16页/共75页
与选择估计方法和样本一样,需要指定均值方程和方差
方程。
(一)均值方程 在因变量编辑栏中输入均值方程形式,均值方程的形式可 以用回归列表形式列出因变量及解释变量。如果方程包含常 数,可在列表中加入C。如果需要一个更复杂的均值方程,可 以用公式的形式输入均值方程。 如果解释变量的表达式中含有ARCH—M项,就需要点 击对话框右上方对应的按钮。EViews4.0中,只有3个选项: 1.选项None表示方程中不含有ARCH−M项;
恩格尔和克拉格(Kraft, D., 1983)在分析宏观数据时,发现这样一些 现象:时间序列模型中的扰动方差稳定性比通常假设的要差。恩格尔的结 论说明在分析通货膨胀模型时,大的及小的预测误差会大量出现,表明存 在一种异方差,其中预测误差的方差取决于后续扰动项的大小。
从事于股票价格、通货膨胀率、外汇汇率等金融时间序列预测的研究 工作者,曾发现他们对这些变量的预测能力随时期的不同而有相当大的变 化。预测的误差在某一时期里相对地小,而在某一时期里则相对地大,然 后,在另一时期又是较小的。这种变异很可能由于金融市场的波动性易受 谣言、政局变动、政府货币与财政政策变化等等的影响。从而说明预测误 差的方差中有某种相关性。
arch模型的原理 -回复

arch模型的原理-回复ARCH模型,即自回归条件异方差模型(Autoregressive Conditional Heteroskedasticity Model),是为了捕捉时间序列数据中异方差(heteroskedasticity)现象而生的一种经济计量模型。
在本文中,将一步一步回答“ARCH模型的原理”。
第一步,我们先了解什么是异方差。
异方差是指时间序列数据中,随着时间的推移,序列的方差出现明显变化的情况。
在金融市场,股票价格或金融资产的收益率常常呈现出异方差现象,即在某些时期波动较小,而在其他时期波动较大。
这种异方差现象对于风险度量和预测模型的构建都有很大的影响。
第二步,ARCH模型的基本思想是通过引入时间序列自己的过去序列的方差来解释序列的异方差现象。
也就是说,ARCH模型假设时间序列数据的方差是由过去的误差平方项决定的。
如果过去的方差较大,那么未来的方差也会较大;反之,如果过去的方差较小,那么未来的方差也会较小。
第三步,ARCH模型的具体形式是通过引入一个滞后期数的误差项平方的线性组合来表示方差的变化。
以ARCH(p)模型为例,其表达式为:σ^2_t = α_0 + α_1 * ε^2_(t-1) + α_2 * ε^2_(t-2) + ... + α_p * ε^2_(t-p)其中,σ^2_t表示时间t的方差,α_0为常数项,α_i(i=1,2,...,p)为参数,ε_t(t=1,2,...,p)为误差项。
在ARCH(p)模型中,根据过去p期的误差项平方的线性组合来估计当前时间的方差。
第四步,ARCH模型的参数估计可以使用最大似然估计法(Maximum Likelihood Estimation,简称MLE)进行。
MLE的思想是找到一组参数值,使得模型产生的数据的概率最大化。
对于ARCH模型,我们需要对误差项的平方进行参数估计,然后利用MLE来求解最优的参数。
第五步,ARCH模型的估计和预测过程需要进行模型检验。
math.h常用函数 -回复

math.h常用函数-回复math.h是C语言中的数学库,它包含了许多常用的数学函数,可以用于各种数学运算和问题的求解。
本文将以math.h常用函数为主题,逐步讲解各个函数的功能和用法。
我们将介绍的函数包括数学运算函数、三角函数、指数和对数函数、常数以及其他的辅助函数。
首先,我们来了解一下数学运算函数。
这些函数可以执行常见的数学运算,如加法、减法、乘法、除法、取余等。
其中常用的函数有:1. fabs(x):返回x的绝对值。
例如,当x为-5时,fabs(x)的返回值为5。
2. sqrt(x):返回x的平方根。
例如,sqrt(9)的返回值为3。
3. pow(x, y):返回x的y次幂。
例如,pow(2, 3)的返回值为8。
4. ceil(x):返回不小于x的最小整数值。
例如,ceil(3.2)的返回值为4。
5. floor(x):返回不大于x的最大整数值。
例如,floor(3.9)的返回值为3。
6. fmod(x, y):返回x除以y的余数。
例如,fmod(10, 3)的返回值为1。
接下来,我们将介绍一些常用的三角函数。
三角函数在几何学和物理学等领域经常被使用。
下面列出了一些常见的三角函数及其功能:1. sin(x):返回x的正弦值。
例如,sin(0)的返回值为0。
2. cos(x):返回x的余弦值。
例如,cos(0)的返回值为1。
3. tan(x):返回x的正切值。
例如,tan(0)的返回值为0。
4. asin(x):返回x的反正弦值。
返回值的范围是[-π/2, π/2]。
例如,asin(1)的返回值为π/2。
5. acos(x):返回x的反余弦值。
返回值的范围是[0, π]。
例如,acos(0)的返回值为π/2。
6. atan(x):返回x的反正切值。
返回值的范围是[-π/2, π/2]。
例如,atan(1)的返回值为π/4。
接下来,让我们来介绍指数和对数函数。
这些函数对于数字的增长和减弱方面非常有用。
arch模型
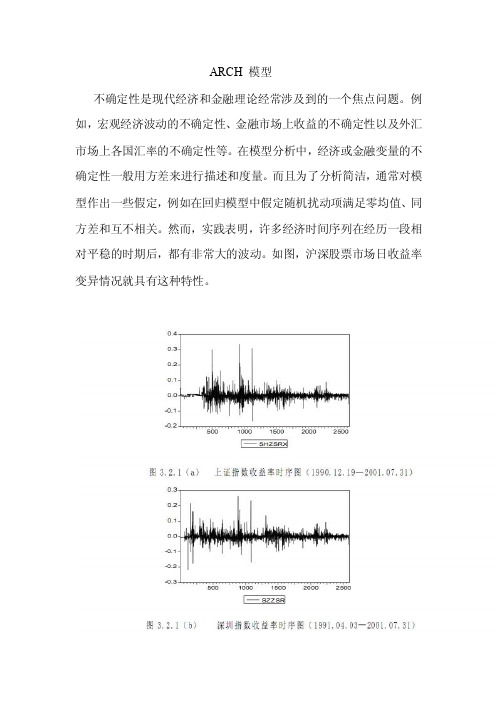
ARCH 模型不确定性是现代经济和金融理论经常涉及到的一个焦点问题。
例如,宏观经济波动的不确定性、金融市场上收益的不确定性以及外汇市场上各国汇率的不确定性等。
在模型分析中,经济或金融变量的不确定性一般用方差来进行描述和度量。
而且为了分析简洁,通常对模型作出一些假定,例如在回归模型中假定随机扰动项满足零均值、同方差和互不相关。
然而,实践表明,许多经济时间序列在经历一段相对平稳的时期后,都有非常大的波动。
如图,沪深股票市场日收益率变异情况就具有这种特性。
在这种情况下,同方差假定是不恰当的。
在这种情况下,人们关心的是如何预测序列的条件方差。
例如,作为资产持有者,他既关心收益率的预测值,同时也关心持有期内方差的大小。
如果一位投资者计划在第 t 时期买入某项资产,在第 t+1 时期售出,则无条件方差(即方差的长期预测值)对他来讲就不重要了。
对于这一类问题,可以使用自回归条件异方差模型 (autoregressive conditiona heteroskedastic model ,简称 ARCH 模型)来进行分析。
最早的 ARCH 模型是由 Robert Engle 于 1982 年建立的,因此它的发展历史不长。
但是,这种模型及其各种推广形式已被广泛应用于经济和金融数据序列的分析,ARCH 模型族已成为研究经济变量变异聚类特性的有效工具。
第一节 ARCH 模型的概念与性质 1、ARCH 过程ARCH 模型的一般性定义如下。
假设时间序列{}t y 服从如下回归模型:'t t ty x u ξ=+(8.1.1)其中 t x 是外生变量向量,它可以包含被解释变量的滞后项,ξ是回归参数向量。
如果扰动项序列{}t u 满足:11|~(0,)(,,)t t t t t t q u N h h h u u ---Ω= (8.1.2)其中:11122{,',,'}t t t t t y x y x -----Ω= 为t 时期以前的信息集。
ARCH与GARCH模型

3.1ARCH 与GARCH 模型例1. 自回回条件异方差模型3.咨询题的提出对异方差误差分布的修正能够导致更加有效的参数估量。
例如在回回方程εβββttttx x y +++=33221〔3.1.1〕中的εt的方差可能与xt22成正比,在这种情况下,我们能够使用加权最小二乘法,即令方程的两边同时除以变量xt2,然后用一般最小二乘法估量变化后的回回方程εβββ*23322121ttttttxx x x y +++=〔3.1.2〕在有些应用场合下,能够认为误差项是随时刻变化的同时依靠于过往的误差大小。
通货膨胀以及股票市场收益都属于这种情形。
在这些实际应用中,经常有大的误差与小的误差成群出现的情形,换句话讲,存在着一种特别的异方差形式,回回误差的方差依靠于过往不久误差的变化程度。
一个被广泛采纳以解决这类异方差模型是由RobertEngle 研究开展出来的,他认为用一个自回回条件异方差模型〔Autoregressiveconditionalheteroscedasticitymodel ,简计为ARCH 模型〕会提高有效性。
3.定义一般的,公式〔1〕中随机误差项t ε的方差2t σ能够依靠于任意多个滞后变化量it -ε〔i=1,2,…p 〕,记作ARCH 〔p 〕εαεαεαασ222221102.......p t p t t t---++++=〔3.1.3〕注重:(1) 为了保证在给定i t -2ε条件下,02≥t σ,就必须要求0≥α〔p ,,1,0 =α〕; (2) 要保证误差序列t ε的平稳性,系数必须满足:121 p ααα++。
3.检验3..1Breusch-Pagan 检验 在同方差的假设下条件下:SSR/2~X 2(1)依据Eviews3.1OLS 处理结果,可依据下式计算检验的统计量SSR/2查自由度为1时的2χ分布表,寻出给定显著性水平α条件下临界值,比立检验统计量与临界值的大小,以确定同意依旧拒尽模型同方差的零假设3.1.3.2拉格朗日乘子检验法〔LM〕差不多讨论过两种假设检验法:F 检验〔Wald 检验〕法(第5章)和似然比检验法。
GARCH模型及拟合案例

GARCH模型及拟合案例GARCH(Generalized Autoregressive Conditional Heteroskedasticity)模型是用于描述金融时间序列数据中的波动性的统计模型。
它是ARCH(Autoregressive Conditional Heteroskedasticity)模型的扩展,能够更好地捕捉到波动性的变化。
GARCH模型是基于时间序列的建模方法,它可以用来预测和解释金融市场的波动。
GARCH模型通常由两个方程组成,一个是用于建模均值的自回归模型,另一个是用于建模方差的GARCH模型。
GARCH模型的核心思想是通过自适应地调整方差的权重,对波动进行建模。
这种建模方法既能够反映出历史波动的影响,又能够根据当前的情况进行预测。
下面我们以一个实际的金融时间序列数据为例,来拟合一个GARCH模型。
我们选取了标准普尔500指数的日收益率数据作为例子。
首先,我们需要对数据进行预处理,计算每日的收益率,并将数据分为训练集和测试集。
import pandas as pdimport numpy as npimport arch#读取数据data = pd.read_csv('sp500.csv')#计算每日收益率data['returns'] = np.log(data['close'] /data['close'].shift(1))#划分训练集和测试集train_data = data[data['date'] < '2024-01-01']test_data = data[data['date'] >= '2024-01-01']接下来,我们可以使用arch包中的GARCH函数来拟合一个GARCH模型。
在拟合模型之前,我们首先需要选择一个合适的模型阶数。
时间序列模型stata 基本命令汇总..

时间序列模型结构模型虽然有助于人们理解变量之间的影响关系,但模型的预测精度比较低。
在一些大规模的联立方程中,情况更是如此。
而早期的单变量时间序列模型有较少的参数却可以得到非常精确的预测,因此随着Box and Jenkins(1984)等奠基性的研究,时间序列方法得到迅速发展。
从单变量时间序列到多元时间序列模型,从平稳过程到非平稳过程,时间序列分析方法被广泛应用于经济、气象和过程控制等领域。
本章将介绍如下时间序列分析方法,ARIMA模型、ARCH族模型、VAR模型、VEC模型、单位根检验及协整检验等。
一、基本命令1.1时间序列数据的处理1)声明时间序列:tsset 命令use gnp96.dta, clearlist in 1/20gen Lgnp = L.gnptsset datelist in 1/20gen Lgnp = L.gnp2)检查是否有断点:tsreport, reportuse gnp96.dta, cleartsset datetsreport, reportdrop in 10/10list in 1/12tsreport, reporttsreport, report list /*列出存在断点的样本信息*/3)填充缺漏值:tsfilltsfilltsreport, report listlist in 1/124)追加样本:tsappenduse gnp96.dta, cleartsset datelist in -10/-1sumtsappend , add(5) /*追加5个观察值*/list in -10/-1sum5)应用:样本外预测: predictreg gnp96 L.gnp96predict gnp_hatlist in -10/-16)清除时间标识: tsset, cleartsset, clear1.2变量的生成与处理1)滞后项、超前项和差分项 help tsvarlistuse gnp96.dta, cleartsset dategen Lgnp = L.gnp96 /*一阶滞后*/gen L2gnp = L2.gnp96gen Fgnp = F.gnp96 /*一阶超前*/gen F2gnp = F2.gnp96gen Dgnp = D.gnp96 /*一阶差分*/gen D2gnp = D2.gnp96list in 1/10list in -10/-12)产生增长率变量: 对数差分gen lngnp = ln(gnp96)gen growth = D.lngnpgen growth2 = (gnp96-L.gnp96)/L.gnp96gen diff = growth - growth2 /*表明对数差分和变量的增长率差别很小*/ list date gnp96 lngnp growth* diff in 1/101.3日期的处理日期的格式 help tsfmt基本时点:整数数值,如 -3, -2, -1, 0, 1, 2, 3 ....1960年1月1日,取值为 0;1)使用 tsset 命令指定显示格式use B6_tsset.dta, cleartsset t, dailylistuse B6_tsset.dta, cleartsset t, weeklylist2)指定起始时点cap drop monthgenerate month = m(1990-1) + _n - 1format month %tmlist t month in 1/20cap drop yeargen year = y(1952) + _n - 1format year %tylist t year in 1/203)自己设定不同的显示格式日期的显示格式 %d (%td) 定义如下:%[-][t]d<描述特定的显示格式>具体项目释义:“<描述特定的显示格式>”中可包含如下字母或字符c y m l nd j h q w _ . , : - / ' !cC Y M L ND J W定义如下:c and C 世纪值(个位数不附加/附加0)y and Y 不含世纪值的年份(个位数不附加/附加0)m 三个英文字母的月份简写(第一个字母大写) M 英文字母拼写的月份(第一个字母大写)n and N 数字月份(个位数不附加/附加0)d and D 一个月中的第几日(个位数不附加/附加0)j and J 一年中的第几日(个位数不附加/附加0)h 一年中的第几半年 (1 or 2)q 一年中的第几季度 (1, 2, 3, or 4)w and W 一年中的第几周(个位数不附加/附加0)_ display a blank (空格). display a period(句号), display a comma(逗号): display a colon(冒号)- display a dash (短线)/ display a slash(斜线)' display a close single quote(右引号)!c display character c (code !! to display an exclamation point)样式1:Format Sample date in format-----------------------------------%td 07jul1948%tdM_d,_CY July 7, 1948%tdY/M/D 48/07/11%tdM-D-CY 07-11-1948%tqCY.q 1999.2%tqCY:q 1992:2%twCY,_w 2010, 48-----------------------------------样式2:Format Sample date in format----------------------------------%d 11jul1948%dDlCY 11jul1948%dDlY 11jul48%dM_d,_CY July 11, 1948%dd_M_CY 11 July 1948%dN/D/Y 07/11/48%dD/N/Y 11/07/48%dY/N/D 48/07/11%dN-D-CY 07-11-1948----------------------------------clearset obs 100gen t = _n + d(13feb1978)list t in 1/5format t %dCY-N-D /*1978-02-14*/list t in 1/5format t %dcy_n_d /*1978 2 14*/list t in 1/5use B6_tsset, clearlisttsset t, format(%twCY-m)list4)一个实例:生成连续的时间变量use e1920.dta, clearlist year month in 1/30sort year monthgen time = _ntsset timelist year month time in 1/30generate newmonth = m(1920-1) + time - 1tsset newmonth, monthlylist year month time newmonth in 1/301.4图解时间序列1)例1:clearset seed 13579113sim_arma ar2, ar(0.7 0.2) nobs(200)sim_arma ma2, ma(0.7 0.2)tsset _ttsline ar2 ma2* 亦可采用 twoway line 命令绘制,但较为繁琐twoway line ar2 ma2 _t2)例2:增加文字标注sysuse tsline2, cleartsset daytsline calories, ttick(28nov2002 25dec2002, tpos(in)) /// ttext(3470 28nov2002 "thanks" ///3470 25dec2002 "x-mas", orient(vert)) 3)例3:增加两条纵向的标示线sysuse tsline2, cleartsset daytsline calories, tline(28nov2002 25dec2002) * 或采用 twoway line 命令 local d1 = d(28nov2002) local d2 = d(25dec2002)line calories day, xline(`d1' `d2')4)例4:改变标签tsline calories, tlabel(, format(%tdmd)) ttitle("Date (2002)") tsline calories, tlabel(, format(%td))二、ARIMA 模型和SARMIA 模型ARIMA 模型的基本思想是:将预测对象随时间推移而形成的数据序列视为一个随机序列,用一定的数学模型来近似描述这个序列。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
arch_model函数的返回值
ARCH模型是金融领域中常用的一种时间序列分析方法,它用来对时间序列中的波动性进行建模。
其中,arch_model函数是ARCH模型中常用的一个函数,该函数的返回值包括经过拟合的ARCH模型的拟合结果和一些统计信息,本文将围绕这个函数的返回值进行详细讲解。
首先,arch_model函数是Python的statsmodels包中的一个函数,它可以用来拟合各种形式的ARCH模型,包括GARCH、EGARCH、TGARCH等,其基本语法为:
arch_model(data, [lag], [vol], ...)
其中,data是需要拟合的时间序列数据;lag是进行拟合时考虑的滞后阶数,vol是ARCH模型中方差方程的形式。
函数返回的对象是一个ARCHModelResults类的实例,其中包含经过拟合的模型的结果和一些统计信息。
下面,我们将从返回对象的不同属性入手,逐步解析arch_model 函数的返回值:
1.模型的参数估计结果
使用ARCH模型研究金融数据的目的通常是为了研究其波动性,并根据波动性的特点来制定相应的风险管理策略。
因此,ARCH模型中的参数估计结果是最为重要的内容之一。
arch_model函数返回的ARCHModelResults类实例中包含了各个参数的估计值和其对应的标准误,同时还包括相应的置信区间和显著性水平。
这些参数的值可以用来判断模型的拟合质量,其中标准误的估计值越小,说明模型的拟合越好。
2.模型的统计信息
在分析ARCH模型时,需要对其进行各种统计检验来验证模型的有效性。
arch_model函数返回的ARCHModelResults类实例中包含了诸如对残差的Jarque-Bera检验、正态性检验、异方差性稳定性检验等常用的统计检验结果。
这些统计检验的结果可以反映模型的有效性和
拟合程度。
3.模型拟合数据信息
arch_model函数返回的ARCHModelResults类实例中还包括了一
些用于拟合数据的信息,例如残差、拟合值和标准化残差等。
这些数
据可以用来评估模型的预测能力和鲁棒性,例如可以将拟合值和实际
观测值进行对比,来评估模型对未来数据的预测能力。
总体来说,arch_model函数的返回值包含了可以用来评估ARCH
模型的多种信息,包括参数估计结果、统计信息以及拟合数据信息等。
在实际应用中,这些信息可以帮助我们对模型进行评估和选择,以便
制定相应的风险管理策略。
