ARCH等效应分析
人民币汇率与股价的ARCH效应检验及模型分析

在股票价格、汇率的应用分析 当中,常常有
大的误差与小的误差成群 出现的情况。为此 ,恩 格 尔 ( oe nl) 等 先 后 提 出 了 A C R br E g t e R H、 G R H、E A C 等 一 系 列 模 型。最 简 单 的 AC G RH G R H模型是 G R H(1, AC AC 1)模型 :
时刻的方差 (G R H项 ) AC 。在对 A C R H效应 的
的理论 :汇率决定 的流量导向模型和股票导向模
型。前者强调经常项 目或贸易平衡 , 认为存在 由 汇率到股价的反向关系;而后者强调资本项 目是
动态汇率的主要决定因素 ,认为存在 由股价到汇 率的正 向关系。国内外学者也已对两者的关系作 过 细 致 的 实 证 研 究 ,如 A t ( 0 1 通 过 p e 20 ) EA C G R H模型研 究 了印度的名义 汇率与股市 发 散性的关系 ,数据选择为从 19 — 00年的汇 9 1 20
率 ( 美元/ 印度卢 比)和股价指数 的收盘价 。研 有 E A C G R H模型 ( e o ,19 ) N ln 9 1 。 s
[ 收稿 日期 ]2 0 0 5一l 0 0一l [ 回日期 ]20 修 0 5—1 0 2— 7
[ 作者简介]陈雁云 (90 ) 17 一 ,江西吉水人,讲师,博士生 ,主要从事产业组织理论、金融产业研究。
应 ,则 建 立 G R H 及 E A C 模 型 。L S O、 A C GRH DT L R T D A 1 D A 2分 别 为 股 指 、美 元 D A 、L R T 、L R T
[ 摘要 ]随着人 民币汇率 弹性 的加 大 ,汇率 与股 价的 关联 效应 开始显 现 出来 ,有可 能导致 外 汇市场 、 股票市场乃至整个金融市场的紊乱 ,所 以两者 的关联研 究对于 整个金融 市场 的安 全与发展具 有较大 的现实 意义 。通过对人 民币各种汇率与股价 的逐 日数 据所作 的 A C R H效应检 验 ,得 出相应 的 G R H和 E A C AC GRH
arch模型
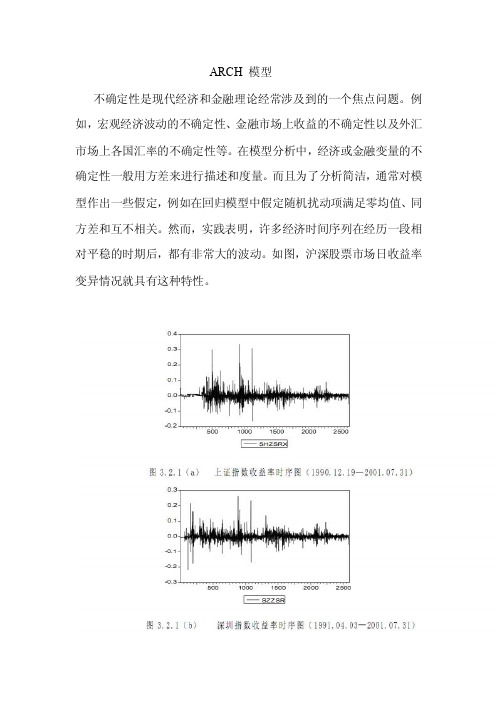
ARCH 模型不确定性是现代经济和金融理论经常涉及到的一个焦点问题。
例如,宏观经济波动的不确定性、金融市场上收益的不确定性以及外汇市场上各国汇率的不确定性等。
在模型分析中,经济或金融变量的不确定性一般用方差来进行描述和度量。
而且为了分析简洁,通常对模型作出一些假定,例如在回归模型中假定随机扰动项满足零均值、同方差和互不相关。
然而,实践表明,许多经济时间序列在经历一段相对平稳的时期后,都有非常大的波动。
如图,沪深股票市场日收益率变异情况就具有这种特性。
在这种情况下,同方差假定是不恰当的。
在这种情况下,人们关心的是如何预测序列的条件方差。
例如,作为资产持有者,他既关心收益率的预测值,同时也关心持有期内方差的大小。
如果一位投资者计划在第 t 时期买入某项资产,在第 t+1 时期售出,则无条件方差(即方差的长期预测值)对他来讲就不重要了。
对于这一类问题,可以使用自回归条件异方差模型 (autoregressive conditiona heteroskedastic model ,简称 ARCH 模型)来进行分析。
最早的 ARCH 模型是由 Robert Engle 于 1982 年建立的,因此它的发展历史不长。
但是,这种模型及其各种推广形式已被广泛应用于经济和金融数据序列的分析,ARCH 模型族已成为研究经济变量变异聚类特性的有效工具。
第一节 ARCH 模型的概念与性质 1、ARCH 过程ARCH 模型的一般性定义如下。
假设时间序列{}t y 服从如下回归模型:'t t ty x u ξ=+(8.1.1)其中 t x 是外生变量向量,它可以包含被解释变量的滞后项,ξ是回归参数向量。
如果扰动项序列{}t u 满足:11|~(0,)(,,)t t t t t t q u N h h h u u ---Ω= (8.1.2)其中:11122{,',,'}t t t t t y x y x -----Ω= 为t 时期以前的信息集。
第六章-ARCH和GARCH效应的检验
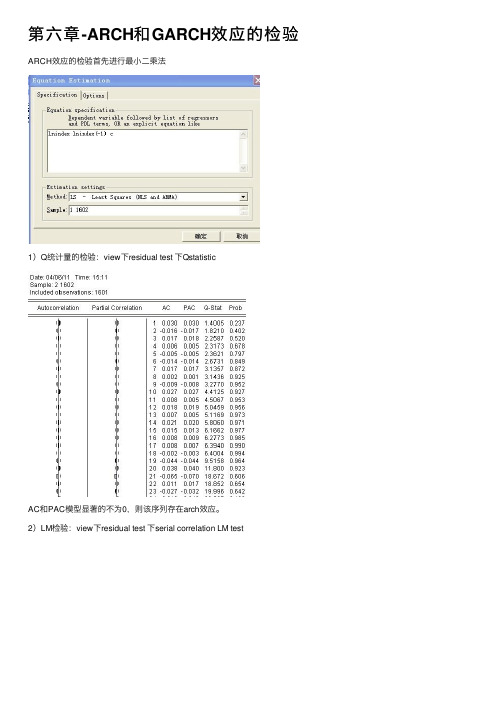
第六章-ARCH和GARCH效应的检验ARCH效应的检验⾸先进⾏最⼩⼆乘法
1)Q统计量的检验:view下residual test 下Qstatistic
AC和PAC模型显著的不为0,则该序列存在arch效应。
2)LM检验:view下residual test 下serial correlation LM test
以⼀个例⼦为例,主要检验以下变量:
GARCH模型的检验
右边的arch-m则为加⼊均值项,下拉项有两种形式:对数与条件标准差形式
均值下⾯的为有⼏种选项,默认为标准的garch模型,指数garch模型、成分garch模型
表⽰滞后阶数
门槛值的设定,只在指数garch模型的时候才有效
⽅差模型的设定,该变量的输⼊只要求输⼊“garch定义的⽅程之外的影响变量(除去残差的⽅差与滞后n阶的⽅差)”,没有则不⽤输⼊
设定的图为下列:
其结果如下:
解释:上⾯为均值⽅程,下⾯为⽅差⽅程。
基于图模型方法的ARCH效应检验

法 .与传 统 的方 法口 比较 ,本 文 的方 法更 直观 ,计算 也 比较 简单 .
1 图的基 本 概 念
定义 非 空 有 限集 是 一个 有 序 的 二元 对 ( E) , ,其 中 中 的元 素称 为 顶 点 , E 为 有 向边或
无 向边构 成 的集 合 ,可记 作 a b a—b. 设 X :( ( , ()… , d ) d维平 稳 时问序 , 假 X X , () ) 为
(, u - bf § - 或X ( JX ( l yfu{ 6 f . nt ) (, 嗟E - ) r e O f . 6 )x ( ) f ) x }) (1
其中 xAf:{ () <f表示子过程 XA —( ) XA , S j 在时刻 以前的信息.
对于平 稳 的 A C ( )模 型 : R H p
DOI 03 7  ̄is.643 6 . 1. . 1 :1 .8 5 . n17 —5 32 00 0 s 0 4 0
图模 型是 统计 学 中一 个 崭新 的研 究领 域 ,它将 传 统 的多 元统 计 中描述 多个 变 量 之 间关 系 的统 计 模 型 图形化 .图模 型 方法 的主要 思想 是 通过 揭示 图 中多维 随机 向量 的相 依 结构 来刻 画 向量之 间
的条件 独 立性 I J 年 来 ,该方 法 已成 为 高维数 据 统计 分 析 的重要 工具 .目前 ,该方 法 已被运 用 J .近 到 多 维 时间序 列 的研 究 中 ,详细 的背景 介 绍可 见文 献 f.】 46 .描述 多维 时 间序 列 的 图主 要有 偏 相关 图 ( C 图)、 时 间序列 链 图 ( S . )和 混合 图 ( x 图 ). P一 T C图 Mi.
作 者简介 :蔡风 景 (9 7 ) 17 一 ,男 ,浙江瑞 安人 ,讲 师,博士研究生 ,研 究方 向:数量经济 ,金融统计
我国股市ARCH效应的实证研究

!
金融与经济 !""#$ %! 金融与经济 $%%&’ ($
!"#"$% #"& %$’"’()
从表 ! 中对数收益率的描述性统计量可以看出,深 沪两市收益率序列的均值均较小,对应的标准差却较 ( ") 存在明显的尖峰、 厚尾特 大, 峰态系数 均为大于 # , 征,$% 统计量表明收益率序列拒绝正态分布假定,这与 大多文献的结论一致。两市日收益率的“尖峰厚尾 ”特 征, 初步判断两市序列 &’ 可能存在 (&)* 现象。两市收 益率的峰态系数均为大于 # 。对美国股市类似的研究显 (+) 示, 一般, 偏态系数 在 , -. # 左右, 峰态系数在 #. / 左 右, 与此相比, 我国股市的偏态系数更趋近于零, 尤其在
三、 实证分析 (一 ) 数据说明。
&’ # "? @ % ""!0 ’ ( " @ % #A &’ ( A 为保证条件方差 &’ B ? , 要求 "? B ? , …, "" & ? , " # $, 0, !, …, #A & ? , A # $, 0, %,
($ )
数据来源为沪深两市综合股价指数的日收盘价及 交易量, 时间跨度为 $888 年 P 月 $? 日至 0??9 年 P 月 P$ 日。选择依据为: 自 $888 年起, 上市公司初具规模; 股市 开始实施 $?X 涨跌停板限制和 S @ $ 的交易制度,制度 层面已经成形;股市结束了设立初期的大幅波动阶段, 逐渐步入正轨。 股票市场日收益率 ,’ 以相邻营业日收盘 的综合股价指数的对数一阶差分表示, 即: ,’ # 43E K Y’ L ( 43E K Y’ ( $ L 。数据处理采用 D7"5Z6[1 ? 软件。 (<,G)是两市股票日收益率的线性图。可以看 图$ 出,股票日收益率的波动比较平稳,没有大幅度的波 动。但收益率异常值出现的频率比较高,并较多情况集 中在一个特定的时期出现,显示出波动的聚类 (\4V6’5*";E) 现象, 即收益率序列随着时间的变化而变化, 同时, 表现出一段时间内的连续偏高或偏低。
arch效应一元回归模型

arch效应一元回归模型arch效应是指在金融市场中存在的时间序列的波动率聚集性现象。
在金融市场中,价格的波动性是投资者非常关注的一个指标,因为波动率的变化会对投资决策产生重要影响。
arch效应的提出为我们解释金融市场中价格波动性的聚集性提供了一个重要的理论框架。
arch模型是用来描述金融市场中的波动性聚集性现象的一种经济学模型。
它是由罗伯特·恩格尔(Robert F. Engle)于1982年提出的,因此也被称为“恩格尔的arch模型”。
arch模型是一种条件异方差模型,它假设金融时间序列的波动率是与其历史波动率相关的。
在arch模型中,波动率被认为是时间序列中的一个随机变量,它的变化是受到历史波动率的影响的。
arch模型可以用来对金融市场中的价格波动性进行建模和预测。
在arch模型中,条件异方差被认为是一个滞后变量的函数,它可以通过对历史波动率的估计来预测未来的波动率。
arch模型的核心思想是,当前的波动率与过去的波动率有关,较高的波动率往往会导致未来较高的波动率,较低的波动率会导致未来较低的波动率。
arch 模型可以帮助我们理解金融市场中的波动率聚集性现象,并对未来的波动率进行预测。
arch模型的估计方法主要有两种,一种是最大似然估计法,另一种是广义最小二乘法。
最大似然估计法是通过最大化似然函数来估计模型的参数,而广义最小二乘法是通过最小化模型的加权残差平方和来估计模型的参数。
这两种方法在实际应用中都有一定的优缺点,选择哪种方法要根据实际情况来决定。
arch模型在金融领域中有着广泛的应用。
它可以用来对金融市场中的风险进行度量和管理,可以帮助投资者进行风险控制和资产配置。
arch模型还可以用来对金融市场中的波动率进行预测,帮助投资者做出更准确的投资决策。
此外,arch模型还可以用来对金融市场中的高频数据进行建模和分析,以及对金融市场中的异常波动进行检测和解释。
尽管arch模型在金融领域中有着广泛的应用,但它也存在一些局限性。
上证指数收益率ARCH效应分析

上证指数收益率ARCH效应分析本文以上证指数为研究对象,选取了从2001年1月2日到2006年12月29日一个时间窗口总共1444个收盘价P i(i=1,2…..1444),并用这1444个收盘价计算出对数收益率Log(sh/sh(-1))为样本数据,利用Eviews软件对上证指数收益率ARCH效应进行分析。
一、序列平稳性检验将收盘价对数处理化后的对数收益率导入Eviews,利用单位根检验,经处理后的数据如图1所示。
图1、上证对数收益率ADF检验结果生成图如图可以看出,P值很小,且ADF统计值在1%,5%及10%的显著水平下,单位根检验的临界值分别为-3.964421,-3.412930及-3.128458,检验统计量值为-37.06543且绝对值很大,远小于相应的DW临界值。
从而拒绝H0,表明2001年1月2日到2006年12月29日的对数收益率为平衡时间序列,不存在单位根,也可通过下面的时序图看出。
由时间序列图可以看出,在相当长的时间内,上证对数收益率波动都比较小,可见序列是平稳的。
二、自相关性检验自相关系数表示的是当前值与滞后值的相关系数,偏自相关系数考虑了所有滞后值之后的预测能力而计算当前和滞后序列的相关性。
用EVIEWS 中的VIEW-CORRELOGRAM 生成自相关图,滞后阶数为25,通过自相关图可以看出,上证收益率具有自相关性。
图3、上证对数收益率相关图三、模型选择由模型定阶可以发现,在ARMA (p,q )中,分别选取(p,q )为(1,1),(2,2), ,(3,3),(3,4)几个数据进行模型估计,观察各模型的P 值和T 统计量。
图2、上证对数收益率时序图MA Backcast: 1MA Backcast: 1 2MA Backcast: 1 3MA Backcast: 0 3通过上面的数据可以看出,在选取P=3,Q=3时,所对应的P值最小,T统计量最大。
运用该ARMA(3,3) 输出结果如下图4 ARMA模型输出结果图结果图形,可写出输出结果的表达式:R t=0.7842εt-3-0.7773R t-3+μt(4.34) (-4.25) R2=0.003481 DW=1.941483四、异方差性检验赤池信息量准则AIC建立的ARMA模型,在P=3,Q=3时AIC值最小,故确定ARMA(3,3)来描述上证指数收益率。
基于上证指数的中国股市ARCH效应分析

基于上证指数的中国股市ARCH效应分析张婧【摘要】The frequent fluctuation of the stock price is one of the most obvious characteristics of the stock market. This paper takes the daily yield of Shanghai stock index as the research object to examine if the volatility of the stock price index has conditional heteroskedasticity or not. If the answer is "yes", the research of the stock index volatility of stock index yield can be done by the ARCH model.%股票价格频繁的波动是股票市场最明显的特征之一。
本文以上证指数每日收益率为研究对象,检验股票价格指数的波动是否具有条件异方差性,检验得到肯定回答后,通过ARCH族模型来研究股价指数收益率的波动性。
【期刊名称】《价值工程》【年(卷),期】2014(000)032【总页数】2页(P230-231)【关键词】波动性;ARCH模型;上证指数【作者】张婧【作者单位】中国农业银行公司与投行业务部,北京100005【正文语种】中文【中图分类】F830.910 引言股票价格频繁的波动是股票市场最明显的特征之一,2014年中国股市能够走出低迷,其前景将是一片光明吗?本文利用ARCH 模型族对中国上海股票市场股价收益率的波动进行实证分析,想发现其中的规律,为股民的投资决策做出指导。
金融市场上收益的风险和价格的不确定性往往是用方差来测试,大量对金融数据的实证研究表明收益率的变化存在波动的聚集性(Volatility clustering)现象,即存在条件异方差性。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
ARCH等效应分析
ARCH(Autoregressive Conditional Heteroskedasticity)等效应
分析是一种金融计量模型,用于研究时间序列数据中的波动性。
本文将介
绍ARCH等效应分析的基本原理和应用,并探讨其在金融市场中的重要性。
1.收集数据:首先,需要收集和整理所需的时间序列数据,这些数据
通常包括金融资产价格、收益或波动性等。
2. 模型设定:在进行ARCH等效应分析之前,需要根据经验和理论设
定一个适当的模型。
常用的模型包括ARCH、GARCH(Generalized Autoregressive Conditional Heteroskedasticity)和EGARCH (Exponential GARCH)等。
3. 参数估计:使用最大似然法(Maximum likelihood estimation,
简称MLE)或其他估计方法对模型参数进行估计。
这些参数包括条件方差
的自回归系数、条件方差的滞后期数等。
4.模型检验和诊断:在估计参数之后,需要对所建立的模型进行检验
和诊断。
常用的方法包括残差平方序列的平稳性检验、残差自相关图的观
察等。
5. 模型预测和应用:基于所估计的模型,可以进行波动性的预测和
应用分析,如计算风险价值(Value at Risk)等。
ARCH等效应分析在金融市场中具有重要的应用和意义。
首先,它可
以帮助研究人员和投资者理解金融市场中的波动性特征。
波动性是金融市
场中的关键概念,它反映了市场参与者对未来风险的预期和态度。
通过建
立ARCH模型,可以揭示金融市场中的波动性特征,帮助投资者更好地理
解市场风险。
其次,ARCH等效应分析可以用于风险管理和投资组合优化。
波动性
是计量金融和风险管理的核心问题之一、通过建立ARCH模型,可以预测
和估计资产收益或波动性的风险水平,从而为投资者制定合理的风险管理
策略和资产配置方案提供重要参考。
另外,ARCH等效应分析还可以用于金融衍生品的定价和风险管理。
金融衍生品(如期权和期货)的定价和风险管理需要考虑市场波动性的影响。
通过建立ARCH模型,可以研究金融衍生品价格和波动性之间的关系,为金融衍生品的定价和风险管理提供重要参考。
总之,ARCH等效应分析是一种重要的金融计量模型,可以揭示金融
市场中的波动性特征,帮助投资者理解市场风险,优化投资组合和制定风
险管理策略。
随着金融市场的不断发展和创新,ARCH等效应分析将继续
在金融理论和实践中发挥重要作用。
