广雅中学数学试卷
广东省广州市广雅中学2025届高三3月份模拟考试数学试题含解析

广东省广州市广雅中学2025届高三3月份模拟考试数学试题注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案标号。
回答非选择题时,将答案写在答题卡上,写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知复数41i z i =+,则z 对应的点在复平面内位于( ) A .第一象限B .第二象限C .第三象限D .第四象限2.在ABC ∆中,60BAC ∠=︒,3AB =,4AC =,点M 满足2B M M C =,则AB AM ⋅等于( ) A .10 B .9 C .8 D .73.秦九韶是我国南宋时期的数学家,普州(现四川省安岳县)人,他在所著的《数书九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法.如图的程序框图给出了利用秦九韶算法求某多项式值的一个实例,若输入x 的值为2,则输出的v 值为( )A .10922⨯-B .10922⨯+C .11922⨯+D .11922⨯- 4.已知圆截直线所得线段的长度是,则圆与圆的位置关系是( )A .内切B .相交C .外切D .相离5.已知集合1|2A x x ⎧⎫=<-⎨⎬⎩⎭,{|10}B x x =-<<则A B =( )A .{|0}x x <B .1|2x xC .1|12x x ⎧⎫-<<-⎨⎬⎩⎭ D .{|1}x x >-6.如图所示的程序框图,当其运行结果为31时,则图中判断框①处应填入的是( )A .3?i ≤B .4?i ≤C .5?i ≤D .6?i ≤7.金庸先生的武侠小说《射雕英雄传》第12回中有这样一段情节,“……洪七公道:肉只五种,但猪羊混咬是一般滋味,獐牛同嚼又是一般滋味,一共有几般变化,我可算不出了”.现有五种不同的肉,任何两种(含两种)以上的肉混合后的滋味都不一样,则混合后可以组成的所有不同的滋味种数为( )A .20B .24C .25D .268.下列函数中,在定义域上单调递增,且值域为[)0,+∞的是( )A .()lg 1y x =+B .12y x =C .2x y =D .ln y x =9.点(,)P x y 为不等式组+40x y y x y ≤⎧⎪≤⎨⎪≥⎩所表示的平面区域上的动点,则+22-y x 的取值范围是( ) A .()(),21,-∞-⋃+∞ B .(][),11,-∞-+∞ C .()2,1- D .[]2,1-10.已知双曲线()2222:10,0x y C a b a b-=>>的右焦点为,F O 为坐标原点,以OF 为直径的圆与双 曲线C 的一条渐近线交于点O 及点332A ⎛ ⎝⎭,则双曲线C 的方程为( )A .2213y x -= B .22126x y -= C .2213x y -= D .22162x y -= 11.已知实数x 、y 满足不等式组2102100x y x y y -+≥⎧⎪--≤⎨⎪≥⎩,则3z x y =-+的最大值为( )A .3B .2C .32- D .2- 12.若集合{}A=|2x x x R ≤∈,,{}2B=|y y x x R =-∈,,则A B ⋂=( )A .{}|02x x ≤≤B .{}2|x x ≤C .{}2|0x x -≤≤D .∅ 二、填空题:本题共4小题,每小题5分,共20分。
广东广雅中学2024~2025学年九年级上学期开学考试数学试题(解析版)

2024学年第一学期九年级综合素质评估试卷数学本试卷分选择题和非选择题两部分,共4页,共25小题,满分120分,考试用时120分钟.注意事项:1.开考前,考生务必用黑色字迹的钢笔或签字笔将自己的校名、姓名、班级、考号等相关信息填写在答题卡指定区域内.2.选择题每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑;如需改动,用橡皮擦干净后,再选涂其它答案;不能答在试卷上.3.非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内的相应位置上:如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液.不按以上要求作答的答案无效.4.考生必须保持答题卡的整洁.第一部分选择题部分一、选择题(本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1. 下列各式中,属于最简二次根式的是()A. B. C. D.【答案】A【解析】【分析】本题考查了最简二次根式以及二次根式的性质,根据最简二次根式的定义:二次根式的被开方式中不含分母,并且不含有能开得尽方的因式或因数,进行判断即可.【详解】解:AB=C=,不是最简二次根式,不符合题意;D故选:A.2. 一组数据5,4,5,6,5,3,4的众数是()A. 3B. 4C. 5D. 6【答案】C【解析】【分析】此题考查众数的定义,根据众数的概念,找到该组数据中出现次数最多的数即可选出正确答案.【详解】解:数据5出现了3次,最多, 所以众数为5,故选:C .3. 下列各组数据中,是勾股数的是( )A.B. 6,7,8C. 1,2,3D. 9,12,15【答案】D【解析】【分析】本题考查勾股定理逆定理,两条较短线段的平方和等于较长线段的平方.根据勾股定理逆定理判断即可.【详解】解:A 、222+≠,不能组成直角三角形,不符合题意;B 、222678+≠,不能组成直角三角形,不符合题意;C 、123+=,不能组成三角形,不符合题意;D 、22291215+=,能组成直角三角形,符合题意;故选:D .4. 甲、乙、丙、丁四人参加射击比赛,经过几轮初赛后,他们的平均数相同,方差分别为:22220.34,0.21,0.4,0.5s s s s ≡===甲乙丁丙.如果要从这四人中选取成绩稳定的一人参加决赛,你认为最应该派去参加决赛的是( )A. 甲B. 乙C. 丙D. 丁【答案】B【解析】【分析】本题主要考查方差,解题的关键是掌握方差的意义,根据方差的定义进行判断即可得出答案.【详解】解:∵22220.34,0.21,0.4,0.5s s s s ≡===甲乙丁丙, 2222s s s s ∴<<<乙甲丁丙, ∴乙的成绩更加稳定,故选:B .5. 如图,已知四边形ABCD 是平行四边形,下列说法正确的是( )A. 若AB BC ⊥,则ABCD 是菱形B. 若AC BD ⊥,则ABCD 是正方形C. 若AC BD =,则ABCD 是矩形D. 若AB AD =,则ABCD 是正方形【答案】C【解析】 【分析】本题主要考查了矩形和正方形以及菱形的判定,熟练掌握矩形和正方形以及菱形的判定定理是解题的关键.根据矩形和正方形以及菱形的判定定理逐项判断,即可解答.【详解】解:A 、邻边互相垂直的平行四边形不一定是菱形,故A 错误,不符合题意;B 、因为对角线互相垂直的平行四边形是菱形,故B 错误,不符合题意;C 、若AC BD =,则ABCD 是矩形,故C 正确,符合题意;D 、因为邻边相等的平行四边形是菱形,故D 错误,不符合题意;故选:C .6. 已知方程2210kx x +−=有实数根,则k 的取值范围是( )A. 1k ≥−B. 1k ≥C. 1k ≤且0k ≠D. 1k ≥−且0k ≠ 【答案】A【解析】【分析】本题考查了根的判别式.讨论:当0k =时,方程化为一元一次方程,有一个实数解;当0k ≠时,根据根的判别式的意义得到224(1)0k ∆=−×−≥,解得1k ≥−且0k ≠,然后综合两种情况得到k 的取值范围.【详解】解:当0k =时,方程化为210x −=, 解得12x =; 当0k ≠时,则224(1)0k ∆=−×−≥,解得1k ≥−且0k ≠,综上所述,k 取值范围为1k ≥−.故选:A .7. 如图,矩形ABCD 中,8AB =,12AD =,E 为AD 的中点,F 为CD 边上任意一点,G ,H 分别为EF,的BF 的中点,则GH 的长是( )A. 6B. 5.5C. 6.5D. 5【答案】D【解析】 【分析】本题考查矩形的性质,三角形中位线定理,勾股定理,关键是由三角形中位线定理推出12GH BE =,由勾股定理求出BE 的长.连接BE ,由矩形的性质得到90A ∠=°,由勾股定理求出10BE,由三角形中位线定理得到152GH BE ==. 【详解】解:连接BE ,∵四边形ABCD 是矩形,90A ∴∠=°,12AD =∵,E 为AD 中点,162AE AD ∴==, 8AB = ,10BE ∴=,∵G ,H 分别为EF ,BF 中点,GH ∴是BEF △的中位线,152GH BE ∴==. 故选:D .8. 已知直线1l :y kx b =−+与直线2l :3y kx b =−在同一平面直角坐标系中的大致图象可能是( )A. B.C. D.【答案】B【解析】【分析】本题考查了一次函数的图象与性质,掌握一次函数的图象与性质,数形结合是本题的关键.根据两个一次函数的图象逐一分析系数符号即可解决.【详解】解:A 、直线1:l y kx b =−+中0k >,0b >,2:3l y kx b =−中0k >,0b <,b 的取值相矛盾,故本选项不符合题意;B 、直线1:l y kx b =−+中0k <,0b >,2:3l y kx b =−中0k <,0b >,k 、b 的取值一致,故本选项符合题意;C 、直线1:l y kx b =−+中0k >,0b >,2:3l y kx b =−中0k <,0b >,k 的取值相矛盾,故本选项不符合题意;D 、直线1:l y kx b =−+中0k <,0b <,2:3l y kx b =−中0k <,0b >,b 的取值相矛盾,故本选项不符合题意.故选:B .9. 在平面直角坐标系中,以方程组1y x m y x =−+ =−的解为坐标的点位于第三象限,则m 的取值范围是( ) A. 1m <−B. 1m <C. 1m >D. 11m −<<【答案】A【解析】【分析】此题考查了解不等式组、解二元一次方程组,利用了消去的思想,消去的方法有:加减消去法与代入消元法,还考查了点的坐标.先求出方程组1y x m y x =−+ =−的解.根据以方程组的解为坐标的点位于第三象限列出不等式组求解即可; 【详解】解:解方程组1y x m y x =−+ =− 得:1212m x m y + = − =, ∵以方程组1y x m y x =−+ =− 的解为坐标的点位于第三象限, ∴102102m m + < − <, 解得:1m <−,故选:A .10. 如图,在矩形ABCD 中,点E 在BC 上,10AE AD ==,6CD =,作AF DE ⊥于点G ,交CCCC 于F ,则CCCC 的长是( )A. 103B. 83C. 3D. 2【答案】B【解析】【分析】根据题意,10AD BC AE ===,6AB CD ==,可得8BE =,这样得2EC BC BE =−=,设CF x =,则6FE DF x ==−,利用勾股定理计算即可.本题考查了矩形的性质,勾股定理,线段的垂直平分线的判定和性质,熟练掌握勾股定理,线段的垂直平分线的判定和性质是解题的关键.【详解】解:∵矩形 ABCD ,10AD AE ==,6CD =,∴10AD BC AE ===,6AB CD ==,90B C ∠=∠=°,∴8BE =,∴2EC BC BE =−=,∵10AD AE ==,AF DE ⊥,∴直线AF 是线段DE 的垂直平分线,∴FE FD =,设CF x =,则6FE DF x ==−,则()2264x x −=+, 解得83x =, 故选:B .二、填空题(本大题共6小题,每小题3分,共18分.)11. 在实数范围内有意义,则x 的取值范围是__________.【答案】3x ≥【解析】【分析】根据二次根式被开方数的非负性求出答案.【详解】解:由题意得30x −≥,解得3x ≥,故答案为:3x ≥.【点睛】此题考查了二次根式的非负性,熟记二次根式的被开方数大于等于零的性质是解题的关键. 12. 已知()211350mm x x +−+−=是关于x 的一元二次方程,则m 的值为______. 【答案】1−【解析】【分析】此题主要考查了一元二次方程的定义:含有一个未知数,且未知数的最高次幂是2次的整式方程,特别注意二次项系数不为0,正确把握定义是解题关键.直接利用一元二次方程的定义知道二次项系数不为0同时x 的最高次幂为2,得出m 的值进而得出答案.【详解】解:由题意知:212m +=且10m −≠,解得1m =−,故答案为:1−.13. 已知正比例函数的图象过点()2,1A −,则该函数的解析式为______. 【答案】12y x =−【解析】【分析】本题考查的是求解正比例函数的解析式,直接利用待定系数法求解函数解析式即可.【详解】解:设正比例函数解析式为y kx =,∵正比例函数的图象过点()2,1A −21k ∴−=, 解得:12k =−, ∴该函数的解析式为12y x =−; 故答案为:12y x =− 14.已知1x =,1y =−,则22x y −的值为____________.【答案】【解析】【分析】先将22x y −因式分解,然后将1x =+、1y =−代入计算即可.详解】解:()())221111x y x y x y −=+−+++=−+故答案为键.15. 若关于x 的一元二次方程()200ax bx c a ++=≠的两根分别为13x =,22x =−,则方程()()2(1)100a x b x c a −+−+=≠的两根分别为______.【答案】14x =,21x =−【解析】【分析】本题考查一元二次方程的解的概念,根据一元二次方程的解即可求得结果.关键是把方程()()22230a x b x ++++=中的2x +看成一个新的未知数,则关于2x +的方程的解等于关于x 的一元二次方程230ax bx ++=的解. 【详解】解:由题意得:关于1x −的方程()()2(1)100a x b x c a −+−+=≠的解为:13x −=,12x −=−,【解得:14x =,21x =−,故答案为:14x =,21x =−.16. 如图,点()03B ,,A 为x 轴上一动点,将线段AB 绕点A 顺时针旋转90°得到.AC 连接.OC 当OC 取最小值时,点A 的坐标是_______________.【答案】302 −, 【解析】【分析】本题考查了直线与图形的变化,垂线段最短,全等三角形的判定和性质等知识,解题的关键是学会添加常用辅助线面构造全等三角形解决问题;如图,在x 轴的正半轴上取一点H ,使得3OH OB ==,在OB 上取一点D ,使得OD OA =.证明点C 在直线3y x =−上运动,根据垂线段最短即可解决问题.【详解】解:在x 轴的正半轴上取一点H ,使得3OH OB ==,在OB 上取一点D ,使得OD OA =.OB OH = ,OD OA =,BD AH ∴=,90HAC OAB ∠+∠=° ,90OAB ABO∠+∠=°, HAC DBA ∴∠=∠,BA AC = ,()SAS BDA AHC ∴ ≌,AHC ADB ∴∠=∠,OD OA = ,90AOD ∠=°,45ADO ∴∠=°,135AHC ADB ∴∠=∠=°,45CHx ∴∠=°,设直线CH 的解析式为y x b =+,()30H ,,∴直线CH 的解析式为3y x =−,∴点C 在直线3y x =−上运动,作OP CH ⊥于点P ,OP = 此时点3322P − ,,即3322C −,,设()0A m ,, AB AC = ,222233322m m ∴+=−+, 解得32m =−, ∴点302A −, 故答案为:3,02 −. 三、解答题(本大题共9小题,共72分.解答应写出文字说明、证明过程或演算步骤.)17. ()03π1−−. 【答案】3−【解析】【分析】本题主要考查了二次根式的混合运算,解题的关键是熟练掌握二次根式混合运算法则,准确计算. 先算乘除法和零次幂,并化简二次根式,最后合并同类二次根式即可.()03π1+−1= 261=−+3=−18. 如图,在ABCD 中,E ,F 分别是,AB CD 的中点.求证:AF CE =.【答案】见解析【解析】【分析】本题考查平行四边形的判定和性质,线段中点的有关计算,解题的关键是掌握平行四边形的判定和性质.根据平行四边形的判定和性质和线段中点的有关计算,证明四边形AECF 是平行四边形,进而即可证明.【详解】证明: 四边形ABCD 是平行四边形,∴AB CD ∥,AB CD =,E ,F 分别是ABCD 的边AB ,CD 上的中点, ∴12CF CD =,12AE AB =, ∴CF AE =,CF AE ∥,∴四边形AECF 是平行四边形,∴AF CE =.19. 如图,已知CD AB ⊥,垂足为D ,1BD =,2CD =,4=AD .判断ABC 的形状,并说明理由.【答案】ABC 是直角三角形,理由见解析【解析】【分析】根据勾股定理分别求出2BC ,2AC ,再根据勾股定理逆定理,即可得出结论.【详解】解:ABC 是直角三角形.理由:CD AB ⊥ ,垂足为D ,1BD =,2CD =,4=AD .22222125BC BD CD ∴=+=+=,222224220AC AD CD =+=+=.415AB AD BD =+=+= ,22225205AB AC BC ∴==+=+.ABC ∴ 是直角三角形.【点睛】本题主要考查了勾股定理和勾股定理逆定理,解题的关键是掌握直角三角形两直角边平方和等于斜边平方,两边平方和等于第三边平方的三角形是直角三角形.20. (1)化简:24211326x x x x −+ −÷ ++; (2)若x 是一元二次方程2320x x −+=的解,请求出上面化简后的代数式的值.【答案】(1)21x −;(2)2 【解析】【分析】本题考查分式的化简求值、解一元二次方程,解答本题的关键是明确分式化简求值的方法. (1)根据分式的加法和除法可以化简题目中的式子即可;(2)根据因式分解法解一元二次方程,可以得到x 的值,然后将使得原分式有意义的x 的值代入化简后的式子即可解答本题. 【详解】解:(1)24211326x x x x −+ −÷ ++ 234(1)32(3)x x x x +−−÷++ 212(3)3(1)x x x x −+×+− 21x =−; (2)解方程:2320x x −+=∴(1)(2)0x x −−=∴121,2x x ==, ∵1x =时分式无意义∴当xx =2 时,原式2221=−. 21. 某校学生会决定从三名学生会干事中选拔一名干事,对甲、乙、丙三名候选人进行了笔试和面试,三人的测试成绩如下表所示:根据录用程序,学校组织200名学生采用投票推荐的方式,对三人进行民主测评,三人得票率(没有弃权,每位同学只能推荐1人)如扇形统计图所示,每得一票记1分.(1)分别计算三人民主评议的得分;(2)根据实际需要,学校将笔试、面试、民主评议三项得分按4:3:3的比例确定个人成绩,三人中谁的得分最高?【答案】(1)甲50,乙80,丙70;(2)丙.【解析】【分析】本题考查了加权平均数、扇形统计图等知识点,熟记相关公式是解题关键.(1)分别用200乘以三人的得票率,求出三人民主评议的得分各是多少即可.(2)根据加权平均数的计算方法列式计算,分别求出三人的得分各是多少;然后比较大小,判断出三人中谁的得分最高即可.小问1详解】解:甲民主评议得分是:20025%50×=(分); 乙民主评议的得分是:20040%80×=(分); 丙民主评议的得分是:20035%70×=(分). 【小问2详解】解:甲的成绩是:()()7549335034337291072.9×+×+×÷++=÷=(分), 乙的成绩是:()()8047038034337701077×+×+×÷++=÷=(分), 丙的成绩是:()()9046837034337741077.4×+×+×÷++=÷=(分),【的∵77.47772.9>>,∴丙的得分最高.22. 如图,在平面直角坐标中,直线26y x =−+与x 轴相交于点B ,与直线2y x =相交于点A .(1)求AOB 的面积;(2)点P 为y 轴上一点,当PA PB +取最小值时,求点P 的坐标,【答案】(1)92(2)()0,2P【解析】【分析】本题考查两直线相交问题,一次函数的性质以及轴对称−最短线路问题,解题的关键是掌握待定系数法.(1)先求出点B 的坐标,联立两直线解析式构成方程组,得262y x y x=−+= ,解方程组求出3,32A 即可求解; (2)直线26y x =−+与y 轴的交点()3,0B ,作点B 关于y 轴的对称点(3,0)B ′−,连接,AB PB ′,交x 轴于点P ,利用待定系数法求出AB ′的解析式并令函数值为0即可求出点P 的坐标.【小问1详解】解: 026B x =−+, ∴3B x =,即()3,0B ,联立262y x y x =−+ =, 解得:323x y = = ,∴点A 的坐标为3,32, ∴AOB 的面积为:11933222A OB y ⋅=××=; 【小问2详解】解:作点B 关于y 轴的对称点B ′,连接AB ′,交y 轴于点P ,PB PB ′= ,PB PA PB PA ′∴+=+,此时,,,B P A ′三点共线,PB PA +有最小值,()3,0B ,3,32A, (3,0)B ′∴−设直线AB ′的解析式为y k x b ′′=+, 代入(3,0)B ′−,3,32A ,的坐标得03332k b k b ′′′=−+ =+, 解得:223b k ==′′, ∴直线AB ′的解析式为223yx =+, 令0x =,得2y =, ∴点()0,2P 使PB PC +最小.23. 为积极响应新旧动能转换,提高公司经济效益,某科技公司近期研发出一种新型高科技设备,每台设备成本价为30万元.经过市场调研发现,每台售价为35万元时,年销售量为550台;每台售价为40万元时,年销售量为500台.假定该设备的年销售量y (单位:台)和销售单价x(单位:万元)成一次函数关系.(1)求年销售量y 与销售单价x 的函数关系式;(2)根据相关规定,此设备的销售单价不得高于60万元,如果该公司想获得8000万元的年利润.则该设备的销售单价应是多少万元?【答案】(1)10900y x =−+ (2)50万元【解析】【分析】(1)设年销售量y 与销售单价x 的函数关系式yy =kkxx +bb (kk ≠0),根据点的坐标,利用待定系数法即可求解;(2)设此设备的销售单价为m 万元/台,则每台设备的利润为()30m −万元,销售数量为()10900m −+台,根据总利润=单台利润×销售数量,即可得出关于m 的一元二次方程,解之取其小于60的值即可得出结论. 【小问1详解】解:设年销售量y 与销售单价x 的函数关系式yy =kkxx +bb (kk ≠0),将()35,550,()40,500代入解析式,得:3555040500k b k b += +=, 解得:10900k b =− =, ∴年销售量y 与销售单价x 的函数关系式为10900y x =−+; 【小问2详解】设此设备的销售单价为m 万元/台,则每台设备的利润为()30m −万元,销售数量为()10900m −+台,根据题意得:()()30109008000m m −−+=, 整理得:212035000m m −+=,解得:150m =, 270m =,此设备的销售单价不得高于60万元,50m ∴=,则该设备的销售单价应是50万元.【点睛】本题考查了待定系数法求一次函数解析式以及一元二次方程的应用,解题的关键是:(1)根据点的坐标,利用待定系数法求出函数关系式;(2)找准等量关系,正确列出一元二次方程.24. 某条城际铁路线共有A ,B ,C 三个车站,每日上午均有两班次列车从A 站驶往C 站,其中D 1001次列车从A 站始发,经停B 站后到达C 站,G 1002次列车从A 站始发,直达C 站,两个车次的列车在行驶过程中保持各自的行驶速度不变.某校数学学习小组对列车运行情况进行研究,收集到列车运行信息如下表所示.列车运行时刻表 车次A 站B 站C 站 发车时刻 到站时刻 发车时刻 到站时刻D 10018:00 9:30 9:50 10:50 G 1002 8:25 途经B 站,不停车10:30 请根据表格中的信息,解答下列问题:(1)D 1001次列车从A 站到B 站行驶了______分钟,从B 站到C 站行驶了______分钟;(2)记D 1001次列车的行驶速度为1v ,离A 站的路程为1d ;G 1002次列车的行驶速度为2v ,离A 站的路程为2d .①12v v =______; ②从上午8:00开始计时,时长记为t 分钟(如:上午9:15,则75t =),已知1240v =千米/小时(可换算为4千米/分钟),在G 1002次列车的行驶过程中()25150t ≤≤,若1260d d −=,求t 的值. 【答案】(1)90,60(2)①56;②75t =或125 【解析】【分析】本题考查了一元一次方程的应用,速度、时间、路程的关系,明确题意,合理分类讨论是解题的关键.(1)直接根据表中数据解答即可;(2)①分别求出D 1001次列车、G 1002次列车从A 站到C 站的时间,然后根据路程等于速度乘以时间求解即可;②先求出2v , A 与B 站之间的路程,G 1002次列车经过B 站时,对应t 的值,从而得出当90110t ≤≤时,D 1001次列车在B 站停车. G 1002次列车经过B 站时,D 1001次列车正在B 站停车,然后分2590t ≤<,90100t ≤≤,100110t <≤,110150t <≤讨论,根据题意列出关于t 的方程求解即可.【小问1详解】解:D 1001次列车从A 站到B 站行驶了90分钟,从B 站到C 站行驶了60分钟,故答案为:90,60;【小问2详解】解:①根据题意得:D 1001次列车从A 站到C 站共需9060150+=分钟,G 1002次列车从A 站到C 站共需356030125++=分钟,∴12150125v v =, ∴1256v v =, 故答案为:56; ②14v = (千米/分钟),1256v v =, 2 4.8v ∴=(千米/分钟).490360×= ,∴A 与B 站之间的路程为360.360 4.875÷=, ∴当100t =时,G 1002次列车经过B 站.由题意可如,当90110t ≤≤时,D 1001次列车在B 站停车.∴G 1002次列车经过B 站时,D 1001次列车正在B 站停车.ⅰ.当2590t ≤<时,12d d >,1212d d d d ∴−=−,()4 4.82560t t ∴−−=,75t =(分钟);ⅱ.当90100t ≤≤时,12d d ≥,1212d d d d ∴−=−,()360 4.82560t ∴−−=,87.5t =(分钟),不合题意,舍去; ⅲ.当100110t <≤时,12d d <,1221d d d d ∴−=−,()4.82536060t ∴−−=,112.5t =(分钟),不合题意,舍去;ⅳ.当110150t <≤时,12d d <,1221d d d d ∴−=−,()()4.825360411060t t ∴−−+−=,125t =(分钟). 综上所述,当75t =或125时,1260d d −=. 25. 如图,等边ABD △中,8AB =.(1)尺规作图:在图1中作点A 关于BD 的对称点C ,连接BC DC ,,并证明四边形ABCD 是菱形; (2)在(1)的条件下,点O 是四边形ABCD 对角线交点,动点E ,F ,G 分别在线段CD AC BC ,,上,且满足EF AD EG EF ⊥∥,,H 是FG 中点;①当OH AB ∥时,求证12OH DE =; ②当OH BC ⊥时,求OH 长度.【答案】(1)作图见解析,证明见解析(2 【解析】【分析】(1)作BAD ∠的平分线,交BD 于O ,截取OC OA =,点C 即为所作;由等边ABD △,可得AC 垂直平分BD ,即AC BD ⊥,OD OB =,进而可证四边形ABCD 是菱形;(2)①由题意证,EF CE =,如图2,作EP CF ⊥,则EP BD ∥,由EF CE =,可得P 是CF 的中点,如图2,连接PH ,则PH CG ∥,由OH AB ∥,AB CD ∥,可得30POH BAC OPH ∠=∠=°=∠,OH CD ∥,则OH PH =,如图2,作HQ EP ∥交EF 于M ,则HQ OD ∥,证明四边形ODQH 是平行四边形,证明四边形MEPH 是平行四边形,证明MEQ △是等边三角形,则QE ME PH ==,由2DE DQ QE OH PH OH =+=+=,可得12OH DE =;②由题意求2BP =,6CP =,2CE CG =,如图3,作EN CF 于H ,连接HN ,延长OH ,交BC 于P ,交EF于Q ,则四边形EGPQ 是矩形,QE PG PQ EG ==,,设CG a PG b ==,,则2EF CE a ==,PQ EG =,12HN a =,QE PG b ==,2FQ EF QE a b =−=−,6a b +=,证明()AAS FHQ GHP ≌,则12QH PH PQ ===,由题意知,2OF OQ =,2ON OH =,由勾股定理得,2FQ a b =−,则OQ =OH =,由QH OQ OH =++,可求a b =,则3a b ==,进而可求OH 的长. 【小问1详解】 解:作BAD ∠的平分线,交BD 于O ,截取OC OA =,点C 即为所作; ∵等边ABD △,∴AC 垂直平分BD ,即AC BD ⊥,OD OB =, 又∵OC OA =,∴四边形ABCD 菱形;【小问2详解】①证明:∵菱形ABCD ,∴30DAC DCA BAC BCA ∠=∠=∠=∠=°,60CDB ∠=°,120ADC ∠=°,BD AC ⊥,AB CD ∥,∵EF AD ∥,∴EFC DAC DCA ∠=∠=∠,120FEC ADC ∠=∠=°,60DEF ∠=°, ∴EF CE =,如图2,作EP CF ⊥,则EP BD∥,是图2∵EF CE =,∴P 是CF 的中点,如图2,连接PH ,∵H 是FG 中点,∴PH CG ∥,∴30OPH ACB ∠=∠=°, ∵OH AB ∥,AB CD ∥,∴30POH BAC OPH ∠=∠=°=∠,OH CD ∥,∴OH PH =,如图2,作HQ EP ∥交EF 于M ,则HQ OD ∥,∴四边形ODQH 是平行四边形,60CQH CDB ∠=∠=°, ∴DQ OH =,∵120EPH EPF OPH ∠=∠+∠=°,1602FEP CEF ∠=∠=°, ∴180EPH FEP ∠+∠=°,∴PH ME ∥,∴四边形MEPH 是平行四边形,∴PH ME =,∵60QEM MQE ∠=°=∠,∴MEQ △是等边三角形, ∴QEME PH ==, ∴2DE DQ QE OH PH OH =+=+=, ∴12OH DE =; ②解:∵菱形ABCD ,8AB =, ∴11422OB BD AB ===, ∵60DBC ∠=°,OHBC ⊥,∴30BOP ∠=°,∴2BP =,6CP =,∵60BCD ∠=°,90EGC FEG ∠=∠=°,∴30CEG ∠=°,∴2CE CG =,如图3,作EN CF 于H ,连接HN ,延长OH ,交BC 于P ,交EF 于Q ,则四边形EGPQ 是矩形,图3∴QE PGPQ EG ==,, 由①可知,EF CE =,HN CG ∥,12HN CG =, ∴90OHN QPC ∠=∠=°,30ONH BCA ∠=∠=°,设CG a PG b ==,,则2EF CE a ==,PQ EG =,12HN a =,QE PG b ==,2FQ EF QE a b =−=−,6a b +=,∵90FQH GPH ∠=°=∠,FHQ GHP ∠=∠,FH GH =, ∴()AAS FHQ GHP ≌,∴12QH PH PQ ===, 由题意知,2OF OQ =,2ON OH =,由勾股定理得,2FQ a b =−,解得,OQ =,同理,OH =, ∵QHOQ OH =+,a ,解得,a b =,∴3a b ==,∴OH =∴OH 【点睛】本题考查了作角平分线,等边三角形的判定与性质,菱形的判定与性质,中位线,等腰三角形的判定与性质,平行四边形的判定与性质,矩形的判定与性质,含30°的直角三角形,勾股定理等知识.熟练掌握作角平分线,等边三角形的判定与性质,菱形的判定与性质,中位线,等腰三角形的判定与性质,平行四边形的判定与性质,矩形的判定与性质,含30°的直角三角形,勾股定理是解题的关键.。
广东省江门市广雅中学2024-2025学年高一上学期9月月考数学试题B卷(含答案解析)

广东省江门市广雅中学2024-2025学年高一上学期9月月考数学试题B 卷学校:___________姓名:___________班级:___________考号:___________一、单选题1.已知集合{}03A x x =≤≤∣,{14}B x x =<<∣,则A B = ()A .{13}xx <≤∣B .{04}xx ≤<∣C .{}13xx ≤≤∣D .{04}xx <<∣2.命题“0x ∀>,210x x ++≥,”的否定是()A .0x ∃≤,210x x ++<B .0x ∃>,210x x ++<C .0x ∃≤,210x x ++≥D .0x ∀>,210x x ++<3.已知a 、b 为非零实数,且a b <,则下列不等式成立的是()A .22a b <B .11a b<C .33a b <D .ac bc<4.甲乙丙丁四位同学在玩一个猜数字游戏,甲乙丙共同写出三个集合:{}0Δ2A x x =<<,{}235,03B x x C x x ⎧⎫=-≤≤=<<⎨⎬⎩⎭,然后他们三人各用一句话来正确的描述“Δ”中的数字,让丁同学找出该数字,以下是甲、乙、丙三位同学的描述,甲:此数为小于5的正整数;乙:B 是A 成立的必要不充分条件;丙:C 是A 成立的充分不必要条件.则“Δ”中的数字可以是()A .3或4B .2或3C .1或2D .1或35.已知二次函数221=-+y x ax 在区间(2,3)内是单调函数,则实数a 的取值范围是()A .2a ≤或3a ≥B .23a ≤≤C .3a ≤-或2a ≥-D .32a --≤≤6.若函数223,1()1,1x ax x f x ax x ⎧++≤=⎨+>⎩是R 上的减函数,则a 的取值范围是A .[3,1]--B .(,1]-∞-C .[1,0)-D .[2,0)-7.已知命题p :x ∀∈R ,210ax ax -+>;q :x ∃∈R ,20x x a -+=.均为真命题,则a 的取值范围是()A .(),4-∞B .[)0,4C .10,4⎛⎤ ⎝⎦D .10,4⎡⎤⎢⎥⎣⎦8.对任意实数,a b 定义运算“ ”,,,,b a b a b a a b≥⎧=⎨<⎩ ,设2()(2)(4)f x x x =-- ,有下列四个结论:①()f x 最大値为2;②()f x 有3个单调递减区间;③()f x 在3[,1]2--是减函数;④()f x 图象与直线y m =有四个交点,则02m ≤<,其中正确结论有()A .4个B .3个C .2个D .1个二、多选题9.21x ≤的一个充分不必要条件是()A .10x -≤<B .1x ≥C .01x <≤D .11x -≤≤10.下列各组函数能表示同一个函数的是()A .()()f x g x x==B .()()2,x f x x g x x==C .()()f x g x ==D .()()222,2f x x x g u u u=-=-11.已知正实数x ,y 满足xy x y =+,则下列结论正确的是()A .xy的最小值为4B .2x y +的最小值为3+C .22x y +的最大值为8D .112x y+的最小值为4三、填空题12.已知函数()f x 的图象如图所示,则()()2f f =.13.函数()f x =的单调递增区间是.14.已知关于x 的不等式()())R (110ax x a +-≤∈,若2a =-,则该不等式的解集是,若该不等式对任意的11x -≤≤均成立,则实数a 的取值范围是.四、解答题15.已知集合{}240A x x =-<,{}012B x x =≤-≤.(1)求A B ;(2)若集合{}11C x m x m =-≤≤+,A C ⋂=∅,求实数m 的取值集合.16.已知函数()1f x x x=+.(1)请用定义证明函数()f x 在()0.1上单调递减;(2)若存在11,42x ⎡⎤∈⎢⎣⎦,使得210x ax -+≥成立,求实数a 的取值范围.17.某乡镇响应“绿水青山就是金山银山”的号召,因地制宜的将该镇打造成“生态水果特色小镇”经调研发现.某珍稀水果树的单株产量即(单位:千克)与施用肥料x (单位:千克)满足如下关系:()()()()253025050251x x W x x x ⎧+≤≤⎪=⎨-<≤⎪+⎩,肥料成本投入为10x 元,其它成本投入(如培育管理、施肥等人工费)20x 元.已知这种水果的市场售价大约为15元/千克,且销路畅通供不应求记该水果树的单株利润为()f x (单位:元).(1)求()f x 的函数关系式;(2)当施用肥料为多少千克时,该水果树的单株利润最大?最大利润是多少?18.已知函数2()2y x a b x a =-++.(1)若关于x 的不等式0y <的解集为{|12}x x <<,求a ,b 的值;(2)当2b =时,解关于x 的不等式0y >.19.已知()f x 是二次函数,且满足()()()02,123f f x f x x =+-=+.(1)求函数()f x 的解析式;(2)设函数()()()2g x f x t x =-+,求()g x 在区间[]1,2上的最小值()h t 的表达式.(3)在(2)的条件下,对任意的[]0,6t ∈,存在[]0,2m ∈,使得()28h t mk mk m ≤+-+成立,求k 的取值范围.参考答案:题号12345678910答案B BCCAADCACAD题号11答案AB1.B【分析】根据并集的知识确定正确答案.【详解】{}=|04A B x x ⋃=≤<.故选:B 2.B【分析】根据全称量词命题的否定的知识求得正确答案.【详解】原命题的全称量词命题,其否定是存在量词命题,注意到要否定结论而不是否定条件,所以B 选项符合.故选:B 3.C【分析】利用特殊值法可判断出A 、B 、D 三个选项中不等式的正误,利用作差法可判断C 选项中不等式的正误,由此可得出结论.【详解】对于A 选项,由于a b <,取2a =-,1b =,则22a b >,A 选项中的不等式不成立;对于B 选项,由于a b <,取1a =,2b =,则11a b>,B 选项中的不等式不成立;对于C 选项,()()()2332221324a b a b a ab b a b a b b ⎡⎤⎛⎫-=-++=-++⎢⎥ ⎪⎝⎭⎢⎥⎣⎦,a b < ,所以,a 与b 不可能同时为零,则223024b a ⎛⎫++> ⎪⎝⎭,则330a b -<,即33a b <,C 选项中的不等式成立;对于D 选项,取0c =,由于a b <,则ac bc =,D 选项中的不等式不成立.故选:C.【点睛】本题考查不等式正误的判断,一般利用特殊值法、作差法、不等式的基本性质和函数的单调性进行判断,考查推理能力,属于基础题.4.C【分析】根据此数为小于5的正整数得到20ΔA x x ⎧⎫=<<⎨⎬⎩⎭,再推出C 是A 的真子集,A 是B 的真子集,从而得到不等式,求出2Δ,35⎡⎫∈⎪⎢⎣⎭,得到答案.【详解】因为此数为小于5的正整数,故{}20Δ20ΔA x x x x ⎧⎫=<<=<<⎨⎬⎩⎭,因为B 是A 成立的必要不充分条件,C 是A 成立的充分不必要条件,所以C 是A 的真子集,A 是B 的真子集,故22Δ3>且25Δ≤,解得2Δ,35⎡⎫∈⎪⎢⎣⎭,故“Δ”中的数字可以是1或2.故选:C 5.A【分析】根据二次函数的性质求解.【详解】二次函数221=-+y x ax 的对称轴为0x a =,欲使得()2,3x ∈时是单调的,则对称轴0x a =必须在()2,3区间之外,即2a ≤或者3a ≥;故选:A.6.A【分析】根据分段函数单调性的性质可以得到关于a 的不等式组,解这个不等式组即可求出a 的取值范围.【详解】因为函数()f x 是R 上的减函数,所以有221201231aa a a ⎧-≥⎪⎪<⎨⎪++≥+⎪⎩,解得31a -≤≤-,故本题选A.【点睛】本题考查了已知分段函数的单调性求参数问题,数形结合是解题的关键.7.D【分析】210ax ax -+>,分0a =和0a ≠,结合开口方向,根的判别式得到不等式,求出p 为真命题,需满足04a ≤<,再利用根的判别式得到q 为真命题,需满足14a ≤,求交集得到答案.【详解】210ax ax -+>恒成立,当0a =时,10>,满足要求,当0a ≠时,需满足2Δ40a a a >⎧⎨=-<⎩,解得04a <<,故p 为真命题,需满足04a ≤<,x ∃∈R ,20x x a -+=,则140a ∆=-≥,解得14a ≤,故q 为真命题,需满足14a ≤,综上,a 的取值范围为[)010,4,41,4⎡⎤⎢⎥⎛⎤-∞=⎥⎣⎝⎦⎦故选:D 8.C【分析】根据f x ()的解析式,作出f x ()的图象,根据图象判断每个选项是否正确.【详解】根据定义,作出f x ()的图象(实线部分),可知当2x =±或0时,f x ()取得最大值2,①正确;f x ()单调递减区间为[2,)-+∞,所以②正确;由图象可知,f x ()在3,12⎡⎤--⎢⎥⎣⎦上不单调,③错误;要使f x ()图象与直线y m =有四个交点,则0m =,④不正确.故答案为C.【点睛】以新定义运算为背景,设计出函数性质与图象的综合问题,考查函数的最大值、单调性、图象综合性问题,重在考查学生的转化能力和作图能力,属于中档题.9.AC【解析】由不等式21x ≤,求得11x -≤≤,结合充分条件、必要条件的判定方法,即可求解.【详解】由不等式21x ≤,可得11x -≤≤,结合选项可得:选项A 为21x ≤的一个充分不必要条件;选项B 为21x ≤的一个既不充分也不必要条件;选项C 为21x ≤的一个充分不必要条件;选项D 为21x ≤的一个充要条件,故选:AC.10.AD【分析】根据定义域、值域和对应法则判断即可.【详解】()f x 的定义域为R ,()g x 定义域为R ,即定义域一样,且()||()f x x g x ==,即值域一样,故能表示同一个函数,故A 选项符合题意;()f x 的定义域为R ,()g x 定义域为0x ≠,定义域不一样,故不能表示同一函数,故B 选项不符合题意;()f x 定义域为[2,)+∞(],2∞⋃--,()g x 定义域为[2,)+∞,二者定义域不一样,故不能表示同一函数,故C 选项不符合题意;()f x 定义域为R ,()g u 定义域为R ,且对应法则一样,值域一样,故能表示同一函数,故D 选项正确.故选:AD 11.AB【分析】由基本不等式及“1”的代换求xy 、2x y +的最值,由基本不等式求得4x y +≥,结合二次函数性质求222()2()x y x x y y +=+-+的最值,由1111(122x y x +=+且101x<<求范围,即可判断各项正误.【详解】由题设111x y+=且0,0x y >>,111x y +=≥114xy ≤,故4xy ≥,当且仅当2x y ==时取等号,A 对;1122(2)()333y x x y x yx y x y +=++=++≥+=+1x y =时取等号,B 对;22222()2()2()(1)1x y xy x y x x y x y y =+-=+-=+-++-,而2()4x y xy x y +=+≤,整理有2()4()0x y x y +-+≥,则4x y +≥,当且仅当2x y ==时取等号,所以22x y +≥8,即2x y ==时取等号,C 错;1121111()(1)2222x y x y x y xy xy x x +++==+=+,而101x<<,故111(,1)22x y +∈,D 错.故选:AB 12.4【分析】根据函数()f x 的图象,先求得()2f 的值,进而求得()()2f f 的值,得到答案.【详解】由函数()f x 的图象,可得()20f =,则()()()204f f f ==.故答案为:4.13.[3,)+∞【分析】首先求出函数()f x 的定义域,令256t x x =-+,分别求出256t x x =-+和y 的单调区间,再利用符合函数单调性的性质即可求出()f x 的单调递增区间.【详解】因为2560x x -+≥,得(2)(3)0x x --≥,得2x ≤或3x ≥,解得函数()f x 的定义域为(,2][3,)-∞⋃+∞.令256t x x =-+,y 在[0,)+∞单调递增.因为函数256t x x =-+在[3,)+∞单调递增,由复合函数的单调性知:()f x =[3,)+∞单调递增.故答案为:[3,)+∞【点睛】本题主要考查符合函数的单调性,特别注意先求定义域,利用复合函数“同增异减”为解题的关键,属于容易题.14.[)1,1,2⎛⎤-∞+∞ ⎥⎝⎦ ,[]1,1-.【分析】代入2a =-,化简可得()()2110x x --≥,根据一元二次不等式解法求结论,当1x =时由条件求a 的取值范围,当1<1x ≤-时,化简不等式,由条件求a 的取值范围,由此可得结论.【详解】当2a =-时,不等式()()110ax x +-≤可化为()()2110x x -+-≤,所以()()2110x x --≥,所以1x ≥或12x ≤,所以不等式()()2110x x -+-≤的解集是[)1,1,2∞∞⎛⎤-⋃+ ⎥⎝⎦,由已知对任意的11x -≤≤,不等式()()110ax x +-≤恒成立,当1x =时,()()110ax x +-=,此时R a ∈,当1<1x ≤-时,不等式()()110ax x +-≤,可化为10ax +≥,所以()min 10ax +≥,其中1<1x ≤-,所以1010a a -+≥⎧⎨+≥⎩,所以11a -≤≤,所以不等式对任意的11x -≤≤均成立时,a 的取值范围是[]1,1-.故答案为:[)1,1,2∞∞⎛⎤-⋃+ ⎥⎝⎦,[]1,1-.15.(1){|23}x x -<≤;(2){|3m m ≤-或3}m ≥.【分析】(1)求解不等式,从而求得集合,A B ,再求并集即可;(2)根据交集为空集,结合(1)中所求,列出对应的不等式,求解即可.【详解】(1)因为{}240A x x =-<{|22}x x =-<<,{}012B x x =≤-≤{|13}x x =≤≤,故可得:A B {|23}x x =-<≤.(2)因为{|22}A x x =-<<,{}11C x m x m =-≤≤+,且A C ⋂=∅,故可得:12m +≤-或12m -≥,解得3m ≤-或3m ≥,故实数m 的取值范围为:{|3m m ≤-或3}m ≥.16.(1)证明见解析(2)17(,]4-∞【分析】(1)根据题意,利用函数单调性的定义与判定方法,即可求解;(2)根据题意,转化为存在11,42x ⎡⎤∈⎢⎥⎣⎦,使得1a x x ≤+,由(1)得到()f x 在11,42⎡⎤⎢⎥⎣⎦上为单调递减函数,求得()f x 的最大值,即可求解.【详解】(1)证明:任取()12,0.1x x ∈且12x x <,则()()122121212121211211111()()()x x f x f x x x x x x x x x x x x x --=+--=-+-=-⋅,因为()12,0.1x x ∈且12x x <,可得210x x ->,且1201x x <<,所以1210x x -<,所以()()122121121()0x x f x f x x x x x --=-⋅<,即()()12f x f x >,所以函数()f x 在()0.1上为单调递减函数.(2)解:由11,42x ⎡⎤∈⎢⎥⎣⎦,不等式210x ax -+≥可化为211x a x x x+≤=+,因为存在11,42x ⎡⎤∈⎢⎥⎣⎦,使得210x ax -+≥成立,即max 1()a x x ≤+,由(1)知,函数()1f x x x =+在11,42x ⎡⎤∈⎢⎥⎣⎦为单调递减函数,所以()max 1117()4444f x f ==+=,所以174a ≤,即实数a 的取值范围17(,]4-∞.17.(1)()27530225,027*******,251x x x f x x x x ⎧-+≤≤⎪=⎨--<≤⎪+⎩(2)4千克时,利润最大480元.【分析】(1)利用销售额减去成本投入可得出利润解析式;(2)利用分段函数的单调性及基本不等式计算最值即可.【详解】(1)由已知()()27530225,0215201075075030,251x x x f x W x x x x x x ⎧-+≤≤⎪=--=⎨--<≤⎪+⎩;(2)由(1)得()2175222,025********,251x x f x x x x ⎧⎛⎫-+≤≤⎪ ⎪⎪⎝⎭=⎨⎛⎫⎪-++<≤ ⎪⎪+⎝⎭⎩,即由二次函数的单调性可知,当[]0,2x ∈时,()()max 2465f x f ==,由基本不等式可知当(]2,5x ∈时,()257803017803024801f x x x ⎛⎫=-++≤-⨯ ⎪+⎝⎭,当且仅当4x =时取得最大值,综上,当4x =时取得最大利润,最大利润为480元.18.(1)1a =,2b =(2)答案见解析【分析】(1)依题意可得关于x 的方程2()20x a b x a -++=的两个根为1和2,利用韦达定理得到方程组,解得即可;(2)依题意可得()(2)0x a x -->,再分2a <、2a =、2a >三种情况讨论,分别求出不等式的解集.【详解】(1)因为关于x 的不等式0y <的解集为{|12}x x <<,所以关于x 的方程2()20x a b x a -++=的两个根为1和2,∴322a b a +=⎧⎨=⎩,解得1a =,2b =;(2)当2b =时,原不等式可化为2(2)20x a x a -++>,即()(2)0x a x -->,当2a <时,解得x a <或2x >;当2a =时,解得2x ≠;当2a >时,解得2x <或x a >;综上可知,当2a ≤时,原不等式的解集为()(),2,a -∞+∞ ;当2a >时,原不等式的解集为()(),2,a -∞+∞ .19.(1)()222f x x x =++(2)()23,22,24462,4t t t h t t t t -≤⎧⎪⎪=-<<⎨⎪-≥⎪⎩(3)2k ≥或3k ≤-【分析】(1)利用待定系数法求解;(2)求出()g x 的对称轴为2t x =,然后进行分类讨论求解;(3)将问题转化为()()()2max max 8h t mk mk m ≤+-+,求出()()max 6h t =,然后得到不等式()21140k k m ++-≥,对21k k ++进行分类讨论求解.【详解】(1)设()()20f x ax bx c a =++≠,()02,f = ()02f c ∴==又()()123,f x f x x +-=+ ()22(1)12223a xb x ax bx x ∴++++---=+即223ax a b x ++=+,223a a b =⎧∴⎨+=⎩,解得12a b =⎧⎨=⎩,即()222f x x x =++,(2)由题意得,()()()222g x f x t x x tx =-+=-+,则二次函数()g x 的对称轴为2t x =,若2t ≤时,12t ≤,当1x =时,()g x 的最小值为3t -;若24t <<时,122t <<,当2t x =时,()g x 的最小值为224t -;若4t ≥时,22t ≥,当2x =时,()g x 的最小值为62t -;所以()23,22,24462,4t t t h t t t t -≤⎧⎪⎪=-<<⎨⎪-≥⎪⎩;(3)在(2)的条件下,对任意的[]0,6t ∈,存在[]0,2m ∈,使得()28h t mk mk m ≤+-+成立,即()()()2max max 8h t mk mk m ≤+-+,作如下图形:故()23,22,24462,4t t t h t t t t -≤⎧⎪⎪=-<<⎨⎪-≥⎪⎩是单调递减函数,[]0,6t ∈ ,当0t =时,()03h =,当6t =时,()66h =-,()max 6h t ∴=,()[]2max 86,0,2mk mk m m ∴+-+≥∈,()[]2max 1140,0,2k k m m ⎡⎤∴++-≥∈⎣⎦,因为22133100244k k k ⎛⎫++==-+≥> ⎪⎝⎭所以2m =时()2114k k m ++-取最大值,所以不等式()221140k k ++-≥,解得:2k ≥或3k ≤-;综上所述:2k ≥或3k ≤-.【点睛】本题考查了求解二次函数的解析式,分段函数的解析式及最值问题、不等式中恒成立问题,利用分类讨论的思想及转化思想求解是关键.。
2023-2024学年广东省广雅中学八年级下学期月考数学试卷含详解
A. B.
C. D.
4.关于正比例函数 ,下列说法中,错误的是()
A.其图象经过原点B.其图象是一条直线
C. 随 的增大而增大D.点 在其图象上
5.已知点 , 在一次函数 的图象上,若 ,则 与 的大小关系是()
【详解】解: 与 成正比例, 与 成正比例.
, .
.
当 时, ,当 时, .
.
解得, .
.
故答案为: .
13.已知一次函数 的图象经过点 ,则 ______.
【答案】
【分析】本题考查的是一次函数图象上点的坐标特点,熟知一次函数图像上各点的坐标适合一次函数解析式是解题的关键.本题直接把点 代入一次函数 ,即可求解.
11.若正比例函数 的图象经过第一,第三象限,则 的取值范围是______.
12.已知 , 与 成正比例, 与 成正比例,且当 时, ,当 时, ,则 关于 的函数解析式为______.
13.已知一次函数 的图象经过点 ,则 ______.
14.菱形 在平面直角坐标系中的位置如图所示,点 的坐标为 , ,则点 的坐标为_____.
4.关于正比例函数 ,下列说法中,错误的是()
A.其图象经过原点B.其图象是一条直线
C. 随 的增大而增大D.点 在其图象上
【答案】C
【分析】本题考查了正比例函数 性质.解题的关键是熟练掌握正比例函数的性质.本题根据一次函数的性质,对四选项逐个进行判断即可得出结论.
【详解】解:A,当 时, ,故图象经过原点,说法正确.
.满足对于x的每一个取值,y都有唯一确定的值与之对应关系,可以表示 是 的函数,故该选项不符合题意.
2024年湖北省武汉市二中学广雅中学数学九上开学统考试题【含答案】

2024年湖北省武汉市二中学广雅中学数学九上开学统考试题题号一二三四五总分得分A 卷(100分)一、选择题(本大题共8个小题,每小题4分,共32分,每小题均有四个选项,其中只有一项符合题目要求)1、(4分)古希腊时期,人们认为最美人体的头顶至肚脐的长度与肚脐至足底的长度之比是黄金分割比(黄金分割比≈0.618)著名的“断臂维纳斯”便是如此.此外最美人体的头顶至咽喉的长度与咽喉至肚脐的长度之比也是黄金分割比.若某人满足上述两个黄金分割比例,且腿长为103cm ,头顶至脖子下端的长度为25cm ,则其身高可能是()A .165cm B .170cm C .175cm D .180cm 2、(4分)如图,▱ABCD 的对角线AC ,BD 交于点O ,E 为AB 的中点,G 为BC 延长线上一点,射线EO 与∠ACG 的角平分线交于点F ,若AC =5,BC =6,则线段EF 的长为()A .5B .112C .6D .73、(4分)若反比例函数ky x =的图象经过点()1,2--,则该反比例函数的图象位于()A .第一、二象限B .第二、三象限C .第二、四象限D .第一、三象限4、(4分)已知函数y=2x+k-1的图象经过第一、三、四象限,则k 的值可以是()A .3B .2C .1D .05、(4分)若式子x 的取值范围是()A .x >32B .x <32C .x≥32D.x≤326、(4分)如果a >b ,下列各式中正确的是()A .ac >bc B .a ﹣3>b ﹣3C .﹣2a >﹣2b D .22a b <7、(4分)下列二次根式是最简二次根式的是()A .B C D .8、(4分)下列分式2410xy x ,22a ba b ++,22x y x y -+,221a a a +-最简分式的个数有()A .4个B .3个C .2个D .1个二、填空题(本大题共5个小题,每小题4分,共20分)9、(4分)比较大小:10、(4分)等边三角形中,两条中线所夹的锐角的度数为_____.11、(4分)如图,已知()1,0A ,()3,0B ,()0,1C -,()0,1D,若线段CD 可由线段AB 围绕旋转中心P 旋转而得,则旋转中心P 的坐标是______.12、(4分)在1,2,3,4-这四个数中,任选两个数的积作为k 的值,使反比例函数y kx=的图象在第二、四象限的概率是________.13、(4分)如图,在四边形ABCD 中,AB ∥CD ,AB =BC =BD =2,AD =1,则AC =__________.三、解答题(本大题共5个小题,共48分)14、(12分)如图所示,在中,点在上,于,且平分,.求证:.15、(8分)如图,在平面直角坐标系中,以原点O 为位似中心,将OAB ∆放大到原来的2倍后得到OA B ∆'',其中A 、B 在图中格点上,点A 、B 的对应点分别为A '、B '。
2023-2024学年广东省广雅中学八年级下学期期中模拟数学试卷含详解
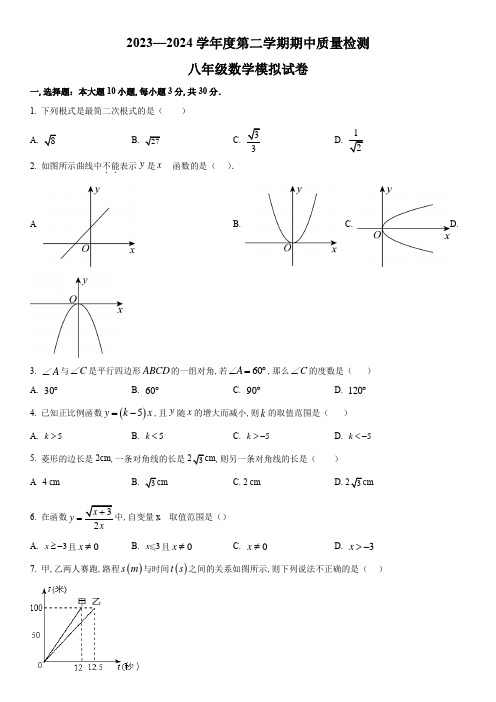
【答案】C
【分析】本题考查函数的概念,设在一个变化过程中有两个变量x与y,对于x的每一个确定的值,y都有唯一的值与其对应,那么就说y是x的函数,由此即可判断.
【详解】解:A,曲线能表示y是x的函数,故A不符合题意.
B,曲线能表示y是x的函数,故B不符合题意.
C,曲线中对于x的每一个确定的值,y都有两个值与之对应,则不能表示y是x的函数,故C符合题意.
2023—2024学年度第二学期期中质量检测
八年级数学模拟试卷
一,选择题:本大题10小题,每小题3分,共30分.
1.下列根式是最简二次根式的是()
A. B. C. D.
2.如图所示曲线中不能表示 是 函数的是().
A B. C. D.
3. 与 是平行四边形 的一组对角,若 ,那么 的度数是()
A. B. C. D.
4.已知正比例函数 ,且 随 的增大而减小,则 的取值范围是()
A. B. C. D.
【答案】B
【分析】正比例函数y随x的增而减小,则系数小于0.
【详解】解:由题意可知,正比例函数y随x的增大而减小.
∴k-5<0.
∴k<5.
故选:B.
【点睛】本题主要考查一次函数系数与图象的关系,了解函数的增减性是解答本题的关键.
10.如图,已知四边形 为正方形, , 为对角线 上一点,连接 ,过点 作 ,交 的延长线于点 ,以 , 为邻边作矩形 ,连接 .以下结论:①矩形 是正方形,② ,③ 平分 ,④ .其中结论正确的序号有().
A.①③④B.①②④C.①②③D.①②③④
【答案】A
【分析】过点E作 于点M,作 于点N,根据正方形性质结合所作辅助线可推出四边形 是正方形,由矩形性质得 ,又可证 ,即可利用“ ”证明 ,即得出 ,说明矩形 是正方形,故①正确,根据正方形性质得 ,推出 ,得到 ,由此推出 平分 ,故③④正确,进而求得 ,故②错误.
2023-2024学年广东省广州市荔湾区广雅中学八年级(上)期中数学试卷
2023-2024学年广东省广州市荔湾区广雅中学八年级(上)期中数学试卷一、选择题(本大题共10小题,每小题3分,满分30分,在每小题给出的四个选项中,只1.(3分)我们生活在一个充满对称的世界中,生活中的轴对称图形随处可见,下面几幅图片是校园中运动场上代表体育项目的图标,其中可以看作是轴对称图形的是()A.乒乓球B.跳远C.举重D.武术2.(3分)下列运算正确的是()A.a2•a4=a8B.a4+a4=a8C.(2ab)3=8a3b3D.(a2)4=a63.(3分)为了使一扇旧木门不变形,木工师傅在木门背面加钉了一根木条,这样做的道理是()A.三角形具有稳定性B.三角形两边之和大于第三边C.两点确定一条直线D.两点之间线段最短4.(3分)在下列各图中,正确画出△ABC边AC上的高的是()A.B.C.D.5.(3分)一个多边形的内角和等于外角和的两倍,那么这个多边形是()A.三边形B.四边形C.五边形D.六边形6.(3分)一个等腰三角形的周长为16cm,其中有一边的长为4cm,则该等腰三角形的腰长为()A.4cm B.6cm C.4cm或6cm D.4cm或8cm7.(3分)如图,△ACB≌△A′CB′,A′B′经过点A,∠BAC=65°,则∠ACA′的度数为()A.20°B.30°C.40°D.50°8.(3分)如图,在△ABC中,∠C=90°,∠A=15°,∠DBC=60°,BC=1,则AD的长为()A.1.5B.2C.3D.49.(3分)如图,在△ACD中,∠CAD=90°,AC=5,AD=12,AB∥CD,点E是CD上一点,BE交AD于点F,若AB=DE,则图中阴影部分的面积为()A.30B.40C.45D.6010.(3分)如图,在△ABC中,∠ABC=45°,CD⊥AB于点D,BE平分∠ABC,且BE⊥AC于点E,与CD相交于点F,DH⊥BC于点H,交BE于点G.下列结论:①BD=CD;②AD+CF=BD;③;④AE=CF.其中正确的是()A.①②B.①③C.①②③D.①②③④二、填空题(本大题共6小题,每小题3分,满分18分)11.(3分)点P(﹣1,2)关于x轴对称的点的坐标是.12.(3分)若a m=2,a n=6,则a m+n=.13.(3分)如图,把两根钢条的中点连在一起,可以做成一个测量工件内槽宽的工具(卡钳)在图中,若测量得A'B'=10cm,则工件内槽宽AB为cm.14.(3分)如图,在△ABC中,分别以点A和点B为圆心,大于的长为半径画弧,两弧相交于点M,N,作直线MN,交AC于点D,交AB于点E,连接BD.若∠C=90°,若∠ABD=2∠CBD,求∠A 的度数是.15.(3分)已知x+y=3,xy=1,则(x﹣2)(y﹣2)=.16.(3分)在△ABC中,AB=AC,∠BAC=40°,点D为直线BC上异于点B,C的一点,若△ABD是等腰三角形,求∠BAD的度数为.三、解答题(本大题共9小题,满分72分.解答应写出文字说明、证明过程或演算步骤。
广东省广州市广雅中学2024届高三下学期教学情况检测(二) 数学试题【含答案】

广东广雅中学2024届教学情况检测(二)数学试题注意事项:1.答卷前,考生务必将自己的姓名、考生号、考场号、座位号填写在答题卡上.2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号.回答非选择题时,将答案写在答题卡上,写在本试卷上无效.3.本卷满分150分,考试时间120分钟.考试结束后,将答题卡交回.一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合{}11P x x =-≤≤,{},M a a =-.若P M P ⋃=,则实数a 的取值范围是()A .{}11a a -≤≤B .{}11a a -<<C .{11a a -<<且}0a ≠D .{11a a -≤≤且}0a ≠2.在5(2)x +的展开式中,2x 项的系数为()A .1B .10C .40D .803.已知直线a ,b 和平面α,a ⊂α,b α⊂,则“//a α”是“//a b ”的()A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分也不必要条件4.2024年2月4日,“龙行中华——甲辰龙年生肖文物大联展”在山东孔子博物馆举行,展览的多件文物都有“龙”的元素或图案.出土于鲁国故城遗址的“出廓双龙勾玉纹黄玉璜”(图1)就是这样一件珍宝.玉璜璜身满刻勾云纹,体扁平,呈扇面状,璜身外镂空雕饰“S ”型双龙,造型精美.现要计算璜身面积(厚度忽略不计),测得各项数据(图2):8AB ≈cm ,2AD ≈cm ,5AO ≈cm ,若3sin 375︒≈,π 3.14≈,则璜身(即曲边四边形ABCD )面积近似为()A .26.8cmB .29.8cmC .214.8cmD .222.4cm 5.甲、乙、丙3人站到共有6级的台阶上,同一级台阶上的人不区分站的位置,则不同的站法种数是()A .156B .210C .211D .2166.记正项等差数列{}n a 的前n 项和为n S ,20100S =,则1011a a ⋅的最大值为()A .9B .16C .25D .507.已知直线:1l y mx m =--,P 为圆22:4210C x y x y +--+=上一动点,设P 到直线l 距离的最大值为()d m ,当()d m 最大时,m 的值为()A .12-B .32-C .23D .28.已知抛物线214y x =和21516y x =-+所围成的封闭曲线如图所示,已知点()0,A a ,若在此封闭曲线上至少存在两对不同的点,满足每一对点关于点A 对称,则实数a 的取值范围是()A .(]1,4B .5,42⎡⎫⎪⎢⎣⎭C .5,32⎡⎫⎪⎢⎣⎭D .(]2,3二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.9.设z 为复数(i 为虚数单位),下列命题正确的有()A .若z ∈R ,则z z =B .若2z ∈R ,则z ∈RC .若()1i 1i z +=-,则1z =D .若210z +=,则iz =10.袋子中有6个相同的球,分别标有数字1,2,3,4,5,6,从中随机取出两个球,设事件A =“取出的球的数字之积为奇数”,事件B =“取出的球的数字之积为偶数”,事件C =“取出的球的数字之和为偶数”,则()A .事件A 与B 是互斥事件B .事件A 与B 是对立事件C .事件B 与C 是互斥事件D .事件B 与C 相互独立11.已知函数()cos sin2xf x x =+,则()A .()f x 在区间π0,6⎛⎫⎪⎝⎭单调递增B .()f x 的图象关于直线πx =对称C .()f x 的值域为90,8⎡⎤⎢⎣⎦D .关于x 的方程()f x a =在区间[0,2π]有实数根,则所有根之和组成的集合为{}π,2π,4π三、填空题:本题共3小题,每小题5分,共15分.12.已知O 为坐标原点,点F 为椭圆2222:1(0)x y C a b a b+=>>的右焦点,点A ,B 在C 上,AB 的中点为F ,OA OB ⊥,则C 的离心率为.13.已知函数()log ab f x x x =-(0a >,0b >)且1b ≠),若()1f x ≥恒成立,则ab 的最小值为.14.已知球O 的表面积为12π,正四面体ABCD 的顶点B ,C ,D 均在球O 的表面上,球心O 为BCD △的外心,棱AB 与球面交于点P .若A ∈平面1α,B ∈平面2α,C ∈平面3α,D ∈平面4α,1//(1,2,3)i i i αα+=且i α与1(1,2,3)i i α+=之间的距离为同一定值,棱AC ,AD 分别与2α交于点Q ,R ,则PQR 的周长为.四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.15.如图,三棱柱111ABC A B C -中,侧面11ABB A 是边长为2的菱形,1π3ABB ∠=,AC =M 为11A B 中点,CM(1)证明:平面ABC ⊥平面11ABB A ;(2)若2BC =,求平面ABC 与平面1ABC 夹角的余弦值.16.“双减”政策执行以来,中学生有更多的时间参加志愿服务和体育锻炼等课后活动.某校为了解学生课后活动的情况,从全校学生中随机选取100人,统计了他们一周参加课后活动的时间(单位:小时),分别位于区间[7,9),[9,11),[11,13),[13,15),[15,17),[17,19],用频率分布直方图表示如下:假设用频率估计概率,且每个学生参加课后活动的时间相互独立.(1)估计全校学生一周参加课后活动的时间位于区间[)13,17的概率;(2)从全校学生中随机选取3人,记ξ表示这3人一周参加课后活动的时间在区间[)15,17的人数,求ξ的分布列和数学期望()E ξ;(3)设全校学生一周参加课后活动的时间的中位数估计值为a 、平均数的估计值为b (计算平均数时,同组中的每个数据都用该组区间的中点值代替),请直接写出,a b 的大小关系.17.双曲线C :()222210,0x y a b a b-=>>32,2T在C 上.(1)求C 的方程;(2)设圆O :222x y +=上任意一点P 处的切线交C 于M 、N 两点,证明:以MN 为直径的圆过定点.18.已知函数()()sin e ln 1xf x x a x =+++.(1)求曲线()y f x =在0x =处的切线方程;(2)当2a ≤-时,求函数()f x 在(]1,0-上的最小值;(3)写出实数a 的一个值,使得()1f x ≥恒成立,并证明.19.已知12:,,,k Q a a a 为有穷正整数数列,且12k a a a ≤≤≤,集合{}1,0,1X =-.若存在,1,2,,i x X i k ∈= ,使得1122k k x a x a x a t +++= ,则称t 为k -可表数,称集合{}1122,,1,2,,k k i T t t x a x a x a x X i k ==+++∈= ∣为k -可表集.(1)若110,2,1,2,,i i k a i k -=== ,判定31,1024是否为k -可表数,并说明理由;(2)若{}1,2,,n T ⊆ ,证明:312k n -≤;(3)设13,1,2,,i i a i k -== ,若{}1,2,,2024T ⊆ ,求k 的最小值.1.D【分析】根据并集结果可知M P ⊆,进而可构造不等式,解不等式求得结果.【详解】解:P M P = ,M P ∴⊆a P ∴∈,a P -∈且a a≠-11a ∴-≤≤,11a -≤-≤,0a ≠,解得:11a -≤≤且0a ≠a ∴的取值范围为{11a a -≤≤且}0a ≠故选:D 2.D【分析】利用通项求解可得.【详解】通项公式为515C 2rrr r T x -+=,当2r =时,232235C 280T x x ==,所以2x 项的系数为80.故选:D 3.B【分析】根据题意,由空间中的线面关系,即可判断.【详解】根据线面平行的判定定理可得,若//a b ,则//a α,即必要性成立,若//a α,则//a b 不一定成立,故充分性不成立,所以“//a α”是“//a b ”的必要不充分条件.故选:B 4.C【分析】根据给定图形求出圆心角AOB ∠,再利用扇形面积公式计算即得.【详解】显然AOB 为等腰三角形,5,8OA OB AB ===,则142cos 5ABOAB OA ∠==,3sin 5OAB ∠=,即37OAB ∠≈ ,于是53π10690AOB ∠==,所以璜身的面积近似为()()()222221153π·5314.8cm 2290AOB OA OD ∠-=⨯⨯-≈.故选:C 5.D【分析】共有三种情况,3人站一个台阶,或2人站一个台阶另1人站另一个台阶,或3人各站一个台阶,然后根据分类计数加法原理即可求解.【详解】若三人站在一个台阶上,有1363C A 种站法,若三人站在两个台阶上,有2262A A 种站法,若三人站在三个台阶上,有3363C A 种站法,所以,一共有132233636263C A A A C A 216++=种站法.故选:D.6.C【分析】根据等差数列的求和公式计算可得101110a a +=,利用基本不等式计算即可得出结果.【详解】∵12020201002a a S +=⨯=,120101112010,10.a a a a a a ∴+=∴+=+=又∵10110,0a a >>,∴210111011+100==2524a a a a ⎛⎫⋅≤ ⎪⎝⎭,当且仅当1011==5a a 时,取“=”∴1011a a ⋅的最大值为25.故选:C 7.A【分析】先得出直线l 过定点()1,1A -,再求出圆心坐标,由圆的对称性以及斜率公式得出m 的值.【详解】因为:l (1)(1)y m x --=-,所以直线l 过定点()1,1A -,圆22:4210C x y x y +--+=可化为22(2)(1)4x y -+-=,则圆心()2,1C ,2r =,由圆的对称性可知,当AC l ⊥时,P 到直线l 距离的最大,则1(1)221AC k --==-,112AC m k =-=-.故选:A 8.B【分析】先联立两抛物线方程求出抛物线交点的横坐标为4±,再根据题意知在某一支抛物线必存在一对点满足题意,故必定还存在两支曲线上的不同点关于(0,)A a 对称,设抛物线214y x =上的点21(,)4P t t ,则P 关于A 的对称点21(,2)4P t a t '--在21516y x =-+上,从而可得关于t 的方程:221125416a t t -=-+在(4,4)t ∈-上有解,最后参变分离转化为函数的值域,即可求解.【详解】联立22141516y x y x ⎧=⎪⎪⎨⎪=-+⎪⎩,可得216x =,所以4x =±,故两抛物线交点的横坐标为4±,显然在某一支抛物线上必存在一对点满足题意,故必定还存在两支曲线上的不同点关于(0,)A a 对称,不妨设抛物线214y x =上的点21(,)4P t t ,则P 关于A 的对称点21(,2)4P t a t '--在21516y x =-+上,所以关于t 的方程:221125416a t t -=-+在(4,4)t ∈-上有解,即232516a t =+在(4,4)t ∈-上有解,因为[)20,16t ∈,所以[)2355,816t +∈,所以[)25,8a ∈,即5,42a ⎡⎫∈⎪⎢⎣⎭.故选:B 9.AC【分析】利用共轭复数的定义可判断A 选项;利用特殊值法可判断B 选项;利用复数的除法化简复数z ,利用复数的模长公式可判断C 选项;解方程210z +=,可判断D 选项.【详解】对于A 选项,若z ∈R ,则z z =,A 对;对于B 选项,若2z ∈R ,不妨取i z =,则21z =-∈R ,但z ∉R ,B 错;对于C 选项,若()1i 1i z +=-,则()()()21i 1i i 1i 1i 1i z --===-++-,故1z =,C 对;对于D 选项,若210z +=,则21z =-,解得i z =±,D 错.故选:AC.10.AB【分析】利用互斥,对立,相互独立的概念逐一判断.【详解】对于AB :取出的球的数字之积为奇数和取出的球的数字之积为偶数不可能同时发生,且必有一个发生,故事件A 与B 是互斥事件,也是对立事件,AB 正确;对于C :如果取出的数为2,4,则事件B 与事件C 均发生,不互斥,C 错误;对于D :()()()22223333222666C C C C 4211,,C 5C 5C 5P B P C P BC +=-=====,则()()()P B P C P BC ≠,即事件B 与C 不相互独立,D 错误;故选:AB.11.BCD【分析】利用符合函数的单调性判断A ,计算出()()2πf x f x -=即可判断B ,利用换元法求出函数的值域,即可判断C ,求出函数在[0,2π]上的单调性,即可画出函数()f x 在区间[0,2π]的图象,结合图象分类讨论,即可判断D.【详解】对于A :当π0,6x ⎛⎫∈ ⎪⎝⎭时sin 02x >,所以2()cos sin 12sin sin 222x xx f x x =+=-+,因为sin 2x y =在π0,6⎛⎫ ⎪⎝⎭上单调递增,又πsin 124===,所以62sin 24x ⎛⎫∈ ⎪ ⎪⎝⎭,因为49316>,即74>172044=>,即124>,12>,所以π1sin 124=,又221y x x =-++在1,4∞⎛⎫- ⎪⎝⎭上单调递增,在1,4⎛⎫+∞ ⎪⎝⎭上单调递减,所以212sin sin 22xx y =-+在π0,6⎛⎫ ⎪⎝⎭上不单调,即()f x 在区间π0,6⎛⎫ ⎪⎝⎭不单调,故A 错误;对于B :因为()()()2π2πcos 2πsincos sin 22x xf x x x f x --=-+=+=,所以()f x 的图象关于直线πx =对称,故B 正确;对于C :因为()22cos sin 12sin sin 12sin sin 22222x x x x xf x x =+=-+=-+,令sin2x t =,则[]0,1t ∈,令()212h t t t =-+,[]0,1t ∈,则()h t 在10,4⎡⎤⎢⎥⎣⎦上单调递增,在1,14⎡⎤⎢⎥⎣⎦上单调递减,又()01h =,()10h =,1948h ⎛⎫= ⎪⎝⎭,所以()90,8h t ⎡⎤∈⎢⎥⎣⎦,所以()f x 的值域为90,8⎡⎤⎢⎥⎣⎦,故C 正确;对于D :当[0,2π]x ∈时sin02x ≥,所以()2cos sin 12sin sin 222x x xf x x =+=-+,由A 选项可令π0,6α⎡⎤∈⎢⎣⎦且1sin 24α=,则当[]0,x α∈时()f x 单调递增,令π222x α<<,即πx α<<时sin 2x y =在(),πα上单调递增,且1sin 142x<<,所以()f x 在(),πα上单调递减,又2π1sinsin 224αα-==,令π2π222x α-<<,即π2πx α<<-时sin 2xy =在()π,2πα-上单调递减,且1sin 142x<<,所以()f x 在()π,2πα-上单调递增,当2ππ22x α-<<,即2π2πx α-<<时sin 2x y =在()2π,2πα-上单调递减,且10sin 24x <<,所以()f x 在()2π,2πα-上单调递减,又()()02π1f f ==,()π0f =,()()92π8f f αα=-=,所以()f x 在[0,2π]上的函数图象如下所示:由图可知:①当0a =时()y f x =与y a =有且仅有一个交点,即关于x 的方程()f x a =在区间[0,2π]的实数根为π;②当01a <<或98a =时()y f x =与y a =有两个交点,即关于x 的方程()f x a =在区间[0,2π]有两个实数根,且两根关于πx =对称,所以两根之和为2π;③当918a ≤<时()y f x =与y a =有四个交点,即关于x 的方程()f x a =在区间[0,2π]有四个实数根,不妨设为1234,,,x x x x 且1234x x x x <<<,所以1x 与4x 关于πx =对称,2x 与3x 关于πx =对称,所以12344πx x x x +++=;④当a<0或98a >时()y f x =与y a =无交点,即关于x 的方程()f x a =在区间[0,2π]无实数根;综上可得,若关于x 的方程()f x a =在区间[0,2π]有实数根,则所有根之和组成的集合为{}π,2π,4π,故D 正确;故选:BCD【点睛】关键点点睛:对于D 选项关键是分析出函数的单调性,结合函数图象,将方程的解转化为函数与函数的交点问题,结合函数的对称性求出方程的根的和.12.12【分析】先结合图形求得(),A c c ,代入椭圆方程构造齐次式,然后可解.【详解】由椭圆的对称性可知,AB 垂直于x 轴,又OA OB ⊥,所以π4AOF ∠=,所以AOF 为等腰直角三角形,故(),A c c ,所以22221c c a b+=,即222222a c b c a b +=,所以()()22222222a c a c c a a c +-=-,整理得42310e e -+=,解得2352e -=或2352e +=(舍去),故2355151222e ⎛⎫---=== ⎪ ⎪⎝⎭.故答案为:512-13.e【分析】根据题意分类讨论01b <<,1b >两种情况,通过导数求导得到ln bab b=,再构造函数()()1ln bg b b b=>及导数方法求出其最小值,从而求解.【详解】函数()log ab f x x x =-的定义域为()0,+∞,当01b <<时,可得()f x 在()0,+∞上单调递增,()0110a f b b b =-<-=,不合题意;当1b >时,()111ln ln a a a f x axx x b x a b -⎛⎫=--'= ⎝⎭,令()00f x '=,解得101ln a x a b ⎛⎫= ⎪⎝⎭,当()00,x x ∈时,()0f x '<,()f x 单调递减,当()0,x x ∈+∞时,()0f x '>,()f x 单调递增,所以当0x x =时,()f x 有极小值,也是最小值,又因为()11f ≥且()11f =,所以()()0min 011f x f x x ⎧==⎨=⎩,则1011ln ax a b ⎛⎫== ⎪⎝⎭,得ln 1a b =,所以ln b ab b =,设()()1ln b g b b b=>,()()2ln 1ln b g b b -'=,令()0g b '=,得e b =,当()1,e b ∈,()0g b '<,当()e,b ∈+∞,()0g b '>,所以()g b 在区间()1,e 单调递减,()e,+∞单调递增,所以()()min e e g b g ==,即ab 的最小值为e .故答案为:e .【点睛】方法点睛:通过分类讨论01b <<,1b >两种情况得到符合的情况,通过导数求导得到ln b ab b =,再构造函数()()1ln bg b b b=>并利用导数求出其最小值即可.14.1+1【分析】结合球的表面积公式,根据正三角形外接圆的性质求得边长,利用三点共线及数量积的运算律求得113AP AB ==,然后利用平行平面的性质求得1AR =,32AQ =,再利用余弦定理求得PQ RQ ==PQR 的周长.【详解】设i α与1(1,2,3)i i α+=之间的距离为d ,设球O 的半径为R ,则由题意得24π12πR =,解得R =所以OB OP ==,所以3AB BC ===,所以OA ,由A ,P ,B 三点共线,故存在实数λ使得()()101OP OA OB λλλ=+-<< ,所以()()22222121OP OA OB OA OB λλλλ=+-+-⋅,所以()223631λλ=+-,即2320λλ-=,解得23λ=,所以2133OP OA OB =+ ,所以12AP PB =,所以113AP AB ==,又1//(1,2,3)i i i αα+=且i α与1(1,2,3)i i α+=之间的距离为d ,则133AR d AD d ==,122AQ d AC d ==,所以1AR =,32AQ =,所以93171214222PQ RQ ==+-⨯⨯⨯=,又113PR BD ==,所以PQR 的周长为712172+⨯=+.故答案为:17+【点睛】关键点点睛:本题考查学生的空间想象能力,解题关键是找到点,,P Q R 的位置.本题中应用正四面体的性质结合球的半径,求出边长,利用平行平面的距离,得到所求三角形的边长即可求解.15.(1)证明见解析(2)77【分析】(1)连接1,AM AB ,证明AM AB ⊥,继而证明AM AC ⊥,即可证明AM ⊥平面ABC ,根据面面垂直的判定定理,即可证明结论;(2)建立空间直角坐标,求得相关点坐标,求出平面ABC 与平面1ABC 的法向量,根据空间角的向量求法,即可求得答案.【详解】(1)连接1,AM AB ,在菱形11ABB A 中,111π2,3A A AB AA B ==∠=,故1AA B 为正三角形,又M 为11A B 中点,故11AM A B ⊥,且3AM =又11AB A B ∥,故AM AB ⊥,CM =AC =222AM AC C M +=,故AM AC ⊥,而,,AB AC A AB AC =⊂ 平面ABC ,故AM ⊥平面ABC ,又AM ⊂平面11ABB A ,故平面ABC ⊥平面11ABB A ;(2)由于2BC AB ==,AC =222BC BA AC +=,故CB AB ⊥,又平面ABC ⊥平面11ABB A ,平面ABC ⋂平面11ABB A AB =,而CB ⊂平面ABC ,故CB ⊥平面11ABB A ,取1BB 中点为O ,则1ABB 为正三角形,则1AO BB ⊥,作OH BC ∥,交1CC 于H ,故OH ⊥平面11ABB A ,1BB ,OA ⊂平面11ABB A ,故1,OH OA OH OB ⊥⊥,则1,,OA OB OH 两两垂直,分别以1,,OA OB OH 所在直线为,,x y z轴,建立空间直角坐标系,则)()()()13,0,1,0,0,1,2,0,1,2,,,022AB C C M ⎛⎫-- ⎪ ⎪⎝⎭,)()1,0,2,2BA BC ==,因为AM ⊥平面ABC,故3,,022AM ⎛⎫= ⎪ ⎪⎝⎭可作为平面ABC 的法向量,设平面1ABC 的法向量为(),,n x y z = ,则100n BA n BC ⎧⋅=⎪⎨⋅=⎪⎩ ,即0220y y z +=+=⎪⎩,令y =(1,n = ,故cos ,n AM n AM n AM ⋅===⋅,而平面ABC 与平面1ABC 夹角的范围为π[0,2,故平面ABC 与平面1ABC夹角的余弦值为7.16.(1)0.65(2)分布列见解析,期望为1.2(3)b a<【分析】(1)根据频率分布直方图计算出对应频率即为所求;(2)由题意可得ξ服从二项分布,再根据二项分布的分布列及期望公式求解即可;(3)根据公式计算平均数和中位数,再比较大小即可.【详解】(1)根据频率分布直方图,可得学生一周参加课后活动的时间位于区间[)13,17的频率为()0.1250.20020.65+⨯=,因此估计全校学生一周参加课后活动的时间位于区间[)13,17的概率为0.65;(2)从全校学生中随机选取1人,其一周参加课后活动的时间在区间[)15,17的概率为0.4,因此()3,0.4B ξ ,ξ可取0,1,2,3,()()311230(10.4)0.216,1C 0.4(10.4)0.432P P ξξ==-===⨯⨯-=,()()221332C 0.4(10.4)0.288,30.40.064P P ξξ==⨯⨯-====.则ξ的分布列为:ξ0123P0.2160.4320.2880.064()30.4 1.2E ξ=⨯=;(3)因为()0.0250.0500.07520.30.5++⨯=<,()0.0250.0500.0750.12520.550.5+++⨯=>,故中位数a 在区间[)13,15上,则()130.1250.50.30.2a -⨯=-=,14.6a =;()280.025100.050120.075140.125160.200180.02514b =⨯⨯+⨯+⨯+⨯+⨯+⨯=,故b a <.17.(1)2212y x -=(2)证明见解析【分析】(1)结合题目所给条件可列出不等式组,解出即可得;(2)可结合双曲线及圆的对称性得出,若存在定点,则该定点必为原点,从而先猜后证,简化过程;或根据圆的方程,结合韦达定理表示出该圆方程,即可得定点坐标.【详解】(1)依题意有22222221a b c a b c a ⎧-=⎪⎪=+⎨⎪⎪⎩,即有22222212a b a b⎧-=⎪⎨⎪=⎩,解得:21a =,22b =,所以双曲线方程为2212y x -=;(2)方法一:设()11,M x y ,()22,N x y ,①当切线斜率存在时,设直线方程为y kx m =+,=2222m k =+,联立()22222122202y x k x kmx m y kx m ⎧-=⎪⇒----=⎨⎪=+⎩,()()()222222Δ4422820k m k m m k =+-+=+->,则12222km x x k +=-,212222m x x k --=-,由对称性知,若以MN 为直径的圆过定点,则定点必为原点.1212OM ON x x y y ⋅=+()()()()22121212121x x kx m kx m kx xmk x x m =+++=++++()2222222122m kmkmk m k k--=+++--222222m k k--=-,又2222m k =+,所以0OM ON ⋅=,所以OM ON ⊥,故以MN 为直径的圆过原点;②当直线斜率不存在时,直线方程x =此时,MN或,MN,此时圆方程为(222x y +=,恒过原点;或((,M N或((,M N ,此时圆方程为(222x y +=,恒过原点;综上所述,以MN 为直径的圆过原点.方法二:设()11,M x y ,()22,N x y ,①当切线斜率存在时,设直线方程为y kx m =+,=2222m k =+,联立()22222122202y x k x kmx m y kx m ⎧-=⎪⇒----=⎨⎪=+⎩,()()()222222Δ4422820k m k m m k =+-+=+->,则12222km x x k +=-,212222m x x k --=-,以()11,M x y ,()22,N x y 为直径的圆的方程为()()()()12120x x x x y y y y --+--=,即()()22121212120x x x x x x y y y y y y -+++-++=,因为()()()()221212121212121x x y y x x kx m kx m k x x km x x m +=+++=++++,所以()222221212222222210222m km m k x x y y k km m k k k ----+=+⋅+⋅+==---,且()121222242222km my y k x x m k m k k +=++=⋅+=--,所以所求的圆的方程为222224022km m x x y y k k -+-=--,所以MN 为直径的圆过原点;②当直线斜率不存在时,同法一,此时圆方程为(222x y +=,恒过原点;综上所述,以MN 为直径的圆过原点.【点睛】方法点睛:利用韦达定理法解决直线与圆锥曲线相交问题的基本步骤如下:(1)设直线方程,设交点坐标为()()1122,,,x y x y ;(2)联立直线与圆锥曲线的方程,得到关于x (或y )的一元二次方程,注意∆的判断;(3)列出韦达定理;(4)将所求问题或题中的关系转化为12x x +、12x x (或12y y +、12y y )的形式;(5)代入韦达定理求解.18.(1)()210a x y +-+=(2)1(3)2a =-,证明见解析【分析】(1)由()()02,01f a f k =+'==直接写出切线方程;(2)先证()f x 单调递减再求最小值.(3)2a =-时,()f x 在(]1,0-上单调递减,在()0,∞+上单调递增,得()()01f x f =≥.【详解】(1)因为()()sin e ln 1xf x x a x =+++,所以()cos e 1xa f x x x =+++',所以()()02,01f a f =+=',所以切线方程为()21y a x =++,即()210a x y +-+=.(2)当2a ≤-时,()()()sin e ln 1,cos e 1x xa f x x a x f x x x =+++=+'++.当(]1,0x ∈-时,cos e 2,21xax x +≤≤-+,所以()0f x '≤恒成立,()f x 单调递减.所以()min ()01f x f ==.(3)2a =-.证明:当2a =-时,()2cos e 1xf x x x =+-+',根据(2),当(]1,0x ∈-时,()f x 单调递减.当()0,x ∈+∞时,设()2cos e 1x g x x x =+-+,则()22e sin (1)xg x x x =+-+',2222e sin 110(1)(1)x x x x +->+->++,所以()2cos e 1xf x x x =+-+'单调递增,()()00f x f ''>=,所以()f x 单调递增.综上所述,()f x 在(]1,0-上单调递减,在()0,∞+上单调递增,所以()()01f x f =≥.19.(1)31是k -可表数,1024不是k -可表数,理由见解析;(2)证明见解析;(3)8【分析】(1)根据定义赋值及数列求和计算验证即可;(2)根据定义判定s T ∈则有s T -∈,从而可知{}1,2,,,0n T ±±±⊆ ,利用集合间的基本关系得出T 中最多含有3k 个元素,解不等式即可证明;(3)利用第二问的结论可设N ,N n m **∀∈∃∈,有1313122m m n ---<≤,然后利用定义先证n 为m -可表数,再根据三进制的基本事实确定k 的最小值为满足1313122m mn ---<≤成立的m ,代入2024n =求m 即可.【详解】(1)31是,1024不是,理由如下:由题意可知1122k k x a x a x a t +++= ,当12,10i i a k -==时,有{}9121022,1,0,1i x x x t x +++=∈- ,显然若{}()161,1,02,3,4,5,7,8,9,10i x x x i =-==∈时,31t =,而012910212121212110231024t ≤⨯+⨯+⨯++⨯=-=< ,故31是k -可表数,1024不是k -可表数;(2)由题意可知若00i x t =⇒=,即0T ∈,设s T ∈,即{}1,0,1i x ∃∈-使得1122k k x a x a x a s +++= ,所以()()()1122k k x a x a x a s -+-++-=- ,且{}1,0,1i x -∈-成立,故s T -∈,所以若{}1,2,,n T ⊆ ,则{}1,2,,,0n T ±±±⊆ ,即{}1,2,,0n ±±± 中的元素个数不能超过T 中的元素,对于确定的Q ,T 中最多有3k 个元素,所以312132k kn n -+≤⇒≤;(3)由题意可设N ,N n m **∀∈∃∈,使1313122m m n ---<≤,又122221231311333111313132m m m m x x x x -----⨯+⨯+⨯++⨯≤⨯+⨯+⨯++⨯= ,所以1k m >-,即k m ≥,而2131111313132m m --⨯+⨯+⨯++⨯= ,即当312m n -=时,取1121,3,3m m a a a -=== 时,n 为m -可表数,因为()21312111313132312m m m--⨯⨯+⨯+⨯++⨯=⨯=- ,由三进制的基本事实可知,对任意的031m p ≤≤-,存在{}()0,1,21,2,,,i r i m ∈= ,使01112333m m p r r r -=⨯+⨯+⨯ ,所以()()01101112313333332m m m m p r r r ----=⨯+⨯+⨯-+++ ()()()01112131313m m r r r -=-⨯+-⨯++-⨯ ,令1i i x r =-,则有{}1,0,1,1,2,,i x i m ∈-= ,设313131222m m m t p t ---=-⇒-≤≤,由p 的任意性,对任意的3131,Z 22m mt t ---≤≤∈,都有{}01112333,1,0,1,1,2,,m m i t x x x x i m -=⨯+⨯++⨯∈-= ,又因为312m n -≤,所以对于任意的,Z n t n t -≤≤∈,t 为m -可表数,综上,可知k 的最小值为m ,其中m 满足1313122m m n ---<≤,又当2024n =时,78313122n --<≤,所以k 的最小值为8.【点睛】难点点睛:第二问关键是根据定义可确定T 中元素互为相反数,再利用集合间的基本关系确定元素个数的关系计算即可;第三问利用第二问的结论可设N ,N n m **∀∈∃∈,有1313122m m n ---<≤,利用定义先证n 为m -可表数,再根据三进制的基本事实设任意的031m p ≤≤-,存在{}()0,1,21,2,,,i r i m ∈= ,使01112333m m p r r r -=⨯+⨯+⨯ ,得出312m t p -=-并结合定义确定t 为m -可表数,从而确定k 的最小值为满足1313122m m n ---<≤成立的m ,代入2024n =求m 即可.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
广州市广雅中学11-12学年高一上学期期中考试
数学试题
命题人:高一数学备课组 统审人:何其峰 审核人:徐广华 本试卷满分为150分,考试用时120分钟。
第一部分 选择题 (共40分)
一、选择题:本大题共8小题,每小题5分,共40分. 在每小题给出的四个选项中,只有
一项是符合题目要求的.
1. 函数)1(log 2
1-=x y 的定义域是
A .0(,)+∞
B .1(,)+∞
C .2(,)+∞
D .12(,)
2.已知{}{}1,2,3,2,4A B ==,定义{}|A B x x A x B -=∈∉且,则A B -=
A. {}1,2,3
B. {}2,4
C. {}1,3
D. {}2
3.下列函数中,在其定义域内既是奇函数又是增函数的是
A .R x x y ∈-=,
B .R x y x ∈=,2
C .R x x y ∈=,3
D .,y x x R =
4.已知2m >,点123(1,),(,),(1,)m y m y m y -+都在二次函数2
2y x x =-的图象上,则
A. 123y y y <<
B. 321y y y <<
C. 312y y y <<
D. 213y y y <<
5. 已知函数x e y =的图象与函数)(x f y =的图象关于直线x y =对称,则
A .()()22x f x e x R =
B .()ln ln ()220f x x x =>
C .()()22x f x e x R =
D .()ln ln ()220f x x x =+>
6. 函数(01)x
y a a =<<的图象是
7. 设函数⎩⎨⎧<+≥+-=0
,60,64)(2x x x x x x f 则不等式)1()(f x f >的解集是
A .),3()1,3(+∞⋃-
B .),2()1,3(+∞⋃-
C .),3()1,1(+∞⋃-
D .)3,1()3,(⋃--∞
8. ()f x 在(1,1)-上既是奇函数,又为减函数. 若2(1)(1)0f t f t -+->,则t 的取值范围是
A .12t t ><-或
B .1t <<
C .21t -<<
D .1t t <>或
第二部分 非选择题 (共110分)
二、填空题:本大题共6小题,每小题5分,共30分.
9. 若函数 1 (0)() 4 (0)
x x f x x x +≥⎧=⎨
--<⎩,则()5f f -=⎡⎤⎣⎦ .
10. 计算222log 10log 0.04+= .
11.函数()20.5log (32)f x x x =--的单调递增区间是 .
12. 若函数1()42
3x x f x +=-+的定义域为[1,1]-,则()f x 值域为 .
13. 已知()f x 在R 上是奇函数,且当0x ≥时,2()ln(1)f x x x =-+;则当0x <时, ()f x 的解析式为()f x = .
14. 方程0122=++ax x 一个根大于1,一个根小于1,则实数a 的取值范围是 .
三、解答题:本大题共6小题,共 80 分. 解答应写出文字说明、证明过程或演算步骤.
15.(本题满分13分)
设全集为U ,集合}6,4,2,0{=A ,{1,3,1,3}U A =--ð,{1
,0,2}U B =-ð,求B A 和B A
16.(本题满分13分)
若函数22,0()22,0x x f x x x x ⎧>⎪=⎨---≤⎪⎩
, (Ⅰ)在给定的平面直角坐标系中画出函数()f x 图象;
(Ⅱ)利用图象写出函数()f x 的值域、单调区间.
17.(本题满分13分) 已知1()log 1a x f x x
+=-(0a >且1a ≠) (Ⅰ)求()f x 的定义域;
(Ⅱ)判断()f x 的奇偶性并证明;
(Ⅲ)求使()0f x >成立的x 的取值范围.
18.(本题满分14分) 已知函数2142
a y x ax =-+-
+在区间[0,1]上的最大值是2,求实数a 的值.
19.(本题满分13分)
一片森林原来面积为a ,计划每年砍伐一些树,且每年砍伐面积的百分比相等,当砍伐到面
积的一半时,所用时间是10年,为保护生态环境,森林面积至少要保留原面积的14,已知到今
. (Ⅰ)求每年砍伐面积的百分比;
(Ⅱ)到今年为止,该森林已砍伐了多少年?
(Ⅲ)今后最多还能砍伐多少年?
20.(本题满分14分)
函数()f x 对一切实数x ,y 均有()()(21)f x y f y x y x +-=++成立,且(1)0f =. (Ⅰ)求(0)f 的值;
(Ⅱ)求函数()f x 的解析式; (Ⅲ)对任意的11(0,)2x ∈,21(0,)2
x ∈,都有12()2log a f x x +<成立时,求a 的取值范围.
广东广雅中学2011学年度上学期期中必修1模块考试
参考答案及评分标准(共3页)
16.(本题满分13分)
解:
…………………………7分
()10,012<<∴<-∴x x x …………10分
10<<a 当时,由()0f x >得 1011x x
+<<-, 则由1101101x x x x
+⎧+>⎪⎪-⎨+⎪<⎪-⎩解得01<<-x …………………………12分 综上,当1a >时,使()0f x >的x 的取值范围为(0,1);
10<<a 当时,使()0f x >的x 的取值范围为(1,0)-. …………………13分
123456-1-2-3-4-5-6-1
-2-3
-4
-5
12
345
x y 0
(Ⅱ)设经过m 年
剩余面积为原来的2
,则 a x a m 22)1(=-, 即2110)2
1()21(=m ,2110=m ,解得5=m 故到今年为止,已砍伐了5年。
………………………………8分 (Ⅲ)设从今年开始,以后砍了n 年,则n 年后剩余面积为n x a )1(2
2- 令n x a )1(2
2-≥a 41,即n x )1(-≥42, 10)21(n ≥23
)21(,10n ≤23,解得n ≤15 故今后最多还能砍伐15年。
………………………13分。
