基本图元的生成算法
第4章 基本图元的生成

putpixel(xc+x,yc-y);
{ plotC(x,y,xc,yc); if(d<0)
putpixel(xc-x,yc+y); putpixel(xc-x,yc-y);
d+=4*x+6;
putpixel(xc+y,yc+x);
else {
putpixel(xc+y,yc-x);
d+=4*(x-y)+10;
d 1=F(xp+2, yp+1.5)=a(xp+2)+b(yp+1.5)+c=d+a+b
增量d1-d=a+b * d>=0时,应取正右方的P1。 接着判断再下一个像素的选取,则需计算:
d2=F(xp+2, yp+0.5)=a(xp+2)+b(yp+0.5)+c=d+a
增量d2-d=a * d的初值d0=F(x0+1,y0+0.5)=a(x0+1)+b(y0+0.5)+c
原理:每一步考察两个可能
Pi-1
Ti
的像素点中那一个更靠近理
t
论圆周,从而推出沿圆周的
s
整数位置。
为计算方便,先将圆心(xc,yc)
Si
移到原点(0,0)。
算法:
* 沿x方向每次递增1个单位,从x=0开始,x=y结束,起点坐
标(0,r)
* 已知Pi-1(xi-1,yi-1)是最接近圆周的像素点,那么下一个像素点 只有可能是Ti(xi-1+1,yi-1)或Si(xi-1+1,yi-1-1)
【计算机图形学】基本图形元素:圆的生成算法

【计算机图形学】基本图形元素:圆的⽣成算法圆的特征圆被定义为到给定中⼼位置(xc,yc)距离为r的点集。
圆⼼位于原点的圆有四条对称轴x=0,y=0, x=y和x=-y。
若已知圆弧上⼀点(x,y),可以得到其关于四条对称轴的其它7个点,这种性质称为⼋分对称性。
因此,只要扫描转换⼋分之⼀圆弧,就可以求出整个圆弧的象素集。
显⽰圆弧上的⼋个对称点的算法:void CirclePoints(int x,int y,int color){ Putpixel(x,y,color); Putpixel(y,x,color);Putpixel(-x,y,color); Putpixel(y,-x,color);Putpixel(x,-y,color); Putpixel(-y,x,color);Putpixel(-x,-y,color); Putpixel(-y,-x,color);}中点画圆算法果我们构造函数 F(x,y)=x2+y2-R2,则对于圆上的点有F(x,y)=0,对于圆外的点有F(x,y)>0,对于圆内的点F(x,y)<0 。
与中点画线法⼀样,构造判别式:d=F(M)=F(xp+1,yp-0.5)=(xp+1)2+(yp-0.5)2-R2若 d<0,则应取P1为下⼀象素,⽽且再下⼀象素的判别式为:d=F(xp+2,yp-0.5)=(xp+2)2+(yp-0.5)2-R2=d+2xp+3若d≥0,则应取P2为下⼀象素,⽽且下⼀象素的判别式为d=F(xp+2,yp-1.5)=(xp+2)2+(yp-1.5)2-R2=d+2(xp-yp)+5我们这⾥讨论的第⼀个象素是(0,R),判别式d的初始值为:d0=F(1,R-0.5)=1.25-R【算法流程图】【算法代码】void PaintArea::drawCircleMiddle(QPainter &painter,const QPoint ¢er, int r) {int x,y,deltax,deltay,d;x=0;y=r;deltax=3;deltay=2-3-3;d=1-r;while(x<y){if(d<0){d+=deltax;deltax+=2;x++;}else{d+=(deltax+deltay);deltax+=2;deltay+=2;x++;y++;}painter.drawPoint(center.x()+x,center.y()+y);painter.drawPoint(center.x()+x,center.y()-y);painter.drawPoint(center.x()-x,center.y()+y);painter.drawPoint(center.x()-x,center.y()-y);painter.drawPoint(center.x()+y,center.y()+x);painter.drawPoint(center.x()+y,center.y()-x);painter.drawPoint(center.x()-y,center.y()+x);painter.drawPoint(center.x()-y,center.y()-x);}}Bresenham画圆算法思想参见直线的Bresenham画法【算法流程图】【算法代码】void PaintArea::drawCircleBresenham(QPainter &painter,const QPoint ¢er, int r) {int x,y,delta,delta1,delta2,direction;x=0;y=r;delta=2*(1-r);while(y>=0){painter.drawPoint(x,y);if(delta<0){ delta1=2*(delta+y)-1;if(delta1<=0)direction=1; else direction=2; }else if(delta>0){ delta2=2*(delta-x)-1;if(delta2<=0)direction=2; else direction=3; }else direction=2;switch(direction){case 1:x++;delta+=2*x+1; break;case 2:x++; y--; delta+=2*(x-y+1); break;case 3:y--;delta+=(-2*y+1); break;}}}椭圆弧⽣成算法基本同圆弧算法,只是⽅程变得复杂F(x,y)=(bx)^2+(ay)^2-(ab)^2.对称性:4分对称,画第⼀象限分段依据:斜率为⼀点上段圆弧:下段圆弧:【椭圆中点算法流程图】【算法代码】void PaintArea::drawEllipseMiddle(QPainter &painter,int xCenter,int yCenter, int Rx, int Ry) {int Rx2=Rx*Rx;int Ry2=Ry*Ry;int twoRx2=2*Rx2;int twoRy2=2*Ry2;int p,x=0,y=Ry,px=0,py=twoRx2*y;void ellipsePlotPoints(QPainter&,int,int,int,int);ellipsePlotPoints(painter,xCenter,yCenter,x,y);//Region1p=round(Ry-(Rx2*Ry)+(0.25*Rx2));while(px<py){x++;px+=twoRy2;if(p<0)p+=Ry2+px;else{y--;py-=twoRx2;p+=Ry2+px-py;}ellipsePlotPoints(painter,xCenter,yCenter,x,y);}//Region2p=round(Ry2*(x+0.5)*(x+0.5)+Rx2*(y-1)*(y-1)-Rx2*Ry2);while(y>0){y--;py-=twoRx2;if(p>0)p+=Rx2-py;else{ x++;px+=twoRy2;p+=Rx2-py+px;}ellipsePlotPoints(painter,xCenter,yCenter,x,y);}}void ellipsePlotPoints(QPainter &painter,int xCenter,int yCenter,int x,int y){ painter.drawPoint(xCenter+x,yCenter+y);painter.drawPoint(xCenter-x,yCenter+y);painter.drawPoint(xCenter+x,yCenter-y);painter.drawPoint(xCenter-x,yCenter-y);}软件截图这个绘图软件是⽤QT写的,我会另外写⼀篇介绍编程结构,待续~转载请注明出处:。
计算机图形学第3章 基本图形生成算法

例题:有点P0(4,3);P1(6,5);P2(10,
6 );P3(12,4),用以上4点构造2次B样条曲线。
2.1.7 非均匀有理B样条
非均匀有理B样条NURBS(Non Uniform Rational BSpline);
3.2.2
Bresenham画圆法
该算法是最有效的算法之一。
不失一般性,假设圆心(xc,yc) ,圆上的点(x′,y′),则:
x' x xc
y ' y yc
圆心为原点,半径为R的位于第一象限1/8圆弧的画法,即(0, R)~( R , R )。
2 2
yi ), 思想:每一步都选择一个距离理想圆周最近的点P( xi , 使其误差项最小。
画其他曲线。
3.3
自由曲线的生成
正弦函数曲线
指数函数曲线
多项式函数曲线
自 由 曲 线
概率分布曲线及样条函数曲线
3.3.1 曲线的基本理论
基本概念
2.1.4
规则曲线:可用数学方程式表示出来的,如抛物 线等。
自由曲线:很难用一个数学方程式描述的,如高
速公路等。可通过曲线拟合(插值、逼近)的方法来
例题: 利用Bresenham算法生成P (0,0)到Q(6,5)的直 线所经过的像素点。要求先 列出计算式算出各点的坐标 值,然后在方格中标出各点。
(1,1)
3.1.5 双步画线法 原理
模式1:当右像素位于右下角时,中间像素位于底线 模式4:当右边像素位右上角时,中间像素位于中线 模式2和模式3:当右像素位于中线时,中间像素可能位于底线 上,也可能位于中线上,分别对应于模式2和模式3,需进一步 判断。 当0≤k≤1/2时,模式4不可能出现,当1/2≤k≤1时,模式1不 可能出现。
电脑图形教程基本图形生成算法

P2
e’
e P P1
y方向不走步
P2
e
e’
P
P1
Bresenham画线算法(6/7)
下一步误差的计算
当e≥0时,y方向走一步
e’=2y/ x - 1 =e + y/ x - 1 e’=e + 2y - 2x
当e<0时,y方向不走步
e’=2y/ x=e + y/ x e’=e + 2y
P2
光栅图形中点的表示
Address(x,y) = (xmax-xmin) * (y-ymin) + (x-xmin) + 基地址 = k1 + k2y + x
对像素连续寻址时,如何减少计算量?
Address(x±1,y) = k1 + k2y + (x±1) = Address(x,y) ± 1 Address(x,y±1) = k1 + k2(y ±1) + x = Address(x,y) ± k2 Address(x±1,y±1) = k1 + k2(y ±1) + (x±1)
实区域填充 字符 图形反走样
光栅图形中点的表示
…
地址线性表 1D表示
(x,y)坐标
显示屏幕 2D表示
像素由其左下角坐标表示
光栅图形中点的表示
y ymax
ymin xmin
x xmax
地址 = (xmax-xmin) * (y-ymin) + (x-xmin) + 基地址
每行像素点数
行数
行中位置
P2
M (Xp+1,Yp+0.5)
P
第2章基本图形生成算法

if (Flag) { //X方向单位增量
for (n=0; n<= Length; n++) {//X方向插补过程
WritePixel(ix, Round(y), value); ix+=idx; y+=dy; } //End of for } //End of if else { //Y方向斜率增量
第 2 章 基本图形生成算法(Ⅰ)
1) Bresenham的基本原理
假定直线斜率 k在 0~1之间 。 此时 , 只需考
虑 x方向每次递增 1个单位 , 决定 y方向每次 递增 0或 1。
设直线的
当前点为 (xi,y) 当前光栅点为 (xi,yi)
下一个
直线的点应为 (xi+1,y+k) 直线的光栅点
y
y 2
y1
k
x x2 x1
第 2 章 基本图形生成算法(Ⅰ)
1)David F. Rogers 描述描述
如果已知第 i点的坐标 , 可用步长 StepX 和 StepY得到
第 i+1点的坐标为 : – xi+1=xi+ StepX – yi+1=yi+ StepY 或 yi+1=yi+ k * StepX
Bresenham算法
– 基本原理 – Bresenham算法 – 整数 Bresenham算法 – 一般整数 Bresenham算法
第 2 章 基本图形生成算法(Ⅰ)
2.1.1 DDA算法算法
1)David F. Rogers 描述描述
直线的基本微分方程是 :
dy dx = 常数 (k)
设直线通过点 P1(x1,y1)和P2(x2,y2) , 则直线方程可表示为 :
CG No3-基本图元生成-1

LinYi University School of Informatics Wang Libo
Computer Graphics 计算机图形学
程序实现
DDALine(int X0,int Y0,int X0,int Y0,Color color) { int X float dx,dy,k,y dx=x1-x0; dy=y1-y0; k=dy/dx; y=Y0; for(x=X0;x<=X1;x++){ putpixel(x,int(y+0.5),Color); y=y+k; } }
getch(); closegraph( ); }
LinYi University School of Informatics Wang Libo
Computer Graphics 计算机图形学
2、逐点比较法
1.偏差计算 <0 画笔在OA下方,走+y 一步 d=tgβ-tgα = =0 画笔在OA上,走+x 一步 >0 画笔在OA上方,走+ x 一步 第一象限: d=ym/xm—yA/xA=(ymxA-yAxm)/xAxm 判别式:Fm=ymxA-xmyA >=0 走+x <0 走+y
Computer Graphics 计算机图形学
Computer Graphics
计算机图形学
基本图元的生成
LinYi University School of Informatics Wang Libo
Computer Graphics 计算机图形学
第二章 基本图元生成算法
几何图形G={Pi | Pi 最接近图形的象素 }
基本图形元素生成算法
实验一基本图形元素生成算法1.实验目的:(1)掌握基本图形元素生成算法。
(2)了解高级语言的图形模式的设定和对基本图形类(或函数)的调用方法。
2.实验内容:选定Bresenham算法,编写生成该基本图形的源程序,并能在计算机上编译运行,画出正确的图形。
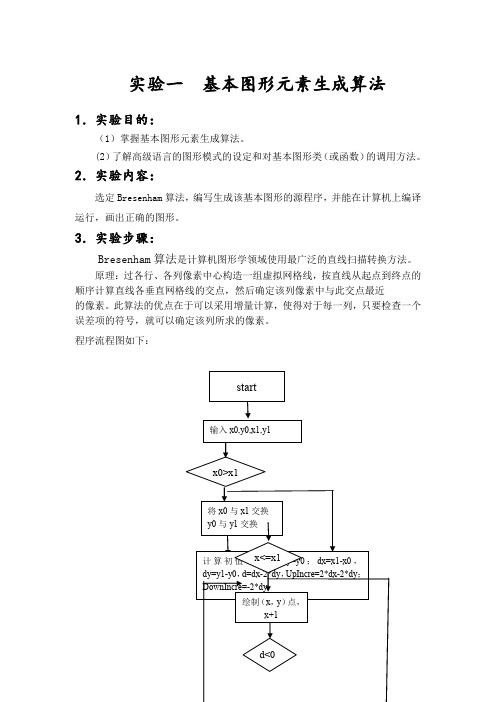
3.实验步骤:Bresenham算法是计算机图形学领域使用最广泛的直线扫描转换方法。
原理:过各行、各列像素中心构造一组虚拟网格线,按直线从起点到终点的顺序计算直线各垂直网格线的交点,然后确定该列像素中与此交点最近的像素。
此算法的优点在于可以采用增量计算,使得对于每一列,只要检查一个误差项的符号,就可以确定该列所求的像素。
程序流程图如下:程序如下function MidBresenhamline( x0, y0, x1,y1) if x0>x1x=x1;x1=x0;x0=x;y=y1;y1=y0;y0=y;endx=x0;y=y0;dx=x1-x0;dy=y1-y0;d=dx-2*dy;UpIncre=2*dx-2*dy;DownIncre=-2*dy;while x<=x1axis([x0 x1 y0 y1])plot([x],[y],'*');grid onhold onx=x+1;if d<0y=y+1;d=d+UpIncre;elsed=d+DownIncre;endpause(0.1);endt=x0:1:x1yy=(y1-y0)./(x1-x0)*t+(y1-((y1-y0)./(x1-x0)*x1)); plot(t,yy)程序运行如下>> MidBresenhamline( 0, 0, 8,5)t =0 1 2 3 4 5 6 7 8>> MidBresenhamline( 0, 0, 500,750)运行过程中的截图效果4.实验总结:1.通过学习使用中点Bresenham算法画直线,对于斜率大于1的直线段,只需交换x和y之间的规则即可。
实验二 二维基本图元的生成

yIncrement = float (dy) / float (steps);
setPixel (round (x), round (y));
for (k = 0; k < steps; k++) {
x += xIncrement;
}
注意:
(1)代码没有主函数及其它OpenGL的初始化函数,请用前面实验一中的代码进行添加,该函数在回调函数myDraw()中调用执行;
(2)代码中出现的
class scrPt {
public:
GLint x, y;
};
是C++中的类定义,对于没有学习过C++的读者,这里可看作是C语言中的一个结构体:
{
setPixel (xCenter + x, yCenter + y);
setPixel (xCenter - x, yCenter + y);
setPixel (xCenter + x, yCenter - y);
setPixel (xCenter - x, yCenter - y);
}
注意:
(1)代码没有主函数及其它OpenGL的初始化函数,请用前面实验一中的代码进行添加,该函数在回调函数myDraw()中调用执行;
*/
void ellipseMidpoint (int xCenter, int yCenter, int Rx, int Ry)
{
int Rx2 = Rx * Rx;
int Ry2 = Ry * Ry;
int twoRx2 = 2 * Rx2;
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
基本图元的生成算法一、实验目的1、初步了解显示窗口与视区的关系2、掌握OpengGL点、直线、多边形的绘制3、掌握DDA直线生成算法。
4、掌握Bresenham直线生成算法二、实验环境硬件要求:PC机,主流配置,最好为独立显卡,显存512M以上。
软件环境:操作系统:Windows XP。
语言开发工具:VC6.0。
三、实验内容与要求1、调出实验一的源代码运行,调整修改使得显示窗口大小改变时,绘制的矩形大小随之改变。
如图2-1所示。
提示:(1)在main函数里添加注册窗口变化函数glutReshapeFunc(myreshape); (放在glutMainLoop()之前)(2)在程序中添加窗口改变子函数,参数w,h为当前显示窗口的宽和高void myreshape(GLsizei w, GLsizei h){glViewport(0,0,w,h); //设置视区位置glMatrixMode(GL_PROJECTION);//设置投影变换模式glLoadIdentity(); //调单位矩阵,清空当前矩阵堆栈if(w<=h)gluOrtho2D(0,300,0,300*(GLfloat)h/(GLfloat)w);//设置裁剪窗口大小elsegluOrtho2D(0,300*(GLfloat)w/(GLfloat)h,0,300);}a) 显示窗口改变前 b)显示窗口变大后未修改前的初始源程序参考如下:/*my first program.cpp*/#include <glut.h>void display(void){glClear(GL_COLOR_BUFFER_BIT); //刷新颜色缓冲区glRectf(0,0,0.5,0.5);glFlush(); //用于刷新命令队列和缓冲区,使所有尚未被执行的OpenGL命令得到执行}void main(int argc, char** argv){glutInit(&argc, argv); //初始化GLUT库glutInitDisplayMode(GLUT_SINGLE|GLUT_RGB); //设置显示模式 glutInitWindowSize(100, 200);glutCreateWindow("hello"); //创建窗口,标题为“hello”glutDisplayFunc(display); //用于绘制当前窗口glutMainLoop(); //表示开始运行程序,用于程序的结尾}2、自己参照讲义或教材按照自己的构思画二维平面图形, 修改样本程序circle-algorithm.cpp将上面的矩形替换成自己构思的二维平面图形。
注意顶点的顺序。
参考函数:(1)、点绘制举例glPointSize(2.0) //点的大小设置glBegin(GL_POINTS);glColor3f(1.0,1.0,1.0);glVertex2f(-0.5,-0.5); //顶点glColor3f(1.0,0.0,1.0);glVertex2f(-0.5,0.5);glColor3f(0.0,1.0,1.0);glVertex2f(0.5,0.5);glColor3f(1.0,1.0,0.0);glVertex2f(0.5,-0.5);glEnd()(2)、直线/三角形/四边形绘制举例glLineWidth(2.0);glBegin(GL_LINES);// glBegin(GL_LINE_STRIP);// glBegin(GL_LINE_LOOP);// glBegin(GL_TRIANGLES);// glBegin(GL_TRIANGLE_STRIP);// glBegin(GL_TRIANGLE_FAN);// glBegin(GL_QUADS);// glBegin(GL_TRIANGLE_STRIP);glVertex2f(-0.5,0.5);glVertex2f(-0.5,-0.5);glColor3f(1.0,1.0,1.0);glVertex2f(-0.5,0.5);glColor3f(1.0,1.0,0.0);glVertex2f(0.5,-0.5);glEnd();(3)、多边形举例glBegin(GL_POLYGON);glVertex2f(-0.5,0.5);glVertex2f(-0.5,-0.5);glColor3f(1.0,1.0,1.0);glVertex2f(0,-0.5);glColor3f(1.0,1.0,0.0);glVertex2f(0.5,-0.5);glVertex2f(0.5,0.5);glEnd();3、读懂DDA直线生成算法伪代码,并修改伪代码,使之变成可行的OpenGL代码,验证DDA直线生成算法。
DDA直线生成伪代码//x0,y0 表示直线的起始点, x1,y1表示直线的终止点,color表示直线的绘制颜色void DDA_line(int x0, int y0, int x1, int y1,int color){int dx = x1 – x0, dy = y1 – y0, k;float xIncrement , yIncrement ,steps, x = x0, y = y0;if (abs (dx) > abs (dy)) steps = abs (dx);else steps = abs (dy);xIncrement = (float) (dx) /steps;yIncrement = (float) (dy) /steps;for (k =0; k<steps; k++){Setpixel(round(x), round(y),color);x += xIncrement; y += yIncrement;}}提示:使用学过的画点函数替换setpixel(round(x), round(y),color)函数。
图2-24、读懂Bresenham直线生成算法伪代码,并修改伪代码,使之变成可行的OpenGL代码,验证Bresenham直线生成算法。
要求在函数void Bresenham_Circle_Algorithm(int cx, int cy, int radius)中写出自己的Bresenham画圆法代码。
思考选做:5、DDA算法来绘制N多边形。
用n多边形逼近圆,最小多边形为3角形。
将自己的代码写在函数NSidedPolygon(int n, int cx, int cy,int radius)里,使用DDA算法来绘制N多边形(不要使用OpenGL绘制多边形的函数)。
我们知道OpenGL画点功能为:glBegin(GL_Points);glVertex2f(x,y);glEnd();由于n多边形有n条边,所以必须画n条直线。
将画直线的代码写在函数 DrawLine(int x1, int y1, int x2, int y2)中,考虑n多边形的n条直线是各个方向,即有斜率|k|>=1的情况,又有斜率|k|<1的情况,你可以使用学过的画直线方法,如DDA算法。
阅读样本程序,参见circle-algorithm.cpp:附:样本程序circle-algoritm.cpp#include <glut.h>#include <stdio.h>#include <stdlib.h>#include <math.h>// set some initial parameters, such as the center of the circle(cx,cy), the radius of the circle,int cx=150,cy=150,radius=80;void DDA_Line(int x1,int y1,int x2,int y2);void Bresenham_DrawLine(int x1,int y1,int x2,int y2);void NSidedPolygon(int n, int cx, int cy, int radius);void Display(void);void Reshape(int w, int h);int main(int argc, char** argv){glutInit(&argc, argv);glutInitWindowPosition(0, 0);glutInitWindowSize(window_width, window_height); glutInitDisplayMode(GLUT_DOUBLE | GLUT_RGB);glutCreateWindow("Circle Generation Algorithm"); glutDisplayFunc(Display);glutReshapeFunc(Reshape);glutMainLoop();return 0;}void Display(void){/* YOUR CODE HERE */glutSwapBuffers();}void Reshape(int w, int h){glMatrixMode(GL_PROJECTION);glLoadIdentity();glViewport(0, 0, w, h);gluOrtho2D(0, w, 0, h);// glutPostRedisplay();}void DDA_Line(int x1,int y1,int x2,int y2);{/* YOUR CODE HERE */}void Bresenham_DrawLine(int x1,int y1,int x2,int y2); {/* YOUR CODE HERE */}void NSidedPolygon(int n, int cx, int cy, int radius) {/* YOUR CODE HERE */}。
