2019-2020年初二数学竞赛初赛试题及答案
2019-2020年初二数学竞赛初赛试题及答案

2019-2020年初二数学竞赛初赛试题及答案一、选择题(每小题4分,共40分。
)以下每题的四个选项中,仅有一个是正确的,请将正确答案前的英文字母写在下面的表格内。
1、 将a 千克含盐10﹪的盐水配制成含盐15﹪的盐水,需加盐x 千克,则由此可列出方程( )(A )()()().001510101-+=-x a a (B )().00150010•+=•x a a(C ).00150010•=+•a x a (D )()().0015100101-=-x a2、一辆汽车从A 地匀速驶往B 地,如果汽车行驶的速度增加a ﹪,则所用的时间减少b ﹪,则a 、b 的关系是( ) (A )001100a a b +=(B )001100a b += (C )a a b +=1 (D )a a b +=100100 3、当1≥x 时,不等式211--≥-++x m x x 恒成立,那么实数m 的最大值是( ) (A )1. (B )2。
(C )3。
(D )4。
4、在平面直角坐标系中,横、纵坐标都是整数的点称为整点,已知k 为整数,若函数12-=x y 与k kx y +=的图象的交点是整点,则k 的值有( )个(A )2. (B )3。
(C )4。
(D )5。
5、(英语意译)已知整数x 满足不等式6122≤-≤x ,则x 的值是( ) (A )8. (B )5。
(C )2。
(D )0。
6、若三角形的三条边的长分别为a 、b 、c ,且.03222=-+-b c b c a b a 则这个三角形一定是( )(A )等腰三角形 (B )直角三角形 (C )等边三角形 (D )等腰直角三角形7、如图1,点C 在线段BG 上,四边形ABCD 是一个正方形,AG 与BD 、CD 分别相交于点E 和F ,如果AE=5,EF=3,则FG=( ) (A )316。
(B )38。
(C )4。
(D )5。
2019-2020年八年级数学竞赛试题含答案_.docx

2019-2020 年八年级数学竞赛试题含答案_学校姓名成一、 (每小 8 分,共 64 分 )以下每个的四个中,有一个是正确的,将正确答案的英文字母填在后的括号内.1.用 11 到 2006 些自然数依次成下列算式:1112 + 1314, 1516 + 1718 ,1920 + 2122, 2324 + 2526,⋯⋯ 20032004 + 20052006.其中,能被 4整除的算式有() (A)0 个(B) 125 个( C)250 个(D)499 个2.中的五角星是用螺栓将两端打有孔的 5 根木条接而构成的,它的形状不定.如果用在中木条交叉点打孔加装螺栓的法来达到使其形状定的目的,且所加螺栓尽可能少,那么需要要添加螺栓()(A)1 个(B)2 个(C)3 个(D)4 个3.把度 4 的段分成四小段.若要以四小段构成一个四形,其中每一小段的度足的条件是()11(A) 不大于 1(B) 大于2且小于 1(C) 小于 2(D) 大于4!未定。
且小于 24.如,有一个均匀的片,两面上分写有1、 2,有—个均匀的三棱旋器和一个均匀的四棱旋器,它的面上分写有1、2、3 和 1、2、3、 4.在桌面上同旋三件器物,停下来后,面向桌面的三个数字的奇数的概率是()1111(A) 2(B)3(C)6(D)85.同价格的某种商品在三个商都行了两次提价.甲商第一次提价的百分率a,第二次提价的百分率b;乙商两次提价的百分率都a + b2;丙商第一次提价的百分率 b,第二次提价的百分率a.若 a > b > 0 ,提价最多的商是()(A) 甲(B) 乙(C)丙(D) 不能确定的6.一本册内有24 份卷,共有 426道,每份卷中有25 或 20或 16 .那么本册中有25 的卷的份数()(A) 1(B) 2( C)3(D)47.把一个正方体切成两个方体,如果两者表面乏比l: 2,那么两者体之比()(A)1:2(B) 1 :3( C)1: 5(D) 1:68.有七个大小相同的正方体,每个正方体的六个面上分写有1 到 6 六个整数,并且任意两个相面上的两数之和7.把些正方体如所示一个挨—个地接起来,使相的两个面上的两数之和 8,“※”所在面上的数是()(A)4(B)3( C)2(D)1二、填空 (每小8 分,共 96 分)9. 算:19972 –19982 +19992 –20002 +⋯ +20052 –20062 =.10.把 (1) 的正方体表面展开成 4 条棱都没有被剪开, 个面是正方形表示 ).(2) ,有—个面的(用字母次是 11.如 ,一个六 形的每个内角都是2. 7、3、 5、 2, 六 形的周 是120 °, 四 的 依.12.小王 置的某种四位密 ,每个密 的各位数字只能是0、 1、 2 或 3,且 0 不能出 在1、 2、3 的后面, 共可以 置 个不同的密 .13.有 度分 1、2、3、4、5、6、7、 8、 9 ( 位: cm)的 木棒各1 根,利用它 (允 接加 但不允 折断)能 成的周 不同的等 三角形共有种.14.在一个 周上均匀地写了任意四个整数. 定算法是:把每相 两数之和放在 两 数之 , 然后把原来的四个数抹去, 就算一次操作. 当开始 在 周上所写的四个整数不全是偶数 ,最多只要次操作,就一定能使 周上所得的四个数都 成偶数.15.《 代数学学 》 志2007 年 3 月将改版 《 代学 ·数学周刊》,其徽 是我国古代“弦 ”的 形 ( 示意 ). 可由直角三角形 ABC 点 O 同向 旋 三次 (每次旋90°)而得.因此有“数学 ”的 感.假 中 小正方形的面 1,整个徽(含中 小正方形 )的面 92, AD = 2 , 徽 的外 周.16.如 ,四 形 ABCD 中, E 、 F 、G 、 H 依次是各 中点,O 是形内一点.若 S四边形AEOH = 3, S四边形BFOE = 4,S四边形CGOF = 5,S 四边形 DHOG =.17. 徒加工某零件,加工1 个零件, 傅比徒弟少用 2. 5 小 ;加工 10 小 , 傅比徒弟多做 9 个零件. 徒合做3 个零件,需要小 .x 215x 4 –3x 2 + 518.如果 x 4 + x 2 + 1 =4 ,那么3x 2 =.19.如 ,∠ CAD 和∠ CBD 的平分 相交于点 P . ∠ CAD 、∠CBD 、∠ C 、∠ D 的度数依次 a 、 b 、 c 、 d ,用 含其中 2 个字母的代数式来表示∠P 的度数:.20.如 ,在每个小正方形1 的网格中取出12 个格点,以 些格点 点的等腰直角三角形的腰 可以是,能得到位置不同的等腰直角三角形 共有个.2008 年从化二中八年级数学竞赛试题参考答案与评分标准一、选择题:(每题 8 分,共 64 分 )题号12345678答案AACCBBCB二、填空题: (每题 8分,共 96 分)-9.–2001510.EFGH (CDHG )11. 20.712. 12113. 1114. 4c + d15. 4816. 4 17.218. 419.220. 1,2, 2 , 5 ;45.说明:第 10 题写出一个正确结果就给8 分,第 20题第一空共有 4 个值,每填 1 个值得1 分,填错 1 个扣 1 分,第二空 4 分.。
2019-2020年初中数学竞赛试题及答案

2019-2020年初中数学竞赛试题及答案一、选择题:(每小题6分,共30分)1、已知a 、b 、c 都是实数,并且c b a >>,那么下列式子中正确的是( ) (A)bc ab >(B)c b b a +>+(C)c b b a ->-(D)cb c a > 2、如果方程()0012>=++p px x 的两根之差是1,那么p 的值为( ) (A)2(B)4(C)3(D)53、在△ABC 中,已知BD 和CE 分别是两边上的中线,并且BD ⊥CE ,BD=4,CE=6,那么△ABC 的面积等于( )(A)12(B)14(C)16(D)18 4、已知0≠abc ,并且p bac a c b c b a =+=+=+,那么直线p px y +=一定通过第( )象限(A)一、二(B)二、三(C)三、四(D)一、四 5、如果不等式组⎩⎨⎧<-≥-0809b x a x 的整数解仅为1,2,3,那么适合这个不等式组的整数a 、b 的有序数对(a 、b )共有( )(A)17个(B)64个(C)72个(D)81个 二、填空题:(每小题6分,共30分)6、在矩形ABCD 中,已知两邻边AD=12,AB=5,P 是AD 边上任意一点,PE ⊥BD ,PF ⊥AC ,E 、F 分别是垂足,那么PE+PF=___________。
7、已知直线32+-=x y 与抛物线2x y =相交于A 、B 两点,O 为坐标原点,那么△OAB 的面积等于___________。
8、已知圆环内直径为a cm ,外直径为b cm ,将50个这样的圆环一个接一个环套地连成一条锁链,那么这条锁链拉直后的长度为___________cm 。
9、已知方程()015132832222=+-+--a a x a a x a (其中a 是非负整数),至少有一个整数根,那么a =___________。
2019-2020年初中数学竞赛(海南赛区)初赛试题(含答案).docx
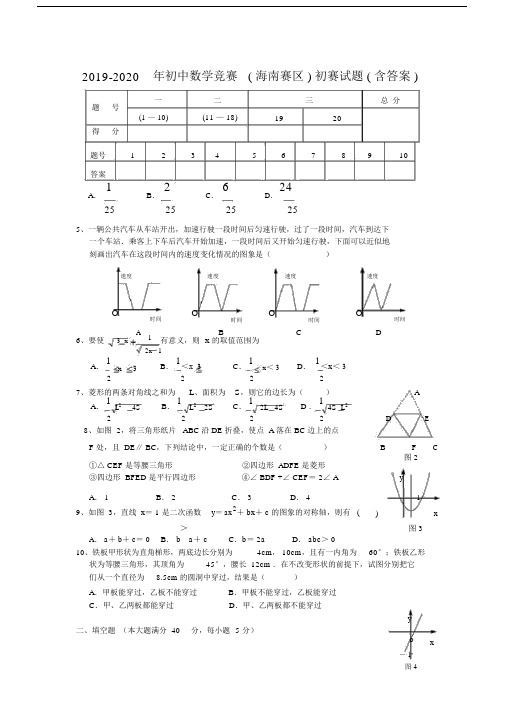
2019-2020 年初中数学竞赛 ( 海南赛区 ) 初赛试题 ( 含答案 )题号 一二三总 分(1 — 10)(11 — 18)1920得 分题号 12345678910答案A .1B .2C .6D .2425 25 25 255、一辆公共汽车从车站开出,加速行驶一段时间后匀速行驶,过了一段时间,汽车到达下一个车站.乘客上下车后汽车开始加速,一段时间后又开始匀速行驶,下面可以近似地刻画出汽车在这段时间内的速度变化情况的图象是()速度速度 速度速度O时间O时间O时间O时间A1BCD6、要使3 x有意义,则 x 的取值范围为2x1A .1x3B . 1<x 3C .1x < 3D . 1<x < 322227、菱形的两条对角线之和为L 、面积为 S ,则它的边长为()AA .1L24SB .1L22SC .12L 4SD .14S L 2E222 2 D8、如图 2,将三角形纸片 ABC 沿 DE 折叠,使点 A 落在 BC 边上的点F 处,且 DE ∥ BC ,下列结论中,一定正确的个数是( )BF C①△ CEF 是等腰三角形②四边形 ADFE 是菱形图 2y③四边形 BFED 是平行四边形④∠ BDF +∠ CEF = 2∠ AA . 1B . 2C . 3D . 41x9、如图 3,直线 x = 1 是二次函数y = ax 2+ bx + c 的图象的对称轴,则有 ()A . a + b + c = 0>a + cC .b = 2aD . abc > 0图 3B . b10、铁板甲形状为直角梯形,两底边长分别为 4cm , 10cm ,且有一内角为 60°;铁板乙形状为等腰三角形,其顶角为45°,腰长 12cm .在不改变形状的前提下,试图分别把它 们从一个直径为8.5cm 的圆洞中穿过,结果是()A .甲板能穿过,乙板不能穿过B .甲板不能穿过,乙板能穿过C .甲、乙两板都能穿过D .甲、乙两板都不能穿过y 二、填空题 (本大题满分 40 分,每小题 5 分)ox- 1图 411、 x 与 y 互为相反数,且x y 3 ,那么x22xy 1的值为__________.12、一次函数 y=ax+b 的图象如图 4 所示,则化简 a b b 1得 ________.13、若 x= -1 是关于 x 的方程 a2 x2+2011ax- 2012=0 的一个根,则 a 的值为 __________.14、一只船从 A 码头顺水航行到 B 码头用 6 小时,由 B 码头逆水航行到 A 码头需 8 小时,则一块塑料泡沫从 A 码头顺水漂流到 B 码头要用 ______小时(设水流速度和船在静水中的速度不变).15、如图 5,边长为 1 的正方形 ABCD 的对角线相交于点O,过点 O 的直线分别交AD、BC于 E、 F ,则阴影部分的面积是.16、如图 6,直线 l 平行于射线AM ,要在直线l 与射线 AM 上各找一点 B 和 C,使得以A、B、 C 为顶点的三角形是等腰直角三角形,这样的三角形最多能画_______个.A EA DlEO B CB FC A M D图 5图 6图 717、如图 7,△与△均是等边三角形,若∠=145°,则∠的度数是 ________.ABC CDE AEB DBE18、如图 8 所示,矩形纸片ABCD 中, AB= 4cm, BC= 3cm,把∠ B、∠ D 分别沿 CE、 AG 翻折,点 B、D 分别落在对角线AC 的点 B'和 D'上,则线段EG 的长度是 ________.D G CB'D'AEB图 8三、解答题 (本大题满分30 分,每小题15 分 )19、某市道路改造工程,如果让甲工程队单独工作,需要30 天完成,如果让乙工程队单独工作,则需要60 天方可完成;甲工程队施工每天需付施工费 2.5 万元,乙工程队施工每天需付施工费 1 万元 . 请解答下列问题:(1)甲、乙两个工程队一起合作几天就可以完成此项工程?(2)甲、乙两个工程队一起合作 10 天后,甲工程队因另有任务调离,剩下的部分由乙工程队单独做,请问共需多少天才能完成此项工程?(3)如果要使整个工程施工费不超过65 万元,甲、乙两个工程队最多能合作几天?(4)如果工程必须在 24 天内(含 24 天)完成,你如何安排两个工程队施工,才能使施工费最少?请说出你的安排方法,并求出所需要的施工费.20、如图 9,四边形 ABCD 是矩形,点P 是直线 AD 与 BC 外的任意一点,连接PA、 PB、PC、 PD.请解答下列问题:(1)如图 9( 1),当点P在线段BC的垂直平分线 MN 上(对角线 AC 与 BD 的交点Q除外)时,证明△ PAC ≌△ PDB ;(2)如图 9( 2),当点 P 在矩形 ABCD 内部时,求证: PA2+PC2=PB2+PD 2;(3)若矩形 ABCD 在平面直角坐标系 xoy 中,点 B 的坐标为( 1,1),点 D 的坐标为( 5,3),如图9( 3)所示,设△PBC 的面积为y,△ PAD 的面积为x,求 y 与 x 之间的函数关系式.MPA DQB N C图 9(1)A DPB C图9 (2)yA DB CO x图 9(3)参考答案一、选择题(本大题满分50 分,每小题 5 分)题号12345678910答案C D D A C B A B D B7、提示:可设菱形的两条对角线长分别为、b,利用对角线互相垂直进行解答 . a9、分析 :由函数的图象可知:当x=1时有a+b+c<0,当x=-1时有a-b+c>0,即a+c>b,即b<a+c,函数的对称轴为x b,则 b=-2a,因为抛物线的开口向上,所以 a>0,抛物线12a与 y 轴的交点在负半轴,所以c<0,由 b=-2a 可得 b<0.所以 abc>0,因而正确答案为 D10、分析:分别计算铁板的最窄处便可知,如图A,直角梯形, AD=4cm,BC=10cm,∠ C=60°,过点 A过 AE// CD,交 BC于点 E,过点 B作 BE⊥ CD于点 F,可求得 AB=6 3 cm>8.5cm,BE=5 3 cmA D AFDB EC BC图B>8.5 cm 铁板甲不能穿过,如图 B,等腰三角形 ABC 中,顶角∠ A =45°,作腰上的高线 BD ,可求得 BD =6 2 cm < 8.5 cm ,所以铁板乙可以穿过;所以选择 B二、填空题 (本大题满分 40 分,每小题 5 分)11、5 12 、 a+1 13、a=2012,a2=-114、 48A4115、 1单位面积16、3个17、85° 18、 10E4BC17、分析: 易证△ CEA 与△ CDB 全等,从而有∠ DBC =∠ EAC ,因为,∠ABE +∠ BAE =180°- 145° =35°所以有∠ EAC +∠ EBC =120°- 35° =85°,D图 7所以∠ EBD =∠ EBC +∠DBC =85°18、分析: AB = 4cm , BC =3cm ,可求得 AC=5cm ,由题意可知GCC B '=BC=3 cm ,A B ' =2cm 设 BE=x ,则 AE=4-x ,则有 (4-x)2- x 2 =2 2,DBx=1.5cm ,即 BE=DG =1.5cm ,过点 G 作 GF ⊥ AB 于点 F ,则' D 'FAB可求出 EF=1 cm ,所以 EG=123210图 8E三、解答题 (本大题满分 30 分,每小题 15 分)19 、本题满分 15 分,第( 1)、( 2)、( 3)小题,每小题 4 分,第( 4)小题 3 分 .解:( 1)设甲、乙两个工程队一起合作x 天就可以完成此项工程,依题意得:(11)x 1 ,解得: x=20答:甲、乙两个工程队一起合作20 天就可以完成此项工程 .30 60(2)设完成这项道路改造工程共需y 天,依题意得:110 y 1 ,解得 y=40 。
2019-八年级(下)数学竞赛试卷及答案

2019-2020 年八年级(下)数学比赛试卷及答案班级姓名得分一、(每7 分,共 21 分)1.如,正方形ABCD外有一点 P,P 在 BC外,并在平行AB与 CD之,若 PA=17 ,PB= 2 ,PC= 5 ,PD=()A.25B.19C.32D.172.如,四形ABCD中,∠ A=∠ C= 90°,∠ ABC= 60°, AD= 4, CD= 10, BD的等于()A. 413B.8 3C. 12D.103 3.如,△ ABC中, AB= AC=2, BC上有 10 个不一样的点P1, P2,⋯⋯ P10, M i AP i2P i B P i C(i=1,2,⋯⋯,10),那么M1M 2M 10的()A. 4 C. 40 D.不可以确立(第 1 )(第2)(第3)二、填空(每7 分,共 28 分)1.若一个等腰三角形的三均足方程x2- 6x+8= 0,个等腰三角形的周。
2. 已知:ab1,且5a22010a 8 0 ,8b22010b 5 0 ,a=。
b3. 如,从等三角形内一点向三作垂,已知三条垂段的分1、3、5,个等三角形的。
4. 如, P 正方形ABCD内一点, PA∶PB∶ PC=1∶ 2∶ 3,∠ APD=。
(第 3 )(第4)三、解答以下各(每17 分,共 51 分)1. 已知: m , n 知足 m210m 10 , n 210n10 , 求 n m的值。
m na b822.已知:ab,试求方程, ,c 三实数知足方程组28bx cx aab c3c 48的根。
3.若△ ADE 、△ BEF 、△ CDF 的面积分别为 5、 3、 4,求△ DEF 的面积。
滁州市第五中学八年级数学比赛试卷答案一、选择题1. A2. A3. C 二、填空题1. 6 或 10 或 12;2.8; 3.6 3 ; °。
5三、解答以下各题 1. 当 m n 时,n m 1 2 ,m1n当 mn 时, m , n 是方程 x 210 x 10 0 的两个根,则 m n 10, mn10 。
2019最新八年级数学竞赛初赛试题(含答案)

5 人,租金 24 元,则该班至少要花租金
元。
13、正三角形△ ABC所在平面内有一点 P,使得△ PAB、△ PBC、△ PCA都是等腰三角形,则
这样的 P 点有
个。
14、若 6 表示一个数,则整数 m可取值的个数是
个。
m1
15、已知 x 和 y 满足 2x+3y=5,则当 x=4 时,代数式 3x2 12xy y2 的值是
2
2) 1
,其中
32
无理数有
个。
7、若 A= ( a2 9) 4,则 A 的算术平方根是
。
8、如图 2,在△ ABC中, AB=AC, G是三角形的重心,那么图中例行
A
DG
E
全等的三角形的对数是
对。
B
9、足球比赛的记分规则是:胜一场记 3 分,平一场记 1 分,负一场
F
C
(图 2 )
记 0 分;一支中学生足球队参加了 15 场比赛,负了 4 场,共得 29 分,则这支球队胜了
。
4、如图 1,正方形 ABCD 的边长为 1cm,以对角线 AC 为边长再作一个正方形,则正方
形 ACEF 的面积是
cm2 .
5、已知四个命题:① 1 是 1 的平方根,②负数没有立方根,③无限小数不一定是无理数,
④ 3a 一定没有意义;其中正确的命题
有
个。
6、已知 7 个数: 1 ,3 8,0.236,(1- 2)2,3.1416, ,( 3 2
9y3 z应排在第
位。
19、一块等边三角形的木板,边长为 始至结束走过的路径长度为
1,现将木板沿水平线翻滚(如图 5),那么 B 点从开
A
B1
2019最新八年级数学竞赛初赛试题(含答案)

八年级数学竞赛初赛试题一、填空题:每小题2分,共40分。
1、使等式x x x =-成立的的值是 。
2、扇形统计图中扇形占圆的30%,则此时扇形所对的圆心角为 。
3、如果点A (3,a )是点B (3,4)关于y 轴的对称点,那(图1)FEDCBA么a的值是。
4、如图1,正方形ABCD的边长为1cm,以对角线AC为边长再作一个正方形,则正方形ACEF的面积是2cm .5、已知四个命题:①1是1的平方根,②负数没有立方根,③无限小数不一定是无理数,一定没有意义;其中正确的命题有个。
6、已知72π⎡--⎢⎣,,,其中无理数有个。
7、若A的算术平方根是。
8、如图2,在△ABC中,AB=AC,G是三角形的重心,那么图中例行全等的三角形的对数是对。
9、足球比赛的记分规则是:胜一场记3分,平一场记1分,负一场记0分;一支中学生足球队参加了15场比赛,负了4场,共得29分,则这支球队胜了场。
10、若方程组4101,43x y kx y kx y+=+⎧<+<⎨+=⎩的解满足则围是。
11、如图3,在一个正方体的两个面上画两条对角线AB,AC,那么这两条对角线的夹角等于。
(图2)FGEDC BA(图3)(图5)12、某班级共48人,春游时到杭州西湖划船,每只小船坐3人,租金16元,每只大船坐5人,租金24元,则该班至少要花租金 元。
13、正三角形△ABC 所在平面内有一点P ,使得△PAB 、△PBC 、△PCA 都是等腰三角形,则这样的P 点有 个。
14、若61m m -表示一个数,则整数可取值的个数是 个。
15、已知x 和y 满足2x+3y=5,则当x=4时,代数式22312x xy y ++的值是 。
16、方程550x x -+-=的解的个数为 个。
17、如图4,△ABC 为等边三角形,且BM=CN ,AM 与BN 相交于点P ,则∠APN= . 18、已知有如下一组,x y z 和的单项式:3232242323117 8 3 9 9 0.325x z x y x yz xy z x zy zy xyz y z xz y z --,,,,,,,,,我们用下面的方法确定它们的先后次序:对任两个单项式,先看x 的次幂,规定x 幂次高的单项式排在x 幂次低的单项式的前面;再先看y 的次幂,规定y 幂次高的单项式排在y 幂次低的单项式的前面;再先看z 的次幂,规定z 幂次高的单项式排在z 幂次低的单项式的前面。
2019-2020年八年级上数学竞赛试题

(C ).第二、四象限内两坐标轴夹角平分线上 ( D).平行于 y 轴的直线上
三 解答题 ( 16、 17 两题中任选一题 10 分; 18 题必做 10 分;计 20 分)
16、如果 a 2
3a 1
2a 5 0 ,试求代数式
5a 4 2a 3 a2 1
8a 2 的值。
1
1
1
17、计算:
3 3 53 35 75 57
的值是 …………………………………………………………………………………
【】
( A)、 32 ( B)、- 32 ( C)、 1024
(D )、- 1024
15、若 A(a,b) ,B(b,a) 表示同一点, 那么这一点在 ………………………………………… 【 】
(A ).第一、三象限内两坐标轴夹角平分线上 ( B).第一象限内两坐标轴夹角平分线上
。
4、已知 a ,b ,c 为△ ABC 的三边,则化简 a b c ( a b c )2
。
5、直角三角形的三边长分别是 5,12,13,若此三角形内一点到三边的距离均为 x,则 x= .
6、某音像社对外出租光盘的收费方法是:每张光盘在出租的头三天每天收
0.8 元 , 以后每
天收 0.4 元,那么一张光盘在租出后第 n 天应收租金
【】
(A)M=P
(B)M>P
(C)M<P
(D)不能确定
12、代数式 2x 3 4x 13 的最小值是 …………………………………………… 【 】
( A)、 0 ( B)、 3 ( C )、3.5
( D )、1
13、现已知有两个角,锐角 α ,钝角 β ,赵,钱,孙,李四位同学分别计算 1 ( 4
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2019-2020年初二数学竞赛初赛试题及答案一、选择题(每小题4分,共40分。
)以下每题的四个选项中,仅有一个是正确的,请将正确答案前的英文字母写在下面的表格内。
1、 将a 千克含盐10﹪的盐水配制成含盐15﹪的盐水,需加盐x 千克,则由此可列出方程( )(A )()()().001510101-+=-x a a (B )().00150010•+=•x a a(C ).00150010•=+•a x a (D )()().0015100101-=-x a2、一辆汽车从A 地匀速驶往B 地,如果汽车行驶的速度增加a ﹪,则所用的时间减少b ﹪,则a 、b 的关系是( ) (A )001100a a b +=(B )001100a b += (C )a a b +=1 (D )a a b +=100100 3、当1≥x 时,不等式211--≥-++x m x x 恒成立,那么实数m 的最大值是( ) (A )1. (B )2。
(C )3。
(D )4。
4、在平面直角坐标系中,横、纵坐标都是整数的点称为整点,已知k 为整数,若函数12-=x y 与k kx y +=的图象的交点是整点,则k 的值有( )个(A )2. (B )3。
(C )4。
(D )5。
5、(英语意译)已知整数x 满足不等式6122≤-≤x ,则x 的值是( ) (A )8. (B )5。
(C )2。
(D )0。
6、若三角形的三条边的长分别为a 、b 、c ,且.03222=-+-b c b c a b a 则这个三角形一定是( )(A )等腰三角形 (B )直角三角形 (C )等边三角形 (D )等腰直角三角形7、如图1,点C 在线段BG 上,四边形ABCD 是一个正方形,AG 与BD 、CD 分别相交于点E 和F ,如果AE=5,EF=3,则FG=( ) (A )316。
(B )38。
(C )4。
(D )5。
8、1216-能分解成n 个质因数的乘积,n 的值是( ) (A )6. (B )5。
(C )4。
(D )3。
9、若关于x 、y 的方程组⎩⎨⎧=+-=++02,01a y bx ay x 没有实数解,则( )(A )2-=ab (B )且2-=ab .1≠a (C )2-≠ab (D )且 10、如图2,∠AOB= 450,OP 平分∠AOB ,PC ⊥OB 于点C 。
若PC=2,则OC 的长是( ) (A )7.(B )6。
(C )222+。
(D )32+。
二、A 组填空题(每小题4分,共40分。
)11、化简:=++52549 。
12、若关于x 、y 的方程组⎩⎨⎧=--=+232123y x k y x 的解使,274>+y x 则k的取值范围是 。
13、如图3,平行于BC 的线段MN 把等边⊿ABC 边形,已知⊿AMN 和四边形MBCN 的周长相等,则BC 与MN 的长度之比是 。
14、小华测得自家冰箱的压缩机运转很有规律,每运转5分钟,停机15分钟,再运转5分钟,再停机15分钟,…,又知8月份这台冰箱的耗电量是24.18度(1度=1千瓦时),则这台冰箱的压缩机运转时的功率是 瓦。
15、已知自然数a 、b 、c 满足c b a c b a 124442222++<+++和022>--a a ,则代数式cb a 111++的值是 。
16、已知A 、B 是反比例函数xy 2=的图象上的两点,A 、B 的横坐标分别是3,5。
设O 为原点,则⊿AOB 的面积是 。
17、设完全平方数A 是11个连续整数的平方和,则A 的最小值是 。
18、将100个连续的偶数从小到大排成一行,其中第38个数与第63个数的和为218,则首尾两个数的和是 。
19、A 、B 两地相距15km ,甲、乙两人同时从A 地出发去B 地。
甲先乘汽车到达A 、B 之间的C 地,然后下车步行,乙全程骑自行车,结果两人同时到达。
已知甲步行的速度是乙骑自行车速度的一半,乙骑自行车的速度是甲乘汽车速度的一半,那么,C 地与A 地相距 km 。
20、已知k cba b c a a c b =+=+=+,则直线k kx y +=必经过点 。
三、B 组填空题(每小题8分,共40分。
)21、等腰三角形的两个内角之比是2:5,则这个三角形的最大内角的度数是 或 。
22、已知10个数x 1,x 2,x 3,…,x 10中,x 1=10,对于整数1>n ,有,1-=n n x n x 则=21x x,=1032x x x 。
23、从甲、乙、丙三名男生和A 、B 两名女生中选出一名男生和一名女生,则所有可能出现的结果有 种;恰好选中男生甲和女生A 的概率是 。
24、若关于x 的方程a b a x b x +=+的解是ab x a x ==21,,那么方程1212--=--a a x x 的解是x 1 = ,x 2 = 。
25、若两个自然数的差是一个数码相同的两位数,它们的积是一个数码相同的三位数,那么这两个自然数是 和 。
第二十二届“希望杯”全国数学邀请赛(含提示)初二 第一试2011年3月13日 上午8:30至10:00 得分一、选择题(每小题4分,共40分。
)以下每题的四个选项中,仅有一个是正确的,请将正确答案前的英文字母写在下面的表格内。
2、 将a 千克含盐10﹪的盐水配制成含盐15﹪的盐水,需加盐x 千克,则由此可列出方程( )(A )()()().001510101-+=-x a a (B )().00150010•+=•x a a(C ).00150010•=+•a x a (D )()().0015100101-=-x a提示:配制问题——只加溶质,溶剂量不变;只加溶剂,溶质不变。
2、一辆汽车从A 地匀速驶往B 地,如果汽车行驶的速度增加a ﹪,则所用的时间减少b ﹪,则a 、b 的关系是( ) (A )001100a a b +=(B )001100a b += (C )a a b +=1 (D )a a b +=100100 提示:行程问题——时间=路程÷速度;最好在时间上找等量关系,即 方程。
3、当1≥x 时,不等式211--≥-++x m x x 恒成立,那么实数m 的最大值是( ) (A )1. (B )2。
(C )3。
(D )4。
提示:根据绝对值的意义,结合x 的取值范围化简不等式,采用验证法,从最大的4开始验证。
(题目问的是最大值!)4、在平面直角坐标系中,横、纵坐标都是整数的点称为整点,已知k 为整数,若函数12-=x y 与k kx y +=的图象的交点是整点,则k 的值有( )个(A )2. (B )3。
(C )4。
(D )5。
提示:图象的交点坐标即是对应方程组的解。
采用验证法求解。
5、(英语意译)已知正整数x 满足不等式6122≤-≤x ,则x 的值是( ) (A )8. (B )5。
(C )2。
(D )0。
提示:根据绝对值的意义,结合x 的取值范围解不等式。
6、若三角形的三条边的长分别为a 、b 、c ,且.03222=-+-b c b c a b a 则这个三角形一定是( )(A )等腰三角形 (B )直角三角形 (C )等边三角形 (D )等腰直角三角形提示:用分组分解法、提公因式法分解因式,再根据“如果两个数的积等于0,那么这两个数中至少有一个是0。
”解答问题。
7、如图1,点C 在线段BG 上,四边形ABCD 是一个正方形,AG 与BD 、CD 分别相交于点E 和F ,如果AE=5,EF=3,则FG=( )(A )316。
(B )38。
(C )4。
(D )5。
提示:建议用比例测量法或已知数据组合法求解。
8、1216-能分解成n 个质因数的乘积,n 的值是( ) (A )6. (B )5。
(C )4。
(D )3。
提示:利用平方差公式因式分解,再根据“任何一个完全平方数与1的和(或差)都是质数”轻松求n 值。
9、若关于x 、y 的方程组⎩⎨⎧=+-=++02,01a y bx ay x 没有实数解,则( )(A )2-=ab (B )且2-=ab .1≠a (C )2-≠ab 提示:方程组没有实数解其实就是方程对应函数的图象没有交点,把方程组中的两个方程变形成一次函数的一般形式后,它们的“k ”值相等而“b ”值不相等!10、如图2,∠AOB= 450,OP 平分∠AOB ,PC ⊥OB于点C 。
若PC=2,则OC 的长是( ) (A )7.(B )6。
(C )222+。
(D )32+。
提示:以点P 为顶点作∠OPD=450,交OC 边于点D ,再借用勾股定理、“等角对等边”即可代换出正确选项。
二、A 组填空题(每小题4分,共40分。
)11、化简:=++52549 。
提示:()252549+=+ 12、若关于x 、y 的方程组⎩⎨⎧=--=+232123y x k y x 的解使,274>+y x 则k 的取值范围是 。
提示:上式×2-下式即可与274>+y x 代换出需要的不等式,进而求解。
13、如图3,平行于BC 的线段MN 把等边⊿ABC ⊿AMN 和四边形MBCN 的周长相等,则BC 与MN 的长度之比是 。
提示:BC ∥MN 可知⊿AMN 也是等边三角形,设AM=x ,根据“⊿AMN 和四边形MBCN 的周长相等”列方程可求解。
14、小华测得自家冰箱的压缩机运转很有规律,每运转5分钟,停机15分钟,再运转5分钟,再停机15分钟,…,又知8月份这台冰箱的耗电量是24.18度(1度=1千瓦时),则这台冰箱的压缩机运转时的功率是 瓦。
提示:每年的8月份都是31天;“每运转5分钟,停机15分钟,再运转5分钟,再停机15分钟,…,”即“每20分钟只运转5分钟”;功耗=功率×做工时间。
15、已知自然数a 、b 、c 满足c b a c b a 124442222++<+++和022>--a a ,则代数式cb a 111++的值是 。
提示:利用完全平方公式对前一个式子进行变形;解不等式022>--a a 得出a 的取值范围,在a 的取值范围内取定一个值,用观察法可得出b 、c 的对应值一组,代入即可求值。
16、已知A 、B 是反比例函数xy 2=的图象上的两点,A 、B 的横坐标分别是3,5。
设O 为原点,则⊿AOB 的面积是 。
提示:由已知画出示意图,用面积“割补法”求其面积。
17、设完全平方数A 是11个连续整数的平方和,则A 的最小值是 。
提示:设连续整数的第六个整数为x ;当x= 时,11x 2+110的值最小。
18、将100个连续的偶数从小到大排成一行,其中第38个数与第63个数的和为218,则首尾两个数的和是 。
