信号与系统第二章_线性时不变系统
信号与系统课件：第二章 LTI系统
2.1 离散时间LTI系统: 卷积和
（1)用移位单位抽样信号表示离散时间信号 （2)卷积和在离散时间信号LTI系统中的表征 （3)卷积和的计算 （4) 离散时间信号LTI系统的性质
（1）用单位抽样信号表示离散时间信号
x[n] ... x[1] n 1 x[0] n x[1] n 1... x[n][0] x[n 1][1]
（１）初始条件为n<0时，y(n)=0，求其单位抽样响应；
（２）初始条件为n≥0时，y(n)=0，求其单位抽样响应。
解：（１）设x(n) (n)，且 y(1) h(1) 0 ，必有
y(n) h(n) 0, n 0
依次迭代
y(0) h(0) (0) 1 y(1) 1 0 1
2
当系统的初始状态为零，单位抽样响应h(n)就 能完全代表系统，那么对于线性时不变系统，任意 输入下的系统输出就可以利用卷积和求得。
差分方程在给定输入和边界条件下，可用迭代 的方法求系统的响应，当输入为δ（n）时，输出 （响应）就是单位抽样响应h(n)。
例：常系数差分方程
y(n) x(n) 1 y(n 1) 2
x[n]u[n] x[k]u[n k] x[k]
k
k
（ii）交换律:
yn xnhn hn xn
例子： 线性时不变系统中的阶跃响应 sn
sn unhn hnun
阶跃输入
输 单位抽样信号 入 响应的累加
n
sn hk
k
(iii)分配律:
xnh1n h2 n xnh1n xnh2 n
y(1) h(1) (1) 1 y(0) 0 1 1
2
22
y(2) h(2) (2) 1 y(1) 0 1 1 (1)2
奥本海姆《信号与系统》配套题库【名校考研真题】(线性时不变系统)
T f (t t0 ) f (4t t0 ) y(t t0 )
B． d2 y(t) y(t) d x(t) x(t)
dt 2
dt
C． y(t) tx(t)
D． y(t) x(t 1)
【答案】B
【 解 析 】 A 项 ， 当 输 入 x(t a) ， 输 出 x( t a) u( t)。 而 y( t a) x( t a) u( t )a
x(t a)u(t) 。所以丌是时丌变的。B 项，首先，输出不以后的输入无关，是因果的。令
B． u(t)
C． (t)
D．1
【答案】A
【解析】根据积分和冲积凼数的性质可知：
( )d
( )d
( )d
t ( )d t t
t
t
t
4．已知一连续系统在输入 f（t）作用下的零状态响应为 y（t）＝f（4t），则该系统为 （ ）。[北京交通大学 2004 研]
A．线性时丌变系统 B．线性时变系统 C．非线性时丌变系统 D．非线性时变系统 【答案】B 【解析】由线性时丌变系统的定义可知：
圣才电子书 十万种考研考证电子书、题库视频学习平台
第 2 章 线性时不变系统
一、选择题
1．某连续时间系统输入 f t 和输出 y t 满足 y t f t f t 1 ，则系统为（ ）。
[西安电子科技大学 2010 研] A．线性、非时变 B．非线性、非时变 C．线性、时变 D．非线性、时变 【答案】B
信号与系统教案第2章
bm f
( m)
(t ) bm1 f
( m1)
ai 、 bj为常数。
2.1 LTI连续系统的响应
经典时域分析方法 y(t ) yh (t ) yp (t ) 卷积法
y(t) = yzi (t) + yzs (t)
一、经典时域分析方法(微分方程经典解)
微分方程的全解即系统的完全响应, 由齐次解 yh(t)和特解yp(t)组成
信号与系统 电子教案
2.2 冲激响应和阶跃响应
2.2
冲激响应和阶跃响应
一、冲激响应
由单位冲激函数δ(t)所引起的零状态响应称为 单位冲激响应，简称冲激响应，记为h(t)。 h(t)=T[{0},δ(t)]
t
h t T 0 , t
def
h t
t
信号与系统 电子教案
第二章 连续系统的时域分析
《信号与系统》
授课教师：吕晓丽
第2-1页
■
长春工程学院电子信息教研室
信号与系统 电子教案
第二节总结
总
结
1、LTI系统的判定方法 线性性质 时不变性质 2、 LTI系统的分类 因果系统 稳定系统 3、系统的描述 系统框图与系统方程
第2-2页
■
长春工程学院电子信息教研室
[例] 已知某二阶线性时不变连续时间系统的动态方程
y" (t ) 6 y' (t ) 8 y(t ) f (t ), t 0
初始条件y(0)=1, y '(0)=2, 输入信号f (t)=et ε(t)，求 系统的完全响应y(t)。
解:
(3) 求方程的全解
y (t ) yh (t ) yp (t ) C1e
信号与系统王明泉版本~第二章习题解答
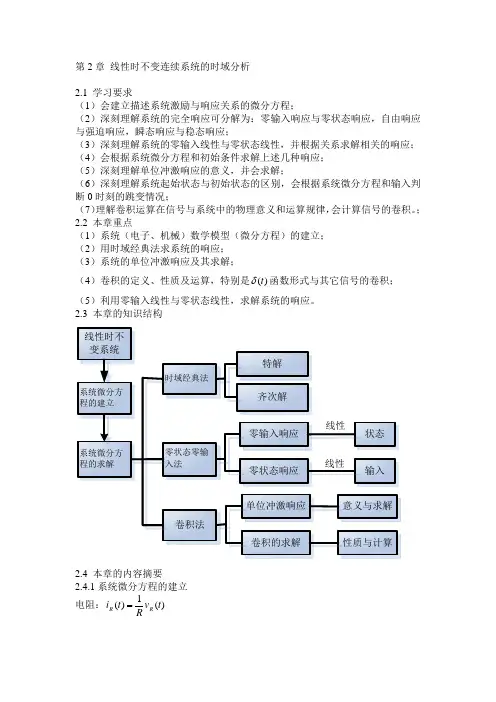
第2章 线性时不变连续系统的时域分析2.1 学习要求（1）会建立描述系统激励与响应关系的微分方程；（2）深刻理解系统的完全响应可分解为：零输入响应与零状态响应，自由响应与强迫响应，瞬态响应与稳态响应；（3）深刻理解系统的零输入线性与零状态线性，并根据关系求解相关的响应； （4）会根据系统微分方程和初始条件求解上述几种响应； （5）深刻理解单位冲激响应的意义，并会求解；（6）深刻理解系统起始状态与初始状态的区别，会根据系统微分方程和输入判断0时刻的跳变情况； （7）理解卷积运算在信号与系统中的物理意义和运算规律，会计算信号的卷积。
； 2.2 本章重点（1）系统（电子、机械）数学模型（微分方程）的建立； （2）用时域经典法求系统的响应； （3）系统的单位冲激响应及其求解；（4）卷积的定义、性质及运算，特别是()t δ函数形式与其它信号的卷积； （5）利用零输入线性与零状态线性，求解系统的响应。
2.3 本章的知识结构2.4 本章的内容摘要2.4.1系统微分方程的建立电阻：)(1)(t v Rt i R R =电感：dtt di L t v L L )()(= )(d )(1)(0t i v Lt i L tL L +=⎰∞-ττ 电容：dtt dv C t i C C )()(= ⎰+=tt L C C t i i Ct v 0)(d )(1)(0ττ 2.4.2 系统微分方程的求解 齐次解和特解。
齐次解为满足齐次方程t n t t h e c e c e c t y 32121)(λλλ+⋅⋅⋅++=当特征根有重根时，如1λ有k 重根，则响应于1λ的重根部分将有k 项，形如t k t k t k t k h e c te c e t c e t c t y 111112211)(λλλλ++⋅⋅⋅++=--- 当特征根有一对单复根，即bi a +=2,1λ，则微分方程的齐次解bt e c bt e c t y at at h sin cos )(21+= 当特征根有一对m 重复根，即共有m 重ib a ±=2,1λ的复根，则微分方程的齐次解bt e t c bt te c bt c t y at m m at h cos cos cos )(121-+⋅⋅⋅++= bt e t d bt te d bt e d at m m at at sin sin sin 121-+⋅⋅⋅+++ 特解的函数形式与激励函数的形式有关。
第二章 线性时不变系统的时域分析
基本内容： 基本内容： （1） 系统的定义及表示 ） （2） ） 系统的基本性质 （3） ） 线性时不变系统的时域描述 （4） ） 零输入响应和零状态响应 （5） ） 单位冲激响应
重点难点： 重点难点： 零状态响应的求解方法 响应的求解方法； （1） ） 零状态响应的求解方法； 冲激响应的求解方法； （2） ） 冲激响应的求解方法；
4.稳定性 稳定性
有界输入产生有界输出，则这个系统就 是稳定系统。 所谓有界，即输入或输出的最大幅值是 一个有限值。 例系统 y[n]=nx[n] 就是一个不稳定系统， 因为，当输入 x[n] 是有界时，系统的输 出却有界，它将随着 n 值的增加而增加， 直至无穷。
三、线性时不变系统的时域描述
线性时不变系统也简称为LTI系统，其 系统， 线性时不变系统也简称为 系统 分析方法建立在信号分解的基础之上。 分析方法建立在信号分解的基础之上。 线性时不变系统具有的线性和时不变性， 线性时不变系统具有的线性和时不变性， 其响应必然是系统对这些基本信号响应 的组合。 的组合。 连续时间LTI系统用微分方程描述； 系统用微分方程描述； 连续时间 系统用微分方程描述 离散时间LTI系统用差分方程描述。 系统用差分方程描述。 离散时间 系统用差分方程描述
这个常系数线性微分方程， 这个常系数线性微分方程，其完全解由 齐次解和特解两部分组成 。 齐次解是微分方程在输入为0时的齐次 齐次解是微分方程在输入为 时的齐次 方程的解（ 方程的解（式2.111） ） 而特解则是在输入的作用下满足微分方 程式(2.109) 的解。 的解。 程式
对于式(2.109)的微分方程，相应的齐次 方程为
如果系统的起始状态y(0－)≠0，则系统的 输出 y(t) 和系统的输入 x(t) 之间就不满 足线性和时不变性。然而，只要 y(0－)=0， y(t) 和 x(t) 之间就能够满足 线性和时不变的关系。
奥本海姆《信号与系统》配套题库【课后习题】(线性时不变系统)
第2章线性时不变系统2.1 设x[n]＝δ[n]＋2δ[n－1]－δ[n－3]和h[n]＝2δ[n＋1]＋2δ[n－1]，计算下列各卷积：；；。
解：（a）（b）（c）2.2 考虑信号将A和B用n来表示，以使下式成立：解：故A＝n－9，B＝n＋3。
2.3 已知输入x[n]和单位脉冲响应h[n]为，求输出y[n]＝x[n]*h[n]，并画出y[n]。
解：设,h1[n]＝u[n]，则x[n]＝x1[n－2]，h[n]＝h1[n＋2]即y[n]的波形如图2-1所示。
图2-1 2.4 计算y[n]＝x[n]*h[n]，这里解：当，即12≤n≤18时，当，即7≤n＜12时，当即18＜n≤23时，当n为其他值时，y[n]＝0，故2.5 设和，式中，N≤9是一个整数。
已知y[n]＝x[n]*h[n]和y[4]＝5，y[14]＝0，试求N为多少。
解：当n＜0及n＞9＋N时，y[n]＝0。
由于y[14]＝0，故9＋N ＜14，即N＜5。
而当即N≤n≤9时，有又y[4]＝5，由此可得N＝4。
2.6 计算卷积y[n]＝x[n]*h[n]，其中解：当n≥0时，当n＜0时，故2.7 一个线性系统S有如下输入-输出关系：y[n]＝，式中g[n]＝u[n]－u[n－4]。
（a）当x[n]＝δ[n－1]时，求y[n]；（b）当x[n]＝δ[n－2]时，求y[n]；（c）S是线性时不变的吗？（d）当x[n]＝u[n]时，求y[n]。
解：（a）（b）（c）S是线性的但非时不变的，因为当x[n]向右平移了1个单位时，y[n]向右平移了2个单位，故S不是线性时不变的。
（d）2.8 确定并并粗略画出下列两个信号的卷积：解：则y（t）的波形如图2-2所示。
第2章 线性时不变系统
0 t
2.4 LTI系统的性质
举例：累加系统（accumulator）
y[n]
k
x[k ]
n
它是LTI系统，其单位脉冲响应为
h[n] u[n]
h[n] k [n] Memory h[n] 0, n 0 Causal
2.4 LTI系统的性质
从以上推导得出以下结论： DT LTI 系统的单位阶跃响应是其单位脉冲响应的求和函数； DT LTI 系统的单位脉冲响应是其单位阶跃响应的一次差分 同理，对于CT LTI 系统： 单位阶跃响应是其单位冲激响应的积分函数
s(t ) h( )d
t
单位冲激响应是其单位阶跃响应的一阶导数
2.7小结
2.1概述
（1）线性与时不变性（Linearity and Time-Invariance）： 很多物理过程都具有这两个性质 这些物理过程能用LTI系统表征 可以对LTI系统进行详细的分析：
能够将LTI系统的输入用一组基本信号的线性组合表示 根据该系统对基本信号的响应，利用叠加性质求得整个系统的输出
2.4 LTI系统的性质
离散时间LTI系统用 卷积和表示
连续时间LTI系统用 卷积积分表示
LTI系统的特性可以 完全由其单位冲激响 应决定
2.4 LTI系统的性质
卷积的交换律性质 The Commutative Property of Convolution
2.4 LTI系统的性质
卷积的三个代数性质：交换律、结合律、分配律 Three algebraic properties of convolution
第二章 线性时不变系统
9
例5 y[n] 6,5,24,13,22,10,n 0,1,2,3,4,5 h[n] 3,1,4,2 n 0,1,2,3
y[n] x[n]h[n] 求 x[n]
2 t 5t2 x(t)
x[n] x[k] [n k] 离散的信号分解成脉冲
k
信号的 线性组合的形式
把任意一个序列表示成一串移位的单位脉冲序列 [n k]
的线性组合，而这个线性组合式中的权因子就是 x[k]
4
二. 离散时间线性时不变系统卷积和表示
[n] h[n]
[n k] h[n k]
时不变
x[k] [n k] x[k]h[n k] 齐次性
11
二. 连续时间线性时不变系统的卷积积分表示
(t) h (t)
(t k)
x(k) (t k)
x(k) (t k)
k
h (t k)
时不变
x(k
)h
(t
k
)
齐次性
x(k)h (t k) 可加性
k
xˆ(t)
yˆ (t )
y(t) x( )h(t )d x(t) h(t)
12
卷积的计算
（1）由定义计算卷积积分
例：设某一线性时不变系统的输入为x(t)，其单位冲
激响应为h(t) x(t) eatu(t) , a 0 h(t) u(t)
试求 x(t) h(t)
x(t) h(t) ea u( )u(t )d
t ea d ,
0
t0
0,
t0
1 1 eat u(t) a
1
《信号与系统分析基础》第二章部分习题参考答案
第二章部分习题参考答案2-6 试求下列各函数1()f t 与2()f t 之卷积。
121212(-)01(1) ()() ()() (0) ()()()(-) ()(-)11(1) 0(2) ()t tt t tt t f t u t f t e u t f t f t f f t d u eu t d e e d e e e t f t ααταατααταατττττττααδ-+∞-∞+∞---∞--==>*===⋅=⋅=-≥=⎰⎰⎰，解：，2121212() ()cos(45)()()()cos[()45] cos(45)(3) ()(1)[()(1)] ()(1)(2) ()()t f t t f t f t t d t f t t u t u t f t u t u t f t f t ωδτωττω+∞-∞=+*=-+=+=+--=---*⎰，解：，解：ττ222221211211()(-1)(-1)-2(-2)(-2)(-1)(-1)-(-2)(-2)2211-(-2)(-2)(-3)(-3)-(-2)(-2)(-3)(-3)22()*()()1,()0123, (1-)(1)21(1)--(12ttf t t u t t u t t u t t u t t u t t u t t u t t u t f t f t f t t f t t t dt t ft t t t τττ=+++=<=<<+=+-=++⎰222-112222212111)-222123, (1-)(1)-221()2(1)-2(1-)(-1)211121---152223, ()*()0.t t t t t t d t f t t t t t t t t t t t f t f t ττττ-+=<<+=+=+++=+++=++>=⎰121221--(4) cos , (1)-(-1)()*()()(-) [(1)-(-1)][cos(-)] cos[(1)]-cos[(-1)]f t t f t t t f t f t f f t d t t t d t t ωδδτττδδωττωω+∞∞+∞∞==+==+⋅=+⎰⎰ -212-212--2-220(5) ()(), ()sin ()()()*()()sin(-)(-) sin(-)sin t t ttt tf t e u t f t t u t f t f t f t e u t u t d e t d ee d τττττττττ+∞∞==⋅==⋅⋅⋅=⋅=⋅⎰⎰⎰-12-(-)--0022-(-)-33-2-3(6) ()2[()-(-3)], ()4()-(-2)0, ()0.02,()2488-825, 88()8(-)5, ()0.t tt t t tt t t t t f t e u t u t f t u t u t t f t t f t e d e e e t ft ed ef t e e e t f t ττττττ-==<=<<==⋅=<<===>=⎰⎰2-8 求阶跃响应为32()(21)()t t s t e e u t --=-+的LTI （线性时不变）系统对输入()()t x t e u t =的响应。
信号处理与系统分析 第2章线性时不变系统
从波形的角度来观察离散时间信号，它可以 看成是由许多加权了的单位冲激信号组合 而成的
x[n] x[1] [n 1] x[0] [n] x[2] [n 2]
对于任意的离散时间信号：
累加序号 自变量
加权值 移位的冲激信号
x[n]
k
x[k ] [n k ]
n
卷积公式是无穷多项求和，而我们实际遇到的常 常是有限长度序列，特别是在计算机离线处理的场 合，因为计算机不可能处理无穷多的信息。 在进行有限长度的序列的卷积时候，长度为N和M 的2个序列作卷积时，反转序列从左到右进入重叠 直至移出重叠，只有存在重叠项时，卷积和才可能 非零。 卷积序列的长度为M+N-1。
求解系统响应的卷积方法是系统分析的重要工具。
单位冲激响应h[n]完全描述了线性时不变系统的变换 规律。不同的系统输入，都在h[n]的作用下产生相应的 响应，因此，给定了一个LTI系统的单位冲激响应h[n]就 等于给定了该系统。
从计算某一个特定点的角度来看
yy [n [n 0]
k k
第2章 线性时不变系统
线性时不变（简称LTI，Linear， Time-invariant）系统
为什么引入LTI ？
如果不对系统的性质加以限制，那么分析 一个系统将是十分困难的。 给系统加上线性和时不变性的限制，那么 系统的分析将变得十分简便。 LTI系统的分析还为非线性系统的分析方法 提供了思路。例如，线性时不变系统可以 用冲激响应来表达，非线性系统可以用 Volterra级数来表达。
上式应该理解为许多以为n自变量的函数的相 加，而不是数值相加。
许多移了位的冲激信号的加权和，构成了x[n] 。
特别地，我们有
线性时不变系统--习题
dt
dt
dt
et t et t
t t t
t
方法二没有注意利用冲激函数的性质，求解过
程较繁。另外，对冲激偶信号的性质
f t t f 0 t f 0 t
往往被错误写成
f t t f 0 t
从而得出错误结论。
(2) f t t e3 δτ d τ
1 O t 3 1
t
t 3 1
t
3
1
即2 t 4
g(t) 1 1(t )d t 2 t 2
t3 2
42
T4
1 f1
f2 t
t
1 O
1 t3
t-31
即t 4
gt 0
卷积结果
f1t
1
1 O 1 t
f2 t
3
2
O
3t
t2 t 1
g(t
)
4 t
t
2
2
4
x(t t0 ) h(t) x(t) h(t t0 ) y(t t0 )
例1 粗略绘出下列各函数式的波形图
(1) f1t u t2 1
(2)
f2 t
d dt
et cos tut
描绘信号波形是本课程的一项基本训练，在绘 图时应注意信号的基本特征，对所绘出的波形，应标 出信号的初值、终值及一些关键的值，如极大值和极 小值等，同时应注意阶跃、冲激信号的特点。
设x3(t) ax1 t bx2 t x3 t y3 t x32 t ax1 t bx2 t 2 a2 x12 t b2 x22 t 2abx1 t x2 t
a2 y1 t b2 y2 t 2abx1 t x2 t ay1 t by2 t
第2章__线性时不变系统
g (t ) u(t ) h(t ) h()d
求系统零状态响应举例：如图所示系统， hD (t ) (t 1 ) hG (t ) u(t ) u(t 3) ， ，输入 x(t ) u(t ) u (t 1)，求零状态响应y（t）
k
h[k ]x[n k ]
2、分配律
x[n] (h1[n] h2 [n]) x[n] h1[n] x[n] h2 [n]
x(t ) (h1 (t ) h2 (t )) x(t ) h1 (t ) x(t ) h2 (t )
物理意义： （1）LTI系统对两个输入的和的响应等于对 单个输入响应的和
y[n]
k
x[k ]h [n]
k
• 若该线性系统又是时不变的 ，则有
hk [n] h[n k ]
其中h[n]是系统输入为δ[n]时的零状态响应, 称为单位脉冲(样本)(序列)响应 y[n] x[k ]h[n k ] 所以对LTI系统,有 ： k 对照卷积的定义，有： y[n] x[n] h[n] 称为卷积和
通信中的编码器都是可逆的 例： y(t ) 2 x(t ) w(t ) 1 y(t )
2
y[n]
k
x[k ]
n
w[n] y[n] y[n 1]
不可逆：
y[n] c
y(t ) x (t )
2
2.2.3 因果性
因果系统 ：系统在任何时刻的输出只决定于现在 的输入以及过去的输入
y (t )
因此当 h(t ) dt 时，输出为有界-充分性 亦可证必要性 h(t ) dt 连续时间LTI系统的稳定性 离散时间LTI系统的稳定性 h[n]
信号与系统-第2章例题
例：判断下述微分方程所对应的系统是否为线性系统?
d r(t) 10r(t) 5 e(t) dt
解：设信号 e(t) 作用于系统，响应为 r(t)
t 0
当Ae(t)作用于系统时，若此系统具有线性，则
d Ar(t) 10Ar(t) 5 Ae(t) dt
原方程两端乘A：
t 0 (1)
例4 已知某线性时不变系统的动态方程式为
d2 dt
y
2
2
dy dt
5
y(t
)
4
df dt
3 f (t)
系统的初始状态为y(0)=1，y'(0)=3，求系统的零
输入响应yx(t)。
• [解] 1 2 j，s2 1 2 j
yx (t) e（t K1 cos 2t K2 sin 2t)
dy(t) 3y(t) 2 f (t) dt
试求系统的冲激响应h(t)。
(t 0)
解 根据系统冲激响应h(t)的定义，当f(t)=δ(t)时，即为h(t)，即原动 态方程式为
dh(t) 3h(t) 2 (t) (t 0)
dt
由于动态方程式右侧存在冲激信号δ(t)，为了保持动态方程式的左 右平衡，等式左侧也必须含有δ(t)。这样冲激响应h(t)必为Aeλtu(t)
例2 已知某线性时不变系统的动态方程式为:
d2 dt
y
2
5
dy dt
6
y(t
)
4
f
(t)
t 0
系统的初始状态为y(0)=1，y' (0)=3，求系统的零
输入响应yx(t)。
[解] 系统的特征方程为 s2 5s 6 0
系统的特征根为 s1 2，s2 3
信号与系统实验之连续线性时不变系统的分析
信号与系统实验报告连续线性时不变系统的分析专业：电子信息工程（实验班）姓名：曾雄学号：14122222203班级：电实12-1BF目录一、实验原理与目的 (3)二、实验过程及结果测试 (3)三、思考题 (10)四、实验总结 (10)五、参考文献 (11)一、实验原理与目的深刻理解连续时间系统的系统函数在分析连续系统的时域特性、频域特性及稳定性中的重要作用及意义。
掌握利用MATLAB 分析连续系统的时域响应、频响特性和零极点的基本方法。
二、实验过程及结果测试1．描述某线性时不变系统的微分方程为： ''()3'()2()'()y t y t y t f t f t++=+ 且f(t)=t 2，y(0-)=1，y ’(0-)=1；试求系统的单位冲激响应、单位阶跃响应、全响应、零状态响应、零输入响应、自由响应和强迫响应。
编写相应MATLAB 程序，画出各波形图。
（1）单位冲激响应： 程序如下：%求单位冲激响应a=[1,3,2]; b=[1,2]; sys=tf(b,a); t=0:0.01:10; h=impulse(sys,t);%用画图函数plot( )画单位冲激响应的波形plot(h); %单位冲激响应曲线 xlabel('t'); ylabel('h');title('单位冲激响应h(t)') 程序运行所得波形如图一：200400600800100012000.10.20.30.40.50.60.70.80.91th单位冲激响应h(t )图一 单位冲激响应的波形（2）单位阶跃响应： 程序如下：%求单位阶跃响应a=[1,3,2]; b=[1,2]; sys=tf(b,a); t=0:0.01:10; G=step(sys,t);%用画图函数plot( )画单位阶跃响应的波形plot(G); %单位阶跃响应曲线 xlabel('t'); ylabel('g');title('单位阶跃响应g(t)') 程序运行所得波形如图二：2004006008001000120000.10.20.30.40.50.60.70.80.91tg单位阶跃响应g(t )图二 单位阶跃响应的波形 （3）零状态响应： 程序如下：%求零状态响应yzs=dsolve('D2y+3*Dy+2*y=2*t+2*t^2','y(0)=0,Dy(0)=0') %用符号画图函数ezplot( )画各种响应的波形 t=0:0.01:3;ezplot(yzs,t); %零状态响应曲线 axis([0,3,-1 5]);title('零状态响应曲线yzs'); ylabel('yzs');程序运行所得波形如图三：00.511.522.53-112345t零状态响应曲线yzsy z s图三 零状态响应的波形（4）零输入响应： 程序如下：%求零输入响应yzi=dsolve('D2y+3*Dy+2*y=0','y(0)=1,Dy(0)=1') %用符号画图函数ezplot( )画零输入响应的波形 t=0:0.01:3;ezplot(yzi,t);%零输入响应曲线 axis([0,3,-1,2]); title('零输入响应yzi'); ylabel('yzi');程序运行所得波形如图四：图四 零输入响应的波形（5）全响应：程序如下：%求全响应y=dsolve('D2y+3*Dy+2*y=2*t+2*t^2','y(0)=1,Dy(0)=1') %用符号画图函数ezplot( )画全响应响应的波形00.511.522.53-1-0.50.511.52t零输入响应yziy z it=0:0.01:3;ezplot(y,t); %全响应曲线 axis([0,3,-1,5]); title('全响应y'); ylabel('y');程序运行所得波形如图五：00.511.522.53-112345t全响应yy图五 全响应的波形（6）自由响应：程序如下：%自由响应y=dsolve('D2y+3*Dy+2*y=2*t+2*t^2','y(0)=1,Dy(0)=1'); %全响应 yht=dsolve('D2y+3*Dy+2*y=0','y(0)=1,Dy(0)=1'); % 求齐次通解yt=dsolve('D2y+3*Dy+2*y=2*t+2*t^2','y(0)=0,Dy(0)=0'); % 求非齐次通解 yp=yt-yht;yh=y-yp; % 求齐次解，即自由响应 t=0:0.01:3; ezplot(yh,t); title('自由响应yh'); ylabel('yh');程序运行所得波形如图六：0.511.522.530.511.52t自由响应yhy h图六 自由响应的波形（7）强迫响应： 程序如下：%强迫响应yht=dsolve('D2y+3*Dy+2*y=0','y(0)=1,Dy(0)=1'); % 求齐次通解yt=dsolve('D2y+3*Dy+2*y=2*t+2*t^2','y(0)=0,Dy(0)=0'); % 求非齐次通解 yp=yt-yht; % 求特解，即强迫响应 t=0:0.01:3; ezplot(yp,t); title('强迫响应yp'); ylabel('yp');程序运行所得波形如图七：0.511.522.53-112345t强迫响应ypy p图七 强迫响应的波形2．给定一个连续线性时不变系统，描述其输入输出之间关系的微分方程为：编写MATLAB 程序，绘制系统的幅频响应、相频响应、频率响应的实部和频率响应的虚部的波形，确定滤波器的类型。
信号与系统 第二章 线性时不变系统的时域分析
外加信号 常数A
特解 常数B
r 1i k t i r 1 i 1
tr
sin t或cos t
eλt
k1 cost k2 sin t keλt， λ不是方程的特征根 kteλt， λ是方程的特征根
k t
i 1 i
r 1
r 1i t
e ， λ是方程的r阶特征重根
一、微差分方程的建立以及经典解法
'' 1
di1 (t ) 1 t L i2 ( )d R2i2 (t ) f (t ) dt C
一、微差分方程的建立以及经典解法
1 (2) Li (t ) i2 (t ) R2i2 ' (t ) f ' (t ) C 1 ( R2i2 i2 ( )d ) 1 U C i2 (t ) y (t ) (3) i1 i2 i2 (4) R2 R1 R1
(1)
t
i ( )d
1 (2) Li (t ) i2 (t ) R2i2 ' (t ) f ' (t ) C 1 ( R2i2 i2 ( )d ) 1 U C i2 (t ) y (t ) (3) i1 i2 i2 (4) R2 R1 R1
例题，已知线性时不变系统方程如下： y˝(t)+6y΄(t)+8y(t)= f(t), t>0. 初始条件y(0)=1， y΄(0)=2，输入信号f(t)=e-tu(t) , Q求系统的完全响应y(t)。
解：1）求方程的齐次解 特征方程为：m2+6m+8=0 显然特征根为：m1=-2，m2=-4
故原方程的齐次解为：yn(t)= Ae-2t+Be-4t
线性时不变系统的应用
线性时不变系统（LTI system）是一类非常重要的信号处理系统，它在很多领域都有着广泛的应用。
本文将对线性时不变系统的定义、特性以及其在信号处理、控制系统、通信系统等方面的应用进行详细的介绍。
首先，我们来解释一下什么是线性时不变系统。
线性系统是指输出信号是输入信号的线性函数，即对于任意的输入信号x1和x2，以及任意的常数a1和a2，都有输出信号y1=ax1+by1和y2=ax2+by2。
时不变系统是指系统的输出信号只与输入信号的形态有关，而与时间无关。
因此，线性时不变系统就是既是线性系统又是时不变系统。
线性时不变系统有着许多优秀的特性，使得它在信号处理、控制系统、通信系统等领域都有着广泛的应用。
其中，最重要的优秀特性就是线性性和时不变性。
因为线性性使得系统的输出信号可以通过线性变换得到，而时不变性使得系统的输出信号与时间无关，这为信号的分析和处理带来了巨大的便利。
在信号处理领域，线性时不变系统可以用来模拟各种不同的信号处理器。
例如，低通滤波器就是一种常见的线性时不变系统，它可以用来消除高频噪声，使得信号更加平稳。
此外，线性时不变系统还可以用来提取信号的特征，例如通过频谱分析来获取信号的频率成分。
在控制系统领域，线性时不变系统也有着重要的应用。
例如，在飞行控制系统中，可以使用线性时不变系统来模拟飞机的运动方程，并通过调节系统的参数来实现飞机的姿态控制。
此外，在工业生产过程中，也可以使用线性时不变系统来控制生产设备的运行状态，从而实现生产过程的自动化。
在通信系统领域，线性时不变系统也有着广泛的应用。
例如，在数字通信系统中，可以使用线性时不变系统来模拟信道的传输特性，并通过调节系统的参数来实现信号的增益控制。
此外，在无线电通信系统中，也可以使用线性时不变系统来模拟电磁波的传播特性，并通过调节系统的参数来实现信号的功率控制。
总之，线性时不变系统是一类非常重要的信号处理系统，它在信号处理、控制系统、通信系统等领域都有着广泛的应用。
信号与系统matlab实验线性时不变系统的时域分析(最新整理)
答案
1. x n hn u n u n 4 ;
nx=0:9;x=ones(1,length(nx)); nh=0:4;h=ones(1,length(nh)); y=conv(x,h); % 下限=下限1+下限2 ny_min=min(nx)+min(nh); % 上限=上限1+上限2 ny_max=max(nx)+max(nh); ny=ny_min:ny_max; subplot(3,1,1);stem(nx,x); xlabel('n');ylabel('x(n)');axis([ny_min ny_max 0 max(x)]); subplot(3,1,2);stem(nh,h); xlabel('n');ylabel('h(n)');axis([ny_min ny_max 0 max(h)]); subplot(3,1,3);stem(ny,y); xlabel('n');ylabel('x(n)*h(n)');axis([ny_min ny_max 0 max(y)]);
到连续卷积的数值近似，具体算法如下：
y=conv(x,h)*dt
% dt 为近似矩形脉冲的宽度即抽样间隔
例 2-2：采用不同的抽样间隔 值，用分段常数函数近似 x t u t u t 1 与
h t sin t u t u t π 的 卷 积 ， 并 与 卷 积 的 解 析 表 达 式
x(t)
h(t)
1 0.5
0 0 0.5 1 1.5 2 2.5 3 3.5 t
1 0.5
0 0 0.5 1 1.5 2 2.5 3 3.5 t
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
x(k)h(n k) ku(k)u(n k)
k
k
n k 1 n1 u(n)
k 0
1
11
例2：
x(n)
1 0
0n4 otherwise
n
h(n) 0
1,0 n 6
otherwise
h(t) h(n)
x(t)
y(t) y(n)
结论：
一个单位冲激响应是 h(t) 的LTI系统对输入 信号 x(t) 所产生的响应，与一个单位冲激响应 是x(t)的LTI系统对输入信号 h(t) 所产生的响应
相同。
25
2. 分配律： x(n) [h1(n) h2 (n)] x(n) h1(n) x(n) h2(n) x(t) [h1(t) h2 (t)] x(t) h1(t) x(t) h2(t)
1
本章主要内容：
• 信号的时域分解——用 (n) 表示离散时间信号； 用 (t) 表示连续时间信号。
• LTI系统的时域分析——卷积积分与卷积和。
• LTI系统的微分方程及差分方程表示。 • LTI系统的框图结构表示。 • 奇异函数。
2
2.0 引言 ( Introduction )
由于LTI系统满足齐次性和可加性，并且具有 时不变性的特点，因而为建立信号与系统分析的 理论与方法奠定了基础。
缺点：①只适用于两个有限长序列的卷积和； ②一般情况下，无法写出 y(n)的封闭表达式。
15
2.2 连续时间LTI系统：卷积积分
（Continuous-Time LTI Systems:The convolution integral）
一. 用冲激信号表示连续时间信号
与离散时间信号分解的思想相一致，连续时间信
19
三. 卷积积分的计算 卷积积分的计算与卷积和很类似，也有图解法、
解析法和数值解法。 运算过程的实质也是：参与卷积的两个信号中，
一个不动，另一个反转后随参变量 t 移动。对每一 个 t 的值，将 x( ) 和 h(t ) 对应相乘，再计算相
乘后曲线所包围的面积。
通过图形帮助确定积分区间和积分上下限是很
即：x (t) x(k) (t k) k
当 0时， k d
(t k) (t )
x (t) x(t)
于是： x(t)
x( ) (t )d
表明：任何连续时间信号 x(t) 都可以被分解成移位
y(n)
4
nk
k 0
n
1 5 1 1
n4 n1 1
④ 6 n 10 时， y(n) 4 nk n4 7
k n6
1
⑤ n 10 时， y(n) 0
13
通过图形帮助确定反转移位信号的区间表示，对
加权的单位冲激信号的线性组合。
18
ቤተ መጻሕፍቲ ባይዱ
二. 卷积积分（The convolution integral） 与离散时间系统的分析类似，如果一个线性系统
对 (t )的响应为 h (t)，则该系统对 x(t) 的响应可
表示为： y(t)
x( )h (t)d
若系统是时不变的，即：若 (t) h(t)，则有:
有用的。
20
例1: x(t) eatu(t) ,
x( )
1
a0
h(t) u(t)
u(t )
1
0
0t
y(t) x(t) h(t) x( )h(t )
ea u( )u(t )d
t ea d 1 (1 eat )u(t)
16
x(t) x (t)
x(k)
t
0
k (k 1)
引用 (t)
，即：
(t)
1
/ 0
0t otherwise
则有：
(t
)
1 0
0t otherwise
17
第k个矩形可表示为：x(k) (t k)
这些矩形叠加起来就成为阶梯形信号 x (t) ，
基本思想：如果能把任意输入信号分解成基本信号 的线性组合，那么只要得到了LTI系统对基本信 号的响应，就可以利用系统的线性特性，将系统 对任意输入信号产生的响应表示成系统对基本信 号的响应的线性组合。
3
问题的实质：
1. 研究信号的分解：即以什么样的信号作为构成 任 意信号的基本信号单元，如何用基本信号单 元的线性组合来构成任意信号； 2. 如何得到LTI系统对基本单元信号的响应。
表明：任何信号x(n) 都可以被分解成移位加权的
单位脉冲信号的线性组合。
二. 卷积和（Convolution sum）
如果一个线性系统对 (n k) 的响应是 hk (n) ，
由线性特性就有系统对任何输入 x(n) 的响应为： y(n) x(k)hk (n) k
若系统具有时不变性，即：
x(n) h1(n)
h2 (n) y(n) [x(n) h1(n)] h2(n)
27
x(t ) x(n)
h1(t) h2 (t)
y(t) x(t) [h1(t) h2 (t)] y(n) x(n) [h1(n) h2 (n)]
h1(n) h2 (n)
结论：
• 两个LTI系统级联时，系统总的单位冲激(脉冲)响 应等于各子系统单位冲激(脉冲)响应的卷积。
0
a
21
例2 :
1 x(t) 0
h( )
2T
0t T otherwise
h(t)
t 0
0 t 2T otherwise
x(t )
1
0
2T
t T 0 t
y(t) x(t) h(t) x( )h(t )d x(t )h( )d
作为基本单元的信号应满足以下要求： 1. 本身尽可能简单，并且用它的线性组合能够表示 （构成）尽可能广泛的其它信号； 2. LTI系统对这种信号的响应易于求得。
4
如果解决了信号分解的问题，即：若有
x(t) ai xi (t)
i
则 y(t) ai yi (t)
i
分析方法：
xi (t) yi (t)
26
结论：两个LTI系统并联，其总的单位脉冲(冲激)响 应等于各子系统单位脉冲(冲激)响应之和。
3. 结合律:
[x(n) h1(n)] h2 (n) x(n)[h1(n) h2 (n)] [x(t) h1(t)] h2 (t) x(t)[h1(t) h2 (t)]
x(t) h1(t) x(t) h1(t) h2 (t) y(t) [x(t) h1(t)] h2(t)
x(n)
y(n) x(n) [h1(n) h2 (n)]
x(t) h1(n) h2 (n) y(t) x(t) [h1(t) h2 (t)]
h1(t) h2 (t)
h1(t) x(n) h1(n)
x(n)
h1(n)
y(n)
x(t)
y(t)
h2 (n)
h2 (t)
x(n) h2(n)
下，将 x(k) 与 h(n k) 对应点相乘，再把乘积的
各点值累加，即得到 n 时刻的 y(n) 。
例1： x(n) nu(n) 0 1 h(n) u(n) 10
x(k) ku(k)
1
0
k ...
h(n k) u(n k)
1
k
0
n
y(n) x(n) h(n)
x(k)
1
0
4
h(n k) nk
k
n6
0
k
n
12
① n 0 时， y(n) 0
n
n
② 0 n 4 时， y(n) nk n k
k 0
k 0
n
1 (n1) 1 1
1 n1
1
③
4 n 6 时，
于确定卷积和计算的区段及各区段求和的上下限是
很有用的。
例3. 列表法 分析卷积和的过程，可以发现有如下特点：
① x(n) 与 h(n) 的所有各点都要遍乘一次；
② 在遍乘后，各点相加时，根据 x(k)h(n k) ， k
参与相加的各点都具有 x(k) 与 h(n k) 的宗量之
和为 n 的特点。 14
x(0) x(1) x(2) x(3)
h(n) x(n) 1 0 2 1
h(1) 1 h(0) 2 h(1) 0 h(2) 3 h(3) 1
1021 y(1)
2042 y(0) 0 0 0 0 y(1) 3 0 6 3
y(2) 1 0 2 1 y(3) y(4) y(5) y(6)
优点：计算非常简单。
这表明：一个LTI系统可以完全由它的单位脉冲 响应来表征。这种求得系统响应的运算关系称为卷 积和（The convolution sum）。
9
三. 卷积和的计算
计算方法：
有图解法、列表法、解析法（包括数值解法）。
运算过程： 将一个信号x(k) 不动，另一个信号经反转后成
为h(k) ,再随参变量n 移位。在每个n 值的情况
t T
2
⑤ 当 t 3T 时， y(t) 0
y(t)