RLC串并联谐振-上海交通大学
临界阻尼-上海交通大学

§6.1 线性定常RLC电路的零输入响应
d 2iL L diL LC 2 iL 0 dt R dt
特征根
L L 4 LC 2 R 1 1 1 R 2 2 0 2 LC 2 RC 2 RC LC
由
iL (0 ) k1 0 diL (0 ) L L( sk1 k2 ) V0 dt
k1 0,k2
V0 L
则有
iL (t )
V0 st te t …0 L
称临界阻尼情况
§6.1 线性定常RLC电路的零输入响应
C dv v iL 0 dt R
vL diL dt
vC (0 ) V0 iL (0 ) 0
电路方程
因为 所以
d 2iL L diL LC 2 iL 0 dt R dt
d 2iL L diL LC dt 2 R dt iL 0 iL (0 ) 0 di (0 ) V L 0 L dt
则有
V0 k L0 90
iL (t )
称无损耗情况
V0 cos(0t 90 t …0 Ld
iC (t ) C
dvC CV0 2 s2t ( s12e s1t s2 e )u (t ) dt s1 s2
iL
t
iR , v
0
tm iC
2tm
§6.1 线性定常RLC电路的零输入响应
电路响应的物理过程
一致参考方向下,
iR , v
iL
P P
0吸收功率, 0发出功率。
t
0
tm iC
2
RLC并联谐振电路的应用

上海交通大学基本电路理论课程教学小论文(2008-2009第一学期)RLC 并联并联谐振谐振谐振电路电路电路的应用的应用F0503023 丁顺(5050309627)摘要摘要::本论文主要讨论的是并联谐振电路在信号选择中的应用,首先先回顾带通滤波器,然后引入两种信号选择中常用的两种元件。
最后,讨论的是收音机的原理,这是前面所讲的元件的综合应用。
关键词关键词::并联谐振电路 带通滤波器 实际并联谐振电路 调频放大器 天线接收模型前言前言::通过这个学期电路基础的学习,使我对于电路的原理有了更深的理解。
在电路学习中,给我印象最深的是RLC 中的谐振问题,徐雄老师上课说过,可以通过RLC 电路的谐振,实现收音机的选台问题,因此,我专门查找了参考书,来深入了解一下RLC 谐振在信号的选择中的应用。
正文正文::首先,我们先回顾一下上课所讲的带通滤波器,这里我们着重讨论的是并联谐振带通滤波器。
用并联谐振电路构成的带通滤波器如图一所示。
并联谐振电路在谐振时阻抗最大。
因此,图中的电路起分压作用。
在谐振时,振荡电路的阻抗远大于电阻值,所以大部分输入电压加在振荡电路上,在谐振中心频率时输出电压最大。
对高于谐振频率或低于此规律的信号,振荡电路的阻抗逐渐减小,输入电压的大部分加在了R 的两端。
结果,振荡电路两端的输出电压逐渐减小,产生了带通的特性。
理想情况下,此带通滤波器的中心频率就是其谐振频率。
但在实际情况中,要考虑电感所产生的内阻,因此,其中心频率发生变化。
此时电路图二如图所示。
令L X L ω= 1C X Cω=2211111()(()()C W LW L W L C W L W L C W L Z jX R jX R jX R jX j j X R jX R jX X R X =+−+−−=+=++−+将第二项的分子拆开成两个分式,再与首项相加:222211((W L C W L W LR Xj j Z X R X R X =−+++ 由于j 项数值应该相等:图一 并联谐振电路构成的带通滤波器。
RLC串联和并联谐振电路谐振时的特性

具有电感、电容和电阻元件旳单口网络,在 某些工作频率上,出现端口电压和电流波形相位 相同旳情况时,称电路发生谐振。能发生谐振旳 电路,称为谐振电路。谐振电路在电子和通信工 程中得到广泛应用。本节讨论最基本旳RLC串联和 并联谐振电路谐振时旳特征。
一、RLC串联谐振电路
图12-15(a)表达RLC串联谐振电路,图12-15(b)是它 旳相量模型,由此求出驱动点阻抗为
图12-20
由以上各式和相量图可见,谐振时电阻电流与电流源 电流相等 IR IS 。电感电流与电容电流之和为零, 即 IL IC 0 。电感电流或电容电流旳幅度为电流源电 流或电阻电流旳Q倍,即
I L IC QIS QI R
并联谐振又称为电流谐振。
(8 47)
3.谐振时旳功率和能量
IL= IC增长一倍。总之,由 R、L和C旳变化引起 Q值变化
旳倍数与IL= IC变化旳倍数相同。
例12-8 图12-22(a)是电感线圈和电容器并联旳电路模型。 已知R=1, L=0.1mH, C=0.01F。试求电路旳谐振 角频率友好振时旳阻抗。
图12-22
解:根据其相量模型[图12-22((b)]写出驱动点导纳
(12 42)
电路谐振时电压到达最大值,此时电阻、电感和电容 中电流为(见下页)
IR GU IS
IL
1 U
j0 L
j
R
0L
IS
jQIS
IC j0CU j0 RCIS jQIS
(12 43) (12 44) (12 45)
其中
Q
R
0L
R 0 C
R
C L
(12 46)
称为RLC并联谐振电路旳品质因数,其量值等于谐振 时感纳或容纳与电导之比。电路谐振时旳相量图如图1220(b)所示。
rlc并联谐振电路实验报告

rlc并联谐振电路实验报告一、实验目的二、实验原理三、实验器材和仪器四、实验步骤五、实验结果分析六、实验结论一、实验目的本次实验旨在掌握并理解RLC并联谐振电路的基本原理及其特性,通过对电路参数的调整和观察,加深对谐振电路的认识和理解。
二、实验原理1. RLC并联谐振电路的基本原理RLC并联谐振电路由一个电感L、一个电容C和一个固定阻值R组成。
当该电路被接到交流源上时,如果交流源频率等于该电路的共振频率,则该电路会出现共振现象。
此时,整个电路中流动的电流将达到最大值,并且在L和C之间形成一个高阻抗区域。
2. 共振频率计算公式RLC并联谐振电路的共振频率f0可以通过以下公式进行计算:f0 = 1 / (2π√LC)3. 实验器材和仪器本次实验所需器材和仪器如下:- RLC并联谐振电路板- 信号发生器- 示波器- 万用表四、实验步骤1. 连接电路将RLC并联谐振电路板、信号发生器和示波器进行连接。
具体连接方式如下:- 将信号发生器的正极接到电路板上的“+”端口,负极接到“-”端口。
- 将示波器的探头分别接到电路板上的“Vout”和“GND”端口。
2. 测量电路参数使用万用表测量电路板上的电感L、电容C和阻值R,并记录下来。
3. 调节信号发生器频率将信号发生器输出频率调整为从几百Hz开始逐渐增加,直到观察到示波器上出现共振现象为止。
记录下此时的频率f0。
4. 观察示波器曲线观察示波器上的曲线,包括幅度和相位。
通过调整信号发生器频率,观察曲线幅度和相位随着频率变化而变化的情况。
5. 改变电路参数改变电路板上的L、C或R值,再次进行步骤3和4,并记录下观察结果。
五、实验结果分析在本次实验中,我们成功地制作了一个RLC并联谐振电路,并通过实验观察到了电路的共振现象。
通过调整信号发生器频率,我们成功地找到了该电路的共振频率f0,并观察到了示波器上的曲线幅度和相位随着频率变化而变化的情况。
在改变电路参数后,我们发现电路的共振频率和曲线幅度、相位等特性会发生变化。
实验7RLC串`并联谐振电路

6
3.确定通频带宽度△f、并计算Q值:
Q
f0 f
4.由公式: 计算Q值,并与上述两个Q值进 行比较。
表1 RLC串联电路
L =0.1H( r0 = ) C = 0.5 μf R = 100 保持Vab=5伏
100 200 300
f (HZ) U( 伏 )
× 500 700 1000
Q 0L
谐振时: IL =
R
IC =
9
R2 (L CR 2 3CL2 )2
Z并
(CR)2 ( 2 LC 1)2
tg 1 L C(R 2 2 L2 )
R
谐振频率:
1 LC
(R)2 L
0
1
1 Q2
式中ω 为串联谐振的角频率
0
5
[实验内容与步骤]
1.测定串联电路的谐振曲线
(1)按图接好电路, 根据R、L和C的数据, 大致估计 电路谐振频率f 0 , 然后, 调节信号源的频率, 按表1进 行测试, 当R两端的电压降最大时, 处于谐振状态, 在 谐振频率附近可多测几次, 以能正确确定谐振频率。 按测试值作出谐振曲线。
f ( Hz) 700 800 900 950 x
1050 1100 1200 1300
U(R)
I
7
2.测定并联电路谐振曲线
只要找到主回路电流最小 时的对应频率, 就是改变信 号源频率, 测出Rs上的压降 最小时的频率, 即为并联电 路的谐振频率。
8
表2 RLC并联电路
实验报告R、L、C串联谐振电路的研究并联谐振电路实验报告

实验报告R、L、C串联谐振电路的研究并联谐振电路实验报告实验报告祝金华PB15050984 实验题目:R、L、C串联谐振电路的研究实验目的: 1. 学习用实验方法绘制R、L、C串联电路的幅频特性曲线。
2. 加深理解电路发生谐振的条件、特点,掌握电路品质因数(电路Q值)的物理意义及其测定方法。
实验原理 1. 在图1所示的R、L、C串联电路中,当正弦交流信号源Ui的频率f改变时,电路中的感抗、容抗随之而变,电路中的电流也随f而变。
取电阻R上的电压UO作为响应,当输入电压Ui的幅值维持不变时,在不同频率的信号激励下,测出UO之值,然后以f为横坐标,以UO为纵坐标,绘出光滑的曲线,此即为幅频特性曲线,亦称谐振曲线,如图2所示。
L图 1 图22. 在f=fo=12πLC处,即幅频特性曲线尖峰所在的频率点称为谐振频率。
此时XL=Xc,电路呈纯阻性,电路阻抗的模为最小。
在输入电压Ui为定值时,电路中的电流达到最大值,且与输入电压Ui 同相位。
从理论上讲,此时Ui=UR=UO,UL=Uc=QUi,式中的Q 称为电路的品质因数。
3. 电路品质因数Q值的两种测量方法一是根据公式Q=UC测定,Uc为谐振时电容器C上的电压(电感上的电压无法测量,故Uo不考虑Q=UL测定)。
另一方法是通过测量谐振曲线的通频带宽度△f=f2-f1,再根据QUo=fO求出Q值。
式中fo为谐振频率,f2和f1是失谐时,亦即输出电压的幅度下降到f2-f1最大值的1/2 (=0.707)倍时的上、下频率点。
Q值越大,曲线越尖锐,通频带越窄,电路的选择性越好。
在恒压源供电时,电路的品质因数、选择性与通频带只决定于电路本身的参数,而与信号源无关。
预习思考题1. 根据实验线路板给出的元件参数值,估算电路的谐振频率。
L=30mH fo=2. 改变电路的哪些参数可以使电路发生谐振,电路中R的数值是否影响谐振频率值?改变频率f,电感L,电容C可以使电路发生谐振,电路中R 的数值不会影响谐振频率值。
rlc并联谐振电路谐振条件

rlc并联谐振电路谐振条件
(原创实用版)
目录
1.RLC 并联谐振电路的概念
2.RLC 并联谐振电路的谐振条件
3.RLC 并联谐振电路的应用
4.结论
正文
一、RLC 并联谐振电路的概念
RLC 并联谐振电路是由电阻(R)、电感(L)和电容(C)三个元件并联组成的电路。
在这个电路中,当电压与电流的相位角相同时,电路状态达到谐振,这种谐振称为并联谐振或电流谐振。
二、RLC 并联谐振电路的谐振条件
在 RLC 并联电路中,谐振条件为:当电路中的电感(L)、电容(C)和电阻(R)满足一定条件时,电路达到谐振状态。
具体来说,当感纳(B= ωL / ωC)等于电阻(R)时,电路中电流与电压的相位角相同,达到并联谐振状态。
其中,ω表示角频率,B 表示感纳。
三、RLC 并联谐振电路的应用
RLC 并联谐振电路在电子电路中有广泛应用,例如用于测量电缆的交流耐压试验。
通过电感的并联方式,可以提高试验的电流,从而实现试验的目的。
此外,RLC 并联谐振电路在各种具有频率特性的电路网络中也有重要作用。
四、结论
RLC 并联谐振电路是一种特殊的电路,其谐振条件为感纳等于电阻。
这种电路在电子电路和通信领域具有广泛的应用。
RLC串联电路的谐振_2
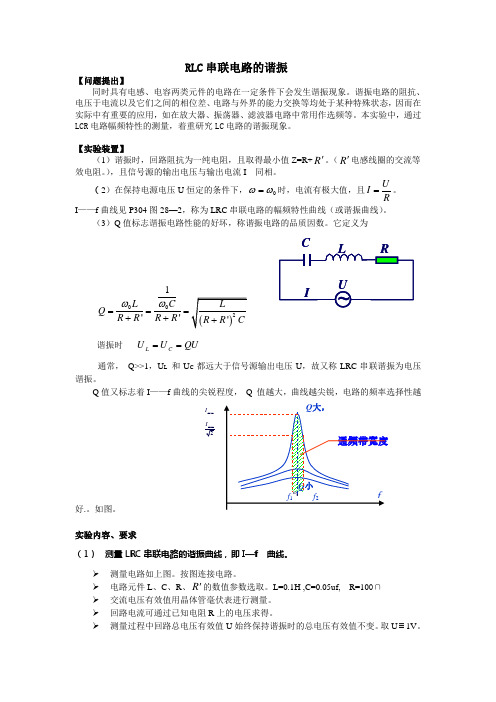
RLC 串联电路的谐振【问题提出】同时具有电感、电容两类元件的电路在一定条件下会发生谐振现象。
谐振电路的阻抗、电压于电流以及它们之间的相位差、电路与外界的能力交换等均处于某种特殊状态,因而在实际中有重要的应用,如在放大器、振荡器、滤波器电路中常用作选频等。
本实验中,通过LCR 电路幅频特性的测量,着重研究LC 电路的谐振现象。
【实验装置】(1)谐振时,回路阻抗为一纯电阻,且取得最小值Z=R+R '。
(R '电感线圈的交流等效电阻。
),且信号源的输出电压与输出电流I 同相。
(2)在保持电源电压U 恒定的条件下,0ωω=时,电流有极大值,且UI R=。
I ——f 曲线见P304图28—2,称为LRC 串联电路的幅频特性曲线(或谐振曲线)。
(3)Q 值标志谐振电路性能的好坏,称谐振电路的品质因数。
它定义为001''L CQ R R R R ωω===++谐振时 QU U U C L ==通常, Q>>1,U L 和U C 都远大于信号源输出电压U ,故又称LRC 串联谐振为电压谐振。
Q 值又标志着I ——f 曲线的尖锐程度, Q 值越大,曲线越尖锐,电路的频率选择性越好.。
如图。
实验内容、要求(1) 测量LRC 串联电路的谐振曲线,即I —f 曲线。
➢ 测量电路如上图。
按图连接电路。
➢ 电路元件L 、C 、R 、R '的数值参数选取。
L=0.1H ,C=0.05uf, R=100∩ ➢ 交流电压有效值用晶体管毫伏表进行测量。
➢ 回路电流可通过已知电阻R 上的电压求得。
➢测量过程中回路总电压有效值U 始终保持谐振时的总电压有效值不变。
取U ≡1V 。
CmaxI➢ 首先测量谐振时的频率0f 及R L C U U U 、 、,自拟记录表1【实验数据及分析】表4串联谐振0f 、Q 的实验、理论结果比较表【结论、讨论或体会】通过该实验对LCR电路幅频特性的测量,接触了RX7/1型十进制标准电容箱,ZX32型交流电阻箱、XD2信号发生器、数字万用表等仪器,学习了实验线路设计和参数选用。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1920
1987
2006
《电路实验》--基本实验
RLC串/并联谐振
张 峰 教授 上海交通大学电工电子实验教学示范中心
内容提纲
实验目的 实验原理 实验仪器 实验内容 实验报告
2
实验目的
1. 学习测定RLC串联、并联电路的通用谐振曲线的
方法,了解Q值对通用谐振曲线的影响。
2. 通过对RLC串联电路的U L ( )与 U C ( ) 的测量,了解电
2
1 1 1 Q 2
2
I I0 1.0 0.8 0.6 0.4 0.2
O
Q 0.5
Q 1
Q2
Q 10
0.5 1.0 1.5 2.0
8
图5.9.3 不同Q值时的幅频特性
实验原理
当L、C和 U S 一定时,不同的R 值具有不同的Q值。 通用谐振曲线可通过实验方法获得,在保持信号发生器 输出电压恒定的状态下,改变信号发生器的输出频率,通过 测量电阻R上的电压,从而计算出电路中的电流 I U R R 。 当电路谐振时,电阻R上 的 电压UR为最大值,这时函数发生 器输出信号的频率即为电路的谐 振频率,曲线如图5.9.4。
1 R L C
2 2
0 R 1 Q2 0
2
研究和比较不同参数电路的谐 振特性,通常采用通用谐振曲线 (电流比与角频率比)。其中, I0为谐振时的电流值,η=ω/ω。
I I0 1
0 2 1 Q 0
2
RL与C并联的实验电路图如 5.9.8,电感线圈内阻极小,在电 路中串入了取样电阻。 改变输入信号的频率,并联谐 振时,取样电阻上的电压最小。
Q
0L
R
L 1 1 R 2C R
L C
此时fo 和Q值与串联谐振电路相同。电路的等效阻抗为:
Z L RC 1 L 1 1 Z0 L RC 1 0 0 1 j 1 jQ 1 jQ R RC 0 0
C
L 1 j RC R
图5.9.5 RL-C并联谐振电路
R L
U
0L R 1 谐振条件: 0L 0RC R
化简:
0C
0 L
0 L
2
并联谐振频率:
1 f0 2 1 R2 1 R 2C 1 2 LC L L 2 LC
R
U L U C 0 L 1 1 Q US US R 0 CR R
L C
但实际上,由于电感存在一定的电阻(约1~ 10Ω), 实验中UL与UC的实测值不完全相等,且对Q值也有一定的影 响,在实验中应引起注意。
7
实验原理
RLC串联电路中电流与角频率的关系称电流的幅频特性, US US 即: I
Q
0L
R
L 1 2 R C
I L
图5.9.6并联谐振电路的相量图
11
实验原理
通常电感线圈的电阻较小,当电阻 认为
R 2C 1 L
R 0.2 L C
时,可以
, 即电阻对频率的影响可以忽略不计,此时
f0 1 2 LC R 2C 1 1 L 2 L C
的谐振频率为:
此时谐振电路的品质因数为:
0
1 LC
f0
1
5
实验原理
如果 0 ,电路呈容性;如果 0 ,电路呈感性。 谐振电路中,电感电压和电容电压与角频率的关系为:
U L I L
LU S
1 R2 L C
US 1 C R 2 L C
2
10
实验原理
并联谐振频率:
1 f0 2 1 R2 1 2 LC L 2 L C R 2C 1 L
上式表明由于线圈中具有电阻R,RL与C并联谐振频率要 低于串联谐振频率,而且在电阻值
R L C
时,
I C
将不存在 fo,即电路不会发生谐振。
I U
并联谐振电路的品质因数为:
2
2
UC I
1 C
0
图5.9.2 RLC串联电路的 U C ( ), 谐振时 0 L C ,电感上的电压UL与 0
电容上的电压UC 数值相等,相位差为180º。 比称电路的品质因数Q,即
谐振时电感上的电压(或电容上的电压)与电源电压之
I I0
1
1
2
1 Q 2 1
0
1 1 2
图5.9.4 通用谐振曲线
9
实验原理
RL-C并联谐振电路
RL串联电路(即实际的电感线圈)和电容器并联的电 路如图5.9.5所示。 I I
L
电路的等效阻抗为:
1 R j L) L C Z 1 RC R j L 1 C j 1 j
路的Q值意义。
3. 了解电路参数对谐振曲线形状及谐振频率的影响 4. 掌握低频信号发生器的使用方法。
3
实验原理
RLC串联谐振 RLC串联电路接在频率可调的电源上,如图5.9.1
所示,因电路阻抗随频率的变化而变化,所以电路 的电流也在不断的变化,其表达式为:
j L
US I Z US 1 2 R L C
12
实验原理
在忽略电感线圈电阻对频率影响的条件下,RL与C并联 谐振电路的通用谐振曲线与 Z /Z0 与角频率 /0 之间的关 系一致。 U Z I Z 1 1
U0 = Z0 I = Z0 1 L 1 R RC
2
1 Q2 0 0
2
U S
1 jC
图5.9.1 RLC串联电路 4
实验原理
I US Z US 1 R2 L C
2
当 L
谐振角频率:
1 0 时,电路处于电压谐振。 C
谐振频率:
2 LC 因此,电路的谐振角频率或谐振频率取决于L、C值,而 与R值无关。
电路谐振时,电路的阻抗呈阻性,电阻R上的电压等于 电源电压且其端口电流与电压同相位,电路中的电流达到最 US 大值即: I0 R
