八年级数学第一章 轴对称图形 单元测试
数学八年级上册《轴对称》单元检测(含答案)

9.如图,在 中, , , 平分 , ,则图中共有等腰三角形( )
A. 个B. 个C. 个D. 个
[答案]D
[解析]
[分析]
根据等腰三角形性质和三角形内角和定理求出∠A C B=∠B= (180°−∠A)=72°,求出∠A C D=∠B C D= ∠A C B=36°,求出∠C D B=∠A+∠A C D=72°,根据平行线的性质得出∠ED B=∠A=36°,∠DEB=∠A C B=72°,∠C DE=∠A C D=36°,推出∠A=∠A C D=∠B C D=∠C DE=36°,∠B=∠A C D=∠DEB=∠C D B=72°即可.
A. B. C. D.
3.一个角是 等腰三角形是( )
A.等腰直角三角形B.等边三角形C.直角三角形D.上述都正确
4.如图,在一个规格为 (即 个小正方形)的球台上,有两个小球 , .若击打小球 ,经过球台边的反弹后,恰好击中小球 ,那么小球 击出时,应瞄准球台边上的点( )
A. B. C. D.
5.如图,桌面上有M、N两球,若要将M球射向桌面的任意一边,使一次反弹后击中N球,则4个点中,可以瞄准的是( )
[详解]解:∵A B=A C,
∴∠A B C=∠C,
∵B D=B A,
∴∠A=∠B D A,
∴∠A>∠C,
∴2∠A<180°且3∠A>180°,
∴60°<∠A<90°,即60<x<90.
故选C.
[点睛]此题考查了等腰三角形的性质,三角形内角和为180°和三角形外角的性质,关键是得到2∠A<180°且3∠A>180°.
[答案]D
[解析]
[分析]
此题根据△A B C中∠A为锐角与钝角分为两种情况解答.
八年级上册数学《轴对称》单元测试卷附答案

(3)将图4中的△A C D绕点C顺时针旋转任意角度(交点F至少在B D、AE中的一条线段上),变成如图5所示的情形,若∠A C D=α,则∠AFB与α的有何数量关系?并给予证明.
24.如图,在平面直角坐标系中,一次函数y=x的图象为直线l.
(B类)已知如图,四边形A B C D中,A B=B C,∠A=∠C,求证:A D=C D.
23.已知点C为线段A B上一点,分别以A C、B C为边在线段A B同侧作△A C D和△B CE,且C A=C D,C B=CE,∠A C D=∠B CE,直线AE与B D交于点F,
(1)如图1,若∠A C D=60°,则∠AFB=;如图2,若∠A C D=90°,则∠AFB=;如图3,若∠A C D=120°,则∠AFB=;
[答案]A
[解析]
[分析]
根据镜面对称的性质,在平面镜中的像与现实中的事物恰好顺序颠倒,且关于镜面对称.
[详解]由图分析可得题中所给的”20∶15”与”21∶05”成轴对称,这时的时间应是21∶05,故答案选A.
[点睛]本题主要考查了镜面反射的原理与性质,解本题的要点在于应认真观察,注意技巧.
9.如图,△A B C与△A D C关于A C所在的直线对称,∠B C A=35°,∠D=80°,则∠B A D的度数为( )
2.关于”线段、角、正方形、平行四边形、圆”这些图形中,其中是轴对称图形的个数为( )
A.2B.3C.4D.5
[答案]C
[解析]
[分析]
根据轴对称图形的概念即可解答.
[详解]线段、角、正方形、圆是轴对称图形,共4个.
故选C.
[点睛]本题考查了轴对称图形的概念,确定轴对称图形的关键是寻找对称轴,图形两部分沿对称轴折叠后可重合.
人教版数学八年级上册《轴对称》单元检测卷带答案

《轴对称》单元测试
(时间:120分钟 满分:150分)
一、选择题(本大题共10小题,共40.0分)
1.在4×4的正方形网格中,已将图中的四个小正方形涂上阴影,若再从其余小正方形中任选一个也涂上阴影,是整个阴影部分组成的图形成轴对称图形,那么符合条件的小正方形共有()
A 4个B.3个C.2个D.1个
故答案为两,一.
【点睛】考查轴对称和轴对称图形的概念,熟练掌握它们的概念,找到它们的区别与联系是解题的关键.
12.点 与点 关于______对称.
【答案】y轴
【解析】
【分析】
根据关于y轴对称点的坐标特点:横坐标互为相反数,纵坐标不变可以直接得到答案.
【详解】∵点A(−3,2),点B(3,2),
纵坐标相等,横坐标互为相反数,
【详解】如图:△ABC中,AB=AC,BD是边AC上的高.
∵ 且AB=AC,
∴
在Rt△BDC中,
∴
故答案为
【点睛】考查等腰三角形的性质,熟练掌握等腰三角形两个底角相等是解题的关键.
14.在等边三角形ABC中,点D在AB边上,点E在BC边上,且 连接AE、CD交于点P,则 ______.
【答案】
【解析】
解:将矩形纸片ABCD折叠,使点D与点B重合,点C落在C′处,折痕为EF,
由折叠特性可得,CD=BC′=AB,∠FC′B=∠EAB=90°,∠EBC′=∠ABC=90°,
∵∠ABE+∠EBF=∠C′BF+∠EBF=90°
∴∠ABE=∠C′BF
在△BAE和△BC′F中,
∴△BAE≌△BC′F(ASA),
13.已知等腰三角形的顶角为40°,则它一腰上的高与底边的夹角为____.
数学八年级上册《轴对称》单元检测题附答案

A.40°B.55°C.70°D.110°
[答案]C
[解析]
试题解析:∵m∥n,
∴
∵A B=B C,
∴
故选C.
点睛:平行线的性质:两直线平行,内错角相等.
5.如图,已知DE∥B C,A B=A C,∠1=125°,则∠C的度数是( )
一、选择题(共12小题,总分36分)
1.下列图案是轴对称图形的有 个.
A.1B.2C.3D.4
[答案]B
[解析]
试题分析:根据轴对称图形的概念(延某条直线对折,两部分能够完全重合)可知第一和第四个是轴对称图形.
故选B
考点:轴对称图形
2.点A(-2,5)关于x轴对称的点的坐标是( )
A.(2,5)B.(-2,-5)C.(2,-5)D.(5,-2)
(1)试判定△ODE的形状,并说明你的理由;
(2)线段B D、DE、EC三者有什么关系,写出你的判断过程.
25.如图所示,点O是等边三角形A B C内一点,∠AOB=110°,∠BOC=α,以OC为边作等边三角形OC D,连接A D.
(1)当α=150°时,试判断△AOD 形状,并说明理由;
(2)探究:当A为多少度时,△AOD是等腰三角形?
A. 31°B. 32°C. 59°D. 62°
11.如图,等边三角形A B C与互相平行的直线A,B相交,若∠1=25°,则∠2的大小为( )
A. 25°B. 35°C. 45°D. 55°
12.如图,在射线OA,OB上分别截取OA1=OB1,连接A1B1,在B1A1,B1B上分别截取B1A2=B1B2,连接A2B2,…按此规律作下去,若∠A1B1O=α,则∠A10B10O=( )
八年级上册数学《轴对称》单元测试(含答案)
A. B. C. D.
二、填空题(每小题3分,共24分)
11.一个正五边形的对称轴共____条.
12.如图,在等边△A B C中,A D是高,若A B=6,则C D的长为:_____
13.已知点P(3,-1)关于y轴 对称点Q的坐标是(A+B,1-B),则A B的值为______.
A. B. C. D.
[答案]A
[解析]
[分析]
根据直角三角形的性质得到A B=2B C,根据线段垂直平分线的性质得到D A=D B,根据直角三角形的性质、角平分线的性质判断即可.
[详解]∵∠C=90°,∠A=30°,
∴∠A B C=60°,A B=2B C,
∵DE是A B的垂直平分线,
∴D A=D B,故B正确,不符合题意;
三、解答题(共66分)
19.如图,已知A B=A C,AE平分∠D A C,那么AE∥B C吗?为什么?
20.(8分)如图,在△A B C中,∠C=∠A B C,BE⊥A C,△B DE是正三角形.求∠C的度数.
21.如图,在平面直角坐标系中,A(﹣1,5),B(﹣1,0),C(﹣4,3).
(1)在图中 点上标出相应字母A、B、C,并求出△A B C的面积;
5.如图,已知A B=A1B,A1B1=A1A2,A2B2=A2A3,A3B3=A3A4,….若∠A=70°,则∠Bn-1AnAn-1的度数为()
A. B. C. D.
[答案]C
[解析]
在△A B A1中,∵∠A=70°,A B=A1B,∴∠B A1A=∠A=70°.
∵A1A2=A1B1,∠B A1A是△A1A2B1的外角,∴∠B1A2A1= =35°.
八年级数学 第一章 轴对称图形单元测试试题 试题

盱眙县八年级数学第一章单元测试〔试卷一共120分〕一.选择题:〔每一小题3分,一共24分〕1、以下图案中是轴对称图形的是〔〕2021年2021年雅典1988年汉城1980年莫斯科ABCD2、以下说法正确的选项是( ).A.等腰梯形不是轴对称图形 B.等腰梯形相邻两内角都相等C.等腰梯形两对角线相等 D.任一梯形都是轴对称图形3、在△ABC中,①假设AB=BC=CA,那么△ABC为等边三角形;②假设∠A=∠B=∠C,那么△ABC为等边三角形;③有两个角都是60°的三角形是等边三角形;④一个角为60°的等腰三角形是等边三角形.上述结论中正确的有〔〕A.1个B.2个C.3个D.4个4 、如图,在△ABC中,AB=AC,AD平分∠BAC,DE⊥AB,DF⊥AC,E、F为垂足,那么以下四个结论,①∠DEF=∠DFE ②AE=AF ③AD垂直平分EF ④EF垂直平分AD,其中正确的个数是〔〕 A.1个B.2个 C.3个 D.4个5、如图,△ABC中,AB<AC,BC边上的垂直平分线DE交BC于点D,交AC于E, 假设AC=8cm,△ABE的周长为15cm,那么AB的长为〔〕A.6cmB.7cmC.8cmD.9cm第4题 第5题 第7题 第8题 6、以下语句中正确的有〔 〕句.①关于一条直线对称的两个图形一定能重合;②两个能重合的图形一定关于某条直线对称;③一个轴对称图形不一定只有一条对称轴;④两个轴对称图形的对应点一定在对称轴的两侧. A 1 B 2 C 3 D 47、如图,在等腰梯形ABCD 中,AB ∥CD ,对角线AC 、BD 交于点O ,那么图中全等三角形有( ). A .1对 B .2对 C .3对 D .4对8. 如图甲,四边形ABCD 是等腰梯形,AB∥DC.由4个这样的等腰梯形可以拼出图乙所示的平行四边形,那么∠A° B. 60° C. 70° D. 80°二.填空题:〔每一小题3分,一共24分9、在镜子中看到时钟显示的时间是是,那么实际时间是是10、长方形有 条对称轴,正方形有 条对称轴,圆有 条对称轴. 11、等腰三角形两边长分别是4和6,那么第三边长是 ;等腰三角形两边长分别是4和9,那么周长是 .12、等腰三角形的一个外角等于100,那么它的顶角是 .13、代号为①、②、③、④的4张三角形纸片都有一个角为50°.假如它们另有一个角分CD BE FADA别为50°、70°、80°、90°,那么其中只有代号为 的纸片能沿直线剪一刀得到等腰梯形.第14题 第15题 第16题 14、(1)如图,由Rt△CDE ≌Rt△ACF,可得∠DCE +∠ACF = ,从而∠ACB= .(2)设小方格的边长为1,那么AB= ;(3)取AB 中点M ,连接CM .那么CM= ,理由是: 15、如图,在梯形ABCD 中,AD∥BC,DE∥AB,AD=4 cm ,△DEC 的周长为12 cm ,那么BE= ,梯形ABCD 的周长= .16、如图,ABC △中,AB AC =,90BAC ∠=,直角EPF ∠的顶点P 是BC 中点,两边PE ,PF 分别交AB ,AC 于点E ,F ,给出以下四个结论:①APE CPF ∠=∠,② AE CF =,③EPF △是等腰直角三角形,④EF AP =。
人教版八年级上册数学《轴对称》单元测试卷(含答案)

人教版八年级上册数学《轴对称》单元测试卷姓名:__________班级:__________考号:__________一、选择题(本大题共10小题,每小题3分,共30分。
在每小题给出的四个选项中,只有一个选项是符合题目要求的)1.如图,阴影部分是由5个小正方形涂黑组成的一个直角图形,再将方格内空白的两个小正方形涂黑,得到新的图形(阴影部分),其中不是轴对称图形的是()A B C D2...将一个正方形纸片依次..........下.图的方式对折,然后沿图...........c.中的虚线裁剪,成图.........d.样式,...将纸展开铺平,所得到的图形是(...............).3.如图,是小华画的正方形风筝图案,他以图中的对角线AB为对称轴,在对角线的下方再画一个三角形,使得新的风筝图案成为轴对称图形,若下列有一图形为此对称图形,则此图为()A B C D4.如图,在ABC ∆中,AB AC =,ABC ∠,ACB ∠的平分线相交于点F ,过F 作DE BC ∥ ,交AB 于点D ,交AC 于E .图中是等腰三角形有( )个. A .3 B .4 C .5 D .65.已知等腰三角形的周长为24cm ,一腰长是底边长的2倍,则腰长是( )A .4.8cmB .9.6cmC .2.4cmD .1.2cm6.若等腰三角形中有一个角等于50︒,则这个等腰三角形的顶角的度数为( )A .50︒B .80︒C .65︒或50︒D .50︒或80︒7.如图a 是长方形纸带,∠DEF =20°,将纸带沿EF 折叠成图b ,再沿BF 折叠成图c ,则图c 中的∠CFE 的度数是( )A 、110°B 、120°C 、140°D 、150° 8.如图,A 在DE 上,F 在AB 上,且AC CE =,123∠=∠=∠,则DE 的长等于( )FE CBADA.DCB.BCC.ABD.AE AC9.将一矩形纸片按如图方式折叠,BC、BD为折痕,折叠后A′B与E′B在同一条直线上,则∠CBD的度数()A、大于90°B、小于90°C、等于90°D、不能确定二、填空题(本大题共5小题,每小题3分,共15分)11.已知:如图,四边形ABCD中,AC平分∠BAD,CD∥AB,BC=6cm,∠BAD=30°,∠B=90°.求CD的长______.F321EDCBAE'A'EDCBA12....已知:如图,Δ.......ABC ...是等边三角形,.......AE ..⊥.BC ..于.E .,.AD ..⊥.CD ..于.D .,若..AB ..∥.CD ..,则图...中.60..°的角有... 个...13.如图,将OAB ∆绕点O 按逆时针方向旋转至''OA B ∆,使点B 恰好落在边''A B 上,已知4AB =cm , '1BB =cm ,则'A B 的长是________cm14....如图..8.-.3.,已知Δ....ABC ...中,..AB ..=.AC ..,∠..BAC ...=.120...°,.DE ..垂直平分....AC ..交.BC ..于.D .,.垂足为...E .,若..DE ..=.2cm ...,则..BC ..=._____cm.........15.如图所示,在△ABC 中,∠BAC=106°,EF 、MN 分别是AB 、AC 的垂直平分线,点E 、M 在BC 上,则∠EAM=三 、解答题(本大题共7小题,共55分)16.下列为边长为1的小正方形组成的网格图.①请画出△ABC 关于直线a 对称的图形(不要求写作法); ②求△ABC 的面积(直接写出即可).B'A'BAONMFE CB A17.如图,在等腰Rt ABC ∆中,3CA CB ==,E 的BC 上一点,满足2BE =,在斜边AB上求作一点P 使得PC PE +长度之和最小。
八年级上册数学《轴对称》单元综合测试附答案
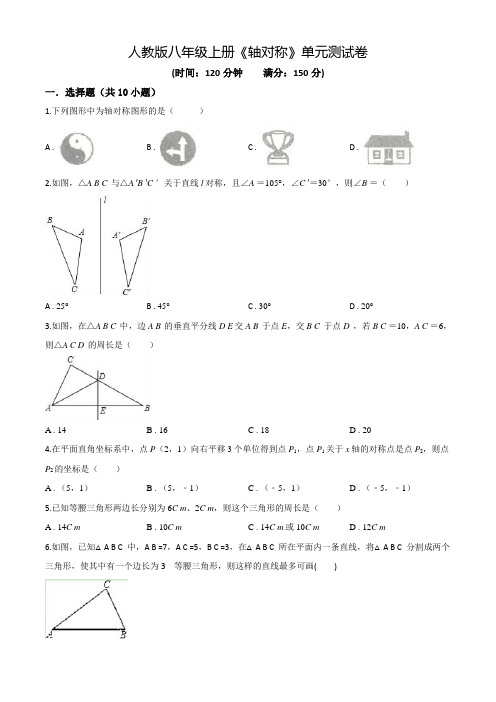
[点睛]本题考查了线段垂直平分线的性质.此题难度不大,注意掌握数形结合思想与转化思想的应用.
4.在平面直角坐标系中,点P(2,1)向右平移3个单位得到点P1,点P1关于x轴的对称点是点P2,则点P2的坐标是( )
A.(5,1)B.(5,﹣1)C.(﹣5,1)D.(﹣5,﹣1)
[答案]B
[解析]
人教版八年级上册《轴对称》单元测试卷
(时间:120分钟 满分:150分)
一.选择题(共10小题)
1.下列图形中为轴对称图形的是( )
A. B. C. D.
2.如图,△A B )
A.25°B.45°C.30°D.20°
3.如图,在△A B C中,边A B的垂直平分线DE交A B于点E,交B C于点D,若B C=10,A C=6,则△A C D的周长是( )
C.三个角都相等的三角形,内角一定为60°是等边三角形,不合题意,故此选项错误;
D.边上的高也是这边的中线的三角形,也可能是等腰三角形,符合题意,故此选项正确.
故选D.
[点睛]本题主要考查了等边三角形的判定,注意熟练掌握:由定义判定:三条边都相等的三角形是等边三角形.(2)判定定理1:三个角都相等的三角形是等边三角形.(3)判定定理2:有一个角是60°的等腰三角形是等边三角形.
22.已知等腰三角形△A B C 一边长为5,周长为22.求△A B C另两边的长.
23.如图,在△A B C中,∠B A C=90°,A D⊥B C于点D,BF平分∠A B C交A D于点E,交A C于点F,求证:AE=AF.
24.如图,△A B C中,点O是∠B C A与∠A B C的平分线的交点,过O作与B C平行的直线分别交AB、A C于D、E.已知△A B C的周长为15,B C的长为6,求△A DE的周长.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一章轴对称图形单元测试(附答案)
(时间:45分钟满分:100分)
一、选择题(每题3分,其30分)
1.“羊”字象征吉祥和美好,下图的图案与羊有关,其中是轴对称图形的个数是( )
A.1 B.2 C.3 D.4
2.平面上有A、B两个点,以线段AB为一边作等腰直角三角形能作( ) A.3个B.4个C.6个D.无数个
3.如图,已知∠AOB=40°,OM平分∠AOB,MA⊥OA,MB⊥OB,垂足分别为A、B两点,则∠MAB等于( )
A.50°B.40°
C.30°D.20°
4.已知等腰三角形的一个外角等于100°,则它的顶角是( )
A.80°B.20°C.80°或20°D.不能确定
5.直角三角形三边垂直平分线的交点位于三角形的( ) A.三角形内B.三角形外C.斜边的中点D.不能确定6.已知等腰三角形的一边等于3,一边等于6,那么它的周长等于( ) A.12 B.12或15 C.15 D.15或18
7.如图,在△ABC中,AB=AC,∠A=36°,两条角平分线BD、CE相交于点F,则图中的等腰三角形共有( )
A.6个B.7个C.8个D.9个
8.如图,把一个正方形三次对折后沿虚线剪下,则所得图形大致是( )
9.如图,DE是△ABC中边AC的垂直平分线,若BC=18 cm,AB=10 cm,则△ABD的周长为( )
A.16 cm B.28 cm
C.26 cm D.18 cm
10.下列语句中,正确的有( )
①关于一条直线对称的两个图形一定能重合;
②两个能重合的图形一定关于某条直线对称;
③一个轴对称图形不一定只有一条对称轴;
④两个轴对称图形的对应点一定在对称轴的两侧.
A.1个B.2个C.3个D.4个
二、细心填一填(每题3分,共30分)
11.若直角三角形斜边上的高和中线长分别是5 cm,6 cm,则它的面积是________.12.如图,在等腰梯形ABCD中,AD∥BC,AB=DC,AC=BC,E是BA、CD延长线上的交点,∠E=40°,则∠ACD=___________.
13.如图,OE是∠AOB的平分线,BD⊥OA于点D,AC⊥BO于点C,则关于直线OE 对称的三角形共有_________对.
14.如图,在∠MON的两边上顺次取点.使DE=CD=BC=AB=OA,若∠MON=22°,则∠NDE=__________.
15.如图,AB=AC=4 cm,DB=DC,若∠ABC为60度,则BE为__________.
16.在△ABC中,AB=BC,其周长为20 cm,若AB=8 cm,则AC=__________.17.△ABC和△DEF关于直线l对称,若△ABC的周长为12 cm,△DEF的面积为8 cm2,则△DEF的周长为__________,△ABC的面积为__________.
18.如图,以正方形ABCD的一边CD为边向形外作等边三角形CDE,则∠AEB=_______.
19.数的计算中有一些有趣的对称,形式如:12×231=132×21.仿照上面的形式填空,
并判断等式是否成立:(1)12×462=_________×_________( ),(2)18×891=________×__________( ).
20.如图,点D 、E 分别为边AB 、AC 的中点,将△ABC 沿线段DE 折叠,使点A 落在
点F 处,若∠B=50°,则∠BDF=_________.
三、耐心解一解(第21题6分,第25题10分,其余每题8分,共40分)
21.如图,求作点P ,使点P 同时满足:①PA=PB ;②到直线m ,n 的距离相等.(尺规作
图,保留作图痕迹)
22、在△ABC 中,∠C =90°,DE 垂直平分斜边AB ,分别交AB ,BC 于D ,E .若∠CAE =∠B +30°,求∠AEB .(5分)
23.如图,在梯形ABCD 中,AD ∥BC ,∠B=∠C ,点E 是BC 边的中点. 试说明:AE=DE .
(第22题)
E B
D C
A
24.如图,在△ABC中,AB=AC,点D在BC边上,且BD=AD,DC=AC.将图中的等腰三角形全都写出来.并求∠B的度数.
90,AB=14cm,AD=18cm,BC=21cm,25.如图,在梯形ABCD中,AD∥BC,∠B=0
点P从点A出发,沿边AD向点D以1cm/s的速度移动,点Q从点C出发沿边CB向点B以2cm/s的速度移动,若有一点运动端点时,另一点也随之停止。
如果P、Q同时出发,能否有四边形PQCD成等腰梯形?如果存在,求经过几秒后;如果不存在,请说明理由。
参考答案
1.B 2.C 3.D 4.C 5.C 6.C 7.C 8.C 9.B 10.B 11.30 cm 2 12.30° 13.4 14.110° 15.2 16.4 17.12 cm 8 cm 2 18.30° 19.264 21 √; 198 81 √ 20.80° 21.略 22.140°
23.∵ 四边形ABCD 为梯形,∠B=∠C ,
∴ 梯形ABCD 为等腰梯形.(同一底上底角相等的梯形为等腰梯形) ∴ AB=DC .
∵ 点E 为BC 中点, ∴ BE=CE .
在△ABE 与△DCE 中,.AB DC B C BE CE =⎧⎪
∠=∠⎨⎪=⎩
,,
∴ △ABE ≌△DCE(SAS).
∴ AE=DE .(全等三角形对应边相等)
24.△ABC 、△DAB 、△CAD 均为等腰三角形,∠B=36°. 设∠B=x °, ∵ AB=AC , ∴ ∠C=∠B=x . 又DB=DA ,
∴∠DAB=∠B=x . ∴∠CDA=2x . 又CM=CD ,
∴∠CAD=∠CDA=2x .
在△CAD 中,∠C+∠CDA+∠CAD=180°, ∴ x+2x+2x=180°. ∴x=36.
25.能,经过8秒.。
