轴对称 平移与旋转单元测试题
四年级下册数学单元测试-1.平移、旋转和轴对称 苏教版(含答案)

四年级下册数学单元测试-1。
平移、旋转和轴对称一、单选题1.下面各图形,不是轴对称图形的是()A. B. C.2.下列现象中,()属于旋转.A. 拉衣服的拉链B. 拧瓶盖C. 跳远时的腿部运动3.下面()的运动是旋转。
A. 旋转的呼啦圈B. 观光电梯C. 拨算珠4.下面()是顺时针旋转一周后的图形。
A. B. C. D.二、判断题5.数学“3”是轴对称图形。
()6.旋转改变了图形的大小和形状.()7.平移不改变图形的大小,只改变图形的位置.()8.圆绕中心点无论旋转多少度都与原来的图形重合,旋转一周可以重合无数次。
()三、填空题9.下列现象哪些是平移,画“√”;哪些是旋转,画“○”。
________ ________________ ________10.把一个图形绕某个点旋转,会得到一个新的图形,新图形与原图形的________和________完全相同。
11.下面的图案各是从哪张纸上剪下来的,连一连。
________ A、________ B、________ C、________ D、四、解答题12.解决问题如图,正方体中哪些线段可经由线段AB平移得到?线段AD可以由FB平移得到吗?13.(1)沿虚线画出图形的另一半,使它成为一个轴对称图形。
(2)图中的小船是经过向________平移________格,再向________平移________格得来的。
(3)先将三角形向左平移三格,然后绕A点逆时针旋转90°,在方格纸中画出旋转后的图形。
五、应用题14.在下面的方格纸上:①用数对表示三角形A三个顶点的位置.(,)(,)(,)②画出图形A向右平移8格后得到图形B;然后再以MN为对称轴,画出B的轴对称图形.参考答案一、单选题1.【答案】C【解析】【解答】平行四边形不是轴对称图形。
故答案为:C。
【分析】如果一个图形沿着一条直线对折,两侧的图形能够完全重合,这个图形就是轴对称图形,折痕所在的这条直线叫做对称轴。
2023年苏教版四年级数学下册第一单元平移、旋转和轴对称测试卷含答案

《平移、旋转和轴对称》学校:___________姓名:___________班级:___________考号:___________评卷人得分一、选择题(共10分)1.(本题1分)平移所给图形可得()。
A.B.C.D.2.(本题1分)下面图形中,对称轴条数最多的是()。
A.B.C.D.3.(本题1分)街心花园的花圃进行了园艺造型设计(如下图),涂色部分种植月季花,其余部分种植郁金香,从示意图中可以看出种植月季花的面积是整个花圃的()。
A.13B.无法确定C.14D.124.(本题1分)钟表上时针指向2,分针指向12,3小时后,时针旋转了()°。
A.30B.90C.120D.1505.(本题1分)再画一个小正方形,使下图成为轴对称图形,共有()种不同的画法。
A.2B.3C.4D.56.(本题1分)下图都是常见的安全标记,其中()是轴对称图形。
A.B.C.D.7.(本题1分)从6:00到9:00,时针旋转了()度。
A.90°B.180°C.360°D.120°8.(本题1分)下列图形中,()是轴对称图形。
A.B.C.D.9.(本题1分)如图,在图形中再给2个格子涂上颜色,使整个图形成为一个轴对称图形。
有()种不同的涂法。
A.6B.7C.8D.910.(本题1分)这是一个电风扇开关,数字表示风速档。
现在风扇在“1”档运行,如果要关闭,可将旋钮()。
A.按顺时针方向旋转90°B.按顺时针方向旋转120°C.按逆时针方向旋转90°D.按逆时针方向旋转120°评卷人得分二、填空题(共10分)11.(本题1分)下面的图形是绕( )点按( )方向旋转的。
12.(本题1分)(1)图1笑脸平移后得到的图形是( );(2)图2小船平移后得到的图形是( )。
13.(本题1分)如图,指针从“12”出发,绕点O顺时针旋转( )°到“4”。
第二单元《轴对称和平移》(单元测试)(含答案)-2024-2025学年五年级上册数学北师大版

第二单元《轴对称和平移》(单元测试)-2024-2025学年五年级上册数学北师大版一、单选题901.图形中的一个是由另一个绕着某个顶点顺时针旋转得到的,可能的是( )。
A.B.C.D.2.下列图形中,对称轴最多的是( )。
A.B.C.D.3.下列图形中,只有1条对称轴的是( )。
A.圆B.正方形C.长方形D.半圆4.下面图形中,对称轴最多的是( )A.B.C.D.5.如图所示,四幅汽车标志设计中,下面通过平移得到的是( )A.B.C.D.二、判断题6.把一个图形向右平移3格,那么平移前后两个图形之间的距离是3格。
( )7.等边三角形只有1条对称轴。
( )8.将5厘米长的线段向左平移3厘米,平移后的线段长8厘米。
( )9.平行四边形有两条对称轴。
( )10.所有的轴对称图形,都至少有一条对称轴。
( )三、填空题11.等腰梯形有 条对称轴,长方形有 条对称轴,正方形有 条对称轴,圆有 条对称轴。
12.图形①先向 平移 格,再向 平移 格,再绕点O 旋转 °得到图形③。
图形②先绕点O' 旋转90°,再向 平移 格,得到图形④。
13.如图,图形1向右平移 格,与图形2合成一个长方形。
14.如图的图形各有几条对称轴? 条; 条; 条; 条。
15.钟面上从6:00到9:00,时针按 方向旋转 。
四、作图题16.画出下面图形的对称轴,有几条画几条。
五、解决问题17.在( )里填“平移”或“旋转”。
18.观察下面的图形,回答问题。
(1)图形A经过什么变换得到图形B?(2)图形B经过什么变换得到图形D?(3)图形A经过什么变换得到图形C?19.下面4只蝴蝶中,哪一只通过平移可以与右面方框中的蝴蝶重合?圈出来吧。
20.图形A经过怎样的平移才能与图形B组合成一个正方形呢?21.方格纸上每一小格的边长是1厘米。
(1)在上面的方格纸上画出和已知长方形周长相等的正方形,并把正方形的 涂上颜色。
(2)用两个已知这样的长方形可以拼成 形,周长是 。
七年级数学下册《第十章 轴对称、平移与旋》单元测试卷及答案解析-华东师大版

七年级数学下册《第十章 轴对称、平移与旋》单元测试卷及答案解析-华东师大版 一、单选题1.在一些美术字中,有的汉字是轴对称图形.下面4个汉字中,可以看作是轴对称图形的是( ) A .B .C .D .2.下列四个图形中,不能通过其中一个四边形平移得到的是( )A .B .C .D .3.如图,将△ABC 绕点A 逆时针旋转65°得到△AED ,则△BAE 的度数是( )A .65°B .45°C .35°D .25°4.中国“二十四节气”已被正式列入联合国教科文组织人类非物质文化遗产代表作品录,下列四幅作品分别代表“立春”、“谷雨”、“白露”、“大雪”,其中是中心对称图形的是( )A .B .C .D .5.如图,若ABC DEF ≌,则D ∠等于( )A .30︒B .50︒C .60︒D .100︒6.如图,在ABC 中40C ∠=︒,把ABC 沿BC 边上的高AM 所在的直线翻折,点C 落在边CB 的延长线上的点C '处,如果20BAC ∠='︒,则BAC ∠的度数为( )A .80︒B .75︒C .85︒D .70︒7.如图,DEF 经过怎样的平移得到ABC ( )A .把DEF 向左平移4个单位,再向上平移2个单位B .相DEF 向右平移4个单位,再向下平移2个单位C .把DEF 向右平移4个单位,再向上平移2个单位D .把DEF 向左平移4个单位.再向下平移2个单位8.如图,将△AOB 绕点O 按逆时针方向旋转45°后得到△A'OB',若△AOB =15°,则△AOB'的度数是( )A .25°B .30°C .35°D .40°9.下列图案中,既是中心对称图形又是轴对称图形的是( )A .B .C .D .10.如图,在正方形方格中,各正方形的顶点叫做格点,三个顶点都在格点上的三角形称为格点三角形.图中△ABC 是格点三角形,请你找出方格中所有与△ABC 全等,且以A 为顶点的格点三角形,这样的三角形共有( )个(△ABC 除外).A .2B .3C .4D .5二、填空题11.如图,在ABC 中,D 是BC 上一点250ABC BAD ∠=∠=︒,将ABD 沿着AD 翻折得到AED ,则CDE ∠= .12.如图,△ABC 沿BC 所在直线向右平移得到△DEF ,已知EC =4,BF =18,则平移的距离为 .13.两块不同的三角板按如图1所示摆放,AC 边重合4530BAC DAC ∠∠=︒=︒,接着如图2保持三角板ABC 不动,将三角板ACD 绕着点C 按顺时针以每秒10︒的速度旋转90︒后停止.在此旋转过程中,当旋转时间t = 秒时三角板A CD ''有一条边与三角板ABC 的一条边恰好平行.14.三个全等三角形摆成如图所示的形式,则αβγ∠+∠+∠的度数为 .三、作图题15.如图,在正方形网格中,ABC 各顶点都在格点上,点A ,B ,C 的坐标分别为()51-,,()54-,和()14-,.四、解答题16.如图是正方形纸片ABCD ,分别沿AE 、AF ,折叠后边AB 与AD 恰好重叠于AG ,求△EAF 的大小.17.如图,在一块长为20m ,宽为10m 的长方形草地上,修建了宽为1m 的小路,求这块草地的绿地面积.18.如图,已知30BAC ∠=︒,把ABC 绕着点A 顺时针旋转,使得点B 与CA 的延长线上的点D 重合,求AEC ∠的度数.19.如图,点P 是△AOB 外的一点,点Q 与P 关于OA 对称,点R 与P 关于OB 对称,直线QR 分别交OA ,OB 于点M ,N ,若PM=PN=3,MN=4,求线段QR 的长.20.如图,ACB 和DCE 均为等边三角形,点A 、D 、E 在同一直线上,连结BE .试说明AD BE =.聪明的小亮很快就找到了解决该问题的方法,请你帮助小亮把说理过程补充完整.解:∵ACB 和DCE 均为等边三角形∴CA CB =,CD=CE ,ACB ∠= 60=︒(等边三角形的性质) ∴ACD ∠=即ACD 绕点C 按逆时针方向旋转 度,能够与 重合 ∴ACD ≌ (旋转变换的性质) ∴AD BE =( ).五、综合题21.如图,已知110AOB ∠=︒,OC 在AOB ∠内部,OD 在BOC ∠的内部,40COD ∠=︒.(1)若50AOC ∠=︒,则BOD ∠= ;若AOC x ∠=︒,则BOD ∠= (用含x 的代数式表示);(2)若2AOD BOC ∠=∠,求AOC ∠的度数;(3)将AOC ∠以OC 为折痕进行翻折,OA 落在OE 处,将BOD ∠以OD 为折痕进行翻折,OB 落在OF 处,AOC ∠的度数变化时EOF ∠的度数是否发生变化?若变化,请说明理由:若不变,请求出EOF ∠的度数.22.如图,在边长为1个单位长度的小正方形组成的网格中.(1)把△ABC 进行平移,得到△A′B′C′,使点A 与A′对应,请在网格中画出△A′B′C′;(2)线段AA′与线段CC′的关系是 .23.如图1,AB CD 点E ,F 分别在直线CD AB ,上2BEC BEF ∠∠=,过点A 作AG BE ⊥的延长线交于点G ,交CD 于点N ,AK 平分BAG ∠,交EF 于点H ,交BE 于点M.(1)直接写出AHE FAH KEH ∠∠∠,,之间的关系:_ . (2)若12BEF BAK ∠=∠,求AHE ∠. (3)如图2,在(2)的条件下,将KHE 绕着点E 以每秒5°的速度逆时针旋转,旋转时间为t ,当KE 边与射线ED 重合时停止,则在旋转过程中,当KHE 的其中一边与ENG 的某一边平行时直接写出此时t 的值.参考答案与解析1.【答案】B【解析】【解答】解:千里之行,四个字中,可以看作是轴对称图形的是:里;故答案为:B .【分析】根据轴对称图形的定义逐项判断即可。
华东师大版七年级数学下册第10章《轴对称、平移与旋转》单元综合测试题及答案解析

七年级数学下册第10章《轴对称、平移与旋转》单元综合测试题一、单选题(共10题;共30分)1.下列图形既是轴对称图形又是中心对称图形的是()A. B. C. D.2.下列四个圆形图案中,分别以它们所在圆的圆心为旋转中心,顺时针旋转90°后,能与原图形完全重合的是()A. B. C. D.3.如图,△OAB绕点O逆时针旋转80°到△OCD的位置,已知∠AOB=45°,则∠AOD等于()A.55°B.45°C.40°D.35°4.如图,△ABC中,AB=6,BC=4,将△ABC绕点A逆时针旋转得到△AEF,使得AF∥BC,延长BC交AE于点D,则线段CD的长为()A.4B.5C.6D.75.如果齿轮A以逆时针方向旋转,齿轮E旋转的方向()A.顺时针B.逆时针C.顺时针或逆时针D.不能确定6.如图,△ACD和△AEB都是等腰直角三角形,∠CAD=∠EAB=90°,四边形ABCD是平行四边形,下列结论错误的是()A.沿AE所在直线折叠后,△ACE和△ADE重合B.沿AD所在直线折叠后,△ACE和△ADE重合C.以A为旋转中心,把△ACE逆时针旋转90°后与△ADB重合D.以A为旋转中心,把△ACE逆时针旋转270°后与△ADB重合7.如图,在3×3的网格中,与ABC成轴对称,顶点在格点上,且位置不同的三角形有()A.5个B.6个C.7个D.8个8.如图,在方格纸中,△ABC经过变换得到△DEF,正确的变换是()A.把△ABC绕点C逆时针方向旋转90°,再向下平移2格B.把△ABC绕点C顺时针方向旋转90°,再向下平移5格C.把△ABC向下平移4格,再绕点C逆时针方向旋转180°D.把△ABC向下平移5格,再绕点C顺时针方向旋转180°9.如图,矩形纸片ABCD中,AB=4,BC=6,将△ABC沿AC折叠,使点B落在点E处,CE交AD于点F,则DF的长等于()A. B. C. D.10.如图,在4×4的正方形网格中,△MNP绕某点旋转一定的角度,得到△M1N1P1.则其旋转中心一定是点()A.A点B.B点C.C点D.D点二、填空题(共8题;共24分)11.线段、两相交直线、角、等腰三角形、等边三角形、平行四边形、矩形、菱形、正方形、圆等图形中是中心对称图形的有:________.12.正六边形可以看成由基本图形________经过________次旋转而成.13.把汉字“目”绕其中心旋转90°后,所得图形与汉字________相似.14.如图,△ABC中,,,点D,E分别在线段,上,将沿直线DE翻折,使B落在处,,分别交AC于F,G.若,则的度数为________.15.如图所示,直径为4cm的⊙O1平移5cm到⊙O2,则图中阴影部分面积为________cm2.16.如图,Rt△ABC中,∠B=90°,AB=3cm,AC=5cm,将△ABC折叠,使点C与A重合,得折痕DE,则△ABE的周长等于________cm。
新苏教版数学四下第一单元《平移、旋转和轴对称》测试题

《平移、旋转和轴对称》测试题一、细心填写。
(第2题2分.其余每空1分,共16分)1、从3时到6时,时针旋转了( )o。
2、在字母A、B、C、D、E、F、G、H、I、J、K中可以看作轴对称图形的是( )。
3、(1)小帆船先向( )平移了( )格,再向( )平移了( )格。
(2)小十字先向( )平移了( )格,再向( )平移了( )格。
4、从中午12:00到下午3:00,时针旋转了( )o;从中午12:00到12:15分,分针旋转了( )0;从( )到( ),时针旋转了1800.5、等腰梯形有( )条对称轴。
二、谨慎选择。
(每题2分,共14分)1、下面图形不是轴对称图形的是( )。
A、长方形B、等腰梯形C、平行四边形2、在下面四种轿车标志中,( )不是轴对称图形。
3、下列说法正确的是( )。
A、旋转不改变图形的形状和大小B、平移改变图形的形状和大小C、等腰三角形有三条对称轴4、下面的图形中,对称轴条数最多的是( )。
A、正方形B、圆 C.等边三角形5、下面的图形中,可以由“基本图形”平移得到的是( )A、 B、 C、6A、正三角形B、圆C、梯形7、将右图绕点A顺时针旋转900后是( )。
A、 B、 C、三、判断是非。
(每题2分,共10分)1、钟面上的针都是顺时针方向旋转的。
()2、圆、平行四边形、正五边形不都是轴对称图形。
()3、门的运动都是旋转。
()4、圆有无数条对称轴,长方形有4条对称轴。
()5、将新的红领巾对折后能重合。
()四、动手操作。
(共20分)1、下面的图形是轴对称图形吗如果是,2、画出每个图形的对称轴,数一数,画出对称轴,看看可以画几条。
(6分)各画了几条,并填在括号内。
(4分)()()()3、画出左面每个图形的另一半,使它们成为轴对称图形。
(3分)4、(1)画出小亭子向下平移4格后的图形。
(1分)(2)小红旗先向上平移j格.再向右平移4格后移到了现在的位置,画出小红旗原来的位置。
(2分)5、画一画。
华师大数学七年级下册《第10章轴对称、平移与旋转》单元测试卷含试卷分析答题技巧

七年级下册单元测试卷班级姓名第10章轴对称、平移与旋转[时间:90分钟分值:120分]一、选择题(每题3分,共30分)1.[2018·淄博]下列图形中,不是轴对称图形的是()A B C D2.如图的方格纸中,左边图形到右边图形的变换是()A.向右平移7格B.以AB的垂直平分线为对称轴作轴对称变换,再以AB 为对称轴作轴对称变换C.绕AB的中点旋转180°,再以AB为对称轴作轴对称D.以AB为对称轴作轴对称,再向右平移7格3.[2016·长沙模拟]如图,△ABC≌△DEC,则不能得到的结论是()A.AB=DEB.∠A=∠DC.BC=CDD.∠ACD=∠BCE4.如图,△ABC与△DEF关于直线MN成轴对称,则以下结论错误的是()A.AB∥DFB.∠B=∠EC.AB=DED.AD的连线被MN垂直平分5.[2017·崇仁校级模拟]如图,∠A=70°,O是AB上一点,直线OD与AB所夹的∠BOD=82°.要使OD∥AC,直线OD绕点O按逆时针方向至少旋转()A.8°B.10°C.12°D.18°6.[2015·成都模拟]如图,△ABC沿边BC所在直线向右平移得到△DEF,则下列结论错误的是()A.△ABC≌△DEFB.AC=DFC.AB=DED.EC=FC7.[2017·萧山模拟]将一张正方形纸片按如图步骤①、②,沿虚线对折两次,然后沿③中的虚线剪去一个角,展开铺平后的图形为()A B C D8.[2016·哈尔滨模拟]如图,将△ABC纸片绕点A按逆时针方向旋转某个角后得到△AEF,CB、AF的延长线交于点D,AE∥CB,∠D=40°,则∠BAC的度数为()A.30°B.40°C.50°D.60°9.如图,△ABC≌△ADE,∠B=20°,∠E=110°,∠EAB=30°,则∠BAD的度数为()A. 80°B. 110°C. 70°D. 130°10.[2018春·商水县期末]如图,点P在∠MON的内部,点P关于OM、ON的对称点分别为A、B,连结AB,交OM 于点C,交ON于点D,连结PC、PD.若∠MON=50°,则∠CPD=()A.70°B.80°C.90°D.100°二、填空题(每题4分,共24分)11.[2018秋·宁河县期中]把图中的风车图案,绕着它的中心O旋转,旋转角至少为____度时,旋转后的图形能与原来的图形重合.12.[2018春·农安县期末]如图,将锐角△ABC绕点B按顺时针方向旋转35°,得到△A′BC′.若A′C′⊥BC于点D,则∠C的度数是____.13.[2018春·鄄城县期末]某同学从平面镜里看到镜子对面的电子钟的示数如图所示,这时的实际时间是__________.14.如图,正方形ABCD经平移后成为正方形CEFG,其平移的方向为_________________________________的方向,平移的距离为线段______________________________的长;正方形CEFG也能看成是正方形ABCD经过旋转得到的,它的旋转中心为点_______,旋转角度为______.15.如图,将△OAB绕着点O逆时针连续旋转两次得到△OA″B″,每次旋转的角度都是50°.若∠B″OA=120°,则∠AOB=_______.16.如图,某住宅小区内有一长方形地块,若在长方形地块内修筑同样宽的两条“之”字路,余下部分绿化,道路的宽为2 m,则绿化的面积为_______ m2.三、解答题(共66分)17.(9分)如图,∠A=90°,点E为BC上一点,点A 和点E关于BD对称,点B和点C关于DE对称,求∠ABC 和∠C的度数.18.(9分)[2018·温州]如图,P、Q是方格纸中的两格点,请按要求画出以PQ为对角线的格点四边形.(1)在图1中画出一个面积最小的P AQB;(2)在图2中画出一个四边形PCQD,使其是轴对称图形而不是中心对称图形,且另一条对角线CD由线段PQ以某一格点为旋转中心旋转得到.图1图219.(12分)如图,已知△ABC≌△DEF,∠A=30°,∠B =50°,BF=2,求∠DFE的度数和EC的长.20.(12分)[2018秋·濮阳县期中]如图,已知△ABC≌△DBE,点D在AC上,BC与DE交于点P.若AD =DC=2.4,BC=4.1.(1)若∠ABE=162°,∠DBC=30°,求∠CBE的度数;(2)求△DCP与△BPE的周长和.21.(12分)[2018春·黄陂区月考]如图1,将线段AB平移至CD,使A与D对应,B与C对应,连结AD、BC.(1)填空:AB与CD的关系为______________________,∠B与∠D的大小关系为__________;(2)如图2,若∠B=60°,F、E为BC的延长线上的点,∠EFD=∠EDF,DG平分∠CDE交BE于G,求∠FDG;(3)在(2)中,若∠FDG=α,其他条件不变,则∠B=_______.图1图2 22.(12分)如图1,将△ABC绕顶点A顺时针旋转得到△AB′C′,若∠B=30°,∠C=40°.(1)当△ABC当顺时针旋转至少多少度时,旋转后的△AB′C′的顶点B′与原三角形的顶点C和A在同一直线上(如图2)?(2)在(1)的基础上,再继续旋转至少多少度时,点C、A、C′在同一直线上(如图3)?图1图2图3参考答案1.C【解析】选项A、B、D均可以沿一条直线折叠,图形左、右或上、下两部分可以重合,故均为轴对称图形,只有C选项不是轴对称图形.2.D3.C4.A【解析】AB与DF不一定平行,故A项错误;△ABC 与△DEF关于直线MN成轴对称,则∠B=∠E,AB=DE,点A与点D是对应点,AD的连线被MN垂直平分,故B、C、D项正确.5.C【解析】∵AC∥OD′,∴∠BOD′=∠A=70°,∴∠DOD′=∠BOD-∠BOD′=82°-70°=12°.6.D7.D8.B【解析】∵EA∥CB,∴∠EAD=∠D=40°,∴由旋转的性质可知∠BAC=∠EAD=40°.9.A【解析】∵△ABC≌△ADE,∠B=20°,∴∠D=∠B=20°.在△ADE中,∠DAE=180°-∠D-∠E=180°-20°-110°=50°,∴∠BAD=∠DAE+∠EAB=50°+30°=80°.10.B【解析】如答图,连结OA、OB、OP,设P A与OM交于点E,PB与ON交于点F.∵点P关于OM、ON的对称点分别为A、B,∴OA=OP=OB,CA=CP,DP=DB,∠AOC=∠COP,∠POD=∠DOB,∴∠AOB=∠AOC+∠COP+∠POD+∠DOB=2∠COD=100°,∴∠OAB=∠OBA=12(180°-∠AOB)=40°.设∠COP=α,∠DOP=β,则α+β=50°.∵OA=OP,∠AOP=2α,∴∠OP A=∠OAP=12(180°-2α)=90°-α.∵∠OAB=40°,∴∠CP A=∠CAP=∠OAP-∠OAB=50°-α.同理,∠DPB=50°-β.∵∠EPF=360°-∠EOF-∠OEP-∠OFP=360°-50°-90°-90°=130°,∴∠CPD=∠EPF-(∠CP A+∠DPB)=130°-(50°-α+50°-β)=30°+(α+β)=80°.11.9012.55°【解析】∵将锐角△ABC绕点B按顺时针方向旋转35°,得到△A′BC′,∴∠CBC′=35°,∠C=∠C′.∵A′C′⊥BC于点D,∴∠BDC′=90°,∴∠C′=90°-35°=55°,∴∠C=∠C′=55°.13.10:5114.射线AC(答案不唯一,写出一个即可)AC(答案不唯一,写出一个即可) C 180°15.20°【解析】∵∠AOA′=∠A″OA′=∠BOB′=∠B′OB″=50°,∴∠B″OB=100°.∵∠B″OA=120°,∴∠AOB=∠B″OA-∠B″OB=120°-100°=20°.16.540【解析】如答图,把两条“之”字路平移到长方形地块ABCD的最上边和最左边,则余下部分EFCG是长方形,根据长方形的面积公式即可求出结果.∵CF=32-2=30(m),CG=20-2=18(m),∴长方形EFCG的面积=30×18=540(m2).故绿化的面积为540 m2.17.解:∵点A和点E关于BD对称,∴∠ABD=∠EBD,即∠ABC=2∠ABD=2∠EBD.又∵点B和点C关于DE对称,∴∠EBD=∠C,∴∠ABC=2∠C.∵∠A=90°,∴∠ABC+∠C=2∠C+∠C=3∠C=90°,∴∠C=30°,∴∠ABC=2∠C=60°.18.解:(1)画法不唯一,如答图1所示:答图1(2)画法不唯一,如答图2所示:答图2 19.解:∵∠A=30°,∠B=50°,∴∠ACB=180°-∠A-∠B=180°-30°-50°=100°.∵△ABC≌△DEF,∴∠DFE=∠ACB=100°,EF=BC,∴EF-CF=BC-CF,即EC=BF.∵BF=2,∴EC=2.20.解:(1)∵∠ABE=162°,∠DBC=30°,∴∠ABD+∠CBE=132°.∵△ABC≌△DBE,∴∠ABC=∠DBE,∴∠ABD=∠CBE=132°÷2=66°.即∠CBE的度数为66°.(2)∵△ABC≌△DBE,∴DE=AD+DC=4.8,BE=BC=4.1,∴△DCP和△BPE的周长和=DC+DP+CP+BP+PE +BE=DC+DE+BC+BE=15.4.21.(1) AB∥CD,且AB=CD相等(3) 2α【解析】(1)AB∥CD,且AB=CD,∠B与∠D相等.解:(2)∵AB∥CD,∴∠DCE=∠B.由三角形的外角性质,得∠CDF=∠DFE-∠DCE,∴∠CDG=∠CDF+∠FDG=∠DFE-∠DCE+∠FDG.∵在△DEF中,∠DEF=180°-2∠DFE,在△DFG中,∠DGF=180°-∠FDG-∠DFE,∴∠EDG=∠DGF-∠DEF=180°-∠FDG-∠DFE-(180°-2∠DFE)=∠DFE-∠FDG.∵DG平分∠CDE,∴∠CDG=∠EDG,∴∠DFE-∠DCE+∠FDG=∠DFE-∠FDG,∴∠FDG=12∠DCE,即∠FDG=12∠B.又∵∠B=60°,∴∠FDG=12×60°=30°.【解析】(3)思路同(2).∵∠FDG=α,∴∠B=2α.22.解:(1)∵∠B=30°,∠C=40°,∴∠BAC=180°-∠B-∠C=110°.∵将△ABC绕其顶点A顺时针旋转,旋转后的△AB′C′的顶点B′与原三角形的顶点C和A在同一直线上,∴∠BAB′=110°,∴需要旋转至少110°.(2)若在(1)的基础上,再继续旋转,使点C、A、C′在同一直线上,则旋转后∠BAB′=180°,∴∠CAB′=180°-110°=70°.即在(1)的基础上,再继续旋转至少70°时,点C、A、C′在同一直线上.。
【苏教版】三年级上册数学6.平移、旋转和对称轴测试卷_含答案
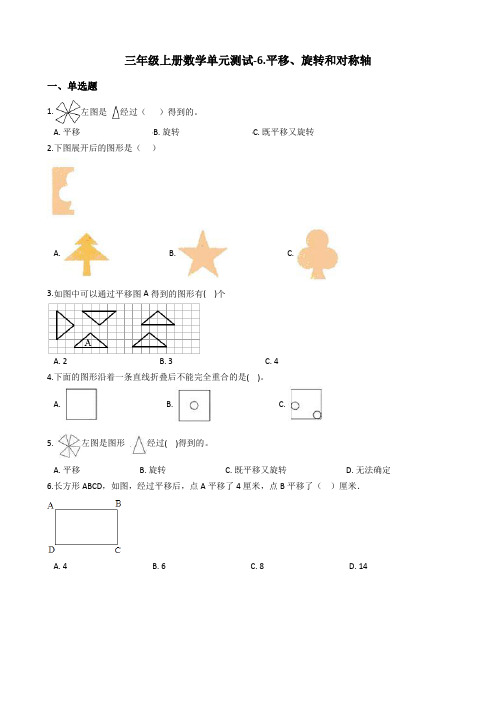
三年级上册数学单元测试-6.平移、旋转和对称轴一、单选题1.左图是经过()得到的。
A. 平移B. 旋转C. 既平移又旋转2.下图展开后的图形是()A. B. C.3.如图中可以通过平移图A得到的图形有( )个A. 2B. 3C. 44.下面的图形沿着一条直线折叠后不能完全重合的是( )。
A. B. C.5.左图是图形经过( )得到的。
A. 平移B. 旋转C. 既平移又旋转D. 无法确定6.长方形ABCD,如图,经过平移后,点A平移了4厘米,点B平移了()厘米.A. 4B. 6C. 8D. 147.将一张正方形的纸连续对折两次(有不同的折法),并在折后的纸中央打一个圆孔,再将纸展开,得到下面不同的图形。
请为下面的折法选择展开后的图形:展开后是()。
A. B. C. D.二、判断题8.旋转改变了图形的大小和形状。
9.一棵小树被扶种好,这棵小树一定绕树脚逆时针方向旋转了90度。
10.将等边三角形绕着中心点旋转120°后,不能与原来的图形重合。
11.火箭升空,是旋转现象。
12.公共汽车出站是平移现象,开冰箱门是旋转现象。
三、填空题13.电风扇扇叶的运动是________现象;拉抽屉现象是________现象.(填“旋转”或者“平移”)14.如图,指针从A开始,顺时针旋转了90°到________点,逆时针旋转了90°到________点;要从A旋转到C,可以按________时针方向旋转________°,也可以按________时针方向旋转________°。
15.汽车沿着直线行驶时,车轮做________运动,车身做________运动.16.电梯的升降属于________现象,汽车行驶时的车轮转动属于________现象.17.平移和旋转都是物体的运动方式,如________、________是平移现象,________、________是旋转现象。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
轴对称、平移与旋转单元测试题
1.如果一个图形沿着一条直线对折,两侧的图形能够完全重合,这样的图形就叫()图形,那条直线就是()。
2.正方形有()条对称轴.
3.移一移,说一说.
(1)向()平移了()格(2)向()平移了()格(3)向()平移了()格4.长方形有条对称轴,圆有条对称轴,正方形有()条对称轴.
A.1
B.2
C.3
D.4 E.无数.
5.你能画出如图所示图形所有的对称轴吗?如果能,请画出来,并填在()里填上适当的数.
三、解答题(共1小题,满分9分)
6.请画出对称图形的另一半.
四、判断对错.(8分)
7.正方形是轴对称图形,它有4条对称轴()。
8.圆不是轴对称图形()。
9.利用平移、对称可以设计许多美丽的图案()。
10.风吹动的小风车是平移现象()。
五、用心选.(6分)
11.下面的图形中,()不能由???通过平移或旋转得到.。
