半导体的霍尔效应
半导体物理基础霍尔效应

离子注入造成的杂质浓度分布曲线一般如下:
浓 度
深度
深度
特点:①杂质浓度最高处位于体内; ②在注入后一般要采取加热圆片(退火)的方法, 来消除损伤和激活注入杂质
离子注入工艺示意图:
衬底
生长外延层 制作掩膜 刻蚀 离子注入掺杂
【实验】
磁场对运动电荷有力的作用——这个力叫洛仑兹力。
【推理与猜想】 磁场对电流有安培力的作用,而电流是由电荷定向运动
扩散工艺所得杂质分布总是表面浓度高、体内浓度低,而 且对扩散系数太低的杂质难于得到要求的杂质浓度。离子 注入工艺可以很好的解决以上问题。
离子注入工艺原理:
在真空中,由高压使杂质离子加速,射向硅表面,加速后 的离子动能很高,能够进入硅中实现掺杂。
离子注入工艺掺杂后其杂质分布特点:
在离开表面一定距离处杂质浓度最高,在其附近呈高斯分 布。如下页图:
• 扩散的方法(扩散工艺)
• 离子注入法
扩 散 工 艺
在物理中我们学过,由于分子热运动和浓度差,在气体、 液体和固体中,都会产生扩散现象。扩散现象在气体和液 体中尤其明显。
那么在硅片中进行掺杂的原理和上面基本一样,可以简单 的画图描述一下,见黑板
扩散工艺造成的杂质浓度分布曲线一般如下:
浓 度 体浓度
形成的。所以磁场对电流的安培力可能是磁场对运动电荷的
作用力的宏观表现。即: 1.安培力是洛伦兹力的宏观表现.
2.洛伦兹力是安培力的微观本质。
一.洛伦兹力的方向
洛伦兹力的方向符合左手定则: ——伸开左手,使大拇指跟其余四指垂直,且处于同一平 面内,把手放入磁场中,磁感线垂直穿过手心,四指指向 正电荷运动的方向(即电流方向),那么,拇指所指的方向 就是正电荷所受洛伦兹力的方向. 若是负电荷运动的方向,那么四指应指向其反方向。
半导体霍尔效应

4
6V 6 降
AC220V
E 2 3 4 5
K3
压 流
A V Ka
接电压表 100Ω 或电位计 mA 取样电阻
整
K1
1
K2
控制部分 36V~5V
其中:样品"1、3","2、4"为电阻率电极, "3、4"为霍尔电极 图 6-6 长条、范德堡法霍尔装置图
二、实验内容
(1) 在预习实验内容基础上设计一套电路,其中包括 B 换向,I 换向待测电压等并列表。 (2) 测Ge长条样品的ρ和RH值。样品电流分别取代 0.5mA、0.8mA两个值,测RH时,B用 1000GS。 (3) 用范德堡法测Si薄片半导体样品ρ和RH值,样品电流取 0.5mA,0.8mA两个值,测RH 时, B取 1000~2000GS。 (4)用范德法测薄片样品的磁阻,样品电流在 0.2mA 取值。
v I
cd ab
压表测另一对接点C、D的电位差Vcd , 由此得出RAB,CD= 流,测D、A间电位差VDA,也同样得到RBC,DA= 样品电阻率ρ与R1、R2构成如下关系: exp(- πρd ⋅ R 1 ) + exp( 式中 d 为样品厚度,由此得到电阻率公式: R ⋅d R + R ρ=π ⋅ ⋅ f ( 2 R ) Ιn 2
对于 Ge,晶格散射时为: (
μH μ
(
μH μ
) P = 1.84
对Байду номын сангаас简并半导体和强磁条件时
=1
在本征导电范围内即电子空穴同时参与导电的情况下则有: σ=po·q·µp + no·q·µn 式中σ为导电率 b = μ n p RH =(
半导体霍尔效应实验

东南大学材料科学与工程实验报告 学生姓名 徐佳乐 班级学号 12011415 实验日期 2014/9/4 批改教师 课程名称 电子信息材料大型实验 批改日期 实验名称 半导体霍尔效应实验 报告成绩一、 实验目的1、 了解半导体中霍尔效应的产生原理,霍尔系数表达式的推导。
2、 掌握霍尔系数和电导率的测量方法。
3、 通过测量数据的处理判别样品的导电类型,计算室温下所测半导体材料的霍尔系数、电导率、载流子浓度和霍尔迁移率。
二、 实验原理霍尔效应的测量是研究半导体性质的重要实验方法。
利用霍尔效应,可以确定半导体的导电类型和载流子浓度。
利用霍尔系数和电导率的联合测量,可以用来研究半导体的导电机制(本征导电和杂质导电)和散射机制(晶格散射和杂质散射),进一步确定半导体的迁移率、禁带宽度、杂质电离能等基本参数。
测量霍尔系数随温度的变化,可以确定半导体的禁带宽度、杂质电离能及迁移率的特性。
1、 霍尔效应和霍尔系数设一块半导体的x 方向上有均匀的电流流过,在z 方向上加有磁场,则在这块半导体的y 方向上出现一横向电势差,这种现象被称为“霍尔效应”, 称为“霍尔电压”,所对应的横向电场称为“霍尔电场”。
霍尔电场强度的大小与流经样品的电流密度和磁感应强度的乘积成正比:ZX H H B J R E ••=式中比例系数称为“霍尔系数”。
半导体样品的长、宽、厚分别为l 、a 、b ,半导体载流子(空穴)的浓度为p ,它们在电场作用下,以平均漂移速度沿x 方向运动,形成电流。
在垂直于电场方向上加一磁场,则运动着的载流子要受到洛仑兹力的作用该洛仑兹力指向-y 方向,因此载流子向-y 方向偏转,这样在样品的左侧面就积累了空穴,从而产生了一个指向+y 方向的电场——霍尔电场。
当该电场对空穴的作用力q 与洛仑兹力相平衡时,空穴在y 方向上所受的合力为零,达到稳态。
在稳态时,有 :若是均匀的,则在样品左、右两侧面间的电位差:而x 方向的电流: 由以上的式子得: 所以对p 型半导体: n 型半导体: 所以的计算式: 2、 半导体电导率半导体电导率:电导率测试公式:结合电导率和霍尔系数的测量,可以计算载流子的迁移率: 实验得出与温度T 的关系曲线如图1.现在以p 型半导体为例分析:(1) 低温区。
半导体的磁效应之一:霍尔效应

两种载流子同时存在时的霍尔系数
• 在磁场作用下电子与空穴的横向运动方向是 相同的,它们引起的横向电流的大小
jt jntg njptg p(njnpjp)B (ne n 2pe 2 p)B0E
• 积累在两侧的电荷产生的霍耳电场引起的电
• 平衡时的横向电场称为霍耳电场,两侧的电势 差称为霍尔电势。
半导体的磁效应之一:霍尔效应
霍尔效应的定量分析
• 1、霍耳系数
• 当霍耳电场引起的力与磁场引起的力最后达到 平衡时,我们有
EvB1(n ev)B1jBR jB
n e
n e
• 由此我们得到一个十分重要的公式。即霍耳电 势与流过样品的电流大小及磁场强度成正比, 比例系数称为霍耳系数,对电子R=-1/ne,对空 穴为R=1/pe。
Rn
hn
1
ne• ,Rp
hp
1 pe
相应的霍耳角、霍耳电势等也要进行修改。
半导体的磁效应之一:霍尔效应
霍尔迁移率
• 对简单能带结构的半导体材料,Rn与Rp 不必修正。
• 由半导体的能带结构可以算出霍耳迁移
率与一般迁移率的比值,它们为
对声学波散射h
3
8
,对电离杂质散射
h
1.9
3,对简并半导体h
半导体的磁效应之一:霍尔效应
2、霍尔角
• 在无磁场时,载流子的漂移运动方向与电流方向相同 或相反,但两者没有夹角(0或180)。
• 磁场引起附加电场,使得载流子的运动方向与外场的 方向有一个夹角,此夹角称为霍耳角。
• 霍耳角的正切应等于霍耳电场与外场的比值, 即tgEh RjBRB,若霍尔电场较小,
实验三 半导体霍尔效应测量实验
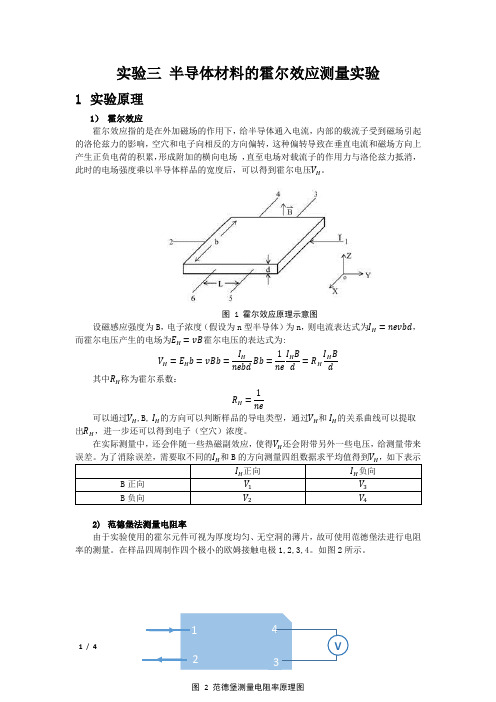
实验三半导体材料的霍尔效应测量实验1实验原理1)霍尔效应霍尔效应指的是在外加磁场的作用下,给半导体通入电流,内部的载流子受到磁场引起的洛伦兹力的影响,空穴和电子向相反的方向偏转,这种偏转导致在垂直电流和磁场方向上产生正负电荷的积累,形成附加的横向电场,直至电场对载流子的作用力与洛伦兹力抵消,此时的电场强度乘以半导体样品的宽度后,可以得到霍尔电压V H。
设磁感应强度为B,电子浓度(假设为n型半导体)为n,则电流表达式为I H=nevbd,而霍尔电压产生的电场为E H=vB霍尔电压的表达式为:V H=E H b=vBb =I HnebdBb =1neI H Bd=R HI H Bd其中R H称为霍尔系数:R H=1 ne可以通过V H,B, I H的方向可以判断样品的导电类型,通过V H和 I H的关系曲线可以提取出R H,进一步还可以得到电子(空穴)浓度。
在实际测量中,还会伴随一些热磁副效应,使得V H还会附带另外一些电压,给测量带来误差。
为了消除误差,需要取不同的I H和B的方向测量四组数据求平均值得到V H,如下表示I H正向I H负向B正向V1V3B负向V2V42)范德堡法测量电阻率由于实验使用的霍尔元件可视为厚度均匀、无空洞的薄片,故可使用范德堡法进行电阻率的测量。
在样品四周制作四个极小的欧姆接触电极1,2,3,4。
如图2所示。
14图 1 霍尔效应原理示意图先在1、2端通电流,3、4端测电压,可以定义一个电阻R1=|V34| I12然后在2、3端通电流,1、4端测电压,求R2=|V14| I23理论上证明样品的电阻率与R1、R2的关系为ρ=πdln2R1+R22f可以通过查表可知范德堡因子f与R1/R2的关系,从而求得样品的电阻率。
2实验内容本实验所用仪器为SH500-A霍尔效应实验仪、恒流电源、高斯计。
实验步骤如下:1)连线掌握仪器性能,连接恒流电源与霍尔效应试验仪之间的各组连线。
2)测量霍尔系数,判断样品的导电类型测量半导体样品的霍尔系数。
半导体霍尔效应研究

半导体霍尔效应研究一、实验目的1.了解半导体中霍尔效应产生的物理过程。
2. 掌握霍尔系数和电导率和测量方法,通过对常温下霍尔系数的测定,确定半导体材料的导电类型和掺杂浓度;了解霍数随温度的变化。
3.了解实验环境条件下可能产生的副效应及其消除方法。
二、实验仪器HL-6A霍尔效应仪、C5特斯拉计三、实验原理与方法(一)霍尔效应如图14-1所示,在一块矩形半导体样的X方向均匀地通以电流Ix,处于同一等势面上的A.B两点间的电位差为零;但若在Z方向加上磁场Bz时,则A.B两点将产生电势差 V ,这一现象称为霍尔效应。
其因为由美国物理学家霍尔研究载流导体在磁场中导电的性质发现而得名。
Z yB Z Y X14-1霍尔效应示意图图14-2 P型半导体的霍尔效应为什么会产生霍尔电势差?假设一块P型半导体宽度为 a,厚度为 b,如图14-2所示。
我们首先讨论其中没有温度梯度且只有一种载流子,所有载流子都具有相同的漂移速度,磁场不太强不考虑磁阻的情况。
令V为空穴速度,P为空穴浓度,p为空穴迁移率。
磁场为Z方向,电流为X方向,电流密度为J。
此时沿X方向运动的空穴在磁场B作用下,受洛沦磁力作用使之横向偏转。
由于样品有边界,有些偏转的载流子在边界累积,产生一横向电场E,我们称之为霍尔电场。
霍尔电势差即由此电场而建立。
这时空穴受力为洛沦磁力与电场力的矢量和:F=e(E+V×B) (14-1)达到稳态时,空穴所受的横向电场力与洛沦磁力恰好抵消,即e(v×B)= eE ( 14-2 )又通过样品的电流为I=pevab则空穴的速度为v=I/peab代入(14-2)式得E==两边同乘以a得V=(14-3)系数=R我们称之为霍尔系数。
又因为电流强度I=J.ab ,V=E a , 故有 V=R..a=R R=(14-4)如果是N型半导体,这时电子沿-X方向运动,在磁场B的作用下受到指向-y方向的洛沦磁力,这样载流子在边缘的累积,在-Y 方向建立霍尔电场E,同理我们可以导出E=-JB R== (n为电子浓度) (14-5)(为电子浓度)(14-5)我们在实验中只要能测出样品电流I,磁场强度B,样品厚度 b及霍尔电位差V,就可以求出霍尔系数R。
半导体物理实验——半导体霍尔效应

实验报告
一、实验目的和任务
1.理解霍尔效应的物理意义;
2.了解霍尔元件的实际应用;
3.掌握判断半导体导电类型,学会测量半导体材料的霍尔系数、电导率、载流子浓度、漂移迁移率及霍
尔迁移率的实验方法。
二、实验原理
将一块宽为2a,厚为d,长为b的半导体样品,在X方向通以均匀电流I X,Z方向上加有均匀的磁场B z 时(见图1.1所示),则在Y方向上使产生一个电势差,这个电势差为霍尔电势差,用U H表示,这种现象就称为霍尔效应。
图 2.1
与霍尔电势对应的电场,叫做霍尔电场,用E Y表示,其大小与电流密度J X和所加磁场强度B z成正比,可以定义如下形式:
E Y = R H·B Z·J X(1)
上式中,R H为比例系数,称为霍尔系数。
霍尔效应的物理意义可做如下解释:半导体中的电流是载流子(电子或空穴)的定向动动引起的,一人以速度υx运动的载流子,将受到沦仑兹力f B = e υx B Z的作用,使载流子沿虚线方向偏转,如图1.2所示,并最后堆积在与Y轴垂直的两个面上,因而产生静电场E Y,此电场对载流子的静电作用力f E=e E Y,它与磁场对运动载流子的沦仑兹力f B大小相等,电荷就能无偏离地通过半导体,因而在Y方向上就有一个恒定的电场E Y。
半导体霍尔效应实验

(1)低温区。在低温区杂质部分电离,杂质电离产生的载流子浓度随温度升高而增加,而且 在低温下主要取决于杂质散射,它也随温度升高而增加。因此, 随T的增加而增加。见图的a段。室温附近,此时杂质已全部电离,载流子浓度基本不变,这时晶格散射起主要作用,使 随T的升高而下降,导致 随T的升高而下降,见图的b段。
将测量样品杆放入电磁铁磁场中(对好位置)。
打开电脑桌面HT648型变温霍尔效应控制程序,进入数据采集状态,选择电压曲线。如果没有进入数据采集状态,则按一下《Ⅰ》复位开关后进入数据采集状态。记录磁场电流正反向的霍尔电压 记录测试所得霍尔电压和霍尔系数数值。
将《Ⅱ》<测量选择>拨至 ,记录电流正反向的电压 记录所得样品的电导率。
(2) 高温区。在这段区域中,本征激发产生的载流子浓度随温度升高而指数地剧增,远远超过 的下降作用,使 随T而迅速增加,如图的c段。
3、 霍尔系数和温度的关系
电子空穴混和半导体材料的霍尔系数表达式:
A:为霍尔因子;b:为电子和空穴迁移率的比,大于1。
霍尔系数与温度的关系如图2:
A:n型半导体 B:p型半导体
1ቤተ መጻሕፍቲ ባይዱ 霍尔效应和霍尔系数
设一块半导体的x方向上有均匀的电流 流过,在z方向上加有磁场 ,则在这块半导体的y方向上出现一横向电势差 ,这种现象被称为“霍尔效应”, 称为“霍尔电压”,所对应的横向电场 称为“霍尔电场”。
霍尔电场强度 的大小与流经样品的电流密度 和磁感应强度 的乘积成正比:
式中比例系数 称为“霍尔系数”。
当该电场对空穴的作用力q 与洛仑兹力相平衡时,空穴在y方向上所受的合力为零,达到稳态。在稳态时,有 :
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
E J
Bz=0,=x
Bz0
§4-5 半导体的霍尔效应
一、P型半导体霍尔效应
1. P型半导体霍耳效应的形成过程
z
y x Bz B
d
I
+
○
fεx
εy
b VH
_
fL
f A
l
qεy
电场力:fε=qεx
磁场力:fL=qVxBz y方向的电场强度为:εy
fL
fεx
平衡后: q y
fL 0
q y f L qV x B z
(1) 本征半导体:n=p=ni
1 b 1 b RH 2 qni (1 b) qni (1 b)
2
RH
(-)
1/T
(2) p型半导体
RH
(+) ( -) (-) (+)
1/T
(3) N 型半导体
RH
(-) (-)
1/T
四、霍尔效应的应用
1.判别极性,测半导体材料的参数
2.霍尔器件
B n y 2 n x
稳定时,横向电流为 0
J y (J p ) y (Jn ) y 0
(nqn pq p ) y (nq pq ) x Bz 0
2 n 2 p
y
p n
2 p
2 n
p p n n
x Bz
J x ( J p ) x ( J n ) x ( pq p nqn ) x
y : qVx Bz
达到稳定时:
q y qVx Bz
V<Vx的空用的方向
εx
V<Vx
vx V>Vx
l
qεy
f
2.同时考虑两种载流子
Bz=0、=x 时, 电子逆电场方向运动,形成电场方向电流Jn
空穴沿电场方向运动,形成电场方向电流Jp 总电流:J0=Jn+Jp
y J x Bz
3.探测器
§4.6 半导体的磁阻效应
由于磁场的存在引起电阻的增 加,称这种效应为磁阻效应。
一、磁阻效应的类型
纵向磁阻效应:
按电磁场的关系分
B//,磁阻变化小,不产生VH
横向磁阻效应:
B,磁阻变化明显,产生VH
按机理分:
由于电阻率变化引起的R变化 —物理磁阻效应
l R s
1 p n y q p p n n
2 p
2 n
2
J x B z J x Bz
2 n
1 p n RH q p p n n
2 p
2
令:
b n p
1 ( p nb ) RH 2 q ( p nb)
2
2.RH 与 T 的关系
1.霍尔效应的形成过程及霍尔系数 RH
有四种横向电流分量:
● 空穴在磁场力作用下,漂移运动发生偏转, B J 使电流产生横向分量,形成的横向电流 py ;
● 电子在磁场力作用下,漂移运动发生偏转, B J 使电流产生横向分量,形成的横向电流 ny ;
● 电子和空穴在 y 方向霍尔场作用下形成的
J J 电流 py , ny
(1) y 方向的空穴电流密度(Jp)y
( J p ) y ( J ) ( J p ) y pq p y pq Bz
B p y 2 p x
(2) y 方向上的电子电流密度(Jn)y
( J n ) y ( J ) ( J n ) y nq Bz nqn y
由于几何尺寸l/s的变化引起的 R变化 —几何磁阻效应
磁阻的大小:
R
或
R B R0 R0 R0
1 1
B 0 B 0 B 0 1 0 0 B 0
二、物理磁阻效应
1.一种载流子
P型:电场加在x方向,磁场在z方向
y : q y
y Vx Bz
J x pqVx Jx Vx pq
J x Bz y J x Bz pq
令:
1 ( RH ) P pq
J x Bz y ( RH ) P J x B z pq
(RH)P为P型材料的霍尔系数。
两种载流子 同时存在
霍尔效应
?
二、两种载流子同时存在时的霍尔效应
– J Jn + + +
– J
Bz
Jp
Jn
εy
Jp
– – –
+
+
(a)
(b)
此种磁阻效应表示为:
2 2 2 R H 0 0 B z 0
npb(1 b) 2 2 (nb p)
2
为横向磁阻系数
RHo为弱磁场时的霍尔系数
三、几何磁阻效应
1.长条样品(N型)
I
Bz
I E
J
