第三章动量守恒定律
动量定理及动量守恒定律

20
动量定理及动量守恒定律
oy N1 − m1g = 0 又f1max = N1μ1
以 m2 为隔离体,m2 受重力W = m2 g ;桌面的支持力 N2 ; m1 的压力 N1′ (大小与 N1 相等); m1 作用在 m2 上的最大静摩擦力 f1max′(大小与 f1max 相等) ;桌面作用在 m2 上的
oA y A W3 − TA′ − TB′ = m3a3
(7)
因为不计滑轮及绳的质量,不计轴承摩擦. 且已知绳不可伸长.
∴ TA = TB = TA′ = TB′ = T
f A ,绳的拉力 TA , A 的动力学方程为
动量定理及动量守恒定律
W1 + N A + f A + TA = m1a1 建立如图 3.5.7(1)所示的坐标系 oA − xA y A .
oA xA TA − f A = m1a1
(1)
oA y A W1 − N A = 0
(2)
且 fA = NAμ
动量定理及动量守恒定律
第三章 动量定理及动量守恒定律
(Momentum and Conservation Law of Momentum)
一、内容简介(Abstract) 1.牛顿第一定律(Newton’s first law)
孤立质点静止或作等速直线运动,即质点在不受力或所受力的合力为零时,将保持静 止或匀速直线运动状态不变.(惯性定律) 2.牛顿第三定律(Newton’s third law)
g
y
x o
N
2
α m2
a2
W2
N1′
图3.5.(5 3)
y′
N1 f∗
m1
第3章动量守恒

v = 2 gl
在其后的一小段时间dt内,对 在其后的一小段时间 内 的绳子, dm = λ dl = λ vdt 的绳子,忽略重力作 y 用,由动量定理可知 Fdt = 0 − dm ⋅ v − dm 2 ∴F = v = − λ v = − 2λ l g dt N = (m + dm) g + F ' ≈ 3λl g
L-l L
例题4 有一条单位长度质量为λ的匀质柔绳,开始 有一条单位长度质量为λ的匀质柔绳, 例题 时盘绕在光滑的水平桌面上,( ,(1 时盘绕在光滑的水平桌面上,(1)若以恒定的加速 向上提起, 时作用于绳端的力; 度a向上提起,当提起的高度为 时作用于绳端的力; 向上提起 当提起的高度为y时作用于绳端的力 若以恒定的速度v向上提起 当提起的高度为y时 向上提起, (2)若以恒定的速度 向上提起,当提起的高度为 时 F 作用于绳端的力。 作用于绳端的力。 取竖直向上为正, 解 :(1)取竖直向上为正 , 当绳加速上升 高度y 高度y时 v = 2ay a 其后一小段时间 dt 内 ,被提起的绳 被提起的绳 y 子将增加 dm = λ dy = λ vdt ,对提起 的绳子, 的绳子,由动量定理
0.2 × 10 = N + 0.2 × 9.8 N = 231N + 1.96 N ≈ 233 N 0 0.01× cos 30 由牛顿第三定律,小球对地面的平均冲力与F大 由牛顿第三定律 , 小球对地面的平均冲力与 大 小相等,方向相反。 小相等,方向相反。 解法二:用分量式求解, 解法二:用分量式求解,选水平竖直平面内直角坐标 系0xy,写出动量定理的分量式: ,写出动量定理的分量式: x方向: 0 = mv sin β − mv0 sin α 方向: 方向 y方向: ( F − mg ) ⋅ ∆t = mv cos β − (− mv0 cos α ) 方向: 方向 两式联立,消去v得 两式联立,消去 得 mv0 ( F − mg ) ⋅ ∆t = sin(α + β ) sin β 因为 α + β = 900 ,故解得 mv0 F= + mg ∆t cos α
动量定理及动量守恒定律

规定m0=1千克(kg),则有
m v 2 / v1 kg
2.动量 · 动量守恒定律 将气桌上两物体的碰撞抽象为两个质点m1和m2的相互作用, 则有
令 v10和v 20
m1v1 m2 v 2
分别表示两质点相互作用后的末速度,则
分别表示两质点相互作用前的初速度,v1和v 2
T cos d / 2 0 N T dT cos d / 2 0
因 d 很小 sin d / 2 d / 2, cos d / 2 1 得到 N Td , dT 0 N dT / T 0 d 4 , 0 0.5, T 积分得 dT / T 0 d ln T / T0 0 T0 5 N ,
d F 21 k m1 v1 dt
d , F 12 k m2 v 2 dt
式中k为常数。在SI中k=1,力的量纲为LMT-2,于是 d d F 21 m1 v1 , F 12 m2 v 2 dt dtFra bibliotek
d 或一般的可写作 F mv dt
r d Fi m dt ma 回旋加速器 (劳伦斯 1930) 2 动力学方程 qvB mv / r v qBr / m
Fin m
粒子运动半周的时间 t r / v m / qB 频率为 qB / 2 m 最早的回旋加速器
R 0.18m, B 1.7T , mD 3.35 1027 kg , q 1.6 1019 C 频率 1.3 107 H 速度 v 1.46 107 m / s z
yl 2
gt 2
第三章-动量守恒定律

cos d
R
2、求半径为 R 、顶角为 2 的均匀扇形薄板的质
心?
习题3-8
3、求质量均匀分布的半球体的质心?
解:
建立坐标系
计算 C z
dz z
由对称性可知,质心在 z 轴上 根据质心定义式 zC
设球体的体密度为
zdm dm
dm ( R 2 z 2 )dz
v10 v1 v2 v20 v10 v20 v2 v1
碰前相互接近的速度 = 碰后相互离开的速度
m1 m2 时 v1 v20 , v2 v10 m1 m2 2m1 v v , v v10 v20 0 时 1 10 2 m1 m2 m1 m2
根据质点动量定理:
t I Fdt p p0 mv mv0 0 mv0
根据平均冲力定义: F I mv0 t t m(v0 ) mv0 F t t
根据质点动能定理: mgh 1 mv 2 0
F
h
mg
m 2 gh F 3.1105 N t
2
v0 2 gh
方向向上
§ 3-2 质点系动量定理和质心运动定理
一、质点系动量定理
1、两个质点构成的质点系
研究对象 受力分析 内力:
F2
f12
2
f 21
F1
1
外力:
运动特点
t0 :
t:
分别对 应用质点动量定理
i
动量守恒定律
当外力矢量和为零时,质点系的总动量保持不变。
说明
分量守恒
第三章 动量守恒定律与能量守恒定律

第三章 动量守恒定律和能量守恒定律3-1 一架以12ms 100.3-⨯的速率水平飞行的飞机,与一只身长为0.20m 、质量为0.50kg 的飞鸟相碰。
设碰撞后飞鸟的尸体与飞机具有同样的速度,而原来飞鸟对于地面的速率很小,可以忽略不计。
估计飞鸟对飞机的冲击力,根据本题的计算结果,你对高速运动的物体与通常情况下不足以引起危害的物体相碰后产生后果的问题有什么体会?解:以飞鸟为研究对象,其初速为0,末速为飞机的速度,由动量定理。
vlt mv t =∆-=∆ ,0F 联立两式可得: N lmv F 521025.2⨯==飞鸟的平均冲力N F F 51025.2'⨯-=-=式中的负号表示飞机受到的冲击力与飞机的运动速度方向相反。
从计算结果可知N F F 51025.2'⨯-=-=大于鸟所受重力的4.5万倍。
可见,冲击力是相当大的。
因此告诉运动的物体与通常情况下不足以引起危险的物体相碰,可能造成严重的后果。
3-2 质量为m 的物体,由水平面上点O 以初速为0v 抛出,0v 与水平面成仰角α。
若不计空气阻力。
求:(1)物体从发射点O 到最高点的过程中,重力的冲量;(2)物体从发射点到落回至同一水平面的过程中,重力的冲量。
解:(1)在垂直方向上,物体m 到达最高点时的动量的变化量是:αsin 01mv P -=∆而重力的冲击力等于物体在垂直方向的动量变化量:ααsin sin 0011mv mv P I -=-=∆=(2)同理,物体从发射点到落回至同一水平面的过程中,重力的冲力等于物体竖直方向上的动量变化量αααsin 2sin sin 1222mv mv mv mv mv P I -=--=-=∆=负号表示冲量的方向向下。
3-3 高空作业时系安全带是非常必要的。
假如一质量为51.0kg 的人,在操作时不慎从高空跌落下来,由于安全带保护,最终使他悬挂起来。
已知此时人离原处的距离为 2.0m ,安全带弹性缓冲作用时间为0.50s 。
大学物理第三章动量守恒定律和能量守恒定律

动量守恒定律的表述
总结词
动量守恒定律表述为系统不受外力或所 受外力之和为零时,系统总动量保持不 变。
VS
详细描述
动量守恒定律是自然界中最基本的定律之 一,它表述为在一个封闭系统中,如果没 有外力作用或者外力之和为零,则系统总 动量保持不变。也就是说,系统的初始动 量和最终动量是相等的。
动量守恒定律的适用条件
能量守恒定律可以通过电磁学 的基本公式推导出来。
能量守恒定律可以通过相对论 的质能方程推导出来。
能量守恒定律的应用实例
01
02
03
04
机械能守恒
在无外力作用的系统中,动能 和势能可以相互转化,但总和
保持不变。
热能守恒
在一个孤立系统中,热量只能 从高温物体传递到低温物体,
最终达到热平衡状态。
电磁能守恒
详细描述
根据牛顿第三定律,作用力和反作用力大小相等、方向相反。如果将一个物体施加一个力F,则该力会产生一个 加速度a,进而改变物体的速度v。由于力的作用是相互的,反作用力也会对另一个物体产生相同大小、相反方向 的加速度和速度变化。因此,在系统内力的相互作用下,系统总动量保持不变。
02
能量守恒定律
能量守恒定律的表述
感谢观看
01
能量守恒定律表述为:在一个封闭系统中,能量不能被创造或消灭, 只能从一种形式转化为另一种形式。
02
能量守恒定律是自然界的基本定律之一,适用于宇宙中的一切物理过 程。
03
能量守恒定律是定量的,可以用数学公式表示。
04
能量守恒定律是绝对的,不受任何物理定律的限制。
能量守恒定律的适用条件
能量守恒定律适用于孤立系统,即系统与外界没有能量 交换。
动量定理及动量守恒定律第三章

在直角坐标系中: , ,
在自然坐标系中: ,
其中 是 、 在坐标轴上的投影,均为代数量,其正负由矢量和坐标轴方向间的夹角小于或大于 来定。方程的数目等于未知数的数目,有时要根据题目中的物理条件列出数字方程。
5解方程,对所得结果进行必要的讨论。
例题讲解:
1如图所示,在光滑的水平地面上放一质量为M的契块,契块底角为 ,斜边光滑,今在其斜边上放一质量为m的物体,求物体沿契块下滑时对契块和对地面的加速度。
解:参考系:地面
研究对象:契块和物体
m
mg
Nm
θ
受力分析: 契块 物体且N‘=-Nm
X
Y
θ
M
m
M
Mg
N
N’
一 章节小结
(一). 惯性定律
1.惯性定律:自由粒子永远保持静止或匀速直线运动状态。
2.惯性参考系 对某一特定物体惯性定律成立的参考系。
其特性:(1)在惯性系中所有物体遵从惯性定律。
(2)一切相对惯性系作匀速直线运动的参考系都是惯性系。
3.相对性原理 对于牛顿动力学规律,一切惯性系都是等价的。
θ
坐标系:如图所示
β
设物体相对地面的加速度为 ,和水平面的夹角为 向下
物体相对契块的加速度为 ,沿斜面,和地面成角
契块相对地面的加速度为 ,沿水平方向后。
根据相对性: ,
例如,对阿特武德机,只能分别选两个物体为研究对象,而不能把两个物体作为一个研究对象来应用牛顿运动定律。
2分析研究对象的受力情况,画出受力图。
3建立坐标系:有了坐标系,才便于把力、加速度等矢量向坐标轴投影,使矢量运算化为标量运算,在动力学中坐标原点的位置可以任意。
大学物理 第三章 动量守恒定律和能量守恒定律 3-9 质心 质心运动定律
第五版
3-9 质心 -
质心运动定律
一 质心
1 质心的概念
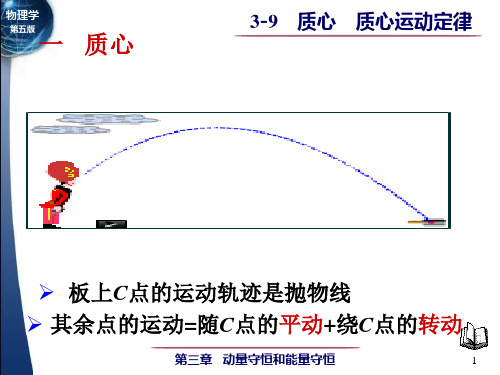
板上C点的运动轨迹是抛物线 板上 点的运动轨迹是抛物线 其余点的运动=随 点的平动+绕 点的 点的平动 点的转动 其余点的运动 随C点的平动 绕C点的转动
第三章 动量守恒和能量守恒
1
物理学
第五版
3-9 质心 -
质心运动定律
2 质心的位置 由n个质点组成 个质点组成 的质点系, 的质点系,其质心 的位置: 的位置:
13
物理学
第五版
3-9 质心 n n v v v m'vC = ∑ mi vi = ∑ pi = p i =1 i =1
质心运动定律
求一阶导数, 再对时间 t 求一阶导数,得
质心加速度
dp v m'aC = dt v v dp ex 根据质点系动量定理 = Fi dt
第三章 动量守恒和能量守恒
}⇒
x2 = 2 xC
17
第三章 动量守恒和能量守恒
物理学
第五版
3-9 质心 -
质心运动定律
例4 用质心运动定律 y F 来讨论以下问题. 来讨论以下问题. 一长为l 一长为 、密度均匀的 y 柔软链条, 柔软链条,其单位长度的质 c yC 量为 λ .将其卷成一堆放在 地面. 若手提链条的一端, 地面. 若手提链条的一端, o 以匀速v 将其上提.当一端 以匀速 将其上提. 被提离地面高度为 y 时,求手的提力. 求手的提力.
竖直方向作用于链条的合外力为 F − λyg
第三章 动量守恒和能量守恒
20
物理学
第五版
3-9 质心 -
质心运动定律
v 得到 F − yλg = lλ ⋅ l
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
——质点系的总动量。 质点系动量定理的积分形式: t1 I Fi dt pi p0 i
t0 i i i
合外力的冲量等于质点系动量的增量,与 内力无关。
例 一辆装煤车以v =3m/s的速率从煤斗下面通过,每秒落入 车厢的煤为m=500kg。若使车厢的速率保持不变,应用多大 的力拉车厢?
物体相互碰撞时, 动量可以在物体间 相互传递,但必须 保持总动量守恒
牛顿摆--法国物理学家伊丹· 马略特
(3)动量守恒式的分量形式:
m v
i
ix
常量
if
if
if
F
i
i
ix
0
0
0
m v
i i
i i
i
iy
iz
常量
常量
F
i
iy
m v
F
iz
当系统在某一方向上合外力为零时,则此 方向上动量守恒。 此时总动量不一定守恒 (4)反冲运动中的动量守恒 (5)动量守恒律在近代物理学中的意义
第三章 动量守恒定律 和能量守恒定律
牛顿三定律给出了“力”的完整定义
力学图景:
力作用于物体,使其在时空中运动
力的时间瞬时效应
牛顿第二定律
三种效应:
力的空间累积效应
能量的概念
力的时间累积效应
动量的概念
§3.1 质点的动量定理
一、冲量和动量 1.力的冲量: 力和作用时间的乘积 ——力对时间的累积效应。
——航天先驱齐奥尔科夫斯基(K.E.
Tsiolkovsky, 1857-1935)
火箭最初质量为m0, 燃料烧完后 火箭的质量为m1 ,火箭最终速度决定 于两者的比值。 单级火箭不能使航天器的最终速度 达到第一宇宙速度. 所以,必须有多级 火箭技术和捆绑火箭技术.
神 舟 七 号 载 人 飞 船
万虎:明代官员,锦衣卫 都指挥使. 他是“第一个企图利用火箭 飞行的人。他用47只最大的火 箭绑在椅子背后,手拿两个大 风筝,想借助火箭的推力和风 筝上升的力量飞向空中。 1970年国际天文学会为了纪 念他,把月球背面的一个环行 山命名为“万虎环行山”。
生活中的碎花瓶理论
雅各布·博尔
丹麦
“雅各布· 博尔定律”:打碎后的物体的碎片按重量的数量 级分类,不同数量级间的表现为统一的倍数关系。花瓶或茶杯 状的物体倍数为16,棒状物约为11,球体则约为40。 约翰· 巴比克
美国
1935年成立了专门从事黏合剂研制生产的BBK公司。 如果用一个完整的玻璃瓶或瓷瓶做花瓶,它只能盛满一缕 缕花朵的芬芳和郁香。而一个人的心灵一旦摔不碎,什么样的 碎片都可能成为他生命的花瓣,飘逸出穿透岁月的清香。 苹果成全了牛顿,茶壶成全了瓦特,花瓶也同样成就了一些人 ;机遇只给那些有准备的人,世界也属于有心人的世界。
答:因为鸡蛋和薄板间的摩擦力很小,若棒打击 时间很短, Ff t 0, p 0 所以鸡蛋就 蛋 掉在杯中.
例 一质量m=140g的垒球,以v=40ms-1的速率沿水平 方向飞向击球手,被击后它以相同的速率沿° 的仰角飞出。求垒球受到的平均打击力。设球和棒 的接触时间t=1.2ms。
则平均冲力
mv 2
)θ
2mv cos 3 F 8 . 1 10 N 大小 t
方向
mv1
)
30
动量定理的应用
? 2、处理变质量物体的运动:
设某物体在 t 时刻质量为 m,速度为 另一质元 dm,以速度 u 运动,在 t+dt 时刻, dm与 m 合并,共同速度为 : v d v 并且在t~t+dt 时间内,有外力 F作用在系统上,求系统运动 规律?
F 1.5 10 ( N )
3
由动量定理:
动量守恒定律
若质点系所受的合外力 Fi 0
则 p mi vi const.
i
i
即:若质点系所受合外力为零,其动量守恒。 讨论 (1)内力不会影响系统的总动量,但可使系统内的 动量一个质点转移到另一个质点。 (2)动量守恒律是牛顿第二、三定律的直接结果; 是空间平移不变性的物理表现。
fdt 0 (vdt )v
地面受力
2m(l h) g f v v f' dt L m F f ' ml g (3l 2h) g L
2
vdt
§3.2 质点系的动量定理和动量守恒定律
质点系:由多个质点组成的系统。
内 外 力:系统内质点间的相互 作用力。 力:系统外物体对质点系的 作用力。 质点系 内力 外力 m1 m2 作用时间 f2 f 1 动量变化 F1 F2
可得: ( F1 F2 )dt d ( p1 p2 )
质点系动量定理的微分形式:
式中: F F1 F2 Fi
Fdt dP
——质点系所受的合外力。 P p1 p2 pi
v,
dm u
dt
u 和 v 分别为
m+dm
m
v
F
vd v
它们相对于地 面的速度
由动量定理:(m dm)(v dv) (mv udm) Fdt dv dm m ( v u) F dt dt
dv dm m vr F dt dt
3
Fy 4.0 103 N
F F F 8.1 10 N
3
arctan
Fy Fx
30
另解 由动量定理:
Ft mv 2 mv1
作矢量三角形如图,求出力的冲量
F t 。 F t
大小 Ft 2mv cos F t 30 方向 2
解 y 取坐标, 由动量定理的分量式:
v2 v1
x
2 x 2 y
F
Fx t mv 2 x mv1 x Fy t mv 2 y mv1 y
Fx t mv cos mv cos
o
Fy t mv sin mv sin
Fx 7.0 10 N
v r 为m相对于 dm的速度
[例1] 已知 M ,m, h,绳拉紧瞬间,绳与m、M 之 间的相互作用时间为t,求:绳子拉紧后,M 与 m 的共同的速度大小。(不计滑轮的质量) [解] 分析物体受力及运动情况:
T
v
M
x
T
m
v0
M
m
h
v
Mg
o
mg
M: (T Mg )t Mv 0 m:(T
mg )t mv (mv0 )
v 0 2 gh
m v 2 gh M m
M
m
h
[练习]一质点受合外力作用,外力为
2 F 10ti 2(2 t ) j 3t k (SI)
求此质点从静止开始在2s内所受合外力的冲量 和质点在2s末的动量。
解: 由冲量定义有 2 2 2 I Fdt 0 [10ti 2( 2 t ) j 3t k ]dt
说明
f1
m1
m2
f2
m1 v 1 m1 v 10 f1 t m2 v 2 m2 v 20 f 2 t
f1 f 2
m1 v 1 m1 v10 m2 v 2 m2 v 20
m1 v 1 m2 v 2 m1 v10 m2 v 20
2 2 2 10tdti 2(2 t )dtj 3t dtk 0 0 0 20i 4 j 8k N s 根据动量定理 I t t pt 2 p0 pt 2 pt 2 20i 4 j 8k N s
世界最强大的战列舰 “衣阿华”号9门主炮右 舷顺次射击,据称可导 致这艘排水量45000吨的 庞然大物侧移10米。
2011年在阿富汗南部坎大 哈省,美军野战队士兵在 前哨基地向本杰瓦尔地区 的火力基地发射榴炮弹 。
反冲运动:
当一个物体向某一方 向射出它的一部分时 ,这个物体的剩余部 分将向相反方向运动
dI Fdt
I
t2
t1
Fdt
2.质点的动量:质点的质量和速度的乘积
p mv
二、动量定理 设质点作任意曲线运动,有
Fdt dp ——动量定理的微分形式 t2 p2 对上式积分 Fdt dp 得:
t1 p1
dv dp F ma m dt dt
风 v1 Δv v2
F横 帆
F帆对风 Δ v
(2)F 方向变化时,I 一般不与其方向同。
F2 t 2
F1t1
I
n I Fi t i
i 1
Fn t n
(3)动量定理的分量形式:
t2
t1 t2
Fx dt mv 2 x mv 1 x
I x p2 x p1 x
t2
t1
Fdt mv 2 mv1 或
I p2 p1
质点的动量定理: 合外力对质点的冲量等于质点动量的增量。
讨论:
I p2 p1
(1)冲量与动量的改变量相联系, 而不是动量本身。
“好船家会 使八面风 ”
“逆风行舟”
演示
逆风行舟
F风对帆
F进
v1 v2
I F ( t )dt
t1
t2
----平均冲力
F ( t 2 t1 )
