专题5图形的旋转
专题05 图形的平移与旋转五种考法(学生版)

专题05图形的平移与旋转五种考法【考法一利用平移的性质求解】例题:(2022·浙江·义乌市绣湖中学教育集团七年级阶段练习)在直角三角形ABC中,∠ACB=90°,AC=6.将三角形ABC沿射线BC方向平移至三角形DEF处.若AG=2,BE=83,则EC=_____【变式训练】1.(2022·广东·汕头市龙湖实验中学七年级期中)如图,把一个三角形纸板的一边紧靠数轴平移,点P平移的距离PP′为()A.2B.3C.4D.52.(2021·浙江省衢州市衢江区实验中学七年级开学考试)如图,直角△ABC沿射线BC的方向平移3个单位长度,得到△DEF,线段DE交AC于点H,已知AB=5,DH=2,则图中阴影部分的面积为()A.12B.24C.48D.不能确定3.(2022·湖北黄石·七年级阶段练习)如图,在直角△ABC 中,90BAC ∠=︒,3AB =,4AC =,5BC =,将ABC 沿直线BC 向右平移2个单位长度得到△DEF ,连接AD 、AE ,则下列结论:①AC DF ∥,AC DF =;②ED DF ⊥;③四边形ABFD 的周长是16;④点D 到线段BF 的距离是2.4.其中正确的有()A .1个B .2个C .3个D .4个4.(2022·广东·惠东县多祝中学七年级阶段练习)如图,三角形DEF 是由三角形ABC 通过平移得到,且点B ,E ,C ,F 在同一条直线上,若BF =10,EC =4,则BE 的长度是________.5.(2021·广东·珠海市凤凰中学七年级期中)如图,点A (-4,0),B (-1,0),将线段AB 平移后得到线段CD ,点A 的对应点C 恰好落在y 轴上,且四边形ABDC 的面积为9,则D 点坐标为_________.6.(2022·山东烟台·八年级期末)如图,己知△ABC 的面积是12,将ABC 沿BC 平移到A B C '''V ,使B '和C 重合,连接AC 交A C '于点D ,则C DC '的面积是___________.7.(2021·河北唐山·七年级期中)如图,在平面直角坐标系中,△DEF 是由△ABC 平移得到的.若()1,4A t -,()3,0E ,()5,0C .(1)指出图中线段AD 的长以及与线段AD 相等的线段;(2)若点A 到y 轴的距离为1,直接写出t 的值与点D 的坐标;(3)求△ABC 的面积;(4)如果将点A 平移到点(),0P m ,直接写出点P 所在位置以及满足条件的点P 的个数.【考法二利用平移解决实际问题】例题:(2022·福建·龙岩二中七年级阶段练习)某宾馆在重新装修后,考虑在大厅内的主楼梯铺设地毯,已知楼梯m的地毯.宽3m,如图,请计算一下,铺此楼梯需购______2【变式训练】1.(2021·山东烟台·模拟预测)如图是一块矩形ABCD的场地,长AB=99米,宽AD=41米,从A,B两处入口的路宽都为1米,两小路汇合处路口宽为2米,其余部分种植草坪面积为()A.3783米2B.3880米2C.3920米2D.4000米22.(2022·山东泰安·八年级期末)如图所示,一块长为18m,宽为12m的草地上有一条宽为2m的曲折的小路,则这块草地的绿地面积是______.3.(2021·湖北武汉·七年级期中)如图,在长方形地块内修筑同样宽的两条“相交”的道路,余下部分作绿化,当道路宽为2米时,绿化的面积为_____平方米.4.(2022·浙江金华·七年级阶段练习)如图,在一块长AB=15m,宽BC=11m的长方形草地上,修建三条宽均为1m的长方形小路,则这块草地的绿地面积(图中空白部分)为_____m2.5.(2022·山东烟台·八年级期末)在边长为8cm的正方形ABCD底座中,放置两张大小相同的正方形纸板,边EF 在AB上,点K,I分别在BC,CD上,若区域Ⅰ的周长比区域Ⅱ与区域Ⅲ的周长之和还大4cm,则正方形纸板的边长为______cm.6.(2022·安徽·合肥市五十中学西校七年级期中)如图,有一长方形空地,其长为a、宽为b,现要在该空地种植两条防风带(图中阴影部分),防风带一边长为c,其中横向防风带为长方形,纵向防风带为平行四边形.(1)用代数式表示剩余空地的面积;(2)若a=2b、c=2,且防风带的面积为116,求原长方形空地的长和宽.【考法三平移、中心对称作图】例题:(2022·重庆市第十一中学校八年级期中)如图,在平面直角坐标系中,已知△ABC的三个顶点坐标分别是A(1,1),B(4,1),C(3,3).(1)将△ABC向下平移5个单位后得到△A1B1C1,请画出△A1B1C1;(2)将△ABC绕原点O逆时针旋转90°后得到△A2B2C2,请画出△A2B2C2;(3)判断以O,A1,B为顶点的三角形的形状,并说明理由.【变式训练】1.(2020·四川泸州·九年级期末)在平面直角坐标系中,△ABC的位置如图所示(每个小方格都是边长为1个单位长度的正方形).(1)将△ABC沿x轴方向向左平移6个单位,画出平移后得到的△A1B1C1;(2)将△ABC绕着点A顺时针旋转90°,画出旋转后得到的△AB2C2,并直接写出点B2、C2的坐标.2.(2022·广东·平洲一中八年级期中)如图,方格纸中每个小正方形的边长都是1个单位长度,Rt △ABC 的三个顶点分别为A (2,﹣2),B (0,﹣5),C (0,﹣2).(1)画△A 1B 1C 1,使它与△ABC 关于点C 成中心对称.(2)平移△ABC ,使点B 的对应点B 2的坐标为(2,3),画出平移后对应的△A 2B 2C 2.(3)若将△A 1B 1C 1绕某一点旋转可得到△A 2B 2C 2,则旋转中心的坐标为.3.(2022·江苏·靖江市实验学校八年级阶段练习)如图,在平面直角坐标系中,即△ABC 的三个顶点分别是()3,2A -,()1,4B -,()0,2C .(1)将△ABC 以点O 为旋转中心旋转180︒,画出旋转后对应的111A B C △;(2)平移△ABC ,若点A 的对应点2A 的坐标为()5,2--,画出平移后对应的222A B C △,求线段BC 在平移过程中扫过的面积;(3)若将111A B C △绕某一点旋转可以得到222A B C △,请直接写出旋转中心的坐标为______.【考法四图形的旋转综合】例题:(2022·湖北·房县教学研究中心一模)把两个等腰直角△ABC 和△ADE 按如图1所示的位置摆放,将ADE 绕点A 按逆时针方向旋转,如图2,连接BD ,EC ,设旋转角()0360a α︒<<︒.(1)当DE AC ⊥时,旋转角α=______度,AD 与BC 的位置关系是______,AE 与BC 的位置关系是______;(2)当点D 在线段BE 上时,请画出图形并求BEC ∠的度数;(3)当旋转角α是多少时,ABD △的面积最大?(直接写出答案,不用推理和证明).【变式训练】1.(2022·广东·佛山市南海区狮山镇罗村第二初级中学八年级阶段练习)如图,在△ABC 中,∠CAB =70°,将△ABC 绕点A 逆时针旋转到△A B C ''的位置,使得CC AB '∥.(1)请判断△ACC '的形状,并说明理由.(2)求∠BAB '的度数.2.(2022·江西赣州·九年级期末)已知△ABC中,∠ACB=135°,将△ABC绕点A顺时针旋转90°,得到△AED,连接CD,CE.(1)求证:△ACD为等腰直角三角形;(2)若BC=1,AC=2,求四边形ACED的面积.3.(2022·河南·罗山县实验中学三模)(1)如图1,在Rt△ABC中,∠BAC=90°,AB=AC,D为BC边上一点(不与点B,C重合),将线段AD绕点A逆时针旋转90°得到AE,连接EC.求证:△ABD≌△ACE;(2)如图2,在Rt△ABC和Rt△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,将△ADE绕点A旋转,使点D落在BC DE,BD,CD之间满足的数量关系,并证明你的结论;(3)如图3,在四边形ABCD中,∠ABC=∠ACB=∠ADC=45°,若BD=6,CD=2,则AD=.4.(2022·湖北武汉·八年级期末)如图,在等边△ABC中,D为BC上一点,DE∥AB,且DE=BD.(1)如图1,若点E在AC边上,求证:AE=CE;(2)如图2,若点E在△ABC内,连接CE,F为CE的中点,连接AF、DF,求证:AF⊥DF;(3)如图3,点N为AB边上一点,连接BE,AN=BE.若CN+CE的值最小时,∠NCE的度数为___________°(直接写出结果).5.(2022·重庆一中九年级阶段练习)如图,在等边ABC中,点D为BC的中点,连接AD,点E为AD上一点,连接EB、CE,将线段EB绕点E顺时针旋转至EF,使点F落在BA的延长线上.(1)如图1,求∠CEF的度数:(2)如图1,探宄线段AB,AE,AF之间的数量关系,并加以证明;(3)如图2,若AB=4,点G为AC的中点,连DG,将△CDG绕点C顺时针旋转得到△CMN,直线BM、AN交于点P,连CP,在△CDG旋转一周过程中,请直接写出△BCP的面积的最大值.6.(2021·浙江温州·一模)如图,在△ABC 中,AB =AC ,∠BAC =135°,E 为BC 边上一点,连结AE ,将点E 绕点A 逆时针旋转135°至点,连结AD ,DE ,CD .(1)求证:CD =BE .(2)若DE ⊥BC ,BE =,求BC 的长.7.(2022·湖南邵阳·八年级期末)如图,在ABC ∆和DCE ∆中,,,90AC BC DC EC ACB DCE ==∠=∠=︒,将DCE ∆绕点C 旋转(其中0180ACD ︒<∠<︒),连接BD 和AE ,BD 与AE AC 、分别交于点O 和点H .(1)求证:BCD ACE ∆≅∆;(2)试确定线段BD 和AE 的数量关系和位置关系;(3)连接AD 和BE ,在旋转过程中,ACD ∆的面积记为1S ,BCE ∆的面积记为2S ,试判断1S 和2S 的大小,并给予证明.8.(2022·四川成都·八年级期末)如图,AB=AC=,∠BAC=α,连接BC,点D在边BC上(点D不与B,C 重合),连接AD,将线段AD绕点A逆时针旋转α得到线段AE,连接CE,DE.(1)求证:△ABD≌△ACE;(2)若α=90°,且AD与BD的数量关系满足AD=BD+2,求△DCE的面积;(3)若α=60°,连接BE,试说明△ABE的面积是一个定值,并求出该定值.9.(2021·四川成都·八年级阶段练习)已知,在△ABC中,∠BAC=90°,AB=AC,点D是BC边上的一点(不与点B,C重合),连接AD.(1)如图1,将线段AD绕点A逆时针方向旋转90°得到线段AE,连接CE.求证:BD=CE,BD⊥CE;(2)如图2,点D,F都在线段BC上,且∠DAF=45°.①试猜想线段DF,BD,CF之间满足的数量关系,井证明结论.②BD=4,CF=3,求△ADF的周长.【考法五轴对称图形与中心对称图形】例题:(2021·四川·渠县崇德实验学校一模)下列图形中是轴对称图形但不是中心对称图形的是()A.B.C.D.【变式训练】1.(2022·山西晋中·一模)下列图案中,既是轴对称图形又是中心对称图形的是()A.B.C.D.2.(2022·广东·平洲二中八年级阶段练习)如图所示的图中,既是轴对称又是中心对称图形的是()A.B.C.D.3.(2022·黑龙江哈尔滨·)A.B.C.D.4.(2022·江苏苏州·一模)下列图形中,既是轴对称图形又是中心对称图形的是()A.B.C.D.5.(2022·安徽铜陵·九年级期末)下列图形中,即是轴对称图形,又是中心对称图形的有()A.1个B.2个C.3个D.4个6.(2022·湖北·前川三中一模)把“武汉加油”的首字母看成图形,既是轴对称图形又是中心对称图形的是()A.B.C.D.7.(2022·广东江门·模拟预测)如图,既是轴对称图形又是中心对称图形的是()A.B.C.D.。
2023年上海市16区数学中考二模专题汇编5 图形的平移、旋转、翻折、新定义(18题)含详解

专题05图形的平移、旋转、翻折、新定义(18题)一、单选题1.(2023·上海黄浦·统考二模)下列轴对称图形中,对称轴条数最多的是()A.等边三角形B.菱形C.等腰梯形D.圆2.(2023·上海嘉定·统考二模)下列图形中既是轴对称图形,又是中心对称图形的是()A.等边三角形B.等腰梯形C.矩形D.正五边形二、填空题5.(2023·上海黄浦A的对应点是点6.(2023·上海静安处,点A落在点7.(2023·上海金山·统考二模)已知线段AC上,如果点E关于直线8.(2023·上海闵行三角形为特征三角形.9.(2023·上海浦东新·于点F.如果2AD AB=10.(2023·上海徐汇·统考二模)如图,抛物线“月牙线”,抛物线1C和抛物线=,那么抛物线果BD CD11.(2023·上海宝山·统考二模)13.(2023·上海闵行·统考二模)如图,在菱形ABCD 中,6AB =,80A ∠=︒,如果将菱形ABCD 绕着点D 逆时针旋转后,点A 恰好落在菱形ABCD 的初始边AB 上的点E 处,那么点E 到直线BD 的距离为___________.14.(2023·上海嘉定·统考二模)如图,在Rt ABC 中,90C ∠=︒,4AC =,2BC =,点D 、E 分别是边BC 、BA 的中点,连接DE .将BDE 绕点B 顺时针方向旋转,点D 、E 的对应点分别是点1D 、1E .如果点1E 落在线段AC 上,那么线段1CD =____.三、解答题15.(2023·上海静安·统考二模)如图,在平面直角坐标系xOy 中,抛物线()240y ax x c a =-+≠与x 轴分别交于点()1,0A 、点()3,0B ,与y 轴交于点C ,连接BC ,点P 在线段BC 上,设点P 的横坐标为m .(1)求直线BC 的表达式;(1)如图,如果点O '恰好落在半圆O 上,求证: O A BC'=;(2)如果30DAB ∠=o ,求EF O D'的值;(3)如果3,1OA O D ==',求OF 的长.17.(2023·上海徐汇·统考二模)如图,已知抛物线2y x bx c =++经过点()2,7A -,与x 轴交于点B 、()5,0C .(1)求抛物线的顶点M 的坐标;(2)点E 在抛物线的对称轴上,且位于x 轴的上方,将BCE 沿直线BE 翻折,如果点C 的对应点F 恰好落在抛物线的对称轴上,求点E 的坐标;(3)点P 在抛物线的对称轴上,点Q 是抛物线上位于第四象限内的点,当CPQ 为等边三角形时,求直线BQ 的表达式.18.(2023·上海松江·统考二模)在平面直角坐标系xOy 中(如图),已知直线2y x =-+与y 轴交于点A ,抛物线()21(0)y x t t =-->的顶点为B .(1)若抛物线经过点A ,求抛物线解析式;(2)将线段OB 绕点B 顺时针旋转90︒,点O 落在点C 处,如果点C 在抛物线上,求点C 的坐标;(3)设抛物线的对称轴与直线2y x =-+交于点D ,且点D 位于x 轴上方,如果45BOD ∠=︒,求t 的值.专题05图形的平移、旋转、翻折、新定义(18题)一、单选题1.(2023·上海黄浦·统考二模)下列轴对称图形中,对称轴条数最多的是()A.等边三角形B.菱形C.等腰梯形D.圆【答案】D【分析】依据轴对称图形的意义,即在同一个平面内,一个图形沿某条直线对折,对折后的两部分都能完全重合,则这个图形就是轴对称图形,这条直线就是其对称轴,从而可以画出它们的对称轴.【详解】解:等边三角形有3条对称轴,菱形有2条对称轴,等腰梯形有1条对称轴,圆形有无数条对称轴,圆的对称轴条数最多,故选:D.【点睛】此题主要考查如何确定轴对称图形的对称轴条数及位置,解题的关键是掌握轴对称的概念.2.(2023·上海嘉定·统考二模)下列图形中既是轴对称图形,又是中心对称图形的是()A.等边三角形B.等腰梯形C.矩形D.正五边形【答案】C【分析】根据轴对称图形的定义、中心对称图形的定义逐项判断即可.【详解】A选项:等边三角形是轴对称图形,不是中心对称图形.故本选项不合题意;B选项:等腰梯形是轴对称图形,不是中心对称图形.故本选项不合题意;C选项:矩形既是轴对称图形,又是中心对称图形.故本选项符合题意;D选项:正五边形是轴对称图形,不是中心对称图形,故本选项不合题意.故选C.【点睛】本题考查轴对称图形、中心对称图形,理解定义,会根据定义判断轴对称图形和中心对称图形是解答的关键.二、填空题在正方形ABCD 和正三角形∴点O ,E 均在BC 的垂直平分线上,∴点E ,O ,P ,G 四三点共线,∵正方形ABCD 和正三角形∴6BC BE ==.116OG BG BC ===⨯=在正方形ABCD 和正三角形∴点O ,E 均在BC 的垂直平分线上,∴点E ,O ,P ,G 四三点共线,∵正方形ABCD 和正三角形∴6BC BE ==.∴11622OG BG BC ===⨯【答案】20【分析】根据旋转可得根据AA B '∠【详解】解:∵∴180ACB ∠=∵将ABC 绕点∴30B A C BAC ∠=∠=''︒,∴(11802CAA CA A ''∠=∠=︒∴AA B CA A B A C '''''∠=∠-∠故答案为:20︒.【点睛】本题考查了旋转的性质,等腰三角形的性质,三角形内角和定理等知识,掌握旋转的性质是关键.A 的对应点是点1A ,点B 的对应点是点1B ),如果点1A 坐标是()20-,,那么点1B 的坐标是________.【答案】()12,【分析】各对应点之间的关系是横坐标减3,纵坐标加3,那么让点B 的横坐标减3,纵坐标加3即为点1B 的坐标.【详解】解:∵()13A -,平移后对应点1A 的坐标为()20-,,∴A 点的平移方法是:先向左平移3个单位,再向上平移3个单位,∴B 点的平移方法与A 点的平移方法是相同的,∴()41B -,平移后的坐标是:()4313--+,即()12,.故答案为:()12,.【点睛】此题主要考查了点的平移规律与图形的平移,关键是掌握平移规律,左右移,纵不变,横减加,上下移,横不变,纵加减.6.(2023·上海静安·统考二模)如图,在ABC 中,AB AC =,将ABC 绕着点B 旋转后,点C 落在AC 边上的点E 处,点A 落在点D 处,DE 与AB 相交于点F ,如果BE BF =,那么DBC ∠的大小是______.【答案】108︒/108度【分析】设A x ∠=,由AB AC =,BE BF =得ABC C ∠∠=,BEF BFE ∠∠=,再由旋转的性质得DEB C ABC DBE ∠∠∠∠===,BE BC =,从而有CBE A x ∠∠==,同理可证:EBF A x ∠∠==,利用三角形的内角和定理构造方程即可求解.【详解】解:设A x ∠=,∵AB AC =,BE BF =,∴ABC C ∠∠=,BEF BFE ∠∠=,∵将ABC 绕着点B 旋转后,点C 落在AC 边上的点E 处,点A 落在点D 处,DE 与AB 相交于点F ,∴DEB C ABC DBE ∠∠∠∠===,BE BC =,∵180BEC C CBE ABC C A ∠∠∠∠∠∠++=++=︒,∴CBE A x ∠∠==,同理可证:EBF A x ∠∠==,【点睛】本题考查解直角三角形,轴对称的性质,掌握垂线段最短是解题的关键.8.(2023·上海闵行·统考二模)阅读理解:如果一个三角形中有两个内角三角形为特征三角形.问题解决:如图,在ABC 中,【答案】253【分析】由题意可分:,A B βα∠=∠=,过点∴A ADC ∠=∠,∵4tan 3A =,∴4tan 3ADC ∠=,∵ABC 是特征三角形,即∴2ABE ABC ∠=∠,∴BC 平分ABE ∠,【答案】35【分析】通过证明AEF △得出边之间的关系,即可求解.【详解】解:∵2=AD AB ∴设,2AB a AD a ==,【点睛】本题主要考查了矩形的折叠问题,以及解直角三角形的方法和步骤.10.(2023·上海徐汇·统考二模)如图,抛物线则tan tan DAC ∠=∠∴t n a CD DAC AC ∠==∴165CD =∴1695BD =-=;作DE AB ⊥于E ,则∵AD AD =,∴Rt △∵,90ACB ∠=︒,设BD x =,则CD DE =【答案】3372-【分析】利用含30度角的直角三角形的性质,分别求出出90DBE ∠=︒,在Rt【答案】3【分析】如图,旋转、菱形的性质可知,180ADE DEA ∠=︒-∠-∠由旋转、菱形的性质可知,∴80DEA A ∠=∠=︒,ABD ∠∴180ADE DEA ∠=︒-∠-∠【答案】355【分析】根据勾股定理求得AB ,根据旋转的性质得出根据相似三角形的性质即可求解.设旋转角为α,∴11ABE CBD ∠=∠,旋转,∴115,1BE BE BD BD ====,三、解答题15.(2023·上海静安·统考二模)如图,在平面直角坐标系xOy 中,抛物线()240y ax x c a =-+≠与x 轴分别交于点(1)求直线BC 的表达式;(2)如果以P 为顶点的新抛物线经过原点,且与①求新抛物线的表达式(用含②过点P 向x 轴作垂线,交原抛物线于点【答案】(1)3y x =-+(2)①()2233m y x m m m-=--+,【分析】(1)先利用待定系数法求出抛物线解析式,进而求出点式即可;(2)①先求出()3P m m -+,,设新抛物线解析式为抛物线解析式,再根据点P 在线段称时,当四边形AEDP 关于PE 【详解】(1)解:把()1,0A 、B ∴13a c =⎧⎨=⎩,∴抛物线解析式为24y x x =-+在243y x x =-+中,令0x =,则∴()0,3C ;设直线BC 的解析式为y kx b =+∴303k b b +=⎧⎨=⎩,∴13k b =-⎧⎨=⎩,∴直线BC 的解析式为y x =-+(2)解:①∵点P 在线段BC【点睛】本题主要考查了待定系数法求二次函数解析式,轴对称的性质,求一次函数解析式等等,灵活运用所学知识是解题的关键.16.(2023·上海松江·统考二模)如图,(1)如图,如果点O '恰好落在半圆O 上,求证: O A BC'=;(2)如果30DAB ∠=o ,求EF O D'的值;(3)如果3,1OA O D ==',求OF 的长.【答案】(1)见解析(2)24(3)97OF =或95OF =.【分析】(1)如图:连接,OC O C ',先根据圆的性质和对称的性质说明OAO ' 是等边三角形,明60COO BOC '∠=∠=︒即可证明结论;(2)设圆O 的半径为2a ,则2O A OA a '==,如图:作ON AD ⊥于N ;先根据对称的性质和等腰三角形的性质可得,30120ODA OAD AOD ︒︒∠=∠=∠=,然后解直角三角形可得()232O D a '=-、EF OE ==∵点O '恰好落在半圆O 上,∴OO OA '=,∵点O '与点O 关于直线AC 对称∴AO OA CO CO ==='',O AC '∠∵,30OA OD OAD =∠=︒,∴,30120ODA OAD AOD ︒∠=∠=∠=在Rt AON △中,sin 30ON OA =⋅︒∵ON AD ⊥,∴FN FM=∴1212AFD OFA AD FM S AD S AO AO FN ⨯==⨯ ,又∵AFD S DF S OF = ,∴FN FM =,∴1212AFD OFA AD FM S AD S AO AO FN ∆∆⨯==⨯,又∵AFD OFA S DF S OF ∆∆=,(1)求抛物线的顶点M 的坐标;(2)点E 在抛物线的对称轴上,且位于的对称轴上,求点E 的坐标;(3)点P 在抛物线的对称轴上,点式.【答案】(1)245y x x =--,顶点坐标为:(2)点E 的坐标为()2,3;(3)直线BQ 的函数表达式为【分析】(1)利用待定系数法求解抛物线的解析式,再化为顶点式,即可得到顶点坐标;(2)先求解抛物线与x 轴交于轴与x 轴交于点H ,则H 点的坐标为2233FH FB BH =-=,(3)连接CF ,证明FCB 于点K ,可得点K 的坐标为【详解】(1)解:∵抛物线∵抛物线与x 轴交于(1,0B -∴6BC =,抛物线的对称轴为直线设抛物线的对称轴与x 轴交于点由翻折得6CB FB ==,由勾股定理,得FH FB =∴点F 的坐标为()2,33,∴60FBH ∠=︒,∴CP CQ =,CB CF =,∠∴FCP BCQ ∠=∠,∴BCQ FCP ≌,∴CBQ CFH ∠=∠,∵BCF △为等边三角形,∴30CFH CBQ ∠=︒=∠,设BP 与x 轴相交于点K ,∴3tan 303OK OB =︒= .(1)若抛物线经过点A ,求抛物线解析式;∵旋转,∴,90OB OC OBC =∠=∴BEO OBC BDC ∠=∠=∠∴90OBE CBD ∠=︒-∠由2y x =-+,令0y =,得∴2OA OH ==,AH =∴OAH △是等腰直角三角形∵BD y ∥轴,。
培优专题5 平移与旋转 (含解答)-

培优专题5 平移与旋转平移是几何变换中最常用的变换之一,用它可以将一些不在同一三角形中要证的两条线段或两角,进行“搬家”,把它们搬到同一个三角形(或平行四边形)中,再利用图形的性质与题设条件,找到解(或比)的途径.平移法能把分散的条件集中起来,收到事半功倍的效果.旋转也是几何变换中较常用的变换之一,在解决问题中主要应用在以下两个方面:一是在题设条件和结论间联系不易沟通或条件不易集中利用的情形下,通过旋转起到铺路架桥作用;二是图形错综复杂,但图形中的量与量之间的关系多,这时也可以看能否使用旋转的办法,移动部分图形,使题目中隐蔽着的关系明朗起来,从而找到解题途径.平移、旋转两种变换在使用中,一定要善于观察变换前后哪些量变了,哪些量没变.只有这样,我们才能充分发挥两种变换的功能,达到有效解决相关问题的目的.例1如图,在△ABC中,D、E是BC边上两点,BD=CE,试说明AB+AC>AD+AE.分析利用平移变换,•将图中已知条件转化为梯形的对角线之和大于两腰之和.解:把△ABD作平移,使BD与EC重合,分别过点E作AB的平行线,过点A作BC•的平行线,两线交于点F,连结CF.再连结EF交AC于O.则AB=EF,∠ABD=∠FEC.∵BD=CE,∴△ABD≌△FEC.∴AD=CF.在梯形AECF中,AO+OE>AE,FO+OC>CF,∴AO+OE+FO+OC>AE+CF.即AC+EF>AE+CF.∴AB+AC>AD+AE.练习11.如图,梯形ABCD中,AD∥BC,已知AD+BC=3,AC=3,BD=6,求此梯形的面积.2.如图,长方形花园ABCD中,AB=a,AD=b,花园中建有一条长方形道路LMPQ•及一条平行四边形道路RSTK,若LM=RS=c,求花园中可绿化部分的面积.3.如图,△ABC中,E、F分别为AB、AC边上的点,且BE=CF,试说明EF<BC.例2 如图,△ABC中,∠ACB=90°,M是AB的中点,∠PMQ=90°,请说明PQ2=•AP2+BQ2.分析本题中PQ、AP、BQ不在同一个三角形中,•如果将它们平移,•使PQ、BQ分别转化为PD、AD,将三线段转化在同一三角形中,巧妙运用直角三角形中的勾股定理求解.解:将BQ平移到AD,连结PD、MD.∵BQ∥AD,∴∠BAD=∠ABC.∵MA=MB,BQ=AD,∴△AMD≌△BMQ,∴∠AMD=∠BMQ.而∠AMQ+∠BMQ=180°,∴∠AMQ+∠AMD=180°.∴D、M、Q三点共线.∴∠PMD=∠PMQ=90°,MD=MQ.∴PQ=PD.∵∠PAD=∠BAC+∠BAD=∠BAC+∠ABC=90°.∴△PAD为直角三角形,PD2=AP2+AD2.∴PQ2=AP2+BQ2.1.如图,EFGH是正方形ABCD的内接四边形,∠BEG与∠CFH都是锐角,•已知EG=3,FH=4,四边形EFGH的面积为5,求正方形ABCD的面积.2.如图,△ABC中,∠B=90°,M、N分别是AB、BC上的点,AN、CM•交于点P,•若BC=AM,BM=CN,求∠APM的度数.3.如图,六边形ABCDEF中,AB∥DE,BC∥EF,CD∥AF,且AB-ED=CD-AF=EF-BC>0,请问,六边形ABCDEF的六个角是否都相等.例3如图,在正方形ABCD的边BC和CD上分别取点M和点K,并且∠BAM=∠MAK.求证:BM+KD=KA.分析把Rt△BAM绕点A顺时针旋转90°到△ADM′,使BM与DN拼成一条线段的KM′,只要证明KM′=KA即可.证明:把Rt△ABM绕点A旋转90°,则点B变为点D,M变为M′,则Rt•△BAM•≌Rt•△ADM′,∴∠M′=∠BMA∴DM′=BM.∵∠BAM=∠MAK,∴∠KAM′=∠MAD.∴∠KAM′=∠M′.∴AK=KM′.∴BM+KD=AM.1.如图,在正方形ABCD中,N是DC的中点,M是AD上异于D•的点,•且∠NMB=∠MBC,求AMAB的值.2.如图,P是等边△ABC内一点,∠APB、∠BPC、∠CPA的大小之比为5:6:7,•求以PA、PB、PC之比为边的三角形三内角之比(从小到大).3.如图,在四边形ABCD中,AB=AD,∠BAD=∠BCD=90°,AH⊥BC,且AH=1,•求四边形ABCD的面积.例4如图,在等腰三角形ABC中,∠CAB=90°,P是△ABC内一点,且PA=1,PB=3,PC=7,求∠APC 的度数.分析本题将△BAP绕点A旋转90°,得到△CAQ,构造直角三角形,利用勾股定理求解解:将△BAP绕点A旋转90°,使AB与AC重合,得△CAQ,则△CAQ≌△BAP.∴AQ=AP=1,CQ=BP=3,∠CAQ=∠PAB,∴∠PAQ=∠PAC+∠CAQ=∠PAC+∠PAB=90°Rt△AQP中,PQ2=AQ2+AP2=2,∴PQ=2,∴∠APQ=45°.在△CPQ中,PQ=2,CQ=3CP=7,CQ2=CP2+PQ2.∴△CPQ是直角三角形,∠CPQ=90°.∴∠APC=∠CPQ+∠APQ=135°.练习41.等边三角形内一点到三个顶点距离分别为3、4、5,则此等边三角形边长的平方为________.2.如图,P是正方形内的点,若PA=1,PB=2,PC=3,求∠APB的度数.3.如图,正方形ABCD的边长为1,AB、AD各有一点P、Q,若△APQ的周长为2,•求∠PCQ.例5 如图,在△ABC中,AB=3,AC=2,以BC为边的三角形BPC是等边三角形,求AP的最大、最小值.分析通过旋转把AP转移到有两条边确定的三角形中,利用三角形的性质求最值.解:把△ABP绕B点顺时针旋转60°得△DBC,则△ABP≌△DBC.∴DC=AP,BD=BA,∠DBA=60°.∴△ABD是等边三角形,AD=AB=3.在△ACD中,有DC<AD+AC=5,当C在DA的延长线上时才有DC=AD+AC=5,说明DC≤5,•即AP≤5.……①在△ACD中,有DC>AD-AC=1时,当C在DA线段上时才有DC=AD-AC=1,说明DC≥1,•即AP≥1.……②由①②得AP最大值为5,最小值为1.练习51.如图,正方形ABCD中,有一个内接三角形AEF,若∠EAF=45°,AB=8,EF=7,•求△EFC的面积.2.如图,在△ABC中,AB=5,AC=13,过BC上的中线AD=6,求BC的长.3.如图,已知△ABC中,AB=AC,D为三角形内一点,∠ADB>∠ADC.试证明:•CD>BD.答案:练习11.解:将BD 平移到CE 交AD 延长线于点E , 则四边形BDEC 为平行四边形∴DE=BC ,CE=BD ,S △BCD =S △CDE ∵△ABC 与△DBC 同底等高, ∴S △ABC = S △BCD = S △CDE∵S 梯形ABCD = S △ABC + S △ACD = S △CDE + S △ACD = S △ACE . 又AE=AD+DE=3=2236AC CE +=+,∴△ACE 为直角三角形,∠ACE=90°. ∴S 梯形ABCD = S △ACE =12·AC·CE=322.2.解:把长方形和平行四边形道路平移,在移动过程中道路面积不变,如图,则四块空白可组成长(b-c ),宽(a-c )的空白长方形,其面积为(b-c )(a-c )=ab-bc-ac+c 2.3.解:将EF 平移为BG ,BF 平移为FG ,作∠CFG 的角平分线交BC 于D ,连结DG ,•则由平移知四边形BEFG 是平行四边形. ∴EF=BG ,BE=FG . ∵BE=CF ,∴FG=CF . ∵∠1=∠2,FD=FD . ∴△FGD ≌△FCD (SAS ). ∴DG=CD .在△BGD 中, ∵BG<BD+DG ,∴EF<BC .练习21.解:过E 、F 、G 、H 分别平移AD 、AB ,交点分别为P 、Q 、R 、T ,则四边形PQRT•为矩形.设正方形边长为a ,PQ=b ,PT=c ,由勾股定理得b= 223a -,c=224a -, ∵S △AEH =S △TEH ,S △BEF =S △PEF , S △CFG =S △QFG , S △DGH =S △RGH 则S 正方形ABCD +S 矩形PQRT =2S 四边形EFGH ∴a 2+b·c=10. 即a 2+223a -·224a -=10.∴5a2=44,a2=445.∴S正方形ABCD=445.2.解:把MC平移,使点M至A点,过A作MC的平行线,过点C作AB的平行线,•两线交于点D,则MC=AD.∠APM=∠NPC=∠NAD……①∵BM=NC,CD=AM=BC,∠DCN=∠CBM=90°,∴△DCN≌△CBM.从而DN=MC,∴DN=DA……②∴∠CMB=∠DNC.∵∠BCM+∠DMB=90°,∴∠BCM+∠DNC=90°.即MC∥AD.∴ND⊥AD.……③由①,②,③得∠APM=45°.3.解:六个角都相等且都等于120°.将AB沿着BC平移到QC,CD沿着DE平移到ER,EF沿着FA平移到AP,∵AB∥ED,BC∥EF,CD∥AF,∴AB=QC,BC=AQ,CD=ER,DE=CR,EF=AP,FA=PE.∵AB-ED=CD-AF=EF-BC,∴QC-CR=ER-PE=AP-AQ.即PQ=PR=QR.∴∠1=∠2=∠3=60°.由平行线性质知:∠A=∠B=∠C=∠D=∠E=∠F=120°.练习31.解:将△BAM绕B点旋转90°,A点变为C点,M点变为P点,连结MP,则△BAM≌△BCP.∴∠BPC=∠BMA=∠CBM=∠NMB.∵BM=BP,∴∠NMP=∠NPM.∴MN=NP=NC+CP=NC+AM.设AB=1,AM=x,在Rt△MND中,则有12+x=221()(1)2x+-.∴x=13.即AMAB=13.2.解:将△ABP绕B点顺时针旋转60°得△BCP′,连结PP′,则△ABP≌△CBP′.∴AP=P′C,BP=BP′,∠APB=∠CP′B.∵∠PBP′=60°,∴△BPP′是等边三角形.∴PP′=BP,∠BPP′=60°=∠BP′P.∵∠APB:∠BPC:∠CAP=5:6:7,又∠APB+∠BPC+∠CPA=360°,∴∠APB=100°,∠BPC=120°,∠CPA=140°,∴∠1=120°-60°=60°,∠2=100°-60°=40°,∠PCP′=180°-60°-40°=80°.由PA=P′C,PP′=PB,∴△PP′C是由PA、PB、PC组成的三角形.∴三内角之比为2:3:4.3.解:将△ABH绕A点旋转90°得△ADP,则△ABH≌△ADP.∴∠APD=∠AHB=90°,AH=AP.∵∠BAD=∠BCD=90°,∠HAP=90°.∴四边形AHCP是正方形.∵AH=1,∴S正方形AHCP=1=S四边形AHCD+S△ADP.S四边形ABCD=S四边形AHCD+S△ABH.又∵S△AOP =S△ABH.∴S四边形ABCD=S正方形AHCP=1.练习41.解:如图,以A为中心将△ACP绕A顺时针旋转60°,则C与B重合,P与P′重合,连结AP′,BP′,PP′则AP′=AP,BP′=CP,∠PAP′=60°.∴△APP′是等边三角形,PP′=3.△BPP′中,BP=4,PP′=3,BP′=CP=5.由32+42=52.∴△BPP′为直角三角形,∠BPP′=90°.∴∠BPA=150°.过B作BE⊥AP,交AP延长线于E.∵∠EPB=180°-150°=30°,在Rt△BEP中,BP=4,BE=2,EP=23,Rt△ABE中,BE=2,AE=23+3,AB2=22+(23+3)2=25+123.2.解:将△ABP绕B点旋转90°,得△CBP′,连结PP′,则△ABP≌△CBP′.∴PB=BP′=2,AP=P′C=1,∠APB=∠CP′B.在Rt△PBP′中,BP=BP′=2,∴PP′=22,∠BP′P=45°.在△PP′C中,PC=3,P′C=1,PP′=22.有PC2=P′C2+P′P2,∴△PP′C是直角三角形,∠PP′C=90°.∴∠APB=∠CP′B=∠BP′P+∠PP′C=135°.3.解:将△CDQ绕C点旋转90°,得△CBM,则△CDO≌△CBM,∠QCM=90°.∵∠D=90°,∠CBA=90°,∴P、B、M在一条直线上.∵QA+AP+QP=2,DQ+AQ+AP+BP=2,∴QP=DQ+BP.∵BM=DQ,PM=PB+BM,∴QP=PM.又CP=CP,CQ=CM.∴△CQP≌△CMP.∴∠QCP=∠PCM.又∠QCP+∠PCM=∠QCM=900∴∠PCQ=45°.练习51.解:把△ADF绕A点旋转到△ABD′的位置.∵∠D和∠ABC均为直角,∴D′、B、E三点在一条直线上,∵∠EAF=45°,∴∠D′AE=45°.在△AD′E和△AEF中,AD′=AF,AE=AE,∠D′AE=∠EAF,∴△AD′E≌△AFE.∴S△D`EF =2S△AD`E =S ABEFD=S正方形ABCD-S△EFC.∴S△EFC =S正方形ABCD-S ABEFD=S正方形ABCD-2S△AD`E =82-2×12×8×7=8.2.解:将△ADC绕D点旋转180°得△BDE.∵BD=CD.- 11 - ∴C 与B 重合,设A 落到E 处,显然A 、D 、E 共线.在△ABE 中,BE=AC=13,AB=5,AE=2AD=12. 则有132=122+52.∴△ABE 为直角三角形,∠BAE=90°. 在Rt △ABD 中,AB=5,AD=6,则有BD=2256 =61.∴BC=2BD=261.3.证明:将△ABD 绕A 点旋转∠BAC 的度数, 得△ACE ,连结DE .由于AB=AC . ∴B 与C 重合,则△ABD ≌△ACE . ∵AD=AE ,∴∠1=∠2.∵∠AEC=∠ADB>∠ADC .∴∠4>∠3,∴CE<DC .∵BD=CE ,∴CD>BD .。
专题5 旋转(初中数学)
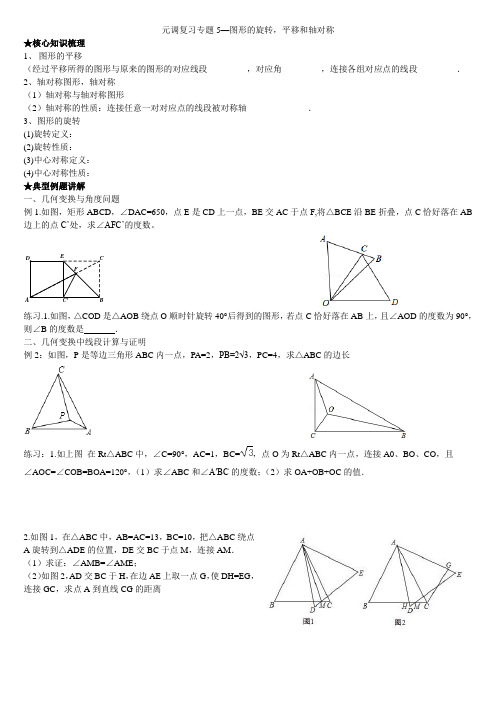
元调复习专题5—图形的旋转,平移和轴对称★核心知识梳理1、 图形的平移(经过平移所得的图形与原来的图形的对应线段_________,对应角_________,连接各组对应点的线段_________.2、轴对称图形,轴对称(1)轴对称与轴对称图形(2)轴对称的性质:连接任意一对对应点的线段被对称轴______________.3、图形的旋转(1)旋转定义:(2)旋转性质:(3)中心对称定义:(4)中心对称性质:★典型例题讲解一、几何变换与角度问题例1.如图,矩形ABCD ,∠DAC=650,点E 是CD 上一点,BE 交AC 于点F,将△BCE 沿BE 折叠,点C 恰好落在AB 边上的点C’处,求∠AFC’的度数。
练习.1.如图,△COD 是△AOB 绕点O 顺时针旋转40°后得到的图形,若点C 恰好落在AB 上,且∠AOD 的度数为90°,则∠B 的度数是 .二、几何变换中线段计算与证明例2:如图,P 是等边三角形ABC 内一点,PA=2,PB=2√3,PC=4,求△ABC 的边长练习:1.如上图 在Rt △ABC 中,∠C=90°,AC=1,BC=,点O 为Rt △ABC 内一点,连接A0、BO 、CO ,且∠AOC=∠COB=BOA=120°,(1)求∠ABC 和∠A′BC 的度数;(2)求OA+OB+OC 的值.2.如图1,在△ABC 中,AB=AC=13,BC=10,把△ABC 绕点A 旋转到△ADE 的位置,DE 交BC 于点M ,连接AM .(1)求证:∠AMB=∠AME ;(2)如图2,AD 交BC 于H ,在边AE 上取一点G ,使DH=EG,连接GC ,求点A 到直线CG 的距离3.如图,等腰Rt△ABC中,∠ACB=90°,AC=BC=1,且AC边在直线a上,将△ABC绕点A顺时针旋转到位置①可得到点P1,此时AP1=;将位置①的三角形绕点P1顺时针旋转到位置②,可得到点P2,此时AP2=1+;将位置②的三角形绕点P2顺时针旋转到位置③,可得到点P3,此时AP3=2+;…,按此规律继续旋转,直至得到点P2014为止.则AP2014= .三、几何变换与点的坐标例3.在平面直角坐标系中,O为原点,点A(-2,0),点B(0,2),点E,点F分别为OA,OB的中点.若正方形OEDF 绕点O顺时针旋转,得正方形OE’D’F’,记旋转角为α.(Ⅰ)如图①,当α=90°,求AE’,BF’ 的长;(Ⅱ)如图②,当α=135°,求证AE’ =BF’,且AE’ ⊥BF’;(Ⅲ)若直线AE’与直线BF’相交于点P,求点P的纵坐标的最大值(直接写出结果即可)练习:1.点A的坐标为(2,0),把点A绕着坐标原点旋转135º到点B,那么点B的坐标是_________ .2.如图,直线443y x=-+与x轴、y轴分别交于A、B两点,把AOB△绕点A顺时针旋转90°后得到AO B''△,则直线A B'的解析式是.3.(2013•武汉)如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(﹣3,2),B(0,4),C(0,2).(1)将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C;平移△ABC,若点A的对应点A2的坐标为(0,﹣4),画出平移后对应的△A2B2C2;(2)若将△A1B1C绕某一点旋转可以得到△A2B2C2;请直接写出旋转中心的坐标;(3)在x轴上有一点P,使得PA+PB的值最小,请直接写出点P的坐标.四、综合题例4. (2015•连云港)在数学兴趣小组活动中,小明进行数学探究活动,将边长为2的正方形ABCD与边长为2的正方形AEFG按图1位置放置,AD与AE在同一直线上,AB与AG在同一直线上.(1)小明发现DG⊥BE,请你帮他说明理由.(2)如图2,小明将正方形ABCD绕点A逆时针旋转,当点B恰好落在线段DG上时,请你帮他求出此时BE的长.(3)如图3,小明将正方形ABCD绕点A继续逆时针旋转,线段DG与线段BE将相交,交点为H,写出△GHE与△BHD 面积之和的最大值,并简要说明理由.练习:(2015北京东城)已知:Rt△A′BC′和Rt△ABC重合,∠A′C′B=∠ACB=90°,∠BA′C′=∠BAC=30°,现将Rt△A′BC′绕点B按逆时针方向旋转角α(60°≤α≤90°),设旋转过程中射线C′C和线段AA′相交于点D,连接BD.(1)当α=60°时,A’B 过点C,如图1所示,判断BD和A′A之间的位置关系,不必证明;BA C (2)当α=90°时,在图2中依题意补全图形,并猜想(1)中的结论是否仍然成立,不必证明;(3)如图3,对旋转角α(60°<α<90°),猜想(1)中的结论是否仍然成立;若成立,请证明你的结论;若不成立,请说明理由.【典型练习基础篇】一、选择题:( ) 1.如图所示的图案绕旋转中心旋转后能够与自身重合,那么它的旋转角可能是A .60ºB .90ºC .72ºD .120º()2.如图,△ABC 绕A 按逆时针方向旋转一定的角度后成为△AB′C′.则下列等式中:①BC=B′C′;②∠BAB′=∠CAC′;③∠ABC=∠AB′C′; ④△ABB′≌△ACC′.其中正确的结论有( )A .1个B .2个C .3个D .4个( )3.在“线段、等腰三角形、等边三角形、矩形、菱形、圆”这几个图形中,既是中心对称图形,又是轴对称图形的个数是 A .6个 B .5个 C .4个 D .3个( )4.在图形旋转中,下列说法错误的是A.图形上各对应点的旋转角度相同;B.对应点到旋转中心距离相等;C.由旋转得到的图形也一定可以由平移得到;D.旋转不改变图形的大小、形状( )5.在平面直角坐标系中,已知点C (0,3),D (1,7),将线段CD 绕点M (3,3)旋转180°后,得到线段AB ,则线段AB 所在直线的函数解析式是A .y=3x+15B .y=3x-15C .y=15x-3D .y=-15x+3( )6. 在等边△ABC 中,D 是边AC 上一点,连接BD ,将△BCD 绕点B 逆时针旋转60°,得到△BAE ,连接ED ,若BC=5,BD=4.则下列结论错误的是A .AE ∥BC ;B .∠ADE=∠BDC ; C .△BDE 是等边三角形;D . △ADE 的周长是9二、填空题7.如图,将Rt △ABC 绕直角顶点C 点逆时针旋转得到△A'CB',若∠A'CB=160º,则此图形旋转角是 度.第7题 第8题 第9题8.如图,在Rt △ABC 中,∠ACB=90°,∠B=60°,BC=2,△A′B′C 可以由△ABC 绕点C 顺时针旋转得到,其中点A′与点A 是对应点,点B′与点B 是对应点,连接AB′,且A 、B′、A′在同一条直线上,则AA′的长为9.如图,P 是正三角形ABC 内的一点,且PA=6,PB=•8,•PC=10,若将△PAC 绕点A 逆时针旋转后,•得到△P •′AB ,•则点P •与点P •′之间的距离为_____,∠APB=_______°.10.若点(a +l ,3)与点(-2,b -2)关于x 轴对称,则点P(-a ,b)关于原点的对称点坐标是 .三、解答题第1题图 第2题图第5题图 第6题图11.(1)点(1,2)绕原点O 逆时针旋转90°得到的点的坐标是 ;(2)直线y=2x 绕原点O 逆时针旋转90°得到的直线解析式是 ;(3)求直线y=2x+3绕原点O 逆时针旋转90°得到的直线解析式.12.(2015•武汉)如图,已知点A (﹣4,2),B (﹣1,﹣2),平行四边形ABCD 的对角线交于坐标原点O .(1)请直接写出点C 、D 的坐标;(2)写出从线段AB 到线段CD 的变换过程;(3)直接写出平行四边形ABCD 的面积.13.如图,正方形ABCD 和平行四边形CPEF ,点P 在射线AB 上,点E 在边AD 上,作FG ⊥AD 于G 。
人教版五年级数学下册第五单元图形的运动(三)——旋转教案

第1课时旋转(1)教学内容教科书P83~84例1、例2及“做一做”,完成教科书P85“练习二十一”中第1~3题。
教学目标1.进一步认识图形的旋转,明确含义,感悟其特征及性质。
会运用数学语言简单描述旋转运动的过程。
2.经历观察实例、操作想象、语言描述等活动,培养学生的推理能力。
积累几何活动经验,发展空间观念。
3.体验数学与生活的联系,学会用数学的眼光观察、思考生活,感受数学的美,体会数学的应用价值。
教学重点通过多种学习活动沟通联系,理解旋转的含义,初步感悟旋转的性质。
教学难点用数学语言描述物体的旋转过程。
教学准备课件,三角尺。
教学过程一、认识旋转要素1.课件出示生活实例,引出研究问题。
师:同学们,你们见过这些现象吗?仔细观察。
师:你们看见了什么?【学情预设】学生可能会说,看见风车在旋转,时钟转动起来等等。
师:看一看这些物体的运动,用我们学过的知识描述一下它们在做怎样的运动。
【学情预设】学生对图形的旋转已经具有了一定的认识,能够比较准确地感知生活中简单的旋转现象,并能对其进行判断。
仅有少数学生能够判断“道闸挡车杆的运动”和“秋千运动”是旋转现象,说明学生对旋转角度不是360°及比较复杂的旋转现象还不能做出正确判断。
师:这些物体的运动,都可以称为旋转运动。
在二年级的时候我们已经初步学习了生活中的旋转现象,能举几个例子吗?学生举例。
师:我也收集了一些生活中的实例,大家一起来看看。
选择一个你喜欢的,说说它是怎样旋转的。
◎教学笔记【教学提示】学生在回答“旋转”时,最好让学生对着具体的物体比画一下是怎样旋转。
课件展示生活中的动态旋转现象。
师:通过刚才的观察,你认为什么样的运动是旋转?学生简单描述后,教师板书课题:旋转(1)。
【设计意图】由于在第一阶段学习时,具体实例多是物体围绕一个点或一个轴做整圆周运动,所以部分学生形成了认识上的误区,认为只有转一圈才是旋转,所以本节课从学生的问题入手,选取学生熟悉的但又有争议的实例作为研究旋转现象的素材,有意识地引导学生探讨:“荡秋千属于平移还是旋转?”学生有明显的争议,以此产生认知冲突,引发探究的欲望。
2022-2023学年初二数学第二学期培优专题05 旋转之线段问题

2022-2023学年初二数学第二学期培优专题05 旋转之线段问题【模型讲解】数学探究课上老师出了这样一道题:“如图,等边ABC 中有一点P ,且3PA =,4PB =,5PC =,试求APB ∠的度数.”小明和小军探讨时发现了一种求APB ∠度数的方法,下面是这种方法的一部分思路,请按照下列思路要求画图或判断.(1)在图中画出APC △绕点A 顺时旋转60°后的1APB △,并判断1APP △的形状是_______;(2)试判断1BPP △的形状,并说明理由;(3)由(1)、(2)两问可知:APB ∠=___________. 【解答】(1)如图,△AP 1 B 为所作;连接PP 1, △AP 1 P 为等边三角形理由如下:∵△APC 绕点A 顺时针旋转60°后得△AP 1 B , ∴AP 1=AP ,∠PAP 1 = 60°, ∴△AP 1P 为等边三角形; (2)∵△AP 1P 为等边三角形;∴PP 1=AP =3,又根据旋转的性质得BP 1=PC =5,PP 12 + PB 2=32+42=25,BP 12=CP 2=52=25,∴PP 12 + PB 2=BP 12∴△BP 1P 为直角三角形,∠BPP 1 = 90°;(3)∵△APP 1为等边三角形,∴∠APP 1 = 60°,而∠BPP 1= 90°; ∴∠APB = 90°+ 60°= 150°,故答案为:150°.【模型演练】1.(1)如图1,P 是锐角ABC 内一动点,把APC △绕点A 逆时针旋转60°得到AP C '',连接PP ',这样就可得出PA PB PC BP PP P C '''++=++,请给出证明过程.(2)图2所示的是一个锐角为30°的直角三角形公园(30B ∠=︒,90C ∠=︒),其中顶点A 、B 、C 为公园的出入口,20km AB =,工人师傅准备在公园内修建一凉亭P ,使该凉亭到三个出入口的距离PA PB PC ++最小,求这个最小的距离.2.(1)如图1,正方形ABCD ,E 、F 分别为BC 、CD 上的点,45EAF ∠=︒,求证:EF BE DF =+小聪把△ABE 绕点A 逆时针旋转90°至△ADG ,从而发现EF BE FD =+,请你利用图1证明上述结论.(2)如图2,若点E 、F 分别在正方形ABCD 的边CB 、DC 的延长线上,45EAF ∠=︒,那么线段EF 、DF 、BE 之间有怎样的数量关系?请证明你的结论.3.旋转是一种重要的图形变换,当图形中有一组邻边相等时,往往可以通过旋转解决问题.如图①,在四边形ABCD 中,AD CD =,120ABC ∠=︒,60ADC ∠=︒,2AB =,1BC =.【问题提出】(1)如图②,在图①的基础上连接BD ,由于AD CD =,所以可将DCB △绕点D 顺时针方向旋转60°,得到DAB ',则BDB '的形状是_______;【尝试解决】(2)在(1)的条件下,求四边形ABCD 的面积; 【类比应用】(3)如图③,等边ABC 的边长为2,BDC 是顶角120BDC ∠=︒的等腰三角形,以D 为顶点作一个60°的角,角的两边分别交AB 于点M ,交AC 于点N ,连接MN ,求AMN 的周长.4.问题:如图(1),点E 、F 分别在正方形ABCD 的边BC 、CD 上,∠EAF =45°,试判断BE 、EF 、FD 之间的数量关系.(1)延长FD 到点G 使DG =BE ,连接AG ,得到至△ADG ,从而可以证明EF =BE +FD ,请你利用图(1)证明上述结论.(2)如图(2),四边形ABCD 中,90≠︒∠BAD ,AB =AD ,∠B +∠D =180°,点E 、F 分别在边BC 、CD 上,则当∠EAF 与∠BAD 满足______数量关系时,仍有EF =BE +FD ,并说明理由. 5.阅读下列材料:问题:如图(1),已知正方形ABCD 中,E 、F 分别是BC 、CD 边上的点,且∠EAF =45°.解决下列问题:(1)图(1)中的线段BE 、EF 、FD 之间的数量关系是______.(2)图(2),已知正方形ABCD 的边长为8,E 、F 分别是BC 、CD 边上的点,且∠EAF =45°,AG ⊥EF 于点G ,求△EFC 的周长.6.在等边BCD △中,DF BC ⊥于点F ,点A 为直线DF 上一动点,以点B 为旋转中心,把BA 顺时针旋转60°至BE .(1)如图1,点A 在线段DF 上,连接CE ,求证:CE DA =;(2)如图2,点A 在线段FD 的延长线上,请在图中画出BE 并连接CE ,当45DEC ∠=︒时,连接AC ,求出BAC ∠的度数;(3)在点A 的运动过程中,若6BD =,求EF 的最小值7.(1)如图1,O 是等边△ABC 内一点,连接OA 、OB 、OC ,且OA =3,OB =4,OC =5,将△BAO 绕点B 顺时针旋转后得到△BCD ,连接OD . 求:①旋转角的度数 ; ②线段OD 的长 ; ③求∠BDC 的度数.(2)如图2所示,O 是等腰直角△ABC (∠ABC =90°)内一点,连接OA 、OB 、OC ,将△BAO 绕点B 顺时针旋转后得到△BCD ,连接OD .当OA 、OB 、OC 满足什么条件时,∠ODC =90°?请给出证明.8.如图所示,正方形ABCD 中,点E 、F 、G 分别是边AD 、AB 、BC 的中点,连接EF ,FG .(1)如图1,直接写出EF与FG的关系______;(2)如图2,若点P为BC延长线上一动点,连接FP,将线段FP以点F为旋转中心,逆时针旋转90°,得到线段FH,连接EH.△;①求证:HFE≌PFG②直接写出EF、EH、BP三者之间的关系;9.如图1,若△ABC和△ADE为等边三角形,M,N分别为EB,CD的中点,易证:CD=BE,△AMN是等边三角形:(1)当把△ADE绕点A旋转到图2的位置时,CD=BE吗?若相等请证明,若不等于请说明理由;(2)当把△ADE绕点A旋转到图3的位置时,△AMN还是等边三角形吗?若是请证明,若不是,请说明理由(可用第一问结论).10.[方法探索]如图1,在等边ABC 中,点P 在ABC 内,且2PA =,4PC =,150APC ∠=︒,求PB 的长. 小敏在解决这个问题时,想到了以下思路:如图1,把APC △绕着点A 顺时针旋转60︒得到'AP B ,连接'PP ,分别证明AP P '△和BP P '△是特殊三角形,从而得解.请在此思路提示下,求出PB 的长.解:把APC △绕着点A 顺时针旋转60︒得到AP B '△,连接PP '. 接着写下去: 11.[方法应用]请借鉴上述利用旋转构图的方法,解决下面问题:①如图2,点P 在等边ABC 外,且3PA PB ==,120APB ∠=︒,若33AB =PBC ∠度数. ②如图3,在ABC 中,90BAC ∠=︒,10AB AC =P 是ABC 外一点,连接PA 、PB 、PC .已知45APB ∠=︒,2PB =.求PC 的长.12.婆罗摩笈多(Brahmagupta )约公元598年生,约660年卒,在数学、天文学方面有所成就. 婆罗摩笈多是印度印多尔北部乌贾因地方人,原籍可能为巴基斯坦的信德. 婆罗摩笈多的一些数学成就在世界数学史上有较高的地位. 例如下列模型就被称为“婆罗摩笈多模型”:如图1,2,3,△ABC 中,分别以AB ,AC 为边作Rt △ABE 和Rt △ACD ,AB =AE ,AC =AD ,∠BAE =∠CAD =90°,则有下列结论:①图1中S △ABC =S △ADE ;②如图2中,若AM 是边BC 上的中线,则ED =2AM ;③如图3中,若AM ⊥BC ,则MA 的延长线平分ED 于点N .(1)上述三个结论中请你选择一个感兴趣的结论进行证明,写出证明过程;(2)能力拓展:将上述图形中的某一个直角三角形旋转到如图4所示的位置:△ABC 与△ADE 均为等腰直角三角形,∠BAC =∠DAE =90°,连接BD ,CE ,若F 为BD 的中点,连接AF ,求证:2AF =CE .13.数学探究课上老师出了这样一道题:“如图,等边ABC 中有一点P ,且3PA =,4PB =,5PC =,试求APB ∠的度数.”小明和小军探讨时发现了一种求APB ∠度数的方法,下面是这种方法的一部分思路,请按照下列思路要求画图或判断.(1)在图中画出APC △绕点A 顺时旋转60°后的1APB △,并判断1APP △的形状是___________; (2)试判断1BPP △的形状,并说明理由;(3)由(1)、(2)两问可知:APB ∠=___________.答案与解析【模型讲解】数学探究课上老师出了这样一道题:“如图,等边ABC 中有一点P ,且3PA =,4PB =,5PC =,试求APB ∠的度数.”小明和小军探讨时发现了一种求APB ∠度数的方法,下面是这种方法的一部分思路,请按照下列思路要求画图或判断.(1)在图中画出APC △绕点A 顺时旋转60°后的1APB △,并判断1APP △的形状是_______;(2)试判断1BPP △的形状,并说明理由;(3)由(1)、(2)两问可知:APB ∠=___________. 【解答】(1)如图,△AP 1 B 为所作;连接PP 1, △AP 1 P 为等边三角形理由如下:∵△APC 绕点A 顺时针旋转60°后得△AP 1 B , ∴AP 1=AP ,∠PAP 1 = 60°, ∴△AP 1P 为等边三角形;(2)∵△AP 1P 为等边三角形;∴PP 1=AP =3,又根据旋转的性质得BP 1=PC =5,PP 12 + PB 2=32+42=25,BP 12=CP 2=52=25,∴PP 12 + PB 2=BP 12∴△BP 1P 为直角三角形,∠BPP 1 = 90°;(3)∵△APP 1为等边三角形,∴∠APP 1 = 60°,而∠BPP 1= 90°; ∴∠APB = 90°+ 60°= 150°,故答案为:150°.【模型演练】1.(1)如图1,P 是锐角ABC 内一动点,把APC △绕点A 逆时针旋转60°得到AP C '',连接PP ',这样就可得出PA PB PC BP PP P C '''++=++,请给出证明过程.(2)图2所示的是一个锐角为30°的直角三角形公园(30B ∠=︒,90C ∠=︒),其中顶点A 、B 、C 为公园的出入口,20km AB =,工人师傅准备在公园内修建一凉亭P ,使该凉亭到三个出入口的距离PA PB PC ++最小,求这个最小的距离.【答案】(1)见解析;(2)107km【分析】(1)根据旋转的性质证明△APP'是等边三角形,即可得出结论;(2)如图,将△BPC绕点B逆时针旋转60度得到△BP′C′,连接PP′,构建直角△ABC',利用勾股定理求AC'的长,即是点P到这个三角形各顶点的距离之和的最小值.【解答】(1)如图1,由旋转得:∠PAP'=60°,PA=P'A,∴△APP'是等边三角形,∴PP'=PA,∵PC=P'C,∴PA+PB+PC=BP+PP′+P′C′;(2)解:在Rt△ACB中,∵AB=20,∠ABC=30°,∴AC=10,BC=103,如图,将△BPC绕点B逆时针旋转60度得到△BP′C′,连接PP′,当A、P、P'、C'在同一直线上时,PA+PB+PC的值为最小,由旋转得:BP=BP',∠PBP'=60°,PC=P'C',BC=BC',∴△BPP′是等边三角形,∴PP'=PB,∵∠ABC=∠APB+∠CBP=∠APB+∠C'BP'=30°,∴∠ABC'=90°,由勾股定理得:222220(103)107,AC AB C B ''=+=+= ∴PA +PB +PC =PA +PP '+P 'C '=AC '=107,则点P 到这个三角形各顶点的距离之和的最小值为107km .【点评】本题主要考查三角形的旋转变换的性质、勾股定理、等边三角形的判定与性质等知识点,将待求线段的和通过旋转变换转化为同一直线上的线段来求是解题的关键,学会利用旋转的方法添加辅助线,构造特殊三角形解决问题.2.(1)如图1,正方形ABCD ,E 、F 分别为BC 、CD 上的点,45EAF ∠=︒,求证:EF BE DF =+小聪把△ABE 绕点A 逆时针旋转90°至△ADG ,从而发现EF BE FD =+,请你利用图1证明上述结论.(2)如图2,若点E 、F 分别在正方形ABCD 的边CB 、DC 的延长线上,45EAF ∠=︒,那么线段EF 、DF 、BE 之间有怎样的数量关系?请证明你的结论.【答案】(1)见解析;(2)DF EF BE =+,理由见解析【分析】(1)根据旋转的性质及全等三角形的判定和性质证明即可;(2)把△ABE 绕点A 逆时针旋转90°至△ADG ,结合(1)中证明方法进行证明即可. 【解答】证明:(1)∵AB AD =,∴把△ABE 绕点A 逆时针旋转90°至△ADG ,可使AB 与AD 重合, ∵90ADC B ∠=∠=︒,∴180FDG ∠=︒,即点F 、D 、G 共线, ∴DAG BAE ∠∠=,AE AG =,+904545FAG FAD GAD FAD EAE EAF =+==︒-︒=︒=∠∠∠∠∠∠,即EAF FAG ∠=∠.∵AF AF =,AE AG =∴AFG AFE ≌∴EF FG =.∴EF DF DG DF BE =+=+,即EF BE DF =+(2)DF EF BE =+.理由:如图2所示.∵AB AD =,∴把△ABE 绕点A 逆时针旋转90°至△ADG ,使AB 与AD 重合,∵90ADC ABE ∠=∠=︒∴点C 、D 、G 在一条直线上.∴EB DG =,AE AG =,EAB GAD ∠=∠.∵90BAG GAD ∠+∠=︒∴90EAG BAD ∠=∠=︒.∵45EAF ∠=︒∴904545FAG EAG EAF ∠=∠-∠=︒-︒=︒∴EAF GAF ∠=∠.∴EAF GAF △≌△∴EF FG =∵FD FG DG =+∴DF EF BE =+.【点评】题目主要考查旋转的性质及全等三角形的判定和性质,正方形的性质等,理解题意,熟练掌握全等三角形的判定和性质是解题关键.3.旋转是一种重要的图形变换,当图形中有一组邻边相等时,往往可以通过旋转解决问题.如图①,在四边形ABCD 中,AD CD =,120ABC ∠=︒,60ADC ∠=︒,2AB =,1BC =.【问题提出】(1)如图②,在图①的基础上连接BD ,由于AD CD =,所以可将DCB △绕点D 顺时针方向旋转60°,得到DAB ',则BDB '的形状是_______;【尝试解决】(2)在(1)的条件下,求四边形ABCD 的面积;【类比应用】(3)如图③,等边ABC 的边长为2,BDC 是顶角120BDC ∠=︒的等腰三角形,以D 为顶点作一个60°的角,角的两边分别交AB 于点M ,交AC 于点N ,连接MN ,求AMN 的周长. 【答案】(1)等边三角形(2)934(3)4【分析】(1)由旋转的性质得出BD =DB ′,∠BDB ′=60°,所以△BDB ′是等边三角形;(2)求出等边三角形的边长为3,求出三角形BDB ′的面积即可;(3)将△BDM 绕点D 顺时针方向旋转120°,得到△DCP ,则△BDM ≌△CDP ,得出MD =PD ,∠MBD =∠DCP ,∠MDB =∠PDC ,证明△NMD ≌△NPD ,证得△AMN 的周长=AB +AC =4.【解答】(1)解:∵将△DCB 绕点D 顺时针方向旋转60°,得到△DAB ′,∴BD =B ′D ,∠BDB ′=60°,∴△BDB ′是等边三角形;故答案为:等边三角形;(2)解:由(1)知,△BCD ≌△B ′AD ,∴四边形ABCD 的面积=等边三角形BDB ′的面积,∵BC =AB ′=1,∴BB ′=AB +AB ′=2+1=3,∴S四边形ABCD=S△BDB′=133933224⨯⨯=;(3)解:将△BDM绕点D顺时针方向旋转120°,得到△DCP,∴△BDM≌△CDP,∴MD=PD,CP=BM,∠MBD=∠DCP,∠MDB=∠PDC,∵△BDC是等腰三角形,且∠BDC=120°,∴BD=CD,∠DBC=∠DCB=30°,又∵△ABC等边三角形,∴∠ABC=∠ACB=60°,∴∠MBD=∠ABC+∠DBC=90°,同理可得∠NCD=90°,∴∠PCD=∠NCD=∠MBD=90°,∴∠DCN+∠DCP=180°,∴N,C,P三点共线,∵∠MDN=60°,∴∠MDB+∠NDC=∠PDC+∠NDC=∠BDC﹣∠MDN=60°,即∠MDN=∠PDN=60°,∴△NMD≌△NPD(SAS),∴MN=PN=NC+CP=NC+BM,∴△AMN的周长=AM+AN+MN=AM+AN+NC+BM=AB+AC=2+2=4.故△AMN的周长为4.【点评】本题是四边形综合题,考查了图形的旋转变换,等边三角形的判定与性质,全等三角形的判定与性质,类比思想等.熟练掌握旋转的性质是解决问题的关键.4.问题:如图(1),点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,试判断BE、EF、FD之间的数量关系.(1)延长FD 到点G 使DG =BE ,连接AG ,得到至△ADG ,从而可以证明EF =BE +FD ,请你利用图(1)证明上述结论.(2)如图(2),四边形ABCD 中,90≠︒∠BAD ,AB =AD ,∠B +∠D =180°,点E 、F 分别在边BC 、CD 上,则当∠EAF 与∠BAD 满足______数量关系时,仍有EF =BE +FD ,并说明理由. 【答案】(1)见解析(2)2BAD EAF ∠∠=,理由见解析【分析】(1)根据旋转变换的性质得到△ADG ≌△ABE ,根据全等三角形的性质得到AG =AE ,∠DAG =∠BAE ,DG =BE ,∠ADG =∠ABE =90°,证明∠AFE ≌△AFG ,根据全等三角形的性质证明;(2)延长CB 至M ,使BM =DF ,连接AM ,证明△EAF ≌△EAM ,根据全等三角形的性质证明;(1)延长FD 到点G 使DG =BE ,连接AG .如图(1),在正方形ABCD 中,AB =AD ,90,BAD ADC B ∠=∠=∠=︒在ABE ∆和ADG ∆中,AB AD ABE ADG BE DG =⎧⎪∠=∠⎨⎪=⎩ABE ∴∆≌ADG ∆(SAS ),BAE GAD AE AG ∴∠=∠=45GAD DAF BAE DAF ∴∠+∠=∠+∠=︒45EAF GAF ∴=∠=∠︒在AEF ∆和AGF ∆中,GA EA GAF EAF AF AF =⎧⎪∠=∠⎨⎪=⎩∴AEF ∆≌AGF ∆EF GF GD DF BE DF ∴==+=+(2)2BAD EAF ∠∠=理由如下:如图,延长CB 至M ,使BM =DF ,连接AM ,180,180ABC D ABC ABM ∠+∠=︒∠+∠=︒D ABM ∠∠∴=在ABM ∆和ADF ∆中,AB AD ABM D BM DF =⎧⎪∠=∠⎨⎪=⎩ABM ∴∆≌ADF ∆,AF AM DAF BAM ∴=∠=∠2BAD EAF ∠∠=DAF BAE BAM BAE EAF ∴∠+∠=∠+∠=∠EAF EAM ∴∠=∠在EAF ∆和ΔEAM 中,AF AM EAF EAM AE AE =⎧⎪∠=∠⎨⎪=⎩∴EAF ∆≌ΔEAMEF EM BE BM BE DF ∴==+=+EF BE DF ∴=+【点评】本题考查的是正方形的性质、旋转变换的性质、正方形的性质,掌握正方形的性质定理、全等三角形的判定定理和性质定理是解题的关键.5.阅读下列材料:问题:如图(1),已知正方形ABCD中,E、F分别是BC、CD边上的点,且∠EAF=45°.解决下列问题:(1)图(1)中的线段BE、EF、FD之间的数量关系是______.(2)图(2),已知正方形ABCD的边长为8,E、F分别是BC、CD边上的点,且∠EAF=45°,AG⊥EF于点G,求△EFC的周长.【答案】(1)EF=BE+DF(2)过程见解析【分析】对于(1),先将△DAF绕点A顺时针旋转90°,得到△BAH,可得△ADF≌△ABH,再根据全等三角形的性质得AF=AH,∠EAF=∠EAH,然后根据“SAS”证明△FAE≌△HAE,根据全等三角形的对应边相等得出答案;对于(2),先根据(1),得△FAE≌△HAE,可得AG=AB=AD,再根据“HL”证明Rt△AEG≌Rt△ABE,得EG=BE,同理GF=DF,可得答案.(1)EF=BE+DF.理由如下:如图,将△DAF绕点A顺时针旋转90°,得到△BAH,∴△ADF≌△ABH,∴∠DAF=∠BAH,AF=AH,∴∠EAF=∠EAH=45°.∵AE=AE,∴△FAE≌△HAE,∴EF=HE=BE+HB,∴EF=BE+DF;(2)由(1),得△FAE ≌△HAE ,AG ,AB 分别是△FAE 和△HAE 的高,∴AG=AB=AD=8.在Rt △AEG 和Rt △ABE 中,AE AE AG AB =⎧⎨=⎩, ∴Rt △AEG ≌Rt △ABE (HL ),∴EG=BE ,同理GF=DF ,∴△EFG 的周长=EC+EF+FC=EC+EG+GF+FC=EC+BE+DF+FC=BC+CD=16.【点评】这是一道关于正方形和旋转的综合题目,考查了旋转的性质,正方形的性质,全等三角形的判定和性质等.6.在等边BCD △中,DF BC ⊥于点F ,点A 为直线DF 上一动点,以点B 为旋转中心,把BA 顺时针旋转60°至BE .(1)如图1,点A 在线段DF 上,连接CE ,求证:CE DA =;(2)如图2,点A 在线段FD 的延长线上,请在图中画出BE 并连接CE ,当45DEC ∠=︒时,连接AC ,求出BAC ∠的度数;(3)在点A 的运动过程中,若6BD =,求EF 的最小值 在DBA 与△BD BC DBA BA BE =∠=∠=DBA ≌△解:如图3,由(1)可知,DBA CBE ≌△△,∴DA CE =,BDA BCE ∠=∠,又∵BCD △是等边三角形,∴60BDC BCD ∠=∠=︒,DB DC =,∵DB DC =,∴△BCD 是等腰三角形,∵DF BC ⊥,∴1302BDF BDC ∠=∠=︒, ∴180150BDA BDF ∠=︒-∠=︒,∴150BCE ∠=︒,360150CDA BDA BDC ∠=︒-∠-∠=︒,∴90DCE BCE BCD ∠=∠-∠=︒,∵45DEC ∠=︒,∴45EDC ∠=︒,∴DEC EDC ∠=∠,∴CE CD =,∴DB DC DA ==,∴180152BDA BAD ︒-∠∠==︒,180152CDA CAD ︒-∠∠==︒, ∴30BAC BAD CAD ∠=∠+∠=︒.(3)解:∵由图1可知,当点A 在线段DF 上时,30BCE BDA ∠=∠=︒;由图3可知,当点A 在线段FD 的延长线上时,150BCE BDA ∠=∠=︒;由图4可知,当点A 在线段DF 的延长线上时,30BCE BDA ∠=∠=︒;∴综上所述,当点A 在直线DF 上运动时,直线CE 与直线BC 的夹角始终为30°,即点E 的运动轨迹为一条直线,过点F 作FE EC '⊥于点E ',则当点E 运动到点E '时,此时EF 的长度最短,∵6BD CD BC ===,DF BC ⊥,∴132CF BC ==,又∵FE EC '⊥,30BCE ∠=︒,∴1322FE CF '==, ∴EF 的最小值为32. 【点评】此考查了旋转的性质、全等三角形的判定和性质、等边三角形的性质、直角三角形的性质、三角形的内角和、等腰三角形的判定和性质等知识,分类讨论是解决问题的关键.7.(1)如图1,O 是等边△ABC 内一点,连接OA 、OB 、OC ,且OA =3,OB =4,OC =5,将△BAO 绕点B 顺时针旋转后得到△BCD ,连接OD .求:①旋转角的度数 ;②线段OD 的长 ;③求∠BDC 的度数.(2)如图2所示,O 是等腰直角△ABC (∠ABC =90°)内一点,连接OA 、OB 、OC ,将△BAO 绕点B 顺时针旋转后得到△BCD ,连接OD .当OA 、OB 、OC 满足什么条件时,∠ODC =90°?请给出证明.【答案】(1)①60°;②4;③150°;(2)当OA、OB、OC满足OA2+2OB2=OC2时,∠ODC=90°,见解析【分析】(1)①根据等边三角形的性质得BA=BC,∠ABC=60°,再根据旋转的性质得∠OBD=∠ABC=60°,于是可确定旋转角的度数为60°;②由旋转的性质得BO=BD,加上∠OBD=60°,则可判断△OBD为等边三角形,所以OD=OB=4;③由△BOD为等边三角形得到∠BDO=60°,再利用旋转的性质得CD=AO=3,然后根据勾股定理的逆定理可证明△OCD为直角三角形,∠ODC=90°,所以∠BDC=∠BDO+∠ODC=150°;(2)根据旋转的性质得∠OBD=∠ABC=90°,BO=BD,CD=AO,则可判断△OBD为等腰直角三角形,则OD=2OB,然后根据勾股定理的逆定理,当222+=时,△OCD为直角三角形,∠ODC=90°.CD OD OC【解答】解:(1)①∵△ABC为等边三角形,∴BA=BC,∠ABC=60°,∵△BAO绕点B顺时针旋转后得到△BCD,∴∠OBD=∠ABC=60°,∴旋转角的度数为60°;②∵△BAO绕点B顺时针旋转后得到△BCD,∴BO=BD,而∠OBD=60°,∴△OBD为等边三角形;∴OD=OB=4;③∵△BOD为等边三角形,∴∠BDO=60°,∵△BAO绕点B顺时针旋转后得到△BCD,∴CD=AO=3,在△OCD中,CD=3,OD=4,OC=5,∵32+42=52,∴CD2+OD2=OC2,∴△OCD为直角三角形,∠ODC=90°,∴∠BDC=∠BDO+∠ODC=60°+90°=150°;(2)OA2+2OB2=OC2时,∠ODC=90°.理由如下:∵△BAO绕点B顺时针旋转后得到△BCD,∴∠OBD=∠ABC=90°,BO=BD,CD=AO,∴△OBD为等腰直角三角形,∴OD=2OB,∵当CD2+OD2=OC2时,△OCD为直角三角形,∠ODC=90°,∴OA2+2OB2=OC2,∴当OA、OB、OC满足OA2+2OB2=OC2时,∠ODC=90°.【点评】本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了等边三角形的判断与性质和勾股定理的逆定理.8.如图所示,正方形ABCD中,点E、F、G分别是边AD、AB、BC的中点,连接EF,FG.(1)如图1,直接写出EF与FG的关系______;(2)如图2,若点P为BC延长线上一动点,连接FP,将线段FP以点F为旋转中心,逆时针旋转90°,得到线段FH,连接EH.①求证:HFE≌PFG△;②直接写出EF、EH、BP三者之间的关系;∴HFE≌△②解:22EF∵HFE≌△EH PG=AE AF==∴22EF AF BG==,∴22BG EF=,∵BG GP BP+=,∴22EF EH BP+=【点评】本题是四边形综合题,考查了正方形的性质,全等三角形的判定和性质,等腰直角三角形的性质,旋转的性质,证明△HFE≌△PFG是解题的关键.9.如图1,若△ABC和△ADE为等边三角形,M,N分别为EB,CD的中点,易证:CD=BE,△AMN是等边三角形:(1)当把△ADE绕点A旋转到图2的位置时,CD=BE吗?若相等请证明,若不等于请说明理由;(2)当把△ADE绕点A旋转到图3的位置时,△AMN还是等边三角形吗?若是请证明,若不是,请说明理由(可用第一问结论).【答案】(1)CD=BE.理由见解析;(2)△AMN是等边三角形.理由见解析.【分析】(1)CD=BE.利用“等边三角形的三条边相等、三个内角都是60°”的性质证得△ABE≌△ACD;然后根据全等三角形的对应边相等即可求得结论CD=BE;(2)△AMN 是等边三角形.首先利用全等三角形“△ABE ≌△ACD ”的对应角相等、已知条件“M 、N 分别是BE 、CD 的中点”、等边△ABC 的性质证得△ABM ≌△ACN ;然后利用全等三角形的对应边相等、对应角相等求得AM =AN 、∠NAM =∠NAC +∠CAM =∠MAB +∠CAM =∠BAC =60°,所以有一个角是60°的等腰三角形的正三角形.【解答】(1)CD =BE .理由如下:∵△ABC 和△ADE 为等边三角形,∴AB =AC ,AD =AE ,∠BAC =∠EAD =60°,∵∠BAE =∠BAC ﹣∠EAC =60°﹣∠EAC ,∠DAC =∠DAE ﹣∠EAC =60°﹣∠EAC ,∴∠BAE =∠DAC ,在△ABE 和△ACD 中,=AB AC BAE DAC AE AD =⎧⎪∠∠⎨⎪=⎩,∴△ABE ≌△ACD (SAS )∴CD =BE ;(2)△AMN 是等边三角形.理由如下:∵△ABE ≌△ACD ,∴∠ABE =∠ACD .∵M 、N 分别是BE 、CD 的中点,∴BM =CN ,∵AB =AC ,∠ABE =∠ACD ,在△ABM 和△ACN 中,=BM CN ABE ACD AB AC =⎧⎪∠∠⎨⎪=⎩,∴△ABM ≌△ACN (SAS ).∴AM =AN ,∠MAB =∠NAC .∴∠NAM =∠NAC +∠CAM =∠MAB +∠CAM =∠BAC =60°.∴△AMN 是等边三角形.【点评】本题考查了等边三角形的性质、全等三角形的判定与性质、旋转的性质.等边三角形的判定:有一个角是60°的等腰三角形是等边三角形.10.[方法探索]如图1,在等边ABC 中,点P 在ABC 内,且2PA =,4PC =,150APC ∠=︒,求PB 的长. 小敏在解决这个问题时,想到了以下思路:如图1,把APC △绕着点A 顺时针旋转60︒得到'AP B ,连接'PP ,分别证明AP P '△和BP P '△是特殊三角形,从而得解.请在此思路提示下,求出PB 的长.解:把APC △绕着点A 顺时针旋转60︒得到AP B '△,连接PP '.接着写下去:11.[方法应用]请借鉴上述利用旋转构图的方法,解决下面问题:①如图2,点P 在等边ABC 外,且3PA PB ==,120APB ∠=︒,若33AB =PBC ∠度数. ②如图3,在ABC 中,90BAC ∠=︒,10AB AC =P 是ABC 外一点,连接PA 、PB 、PC .已知45APB ∠=︒,2PB =.求PC 的长. 【答案】10.PB =25 11.PBC ∠=90°;PC =210【分析】(1)把APC △绕着点A 顺时针旋转60︒得到'AP B ,连接'PP ,易证明AP P '△是等边三角形,BP P '△是直角三角形,根据勾股定理即可求出BP .(2)①把APB △绕着点A 逆时针旋转60︒得到'AP C ,连接'PP ,易证明AP P '△是等边三角形,BP P '△是等边,△BPC 是直角三角形,则可得到PBC ∠=90°.②将△APC 绕点A 逆时针旋转90°得到△'ABP ,连接'PP ,过B 点做BM 垂直于AP 于M 点,易证明△PBM 是等腰直角三角形,△'P PB 是直角三角形,用勾股定理即可求出PC .10.AP B '△由△APC 旋转60°得到∴AP ='AP =2,PC ='BP =4,∠'PAP =60°∴△'PAP 为等边三角形∴ AP ='AP ='PP =2,'AP P ∠=60°150APC ∠=︒∴'BP P ∠=90°在Rt △'BP P 中,由勾股定理可得:BP =22''BP PP +=2224+=2511.把APB △绕着点B 顺时针旋转60︒得到'BP C ,连接'PP'BP C 由△APB 逆时针旋转60°得到∴AP ='P C =3,PB ='BP =3,∠'PBP =60°,'120APB BP C ∠=∠=︒∴△'PBP 为等边三角形,∴'PP =PB =3'BP C ∠=120°,∠'BP P =60°∴∠'CP P =180°,即'C P P 、、三点共线.∴PC ='CP +'PP =6在△PBC 中,PC =6,PB =3,BC =33223223(33)36PB BC PC +=+==∴△PBC 是直角三角形,故PBC ∠=90°.将△APC 绕点A 顺时针旋转90°得到△'ABP ,连接'PP ,过B 点做BM 垂直于AP 于M 点45APB ∠=︒,BM ⊥AP ,PB =2∴PM =BM =2AB =10在Rt △AMB 中,AM =2210222AB BM -=-=∴AP =PM +AM =32△'ABP 由△APC 旋转90°所得∴ AP ='AP =32,∠'PAP =90°,∠'PP A =45°在Rt △'PAP 中,'PP =22'6AP AP +=∠'PP A =45°,45APB ∠=︒∴'P PB =90°在Rt △'P PB 中,22''210P B P P PB =+=∴PC ='P B =210【点评】本题主要考查了旋转和直角三角形相关内容,注意旋转后的图形要能够和原图构造出特殊的三角形才有利于解题,正确的做出旋转后的图形和辅助线是解题的关键.12.婆罗摩笈多(Brahmagupta )约公元598年生,约660年卒,在数学、天文学方面有所成就. 婆罗摩笈多是印度印多尔北部乌贾因地方人,原籍可能为巴基斯坦的信德. 婆罗摩笈多的一些数学成就在世界数学史上有较高的地位. 例如下列模型就被称为“婆罗摩笈多模型”:如图1,2,3,△ABC 中,分别以AB ,AC 为边作Rt △ABE 和Rt △ACD ,AB =AE ,AC =AD ,∠BAE =∠CAD =90°,则有下列结论: ①图1中S △ABC =S △ADE ;②如图2中,若AM 是边BC 上的中线,则ED =2AM ;③如图3中,若AM ⊥BC ,则MA 的延长线平分ED 于点N .(1)上述三个结论中请你选择一个感兴趣的结论进行证明,写出证明过程;(2)能力拓展:将上述图形中的某一个直角三角形旋转到如图4所示的位置:△ABC 与△ADE 均为等腰直角三角形,∠BAC =∠DAE =90°,连接BD ,CE ,若F 为BD 的中点,连接AF ,求证:2AF =CE .【答案】(1)①证明见解答;②证明见解答;③证明见解答;(2)证明见解答.【分析】(1)①取DE 中点F ,过E 作EG ∥AD ,交射线AF 于G ,先证△GEF ≌△ADF (AAS ),得出S △EAD =S △GEA ,再证△GEA ≌△CAB (SAS )即可;②取DE 中点F ,过E 作EG ∥AD ,交射线AF 于G ,先证△GEF ≌△ADF (AAS ),得出∠BAC =∠GEA ,再证△GEA ≌△CAB (SAS ),得出∠EAG =∠ABC ,AC =AG ,由AM 是边BC 上的中线,得出BM =CM =AF ,三证△EAF ≌△ABM (SAS )即可;③过E 作EP ⊥MN 交MN 延长线于O ,过D 作DO ⊥MN 于O ,先证∠ABM =∠EAP ,∠MCA =∠OAD ,证明△EAP ≌△ABM (AAS ),再证△CAM ≌△ADO (AAS ),三证△EPN ≌△DON (AAS )即可.(2)延长AF ,使FQ =AF ,连接DQ ,将△ACE 绕点A 逆时针旋转90°,得△ARD ,由点F 为BD 中点,可得DF =BF ,先证△DQF ≌△BAF (SAS ),DQ =BA =AC ,∠FDQ =∠FBA ,可证DQ ∥BA ,根据△ACE 绕点A 逆时针旋转90°得△ARD ,可得AR =AC =AB =QD ,RD =CE ,证明R 、A 、B 三点共线,再证△DQA ≌△ARD (SAS ),即可.【解答】(1)①图1中S △ABC =S △ADE ;证明:取DE 中点F ,过E 作EG ∥AD ,交射线AF 于G ,∵点F 为DE 中点,∴EF =DF ,∵EG ∥AD ,∴∠GEF =∠ADF ,∠GEA +∠EAD =180°,在△GEF 和△ADF 中,GFE AFD GEF ADF EF DF ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△GEF ≌△ADF (AAS ),∴GE =AD ,∠G =∠DAF ,∴S △GEF =S △ADF ,∴S △EAD =S △GEA ,∵∠BAE =∠CAD =90°,∴∠BAC +∠EAD =360°-∠BAE -∠CAD =180°∴∠BAC +∠EAD =∠GEA +∠EAD =180°∴∠BAC =∠GEA ,∴GE =AD =AC ,在△GEA 和△CAB 中,GE CA GEA CAB EA AB =⎧⎪∠=∠⎨⎪=⎩,∴△GEA ≌△CAB (SAS ),∴S △ABC =S △GEA=S △ADE ;②如图2中,若AM 是边BC 上的中线,则ED =2AM ; 证明:取DE 中点F ,过E 作EG ∥AD ,交射线AF 于G , ∵点F 为DE 中点,∴EF =DF ,∵EG ∥AD ,∴∠GEF =∠ADF ,∠GEA +∠EAD =180°,在△GEF 和△ADF 中,GFE AFD GEF ADF EF DF ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△GEF ≌△ADF (AAS ),∴GE =AD ,GF =AF =12AG ∵∠BAE =∠CAD =90°,∴∠BAC +∠EAD =360°-∠BAE -∠CAD =180°∴∠BAC +∠EAD =∠GEA +∠EAD =180°∴∠BAC =∠GEA ,∴GE =AD =AC ,在△GEA 和△CAB 中,GE CA GEA CAB EA AB =⎧⎪∠=∠⎨⎪=⎩,∴∠EAG =∠ABC ,AC =AG ,∵AM 是边BC 上的中线,∴BM =CM =1122BC AG AF ==, 在△EAF 和△ABM 中,EA AB EAF ABM AF BM =⎧⎪∠=∠⎨⎪=⎩,∴△EAF ≌△ABM (SAS ),∴EF =AM ,∵点F 为DE 中点,∴DE =2EF =2AM ,③如图3中,若AM ⊥BC ,则MA 的延长线平分ED 于点N .证明:过E 作EP ⊥MN 交MN 延长线于O ,过D 作DO ⊥MN 于O ,∵∠BAE =90°,∠DAC =90°,∴∠BAM +∠EAP =90°,∠MAC +∠DAO =90°,∵AM ⊥BC ,∴∠ABM +∠BAM =90°,∠MCA +∠MAC =90°∴∠ABM =∠EAP ,∠MCA =∠OAD ,∵EP ⊥MN ,∴∠EPA =90°在△EAP 和△ABM 中,90EPA AMB EAP ABMEA AB ∠=∠=︒⎧⎪∠=∠⎨⎪=⎩,∴EP =AM ,∵DO ⊥MN ,∴∠AOD =90°,在△CAM 和△ADO 中,CMA AOD MCA OAD AC DA ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△CAM ≌△ADO (AAS )∴AM =DO ,∴EP =DO =AM ,在△EPN 和△DON 中,90EPN DON ENP DNOEP DO ∠=∠=︒⎧⎪∠=∠⎨⎪=⎩∴△EPN ≌△DON (AAS ),∴EN =DN ,∴MA 的延长线平分ED 于点N .(2)延长AF ,使FQ =AF ,连接DQ ,将△ACE 绕点A 逆时针旋转90°,得△ARD∵点F 为BD 中点,∴DF =BF ,在△DQF 和△BAF 中,QF AF DFQ BFA DF BF =⎧⎪∠=∠⎨⎪=⎩∴△DQF ≌△BAF (SAS ),∴DQ =BA =AC ,∠FDQ =∠FBA ,∴DQ ∥BA ,∵△ACE 绕点A 逆时针旋转90°得△ARD∴△ACE ≌△ARD ,∠RAC =90°,∴AR =AC =AB =QD ,RD =CE ,∵∠CAB =90°,∴∠RAB =∠RAC +∠CAB =90°+90°=180°,∴R 、A 、B 三点共线,∵DQ ∥BA ,∴∠QDA =∠RAD ,在△DQA 和△ARD 中,DQ AR QDA RAD DA AD =⎧⎪∠=∠⎨⎪=⎩∴△DQA ≌△ARD (SAS ),∴AQ =DR ,∴2AF =AG =DR =CE ,∴2AF =CE .【点评】本题考查三角形全等判定与性质,三角形面积,中线加倍,三角形中线性质,等腰直角三角形性质,图形旋转变换性质,三点共线,掌握以上知识,尤其是利用辅助线作出准确图形是解题关键.。
中考数学旋转专题中的常见模型

旋转专题1、图形的旋转(1)在平面内,将一个图形绕一个定点沿某个方向旋转一个角度,这样的图形运动称为旋转,这个定点称为旋转中心,转动的角度称为旋转角.(2)性质:①在图形旋转过程中,图形上每一个点都绕旋转中心沿相同方向转动了相同角度;②注意每一对对应点与旋转中心的连线所成的角度都叫旋转角,旋转角都相等; ③对应点到旋转中心的距离相等.2、图形的中心对称(1)把一个图形绕着某一点旋转180°,如果它能够与另一个图形重合,那么这两个图形关于这个点对称或中心对称,该点叫做对称中心. (2)①关于中心对称的两个图形是全等形;②关于中心对称的两个图形,对称点连线都经过对称中心,并且被对称中心平分; ③关于中心对称的两个图形,对应线段平行(或者在同一直线上)且相等.1、三垂直全等模型三垂直全等构造方法:从等腰直角三角形的两个锐角顶点出发向过直角顶点的直线作垂线。
CBE D CAB2、手拉手全等模型CCCABDEABBA方法技巧提炼高频核心考点EDCBAEDCBAEDCBAABCDEEDCBA3、等线段、共端点 (1) 中点旋转(旋转180°)(2) 等腰直角三角形(旋转90°)A'DCBAF'D'FEDCA(3) 等边三角形旋转(旋转60°)(4) 正方形旋转(旋转90°)②①FEDCBAPFEDCBAGFEDCBA例1、如图,设P 是等边△ABC 内的一点,PA=3,PB=4,PC=5,则∠APB 的度数是________。
类型一旋60°,造等边精题精讲精练例2、(1)如图,P是等边△ABC内一点,∠APB、∠BPC、∠CPA的大小之比为5:6:7,则以PA、PB、PC为边的三角形三内角大小之比(从小到大)是().A.2:3:4B.3:4:5C.4:5:6D.以上结果都不对(2)在等边△ABC中,P为BC边上一点,设以AP、BP、CP为边组成的新三角形的最大内角为θ,则() A. θ≥90° B.θ≤120° C.θ=120° D.θ=135°例3、如图所示.△ABD是等边三角形,在△ABC中,BC=a,CA=b,问:当∠ACB为何值时,C,D 两点的距离最大?最大值是多少?例4、(1)如图,在四边形ABCD中,AB=AD,∠BAD=60°,∠BCD=120°,证明:BC+DC=AC.(2)如图,四边形ABCD中,AB=BC,∠ABC=60°,P为四边形ABCD内一点,且∠APD=120°.证明:PA+PD+PC≥BD.如图,P 为等边△ABC 内一点,∠APB =113°,∠APC =123°求证:以AP ,BP ,CP 为边可以构成一个三角形,并确定所构成的三角形的各内角的度数.如图,在四边形ABCD 中,∠ABC=30°,∠ADC =60°,AD=DC.证明:BD 2=AB 2+BC 2.例5、如图,以Rt △ABC 的斜边BC 为一边在△ABC 的同侧作正方形BCEF,设正方形的中心为O,连接AO,如果AB=4,AO=62,那么AC 的长等于________。
图形的旋转课件(通用7篇)

图形的旋转课件(通用7篇)图形的旋转课件1一、教学目标1、知道图形旋转的概念,能找出旋转图形中的旋转中心、旋转角度和对应关系。
2、通过观察、操作、交流、归纳等过程,培养学生探究问题的能力、观察能力,以及与人合作交流的能力。
3、经历对生活中旋转图形的观察、讨论、实践操作,使学生充分感知数学美,培养学生学习数学的兴趣和热爱生活的情感。
二、教学重点掌握旋转的有关概念,探索和发现旋转后图形的形状和大小都没有发生变化;会准确找出对应点、对应线段、对应角,旋转中心、旋转角。
三、教学难点对图形旋转过程中旋转角相等的理解,会准确找出旋转角。
旋转中心不在三角形顶点时旋转角的确定。
四、课时安排:一课时五、教学过程一、出示学习目标1、板书课题同学们,本节课我们一同来学习“图形的旋转”。
本节课的学习目标是(投影)2、出示学习目标(1)通过实例观察,认识并描述图形的旋转。
(2)了解一个简单的图形经过旋转制作复杂图形的过程,知道图形旋转的三要素(点、方向、度数)。
(3)欣赏图形的旋转变换所创造出的美,感受旋转在生活中的应用,体会数学的价值。
二、出示生活图片(一)图形的旋转,旋转中心,旋转角,方向1、[演示]:演示生活中常见的转动,观察转动时各点的运动情况得到图形在转动时,位置始终不变的那一点叫做旋转中心。
图形转动的角度叫做旋转角。
区分顺时针旋转和逆时针旋转,以及旋转的三要素。
2、由钟表的旋转,得到线段转动的旋转角,学生描述钟表的旋转,加深旋转三要素的记忆,同时培养学生的语言表达能力。
再由线段的旋转引申到几何图形的旋转,进一步得到:旋转前后的两个图形形状和大小不变,只是位置发生变化。
(二)感受生活中的旋转在日常生活中,我们可以看到,一些图形绕着某一个点旋转一定角度时,能与自身重合。
你能举出这样的例子吗?(三)全课,巩固方法今天我们学习了图形的一种运动————旋转。
通过学习你有什么收获?(四)布置作业:1、课本习题2、32、动手操作:请设计一个绕一点旋转一定角度后能与自身重合的图形。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
图形的旋转
一、知识点复习:
旋转的定义:把一个图形绕着某一个定点顺(逆)时针旋转某一个角度,这样的图形变换叫做旋转。
这个定点称为旋转中心。
旋转三要素:旋转中心、旋转方向、旋转角度。
旋转的性质:1、旋转前后的两个图形全等。
2、对应点到旋转中心的距离相等。
3、两组对应点分别与旋转中心连线所成的角相等。
旋转的目的:利用旋转将相关条件变换位置后,与其他条件结合以达到解题目的。
友情提醒:旋转变换过程中会发生许多的变化,但也有许多关系不会随着图形的变化而变化,这些旋转变化过程中的不变关系往往是解题的关键。
二、典型例题:
(一)、旋转中心确定问题
通过确定的旋转,让学生熟练旋转的基本性质,抓住旋转的关键不变量,从而达到解题的目的。
例1、如图,在△ABC 中,∠CAB=65°,将△ABC 在平面内绕点 A 旋转到
△AB′C′的位置,使 CC′∥AB,旋转角的度数为.
例2、如图,在△ABC中,AB=AC=5,BC=6,将△ABC绕点B逆时针旋转
60°得到'
△,连接C'A,则C'A的长为.
'A
BC
例3、已知 A 点的坐标为(-1,3),将 A 点绕坐标原点 O 顺时针旋转 90°,
则点 A 的对应的坐标为.
(二)、旋转中心不确定问题
利用旋转的性质,确定旋转中心。
抓住特殊旋转前后对应
线段之间的位置和数量关系,从而找到需要的解答方法。
例1、如图所示,在 8×8 的网格中,我们把△ABC在图中作
旋转变换,已知网格中的线段 MN 是边AB经一次变换后
所得的对应线段,请在图中画出△ABC经一次旋转变换后
的对应三角形,并标出旋转中心O(要求:不写作法,
作图工具不限,但要保留作图痕迹).
例2、如图,在△BDE中,∠BDE=90°,BD=42,点D的坐标是(5,0),
∠BDO =15°,将△BDE经过一次旋转后到△ABC的位置,点C恰好
落在BD上,则旋转中心的坐标为.
(三)、综合运用
题目中没有提示旋转,但利用旋转思想来解题将能达到事半功倍的效果。
例1、如图1,正方形ABCD中,P、Q分别是BC、CD边上的点,且∠PAQ=45°,
试说明:DQ+BP=PQ
例2、如图,等腰直角△ABC中,AC=BC,∠ACB=90°,点O分斜边AB
为BO∶OA=1∶BOC的度数.
例3、在平面直角坐标系中,边长为2的正OABC的两顶点A、C分别在y轴、x轴的正半轴上,点O在原点.现将正方形OABC绕O点顺时针旋转,当A点第一次落在直线y=x上时停止旋转,旋转过程中,AB边交直线y=x于点M,BC边交x轴于点N(如图).(1)求OA在旋转过程中所扫过的面积;
(2)旋转过程中,当MN和AC平行时,求正方形OABC旋转的度数;
(3)设△MBN的周长为p,在正方形OABC旋转的过程中,p值是否有变化?请证明你的结论.
四、课后巩固:
1.如图,在Rt△ABC中,∠ACB=90°,∠ABC=30°,将△ABC绕点C顺时针旋转至△A′B′C,使得点A′恰好落在AB上,则旋转角度为.
2.如图,在Rt△ABC中,∠ACB=90°,∠B=60°,BC=2,△A′B′C可以由△ABC绕点C顺时针旋转得到,其中点A′与点A是对应点,点B′与点B是对应点,连接AB′,且A、B′、A′在同一条直线上,则AA′的长为.
3.如图,边长为1的正方形ABCD绕点A逆时针旋转45°后得到正方形AB
1C
1
D
1
,边B
1
C
1
与CD
交于点O,则四边形AB
1
OD的面积是.
4.如图,已知△ABC中,∠C=90°,AC=BC=,将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置,连接C′B,则C′B的长为.
5.如图,已知正方形ABCD和正方形AEFG,连接EB、DG,问:S
△ABE 与S
△ADG
有怎样的数量关系?
6.(1)如图1,点P是正方形ABCD内的一点,若PA=3,PB=2,PC=5,求∠APB的度数.(2)点P是等边三角形ABC内的一点,若PA=12,PB=5,PC=13,求∠BPA的度数.
8. 如图,抛物线c
-
=2与x轴交与A(1,0),B(-3,0)两点,交Y轴于C,顶点为D,
+
bx
x
y+
对称轴交x轴于点H .将该抛物线沿直线y=x+5的方向平移,当抛物线经过点A时,抛物线与x轴的另一个交点为点F,对称轴为直线m.
①求点F的坐标;
②将△ADH绕某一点旋转180°后,正好有两个顶点落在平移后在抛物线上,直接写出
顶点H的对应点H ’的坐标.。
