七年级数学上册第3章《分段计费问题》同步提升训练(人教版)
七年级上册数学实际问题与一元一次方程--分段计费问题训练

,
所以老李家 月份的用电量超过 度,但不超过 度.
设老李家 月份的用电量为 度.
由题意,得 解得 即老李家 月份的用电量为 度.
(3)因为 ,
所以老李家 月份的用电量超过 度,
设老李家 月份的用电量为 度.
由题意,得 解得 即老李家 月份的用电量为 度.
17.【答案】
(1) (元).
答:乙班比甲班少花费 元;
甲班分两次共购买苹果 千克(第二次购买苹果的质量多于第一次),共花费 元;而乙班一次性购买苹果 千克.
(1)乙班比甲班少花费多少元?
(2)设甲班第一次购买苹果 千克.
①则甲班第二次购买苹果千克;
②甲班第一次、第二次分别购买苹果多少千克?
18.为准备联合韵律操表演,甲、乙两校共 名学生准备统一购买服装(一人买一套)参加表演(其中甲校人数多于乙校人数,且甲校学生不足 人),下面是服装厂给出的演出服装的价格表:
答:甲校有 名学生准备参加表演,乙校有 名学生准备参加表演.
(2) (人).
有如下方案:
①各自购买服装需 (元);
②联合购买服装需 (元);
③联合购买 套服装需 (元).
因为 ,
所以甲、乙两校联合起来购买 套服装最省钱.
(2)① ;
②若第一次购买不超过 千克,第二次购买 千克以上,则有 解得 ,符合题意.
若两次都购买 千克以上,但不超过 千克,则有 (元),不符合题意.
综上,甲班第一次购买苹果 千克,第二次购买苹果 千克.
18.【答案】
(1)设甲校有 名学生准备参加表演,则乙校有 名学生准备参加表演.
根据题意,得 解得 所以 .
6.商店为了对某种商品促销,将定价为 元的商品,以下列方式优惠销售:若购买不超过 件,按原价付款;若一次性购买 件以上,超过部分打八折,如果用 元钱,最多可以购买该商品的件数是.
人教版七年级数学上册作业课件 第三章 一元一次方程 实际问题与一元一次方程 第3课时 分段计费问题

9.某市为更有效地利用水资源,制定了居民用水收费标准:如果一户每月用 水量不超过15立方米,每立方米按1.8元收费;如果超过15立方米,超过部分按每 立方米2.3元收费,其余仍按每立方米1.8元计算,另外,每立方米加收污水处理费 用1元.若某户一月份共支付水费58.5元,求该户一月份用水量.
解:若该用户每月用水量为15立方米,则需支付水费为15×(1.8+1)=42(元)< 58.5元,所以该户一月份用水量超过了15立方米.设该户一月份用水量为x立方米, 根据题意,得42+(x-15)×(2.3+1)=58.5,解得x=20.答:该户一月份用水量为 20立方米
12.小明用的练习本可以到甲商店购买,也可以到乙商店购买,已知两商店的 标价都是每本1元,甲商店的优惠条件是购买10本以上,从第11本开始按标价的 70%卖;乙商店的优惠条件是从第一本按标价的80%卖.
(1)小明要买20本时,到_乙___商店省钱; (2)买_3_0__本时到两个商店买一样; (3)小明现有31元钱,最多可买_4_0__本.
3.某校准备为毕业班制作一本纪念册,甲公司提出:每册收材料费5元,另收 设计费1500元,乙公司提出每册收材料费8元,不收设计费,孙老师经过计算,发 现两公司收费一样,则毕业生有_____人.
4.购买手机的“全球通”卡,5使00用须付“基本月租费”(每月须交的固定费 用)58元,本地主叫限定时间为150分钟,超过的部分按0.25元/分钟计费;购买 “神州行”卡,使用时不收“基本月租费”,但在本地主叫时每分钟话费0.30元, 若某用户每月手机费预算为100元,则在这两种手机卡神中州,行购买_______卡较合 算.
15.某地上网有两种收费方式,用户可以任选其一:A计时制:4元/小时;B包 月制:320元/月.此外,每一种上网方式都加收通讯费0.4元/小时.
七年级上册课分段计费问题与方案选择问题同步试题
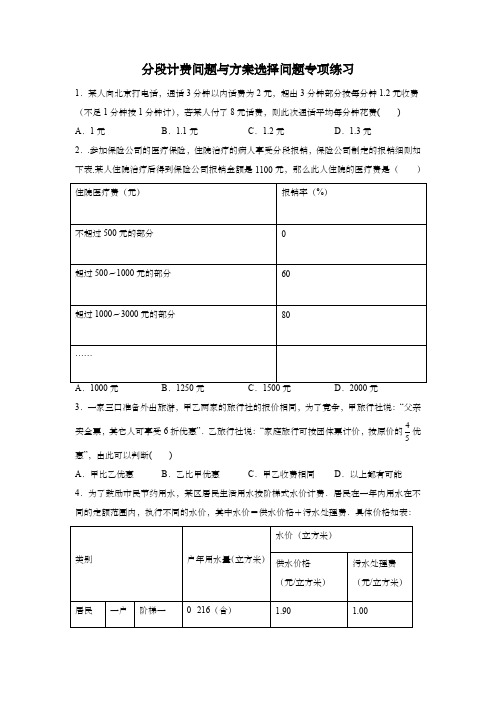
分段计费问题与方案选择问题专项练习1.某人向北京打电话,通话3分钟以内话费为2元,超出3分钟部分按每分钟1.2元收费(不足1分钟按1分钟计),若某人付了8元话费,则此次通话平均每分钟花费( )A.1元B.1.1元C.1.2元D.1.3元2..参加保险公司的医疗保险,住院治疗的病人享受分段报销,保险公司制定的报销细则如下表.某人住院治疗后得到保险公司报销金额是1100元,那么此人住院的医疗费是()3.一家三口准备外出旅游,甲乙两家的旅行社的报价相同,为了竞争,甲旅行社说:“父亲买全票,其它人可享受6折优惠”.乙旅行社说:“家庭旅行可按团体票计价,按原价的4优5惠”,由此可以判断()A.甲比乙优惠B.乙比甲优惠C.甲乙收费相同D.以上都有可能4.为了鼓励市民节约用水,某区居民生活用水按阶梯式水价计费.居民在一年内用水在不同的定额范围内,执行不同的水价,其中水价=供水价格+污水处理费.具体价格如表:月份多了55.6元,则该居民家7月份属阶梯二的用水量为()A.22立方米B.18立方米C.13立方米D.12立方米5.某水果量贩店出售一批菠萝蜜,分两种销售方式:_________kg.6.某市按如下规定收取每月煤气费:用煤气如果不超过60立方米,每立方米按1元收费,如果超过60立方米,超过部分按每月1.5元收费.已知12月份某用户的煤气费平均每立方米1.2元,那么12月份该用户用煤气_______立方米.7.为充分发挥市场机制和价格杠杆在水资源配置中的作用,促进节约用水,提高用水效率,2017年7月1日起某地实行阶梯水价,价目如表(注:水费按月结算,m3表示立方米):3×18+4×(23﹣18)=74(元).(1)若A居民家1月份共用水12m3,则应缴水费元;(2)若B居民家2月份共缴水费66元,则用水m3;(3)若C居民家3月份用水量为am3(a低于18m3,即a<18),且C居民家3、4两个月用水量共40m3,求3、4两个月共缴水费多少元?(用含a的代数式表示)(4)在(3)中,当a =17时,求C 居民家3、4两个月共缴水费多少元? 8.某地试行医保制度,并规定: 一、每位居民年初缴纳医保基金70元;二、居民个人当年看病的医疗费(以定点医院的医疗发票为准,年底按下表所示的方式结算)报销看病的医疗费用.承担的部分和年初缴纳的医保基金)记为y 元. (1)写出如下条件,y 的代数式(可含有,n x ). ①当0x n ≤≤时; ②当6000n x <≤时.(2)已知500n =,若该地居民周大爷某一年个人实际承担的医疗费用是5270元,那么他这一年看病所花费的医疗费共多少元?9.疫情期间,某蛋糕店采用“线上”销售模式,即提前一天线上下单,第二天无接触送货上门.为了吸引客户,在A 、B 两种蛋糕送达时,采用赠代金券的返利方式给顾客意外惊喜.已知返利方式有两种,每种方式返利后A 、B 两种蛋糕的实际利润如下表:蛋糕店每日限量销售A 、B 两种蛋糕共计30盒,且都能售完,每天只推出一种返利方式. (1)若采用方式一返利,某天销售A 、B 两种蛋糕的实际利润共274元,则A 、B 两种蛋糕各售出多少盒?(2)下完订单的当晚,店员M说:“明天无论采用哪种返利方式,销售A、B两种蛋糕的实际总利润都一样”,你觉得她的判断会成立吗?请说明理由.10.某牛奶加工厂有鲜奶9吨,若在市场上直接销售鲜奶,每吨可获取利润500元,制成酸奶销售,每吨可获取利润1200元;制成奶片销售,每吨可获利润2000元,该工厂的生产能力是:若制成酸奶,每天可加工3吨;制成奶片每天可加工1吨,受人员限制,两种加工方式不可同时进行,受气温条件限制,这批牛奶必须在4天内全部销售或加工完毕.为此,该厂某领导提出了两种可行方案:方案1:尽可能多的制成奶片,其余直接销售鲜牛奶;方案2:将一部分制成奶片,其余制成酸奶销售,并恰好4天完成.你认为选择哪种方案获利最多,为什么?参考答案1.A【分析】通话3分钟以内话费为2元,由于付了8元,那么时间一定超过了3分钟,那么等量关系为:2元+超过3分钟的付费=8,可求出通话用的总时间,根据总花费÷总时间即可得出此次通话平均每分钟的花费.【详解】解:设此次通话x分,则2+(x-3)×1.2=8,得:x=8,则此次通话平均每分钟花费=8=1(元).8故选:A.【点睛】本题考查一元一次方程的应用,关键在于找出题目中的等量关系,根据等量关系列出方程解答.2.D【解析】考点:一元一次方程的应用.分析:因为报销金额是1100元,根据分段报销,超过500~1000元的部分报销60%,超过1000~3000元的部分报销80%的情况,设住院医疗费是x元,根据题意可得等量关系:超过500~1000元的部分报销的钱+超过1000~3000元的部分报销的钱=1100元,根据等量关系列出方程求解即可.解:设住院医疗费是x元,由题意得:500×60%+80%(x-1000)=1100,解得:x=2000.答:住院费是2000元.故选D.3.A【解析】【分析】可以设每人的原票价为a元,然后按照旅行社的要求代入数据进行计算即可.【详解】设每人的原票价为a元,如果选择甲,则所需要费用为a+0.6a×2=2.2a(元),如果选择乙,则所需费用为:4×3×a=2.4a(元),5∵2.2a<2.4a,∴甲比乙优惠.故选:A. 【点睛】本题考查列代数式. 4.D 【分析】根据题意,阶梯一、二、三阶段的水价,分别计算6、7月份用水量同在第一、二、三阶段时10方水的价格,得到7月份用水量跨二、三阶段,而六月份用水量在第二阶段,从而得到6月份用水量为8立方米,7月份用水量为18立方米,设7月份第二阶段用水量为x 立方米,则第三阶段用水量为(18-)x 立方米.根据题意列方程求解即可. 【详解】解:根据题意,阶梯一、二、三阶段的水价分别为:2.90/立方米、3.85/立方米、6.70元/立方米;若6、7月份用水量同在第一阶段,则两月水费差应为10 2.9029⨯=元; 若6、7月份用水量同在第二阶段,则两月水费差应为10 3.8538.5⨯=元; 若6、7月份用水量同在第三阶段,则两月水费差应为10 6.7067⨯=元;由于两实际水费差为55.6元,38.5<55.6<67,由题意可知,7月份用水量跨二、三阶段,而六月份用水量在第二阶段,易算出6月份用水量为(86.455.6) 3.85=8-÷立方米,则7月份用水量则为18立方米.设7月份第二阶段用水量为x 立方米,则第三阶段用水量为(18-)x 立方米. 列出方程:3.85 6.7(18)86.4x x +-=; 解得:12x =. 故选D . 【点睛】本题考查了一元一次方程的应用,根据题意确定6、7月份用水量所在阶梯,进而得到两个月的用水量是解题关键. 5.5kg 或10kg 【分析】设菠萝蜜的重量为xkg ,分总价小于50元和大于50元,两种情形求解 【详解】设菠萝蜜的重量为xkg ,则支出为6x 元,可剥果肉30%xkg ,当总价小于50元时,根据题意,得:0.3x×18=6x-3,解得x=5;当总价大于50元时,根据题意,得:0.3x×18=6x-6,解得x=10;故答案为:5或10【点睛】本题考查了一元一次方程的应用,学会运用分类思想,列一元一次方程求解是解题的关键.6.100.【详解】设12月份用了煤气x立方米,12月份的煤气费平均每立方米1.2元,那么煤气一定超过60立方米,等量关系为:60×1+超过60米的立方数×1.5=1.2×所用的立方数,把相关数值代入即可求得所用煤气的立方米数.解:设12月份用了煤气x立方米,由题意得,60×1+(x-60)×1.5=1.2x,解得:x=100,答:12月份该用户用煤气100立方米.故答案为100.7.(1)36;(2)21;(3)①当0<a<15时,共缴水费:187﹣4a;②当15≤a<18时,共缴水费:142﹣a;(4)当a=17时,C居民家3、4两个月共缴水费125元【分析】(1)A居民家1月份共用水3⨯=(元);12m,则按第一档缴费,31236(2)B居民家由于2月份缴水费66元,用水超过了3xm,根据缴费的形式得18m,设用水3到318(18)466x,然后解方程即可;(3)分类讨论:当15≤<,然后根据各段的缴费列代数式即可;a<,当1518a(4)当17a=时,求出代数式142a的值即可.【详解】解:(1)1218,∴应缴水费12336⨯=(元),故答案为:36;(2)设B 居民家2月份用水3xm ,3184(18)66x ,解得21x =. 故答案为:21.(3)①当15a <时,4月份的用水量超过325m 共缴水费:33184(2518)7(4025)1874a a a , ②当1518a ≤<时,4月份的用水量高于322m 且不超过325m 共缴水费:33184(4018)142a a a ,(4)当17a =时,C 居民家3、4两个月共缴水费14217125元. 【点睛】本题考查了一元一次方程的应用及列代数式,解题的关键是:找准等量关系,正确列出一元一次方程,注意分类讨论思想的理解运用.8.(1)①当0x n ≤≤时,70y =;②当6000n x <≤,0040()70y x n =-+;(2)他这一年看病所花费的医疗费共21000元. 【分析】(1)①当0x n ≤≤时,居民个人实际承担的医疗费用只有缴纳的医保基金70元;②当6000n x <≤时,个人承担超过 n 元但不超过 6 000 元的部分,为0040()x n -元,再加医保基金70元.(2)先令6000x =,检验一下此时y 的值,发现医疗费超过6000元,故需要按照第三档计算,由题意得()20%6000x -元即为5270减去医保基金再减去第二档的()40%6000500-元,列方程解之即可. 【详解】解:(1)①当0x n ≤≤时,70y = ②当6000n x <≤,0040()70y x n =-+; (2)设这一年他看病所花费的医疗费共x 元, 当6000x =时, 007055004022705270y =+⨯=<,00005270705500406000,600020x x --⨯∴>-=,21000x =答:他这一年看病所花费的医疗费共 21000 元.本题结合代数式,考查分段计费问题,解决此类问题,要根据不同的数额分到相应的档次进行计算.9.(1)A种蛋糕售出17盒,B种蛋糕售出13盒;(2)店员的判断不成立,见解析【分析】(1)设A种蛋糕售出x盒,则B种蛋糕售出(30−x)盒,根据“采用方式一返利,某天销售A、B两种蛋糕的实际利润共274元,”列出方程求解即可;(2)设A种蛋糕订了y盒,则B种蛋糕订出(30−y)盒,若店员的判断成立,根据“明天无论采用哪种返利方式,销售A、B两种蛋糕的实际总利润都一样”列方程求解,再根据y 只能取整数,即可得出答案.【详解】解:(1)设A种蛋糕售出x盒,则B种蛋糕售出(30−x)盒,根据题意得方程()x x+-=.10830274解得x=.17因此,3013-=.x答:A种蛋糕售出17盒,B种蛋糕售出13盒.(2)设A种蛋糕订了y盒,则B种蛋糕订出(30−y)盒,若店员的判断成立,则可列方程:()()+-=+-y y y y1083091130解得y=22.5y=不符合题意,因此店员的判断不成立.因为y只能取整数,所以22.5【点睛】本题考查了一元一次方程的应用,读懂题意找到等量关系式式解题的关键.10.第二种方案可以多得1500元的利润.【分析】方案一:根据制成奶片每天可加工1吨,求出4天加工的吨数,剩下的直接销售鲜牛奶,求出利润;方案二:设生产x天奶片,(4-x)天酸奶,根据题意列出方程,求出方程的解得到x的值,进而求出利润,比较即可得到结果.解:方案一:最多生产4吨奶片,其余的鲜奶直接销售,则其利润为:4×2000+(9-4)×500=10500(元);方案二:设生产x天奶片,则生产(4-x)天酸奶,根据题意得:x+3(4-x)=9,解得:x=1.5,∴2.5天生产酸奶,加工的鲜奶3×2.5=7.5吨,则利润为:1.5×2000+3×2.5×1200=3000+9000=12000(元),∴12000-10500=1500.得到第二种方案可以多得1500元的利润.【点睛】此题考查了一元一次方程的应用,分析题意,找到关键描述语,找到合适的等量关系是解决问题的关键.。
人教版七年级数学上第三章一元一次方程第3课时 分段计费问题习题课件

自主学习
基础夯实
整合运用
思维拓展
七年级 数学 上册 人教版
2.(曲靖中考)小明所在城市的“阶梯水价”收费办法如下:每户用水不 超过 5 t,每吨水费 x 元;超过 5 t,超过部分每吨加收 2 元.小明家今 年 5 月份用水 t 吨,共交水费 44 元,根据题意可列方程为 55xx++44((xx+2)=+424)=44.
自主学习
基础夯实
整合运用
思维拓展
七年级 数学 上册 人教版
【自主解答】
设小华打折前应付款 x 元, ①打折前购物金额超过 400 元,但不超过 600 元,由题意得 0.9x=504, 解得 x=560,560÷80=7(件);②打折前购物金额超过 600 元,由题意, 得 600×0.8+(x-600)×0.6=504, 解得 x=640,640÷80=8(件), 综上所述,小华在该商场购买商品件数 n 为 7 或 8.
自主学习
基础夯实
整合运用
思维拓展
七年级 数学 上册 人教版
解:(1)按购 A,B 两种,B,C 两种,A,C 两种电视机这三种方案分别计 算,设购 A 种电视机 x 台,B 种电视机 y 台. ①当购 A,B 两种电视机时,B 种电视机购(50-x)台,可得方程:1 500x +2 100(50-x)=90 000, 解得 x=25,则 B 种电视机购 50-25=25(台);
七年级 数学 上册 人教版
第 3 课时 分段计费问题
自主学习
基础夯实
整合运用
思维拓展
七年级 数学 上册 人教版
分段计费问题中,基本的数量关系如下:费用=不不超超过过部部分 分的费用 +超超过过部部分 分的费用.
自主学习
七年级数学上册第3章《分段计费问题》知识点训练(基础)(人教版)

《分段计费问题》基础训练
知识点分段计费问题
1.深圳市出租车的收费标准是:起步价10元(行驶距离不超过2km,都需付10元车费),超过2km时,每增加1km,加收
2.6元.小陈乘出租车到达目的地后共支付车费49元,那么小陈坐车可行驶的路程最远是(不考虑其他收费)()
A. 15km
B. 16km
C. 17km
D. 18km
2.(武汉中考改编)某市按如下规定收取每月煤气费:用户每月用煤气如果不超过60立方米,每立方米按1元收费,如果超过60立方米,超过部分每立方米按1.5元收费.已知12月份某用户的煤气费平均每立方米1.2元,那么12月份该用户用煤气________立方米.
参考答案1.C 2.100。
人教版七年级数学上册第三章一元一次方程3.4实际问题与一元一次方程第4课时分段计费问题课堂练习题

3.4实际问题与一元一次方程第4课时分段计费问题同步课堂练习一、选择填空题1、某超市推出如下优惠方案:(1)一次性购物不超过100元不享受优惠;(2)一次性购物超过100元,但不超过300元一律9折;(3)一次性购物超过300元一律8折.李明两次购物分别付款80元,252元.如果李明一次性购买与这两次相同的物品,则应付款( )A.288元 B.332元C.288元或316元 D.332元或363元2、某班同学一起去看电影,票价每张50元,20张以上(不含20张)打八折,他们一共花了1000元,则共买了()张电影票.A.20 B.25 C.20或25 D.25或303、一家三口准备外出旅游,甲乙两家的旅行社的报价相同,为了竞争,甲旅行社说:“父亲买全票,其它人可享受6折优惠”.乙旅行社说:“家庭旅行可按团体票计价,按原价的优惠”,由此可以判断( )A.甲比乙优惠B.乙比甲优惠C.甲乙收费相同D.以上都有可能4.开学初,小明到某商场购物,发现商场正在进行购物返券活动,活动规则如下:购物每满100元,返购物券50元,此购物券在本商场通用,且用购物券购买商品不再返券,也不得找零. 小明只购物买了单价别为60元,80元和120元的物品各一件,使用购物券后,他的实际花费为_________元.5.张老师带学生乘车外出郊游,甲车主说:”不论师生,每人8折,"乙车主说:“学生9折,老师免费,“张老师算了一下,不论坐谁的车,费用一样,则张老师带的学生人数是________.三、解答题6、某市电话拨号上网有两种收费方式,用户可以任选其一:A.计时制:0.05元/分钟;B.月租制:50元/月(限一部个人住宅电话上网).此外,每种上网方式都得加收通信费0.02元/分钟.(1)小玲说:两种计费方式的收费对她来说是一样的.小玲每月上网多少小时?(2)某用户估计一个月内上网的时间为65小时,你认为采用哪种方式较为合算?为什么?7、甲、乙两家超市以相同的价格出售同样的商品,为了吸引顾客,各自推出不同的优惠方案:在甲超市累计购买商品超出了300元以后,超出部分按原价8折优惠;在乙超市累计购买商品超出200元之后,超出部分按原价8.5折优惠,设顾客预计累计购物x元(x>300).(1)分别列出到甲、乙超市购买商品所需费用(用含x的代数式表示);(2)当x=400元时,到哪家超市购物更优惠?8、某中学拟组织九年级师生去韶山举行毕业联欢活动.下面是年级组长李老师和小芳、小明同学有关租车问题的对话:李老师:“某客运公司有60座和45座两种型号的客车可供租用,60座客车每辆每天的租金比45座的贵200元.”小芳:“我们学校八年级师生昨天在这个客运公司租了4辆60座和2辆45座的客车到韶山参观,一天的租金共计5000元.”小明:“我们九年级师生租用5辆60座和1辆45座的客车正好坐满.”根据以上对话,解答下列问题:(1)此客运公司60座和45座的客车每辆每天的租金分别是多少元?(2)按小明提出的租车方案,九年级师生到该公司租车一天,共需租金多少元?9、这个星期周末,七年级段长准备组织学生观看电影,由各班班长负责买票,票价每张20元,1班班长问售票员买团体票是否可以优惠,售票员说: 50人以上的团体票有两个优惠方案可选择:方案一:全体人员可打8折;方案二:若打9折,有7人可免票。
人教版七年级上册3.4 一元一次方程应用-分段问题专题(含答案)

人教版七年级上册3.4 一元一次方程应用-分段问题专题(含答案)一、解答题1.根据国家发改委实施“阶梯电价”的有关文件要求,某市结合地方实际,决定从2017年5月1日起对居民生活用电试行“阶梯电价”收费,具体收费标准见下表.若2017年5月份,该市居民甲用电100千瓦时,交电费60元.一户居民一个月用电量的范围电费价格(单位:元/千瓦时)不超过150千瓦时 a超过150千瓦时但不超过300千瓦时的部分0.65超过300千瓦时的部分0.9(1)上表中,a=________,若居民乙用电200千瓦时,应交电费________元;(2)若某用户某月用电量超过300千瓦时,设用电量为x千瓦时,请你用含x的代数式表示应交的电费;(3)试行“阶梯电价”收费以后,该市一户居民月用电多少千瓦时,其当月的平均电价不超过0.62元/千瓦时?2.某省公布的居民电阶梯电价听证方案如下:第一档电量第二档电量第三档电量月用电210度以下,每度价格0.52元月用电210度至350度,每度比第一档提价005元月用电350度以上,每度比第一档提价0.30元例:若某户用电量400度,则需交电费为:210×0.52+(350-210)×(0.52+0.05)+(400-350)×(0.52+0.30)=230元如果按此方案计算,小华家5月份的电费为138.84元,请你求出小华家5月份用电量.3.(12分)根据国家发改委实施“阶梯电价”的有关文件要求,某市结合地方实际,决定从2017年5月1日起对居民生活用电试行“阶梯电价”收费,具体收费标准见下表.若2017年5月份,该市居民甲用电100千瓦时,交电费60元.(1)上表中,a=,若居民乙用电200千瓦时,应交电费元;(2)若某用户某月用电量超过300千瓦时,设用电量为x千瓦时,请你用含x的代数式表示应交的电费;(3)试行“阶梯电价”收费以后,该市一户居民月用电多少千瓦时时,其当月的平均电价每千瓦时不超过0.62元?4.某地为鼓励节约用水,水价实行阶梯计费制,其收费标准如下:(1)若某用户上月用水22m3,则应缴水费_____元(用含a的代数式表示).(2)若某用户上月用水36m3,缴水费131元,求a;(3)在(2)的条件下,设每月用水量xm3,请直接用x的代数式表示每月支出的水费.5.某城市居民用水实行阶梯收费,每户每月用水量如果未超过20吨,按每吨元收费如果超过20吨,未超过的部分按每吨元收费,超过的部分按每吨元收费设某户每月用水量为x吨,应收水费为y元.设某户居民每月用水量为m吨,则应收水费为______元用含m的代数式表示;设某户居民每月用水量为m吨,则应收水费为______元用含m的代数式表示;若该城市某户5月份水费平均为每吨元,求该户5月份用水多少吨?6.根据国家发改委实施“阶梯电价”的有关文件要求,某市结合地方实际,决定从2017年4月1日起对居民生活用电试行“阶梯电价”收费,具体收费标准见下表:一户居民一个月用电量的范围电费价格(单位:元/度)不超过150度 a超过150度的部分 b2017年5月份,该市居民甲用电100度,交电费80元;居民乙用电200度,交电费170元.(1)上表中,a=_____,b=_____;(2)试行“阶梯电价”收费以后,该市一户居民2017年8月份平均电价每度为0.9元,求该用户8月用电多少度?7.温州和杭州某厂同时生产某种型号的机器若干台,温州厂可支援外地10台,杭州厂可支援外地4台,现在决定给武汉8台,南昌6台,每台机器的运费如下表,设杭州厂运往南昌的机器为x台,(1)用含x的代数式来表示总运费(单位:元)(2)若总运费为8400元,则杭州厂运往南昌的机器应为多少台?(3)试问有无可能使总运费是7800元?若有可能请写出相应的调动方案;若无可能,请说明理由. 8.重百江津商场元月一日搞促销活动,活动方案如下表:一次性购物优惠方案不超过200元不给于优惠超过200元,而不足500元优惠10%超过500元,而不足1000元其中500元按9折优惠,超过部分按8折优惠超过1000元其中1000元按8.5折优惠,超过部分按7折优惠某人两次购物分别用了134元和913元.(1)此人两次购物其物品如果不打折,值多少钱?(2)在此活动中,他节省了多少钱?(3)若此人将两次购物的钱合起来购相同的商品是更节省还是亏损?说明你的理由.9.甲、乙两商场以同样的价格出售同样的商品,并且又各自推出不同的优惠方案:在甲商场累计购物超过200元后,超过200元的部分按9折收费;在乙商场累计购物超过100元后,超过100元的部分按9.5折收费,顾客到哪家商场购物花费少?10.10.马刚家附近有甲乙两家超市,春节来临之际两个超市分别给出了不同的促销方案:甲超市购物全场8.8折,乙超市购物①不超过200元,不给予优惠;②超过200元而不超过500元,打9折;③超过500元,其中的500元仍打9折,超过500元的部分打8折.(假设两家超市相同商品的标价都一样)(1)当一次性购物标价总额是300元时,甲乙两个超市实付款分别是多少?(2)当标价总额是多少元时,甲乙超市实付款一样?11.某开发商进行商铺促销,广告上写着如下条款:投资者购买商铺后,必须由开发商代租赁5年,5年期满后由开发商以比原商铺标价高20%的价格进行回购,投资者可在以下两种购铺方案中做出选择:方案一:按照商铺标价一次性付清铺款,每年可获得的租金为商铺标价的10%;方案二:按商铺标价的八折一次性付清铺款,前3年商铺的租金收益归开发商所有,3年后每年可获得的租金为商铺标价的9%(1)问投资者选择哪种购铺方案,5年后所获得的投资收益率更高?为什么?(注:投资收益率=投资收益实际投资额×100%)(2)对同一标价的商铺,甲选择了购铺方案一,乙选择了购铺方案二,那么5年后两人获得的收益相差7.2万元.问甲乙两人各投资了多少万元?12.为发展校园足球运动,某县城区四校决定联合购买一批足球运动装备,市场调查发现:甲、乙两商场以同样的价格出售同种品牌的足球队服和足球,已知每套队服比每个足球多50元,两套队服与三个足球的费用相等.经洽谈,甲商场的优惠方案是:每购买10套队服,送1个足球;乙商场的优惠方案是:若购买队服超过80套,则购买足球打八折.(1)每套队服和每个足球的价格分别是多少?(2)若城区四校联合购买100套队服和a个足球,请用含a的式子分别表示出到甲商场和乙商场购买装备所需的费用.(3)假如你是本次购买任务的负责人,你认为到哪家商场购买比较合算?13.春节期间,七年级(1)班的明明、丽丽等同学随家长一同到某公园游玩,如图是购买门票时,明明与他爸爸的对话,试根据图中的信息,解答下列问题:(1)明明他们一共去了几个成人?几个学生?(2)请你帮助明明算一算,用哪种方式购票更省钱?(3)购完票后,明明发现七年级(2)班的张小涛等8个学生和他们的12个家长共20人也来购票,请你为他们设计出最省钱的购票方案,并求出此时的购票费用。
新人教版数学七年级上册同步练习:3.4 第3课时 比赛、分段计费问题与一元一次方程

3.4第3课时比赛、分段计费问题与一元一次方程知识点1比赛问题1.某足球比赛计分规则:胜一场得3分,平一场得1分,负一场得0分.某足球队经过26轮激战,以42分获比赛第五名,其中负6场,那么胜场数为()A.9 B.10 C.11 D.122.一份试卷由50道选择题组成,每道题选对得3分,不选、错选均扣1分.小亮在这次考试中得了102分,则他答对了________道题.3.在一场篮球比赛中,小明投中的两分球、三分球共得28分,且他投中的两分球比三分球多4个,小明投中两分球、三分球各几个?知识点2分段计费问题4.小明所在城市的“阶梯水价”收费办法如下:每户每月用水不超过5吨,每吨收费x 元;超过5吨,超过的部分每吨加收2元.小明家今年5月份用水9吨,共交水费44元,根据题意列出关于x的方程正确的是()A.5x+4(x+2)=44 B.5x+4(x-2)=44C.9(x+2)=44 D.9(x+2)-4×2=445.参加保险公司的医疗保险,住院治疗的病人享受分段报销,保险公司制定的报销细则如下表:某人住院治疗后得到保险公司报销的金额是1100元,那么此人住院的医疗费是() A.1000元B.1250元C.1500元D.2000元6.有一旅客带35 kg行李从郑州到广州,按民航规定,旅客最多可免费携带20 kg行李,超过部分每千克按飞机票价的1.5%购买行李票.已知该旅客购买的行李票为198元,则他的飞机票价为()A.800元B.850元C.880元D.1000元7.某城市按以下规定收取每月煤气费:每月煤气用量如果不超过60立方米,按每立方米0.8元收费;如果超过60立方米,超过部分按每立方米1.2元收费.已知某用户10月份的煤气费为66元,求该用户10月份使用煤气多少立方米.8.你坐过出租车吗?请你帮小明算一算.某市出租车收费标准如下:起步价(3千米及3千米以内)10元,超过3千米的部分每千米1.2元,小明乘坐了x(x>3)千米的路程.(1)请用含x的式子表示他应付的费用;(2)若他支付的费用是23.2元,请你算出他乘坐出租车的路程.9.某市对居民生活用电实行阶梯电价,具体收费标准如下表:已知10月份该市居民老李家用电200度,交电费120元;9月份老李家交电费157元.(1)表中a的值为________;(2)求老李家9月份的用电量;(3)若8月份老李家用电的平均电价为0.7元/度,求老李家8月份的用电量.10.下面的表格是某次篮球比赛积分表:某次篮球比赛积分表(1)如果删去积分表的最后一行,你能求出胜一场和负一场的得分吗?(2)某队的胜场总积分能等于它的负场总积分的2倍吗?(3)某队的负场总积分能等于它的胜场总积分的2倍吗?11.某景点的门票价格如下表:某校七年级(1)、(2)两班计划去游览该景点,其中(1)班人数少于50人,(2)班人数多于50人且少于100人.若两班都以班为单位单独购票,则一共支付1118元;若两班联合起来作为一个团体购票,则只需花费816元.(1)求两个班各有多少名学生.(2)团体购票与单独购票相比较,两个班各能节省多少钱?详解详析1.C[解析] 设胜场数为x,则平场数为(26-6-x).依题意,得3x+(26-6-x)=42,解得x=11.即胜场数为11.故选C.2.38[解析] 设他答对了x道题,则3x-(50-x)=102,解得x=38.3.解:设小明投中两分球x个,则投中三分球(x-4)个.根据题意,得2x+3(x-4)=28,解得x=8,x-4=8-4=4.所以小明投中两分球8个,三分球4个.4.A5.D[解析] 设此人住院的医疗费为x元.因为500×60%=300(元)<1100元,所以x>1000.根据题意,得500×60%+(x-1000)×80%=1100.解这个方程,得x=2000.6.C[解析] 设该旅客的飞机票价为x元,则行李超重部分应购买行李票(15×1.5%x)元.由题意,得15×1.5%x=198,解得x=880.故他的飞机票价为880元.故选C.7.解:因为60×0.8=48(元)<66元,所以该用户10月份的煤气用量超过了60立方米.设该用户10月份使用煤气x立方米,根据题意,得60×0.8+1.2(x-60)=66,解得x=75.答:该用户10月份使用煤气75立方米.8.解:(1)[10+1.2(x-3)]元.(2)根据题意,得10+1.2(x-3)=23.2,解得x=14.所以他乘坐出租车的路程为14千米.9.解:(1)因为老李家10月份用电200度,交电费120元,所以200a=120,解得a=0.6.故答案为0.6.(2)因为240×0.6=144(元),240×0.6+(400-240)×0.65=248(元),144<157<248,所以老李家9月份的用电量超过240度,但不超过400度.设老李家9月份的用电量为x度.由题意,得240×0.6+0.65(x-240)=157,解得x=260.即老李家9月份的用电量为260度.(3)因为0.7>0.65,所以老李家8月份的用电量超过400度.设老李家8月份的用电量为y度.由题意,得240×0.6+(400-240)×0.65+0.9(y-400)=0.7y,解得y =560.即老李家8月份的用电量为560度.10.解:(1)能.利用东方队和光明队的数据设胜1场得x 分, 则东方队负场总积分为(24-10x)分, 说明负1场得24-10x4分;光明队负场总积分为(23-9x)分, 说明负1场得23-9x5分.由此得方程24-10x 4=23-9x5.解得x =2.则24-10x 4=24-10×24=1. 答:胜1场得2分,负1场得1分.(2)能.设一个队胜的场次为y ,则负的场次为(14-y), 由题意,得2y =2(14-y), 解得y =7.所以某队的胜场总积分能等于它的负场总积分的2倍. (3)不能.设一个队胜的场次为z ,则负的场次为(14-z). 由题意,得2×2z =14-z , 解得z =145.因为胜的场次不可能为分数,所以某队的负场总积分不能等于它的胜场总积分的2倍. 11.解:(1)若两班学生人数之和不超过100,设人数之和为w ,则10w=816,则w不是整数,不合题意,故两个班学生人数之和超过100.816÷8=102,所以两个班共有102人.设七年级(1)班有x名学生,则七年级(2)班有(102-x)名学生.由题意,得12x+10(102-x)=1118,解得x=49.102-x=102-49=53.答:七年级(1)班有49名学生,七年级(2)班有53名学生.(2)七年级(1)班能节省(12-8)×49=196(元),七年级(2)班能节省(10-8)×53=106(元).。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《分段计费问题》提升训练
1.参加医疗保险,住院治疗的病人享受分段报销,保险公司制定的报销细则如下表:
某人住院治疗后得到保险公司报销金额是1100元,那么此人住院的医疗费是()
A.1000元
B.1250元
C.1500元
D.2000元
2.据电力部门统计,每天8:00至21:00是用电的高峰期,简称“峰时”,21:00至次日8:00是用电的低谷时期,简称“谷时”,为了缓解供电需求紧张矛盾,某市电力部门于本月初统一换装“峰谷分时”电表,对用电实行“峰谷分时电价”新政策,具体见下表:
(1)小张家上月“峰时”用电50度,“谷时”用电20度,若上月初换表,则相对于换表前小张家的电费是增多了,还是减少了?增多或减少了多少元?请说明理由;
(2)小张家这个月用电95度,经测算比换表前使用95度电节省了5.9元,问小张家这个月使用“峰时电”和“谷时电”分别是多少度?
3.(淄博中考)为鼓励居民节约用电,某省试行阶段电价收费制,具体执行方案如表:
例如:一户居民七月份用电420度,则需缴电费420×0.85=357(元).
某户居民五、六月份共用电500度,缴电费290.5元.已知该用户水月份用电量大于五月份,且五、六月份的用电量均小于400度.问该户居民五、六月份各用电多少度?
参考答案
1.D
2.解:(1)若上月初换表,则相对于换表前小张家的电费是减少了2.9元.(2)小张家这个月使用“峰时电”60度,“谷时电”35度.
3.解:设五月用电量为x 度,则六月份用电量为500x
-
()度,当五份用电小于等于200,六月份用电大于200小于400时,由题意,得0.550.6500290.5
+-=
(),解得190
x x
x=.则x
-=.当五月份、六月份用电均大于200小于400时,由题意,得500310
(),方程无解,所以该情况不符合题意.答:该户居民五、+-=
x x
0.60.6500290.5
六月份分别用电190度、310度.。
