沪科版九年级下册数学综合与实践进球线路与最佳射门角
九下数学(沪科版)课件-综合与实践 进球线路与最佳射门角
(1)证明:连接 OA,过 O 作 OF⊥AE 于 F,∴∠AFO=90°,∴∠EAO+∠AOF
=90°,∵OA=OE,∴∠EOF=∠AOF=12∠AOE,∵∠EDA=21∠AOE, ∴∠EDA=∠AOF,∵∠EAC=∠EDA,∴∠EAC=∠AOF,∵∠EAO+
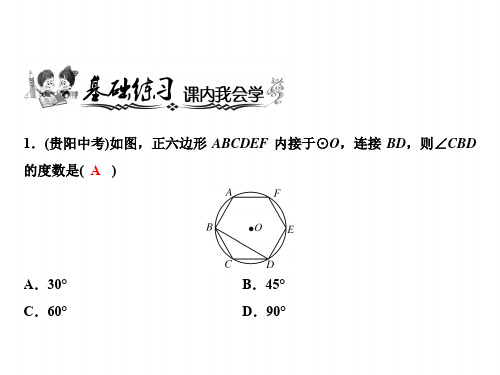
1.(贵阳中考)如图,正六边形 ABCDEF 内接于⊙O,连接 BD,则∠CBD 的度数是( A )
A.30° C.60°
B.45° D.90°
2.(南充中考)如图,在半径为 6 的⊙O 中,点 A、B、C 都在⊙O 上,四边 形 OABC 是平行四边形,则图中阴影部分的面积为( A )
A.6π C.2 3π
11.如图 A、B 表示球门边框的两端点,C 表示射门点,连接 AC、BC,∠
ACB 即为射门角,当球员带球沿直线 l 跑动时(若 l∥AB),则射门点 C 应选
在
处射门角最大( C )
A.点 D C.点 M
B.点 E D.点 N
12.(威海中考)如图,正方形 ABCD 内接于⊙O,其边长为 4,则⊙O 的内 接正三角形 EFG 的边长为 2 6 .
B.3 3π D.2π
3.(枣庄中考)如图,在边长为 4 的正方形 ABCD 中,以点 B 为圆心,AB 为半径画弧,交对角线 BD 于点 E,则图中阴影部分的面积是(结果保留 π)( C )
A.8-π C.8-2π
B.16-2π D.8-π
4.如图,在△ABC 的外接圆中,CP⊥AB,当 C 沿 CP 方向运动时,其点 C 所对弧 AB 的张角的变化情况是( C )
13.在足球比赛射门时,球对球门 AB 张开的角越大球越容易射进.在今年 的世界杯比赛中,如图,队员甲已经把球带到对方球门前 D 处,由于遇到 防守队员死死盯防,他选择带球摆脱然后射门,有 C、E、F、G 四点供选 择,则他选择到点 C 射门效果最好.
上海科学技术出版社初中数学九年级下册 综合与实践 进球线路与最佳射门角 省赛

综合与实践教学设计进球线路与最佳射门角一、教学背景(一)教材分析本节课的内容为进球线路与最佳射门角,选自沪科版九年级数学下册第二十四章《圆》第八节的内容,要求学生能理解进球线路和最佳射门角存在关系,结合圆及相关知识,找到最佳射门角。
本节内容是本章知识的升华和提高,是数学知识与现实生活的紧密联系。
(二)学情分析学生已经学习了圆的知识,对圆周角、圆内角、圆外角的比较已经掌握,并有一定的生活经验。
但本节内容比较抽象,将结合几何画板进行讲解分析,提高直观性。
二、教学目标让学生理解能利用圆的知识分析进球路线与射门角度关系,通过观察分类、观察、思考进球路线与射门角度存在关系。
通过不同进球路线的分析,结合圆周角的知识找到最佳射门角。
让学生感受数学对现实生活的意义,体会分类讨论思想。
培养学生积极参与和勇于探索的精神。
三、教学重点与难点教学重点:理解进球路线和射门角关系。
教学难点:利用圆及相关知识找到最佳射门角。
四、教学方法分析及学习方法指导多媒体教学,利用几何画板辅助理解,让学生通过观察、思考、讨论、交流结合圆的知识,找出最佳进球角。
五、教学过程(一)导入新课足球场上的顺口溜:冲向球门跑,越近就越好;歪着球门跑,射点要选好!足球运动已成为一种世界性的运动,也是我们大家喜欢欣赏的一种体育活动。
在比赛的过程中,运动员在对方球门前不同的位置起脚射门对球门的威胁是不相同的。
设计意图:从生活中的实际问题入手,使学生认识到数学总是与现实问题密不可分,同时激发学生的学习热情。
(二)新授内容1足球场上,常需带球跑动到一定位置后,再进行射门,这个位置为射门点,射门点与球门边框两端点的夹角就是射门角;如果用点A、B表示球门边框(不考虑球门的高度)的两端点,点C表示射门点,连接AC,BC,则∠ACB就是射门角在不考虑其他因素的情况下,一般说来,射门角越大,射门进球的可能性就越大。
2运动员带球跑动的三种常见线路(用直线l表示)设计意图:让实际问题转化为数学知识,让学生感受分类的数学思想。
2综合实践进球线路与最佳射门角PPT课件(沪科版)

α<β<θ
新课讲授
典例分析
例 1 如在足球比赛场上,甲、乙、丙B,D 处 (如图所示),此时甲自己直接射门好,还是迅速将球回传给 乙或丙射门好?若选择回传,则选回传给谁更合理?
新课讲授
练一练
1 如图,点A,B,C表示足球比赛中三个不同的射门位置,估测图
中各角的大小关系,请指出在图中__B__点处射门最好.
2 某处靠近海岸的海域有一片暗礁,当地海洋管理部在海岸上建 造了两座灯塔A,B,通告所有船只不要进入以AB为弦的弓形区 域(阴影部分)内(含边界)以免触礁,如图所示.现有一艘货轮P正 向暗礁区域靠近,当∠APB多大时,才能躲开暗礁? 解:货轮P在航行时,只要∠APB<55°,即 在ACB外行驶,就能躲开暗礁.
A.∠APB>∠AMB
A
B
B.∠APB>∠ANB
C.∠APB<∠AMB D.∠ANB>∠AMB
N
P
M
当堂小练
2. 如图,在足球比赛中,甲带球向对方球门AB进攻,当他带 球冲到C点时,同伴乙、丙已经分别助攻到点D、E,不考虑 防守情况,仅从射门角度考虑,下列说法能够使进球有最佳
射门角度的是( C )
新课讲授
知识点1 最佳射门角
球门
A
B
射门角
C 射门点
足球运动员在球场 上,常需带球跑动到一 定位置后,再进行射门, 这个位置为射门点,射 门点与球门边框两端点 的夹角就是射门角.
∠ACB就是射门角
新课讲授
在不考虑其他因素的情况下:一般地,射门角越大,射门进球 的可能性就越大。
新课讲授
当运动员沿直线 l 横向跑动时,他的位置离球门的中心越近, 射门角越大,离球门的中心最近(点C0)时,射门角最大,我们 把点C0称为直线 l 上的最佳射门点,∠AC0B 称为直线 l 上的最佳 射门角.
2024-2025学年沪科版初中数学九年级(下)教学课件24.8综合与创新进球线路与最佳射门

24.8 综合与实践
进球线路与最佳射门
新课导入
足球运动员在球场上,常需要带球跑动到一定的距离进行射门, 你能确定下最佳射门角度吗?
知识讲解
• 如图:
射门点与射门角
球门
E
A
B
射门角
D
C
射门点
在不考虑其他因素的情况下:一般地,射门角越大,射门 进球的可能性就越大
知识讲解
运动员带球跑动的常见线路
• A、立刻射门
• B、带球到点F射门 • C、传给同伴乙 • D、传给同伴丙
A
B
F
D
E C
知识讲解
探究2:直向跑动时的最佳射门点
A
B
D
C
总结:当直线与过A、B的圆相切时,切点是最佳射门点
知识讲解
例3
已知AB=8,BD=2,当点C是直线l上的最佳射门点时,求CD的长
A
B
D
C
知识讲解
探究2:直向跑动时的最佳射门点
当运动员直向跑动路线垂直穿过球门AB时,分析最佳射门点的位置
A
B
D
C0
C
总结:当运动员由C向AB移动时,∠ACB逐渐增大, 0o<∠ACB<180o,此时直线上没有最佳射门点, 但当点C越靠近AB时,进球的可能性越大。
随堂训练
随堂训练
随堂训练
4.
随堂训练
5.
球门
A
B
射门角
C 射门点
横向跑动
球门
A
B
射门角
C 射门点
直向跑动
球门
A
B
射门角
C 射门点
斜向跑动
知识讲解
沪科版数学九年级下册《综合与实践 进球路线与最佳射门角》教案1

《综合与实践进球路线与最佳射门角》教案(一)教学目标
1.理解圆的概念,了解等圆、等弧的概念,通过观察生活中的圆以及圆的形成过程,学习从具体中提炼抽象概念的方法及发展空间观念。
2. . 初步学会从数学的角度发现问题和提出问题,综合应用已学知识解决简单的实际问
题,增强应用知识,提高实践能力。
3. 体验解决问题方法的多样性,发展创新意识情感态度,激发对数学探索求知的欲望,在数学活动中,体验成功的乐趣,锻炼克服困难的意志,建立自信心,养成独立思考、合作交流、认真勤奋等学习习惯。
教学重、难点
重点:理解圆是由到定点等于定长的点的集合的概念、垂径定理及其应用
难点:使用垂径定理解决实际问题
教学过程
根据实际,使学生理解理解射门点与射门角的概念。
根据本单元所学的相关知识引导学生总结出结论:
一般地,射门角越大,射门进球的可能性就越大
实际生活中两种不同情况
运动员带球跑的常见线路:
一、横向跑动时的最佳射门点
推论1 C点成为直线上的最佳射门点,∠ACB成为直线上的最佳射门角
推论2 直线AB上,圆外角<圆上角<圆内角
二、纵向跑动时的最佳射门点
推论3 沿直线CD跑时,∠ACB越来越大,无最佳射门点
三、练习。
沪科版数学 九年级下册 24.8 综合与实践 进球线路与最佳射门角 课后练习题

一、单选题
1. 如图,足球运动员在球门前横向带球准备射门,下列说法正确的是()
A.在处射门进球的可能性大
B.在处射门进球的可能性大
C.在,两处射门进球的可能性一样大
D.无法判断,两处哪处进球的可能性大
二、填空题
2. 如图,点,,表示足球比赛中三个不同的射门位置,估测图中各角的大小关系,请指出在图中________点处射门最好.
三、解答题
3. 在圆O中,C是弦AB上的一点,联结OC并延长,交劣弧AB于点D,联结AO、BO、
AD、BD.已知圆O的半径长为5,弦AB的长为8.
(1)如图1,当点D是弧AB的中点时,求CD的长;
(2)如图2,设AC=x,=y,求y关于x的函数解析式并写出定义域;
(3)若四边形AOBD是梯形,求AD的长.
4. 足球训练场上,教练在球门前画了一个圆圈进行无人防守的射门训练.如图,甲、乙两名运动员分别在,两处,他们争论不休,都说自己所在的位置对球门的
张角大,如果你是教练,请评一评他们两个人谁的位置对球门的张角大?为什么?
5. 某处靠近海岸的海域有一片暗礁,当地海洋管理部门在海岸上建造了两座灯塔,,通告所有船只不要进入以为弦的弓形区域(阴影部分)内(含边界)以免触礁,如图所示.现有一艘货轮正向暗礁区域靠近,当多大时,才能避开暗礁?。
沪科版数学九年级下册24.8《进球线路与最佳射门角》教学设计
沪科版数学九年级下册24.8《进球线路与最佳射门角》教学设计一. 教材分析《进球线路与最佳射门角》是沪科版数学九年级下册第24章第8节的内容。
本节内容主要通过探究进球线路与射门角的关系,让学生了解数学在实际生活中的应用,提高学生学习数学的兴趣。
教材通过丰富的图片和实例,引导学生利用数学知识解决实际问题,培养学生的数学建模能力和解决问题的能力。
二. 学情分析九年级的学生已经掌握了初中阶段的基本数学知识,具备一定的逻辑思维能力和问题解决能力。
但是,对于将数学知识应用到实际生活中的问题,部分学生可能还存在一定的困难。
因此,在教学过程中,教师需要关注学生的个体差异,引导学生将数学知识与实际生活相结合,提高学生的学习兴趣和积极性。
三. 教学目标1.知识与技能目标:让学生掌握进球线路与射门角的关系,学会利用数学知识解决实际问题。
2.过程与方法目标:通过观察、分析、归纳等方法,培养学生的数学思维能力和问题解决能力。
3.情感态度与价值观目标:激发学生学习数学的兴趣,提高学生对数学的应用意识。
四. 教学重难点1.重点:进球线路与射门角的关系。
2.难点:如何将数学知识应用到实际问题中。
五. 教学方法1.情境教学法:通过丰富的图片和实例,引导学生置身于实际问题中,激发学生的学习兴趣。
2.问题驱动法:教师提出问题,引导学生主动探究,培养学生的问题解决能力。
3.合作学习法:学生分组讨论,共同解决问题,培养学生的团队协作能力。
六. 教学准备1.准备相关图片和实例,用于课堂讲解和引导学生思考。
2.准备进球线路与射门角的动画演示,帮助学生直观地理解概念。
3.准备练习题和拓展题,用于巩固所学知识和提高学生的问题解决能力。
七. 教学过程1.导入(5分钟)利用一张足球比赛的图片,引导学生思考:如何才能更好地进球?激发学生的兴趣,引入本节内容。
2.呈现(10分钟)讲解进球线路与射门角的概念,通过动画演示,让学生直观地理解两者之间的关系。
沪科版(2012)初中数学九年级下册 24.8 综合与实践:射门线路与最佳射门角 教案
24.8综合与实践教学设计进球线路与最佳射门角一、教学背景(一)教材分析本节课的内容为进球线路与最佳射门角,选自沪科版九年级数学下册第二十四章《圆》第八节的内容,要求学生能理解进球线路和最佳射门角存在关系,结合圆及相关知识,找到最佳射门角。
本节内容是本章知识的升华和提高,是数学知识与现实生活的紧密联系。
(二)学情分析学生已经学习了圆的知识,对圆周角、圆内角、圆外角的比较已经掌握,并有一定的生活经验。
但本节内容比较抽象,将结合几何画板进行讲解分析,提高直观性。
二、教学目标让学生理解能利用圆的知识分析进球路线与射门角度关系,通过观察分类、观察、思考进球路线与射门角度存在关系。
通过不同进球路线的分析,结合圆周角的知识找到最佳射门角。
让学生感受数学对现实生活的意义,体会分类讨论思想。
培养学生积极参与和勇于探索的精神。
三、教学重点与难点教学重点:理解进球路线和射门角关系。
教学难点:利用圆及相关知识找到最佳射门角。
四、教学方法分析及学习方法指导多媒体教学,利用几何画板辅助理解,让学生通过观察、思考、讨论、交流结合圆的知识,找出最佳进球角。
五、教学过程(一)导入新课足球场上的顺口溜:冲向球门跑,越近就越好;歪着球门跑,射点要选好!足球运动已成为一种世界性的运动,也是我们大家喜欢欣赏的一种体育活动。
在比赛的过程中,运动员在对方球门前不同的位置起脚射门对球门的威胁是不相同的。
设计意图:从生活中的实际问题入手,使学生认识到数学总是与现实问题密不可分,同时激发学生的学习热情。
(二)新授内容1.足球场上,常需带球跑动到一定位置后,再进行射门,这个位置为射门点,射门点与球门边框两端点的夹角就是射门角;如果用点A、B表示球门边框(不考虑球门的高度)的两端点,点C表示射门点,连接AC,BC,则∠ACB就是射门角.在不考虑其他因素的情况下,一般说来,射门角越大,射门进球的可能性就越大。
2.运动员带球跑动的三种常见线路(用直线l表示)设计意图:让实际问题转化为数学知识,让学生感受分类的数学思想。
秋九年级数学下册(沪科版)课件:24.8 综合与实践 进球线路与最佳射门角(共11张PPT)
•
13、He who seize the right moment, is the right man.谁把握机遇,谁就心想事成。2021/9/102021/9/102021/9/102021/9/109/10/2021 •14、谁要是自己还没有发展培养和教育好,他就不能发展培养和教育别人。2021年9月10日星期五2021/9/102021/9/102021/9/10 •15、一年之计,莫如树谷;十年之计,莫如树木;终身之计,莫如树人。2021年9月2021/9/102021/9/102021/9/109/10/2021 •16、教学的目的是培养学生自己学习,自己研究,用自己的头脑来想,用自己的眼睛看,用自己的手来做这种精神。2021/9/102021/9/10September 10, 2021 •17、儿童是中心,教育的措施便围绕他们而组织起来。2021/9/102021/9/102021/9/102021/9/10
•9、要学生做的事,教职员躬亲共做;要学生学的知识,教职员躬亲共学;要学生守的规则,教职员躬亲共守。2021/9/102021/9/10Friday, September 10, 2021 •10、阅读一切好书如同和过去最杰出的人谈话。2021/9/102021/9/102021/9/109/10/2021 7:20:13 PM •11、只有让学生不把全部时间都用在学习上,而留下许多自由支配的时间,他才能顺利地学习……(这)是教育过程的逻辑。2021/9/102021/9/102021/9/10Sep-2110-Sep-21 •12、要记住,你不仅是教课的教师,也是学生的教育者,生活的导师和道德的引路人。2021/9/102021/9/102021/9/10Friday, September 10, 2021
沪科版(2012)初中数学九年级下册 24.8 综合与实践:进球线路与最佳射门角 教案
24.8综合与实践——进球线路与最佳射门角一、教学目标:1、了解足球运动中射门点,射门角以及最佳射门角的概念;2、了解足球运动员在跑动线路变化时,射门角的大小变化,探究三种常见线路下,最佳射门点的位置;3、通过探究学习,促进学生相互交流,最大限度获得用圆中的知识解决相关实际问题的能力,以及体验用运动的观点来研究图形的思想方法。
二、教学分析:1、内容分析:本节是在学生掌握圆的基本性质,以及圆与点,直线,三角形,正多边形的位置关系的基础上,进一步探讨圆与角的位置关系,本节先从实例出发,探究足球运动中进球线路与最佳射门角的问题。
从三种情形下建立认识,最佳射门角是从直线与圆相切时,进行探究的,从而将实际问题转化成直线与圆相切的位置问题。
教学中注重学生参与探究的过程,指导学生一步一步直线与圆相切的现实意义,体验用运动的观点来研究图形的思想方法。
2、教学重点: (1)、最佳射门角的概念理解; (2)、探求常见的三种线路下最佳射门点的位置。
3、教学难点:三种线路下最佳射门点位置确定与理解。
三、教学设计: 1、情境引入: 2、新知讲解:(1)、射门点与射门角的概念射门点:足球运动员在球场上,常需要带球跑到一定位置后,在进行射门,这个位置就叫射门点;射门角:射门点与球门边框两端点的夹角(不考虑球门的高度),就叫射门角,如图∠ACB 就是射门角。
(2)、探究最佳射门点的位置:如图:运动员带球跑动的三种常见路线C球门射门点(一)横向跑时的最佳射门点确定现在,如图1,我们来证明点C 在直线l 上移动时,∠ACB 是最大角(最佳射门角),参见课本63页的证明过程。
推论1、最佳射门角的大小与直线m 到直线AB 的距离有关,当直线m 与AB 的距离越近,最佳射门角就越大,射门进球的可能性也就越大。
推论2、如果圆过点A,B,而直线AB 同侧的三点D 、C 、E ,分别在圆外、圆上、圆内,则有:圆外角<圆上角<圆内角(二)、再对直向跑动时,如,2,球门AB 与直线m 垂直,点C 是运动员的位置 推论3、当直线与过A 、B 的圆相切时,切点是最佳射门点。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
如图:
射门点与球射门门角
A
B
射门角
C
射门点
在不考虑其他因素的情况下:一般地,射门 角越大,射门进球的可能性就越大
一、横向跑动时的最佳射门点
球门
A
B
射门角
1.正对着球门 2. 红线越近
C 射门点
一、横向跑动时的最佳
射门点
A
B
E
m
D
C
称:C点为直线m上的最佳射门点, ∠ACB为直线m上的最佳射门角
这时点C为过AB的圆也直线m的切点
一、横向跑动时的最佳射门点
A
B
m
D
C
最佳射门角的大小与直线m到直线AB的距离有 关,当直线m与AB的距离越近,最佳射门角就 越大,射门进球的可能性也就越大。
二、直向跑动时的最佳射门点
球门
A
B
射门角越离近球门,进球C 射门点率越高,无最佳射
门角
二、直向跑动时的最佳射门点
佳射门点? C
这时切点就是最佳射门角
三、斜向跑动时的最佳射门点
球门
A
B
射门角
m C
射门点
当C在过AB的圆与直线m切点时
三、斜向跑动时的最佳射门点
A
B
l C
结论:当斜向跑动时,过AB的圆与直线l相 切时,切点与AB所组成的角为最佳射门角
结论:
A
B
E
P m
D
C
如果圆过点A,B,而直线AB同侧的三点 D、C、E分别在圆外、圆上、圆内,
则有: 圆外角<圆周角<圆内角
典例分析1
如图,点P在圆外,点M,N都
在圆上,则下列角度大小关
系正确的是( )
A
B
A、∠APB>∠AMB
B、∠APB>∠ANB C、∠APB<∠AMB D、∠ANB>∠AMB
N
P
M
典例分析2
如图,在足球比赛中,甲带
球向对方球门AB进攻,当他
带球冲到C点时,同伴乙、丙
A
当运动员跑 动路线垂直 穿过球门AB时, 分析最佳射门点 的位置
B D
C
此时,∠ACB越来越大,直线上没有最佳射门点 这时,离球门越近,进球率越高
二、直向跑动时的最佳射门点
球门 A
射门点为过AB的 圆与直线m的切点
B
射门角
C 射门点
m
二、纵向跑动时的最佳射门点
注:当直线与
A
B
过A、B的圆相
D
切时,切点是最
小结:
同学们!今天你学到了什么 知识?
作业:
利用今天所学的知识,课 下几个同学一起到足球感受 今天所学知识应用
谢谢大家! 再见!
谢谢
已经分别助攻到点D、E,不
考虑防守情况,仅从射门角
A
度考虑,下列说法能够使进 球有最佳射门角度的是( )F
A、立刻射门
B、带球到点F射门 C
E
C、传给同伴乙
C
B D
典例分析3
已知:AB=m,BD=n,当点C是直线l上的最 佳射门点时,求CD的长
A
BD
解:
CD:AD=BD:CD
C
CD=AB·BD
CD2=n(m+n)
