数值分析 第二章 非线性方程求解
数值分析中的非线性方程求解与优化

数值分析中的非线性方程求解与优化在数值分析领域中,非线性方程求解是一个重要的问题。
许多实际问题都可以被建模为非线性方程,而求解这些方程对于解决实际问题具有重要意义。
本文将介绍非线性方程求解的基本概念、方法和优化技术。
一、非线性方程求解的概念非线性方程是指方程中包含非线性项的方程。
与线性方程不同,非线性方程的解不再是一条直线,而是一条曲线或曲面。
非线性方程的求解是寻找方程中满足特定条件的变量值或函数的过程。
二、非线性方程求解的方法1. 迭代法迭代法是解决非线性方程求解问题中常用的方法。
迭代法的基本思想是通过不断逼近方程的解,使得迭代序列逐步收敛于方程的解。
常见的迭代法包括牛顿迭代法、割线法和弦截法等。
以牛顿迭代法为例,假设要求解方程f(x) = 0,首先选择一个初始估计值x0,然后通过迭代公式进行迭代计算直到满足收敛条件。
迭代公式为:xn+1 = xn - f(xn)/f'(xn),其中f'(xn)表示f(x)在xn处的导数。
2. 区间划分法区间划分法是通过将求解区间划分为若干个子区间,然后在每个子区间内搜索方程的解。
这种方法常用于求解具有多个解的非线性方程。
一般可以使用二分法、割线法和弦截法等算法进行区间划分和求解。
3. 优化技术优化技术常用于求解非线性方程的最优解。
在数值分析中,优化问题可以理解为寻找使得目标函数达到最大或最小值的变量值。
常用的优化算法包括梯度下降法、拟牛顿法和粒子群算法等。
这些算法通过迭代过程不断调整变量值,使得目标函数逐渐趋于最优解。
三、非线性方程求解与优化的应用非线性方程求解和优化技术在实际问题中具有广泛的应用。
以下是一些应用领域的例子:1. 工程领域:在工程设计中,需要求解非线性方程以确定优化的设计参数。
例如,在机械设计中,可以通过求解非线性方程来确定零件的几何尺寸和运动轨迹。
2. 金融领域:在金融衍生品定价和风险管理中,需要求解非线性方程来估计资产价格和风险敞口。
数值分析_第2章

证:由1。 f '( x) C[a, b],由2。 f '( x)不变号,故f ( x) 知 知 单调,再由3。 唯一的 [a, b],使f ( ) 0. 知
由1 3 知f ( x)在[a, b]上必属于下列四种情形之一:
。 。
f ''( x) 0 f (a) 0, f (b) 0, f '( x) 0(增) f ''( x) 0
二.收敛性:
mn . n .
◆判定二分次数:
1 lim n 1 b0 a0 0 n 2
1 对 0,若要求 mn n 1 b0 a0 2
b0 a0 则2 n log 2 1与取整的 1抵消 .
定理1.(单点法收敛的充分条件) 设f ( x)在[a, b]上二阶 可导,且满足:
。 1. f ''( x)在[a, b]上不变号(凹凸不变性);
2。 f '( x)在[a, b]上不为0(单调性); . 3。 f (a) f (b) 0; . 4。取x0 [a, b], 使f ( x0 ) f ''( x0 ) 0.x1 [a, b], f ( x1 ) f ( x0 ) 0. . 则由(6)所得 xn 单调收敛于f ( x) 0在[a, b]上的唯一根。
列表计算:
n
0 1 2 3 4 5
xn
2 1 1.33333 1.40000 1.41176 1.40378
2
f ( xn )
2 -1 -0.22223 -0.04000 -0.00692
hn
数值分析 第二章 基于MATLAB的科学计算—非线性方程(组)

科学计算—理论、方法及其基于MATLAB 的实现与分析解非线性方程(组)(一)直接法二分法:设方程()0=x f 在区间[]b a ,上有唯一解,并且()()0<b f a f ,如方程()f x x x x x =-++=3223030.sin .(1)首先要确定适当的包含根的区间,这可以依据闭区间上连续函数的介值定理来确定,例如,()f 1110=-+<sin ,()f 222090=->sin .,所以方程 (1)至少有一个实根属于区间[]12,,图1表明区间[]12,中只含有一个根,显然方程 (1)的根不易直接求得。
在区间[-1,0]、[0,1]和[1,2]的情形,如下图1所示 例1 plotNL_fun01.mplotNL_fun01clearx=-1:0.05:2;f=x.^3-2.3*x.^2+x.*sin(x)+0.3; plot(x,f,'r',x,0*x,'k')title('The Image of f(x)=x^3-2.3*x^2+x*sin(x)+0.3') xlabel('\fontsize {12} \fontname {宋体} 图1') axis square二分法的求根过程:用*x 表示方程()0=x f 在区间[]b a ,上的根,对于给定的精度要求0>ε,取区间[]b a ,的中点21ba x +=,并按下式进行判断: ()()()()()⎪⎩⎪⎨⎧∈⇒<∈⇒<=⇒=],[0],[001*11*1*11b x x b f x f x a x a f x f x x x f (2) 以()()01<a f x f 为例,如果ε≤-2ab ,那么区间[]1,x a 内的任何一点都可以作为方程()0=x f 的近似根。
二分法适用于一个方程的场合,收敛速度是线性的,二分次数的估计:()b aN b a N-≤⇒≥--22εεln ln ln (3) 2、黄金分割法:在区间[]b a ,内取对称的两点:()()()⎩⎨⎧-+=--+=a b a x a b a x ββ211 (4) 使得()()()()()618.025125101102221≈+-=−−→−±-=⇒=-+⇒--=--=--=--->ββββββββa b a b ab a x a x a x a b a b按这种方法选取点1x 和2x ,每次去掉的区间长度至少是原区间长度的0.618倍,()()()()()()()()⎪⎪⎩⎪⎪⎨⎧∉∈⇒<⋃∉∈⇒<∉∈⇒<=⇒==⇒=],[],[0],[],[],[0],[],[0002*2*221*21*211*1*1*22*11x a x b x x b f x f b x x a x x x x x f x f b x x x a x a f x f x x x f x x x f (5) 适用于一个方程的场合,收敛速度是线性的,迭代次数的估计:()()215lnln ln 215--->⇔<⎪⎪⎭⎫ ⎝⎛--a b N a b Nεε (6) (二)迭代法首先将方程(组)写成等价的迭代形式:()()0f x x x ϕ=⇔= (7)由此确定了相应的迭代法:()[]10,n n x x x a b ϕ+=⎧⎪⎨∀∈⎪⎩ (8)迭代收敛的图像解释对于非线性方程(组)的迭代法来说,同样面临收敛性问题,为说明收敛性条件,先看下面的例子:例2:让我们来求如下方程的根()f x x x x x =-++=3223030.sin .下面,我们采用迭代法求方程 (1)位于区间]01[,-中的根,为此构造迭代算法如下:()()x x xx g x -+==3.2sin 3.0 (9)()()x g x x x x n n nn n +==+-10323.sin ., n =12,, (10)在区间]01[,-中任取一个迭代初值x 0,如取初值8.00-=x .执行下面的程序:EqutIteration.m:open EqutIteration.m EqutIterationN =29下面欲求1.5附近的根,为此分别取初值4.10=x ,9.10=x ,迭代的结果如下:open Ex_IteraConv01 Ex_IteraConv01N = 31收敛性定理:(收敛的充分性条件)设方程()f x =0在[]a b ,上存在唯一解,()x g x =是方程的等价形式,如果1、()g x 在[]a b ,上连续可微; 2、对任何x a b ∈[],,()g x a b ∈[],; 3、()'≤<g x L 1,则对任何x a b 0∈[],,由迭代算法()x g x n n +=1, (11)生成的序列{}x n 收敛于方程()f x =0在[]a b ,上的唯一解。
数值分析实验报告——非线性方程求根

数值分析实验报告——非线性方程求根一、实验目的:1.掌握求解非线性方程的常用方法;2.了解非线性方程求根问题的数值解法;3.熟悉使用数值分析软件进行非线性方程求根的实现。
二、实验原理:非线性方程指的是形如f(x)=0的方程,其中f(x)是一个非线性函数。
非线性方程求根的常用方法包括二分法、割线法和牛顿法等。
其中,二分法是通过不断缩小区间范围来逼近方程的解;割线法是通过使用割线来逼近方程的解;牛顿法则是通过使用切线来逼近方程的解。
对于给定的非线性方程,可以根据实际情况选择合适的方法进行求根。
三、实验内容:1.编写求解非线性方程的函数,包括二分法、割线法和牛顿法;2.使用编写的函数求解给定的非线性方程,比较各个方法的收敛速度和精确程度;3.根据实际情况分析和选择合适的方法进行求根。
四、实验步骤:1.针对给定的非线性方程,编写二分法的函数实现:(1)首先确定方程的解存在的区间;(2)根据方程的解存在的区间,使用二分法逐步缩小区间范围;(3)根据设定的精度要求,不断循环迭代,直至满足要求或达到迭代次数限制;2.针对给定的非线性方程,编写割线法的函数实现:(1)首先需要确定方程的解存在的初始点;(2)根据方程的解存在的初始点,根据割线的定义进行迭代;(3)设定迭代的精度要求和限制次数,结束迭代;3.针对给定的非线性方程,编写牛顿法的函数实现:(1)首先需要确定方程的解存在的初始点;(2)根据方程的解存在的初始点,根据牛顿法的定义进行迭代;(3)设定迭代的精度要求和限制次数,结束迭代;4.根据给定的非线性方程,分别使用二分法、割线法和牛顿法进行求解,并比较各个方法的收敛速度和精确程度;5.分析实际情况,选择合适的方法进行求解。
五、实验结果:4.通过比较,发现割线法和牛顿法的收敛速度较快,精确程度较高,因此选择割线法进行求解。
六、实验总结:通过本次实验,我掌握了求解非线性方程的常用方法,并使用数值分析软件实现了二分法、割线法和牛顿法。
东南大学-数值分析-第二章-牛顿迭代法

东南大学-数值分析-第二章-牛顿迭代法第二章非线性方程的解法某某某某(学号)某某某某(姓名)算法与程序题目见教材P56上机题目20。
一、算法原理根据题目的要求,是关于用牛顿迭代法法求解方程f(某)0的通用算法。
该法是一种通过斜率迭代的算法,其速度比二分法和简单迭代法都要快。
其简单原理如下:设fC2[a,b],且存在数p[a,b],满足f(p)0。
如果f(p)0,则存在一个数0,对任意初始值p0[p,p],使得由如下定义的迭代序列{pk}k0收敛到p:pkg(pk1)pk1f(pk1),其中k1,2,f(pk1)(1)对于函数f(某)某3/3某=0,则其递推规则是32pkpk21,其中k1,2,3pk1-3(2)定义序列{pk}则序列{pk}也可表示为limpk某现简要证明:k0,k0收敛到某,某对于f(某)某3/3某,得f'(某)某2-1,写出牛顿迭代公式f(某)某3/3某g(某)某某2f(某)某-1(3)该公式可化简为2某3g(某)23某3(4)二、流程图题目要求于用牛顿迭代法法求解方程f(某)0的通用算法。
其计算过程主要第二章非线性方程的解法用到迭代g(某)某f(某),图流程图1所示。
f(某)输入各参数k=1迭代pkg(pk1)pk1f(pk1),其中k1,2,f(pk1)Tbreak计算各误差误差在允许范围之内Fk=k+1k三、计算代码核心代码1)p1=……;2)if(err程序1:Newton.m%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %Decription:牛顿迭代法%Author:panyunqiang%Veroin:1.0%Date:2022-9-21%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%f unction[p0,err,k,y]=Newton(p0,delta,epilon,ma某N)%input-p0itheinitialappro某imationtoazerooff%-deltaithetoleranceforp0%-epilonithetoleranceforthefunctionvaluey%-ma某Nithema某iumnumberofiteration%output-p0itheNewtonappro某imationtoazero%-erritheerroretimateforp0东南大学《数值分析》上机练习——算法与程序设计实验报告%-kithenumberofiteration%-yithefunctionvaluef(p0)fork=1:ma 某N%%递归p1=2某p0^3/(3某p0^2-3);%%计算误差err=ab(p1-p0);relerr=2某err/(ab(p1)+delta);p0=p1;%%当前求出的根的函数值y=p0^3/3-p0;%%判断if(err程序2:Newton_Step.m%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %%%Decription:寻找题目中关于牛顿迭代法收敛的尽可能大的delta%搜索步进为tep=10^(-6),即精确到小数点后六位%Author:panyunqiang%Veroin:1.0%Date:2022-9-21%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %formatlongtep=10^(-6);delta=10^-8;epilon=10^-8;ma某N=1000;p=0.6;[p0,err,k,y]=Newton(p,delta,epilon,ma某N);while((ab(p0)<=epilon)&(p0~=NaN))p=p+tep;[p0,err,k,y]=Newton(p,delta,epilon,ma某N);endp-tep四、计算结果及分析a)运行程序Newton_Step.m,获得Newton局部收敛于某2=0的初始值的范围=0.774596,六位有效数字。
非线性方程的数值解法

2. 2 二分法
二分法的误差估计
由于 x − x* ≤ 1 (b − a ) = b − a k k k k +1 k +1
2
只要有根区间[a 只要有根区间 k+1, bk+1]的长度小于预先给定的误 的长度小于预先给定的误 差ε,那么就可以取 作为所求根x*的第 次近似值。 作为所求根 的第k+1次近似值。其误差估计为 的第
计算机科学与工程系 21
2.3 迭代法
简单迭代法的原理 迭代法的收敛性 迭代加速法
计算机科学与工程系 22
2.3.1 简单迭代法原理
基本思想
将方程f 将方程 (x) = 0化为一个等价的方程 化为一个等价的方程 x = ϕ (x ) 从而构成序列
x k +1 = ϕ ( x k ) k = 0 , 1, 2 , L
计算机科学与工程系
9
2.1.2 根的隔离方法
画图法
f(x)
x0 =
a
x0 + h
x* b
计算机科学与工程系 10
2.1.2 根的隔离方法
逐步扫描法
设单值连续函数f(x)在有根区间 b],从左端点 = 在有根区间[a, ,从左端点x 设单值连续函数 在有根区间 a出发,按某个预先选定的步长 一步一步地向右跨 出发, 出发 按某个预先选定的步长h一步一步地向右跨 每跨一步都检验每步起点x 和终点x 每跨一步都检验每步起点 0和终点 0 + h的函数值 的函数值 如果
1 x − xk ≤ k +1 (b − a) 2
*
计算机科学与工程系 16
1 xk = (ak + bk ) 2
输入 a, b, ε 定义f (x) 是
数值分析(26)非线性方程组的数值方法
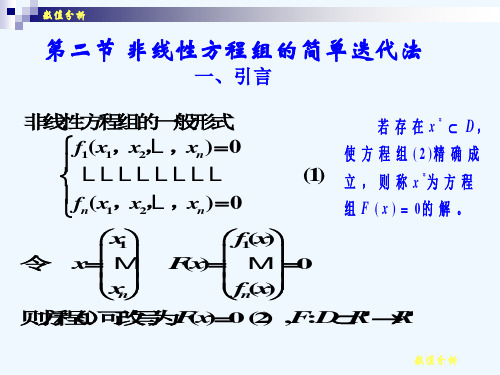
(k )
k0
收 敛 到 x *,
x
*
x (k ) x *
L x (k ) x (k 1) 1 L Lk x (1 ) x ( 0 ) 1 L
数值分析
数值分析
对 压 缩 映 射 原 理 的 认 识 和 讨 论 : ( k 1 ) ( k ) [ 1 ] 条 件 1 ) 是 保 证 由 x ( x ) 产 生 的 迭 代 序 列 ( k ) { x } 仍 在 D 中 , 这 是 证 明 在 D 中 存 在 不 动 点 的 k 0 不 可 少 的 条 件 。
相应的解向量和右端向量分别为
u (u1,1, u2,1,..., uN,1, u1,2 , u2,2 ,..., uN,2 ,..., u 1, N , u2,N ,..., uN,N )T F(u) (F 1,1, F 2,1,..., F N,1, F 1,2 , F 2,2 ,..., F N,2 ,..., F 1, N , T F ,..., F ) 2, N N, N 2 其 中 F 为 非 线 性 函 数 , 含 右 端 项 h f (ih, jh, uij )及 i, j 相 应 边 界 点 ij (ih, jh)。
数值分析
数值分析
写 成 矩 阵 向 量 形 式
2 ln y1) 0 2 -1 y1 h29t1 y 2 2 -1 2 -1 2 h (t2 ln y2) 0 2 2 -1 2 -1 yn1 h (tn1 ln yn1) 0 y h2(t2 ln y ) 0 -1 2 n n n
(1)a 1, 无解 1 1 (2)a , 一个解,x1 x2 4 2 (3)a 0, 两个解,x1 x2 0;x1 x2 1 (4)a 1,四个解,x1 1, x2 0; x1 0, x2 1; 1 x1 x2 (1 5)。 2
数值分析课件第二章非线性方程的数值解法1

Step 5 If x*f(a)<0 , Set b=x; Else Set a=x;
Step 6 Set k=k+1; Compute x=f((a+b)/2);Go To Step 3 ;
Step 7 Output the solution of equation: x; STOP.
思
xk+1 = g(xk), … 若
xk
k0
收敛,即存在 x* 使得
路 lk im xk x*,且 g 连续,则由 lk i m x k 1lk 可 i 知m gxx *k=
g(x* ),即x* 是 g 的不动点,也就是f 的根。
几何意义
y
p1 p0
y=x y=g(x)
x3 1.365230014 x 11 1 .3 6 5 1 3 7 8 2 1 x 4 1.365230013
x 29 1 .3 6 5 2 3 0 0 1 3
法4
x 1 1 .3 4 8 4 0 x 2 1 .3 6 7 3 8 x 3 1 .3 6 4 9 6 x 4 1 .3 6 5 2 6 x 4 1 .3 7 5 1 7 x 5 1 .3 6 5 2 2 5
⑥ lki m xxxxkk1 g(x) ?
L 越 小 收敛越快
lix m * x k 1 lig m (ξ k)x (* x k) g (x *) k x * x k k x * x k
注:条件 ( II ) 可改为 在[a, b] 满足Lipschitz条件, 定理结论仍然成立(定理2.3’)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
y
y cos x
y 3x 1
1 x ( , ) 3 2
*
1 3
x*
2
x
6
求隔根区间的一般方法
2.利用 f '( x) 的正、负与 f ( x ) 的单调性的关系来确定根的大概位置。
例 2:求 f ( x) x4 4 x3 1 0 的隔根区间。
解:令 f '( x) 4 x 12 x 0 ,可得驻点 x1 0, x2 3 .
第二章 非线性方程求解
二分法 迭代法
迭代法基本思想 迭代法的收敛条件 迭代法的收敛速度 Aitk法的变形 计算重根的牛顿法
1
引言
很多科学计算问题常归结为求解方程:
f ( x) 0
n n 1 代数方程:形如 f ( x ) a x a x an (a0 0) 0 1 方程 超越方程:非代数方程
14
§2 迭代法
迭代法的基本思想: 对给定方程 f ( x) 0 , 将它转换成等价的形式 x ( x) 。 给定初 值 x0 ,构造序列 xk 1 ( xk ), k 1,2,3,,如果迭代收敛
k
lim xk 1 lim ( xk ) x* ,
k
x3 2.1875
2.25] 1 1 2 2. [2 | xn x | n 1 (3 2) n 1 10 2 2 3. [2.125 2.25] 2 n 1 2 100 n 1 5.6 4. [2.1875 2.25] lg 2
5. [2.21875
5
求隔根区间的一般方法
1.作图法: 画出 y f ( x) 的草图, 由 f ( x ) 与 x 轴交点的大概位置 来确定有根区间。
例 1:求 f ( x) 3x 1 cos x 0 的隔根区间。
解:将方程变形为 3x 1 cos x 绘出曲线 y 3x 1 及 y cos x , 由右图可知,方程只有一个实根:
定义:如果 f ( x) ( x x* )m g ( x) ,其中 m 为正整数, g ( x) 的分母 不含有因子 ( x x* ) ,且 g ( x* ) 0 ,则称 x 为 f ( x ) 的 m 重
*
零点, x 为 f ( x) 0 的 m 重根。当 m 1 时,称 x 为单根。
*
12
例 4. 方程 f ( x) x2 5 0 在区间 [2,3] 中有一实根, 若用二分法求此 根,使其误差不超过 102 ,问应将区间对分几次?并请用二分法求此 根。
0.[2 3]
解:假设区间对分 n 次,
*
1.[2
2.5]
x0 2.5 x1 2.25
x2 2 . 1 2 5
4
几个重要结论
1 设 f ( x) C[a, b] , 且 f (a) f (b) 0 , 根据连续函数的介值定理, 那 么在区间 ( a, b) 必存在零点; 若 f ( x ) 在 ( a, b) 严格单调, 则 f ( x) 0 在
( a, b) 内只有一个根。
2 n 次代数方程在复数域上恰有 n 个根(一个 r 重根算 r 个根) ,实系 数代数方程的复根会成对出现。
y
y=x
y = (x )
y
y=x
y = (x )
x0 x2 x* x1
x
x* x2 x1
x0
x
20
当然,迭代过程也可能出现下图所示的情况,此时 xn 越来越远离 x , 迭代序列发散。
y=x
y y = (x) y=x
*
y = (x) x3 x1 x* x0
x2
x
x* x0 x1
x2
可以看出:随着 k 的增大,序列收敛于 3。
16
2 xk 3 (2). xk 1 xk
x1 2.750000000000000 ; x2 3.090909090909091 ; x3 2.970588235294118 ; x4 3.009900990099010 ; x5 2.996710526315789 ; x6 3.001097694840834 ; 可以看出:随着 k 的增大,序列收敛于 3。
线性方程:n 1的代数方程 方程 非线性方程:n 1的代数方程、超越方程
问题:如何求解非线性方程?比如
x4 10 x3 35x2 50 x 24 0 ,
或
x e sin 0。 2
x
2
引言
记 非线性方程为 f ( x) 0 。
定义: 如果有一个数 x* , 使得 f ( x* ) 0 , 则称 x* 为方程 f ( x) 0 的根,又称 x* 为函数 f ( x) 的零点。
x4 8.495307 107
迭代格式不同,收敛情况也不同。选择迭代函数的基本原则是: 首先必须保证迭代产生的迭代序列 x0 , x1, x2 ,, xk ,收敛; 其次在收敛的基础上,要求迭代序列尽可能收敛得快。
19
迭代法的几何含义
从几何上看,迭代法是将求曲线 y f ( x) 的零点问题化为 求曲线 y ( x) 与直线 y x 的交点,迭代过程下图所示,
故应将区间对分 6 次。
6.[2.234375
x4 2.21875
x5 2.234375
2.25]
2.25]
取 x6 2.2421875 作为根的近似
二分法优缺点
优点:计算简单,方法可靠,容易估计误差。 缺点:收敛较慢,不能求偶重根,也不能求复根。 因此,一般在求方程近似根时,很少单独使用,常用于 为其它高速收敛算法(如牛顿法)提供初值。
例 6:用迭代法求方程 x 2 x x 3 0 在 [1,1.2] 的实根。
4 2
解:利用等价形式
x 1 ( x) (3 x 2 x )
x 2 ( x)
1 2 4 ;
x 4 1 ;
x 3 ( x) x4 2x2 3
取初始近似值 x0 1 ,分别考虑用迭代公式计算:
x
21
迭代法的收敛条件 –定理1
定理 1:方程 x ( x) , ( x) C[a, b] ,且满足以下两条件:
(1)当 x [a, b] , ( x) [a, b] ; (2) 存 在 常 数 0 L 1 , 对 任 意 的 x, y [a, b] , 有
| ( x ) y ( L ) | |x y | ;
1 2 (3). xk 1 ( xk 3) 2
x1 6.500000000000000 ; x2 19.625000000000000; x3 191.0703125000000 ; x4 18252.43215942383 ; 可以看出:随着 k 的增大,序列不收敛。
17
则 x 即为方程 f ( x) 0 的根。
*
这种求根方法称为迭代法, xk 1 ( xk ) 称为迭代格式, ( x) 称 为迭代函数,若迭代序列收敛,则称迭代格式收敛,否则称为发散。
15
例 5:方程 x 2 x 3 0 有以下三个等价形式:
2
2x 3 1 2 ; x ( x 3) x 2x 3 ; x x 2
18
(1) xk 1 1 ( xk ) (3 xk 2 xk )
(2) xk 1 2 ( xk )
1 2 4 ;
x26 x27 1.124123
xk 4 1 ; x6 x7 1.124123
(3) xk 1 3 ( xk ) xk 4 2xk 2 3 ;x3 96,
若 f ( x0 ) 0 ,则 x0 为方程的根,跳出循环;
a1 b1 若 f (a0 ) f ( x0 ) 0 ,令 a1 a0 , b1 x0 , x1 ; 2 a1 b1 若 f (a0 ) f ( x0 ) 0 ,令 a1 x0 , b1 b0 , x1 ; 2
( a, b) 内至少存在一点 ,使 f ( ) 0 。
二分法基本思想:用对分区间的方法,通过判别函数 f ( x ) 在每个对 分区间中点的符号,逐步将隔根区间缩小,最终求得一个具有相当精 确程度的近似根。
9
二分法具体步骤:
a0 b0 取 a0 a, b0 b, x0 , 2
3 2
x
f '( x) f ( x)
隔根区间
(, 0)
-
0 0 +
(0,3)
-
3
0 -
(3, )
+
减
减
增
(0,3)
(3, )
因 f (4) 0 ,所以,二个隔根区间确定为 (0,3),(3,4) 。
7
求隔根区间的一般方法
3.逐步搜索法:从区间 [ a, b] 的左端点 a 出发,按选定的步长 h 一 步步向右搜索,若:
则(1) x ( x) 在 [a, b] 上有唯一解 x* ; (2) 任取 x0 [a , b ] ,由 xk 1 ( xk ) 得到的序列 {xk } 收敛于
x* ,即有 lim xk x* ;
k
22
迭代法的收敛条件-定理1
(3) 成立误差估计式:
L | xk x | | xk xk 1 | , 1 L
*
(2.1)
k L | xk x* | | x1 x0 |, k 1, 2,3, 。(2.2) 1 L
注 1:(2.1)式称为事后估计式,表示可用相邻两次迭代值之差 的绝对值来估计误差,可作为迭代终止条件。 注 2:(2.2)式称为事前估计式,可以估计出要达到给定精度ε 所需次数 n。
