《通信原理教学资料》Q函数和误差函数表.doc
误差函数表

误差函数表误差函数是数学中常见的一种函数,它在数学、物理、工程等领域中都有广泛的应用。
误差函数表是一份列出了误差函数在不同参数下取值的表格,它是一份重要的参考资料,可以帮助人们更好地理解误差函数的性质和应用。
本文将介绍误差函数的定义、性质和应用,并给出一份常用误差函数表,供读者参考。
一、误差函数的定义误差函数,又称为高斯函数,是一种特殊的积分函数。
它的定义如下:$$erf(x)=frac{2}{sqrt{pi}}int_{0}^{x}e^{-t^2}dt$$其中,$x$为自变量,$erf(x)$为函数值。
误差函数的图像呈现出一种钟形曲线,该曲线在$x=0$处取得最大值$1$,随着$x$的增大或减小,函数值逐渐减小,当$x$趋于正无穷或负无穷时,函数值趋于$1$或$-1$。
二、误差函数的性质1. 对称性误差函数具有对称性,即$erf(-x)=-erf(x)$。
这是因为误差函数的定义式中,$e^{-t^2}$为偶函数,因此积分区间$[0,x]$和$[0,-x]$的积分结果相同,只是符号相反。
2. 奇偶性误差函数具有奇偶性,即$erf(-x)=erf(x)$。
这是因为误差函数的定义式中,积分区间为$[0,x]$,而$e^{-t^2}$为偶函数,因此$erf(x)$为奇函数。
3. 渐进性当$x$趋于正无穷或负无穷时,误差函数的函数值趋于$1$或$-1$。
这是因为误差函数的定义式中,指数函数$e^{-t^2}$比分母中的$sqrt{pi}$增长得更快,因此当$x$趋于无穷时,分母可以忽略不计,误差函数的函数值趋近于$1$或$-1$。
4. 导数性质误差函数的导数具有简单的形式,即:$$frac{d}{dx}erf(x)=frac{2}{sqrt{pi}}e^{-x^2}$$这个导数的形式非常简单,但是它在误差函数的应用中起着重要的作用,比如在概率统计中经常用到的正态分布函数中,就涉及到误差函数的导数。
三、误差函数的应用误差函数在数学、物理、工程等领域中都有广泛的应用,以下列举几个例子:1. 概率统计误差函数在概率统计中应用广泛,特别是在正态分布函数中。
通信原理第3章(樊昌信第七版)

即
Po ( f ) H( f ) H( f ) Pi ( f ) H( f ) 2 Pi ( f )
结论:输出过程的功率谱密度是输入过程的功率谱密度乘 以系统频率响应模值的平方。
应用:由Po( f )的反傅里叶变换求Ro()
20
输出过程o(t)的概率分布
如果线性系统的输入过程是高斯型的,则系统的输出过
量之和。由概率论理论得知,这个“和” 也是高斯随机
变量,因而输出过程也为高斯过程。
注意,与输入高斯过程相比,输出过程的数字特征已经改变了。
21
3.5 窄带随机过程
什么是窄带随机过程?
若随机过程(t)的谱密度集中在中心频率
fc附近相对窄的频带范围f 内,即满足f << fc
的条件,且 fc 远离零频率,则称该(t)为窄带
E[c (t)] 0, E[s (t)] 0
27
(t)的自相关函数:由自相关函数的定义式
R (t,t ) E[ (t) (t )] Rc (t,t ) cosct cosc (t ) Rcs (t,t ) cosct sin c (t ) Rsc (t,t ) sin ct cosc (t ) Rs (t,t ) sin ct sin c (t )
1. 输出过程的均值是一个常数。
E 轾 臌x0 (t) = E 轾 臌xi (t) H (0)=aH (0)
a是输入过程的均值,H(0)是线性系统在f=0时的频率响
应,即直流增益。
15
输出过程o(t)的均值
0(t) h( )i (t )d
对上式两边取统计平均:
QBASIC函数一览表

QBASIC函数一览表函数名函数格式功能ABS y=ABS(n)得到n的绝对值ASC y=ASC(S$)得到字符串头一个字符的ASCII码ATN y=ATN(n)得到反正切值(单位是弧度)CDBL y=CDBL(n)把n转化为双精度浮点格式CHR$ S$=CHR$(n)得到ASCII码n对应的字符CINT y=CINT(n)对n进行舍入取整(奇凑偶CLNG y=CLNG(n)把一个数n转化为长整数COMMAND$S$=COMMAND$在DOS下启动程序时,获得命令行中的其余信息COS y=COS(n)得到自变量n的余弦值CSNG y=CSNG(n)把一个数值转化为单精度数CSRLIN y=CSRLIN返回光标行数位置CVI V%=CVI(2字节的串)字符串转换为整型数CVS V!=CVS(4字节的串)字符串转换为单精度数CVL V&=CVL(4字节的串)字符串转换为长整数CVD V#=CVD(8字节的串)字符串转换为双精度数CVSMBF V!=CVSMBF(4字节MS字符串)转换成IEEE格式单精度数CVDMBF V#=CVDMBF(8字节MS字符串)转换成IEEE格式双精度数DATE$ S$=DATE$把系统日期赋给变量S$ENVIRON$S$=ENVIRON$(X$)S$=ENVIRON$(n)得到环境表中的参数EOF y=EOF(filenum)遇到文件结束则返回真,否则为假ERDEV y=ERDEV返回设备驱动器错误码ERDEV$ S$=DEDEV$返回设备驱动器错误信息ERR y=ERR返回错误的错误号ERL y=ERL返回出错处最近的行号EXP y=EXP(X)指数函数y=exFILEATTR y=FILEATTR(filenum,attr)返回打开文件的信息FIX y=FIX(n)截掉小数部分进行取整FRE y=FRE({S$|-1|-2})得到可以被程序使用的剩余内存空间的大小FREEFILE y=FREEFILE返回下一个自由BASIC文件号HEX$ S$=HEX$(n)把十进制数转换成相应十六进制格式字符串INKEY$ S$=INKEY$从键盘上读数据但不显示INP y=INP(portno)从一个I/O端口读入一个字节INPUT$ S$=INPUT$(m[,[#]n])从键盘或文件中读入指定数量的字符INSTR y=INSTR([n,]targetstring,patternsttring)字符串查找INT y=INT(n)得到一个不大于n的最大整数IOCTL$ S$=IOCTL$[#]n从一个设备驱动器程序接收数据LBOUND y=LBOUND(array[,n])返回数组array第n维的最小下标LCASE$ S$=LCASE$(X$)把字符串X$的大写字母全变为小写LEFT$ S$=LEFT$(X$,n)得到字符串X$最左边的n个字符LEN y=LEN(S$)得到字符串S$的长度LOC y=LOC(n)得到文件中现在所处的位置(当前位置)LOF y=LOF(n)得到磁盘文件的长度或通讯缓冲区剩余空间大小LOG y=LOG(x)自然对数y=InXLPOS y=LPOS(printer)得到打印缓冲区中当前的位置LTRIM$ S$=LTRIM$(x$)返回去掉前导空格的字符串复制品MID$S$=MID$(X$,n[,m])从X$的第n个字符开始取m个字符;省略m,则取完MKD$ S$=MKD$(V#)把双精度数值转化为随机文件中输出字符串MKI$ S$=MKI$(V%)把整数转换为字符串MKL$ S$=MKL$(V&)把长整数转换为字符串MKS$ S$=MKS$(V!)把单精度数转换为字符串MKSMBF$ S$=MKSMBF$(V!)把单精度数转换为MS格式字符串MKDMBF$ S$=MKDMBF$(V#)把双精度数转换为MS格式字符串OCT$ S$=OCT$(n)得到数值n的八进制形式字符串,负数为其补码形式PEEK y=PEEK(offset)得到指定存储单元的值PEN y=PEN(option)读取光笔状态PLAY y=PLAY(x)得到后台音乐缓冲区音符个数PMAP y=PMAP(i,option)把图形屏幕的物理坐标变为实用坐标或反之POINT color=POINT(x,y)y=POINT(n)得到一个象素的颜色得到前一个点的坐标POS y=POS(x)得到光标的列数位置RIGHT$ S$=RIGHT$(x$,n)从字符串X$的右边取n个字符RND y=RND(n)得到0到1之间的随机数,n=0则得到前一个RND值RTRIM$ S$=RTRIM$(X$)返回一个去掉X$尾随空格的字符串SADD y=SADD(S$)返回S$字符串的地址SCREEN y=SCREEN(row,column[,option])得到屏幕上指定字符的ASCII或属SEEK y=SEEK(filenum)返回当前文件位置SETMEM y=SETMEM(n)改变远堆集使用的内存大小SGN y=SGN(n)输出n的符号SIN y=SIN(x)正弦值y=SinXSPACE$ S$=SPACE$(n)输出长度为n的空格字符串SPC SPC(n)在PRINT语句中跳过n个空格SQR y=SQR(n)给出n的平方根STICK y=STICK(n)返回两个操纵杆的坐标STR$ S$=STR$(n)返回一个表示n值的字符串STRIG y=STRIG(n)返回操纵杆触发状态STRING$S$=STRING$(n,x$)返回n个x$第一个字符组成的字符串TAB TAB(column)将输出位置移到column列TAN y=TAN(x)正切值y=tgXTIME$ S$=TIME$获得当前时间TIMER y=TIMER输出自午夜开始后流逝的秒数UBOUND y=UBOUND(array[,n])输出数组array第n维最大下标UCASE$ S$=UCASE$(x$)把字符串x$中所有小写字母变成大写VAL y=VAL(S$)输出字符串S$的相应数值VARPTR y=VARPTR(variable)返回变量的偏移地址VARSEG y=VARSEG(variable)返回变量的段地址VARPTR$S$=VARPTR$(variable)返回变量地址的字符串表示。
通信原理第2章 预备知识

l 信号的分类
数字信号和模拟信号 周期信号和非周期信号 信号分类 确定信号和随机信号 能量信号和功率信号
能量信号:能量有限的信号,只存在有限时间间隔内。
能量: E
T 2
T 2
f (t ) dt
2
1 T2 2 平均功率: S lim f (t ) dt T T T 2 当 T 时,若 S 是大于零的有限值,则 f (t ) 为功率信号。
如对同一台通信机作了n次观测,得到的结果 是不相同的,如图2-1所示。因为通信机的输出噪 声电压随时间的变化是不可预知的,所以,在同 一时刻ti这n次观测的记录结果,可以由随机变量 X(ti)进行表示,而在不同的时刻得到的观测结果 的集合X(t)={ X(t1),X(t2),…,X(ti)},则构成了 通信机输出噪声的随机过程。可以这样理解,随 机过程是依赖于时间参数的随机变量的全体,它 是时间的函数,而在每一个时间点上又可以由一 个随机变量表述。
2 FT ( f ) df
2
P
90%(或95%, 99%)
(2)根据能量谱或功率谱从最大值到下降3dB处所对应 的频率间隔定义带宽 (3)满足等式
B
E ( f )df
2 E (0)
或
B
P( f )df
2 P(0)
2.3 随机信号的分析
2.3.1 概率及随机变量
1. 概率:
* * 结论:时域内能量信号的总能量等于频域内各个频域分量能量的
连续和。周期信号的总的平均功率等于各个频域分量功率的总和。
若
1 1 2 E f (t ) dt F ( ) d E ( )d 2 E ( f )df 0 2 - 2 2
《通信原理》课程导学(学习指南)

《通信原理》课程导学(学习指南)第1章绪论一、重点本章的重点内容包括以下三部分:1. 通信系统的组成及其各组成部分的功能点对点通信系统的一般模型由五大部分“信源、发送设备、信道、接收设备、信宿”组成.根据不同的传输对象和研究内容,有更加具体的通信系统模型。
由通信系统模型可知,在实施通信的过程中,将涉及以下关键技术:“编码、解码、调制、解调、同步”在学习本课程的过程中,应着眼于这些技术的原理、性能和应用。
2. 信息及其度量通信的目的在于传输消息中所包含的信息.对接收者来说,只有消息中不确定的内容才构成信息,而这种不确定程度可以用概率来描述。
因此,消息中所含的信息量与消息发生的概率密切相关,而与消息的种类和重要程度无关。
要重点掌握离散消息的信息量、离散信源的平均信息量(熵)和总信息量的计算方法。
3. 通信系统的性能指标有效性和可靠性是通信系统的两个主要指标。
两者相互矛盾而又相对统一,且可互换。
在模拟通信系统中,有效性可以用带宽来衡量,可靠性可以用输出信噪比来衡量.在数字通信系统中,有效性用码元速率、信息速率和频带利用率表示,可靠性用误码率、误信率表示。
要注意理解每个性能指标的定义、内涵、关系和计算。
二、难点及解决方法本章的难点有:模拟信号与数字信号的区别;熵的计算;比特率和波特率的关系.解决方法:从它们的定义入手,并借助于教学视频中的例题讲解及课后习题的练习,就不难搞清楚它们的含义和区别。
第2章随机过程一、重点本章的重点内容包括以下四部分:1. 随机过程的基本概念和统计特性自然界中事物的变化过程可以大致分成为两类:一类是变化过程具有确定的形式的确定性过程,另一类是没有确定的变化形式的随机过程。
本节课程主要从随机变量和时间函数两个方面研究随机过程:(1) 随机过程的统计特性:概率分布函数、概率密度函数;(2)随机过程的数字特征:数学期望、方差、相关函数.2。
平稳随机过程及各态历经性平稳随机过程是指它的统计特性不随时间推移而变化,通信系统中所遇到信号及噪声大多可视为平稳的随机过程。
通信原理公式总结

第一章 绪论模拟通信系统一般模型:数字通信系统模型:点对点的通信按时间和传递方向可以分为:单工,半双工,全双工通信。
有效性指标 可靠性指标 模拟 频宽利用率输出信噪比数字 传码率,传信率,带宽利用率 误码率,误信率参量: 公式 单位 信息量 )(log 2x P I -=bit 平均信息量/信源熵∑=-=Mi i i x P x P x H 12)(log )()(bit/符号传码率 T R B /1= B 传信率 )(x H R R B b =b/s 带宽利用率B R B =ηB/Hz 误码率P e =错误码元数/码元总数误信率P b =错误比特数/比特总数第二章 确知信号确知信号功率信号 频谱⎰--=2220000)(1T T tnf j n dt et s T C π功率谱密度2|)(|1lim )(f S Tf P T T ∞→=自相关函数dtt s t s T R T T T ⎰-∞→+=2/2)()(1lim )(ττ能量信号 频谱密度∑∞∞--=dt e t s f S ft j π2)()(能量谱密度2|)(|)(f S f G =;)()]([1τR f G F =-自相关函数⎰∞∞-+=)()()(ττt s t s R ;)()]([f G R F =τ第三章 随机过程公式备注 统计均值dxx f t t E )()()]([⎰∞∞-=ξξf (x )是x 的概率密度函数统计自相关函数)]()([)(212,1t t E t t R ξξ==参照统计均值计算方法广义平稳随机过程1. 均值为常数,与时间t 无关2.自相关函数只与时间间隔τ有关时间均值⎰-∞→-=2/2)(1limT T T dt t x T a 时间自相关函数⎰-∞→----+=2/2)()(1lim )(T T T dtt x t x T R ττ各态历经性1.-=a t E )]([ξ 2.-----=)(),(21τR t t R平稳随机过程自相关函数性质)0(R代表平均功率)(∞R代表直流功率(均值的平方))()(ττ-=R R偶函数 )0(|)(|R R ≤τ有上界2)()0(σ=∞-R R方差代表交流功率高斯随机过程:)2)(ex p(21)(22σσπa x x f -- 结论1:线性系统:输出过程的功率谱密度是输入过程的功率谱密度乘以系统频率响应模值的平方,即)(|)(|)(2f P f H f P i o =结论2:如果线性系统的输入是高斯型的,则输出也是高斯型的。
通信原理 第3章
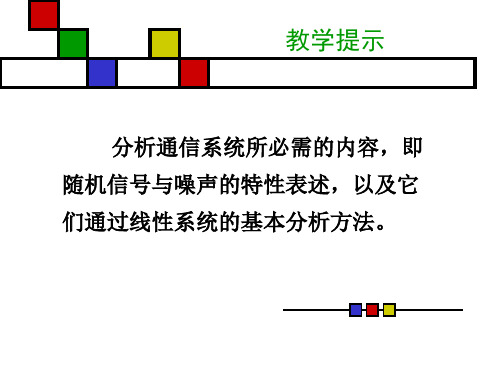
➢ 图3.1-1 n部接收机噪声记录
第3章
2 随机过程的统计特性
① 概率分布——分布函数和概率密度函数:
➢ 设ξ(t) 表示一个随机过程,则在任意一个时刻t1上ξ(t1) 是一个 随机变量。
➢ ξ(t)的一维分布函数: F1(x1,t1)=P [ξ(t1)≤x1]
一个随机过程的均值和自相关函数都具有各态历经性,则 称该随机过程具有各态历经性。
设x1(t)是ξ(t)的一个样本,若下列式子成立,则具有"各态历经
性"的平稳随机过程
注意:只有平稳随机过程才具有各态历经性
即各态历经的随机过程一定是平稳的,而平稳
的随机过程则需要满足一定的条件才是各态历 经的。
第3章
例3.3
例3.4
第3章
3.5 窄带随机过程
一、引言
➢ 1.必要性 ➢ 2.窄带条件
在通信系统中,许多实际信号和噪声都满足“窄带”的假设,
其频谱被限制在“载波”或某中心频率附近一个窄的频带上, 而这个中心频率离开零频率又相当远。
Δf
Ps(f)
本节主要内容:
**窄 窄带带随过-f机程c 过的程统的 计表 特示 性方式0
率和交流功率)。 ➢ 对偶性 R(τ)=R(-τ)
自相关函数R(τ)是τ的偶函数 证明:
第3章
➢ |R(τ)|≤ R(0)
当τ=0时,自相关函数取最大值
证明:
➢ R(∞ )=E2[ξ (t)] (3.2-10)
R(∞ )是ξ(t)的直流功率,在时间
间隔很大的时候,可将二者看成
R(τ)
是相互独立的。
通信系统中的信号及噪声,大多数可视为平稳的随机过程。 因此,研究平稳随机过程有很大的实际意义。
通信原理教学资料-第3章
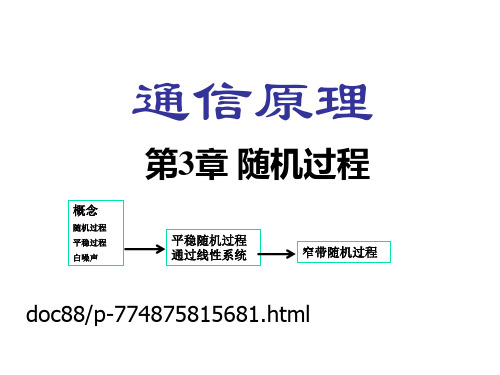
[x 1 a (t1 )x ]2 [a (t2 )f] 2 (x 1 ,x 2 ;t1 ,t2 )d1 d x 2x
式中 a ( t1 ) a ( t2 ) - 在t1和t2时刻得到的 (t)的均值
f2 (x1, x2; t1, t2) - (t)的二维概率密度函数。
3.1 随机过程的基本概念
自相关函数
R(t1,t2) E[(t1)(t2 )]
E[Acos(ct1 ) Acos(ct2 )]
A2 2
E{cosc (t2
t1 )
cos[c (t2
t1 )
2]}
A2 2
cosc (t2
t1 )
A2 2
2 0
cos[c
(t2
t1)
2]
1
2
d
A2 2
cosc (t2
t1 )
0
令t2 – t1 = ,得到
则其时间均值和时间相关函数分别定义为:
ax(t)lim1 T/2 x(t)dt
T T T/2
R()x(t)x(t)lim1 T/2 x(t)x(t)dt
T T T/2
如果平稳过程使下式成立
aa
R(
Байду номын сангаас
)
R(
)
时间平均= 集合平平均
则称该平稳过程具有各态历经性。
3.2 平稳随机过程
“各态历经”的含义是:随机过程中的任一次实现都经 历了随机过程的所有可能状态。因此,在求解各种统计 平均(均值或自相关函数等)时,无需作无限多次的考 察,只要获得一次考察,用一次实现的“时间平均”值 代替过程的“统计平均”值即可,从而使测量和计算的 问题大为简化。
间函数。
