2007年全国中考数学压轴题分类解析
2007年各地中考压轴题汇编(1)

2007年各地中考压轴题汇编(1)1、(安徽)按右图所示的流程,输入一个数据x ,根据y 与x 的关系式就输出一个数据y ,这样可以将一组数据变换成另一组新的数据,要使任意一组都在20~100(含20和100)之间的数据,变换成一组新数据后能满足下列两个要求: (Ⅰ)新数据都在60~100(含60和100)之间;(Ⅱ)新数据之间的大小关系与原数据之间的大小关系一致,即原数据大的对应的新数据也较大。
(1)若y 与x 的关系是y =x +p(100-x),请说明:当p =12时,这种变换满足上述两个要求; (2)若按关系式y=a(x -h)2+k (a>0)将数据进行变换,请写出一个满足上述要求的这种关系式。
(不要求对关系式符合题意作说明,但要写出关系式得出的主要过程) 【解】(1)当P=12时,y=x +()11002x -,即y=1502x +。
∴y 随着x 的增大而增大,即P=12时,满足条件(Ⅱ)……3分又当x=20时,y=1100502⨯+=100。
而原数据都在20~100之间,所以新数据都在60~100之间,即满足条件(Ⅰ),综上可知,当P=12时,这种变换满足要求;……6分(2)本题是开放性问题,答案不唯一。
若所给出的关系式满足:(a )h ≤20;(b )若x=20,100时,y 的对应值m ,n 能落在60~100之间,则这样的关系式都符合要求。
如取h=20,y=()220a x k -+,……8分∵a >0,∴当20≤x ≤100时,y 随着x 的增大…10分 令x=20,y=60,得k=60 ①令x=100,y=100,得a ×802+k=100 ②由①②解得116060a k ⎧=⎪⎨⎪=⎩, ∴()212060160y x =-+。
………14分 2、(常州)已知(1)A m -,与(2B m +,是反比例函数k y x=图象上的两个点.(1)求k 的值;(2)若点(10)C -,,则在反比例函数ky x=图象上是否存在点D ,使得以A B C D ,,,四点为顶点的四边形为梯形?若存在,求出点D 的坐标;若不存在,请说明理由.解:(1)由(1)2(3m m -=+ ,得m =-因此k =.·······················································································(2)如图1,作BE x ⊥轴,E 为垂足,则3CE =,BE =BC =30BCE = ∠.由于点C 与点A 的横坐标相同,因此CA x ⊥轴,从而120ACB =∠. 当AC 为底时,由于过点B 且平行于AC 的直线与双曲线只有一个公共点B ,故不符题意. ································································································ 3分 当BC 为底时,过点A 作BC 的平行线,交双曲线于点D , 过点A D ,分别作x 轴,y 轴的平行线,交于点F .由于30DAF =∠,设11(0)DF m m =>,则1AF ,12AD m =,由点(1A --,,得点11(1)D m --,.因此11(1)()m --=解之得1m =10m =舍去),因此点6D ⎛ ⎝⎭.此时BC 的长度不等,故四边形ADBC 是梯形. ·························· 5分如图2,当AB 为底时,过点C 作AB 的平行线,与双曲线在第一象限内的交点为D .由于AC BC =,因此30CAB= ∠,从而150ACD =∠.作DH x ⊥轴,H 为垂足,则60DCH =∠,设22(0)CH m m =>,则2DH ,22CD m =由点(10)C -,,得点22(1)D m -+, 因此22(1)m -+=解之得22m =(21m =-舍去),因此点(1D .此时4CD =,与AB 的长度不相等,故四边形ABDC 是梯形. ······························ 7分如图3,当过点C 作AB 的平行线,与双曲线在第三象限内的交点为D 时,同理可得,点(2D -,四边形ABCD 是梯形. ············································ 9分 综上所述,函数y x=图象上存在点D ,使得以A B C D ,,,四点为顶点的四边形为梯形,点D 的坐标为:63D ⎛ ⎝⎭,或(1D 或(2D -. ························································ 10分图1图23、(福建龙岩)如图,抛物线254y ax ax =-+经过ABC △的三个顶点,已知BC x ∥轴,点A 在x 轴上,点C 在y 轴上,且AC BC =. (1)求抛物线的对称轴;(2)写出A B C ,,三点的坐标并求抛物线的解析式;(3)探究:若点P 是抛物线对称轴上且在x 轴下方的动点,是否存在PAB △是等腰三角形.若存在,求出所有符合条件的点P 坐标;不存在,请说明理由. 解:(1)抛物线的对称轴5522a x a -=-=………2分 (2)(30)A -, (54)B , (04)C ,…………5分把点A 坐标代入254y ax ax =-+中,解得16a =-………6分215466y x x ∴=-++…………………………………………7分(3)存在符合条件的点P 共有3个.以下分三类情形探索.设抛物线对称轴与x 轴交于N ,与CB 交于M .52BM =过点B 作BQ x ⊥轴于Q ,易得4BQ =,8AQ =, 5.5AN =,① 以AB 为腰且顶角为角A 的PAB △有1个:1PAB △. 222228480AB AQ BQ ∴=+=+= ·········································在1Rt ANP △中,1PN====152P ⎛∴ ⎝⎭, ···················································································· 9分 ②以AB 为腰且顶角为角B 的PAB △有1个:2P AB △. 在2Rt BMP △中,22MP====··· 10分 252P ⎛∴ ⎝⎭················································································ 11分 ③以AB 为底,顶角为角P 的PAB △有1个,即3P AB △.画AB 的垂直平分线交抛物线对称轴于3P ,此时平分线必过等腰ABC △的顶点C . 过点3P 作3P K 垂直y 轴,垂足为K ,显然3Rt Rt PCK BAQ △∽△. 312P K BQ CK AQ ∴==. 3 2.5P K = 5CK ∴= 于是1OK = ····················································· 13分 3(2.51)P ∴-, ························································································ 14分 注:第(3)小题中,只写出点P 的坐标,无任何说明者不得分. 4、(福州)如图12,已知直线12y x =与双曲线(0)ky k x=>交于A B ,两点,且点A 的横坐标为4. (1)求k 的值;(2)若双曲线(0)ky k x=>上一点C 的纵坐标为8,求AOC △的面积; (3)过原点O 的另一条直线l 交双曲线(0)ky k x=>于P Q ,两点(P 点在第一象限),若由点A B P Q ,,,为顶点组成的四边形面积为24,求点P 的坐标.解:(1)∵点A 横坐标为4 , ∴当 x = 4时,y = 2 .∴ 点A 的坐标为( 4,2 ). ∵ 点A 是直线 与双曲线 (k>0)的交点 , ∴ k = 4 ×2 = 8 . (2) 解法一:如图12-1,∵ 点C 在双曲线上,当y = 8时,x = 1∴ 点C 的坐标为 ( 1, 8 ) . 过点A 、C 分别做x 轴、y 轴的垂线,垂足为M 、N ,得矩形DMON . S 矩形ONDM = 32 , S △ONC = 4 , S △CDA = 9, S △OAM = 4 . S △AOC = S 矩形ONDM - S △ONC - S △CDA - S △OAM = 32 - 4 - 9 - 4 = 15 . 解法二:如图12-2,过点 C 、A 分别做x 轴的垂线,垂足为E 、F , ∵ 点C 在双曲线8y x=上,当y = 8时,x = 1 . ∴ 点C 的坐标为 ( 1, 8 ). ∵ 点C 、A 都在双曲线8y x=上 , ∴ S △COE = S △AOF = 4 。
2007年全国中考数学压轴题精选全解之一

年全国各地中考试题压轴题精选全解之一(北京市).我们知道:有两条边相等的三角形叫做等腰三角形.类似地,我们定义:至少有一组对边相等的四边形叫做等对边四边形.()请写出一个你学过的特殊四边形中是等对边四边形的图形的名称; ()如图,在ABC △中,点D E ,分别在AB AC ,上, 设CD BE ,相交于点O ,若60A ∠=°,12DCB EBC A ∠=∠=∠. 请你写出图中一个与A ∠相等的角,并猜想图中哪个四边形 是等对边四边形;()在ABC △中,如果A ∠是不等于60°的锐角,点D E ,分别在AB AC ,上,且12DCB EBC A ∠=∠=∠.探究:满足上述条件的图形中是否存在等对边四边形,并证明你的结论.解:()回答正确的给分(如平行四边形、等腰梯形等). ()答:与A ∠相等的角是BOD ∠(或COE ∠). 四边形DBCE 是等对边四边形.()答:此时存在等对边四边形,是四边形DBCE .证法一:如图,作CG BE ⊥于G 点,作BF CD ⊥交CD 延长线于F 点. 因为12DCB EBC A ∠=∠=∠,BC 为公共边, 所以BCF CBG △≌△.所以BF CG =.因为BDF ABE EBC DCB ∠=∠+∠+∠,BEC ABE A ∠=∠+∠,所以BDF BEC ∠=∠.可证BDF CEG △≌△.所以BD CE =.所以四边形DBCE 是等边四边形.证法二:如图,以C 为顶点作FCB DBC ∠=∠,CF 交BE 于F 点. 因为12DCB EBC A ∠=∠=∠,BC 为公共边, 所以BDC CFB △≌△.所以BD CF =,BDC CFB ∠=∠.所以ADC CFE ∠=∠.因为ADC DCB EBC ABE ∠=∠+∠+∠,FEC A ABE ∠=∠+∠, 所以ADC FEC ∠=∠. 所以FEC CFE ∠=∠. 所以CF CE =. 所以BD CE =.所以四边形DBCE 是等边四边形.说明:当AB AC =时,BD CE =仍成立.只有此证法,只给分.BOA DECBOA D ECF 图 B OA D ECF 图 G(上海市).已知:60MAN =∠,点B 在射线AM 上,4AB =(如图).P 为直线AN 上一动点,以BP 为边作等边三角形BPQ (点B P Q ,,按顺时针排列),O 是BPQ △的外心.()当点P 在射线AN 上运动时,求证:点O 在MAN ∠的平分线上;()当点P 在射线AN 上运动(点P 与点A 不重合)时,AO 与BP 交于点C ,设AP x =,AC AO y =,求y 关于x 的函数解析式,并写出函数的定义域;()若点D 在射线AN 上,2AD =,圆I 为ABD △的内切圆.当BPQ △的边BP 或BQ 与圆I 相切时,请直接写出点A 与点O 的距离.()证明:如图,连结OB OP ,,O 是等边三角形BPQ 的外心,OB OP ∴=,圆心角3601203BOP ∠==. 当OB 不垂直于AM 时,作OH AM ⊥,OT AN ⊥,垂足分别为H T ,. 由360HOT A AHO ATO ∠+∠+∠+∠=,且60A ∠=,90AHO ATO ∠=∠=,120HOT ∴∠=.BOH POT ∴∠=∠.Rt Rt BOH POT ∴△≌△.OH OT ∴=.∴点O 在MAN ∠的平分线上.当OB AM ⊥时,36090APO A BOP OBA ∠=-∠-∠-∠=. 即OP AN ⊥,∴点O 在MAN ∠的平分线上.综上所述,当点P 在射线AN 上运动时,点O 在MAN ∠的平分线上.图备用图()解:如图,AO 平分MAN ∠,且60MAN ∠=,30BAO PAO ∴∠=∠=.由()知,OB OP =,120BOP ∠=,30CBO ∴∠=,CBO PAC ∴∠=∠.BCO PCA ∠=∠,AOB APC ∴∠=∠. ABO ACP ∴△∽△. AB AOAC AP∴=.AC AO AB AP ∴=.4y x ∴=. 定义域为:0x >.()解:①如图,当BP 与圆I相切时,AO = ②如图,当BP 与圆I相切时,AO =; ③如图,当BQ 与圆I 相切时,0AO =.M图()P AM图M图M图M图(天津市). 已知关于的一元二次方程x c bx x =++2有两个实数根21,x x ,且满足01>x ,112>-x x 。
2007年全国100多个地区中考数学试题分类汇编 点、线、相交、平行
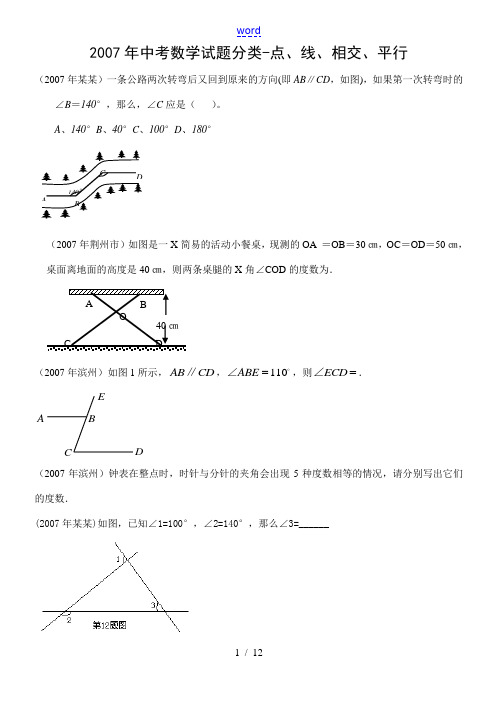
2007年中考数学试题分类-点、线、相交、平行(2007年某某)一条公路两次转弯后又回到原来的方向(即AB ∥CD ,如图),如果第一次转弯时的∠B =140°,那么,∠C 应是( )。
A 、140°B 、40°C 、100°D 、180°(2007年荆州市)如图是一X 简易的活动小餐桌,现测的OA =OB =30㎝,OC =OD =50㎝,桌面离地面的高度是40㎝,则两条桌腿的X 角∠COD 的度数为.(2007年滨州)如图1所示,AB CD ∥,110ABE =∠,则ECD =∠.(2007年滨州)钟表在整点时,时针与分针的夹角会出现5种度数相等的情况,请分别写出它们的度数.(2007年某某)如图,已知∠1=100°,∠2=140°,那么∠3=______ABCD EODCBA40㎝ ABCD140°(2007年某某市)如图所示,直线a b ∥,112330'=∠,则2=∠.(2007年某某市)如图2,直线a b ∥,则A ∠的度数是( ) A.28B.31C.39D.42(2007年某某市)如图,AB CD ∥,40A ∠=,45D ∠=,则1∠=.(2007年某某市)如图12,平面内有公共端点的六条射线OA ,OB ,OC ,OD ,OE ,OF ,从射线OA 开始按逆时针方向依次在射线上写出数字1,2,3,4,5,6,7,…. (1)“17”在射线上.(3分)(2)请任意写出三条射线上数字的排列规律.(3分) (3)“2007”在哪条射线上?(3分)ABCDab70°31°abc12.(2007年某某省)图10-1是三个直立于水平面上的形状完全相同的几何体(下底面为圆面,单位:cm ).将它们拼成如图10-2的新几何体,则该新几何体的体积为cm 3.(计算结果保留 )(2007年某某省)用M ,N ,P ,Q 各代表四种简单几何图形(线段、正三角形、正方形、圆)中的一种.图6-1—图6-4是由M ,N ,P ,Q 中的两种图形组合而成的(组合用“&”表示).那么,下列组合图形中,表示P&Q 的是( )(2007年某某省)如图1,直线a ,b 相交于点O ,若∠1等于40°,则∠2等于( )图10-2图10-1M&PN&PN&QM&Q图6-1图6-2图6-3图6-4A .B .C .D .A .50°B .60°C .140°D .160°(2007年某某市)如图,已知a b ∥,170∠=,则2∠=.(2007年某某市)如图1,直线c 截二平行直线a 、b ,则下列式子中一定成立的是 ( ) A .∠1=∠5 B . ∠1=∠4 C . ∠1=∠3 D . ∠1=∠2(2007年某某市)如图,能判定EB ∥AC 的条件是( )。
2007年全国各地中考试题压轴题精选解析

2007年全国各地中考试题压轴题精选1.(杭州市)24. 在直角梯形ABCD 中,90C ∠=︒,高6C D c m =(如图1)。
动点,P Q 同时从点B 出发,点P 沿,,BA AD DC 运动到点C 停止,点Q 沿BC 运动到点C 停止,两点运动时的速度都是1/cm s 。
而当点P 到达点A 时,点Q 正好到达点C 。
设,P Q 同时从点B 出发,经过的时间为()t s 时,BPQ ∆的面积为()2y cm (如图2)。
分别以,t y 为横、纵坐标建立直角坐标系,已知点P 在AD 边上从A 到D 运动时,y 与t 的函数图象是图3中的线段MN 。
(1)分别求出梯形中,BA AD 的长度; (2)写出图3中,M N 两点的坐标;(3)分别写出点P 在BA 边上和DC 边上运动时,y 与t 的函数关系式(注明自变量的取值范围),并在图3中补全整个运动中y 关于t 的函数关系的大致图象。
2..(湖南省郴州) 27.如图1,矩形ABCD 中,AB =3,BC =4,将矩形ABCD 沿对角线AC 平移,平移后的矩形为EFGH (A 、E 、C 、G 始终在同一条直线上),当点E 与C 重合时停止移动.平移中EF 与BC 交于点N ,GH 与BC 的延长线交于点M ,EH 与DC 交于点P ,FG 与DC 的延长线交于点Q .设S 表示矩形PCMH 的面积,S '表示矩形NFQC 的面积. (1) S 与S '相等吗?请说明理由.(2)设AE =x ,写出S 和x 之间的函数关系式,并求出x 取何值时S 有最大值,最大值是多少? (3)如图2,连结BE ,当AE 为何值时,ABE ∆是等腰三角形.(图1)(图2)(图3)3.(上海市)已知:60MAN =∠,点B 在射线AM 上,4AB =(如图10).P 为直线AN 上一动点,以BP 为边作等边三角形BPQ (点B P Q ,,按顺时针排列),O 是BPQ △的外心. (1)当点P 在射线AN 上运动时,求证:点O 在MAN ∠的平分线上;(2)当点P 在射线AN 上运动(点P 与点A 不重合)时,AO 与BP 交于点C ,设AP x =,AC AO y =,求y 关于x 的函数解析式,并写出函数的定义域;(3)若点D 在射线AN 上,2AD =,圆I 为ABD △的内切圆.当BPQ △的边BP 或BQ 与圆I 相切时,请直接写出点A 与点O 的距离.(1.2)xN MQ PHGFEDCBA图2QPN M HGFED CB A图1图10 M备用图4. (海南省) 24.如图,直线434+-=x y 与x 轴交于点A ,与y 轴交于点C ,已知二次函数的图象经过点A 、C 和点()0,1-B .(1)求该二次函数的关系式;(2)设该二次函数的图象的顶点为M ,求四边形AOCM 的面积; (3)有两动点D 、E 同时从点O 出发,其中点D 以每秒23个单位长度的速度沿折线OAC 按O →A →C 的路线运动,点E 以每秒4个单位长度的速度沿折线OCA 按O →C →A 的路线运动,当D 、E 两点相遇时,它们都停止运动.设D 、E 同时从点O 出发t 秒时,ODE ∆的面积为S . ①请问D 、E 两点在运动过程中,是否存在DE ∥OC ,若存在,请求出此时t 的值;若不存在,请说明理由;②请求出S 关于t 的函数关系式,并写出自变量t 的取值范围; ③设0S 是②中函数习题一1.(长沙市)26. 如图,ABCD 中,4AB =,3BC =,120BAD =∠,E 为BC 上一动点(不与B 重合),作EF AB ⊥于F ,FE ,DC 的延长线交于点G ,设B E x =,DEF △的面积为S .(1)求证:BEF CEG △∽△; (2)求用x 表示S 的函数表达式,并写出x 的取值范围; (3)当E 运动到何处时,S 有最大值,最大值为多少?.2.(扬州市)26.如图,矩形ABCD 中,3AD =厘米,AB a =厘米(3a >).动点M N ,同时从BA CB DE F G点出发,分别沿B A →,B C →运动,速度是1厘米/秒.过M 作直线垂直于AB ,分别交AN ,CD 于P Q ,.当点N 到达终点C 时,点M 也随之停止运动.设运动时间为t 秒.(1)若4a =厘米,1t =秒,则PM =______厘米;(2)若5a =厘米,求时间t ,使PNB PAD △∽△,并求出它们的相似比;(3)若在运动过程中,存在某时刻使梯形PMBN 与梯形PQDA 的面积相等,求a 的取值 范围;(4)是否存在这样的矩形:在运动过程 中,存在某时刻使梯形PMBN ,梯形PQDA ,梯形PQCN 的面积都相等?若存在,求a 的值;若不存在,请说明理由. 3.(温州市)第24题.在ABC ∆中,,4,5,D BC CD 3cm,C Rt AC cm BC cm ∠=∠==点在上,且以=现有两个动点P 、Q 分别从点A 和点B 同时出发,其中点P 以1cm/s 的速度,沿AC 向终点C 移动;点Q 以1.25cm/s 的速度沿BC 向终点C 移动。
2007年全国各地中考数学试题压轴题精选全解之四

2007年全国各地中考试题压轴题精选全解之四63.(某某市)26. 如图,ABCD 中,4AB =,3BC =,120BAD =∠,E 为BC 上一动点(不与B 重合),作EF AB ⊥于F ,FE ,DC 的延长线交于点G ,设BE x =,DEF △的面积为S .(1)求证:BEF CEG △∽△;(2)求用x 表示S 的函数表达式,并写出x 的取值X 围; (3)当E 运动到何处时,S 有最大值,最大值为多少? 解: (1)证明略;(2)由(1)DG 为DEF △中EF 边上的高,在Rt BFE △中,60B =∠,sin EF BE B x ==, 在Rt CEG △中,3CE x =-,3(3)cos602xCG x -=-=, 112xDG DC CG -∴=+=,213288S EF DG x x ∴==-+, 其中03x <≤. (3)308a =-<,对称轴112x =,∴当03x <≤时,S 随x 的增大而增大,∴当3x =,即E 与C 重合时,S 有最大值.S =最大64.(某某省某某) 27.如图,矩形ABCD 中,AB =3,BC =4,将矩形ABCD 沿对角线AC 平移,平移后的矩形为EFGH (A 、E 、C 、G 始终在同一条直线上),当点E 与C 重合时停止移动.平移中EF 与BC 交于点N ,GH 与BC 的延长线交于点M ,EH 与DC 交于点P ,FG 与DC 的延长线交于点Q .设S 表示矩形PCMH 的面积,S '表示矩形NFQC 的面积. (1) S 与S '相等吗?请说明理由.(2)设AE =x ,写出S 和x 之间的函数关系式,并求出x 取何值时S 有最大值,最大值AC B DEF G是多少?(3)如图11,连结BE ,当AE 为何值时,ABE ∆是等腰三角形.解: (1)相等理由是:因为四边形ABCD 、EFGH 是矩形, 所以,,EGH EGF ECN ECP CGQ CGM S S S S S S ∆∆∆∆∆∆===所以,EGH ECP CGM EGF ECN CGQ S S S S S S ∆∆∆∆∆∆--=-- 即:S S '=(2)AB =3,BC =4,AC =5,设AE =x ,则EC =5-x ,34(5),,55PC x MC x =-=所以12(5)25S PC MC x x ==-,即21212(05)255S x x x =-+≤≤ 配方得:2125()3252S x =--+,所以当52x =时, S 有最大值3(3)当AE =AB =3或AE =BE =52或AE =3.6时,ABE ∆是等腰三角形65.(某某省某某市)28. 两个直角边为6的全等的等腰直角三角形Rt AOB △和Rt CED △按图1所示的位置放置A 与C 重合,O 与E 重合. (1)求图1中,A B D ,,三点的坐标.(2)Rt AOB △固定不动,Rt CED △沿x 轴以每秒2个单位长的速度向右运动,当D 点运动到与B 点重合时停止,设运动x 秒后Rt CED △和Rt AOB △重叠部分面积为y ,求y 与x 之间的函数关系式.(3)当Rt CED △以(2)中的速度和方向运动,运动时间4x =秒时Rt CED △运动到如图2所示的位置,求经过A G C ,,三点的抛物线的解析式. (4)现有一半径为2,圆心P 在(3)中的抛物线上运动的动圆,试问P 在运动过程中是xN MQ PHGFEDCBA图11QPNM HGF ED CB A 图10否存在P 与x 轴或y 轴相切的情况,若存在请求出P 的坐标,若不存在请说明理由.解:(1)(06)A ,,(60)B ,,(60)D -, (2)当03x <≤时,位置如图A所示,作GH DB ⊥,垂足为H ,可知:2OE x =,EH x =,62DO x =-,6DH x =-,22()GHD IOD IOHG y S S S ∴==-△△梯形22112(6)(62)22x x ⎡⎤=---⎢⎥⎣⎦223263122x x x x ⎛⎫=-+=-+ ⎪⎝⎭当36x ≤≤时,位置如图B所示. 可知:122DB x =-212DGBy S DB ⎫∴==⎪⎪⎝⎭△2212)12362x x x ⎤=-=-+⎥⎣⎦(求梯形IOHG 的面积及DGB △的面积时只要所用方法适当,所得结论正确均可给分)y ∴与x 的函数关系式为:22312(03)1236(36)x x x y x x x ⎧-+<⎪=⎨-+⎪⎩≤≤≤ (3)图2中,作GH OE ⊥,垂足为H ,当4x =时,28OE x ==,1224DB x =-=122GH DH DB ∴===,1666242OH HB DB =-=-=-=图B∴可知:(06)A ,,(42)G ,,(86)C ,∴经过A G C ,,三点的抛物线的解析式为:221(4)22644x y x x =-+=-+ (4)当P 在运动过程中,存在P 与坐标轴相切的情况,设P 点坐标为00()x y ,当P 与y 轴相切时,有02x =,02x =±,由02x =-得:011y =,1(211)P ∴-,由02x =,得03y =,2(23)P ∴,当P 与x 轴相切时,有02y = 21(4)204y x =-+>02y ∴=,得:04x =,3(42)P ∴,综上所述,符合条件的圆心P 有三个,其坐标分别是:1(211)P -,,2(23)P ,,3(42)P ,66.(某某省永州市) 25、在梯形ABCD 中,AB CD ∥,90ABC ∠=°,5AB =,10BC =,tan 2ADC ∠=.(1)求DC 的长;(2)E 为梯形内一点,F 为梯形外一点,若BF DE =,FBC CDE ∠=∠,试判断ECF △的形状,并说明理由.(3)在(2)的条件下,若BE EC ⊥,:4:3BE EC =,求DE 的长.解(1)过A 点作AG DC ⊥,垂足为G90AB CD BCD ABC ∴∠=∠=∥, ∴四边形ABCG 为矩形510CG AB AG BC ∴====,tan 2AGADG DG∠==510DG DC DG CG ∴=∴=+=,(2)DE BF FBC CDE BC DC =∠=∠=,,DEC BFC ∴△≌△EC CF ECD FCB ∴=∠=∠,9090BCE ECD ECF ∠+∠=∠=,ECF ∴△是等腰直角三角形(3)过F 点作FH BE ⊥BE EC CF CE CE CF =⊥,⊥,∴四边形ECFH 是正方形,6FH EC ∴==:4:390BE EC BEC =∠=, 222BC BE EC ∴=+68ECBE ∴==,2BH BE EH ∴=-=DE BF ∴===67.(某某省某某市) 25.如图6,在平面直角坐标系中,四边形OABC 是矩形,OA=4,AB=2,直线32y x =-+与坐标轴交于D 、E 。
2007年全国各地中考数学试题压轴题精选全解之二

2007年全国各地中考试题压轴题精选全解之二25.(某某市)24. 在直角梯形ABCD 中,90C ∠=︒,高6CD cm =(如图1)。
动点,P Q 同时从点B 出发,点P 沿,,BA AD DC 运动到点C 停止,点Q 沿BC 运动到点C 停止,两点运动时的速度都是1/cm s 。
而当点P 到达点A 时,点Q 正好到达点C 。
设,P Q 同时从点B 出发,经过的时间为()t s 时,BPQ ∆的面积为()2y cm (如图2)。
分别以,t y 为横、纵坐标建立直角坐标系,已知点P 在AD 边上从A 到D 运动时,y 与t 的函数图象是图3中的线段MN 。
(1)分别求出梯形中,BA AD 的长度; (2)写出图3中,M N 两点的坐标;(3)分别写出点P 在BA 边上和DC 边上运动时,y 与t 的函数关系式(注明自变量的取值X 围),并在图3中补全整个运动中y 关于t 的函数关系的大致图象。
解: (1)设动点出发t 秒后,点P 到达点A 且点Q 正好到达点C 时,BC BA t ==,则1630,102BPQ S t t ∆=⨯⨯=∴=(秒)则()()10,2BA cm AD cm ==; (2)可得坐标为()()10,30,12,30M N (3)当点P 在BA 上时,()213sin 010210y t t B t t =⨯⨯⨯=≤<; 当点P 在DC 上时,()()1101859012182y t t t =⨯⨯-=-+<≤ 图象略(图1)(图2)26.(某某市)27.四边形一条对角线所在直线上的点,如果到这条对角线的两端点的距离不相等,但到另一对角线的两个端点的距离相等,则称这点为这个四边形的准等距点.如图l,点P为四边形ABCD对角线AC所在直线上的一点,PD=PB,PA≠PC,则点P为四边形ABCD的准等距点.(1)如图2,画出菱形ABCD的一个准等距点.(2)如图3,作出四边形ABCD的一个准等距点(尺规作图,保留作图痕迹,不要求写作法).(3)如图4,在四边形ABCD中,P是AC上的点,PA≠PC,延长BP交CD于点E,延长DP 交BC于点F,且∠CDF=∠CBE,CE=CF.求证:点P是四边形AB CD的准等距点.(4)试研究四边形的准等距点个数的情况(说出相应四边形的特征及准等距点的个数,不必证明).解:(1)如图2,点P即为所画点.(答案不唯一,但点P不能画在AC中点)。
2007年广东省中考数学压轴题全解全析

2007年广东省中考数学压轴题全解全析2008年中考在即,备受广大师生关注的中考数学中的压轴题,因为这些试题有较强的选拔性,往往在很大的程度上决定了考试的成败,为帮助大家迎接今年的中考,特对2007年广东省各市中考数学压轴题加以整理,希望对大家有所帮助。
1.(深圳) 如图7,在平面直角坐标系中,抛物线2164y x =-与直线12y x =相交于A B ,两点.(1)求线段A B 的长.(2)若一个扇形的周长等于(1)中线段A B 的长,当扇形的半径取何值时,扇形的面积最大,最大面积是多少? (3)如图8,线段A B 的垂直平分线分别交x 轴、y 轴于C D ,两点,垂足为点M ,分别求出O M O C O D ,,的长,并验证等式222111+=是否成立.(4)如图9,在R t AB C △中,90A C B=∠,C D A B ⊥,垂足为D ,设B C a =,A C b =,A B c =.C D b =,试说明:222111abh+=.解(1) ∴A (-4,-2),B (6,3)分别过A 、B 两点作x AE ⊥轴,y BF ⊥轴,垂足分别为E 、F∴AB =OA+OB 22223624+++=55=(2)设扇形的半径为x ,则弧长为)255(x -,扇形的面积为y则)255(21x x y -=x x5252+-=16125)455(2+--=x∵01<-=a ∴当455=x 时,函数有最大值16125=最大y(3)过点A 作AE ⊥x 轴,垂足为点E ∵CD 垂直平分AB ,点M 为垂足∴255225521=-=-=OA AB OM ∵COM EOA OMC AEO ∠=∠∠=∠,图7 图8图9D∴△AEO ∽△CMO ∴COAO OMOE =∴CO52254=∴45415225=⋅⋅=CO同理可得 25=OD∴542520)52()54(112222==+=+OD OC∴5412=OM∴222111OMODOC=+(4)等式222111hba=+成立.理由如下:∵AB CD ACB⊥=∠,90∴2222121b aABh AB ab +=⋅=∴h c ab ⋅=∴ 2222h cba ⋅= ∴22222)(h b aba += ∴22222222222)(hb a hb a hb a ba +=∴222221ba bah+=∴222111bah+=∴222111hba=+2. (梅州 11分)如图12,直角梯形A B C D 中,90643A B C D A A B A D D C ∠====∥,°,,,,动点P 从点A 出发,沿A D C B →→→方向移动,动点Q 从点A 出发,在A B 边上移动.设点P 移动的路程为x ,点Q 移动的路程为y ,线段P Q 平分梯形A B C D 的周长. (1)求y 与x 的函数关系式,并求出x y ,的取值范围; (2)当P Q A C ∥时,求x y ,的值;(3)当P 不在B C 边上时,线段P Q 能否平分梯形A B C D 的 面积?若能,求出此时x 的值;若不能,说明理由.解:(1)过C 作C E A B ⊥于E ,则34C D A E C E ===,,可得5B C =,所以梯形A B C D 的周长为18. ····················································································· 1分 P Q 平分A B C D 的周长,所以9x y +=, ··································································· 2分 因为06y ≤≤,所以39x ≤≤, 所求关系式为:939y x x =-+,≤≤. ················ 3分(2)依题意,P 只能在B C 边上,79x ≤≤. 126P B x B Q y =-=-,,因为P Q A C ∥,所以B P Q B C A △∽△,所以B P B Q B CB A=,得 ······································ 4分12656x y --=,即6542x y -=, 解方程组96542x y x y +=⎧⎨-=⎩, 得87121111x y ==,. ······ 6分 ABCD P Q图12(3)梯形A B C D 的面积为18. ························································································ 7分 当P 不在B C 边上,则37x ≤≤(a )当34x <≤时,P 在A D 边上,12A P Q S x y =△.如果线段P Q 能平分梯形A B C D 的面积,则有192x y =······················································· 8分 可得:918.x y x y +=⎧⎨=⎩,解得36x y =⎧⎨=⎩,;(63x y ==,舍去). ····················································· 9分(b )当47x ≤≤时,点P 在D C 边上,此时14(4)2A D P Q S x y =⨯-+.如果线段P Q 能平分梯形A B C D 的面积,则有14(4)92x y ⨯-+=,可得92217.x y x y +=⎧⎨+=⎩,此方程组无解. 所以当3x =时,线段P Q 能平分梯形A B C D 的面积.11分3. (韶关 9分)如图6,在平面直角坐标系中,四边形OABC 是矩形,OA=4,AB=2,直线32y x =-+与坐标轴交于D 、E 。
2007年广东中考数学压轴题全解全析

2007年广东省中考数学压轴题全解全析2008年中考在即,备受广大师生关注的中考数学中的压轴题,因为这些试题有较强的选拔性,往往在很大的程度上决定了考试的成败,为帮助大家迎接今年的中考,特对2007年广东省各市中考数学压轴题加以整理,希望对大家有所帮助。
1.(深圳) 如图7,在平面直角坐标系中,抛物线2164y x =-与直线12y x =相交于A B ,两点. (1)求线段AB 的长.(2)若一个扇形的周长等于(1)中线段AB 的长,当扇形的半径取何值时,扇形的面积最大,最大面积是多少?(3)如图8,线段AB 的垂直平分线分别交x 轴、y 轴于C D ,两点,垂足为点M ,分别求出OM OC OD ,,的长,并验证等式222111+=是否成立.(4)如图9,在Rt ABC △中,90ACB =∠,CD AB⊥,垂足为D,设BC a =,AC b=,AB c =.CD b =,试说明:222111a b h +=.解(1) ∴A (-4,-2),B (6,3) 分别过A 、B 两点作x AE ⊥轴,y BF ⊥轴,垂足分别为E 、F∴AB =OA+OB 22223624+++=55=(2)设扇形的半径为x ,则弧长为)255(x -,扇形的面积为y则)255(21x x y -=x x 5252+-=16125)455(2+--=x∵01<-=a ∴当455=x 时,函数有最大值16125=最大y (3)过点A 作AE ⊥x 轴,垂足为点E ∵CD 垂直平分AB ,点M 为垂足 ∴255225521=-=-=OA AB OM∵COM EOA OMC AEO ∠=∠∠=∠, 图7图8图9∴△AEO ∽△CMO ∴CO AO OM OE = ∴CO52254=∴45415225=⋅⋅=CO 同理可得 25=OD∴542520)52()54(112222==+=+OD OC ∴5412=OM ∴222111OM OD OC =+(4)等式222111hb a =+成立.理由如下:∵AB CD ACB ⊥=∠,90∴2222121b a AB h AB ab +=⋅= ∴h c ab ⋅=∴ 2222h c b a ⋅= ∴22222)(h b a b a += ∴22222222222)(h b a h b a h b a b a +=∴222221b a b a h += ∴222111b a h += ∴222111h b a =+2. (梅州 11分)如图12,直角梯形ABCD 中,90643AB CD A AB AD DC ∠====∥,°,,,,动点P 从点A 出发,沿A D CB →→→方向移动,动点Q 从点A 出发,在AB 边上移动.设点P 移动的路程为x ,点Q 移动的路程为y ,线段PQ 平分梯形ABCD 的周长.(1)求y 与x 的函数关系式,并求出x y ,的取值范围;(2)当PQ AC ∥时,求x y ,的值;(3)当P 不在BC 边上时,线段PQ 能否平分梯形ABCD 的面积?若能,求出此时x 的值;若不能,说明理由. 解:(1)过C 作CE AB ⊥于E ,则34CD AE CE ===,,可得5BC =,所以梯形ABCD 的周长为18. ····················································································· 1分PQ 平分ABCD 的周长,所以9x y +=, ··································································· 2分 因为06y ≤≤,所以39x ≤≤, 所求关系式为:939y x x =-+,≤≤. ················ 3分(2)依题意,P 只能在BC 边上,79x ≤≤.126PB x BQ y =-=-,,因为PQ AC ∥,所以BPQ BCA △∽△,所以BP BQBC BA=,得 ······································ 4分12656x y --=,即6542x y -=, 解方程组96542x y x y +=⎧⎨-=⎩, 得87121111x y ==,. ······ 6分 ABCDPQ图12(3)梯形ABCD 的面积为18. ························································································ 7分 当P 不在BC 边上,则37x ≤≤(a )当34x <≤时,P 在AD 边上,12APQ S xy =△.如果线段PQ 能平分梯形ABCD 的面积,则有192xy = ······················································· 8分可得:918.x y xy +=⎧⎨=⎩,解得36x y =⎧⎨=⎩,;(63x y ==,舍去). ····················································· 9分(b )当47x ≤≤时,点P 在DC 边上,此时14(4)2ADPQ S x y =⨯-+. 如果线段PQ 能平分梯形ABCD 的面积,则有14(4)92x y ⨯-+=,可得92217.x y x y +=⎧⎨+=⎩,此方程组无解. 所以当3x =时,线段PQ 能平分梯形ABCD 的面积.11分3. (韶关 9分)如图6,在平面直角坐标系中,四边形OABC 是矩形,OA=4,AB=2,直线32y x =-+与坐标轴交于D 、E 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2007年全国中考数学压轴题分类解析从今年的中考数学压轴题中,我们可以看到在考察学生基本运算能力、思维能力的同时,对优生还要着重考查学生灵活运用数学知识分析和解决问题的能力.也着重考查了学生对数学思想方法的理解和掌握.中考压轴题设计特点是知识点多,覆盖面广,条件隐蔽,关系复杂,思路难觅,解法灵活.解数学压轴题,一要树立必胜的信心,二要具备扎实的基础知识和熟练的基本技能,三要掌握常用的解题策略.现归纳几种常见题型给予解答,供初三同学参考. 一.以圆为背景的压轴题例1(2007•上海市第25题)已知:60MAN =∠,点B 在射线AM 上,4AB =(如图1).P 为直线AN 上一动点,以BP 为边作等边三角形BPQ (点B P Q ,,按顺时针排列),O 是BPQ △的外心. (1)当点P 在射线AN 上运动时,求证:点O 在MAN ∠的平分线上;(2)当点P 在射线AN 上运动(点P 与点A 不重合)时,AO 与BP 交于点C ,设AP x =,AC AO y = ,求y 关于x 的函数解析式,并写出函数的定义域;(3)若点D 在射线AN 上,2AD =,圆I 为ABD △的内切圆.当BPQ △的边BP 或BQ 与圆I 相切时,请直接写出点A 与点O解析:(1)证明:如图3,连结OB OP ,,O 是等边三角形BPQ 的外心,OB OP ∴=,圆心角3601203BOP ∠==. 当OB 不垂直于AM 时,作OH AM ⊥,OT AN ⊥,垂足分别为H T ,. 由360HOT A AHO ATO ∠+∠+∠+∠=,且60A ∠=, 90AHO ATO ∠=∠=,120HOT ∴∠= .B O H P O ∴∠=∠. R t R t B O H P O T ∴△≌△. O H O T ∴=.∴点O 在MAN ∠的平分线上. 当OB AM ⊥时,36090APO A BOP OBA ∠=-∠-∠-∠=.即OP AN ⊥,∴点O 在MAN ∠的平分线上.综上所述,当点P 在射线AN 上运动时,点O 在MAN ∠的平分线上.图10 M备用图2(2)解:如图4,AO 平分MAN ∠,且60MAN ∠= ,30BAO PAO ∴∠=∠=.由(1)知,OB OP =,120BOP ∠=, 30CBO ∴∠=,CBO PAC ∴∠=∠.B C OP C ∠=∠ ,AOB APC ∴∠=∠.ABO ACP ∴△∽△. A BA OA CA P∴=.AC AO AB AP ∴= .4y x ∴=. 定义域为:0x >.(3)解:①如图5,当BP 与圆I相切时,AO = ②如图6,当BP 与圆I相切时,AO =; ③如图7,当BQ 与圆I 相切时,0AO =.点评 今年的上海市数学压轴题难度与去年相差不大,是比较传统的压轴题,应该说比较容易上手,考查的知识点较多,综合性较强,第2小题考到了函数思想,第3小题又运用到了分类讨论思想,在解决这种题时应在比较牢固掌握基础知识的同时培养自己运用各种数学思想方法的能力,本题是一道好题,符合上海市二期课改的理念.二、二次函数与圆为背景的压轴题例2(2007•南充市第25题)如图,点M (4,0),以点M 为圆心、2为半径的圆与x 轴交于点A 、B .已知抛物线216y x bx c =++过点A 和B ,与y 轴交于点C . (1)求点C 的坐标,并画出抛物线的大致图象. (2)点Q (8,m )在抛物线216y x bx c =++上,点P 为此抛物线对称轴上一个动点,求PQ +PB 的最小值.图5()P A图6M图7图3图4(3)CE 是过点C 的⊙M 的切线,点E 是切点,求OE 所在直线的解析式. 解析:(1)由已知,得 A (2,0),B (6,0), ∵ 抛物线216y x bx c =++过点A 和B ,则 221220,61660,6b c b c ⎧⨯++=⎪⎪⎨⎪⨯++=⎪⎩ 解得4,32.b c ⎧=-⎪⎨⎪=⎩ 则抛物线的解析式为 214263y x x =-+. 故 C (0,2).(说明:抛物线的大致图象要过点A 、B 、C ,其开口方向、顶点和对称轴相对准确)(2)如图①,抛物线对称轴l 是 x =4. ∵ Q (8,m )抛物线上,∴ m =2.过点Q 作QK ⊥x 轴于点K ,则K (8,0),QK =2,AK =6,∴ AQ=.又∵ B (6,0)与A (2,0)关于对称轴l 对称, ∴ PQ +PB 的最小值=AQ=.(3)如图②,连结EM 和CM . 由已知,得 EM =OC =2.CE 是⊙M 的切线,∴ ∠DEM =90º,则 ∠DEM =∠DOC . 又∵ ∠ODC =∠EDM . 故 △DEM ≌△DOC . ∴ OD =DE ,CD =MD .又在△ODE 和△MDC 中,∠ODE =∠MDC ,∠DOE =∠DEO =∠DCM =∠DMC . 则 OE ∥CM . 设CM 所在直线的解析式为y =kx +b ,CM 过点C (0,2),M (4,0),∴ 40,2,k b b +=⎧⎨=⎩ 解得 1,22,k b ⎧=-⎪⎨⎪=⎩直线CM 的解析式为122y x =-+. 又∵ 直线OE 过原点O ,且OE ∥CM , 则 OE 的解析式为 y =12-x .点评 本题是一道综合性很强也是传统型的压轴题,涉及了函数、方程、平行线、勾股定理、圆等大量初中数学的重点知识,解这类问题要求学生必须稳固的掌握各个领域的数学知识,须注意的是在第3小问中涉及了全等三角形的问题,很有可能会有多解的情况出现,此时就要求学生拥有较强的数形结合思想去探索结论的存在性. 三、折叠型问题压轴题例3(2007•荆门市第28题)如图1,在平面直角坐标系中,有一张矩形纸片OABC ,已知O (0,0),A (4,0),C (0,3),点P 是OA 边上的动点(与点O 、A 不重合).现将△PAB 沿PB 翻折,得到△PDB ;再在OC 边上选取适当的点E ,将△POE 沿PE 翻折,得到△PFE ,并使直线PD 、PF 重合. (1)设P (x ,0),E (0,y ),求y 关于x 的函数关系式,并求y 的最大值;(2)如图2,若翻折后点D 落在BC 边上,求过点P 、B 、E 的抛物线的函数关系式; (3)在(2)的情况下,在该抛物线上是否存在点Q ,使△PEQ 是以PE 为直角边的直角三角形?若不存在,说明理由;若存在,求出点Q 的坐标.解析:(1)由已知PB 平分∠APD ,PE 平分∠OPF ,且PD 、PF 重合,则∠BPE =90°.∴∠OPE +∠APB =90°.又∠APB +∠ABP =90°,∴∠OPE =∠PBA . ∴Rt △POE ∽Rt △BPA . ∴PO BA OE AP =.即34x y x =-.∴y =2114(4)333x x x x -=-+(0<x <4). 且当x =2时,y 有最大值13. (2)由已知,△PAB 、△POE 均为等腰三角形,可得P (1,0),E (0,1),B (4,3).设过此三点的抛物线为y =ax 2+bx +c ,则1,0,164 3.c a b c a b c =⎧⎪++=⎨⎪++=⎩∴1,23,21.a b c ⎧=⎪⎪⎪=-⎨⎪=⎪⎪⎩y =213122x x -+. (3)由(2)知∠EPB =90°,即点Q 与点B 重合时满足条件. 直线PB 为y =x -1,与y 轴交于点(0,-1). 将PB 向上平移2个单位则过点E (0,1),∴该直线为y =x +1.由21,131,22y x y x x =+⎧⎪⎨=-+⎪⎩得5,6.x y =⎧⎨=⎩∴Q(5,6). 故该抛物线上存在两点Q (4,3)、(5,6)满足条件.点评 这是一道以折叠为背景的综合型压轴题,综合性较强,这类试题在各地中考题中出现的频率不小,本题中第1、2小题只需根据折叠的基本性质结合函数知识即可得解,第3小题是探究型问题,是一道检测学生能力的好题.四、以二次函数和四边形的综合为背景的压轴题 例4(2007•江西第25题)实验与探究(1)在图1,2,3中,给出平行四边形ABCD 的顶点A B D ,,的坐标(如图所示),写出图1,2,3中的顶点C 的坐标,它们分别是(52),, , ;(2)在图4中,给出平行四边形ABCD 的顶点A B D ,,的坐标(如图所示),求出顶点C 的坐标(C 点坐标用含a b c d e f ,,,,,的代数式表示);归纳与发现(3)通过对图1,2,3,4的观察和顶点C 的坐标的探究,你会发现:无论平行四边形ABCD 处于直角坐标系中哪个位置,当其顶点坐标为()()()()A a b B c d C m n D e f ,,,,,,,(如图4)时,则四个顶点的横坐标a c m e ,,,之间的等量关系为 ;纵坐标b d n f ,,,之间的等量关系 为 (不必证明); 运用与推广(4)在同一直角坐标系中有抛物线2(53)y x c x c =---和三个点15192222G c c S c c ⎛⎫⎛⎫-⎪ ⎪⎝⎭⎝⎭,,,,(20)H c ,(其中0c >).问当c 为何值时,该抛物线上存在点P ,使得以G S H P ,,,为顶点的四边形是平行四边形?并求出所有符合条件的P 点坐标. 解析:(1)()e c d +,,()c e a d +-,.x图1x图2x图3)x图4(2)分别过点A B C D ,,,作x 轴的垂线,垂足分别为1111A B C D ,,,, 分别过A D ,作1AE BB ⊥于E ,1DF CC ⊥于点F . 在平行四边形ABCD 中,CD BA =,又11BB CC ∥,180EBA ABC BCF ABC BCF FCD ∴∠+∠+∠=∠+∠+∠=EBA FCD ∴∠=∠.又90BEA CFD ∠=∠=,BEA CFD ∴△≌△. A F D F a ∴==-,BE CF d b ==-.设()C x y ,.由e x a c -=-,得x e c a =+-.由y f d b -=-,得y f d b =+-.()C e c a f d b ∴+-+-,. (此问解法多种,此处从略)(3)m c e a =+-,n d f b =+-.或m a c e +=+,n b d f +=+.(4)若GS 为平行四边形的对角线,由(3)可得1(27)P c c -,.要使1P 在抛物线上, 则有274(53)(2)c c c c c =--⨯--,即20c c -=. 10c ∴=(舍去),21c =.此时1(27)P -,. 若SH 为平行四边形的对角线,由(3)可得2(32)P cc ,,同理可得1c =,此时2(32)P ,. 若GH 为平行四边形的对角线,由(3)可得(2)c c -,,同理可得1c =,此时3(12)P -,. 综上所述,当1c =时,抛物线上存在点P ,使得以G S H P ,,,为顶点的四边形是平行四边形. 符合条件的点有1(27)P -,,2(32)P ,,3(12)P -,. 点评 本题以坐标系为桥梁,运用数形结合思想,是比较传统的二次函数型综合题,第3小题是一个很典型的定值问题,考察学生的探究能力.纵观最近几年各地的中考压轴题,绝大部分都是与坐标系有关的,其特点是通过建立点与数即坐标之间的对应关系,一方面可用代数方法研究几何图形的性质,另一方面又可借助几何直观,得到某些代数问题的解答.)x。
