卡方分布概念及表和查表方法
卡方分布表

卡方分布表卡方分布表卡方分布表是一个重要的数学工具,在统计学和实验设计中经常被使用。
卡方分布表揭示了卡方分布在不同程度上的概率密度值,它可根据样本数、自由度和期望值,计算出卡方分布的概率密度函数。
卡方分布表能够帮助统计学家检验假设和求解不同的统计问题,尤其在研究方差分析和卡方检验等方面有着广泛的应用。
卡方分布卡方分布是一种特殊的概率分布,在统计学中有着十分广泛的应用。
卡方分布通常是由一系列相互独立且在总体上是正态分布的变量构成的。
在卡方分布中,每个变量都乘以一个系数,将它们加起来就得到了卡方值。
卡方分布在一个样本的数据分布、两个样本的独立性检验和拟合度检验等方面均有广泛应用。
卡方分布的应用卡方分布在实际应用中有着广泛的应用。
它通常用于试验设计、广告效果分析、市场研究、金融风险管理、医学统计分析等领域。
卡方分布常常被用来检验假设,例如检验两个样本之间的独立性、检验一个样本的频率分布是否符合期望分布等。
卡方分布表则可以帮助统计学家更加轻松地完成一系列检验,提高工作效率。
卡方分布表的使用步骤卡方分布表的使用方法相对简单,主要包括以下几个步骤:1. 计算卡方值:在卡方检验中需要先计算卡方值,其计算公式是:X2=Σ(Oi-Ei)2/Ei。
其中,Oi为观察值,需要通过实验或者数据统计获取;Ei为期望值,通常是由独立性假设或者完全随机假设得出的。
计算出卡方值之后,即可查找相应的卡方分布表。
2. 确定自由度:自由度的数量是根据数据的情况而定。
在卡方分布中,自由度数量即为样本数减1:df=n-1。
3. 查找卡方分布表:在卡方分布表中,根据自由度和显著性水平,可以查到卡方值的概率密度函数值。
4. 进行统计检验:通过比较计算出的卡方值和查找到的卡方分布表中的概率密度函数值,可以判断样本数据是否符合假设,从而进行相应的统计检验。
卡方分布表的注意事项在使用卡方分布表时,需要注意以下几个问题:1. 样本数必须大于等于自由度数,否则不能进行卡方检验。
卡方分布概念及表和查表方法
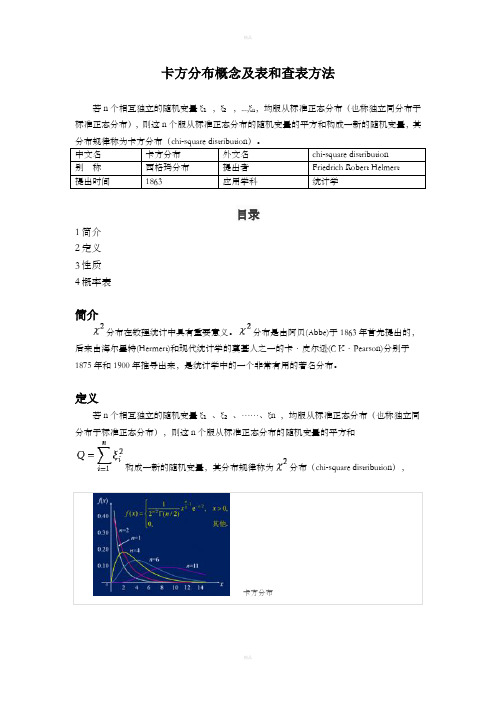
卡方分布概念及表和查表方法若n个相互独立的随机变量ξ₁,ξ₂,...,ξn,均服从标准正态分布(也称独立同分布于标准正态分布),则这n个服从标准正态分布的随机变量的平方和构成一新的随机变量,其分布规律称为卡方分布(chi-square distribution)。
中文名卡方分布外文名chi-square distribution别称西格玛分布提出者Friedrich Robert Helmert提出时间1863应用学科统计学目录1简介2定义3性质4概率表简介分布在数理统计中具有重要意义。
分布是由阿贝(Abbe)于1863年首先提出的,后来由海尔墨特(Hermert)和现代统计学的奠基人之一的卡·皮尔逊(C K·Pearson)分别于1875年和1900年推导出来,是统计学中的一个非常有用的著名分布。
定义若n个相互独立的随机变量ξ₁、ξ₂、……、ξn ,均服从标准正态分布(也称独立同分布于标准正态分布),则这n个服从标准正态分布的随机变量的平方和构成一新的随机变量,其分布规律称为分布(chi-square distribution),卡方分布其中参数称为自由度,正如正态分布中均数或方差不同就是另一个正态分布一样,自由度不同就是另一个分布。
记为或者(其中,为限制条件数)。
卡方分布是由正态分布构造而成的一个新的分布,当自由度很大时,分布近似为正态分布。
对于任意正整数x,自由度为的卡方分布是一个随机变量X的机率分布。
性质1) 分布在第一象限内,卡方值都是正值,呈正偏态(右偏态),随着参数的增大,分布趋近于正态分布;卡方分布密度曲线下的面积都是1。
2) 分布的均值与方差可以看出,随着自由度的增大,分布向正无穷方向延伸(因为均值越来越大),分布曲线也越来越低阔(因为方差越来越大)。
3)不同的自由度决定不同的卡方分布,自由度越小,分布越偏斜。
4) 若互相独立,则:服从分布,自由度为。
5) 分布的均数为自由度,记为E( ) = 。
卡方分布分位表

卡方分布分位表1. 什么是卡方分布?卡方分布(chi-squared distribution )是统计学中常用的概率分布之一,它是一种单参数分布。
卡方分布常用于分析成功与失败之间的关系,比如独立性检验、拟合优度检验等。
2. 卡方分布的概率密度函数卡方分布的概率密度函数(probability density function, PDF )可以表示为:f (x;k )=12k 2Γ(k 2)x k 2−1e −x 2其中,k 是卡方分布的自由度参数,Γ 是伽马函数。
3. 卡方分布分位表的作用卡方分布分位表(chi-squared distribution quantile table )是用于计算卡方分布的分位数的一种表格。
分位数是统计学中用于表示分布特征的关键指标之一。
通过查表可以快速找到给定分布和自由度下的分位数,从而帮助我们进行各种统计分析。
4. 卡方分布分位表的使用方法使用卡方分布分位表,首先需要确定自由度(degrees of freedom, df )和置信水平(confidence level, α)。
然后在表格中找到对应自由度和置信水平的值,就可以得到相应的分位数。
以下是示例卡方分布分位表的一部分: 自由度 (k ) 0.995 0.99 0.975 0.95 0.9 0.1 0.05 0.025 0.01 0.005 10.00004 0.00016 0.00393 0.01579 0.21072 2.70554 3.84146 5.02389 6.63490 7.87944自由度(k) 0.995 0.99 0.975 0.95 0.9 0.1 0.05 0.025 0.01 0.0052 0.01003 0.020100.050640.103180.710724.605175.991467.377769.2103410.596623 0.07172 0.114830.215800.351851.441796.251397.814739.3484011.3448712.83816……………………………例如,如果自由度为3,置信水平为0.95,则对应的分位数为3.84146。
卡方分布概念及表和查表方法

卡方分布概念及表和查表方法若n个相互独立的随机变量ξ₁,ξ₂,...,ξn,均服从标准正态分布(也称独立同分布于标准正态分布),则这n个服从标准正态分布的随机变量的平方和构成一新的随机变量,其分布规律称为卡方分布(chi-square distribution)。
中文名卡方分布外文名chi-square distribution别称西格玛分布提出者Friedrich Robert Helmert提出时间1863应用学科统计学目录1简介2定义3性质4概率表简介分布在数理统计中具有重要意义。
分布是由阿贝(Abbe)于1863年首先提出的,后来由海尔墨特(Hermert)和现代统计学的奠基人之一的卡·皮尔逊(C K·Pearson)分别于1875年和1900年推导出来,是统计学中的一个非常有用的著名分布。
定义若n个相互独立的随机变量ξ₁、ξ₂、……、ξn ,均服从标准正态分布(也称独立同分布于标准正态分布),则这n个服从标准正态分布的随机变量的平方和构成一新的随机变量,其分布规律称为分布(chi-square distribution),卡方分布其中参数称为自由度,正如正态分布中均数或方差不同就是另一个正态分布一样,自由度不同就是另一个分布。
记为或者(其中,为限制条件数)。
卡方分布是由正态分布构造而成的一个新的分布,当自由度很大时,分布近似为正态分布。
对于任意正整数x,自由度为的卡方分布是一个随机变量X的机率分布。
性质1) 分布在第一象限内,卡方值都是正值,呈正偏态(右偏态),随着参数的增大,分布趋近于正态分布;卡方分布密度曲线下的面积都是1。
2) 分布的均值与方差可以看出,随着自由度的增大,分布向正无穷方向延伸(因为均值越来越大),分布曲线也越来越低阔(因为方差越来越大)。
3)不同的自由度决定不同的卡方分布,自由度越小,分布越偏斜。
4) 若互相独立,则:服从分布,自由度为。
5) 分布的均数为自由度,记为E( ) = 。
卡方检验基本公式检验方法

四格表资料分析小结(重要)
n Fisher’s exact probability法均适用 n 卡方检验是一种近似检验
(1)当n≥40,T>5时,可用。然而当P值接近0.05时最好用
Fisher’s exact probability法;
•若
• a (甲+ 乙+)、
• b (甲+ 乙-)、
•
c (甲- 乙+)、
•
d (甲- 乙-)。
•
将a、b、c、d四种情况的对子数填入四格表
P114 例7-3
观察的结果只有阳性、阴性两种可能,清点成对资料时发现 则存在四种情况。
n (1)两种方法都出现阳性(共有11例); n (2)免疫荧光法阳性而乳胶凝集法却是阴性(共有12例); n (3)免疫荧光法阴性而乳胶凝集法却是阳性(共有2例); n (4)两种检测方法均为阴性结果(共有33例)。
McNemar检验的推广
例子
n 某研究所欲比较X线与CT对强直性脊柱炎(AS)骶髂关节 病变的诊断价值,分析临床诊断为AS的患者136例,对272 个骶髂关节分别拍摄X线平片与CT扫描,结果见下。问两 种方法诊断骶髂关节病变的分级有无差别?
•7.4 行×列表资料的•2 检验
•1、多个样本率的比较 •2、样本构成比的比较 •3、双向无序分类资料的关联性检验 •专用公式
99
5
75
21
174
26
104
95.20
200
87.00 (pc)
•
实际频数A (actual frequency)
•
理论频数T (theoretical frequency)
卡方分布

χ2分布的和也是χ2分布,即χ2分布具有可加性。 Σ χ2是一个遵从df= df1+df2+…+dfk的χ2分布.
如果df>2,χ2分布的平均数:μ χ2=df,方差σ χ2
=2df.
χ2分布是连续型分布,有些离散型的分布也近似
χ2分布.
2
χ2分布密度曲线
n=1
n=4 n=10
n=20
概述-3
知道了同一总体不同样本的方 差比率分布,即可分析任意两样 本方差是否取自同一总体了.
F分布密度曲线
m=10,n=∞ m=10,n=50 m=10,n=10 m=10,n=4
F分布的特点-1
1. F分布形态是一个正偏态分布,它的分布 曲线随分子、分母的自由度不同而不同, 随df1与df2的增加而渐趋正态分布。
这无限多个F的分布称做F分布.
概述-112FFra bibliotek
2 2
df1
df2
概
述
2
(Xi X )2
2
(n 1)sn21
2
-2
概 述
代入F
12
df1
2 2
df2
(n1
1)
s2 n1
1
2 1
(n1
1)
(n2
1)
s2 n2
1
22 (n2 1)
-2
s2 n1 1
χ2分布表-1
χ2分布表是根据χ2分布函数计算出 来的,χ2分布曲线下的面积都是1.
随自由度不同,同一χ2 值以下或 以上所含面积与总面积之比率不同。
χ2表要列出自由度及某一χ2值以上 χ2分布曲线下的概率.
卡方分布知识点总结

卡方分布知识点总结一、基本概念1.1 卡方分布的定义卡方分布是一种非对称分布,它是由自由度为n的正态随机变量的平方和构成的。
通常表示为χ^2(n),其中n表示自由度。
卡方分布是一种连续型概率分布,其密度函数为:f(x;n) = (1/2)^(n/2) * x^(n/2-1) * e^(-x/2) / Γ(n/2)其中Γ(n/2)表示Γ函数,n表示自由度。
1.2 卡方分布的特性(1)卡方分布是非对称的,且随着自由度的增大而逐渐对称;(2)当自由度为1时,卡方分布是右偏的;(3)当自由度为2时,卡方分布呈指数分布;(4)卡方分布的均值为自由度n,方差为2n。
1.3 卡方分布与正态分布的关系卡方分布与正态分布之间存在密切的关系,当n足够大时,卡方分布近似于正态分布。
这是由中心极限定理所决定的,即任意独立同分布的随机变量和近似服从正态分布。
1.4 卡方分布的应用卡方分布在统计学中有着广泛的应用,主要用于进行检验各种假设的合理性。
比如用于检验总体方差的假设、检验两个总体方差的比值、检验两个相互独立样本的均值等。
二、卡方分布的应用2.1 卡方检验卡方检验是一种用于定性数据的假设检验方法,它主要用于检验变量之间的相关性以及同一变量在不同条件下的差异性。
通常有单样本卡方检验、两独立样本卡方检验、两相关样本卡方检验等不同类型的卡方检验方法。
2.2 回归分析在回归分析中,卡方分布用于检验回归方程的拟合度。
通常用F检验和卡方检验结合来进行回归模型的拟合度检验。
2.3 方差分析在方差分析中,卡方分布用于检验总体方差的假设。
通常用卡方检验来判断总体方差是否相等,进而进行方差分析。
2.4 生物统计学在生物统计学领域,卡方分布也有着广泛的应用。
比如用于遗传学中分析自由度、检验拟合度等方面。
三、卡方分布的计算方法3.1 卡方分布的计算通常情况下,计算卡方分布的概率值是比较繁琐的,需要借助专门的卡方分布表或统计软件来进行计算。
3.2 卡方检验的计算卡方检验的计算方法通常包括以下几个步骤:(1)建立原假设和备择假设;(2)计算观察频数和期望频数;(3)计算卡方检验统计量;(4)根据自由度和显著性水平查找卡方分布表,得出卡方统计量的临界值;(5)比较实际计算的卡方统计量与临界值,并作出判断。
f分布t分布和卡方分布

§1、4 常用得分布及其分位数1、 卡平方分布卡平方分布、t 分布及F 分布都就是由正态分布所导出得分布,它们与正态分布一起,就是试验统计中常用得分布。
当X 1、X 2、…、Xn 相互独立且都服从N(0,1)时,Z=∑ii X 2 得分布称为自由度等于n 得2χ分布,记作Z ~2χ(n),它得分布密度p(z )=⎪⎪⎩⎪⎪⎨⎧>⎪⎭⎫ ⎝⎛Γ--,,00,2212122其他z e x n z n n 式中得⎪⎭⎫ ⎝⎛Γ2n =u d e u u n ⎰∞+--012,称为Gamma 函数,且()1Γ=1,⎪⎭⎫ ⎝⎛Γ21=π。
2χ分布就是非对称分布,具有可加性,即当Y 与Z 相互独立,且Y ~2χ(n ),Z ~2χ(m ),则Y+Z ~2χ(n+m )。
证明: 先令X 1、X 2、…、X n 、X n+1、X n+2、…、X n+m 相互独立且都服从N(0,1),再根据2χ分布得定义以及上述随机变量得相互独立性,令Y=X 21+X 22+…+X 2n ,Z=X 21+n +X 22+n +…+X 2m n +,Y+Z= X 21+X 22+…+X 2n + X 21+n +X 22+n +…+X 2m n +,即可得到Y+Z ~2χ(n +m )。
2、 t 分布 若X 与Y 相互独立,且X ~N(0,1),Y ~2χ(n ),则Z =n Y X得分布称为自由度等于n 得t 分布,记作Z ~ t (n ),它得分布密度 P(z)=)()(221n nn ΓΓ+2121+-⎪⎪⎭⎫ ⎝⎛+n n z 。
请注意:t 分布得分布密度也就是偶函数,且当n>30时,t 分布与标准正态分布N(0,1)得密度曲线几乎重叠为一。
这时, t 分布得分布函数值查N(0,1)得分布函数值表便可以得到。
3、 F 分布 若X 与Y 相互独立,且X ~2χ(n ),Y ~2χ(m ), 则Z=m Y n X得分布称为第一自由度等于n 、第二自由度等于m 得F 分布,记作Z ~F (n , m ),它得分布密度 p(z)=⎪⎪⎪⎩⎪⎪⎪⎨⎧>++-⎪⎭⎫ ⎝⎛Γ⎪⎭⎫ ⎝⎛Γ⎪⎭⎫ ⎝⎛+Γ•。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
卡方分布概念及表和查表方法
若n个相互独立的随机变量ξ₁,ξ₂,...,ξn,均服从标准正态分布(也称独立同分布于标准正态分布),则这n个服从标准正态分布的随机变量的平方和构成一新的随机变量,其分布规律称为卡方分布(chi-square distribution)。
中文名卡方分布外文名chi-square
distribution
别称西格玛分布提出者Friedrich Robert
Helmert
提出时间1863应用学科统计学
目录
1 简介
2 定义
3 性质
4 概率表
简介
分布在数理统计中具有重要意义。
分布是由阿贝(Abbe)于1863年首先提出的,后来由海尔墨特(Hermert)和现代统计学的奠基人之一的卡·皮尔逊(C K·Pearson)分别于1875年和1900年推导出来,是统计学中的一个非常有用的著名分布。
定义
若n个相互独立的随机变量ξ₁、ξ₂、……、ξn ,均服从标准正态分布(也称独立同分布于标准正态分布),则这n个服从标准正态分布的随机变量的平方和
构成一新的随机变量,其分布规律称为分布(chi-square distribution),
卡方分布
其中参数称为自由度,正如正态分布中均数或方差不同就是另一个正态分布一样,自由度不同就是另一个分布。
记
为或者(其中,为限制条件数)。
卡方分布是由正态分布构造而成的一个新的分布,当自由
度很大时,分布近似为正态分布。
对于任意正整数x,自由度为的卡方分布是一个随机变量X的机率分布。
性质
1) 分布在第一象限内,卡方值都是正值,呈正偏态(右偏态),随着参数
的增大,分布趋近于正态分布;卡方分布密度曲线下的面积都是1。
2) 分布的均值与方差可以看出,随着自由度的增大,分布向正无穷方向延伸(因为均值越来越大),分布曲线也越来越低阔(因为方差越来越大)。
3)不同的自由度决定不同的卡方分布,自由度越小,分布越偏斜。
4) 若互相独立,则:服
从分布,自由度为。
5) 分布的均数为自由度,记为 E( ) = 。
6) 分布的方差为2倍的自由度( ),记为 D( ) = 。
概率表
分布不象正态分布那样将所有正态分布的查表都转化为标准正态分布去查,在
分布中得对每个分布编制相应的概率值,这通过分布表中列出不同的自由度来表示,
卡方分布临界值表
在分布表中还需要如标准正态分布表中给出不同 P 值一样,列出概率值,只不过这里的概率值是值以上分布曲线以下的概率。
由于分布概率表中要列出很多分布的概率值,所以分布中所给出的 P 值就不象标准正态分布中那样给出了400个不同的 P 值,而只给出了有代表性的13个值,因此分布概率表的精度就更差,不过给出了常用的几个值,足够在实际中使用了。
查分布概率表时,按自由度及相应的概率去找到对应
的值。
如上图所示的单侧概率0.05(7)=14.1的查表方法就是,在第一列找到自由度7这一行,在第一行中找到概率0.05这一列,行列的交叉处即是14.1。
表中所给值直接只能查单侧概率值,可以变化一下来查双侧概率值。
例如,要在自由度为7的卡方分布中,得到双侧概率为0.05所对应的上下端点可以这样来考虑:双侧概率指的是在上端和下端各划出概率相等的一部分,两概率之和为给定的概率值,这里是0.05,因此实际上上端点以上的概率为0.05/2=0.025,用概率0.025查表得上端点的值为16,记为0.05/2(7)=16。
下端点以下的概率
也为0.025,因此可以用0.975查得下端点为1.69,记
为1-0.05/2(7)=1.69。
当然也可以按自由度及值去查对应的概率值,不过这往往只能得到一个大概的结果,因为分布概率表的精度有限,只给了13个不同的概率值进行查表。
例如,要在自由度为18 的分布查找=30对应的概率,则先在第一列找到自由度18,然后看这一行可以发现与30接近的有28.9与31.5,它们所在的列是0.05与0.025,所以要查的概率值应于介于0.05与0.025之间,当然这是单侧概率值,它们的双侧概率值界于0.1与0.05之间。
如果要更精确一些可以采用插值的方法得到,这在正态分布的查表中有介绍。
为什么从正态总体中抽取出的样本的方差服从分布?
在抽样分布理论一节里讲到,从正态总体进行一次抽样就相当于独立同分布的n个正态随机变量ξ1,ξ2,…,ξn的一次取值,将n个随机变量针对总体均值与方差进行标准化得(i=1,…,n),显然每个都是服从标准正态分布的,因此按照分布的定义,应该服从参数为的分布。
如果将总体中的方差σ2 用样本方差s2代替,它是否也服
从分布呢?理论上可以证明,它是服从分布的,但是参数不是n而是n-1了,究其原因在于它是n-1个独立同分布于标准正态分布的随机变量的平方和。
我们常常把一个式子中独立变量的个数称为这个式子的“自由度”,确定一个式子自由度的方法是:若式子包含有n个变量,其中k个被限制的样本统计量,则这个表达式的自由度为 n-k。
比如中包含ξ1,ξ2,…,ξn这n个变量,其中ξ1-ξn-1相互独立,ξn 为其余变量的平均值,因此自由度为n-1。
附卡方表
n/P
0.99
50.99
0.97
5
0.950.900.750.500.250.100.05
0.02
5
0.01
0.00
5
1…………0.020.100.451.322.713.845.026.637.88 20.010.020.020.100.210.581.392.774.615.997.389.2110.6
注:1. 当n充分大时,χ2(n)的值近似等于【Zα+ SQRT(2n-1)】的平方/2
2. Z0.05=1.645,Z0.01=2.326。
