卡方检验临界值表
实验报告卡方检验

实验报告卡方检验1. 引言卡方检验是一种用于判断变量之间是否存在关联性的统计方法。
它可以用于比较观察频数和期望频数之间的差异,并通过计算卡方统计量来判断这种差异是否显著。
本实验旨在介绍卡方检验的基本原理和应用方法,并通过一个具体案例来演示其使用过程。
2. 原理卡方检验是基于卡方统计量进行判断的。
卡方统计量的计算公式如下:X^2 = \sum \frac{(O - E)^2}{E}其中,O 表示观察频数,E 表示期望频数。
卡方统计量的值越大,说明观察频数和期望频数之间的差异越大,即变量之间的关联性越强。
卡方检验的步骤如下:1. 建立假设:设H_0为原假设,H_1为备择假设。
H_0 假设不存在变量间的关联性,H_1 假设存在变量间的关联性。
2. 计算观察频数和期望频数:根据给定的数据计算得到观察频数和期望频数。
3. 计算卡方统计量:根据卡方统计量的计算公式,计算得到卡方统计量的值。
4. 设置显著性水平:根据实验需求和数据量,设置显著性水平,通常取0.05或0.01。
5. 判断显著性:根据卡方统计量的值和显著性水平,判断是否拒绝原假设。
如果卡方统计量的值大于显著性水平对应的临界值,则拒绝原假设;否则,接受原假设。
3. 案例演示假设有一张表格,记录了200名学生在选课时选择了哪个学科,包括科学、文学和艺术。
下面是观察频数的数据:科学文学艺术男生数60 40 30女生数45 25 0现在我们要判断学生的性别和选课学科之间是否存在关联性。
3.1. 建立假设原假设H_0: 学生的性别和选课学科之间不存在关联性。
备择假设H_1: 学生的性别和选课学科之间存在关联性。
3.2. 计算观察频数和期望频数首先,我们需要计算每个单元格的期望频数。
期望频数的计算公式如下:E = \frac{(\text{对应行的总计数}) \times (\text{对应列的总计数})}{\text{总样本数}}根据以上公式,我们可以得到下表的期望频数:科学文学艺术-男生数55.71 34.29 40女生数49.29 30.71 353.3. 计算卡方统计量根据卡方统计量的计算公式,我们可以得到卡方统计量的值:X^2 = \frac{(60-55.71)^2}{55.71} + \frac{(40-34.29)^2}{34.29} +\frac{(30-40)^2}{40} + \frac{(45-49.29)^2}{49.29} +\frac{(25-30.71)^2}{30.71} + \frac{(0-35)^2}{35} = 7.1193.4. 设置显著性水平根据实验需求和数据量,我们设置显著性水平为0.05。
卡方检验

卡方检验(Chi-square test)Li Junrongstat9@7.1 四格表资料的χ2检验χ2检验(Chi-square test)是现代统计学的创始人之一,K. Pearson(1857-1936)于1900年提出的一种具有广泛用途的统计方法,可用于两个或多个率(或者构成比)之间的比较,计数资料的关联度分析,拟合优度检验等。
一、卡方检验的基本思想卡方分布⏹属连续型分布⏹可加性是其基本性质⏹唯一参数,即自由度(1) 自由度为1的χ2分布若Z N ~(,),01则Z 2的分布称为自由度为1的χ2分布.(chi-square distribution),记为χ()12或χ21(). 图形:从纵轴某个点开始单调下降,先凸后凹.02468100.00.10.20.3 2220.05(1)0.05/22220.01(1)0.01/23.84(1.96)6.63(2.5758)Z Zχχ======(2) νZ Z Z ,...,,21互相独立,均服从N (,)01,则22221...νZ Z Z +++的分布称自由度为 ν的χ2分布,记为χν()2或)(2νχ,或简记为χ2.* 图形:单峰,正偏峰;自由度ν很大时,2()νχ近似地服从正态分布.有2()2(),22Z ννχνχννν-=服从均数为,方差为的正态分布.00.10.20.30.40.50369121518¿¨·½Öµ×Ý·ß×ÔÓɶȣ½1×ÔÓɶȣ½2×ÔÓɶȣ½3Óɶȣ½62/)12/(2222)2/(21)(χνχνχ--⎪⎪⎭⎫⎝⎛Γ=ef 3.847.8112.59P =0.05的临界值χ2分布(chi-square distribution )性质:若χνχν2122(),()互相独立, 则χνχν2122()()+服从χ2分布, 自由度=+νν12 χνχν2122()()-服从χ2分布, 自由度=-νν12卡方检验的基本思想组别有效无效合计有效率(%)试验组99 5 10495.20(p 1)对照组7521 9678.13(p 2)合计1742620087.00(p c )表7-1两组降低颅内压有效率的比较实际频数A (actual frequency)理论频数T (theoretical frequency)nn n column row T C R =⨯=总例数合计列合计行)()(RC四格表(fourfold table)它反映了理论数与实际数的吻合情况,该统计量近似地服从自由度为ν的卡方分布。
χ2检验
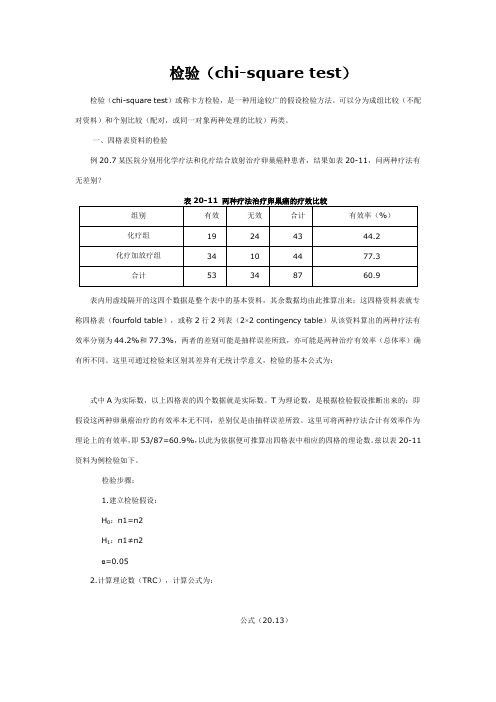
检验(chi-square test)检验(chi-square test)或称卡方检验,是一种用途较广的假设检验方法。
可以分为成组比较(不配对资料)和个别比较(配对,或同一对象两种处理的比较)两类。
一、四格表资料的检验例20.7某医院分别用化学疗法和化疗结合放射治疗卵巢癌肿患者,结果如表20-11,问两种疗法有无差别?表20-11 两种疗法治疗卵巢癌的疗效比较组别有效无效合计有效率(%)化疗组19244344.2化疗加放疗组34104477.3合计53348760.9表内用虚线隔开的这四个数据是整个表中的基本资料,其余数据均由此推算出来;这四格资料表就专称四格表(fourfold table),或称2行2列表(2×2 contingency table)从该资料算出的两种疗法有效率分别为44.2%和77.3%,两者的差别可能是抽样误差所致,亦可能是两种治疗有效率(总体率)确有所不同。
这里可通过检验来区别其差异有无统计学意义,检验的基本公式为:式中A为实际数,以上四格表的四个数据就是实际数。
T为理论数,是根据检验假设推断出来的;即假设这两种卵巢癌治疗的有效率本无不同,差别仅是由抽样误差所致。
这里可将两种疗法合计有效率作为理论上的有效率,即53/87=60.9%,以此为依据便可推算出四格表中相应的四格的理论数。
兹以表20-11资料为例检验如下。
检验步骤:1.建立检验假设:H0:π1=π2H1:π1≠π2α=0.052.计算理论数(TRC),计算公式为:公式(20.13)式中TRC是表示第R行C列格子的理论数,n R为理论数同行的合计数,n C为与理论数同列的合计数,n为总例数。
第1行1列:43×53/87=26.2第1行2列:43×34/87=16.8第2行1列:44×53/87=26.8第2行2列:4×34/87=17.2以推算结果,可与原四项实际数并列成表20-12:表20-12 两种疗法治疗卵巢癌的疗效比较组别有效无效合计化疗组19(26.2)24(16.8)43化疗加放疗组34(26.8)10(17.2)44合计533487因为上表每行和每列合计数都是固定的,所以只要用TRC式求得其中一项理论数(例如T1.1=26.2),则其余三项理论数都可用同行或同列合计数相减,直接求出,示范如下:T1.1=26.2T1.2=43-26.2=16.8T2.1=53-26.2=26.8T2.2=44-26.2=17.23.计算值按公式20.12代入4.查值表求P值在查表之前应知本题自由度。
卡方检验 (Chi-square)

卡方检验 (Chi-square)⏹参数与非参数检验⏹卡方匹配度检验⏹卡方独立性检验⏹卡方检验的前提和限制⏹卡方检验的应用参数与非参数检验⏹参数检验◆用于等比/等距型数据◆对参数的前提:正态分布和方差同质⏹非参数检验◆不用对参数进行假设◆对分布较少有要求,也叫distribution-free tests◆用于类目/顺序型数据◆没有参数检验敏感,效力低◆因此在二者都可用时,总是用参数检验卡方匹配度检验⏹用样本数据检验总体分布的形状或比率,以确定与假设的总体性质的匹配度⏹是对次数分布的检验⏹研究情境◆在医生职业中,男的多还是女的多?◆在三种咖啡中,哪种被国人最喜欢?◆在北京大学中,各国留学生的比例有代表性吗?卡方匹配度检验的公式⏹χ2=∑[(f0-f e)2/f e]⏹f e=p n⏹d f=C-1◆F0:观察次数◆f e:期望次数◆C:类目的个数◆Χ2:统计量卡方独立性检验⏹检验行和列的两个本来变量彼此有无关联卡方独立性检验的公式⏹χ2=∑[(f0-f e)2/f e]⏹f e=(r o w t o t a l)(c o l u m n t o t a l)/n,⏹d f=(R-1)(C-1)◆F0:观察次数◆f e:期望次数◆R:行类目的个数C:列类目的个数◆Χ2:统计量例:х2检验1.计算期望次数fe=(fc*fr)/n2.计算每个单位格的х2值22df=(R-1)(C-1)= (3-1)(2-1)=2,х2的临界值为5.99拒绝Ho,对手表显示的偏好程度与被试的年龄段有关。
卡方检验示例

卡方检验示例卡方检验是一种常用的统计方法,用于检验观察频数与期望频数之间是否存在显著差异。
下面是一个卡方检验的示例:假设有一批学生参加了一次数学考试,考试分为ABC三个难度等级。
我们想知道,这批学生在不同难度等级下的得分情况是否存在显著差异。
我们先统计每个难度等级下考试成绩的频数,得到如下表格: | 难度等级 | 得分0-59 | 得分60-79 | 得分80-100 || :------: | :------: | :-------: | :--------: || A | 6 | 12 | 22 || B | 8 | 16 | 24 || C | 4 | 10 | 26 | 然后我们计算每个难度等级下的期望频数,期望频数的计算公式为:期望频数 = (该难度等级下得分总数÷所有学生的得分总数) ×该难度等级下考试人数比如难度等级为A的期望频数计算如下:得分0-59的期望频数 = (6+8+4) ÷(6+8+4+12+16+10+22+24+26) × (6+12+22) ≈ 4.7得分60-79的期望频数 = (12+16+10) ÷(6+8+4+12+16+10+22+24+26) × (6+12+22) ≈ 9.4得分80-100的期望频数 = (22+24+26) ÷(6+8+4+12+16+10+22+24+26) × (6+12+22) ≈ 18.9将所有难度等级下的期望频数填充到表格中:| 难度等级 | 得分0-59 | 得分60-79 | 得分80-100 || :------: | :------: | :-------: | :--------: || A | 4.7 | 9.4 | 14.9 || B | 5.6 | 11.2 | 17.2 || C | 8.7 | 17.4 | 14.9 | 接下来,我们需要计算卡方值,卡方值的计算公式为:卡方值 = ∑ [(观察频数 - 期望频数) ÷期望频数]比如难度等级为A的卡方值计算如下:卡方值 = [(6-4.7) ÷ 4.7] + [(12-9.4) ÷ 9.4] + [(22-14.9) ÷ 14.9] ≈ 10.5将所有难度等级下的卡方值计算出来,并将其填充到表格中:| 难度等级 | 得分0-59 | 得分60-79 | 得分80-100 | 卡方值 || :------: | :------: | :-------: | :--------: | :-----: || A | 4.7 | 9.4 | 14.9 | 10.5 || B | 5.6 | 11.2 | 17.2 | 6.3 || C | 8.7 | 17.4 | 14.9 | 5.5|最后,我们需要确定卡方分布的自由度,自由度的计算公式为:自由度 = (难度等级个数 - 1) × (得分等级个数 - 1)在这个例子中,难度等级有三个,得分等级有三个,因此自由度为 4。
卡方检验值的取值范围

卡方检验值的取值范围一、卡方检验简介卡方检验是一种常用的统计方法,用于分析分类数据是否存在相关性。
它基于观察值与理论值之间的差异,通过计算卡方检验值来评估样本数据与理论期望的偏离程度。
卡方检验值的取值范围在实际应用中具有一定意义。
二、卡方检验值的计算方法卡方检验值的计算涉及到观察频数和理论频数之间的计算。
一般情况下,我们通过以下步骤来计算卡方检验值:1.建立假设:首先,我们需要明确零假设和备择假设。
零假设表示无关性,备择假设则表示相关性。
2.计算理论频数:根据样本数据和假设下的期望频数,计算理论频数。
理论频数是基于各个变量之间独立的假设计算得到的。
3.计算卡方值:根据观察频数和理论频数之间的差异,计算卡方值。
卡方值表示观察值与理论值之间的偏离程度。
4.计算自由度:根据变量的个数和约束条件,计算卡方检验的自由度。
自由度用于确定卡方检验值的分布。
5.查表或计算P值:根据卡方检验值和自由度,查找卡方分布表来确定P值。
三、卡方检验值的意义卡方检验值的取值范围主要受到样本容量和自由度的影响。
在实际应用中,我们可以根据卡方检验值的大小来进行分析和判断。
1.卡方检验值较小:当卡方检验值较小时,说明观察频数与理论频数之间的差异较小,样本数据与理论期望相符合。
这表明没有足够的证据来拒绝零假设,可以认为变量之间无相关性。
2.卡方检验值适中:当卡方检验值适中时,说明观察频数与理论频数之间存在一定的差异,样本数据与理论期望有一定的偏离。
这表明可能存在一定程度上的相关性,但需要进一步进行分析和判断。
3.卡方检验值较大:当卡方检验值较大时,说明观察频数与理论频数之间的差异较大,样本数据与理论期望明显偏离。
这表明有足够的证据来拒绝零假设,可以认为变量之间存在相关性。
四、卡方检验值的取值范围举例卡方检验值的具体取值范围可以通过卡方分布表来确定。
以常见的显著性水平为0.05为例,我们可以根据自由度找到对应的临界值。
自由度0.05显著性水平下的临界值1 3.8412 5.9913 7.8154 9.4885 11.070以上是自由度为1到5时的卡方分布表的部分数据。
卡方检验
2
3.03 ,
=1
2<3.84=2
按 =0.05 水 准 , 不 拒 绝 H0, …
配对四格表资料的 检验
2
也称McNemar检验(McNemar's test)
例 6-8 表 6-9
甲 法
两种血清学检验结果比较
乙 法 + - 10 (b) 11 (d) 21 90 42 132 合计
n2 n2 n
一般地,
理论频数
n n (行合计)(列合计) = R C 总计 n
例题:计算以下四格表的各理论频数: (1) (2) 35 27 25 8 16 33 15 22
2 检验的基本思想可通过其基本公式来解释:
2
观察值 理论值
理论值
2
A T 2
2
1
2
( / 21)
e
2 / 2
Ý ß ×·
×Ó ¶ £ 1 Ô É È ½
0.2 0.1 0.0 0 3
3.84
×Ó ¶ £ 2 Ô É È ½ ×Ó ¶ £ 3 Ô É È ½ ×Ó ¶ £ 6 Ô É È ½
P=0.05的临界值
7.81 12.59
6
9 12 ¿ ·Ö ¨½ µ
* 图形:单峰,正偏峰; 自由度 很大时, 近似地服从正态分布.有 2 ( ) 2 Z , ( )服从均数为 ,方差为2 的正态分布 2
2 ( )
χ2分布(chi-square distribution)
0.5 0.4 0.3
f ( ) 2( / 2) 2
2
2 =2.734<3.84,P>0.05,不拒绝无效假设H0
卡方检验
——————————————————————
结论:工人患近视眼最多,其次是农民,学生和干部患近视眼都比较少。
2015/12/12
9
计数资料的统计描述
率与构成比的差异(参考答案)
某医院门诊部近视眼患者情况
—————————————————————— 职业 工人 农民 学生 干部 调查人数 2000 2000 1000 1000 患者人数 100 100 100 100 患病率(%) 5.00 5.00 10.00 10.00 ——————————————————————
υ(R 1)(C 1) 1
观察频数 O 理论频数 T(H0:π1=π2)
2
行合计 列合计 T 总例数
2 (ad bc) n 四格表专用公式 χ ν 1 (a b)(c d)(a c)(b d)
2015/12/12
24
计数资料的统推断:假设检验
最简单的χ2检验:四格表Pearson卡方检验
率的标准误(standard error of rate)
用来表示率抽样误差的大小。
公式
2015/12/12
18
计数资料的统推断:参数估计
率的可信区间
公式
当样本含量n较大时,且样本率P和(1- P)均不太小,如 nP和n(1- P) ≧5时,样本率p的分布接近(π,Sp )正态 分布,总体率的1-α的可信区间的正态近似为 ( p u s p)。 如:率95%可信区间为P±1.96×Sp。 当样本含量n较小,nP或n(1- P)<5时,查P400附表。
2015/12/12
13
计数资料的统计描述
标化率(示例参考答案)
甲医院 腋下淋巴 标准 结转移 构成 (人群) 生存率(%)
卡方检验分类变量事物相互独立临界值_解释说明
卡方检验分类变量事物相互独立临界值解释说明1. 引言1.1 概述本篇论文探讨了卡方检验在分类变量相互独立性判断中的应用,并重点关注了临界值的计算方法及其意义。
卡方检验是一种常用的统计方法,可用于确定两个分类变量之间是否存在相关性。
分类变量是指通过将样本分为不同类别或组别来描述数据的变量。
事物相互独立性是指两个分类变量之间没有任何关联或联系。
1.2 文章结构本文分为五个主要部分:引言、卡方检验与分类变量、事物相互独立的概念和判断方法、卡方检验的临界值计算方法与意义解释、结论。
在引言部分中,我们将简要介绍文章的背景和目标,以及各个章节的内容和结构。
1.3 目的本文旨在解释说明卡方检验在分类变量相互独立性判断中的作用,并深入讨论临界值计算方法与其意义。
通过对相关理论和实际案例进行分析,我们将提供一个具有实践价值和学术参考价值的综合指南,帮助读者更好地理解和应用卡方检验在统计分析中的作用。
同时,我们还将评估卡方检验在分类变量相互独立性判断中的应用价值,并展望未来可能的发展方向。
2. 卡方检验与分类变量2.1 卡方检验概述卡方检验是一种统计方法,用于确定两个或多个分类变量之间的相关性。
它基于观察到的频数与期望频数之间的差异来判断分类变量之间是否存在显著关系。
在实际应用中,卡方检验通常用于验证研究假设和分析数据。
2.2 分类变量的定义和特点分类变量指的是可被分配到有限数目类别中的自变量。
例如,性别、民族和教育程度等都是分类变量。
分类变量具有离散性,它们按照不同类别进行排序,并且各个类别之间没有固定顺序。
2.3 卡方检验在分类变量中的应用卡方检验可用于衡量两个或多个分类变量之间的相关性或独立性。
在进行卡方检验时,我们首先建立一个原假设(H0),即假设两个或多个分类变量是相互独立的。
然后,通过计算观察到的频数与期望频数之间的差异来评估原假设。
如果观察到的频数与期望频数之间没有显著差异,则说明两个或多个分类变量之间是相互独立的。
f critical value表
f critical value表临界值表是在统计学中常用的表格之一,用于帮助确定假设检验的结果是否显著。
该表格记录了在给定的显著性水平下,不同自由度条件下的临界值。
本文将对临界值表进行详细介绍,包括其定义、用途、计算方法等方面,以期能够对读者提供清晰明了的理解。
第一部分:定义临界值表是一个统计学工具,用于确定统计显著性检验中的拒绝域。
在统计推断中,我们常常会根据样本数据来推断总体的参数,然后再进行统计检验。
在进行统计检验时,我们会设置一个显著性水平α,并将给定的统计量与临界值进行比较,以判断原假设是否可接受或拒绝。
临界值是样本观测值在假设检验中应达到的临界点,该观测值与临界值的比较可以帮助我们确定是否能够拒绝原假设。
临界值表通常是一个以显著性水平α和自由度为两个参数的表格。
在统计学中,自由度是指样本数据中可以自由变化的部分的个数。
临界值表根据不同的显著性水平和自由度条件,提供了相应的临界值。
第二部分:用途临界值表在统计学中起到了至关重要的作用。
它为统计推断提供了一种明确的参考标准,使我们能够对假设检验结果进行客观、科学的判断。
临界值表的应用涉及到很多领域,包括医学、社会科学、自然科学等等。
以下是临界值表在常见的统计检验中的应用举例:1.单样本t检验:用于比较一个样本的均值与总体均值是否有显著差异。
2.两样本t检验:用于比较两个独立样本的均值是否有显著差异。
3.方差分析:用于比较多个样本均值之间是否存在显著差异。
4.相关分析:用于分析两个变量之间的相关性是否显著。
在以上的各种统计分析中,临界值表起到了决策的作用。
根据计算出的统计量,我们可以在临界值表中查找相应的临界值,如果统计量超过了临界值,那么我们就可以拒绝原假设,否则我们接受原假设。
第三部分:计算方法临界值的计算是基于概率分布的性质进行的。
不同的统计量的分布可能会有所不同,因此根据不同的统计量,我们需要使用不同的概率分布进行计算。
常见的统计量及其相应的概率分布包括:1. t分布:用于单样本t检验和两样本t检验。
